Abstract
The prebiotic mechanism to produce molecular oxygen (O2) in carbon dioxide (CO2)-rich planetary atmospheres is of great importance in understanding astrochemical reactions and is potentially relevant to the origin of life on Earth. Here, we demonstrate that, aside from the direct productions of O2 by photodissociation and dissociative electron attachment, the low-energy ion-molecule reaction between cationic helium in solar winds and molecular CO2 is a noticeable mechanism. Branching ratios of the reaction channels are determined, and their absolute cross-sections are estimated accordingly. The present findings represent a further, indispensable step towards fully understanding the origins of atmospheric O2.
Similar content being viewed by others
Introduction
Before the dramatic rise of atmospheric oxygen during the Great Oxidation Event about 2.4 billion years ago on Earth1,2, few oxygen molecules (O2) already existed in the primitive atmosphere which was nearly full of carbon dioxide (CO2). Those O2 molecules were exclusively produced via abiotic processes. A widely accepted mechanism about the O2 origin in CO2-rich planetary atmosphere is the cascade process induced with vacuum ultraviolet (VUV) photon
where the product O2 can be stabilized efficiently by releasing a third body M3,4,5. A recent experimental study indicated that O2 was directly produced in near extreme ultraviolet (XUV) photodissociation6
More recently, we reported another finding that dissociative electron attachment (DEA) also directly led to the O2 formation7
Since a large quantity of low-energy free electrons were detected in the atmospheres of Venus and Mars, as well as the current Earth8,9,10,11, Eq. (3) and relevant DEA processes that were unheeded over a long period should be incorporated into the atmospheric reaction networks.
Besides VUV/XUV photons and free electrons, He2+ (alpha particle) and He+ are the heavy (respective to H+) ions in the solar wind12,13,14,15. Although the He+/He2+ collisional reactions were confirmed to contribute to the production of O+, O2+, and CO2+ in the Martian ionosphere16,17, there is still no indisputable evidence about the O2 formation18,19,20. Here we demonstrate that O2 and O2+ are certainly produced in the following collisional reactions:
by the measurements of time-of-flight (TOF) mass spectra and ion velocity maps using a crossed-beam apparatus21,22,23.
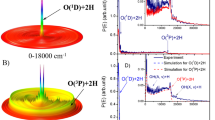
Previously, the experimental drawbacks such as multiple collisions and ionic yield collection or transportation gave rise to a divergence in whether O2 or O2+ could be produced in the thermal-energy reactions of He+ + CO2 (refs. 18,19,20), while those technical troubles are settled in the present measurements. On the other hand, the translational energy of He+ in the Martian atmosphere spreads over a wide range and depends on its sources, for instance, the velocity of He+ is comparable to that of He2+ in the solar wind if He+ is produced by the charge exchange reaction between He2+ and neutral hydrogen13. Besides the thermal-energy collisions, He+ + CO2 reactions at the collision energy of electron volts are particularly interesting, since the products in different electronic states, as shown in Fig. 1, play versatile roles in the subsequent processes.
CO2+ formed in the resonant charge exchange between CO2 and He+ can be populated in the ro-vibrationally excited states of electronic state C̃2Σg+ or the 2Πu-satellite states, but its spontaneous dissociation is highly preferred due to an electron depletion from the bonding orbital 4σg or 1πu of CO2 (refs. 24,25). The channels producing CO+ + O and O+ + CO were found to be dominant in the thermal collisions of He+ + CO2 (refs. 18,19,20,26), and as one of their subsequent processes, the photoemission A͂2Π → X͂2Σ+ of the CO+ yield may contribute to the comet tail glow26. Such scenarios can be further found in Fig. 1. For instance, the phosphorescence from the O2 in singlet states (a1Δg, b1Σg+) was observed in the aurora27. The reactions noted in Fig. 1, once authenticated experimentally, should be of fundamental importance toward understanding the oxygen-related processes in planetary atmospheres.
The present experiments were conducted with our home-made crossed-beam apparatus which was recently updated by introducing the three-dimensional velocity map imaging technique of ionic products22,23. The TOF mass spectra and velocity distributions of all ionic yields can be obtained simultaneously. The collection efficiency of ionic yields is close to 100%, and each peak in the TOF mass spectrum corresponds to the whole Newton spheres of a certain type of ionic yield. The multiple collisions in the ion flowing or the ion drift of cyclotron resonance18,19,20 are absent or reduced significantly in the crossed-beam arrangement where the pulsed reactant ion beam is perpendicular to a supersonic target beam.
Due to the energy redistribution in a collision, the endothermic channels (their energetic thresholds can be found in Table S1 of Supplementary Note 1) in Fig. 1 are possibly accessed. For example, around 3.5 eV of the collision energy, the reactions leading to O2(X͂3Σg¯) + C+(4P1/2) and 2O(3P2) + C+(2P1/2) are allowed in energetics if the collisional or translational energy is completely transformed into the internal energies of the target. However, in the TOF mass spectrometry measurement, the same product, C+ as mentioned above, cannot be distinguished from which channel the ion originates. Different ion production channels could be further identified by the ion velocity imaging measurements. In this work, the combinational measurements were accomplished at three collision energies in the reaction center-of-mass (c.m.) coordinate (Ec.m. = 1.94, 2.49, and 4.75 eV).
Results and discussion
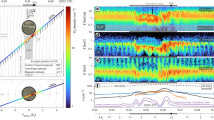
The TOF mass spectrum at Ec.m. = 4.75 eV, as a typical example, is shown in Fig. 2a, in which the C+ and O2+ ions are observed clearly but their relative intensities are much lower than those of other ionic yields. Such low signals of C+ and O2+ certainly brought difficulties in the previous measurements18,19,20,26. Here, we further obtained the branching ratios of the reactions and plotted their collision energy dependences in Fig. 2b. A comparison between the present branching ratios and the previous ones18,19,20 is presented in Table S2 of Supplementary Note 2.
In the reactions at the higher collision energies (10–103 eV), the production ratio γ (C+/CO+) was found to gradually increase with the enhancement of He+ kinetic energy24. Here one can find that the branching ratios of the reactions denoted with Eqs. (4) and (5) decrease with the Ec.m. enhancement. Such different collision-energy dependences should be attributed to reaction dynamics, e.g., diversities of collisional trajectories and dissociation pathways. Usually, the time scale of a charge exchange at the higher collision energy could be shorter than that of molecular vibrational motions. O2 can only be formed via the slow atomic roaming6 or the bending motion with a large amplitude of CO2 (ref. 7). Thereby, similar scenarios should exist for the O2 or O2+ product of the He+ + CO2 reactions at the lower collision energy.
The velocity maps of C+ and O2+ products in Fig. 3 correspond to the ionic three-dimensional Newton spheres projected on the detector or reaction plane, rather than the central slices of the spheres. Nevertheless, we still can find the collision-energy dependences of the velocity distributions. Figure 3a indicates that the C+ yields are primarily located around the target CO2 at the lower collision energies, but most of them are distributed in the forward direction (namely the CO2 flying direction) at Ec.m. = 4.75 eV. In contrast to the C+ velocity maps, as shown in Fig. 3b, most of the O2+ ions are always distributed around CO2 and become crowded at Ec.m. = 4.75 eV. The forward scattering preference and the product distributions around the reactant CO2 indicate that the reactions would like to proceed in the large-parameter collisions, namely, the collisional or translational energy is hardly transferred to the target in such a contactless reaction. Therefore, the higher-threshold channel leading to the fragments 2 O(3P2) + C+(2P1/2) is unfavorable at Ec.m. = 4.75 eV, due to the inefficient translational-to-internal energy transformation. The isotropic angular distributions (red circles in Fig. 3) represent the C+ yield of the CO2+ dissociation where CO2+ is assumed to be rebounded toward the c.m. position and receives 4.75 eV in a head-on collision. What we observed here obviously deviates from this hypothetical model.
Each velocity image is the projection of three-dimensional Newton spheres of C+ or O2+ to the ion detector. Red circles represent the isotropic distributions for O2(X̃3Σg¯) + C+(2P1/2) or O2+(X̃2Πg) + C(3P0) (outer circle) and O2(X̃3Σg¯) + C+(4P1/2) or O2+(a4Πu) + C(3P0) (inner circle) yields that are assumed to be produced in photodissociation of CO2+ at the center-of-mass (c.m.) of the collision. White lines with arrows show the coordinate transformation from the laboratory (the reactants’ velocities are represented with v, broken lines) and the collisional c.m. coordinate (the reactants’ velocities are represented with u, solid lines). The ionic signals in the left and right sides respective to c.m. are defined as the forward and backward scatterings.
The O2 coproduct is likely in b1Σg+ at the lower collision energies, primarily due to near energy-resonance of the channel to O2(b1Σg+) + C+(2P1/2) (see Fig. 1) and partially according to the velocity u(C+) distributions in Fig. S1a. The O2 coproduct could be in X̃3Σg¯ or Ã3Σu+ state at the higher collision energy 4.75 eV. The u(O2+) profiles in Fig. S1b, by contrast, exhibit a preference for the ground-state product O2+(X̃2Πg). O2 or O2+ in other states could be produced as the minor yields. More importantly, the absolute cross sections or production efficiencies of O2 and O2+ are the fundamental data of atmospheric reaction networks, but very few are available so far18,19,20,24,26,28,29. Extrapolating the total cross-sections of the He+ + CO2 reaction (all channels) from the higher collision energies28,29 to the low-energy range and according to the branching ratios obtained in this work, we further derive the absolute cross-sections of about 10−22 m2 of the reactions denoted with Eqs. (4) and (5) in a collision energy range of 1–5 eV (more details can be found in Supplementary Note 3). These cross-sections are a few hundred times larger than that of the direct production of O2 via DEA7.
As discussed previously, oxygen-atom roaming and molecular bending are two feasible pathways to produce O2 from CO2, where the former usually results in the nearly isotropic angular distributions of the products while a distinct anisotropy can be observed for the latter6,7. As proposed above, in the large-parameter collisional reaction, the He atom formed by the prompt charge exchange should be a spectator in the subsequent dissociation. To further reveal this unimolecular-like process, we make a coordinate transformation from the reaction c.m. one (used in Fig. 3) to the CO2 reaction coordinate (more details can be found in Supplementary Note 4). As illustrated in Fig. S2, the CO2 reaction coordinate is also defined with respect to the collision axis, but its scattering angle is different from that in the reaction c.m. coordinate. Figure 4 shows the angular and velocity distributions of C+ and O2+ in the CO2 reaction coordinate.
These distributions after the independent intensity normalizations are plotted in the CO2 reaction coordinate by the transformation from those in the collisional c.m. coordinate and assuming the reactions lead to O2(b1Σg+) + C+(2P1/2) (a, b) or O2+(X͂2Πg) + C(3P0) (c, d). The shades in different colors represent the statistical uncertainties and the ion intensities are normalized independently. Each point in the angular distribution (a, c) corresponds to all ion signals within a range of ±5°.
Figure 4a exhibits the nearly isotropic distributions of C+ at the lower Ec.m. values and a clearly forward preference at 4.75 eV, where O2 and C+ yields are assumed to be in specific states. As indicated in Fig. S3, this collision-energy dependence scarcely relies on the products’ states. A cartoon in the bottom panel of Fig. S3b illustrates a possible molecular orientation, namely, the dissociation undergoes the bended conformation which is almost perpendicular to the collision axis. It is reasonable that such a stereodynamics feature becomes indistinct in the slower collisional reaction. All O2+ angular distributions in Fig. 4c are almost isotropic, which could be attributed to the roaming dynamics, namely, the roaming O+ abstracts the oxygen atom from the CO moiety. The velocities of C+ and O2+ in Fig. 4b and d indicate the lower values at the higher collision energy, due to an enhancement of the products in the higher states.
To further understand the dissociation dynamics of CO2+, we plot the potential energy surfaces of C̃2Σg+ state in Fig. S4 of Supplementary Note 5. Different shapes or patterns of above potential energy surfaces imply that the O2+ or O2 formation hardly undergoes a combinational motion of molecular bending and symmetric bond stretching, but possibly benefits from an asymmetric stretching. The asymmetric stretching should be also responsible for the predominance of the CO+ and O+ products observed in this work and the previous studies18,19,20,24,26,28,29. However, it would be a tough task to simulate the dynamic trajectories leading to O2 or O2+ because of their much lower yields. Furthermore, the nonadiabatic process, for instance, coupling between C̃2Σg+ state and 2Πu-satellite states of CO2+25, may be involved in the reactions.
Conclusions
Based on the previous and present findings, we make a conclusive remark on the origins of atmospheric O2. Since the production efficiency of the photodissociation of CO2 was not high enough to reproduce the measured data30, the other production sources of those O2 molecules must be considered. The He+ + CO2 reaction, particularly in the low collision energy range, is an important mechanism but was ignored before this study. Up to date, we have known different mechanisms for the origin of atmospheric O2. The O atoms produced in the ion-molecule reaction, DEA, and photodissociation can also participate in the formation of O2. Some contributions could be from the O+ and O2+ ions by the electron capture, however, these ions are likely responsible for the oxygen escaping16,17. All-inclusive networks of the atmospheric and interstellar oxygen-related reactions are expected to be established by more and more laboratory studies and astronomical observations.
Methods
Experiments
Our three-dimensional velocity map imaging apparatus has been described elsewhere22, in which the product ion detector consists of a set of multichannel plates and a Delay-Line-Detector (DLD ϕ = 80 mm, commercially available from Roentdek). The ion source that previously produced Ar+ ions21 was updated recently to produce lighter ions (such as He+). In the present experiment, the energy spreads (ΔE/E ~ 7%) of the He+ bunches are comparable to that of the Ar+ bunches. The x−y positions (the plane of the detector) and the time of flight (along z direction) of each ionic signal are recorded simultaneously with the DLD, and then a Newton sphere of a certain type of ionic yield is rebuilt with these data22,23. In Fig. 3, the two-dimensional images are plotted with the raw data of whole Newton spheres of the ionic products projected on the detector, where one pixel corresponds to ca. 200 m/s of C+ or O2+. On the other hand, the TOF mass spectrum can be directly obtained from the measurement of whole Newton spheres, thus the ion collection efficiency is nearly 100%. High-purity (99.99%) samples (He and CO2) are available commercially and used without further purification. The He+ reactant ions are produced in the electron impacts at 30 eV. The kinetic energies and the energy spreads of the reactants He+ and CO2 (its ΔE/E ~ 6%) were calibrated or determined prior to the experiments. During the experiments, the reaction chamber is evacuated under a steady vacuum condition of 2.0 × 10−7 mbar and the reactions happen in the field-free region. The working frequency is 10 kHz, and we need dozens of hours to record the velocity images at a given collision energy.
Calculations
Equilibrium geometry and vibrational frequencies of the ground-state CO2 were calculated at the density functional theory level wb97xd/def2TZVP. This molecular geometry was used as the initial point in scanning the potential energy surfaces along the vibrational motions, i.e., symmetric stretching Q1, bending Q2, and asymmetric stretching Q3. Table S4 shows the corresponding values of real bond length and bond angle for each Q1–Q3. The equation of motion method based on the coupled cluster method limited to singles and doubles excitations and the basis set cc-pVTZ31,32,33,34 (encoded in Guassion16 suit of programs35) were used here to obtain the two-dimensional potential energy surfaces of CO2+(C2Σg+).
Data availability
All data underlying the figures are deposited in the main text or as supplementary information. The calculated data about the potential energy surfaces of CO2+(C2Σg+) are available upon the requests to the corresponding authors.
References
Canfield, D. E. The early history of atmospheric oxygen. Annu. Rev. Earth Planet. Sci. 33, 1–36 (2005).
Bekker, A. et al. Dating the rise of atmospheric oxygen. Nature 427, 117–120 (2004).
Kasting, J. F., Liu, S. & Donahue, T. Oxygen levels in the prebiological atmosphere. J. Geophys. Res. 84, 3097–3107 (1979).
Kasting, J. F. & Walker, J. C. Limits on oxygen concentration in the prebiological atmosphere and the rate of abiotic fixation of nitrogen. J. Geophys. Res. 86, 1147–1158 (1981).
Kasting, J. F., Pollack, J. B. & Crisp, D. Effects of high CO2 levels on surface temperature and atmospheric oxidation state of the early Earth. J. Atmos. Chem. 1, 403–428 (1984).
Lu, Z., Chang, Y.-C., Yin, Q.-Z., Ng, C. Y. & Jackson, W. M. Evidence for direct molecular oxygen production in CO2 photodissociation. Science 346, 61–64 (2014).
Wang, X.-D., Gao, X.-F., Xuan, C.-J. & Tian, S. X. Dissociative electron attachment to CO2 produces molecular oxygen. Nat. Chem. 8, 258–263 (2016).
Pätzold, M. et al. The structure of Venus’ middle atmosphere and ionosphere. Nature 450, 657–660 (2007).
Frahm, R. A. et al. Carbon dioxide photoelectron energy peaks at Mars. Icarus 182, 371–382 (2006).
Lee, J. S., Doering, J. P., Potemral, T. A. & Brace, H. Measurements of the ambient photoelectron spectrum from atmosphere explorer: I. AE-E measurements below 300 km during solar minimum conditions. Planet. Space Sci. 28, 947–971 (1980).
Mantas, G. P. & Hanson, W. B. Photoelectron fluxes in the Martian ionosphere. J. Geophys. Res. 84, 369–385 (1979).
Möbius, E. et al. Direct observation of He+ pick-up ions of interstellar origin in the solar wind. Nature 318, 426–429 (1985).
Swaczyna, P., McComas, D. J. & Zirnstein, E. J. He+ ions comoving with the solar wind in the outer heliosphere. Astrophys. J. 875, 36 (2019).
Barabash, S. & Norberg, O. Indirect detection of the Martian helium corona. Geophys. Res. Lett. 21, 1547–1550 (1994).
Halekas, J. S. & MaFadden, J. P. Using solar wind helium to probe the structure and seasonal variability of the Martian hydrogen corona. J. Geophys. Res.: Planets 126, e2021JE007049 (2021).
Kallio, E. et al. Energisation of O+ and O2+ ions at Mars: an analysis of a 3-D quasi-neutral hybrid model simulation. Space Sci. Rev. 126, 39–62 (2006).
Maes, L., Fraenz, M., McFadden, J. P. & Benna, M. Escape of CO2+ and other heavy minor ions from the ionosphere of Mars. J. Geophys. Res.: Space Phys. 126, e2020JA028608 (2021).
Fehsenfeld, F. C., Schmeltekopf, A. L., Goldan, P. D., Schiff, H. I. & Ferguson, E. E. Thermal energy ion-neutral reaction rates. I. Some reactions with helium ions. J. Chem. Phys. 44, 4087–4098 (1966).
Adams, N. G. & Smith, D. Product-ion distributions for some ion-molecule reaction. J. Phys. B: Mol. Phys. 9, 1439–1450 (1976).
Anicich, V. G., Laudenslager, J. B., Huntress, W. T. Jr. & Futrell, J. H. Product distributions for some thermal energy charge transfer reactions of rare gas ions. J. Chem. Phys. 67, 4340–4350 (1977).
Hu, J., Wu, C.-X. & Tian, S. X. A well-confined pulsed low-energy ion beam: test experiments of Ar+. Rev. Sci. Instrum. 89, 066104 (2018).
Hu, J. et al. Stereodynamics observed in the reactive collisions of low-energy Ar+ with randomly oriented O2. J. Phys. Chem. Lett. 12, 1346–1351 (2021).
Hu, J., Zhi, Y.-Y., Xie, J.-C., Wu, C.-X. & Tian, S. X. Collision-energy dependent stereodynamics of the dissociative charge exchange reaction between Ar+ and CO. J. Phys. Chem. Lett. 12, 7127–7133 (2021).
McMillan, M. R. & Coplan, M. A. Kinematics of He+–CO2 dissociative charge exchange. J. Chem. Phys. 71, 3063–3071 (1979).
Roy, P., Nenner, I., Millie, P., Morin, P. & Roy, D. Experimental and theoretical study of configuration interaction states of CO2+. J. Chem. Phys. 84, 2050–2061 (1980).
Tsuji, M., Endoh, M., Susuki, T., Mizukami, K. & Nishimura, Y. Optical spectroscopic study of thermal-energy charge transfer between He+ and CO2. J. Chem. Phys. 81, 3559–3563 (1984).
Burrage, M. D., Arvin, N., Skinner, W. R. & Hay, P. B. Observations of the O2 atmospheric band nightglow by the high-resolution Doppler imager. J. Geophys. Res. 99, 15017–15023 (1994).
Parker, J. E. & Johnson, C. A. F. A two-state treatment of the electron transfer reactions from carbon dioxide to helium ions. Int. J. Mass Spectrom. Ion-. Proc. 94, 87–99 (1989).
Werbowy, S. & Pranszke, B. Charge-exchange processes in collisions of H+, H2+, H3+, He+, and He2+ ions with CO and CO2 molecules at energies below 1000 eV. Phys. Rev. A. 93, 022713 (2016).
Lo, D. Y., Yelle, R. V. & Lillis, R. J. Carbon photochemistry at Mars: updates with recent data. Icarus 352, 114001 (2020).
Kendall, R. A., Dunning, T. H. Jr. & Harrison, R. J. Electron affinities of the first‐row atoms revisited. Systematic basis sets and wave functions. J. Chem. Phys. 96, 6796–6806 (1992).
Dunning, T. H. Jr. Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen. J. Chem. Phys. 90, 1007–1023 (1989).
Woon, D. E. & Dunning, T. H. Jr. Gaussian-basis sets for use in correlated molecular calculations. III. The atoms aluminum through argon. J. Chem. Phys. 98, 1358–1371 (1993).
Peterson, K. A., Woon, D. E. & Dunning, T. H.Jr. Benchmark calculations with correlated molecular wave functions. IV. The classical barrier height of the H + H2 → H2 + H reaction. J. Chem. Phys. 100, 7410–7415 (1994).
Frisch, M. J. et al. Gaussian 16, Revision C.01 (Gaussian, Inc., Wallingford, CT, 2019).
Acknowledgements
We gratefully acknowledge the financial support from the Strategic Priority Research Program of the Chinese Academy of Sciences (XDB0450202) and the National Natural Science Foundation of China (22233004, 22003062). The numerical calculations are done in the Supercomputing Center of the University of Science and Technology of China.
Author information
Authors and Affiliations
Contributions
S.X.T. conceived this study. S.X.T. and J.H. supervised this study. Y.Z., Q.G., and J.H. carried out the experiments. Y.Z. and J.X. performed the quantum chemistry calculations. Y.Z., Q.G., and J.H. did the data analyses. All authors contributed to the discussion and the manuscript preparation.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Communications Chemistry thanks the anonymous reviewers for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Zhi, Y., Guo, Q., Xie, J. et al. Direct production of molecular oxygen from carbon dioxide and helium ion collisions. Commun Chem 6, 267 (2023). https://doi.org/10.1038/s42004-023-01074-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42004-023-01074-2
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.