Abstract
Ferrihydrite is one of the most important iron-containing minerals on Earth. Yet determination of its atomic-scale structure has been frustrated by its intrinsically poor crystallinity. The key difficulty is that physically-different models can appear consistent with the same experimental data. Using X-ray total scattering and a nancomposite reverse Monte Carlo approach, we evaluate the two principal contending models—one a multi-phase system without tetrahedral iron(III), and the other a single phase with tetrahedral iron(III). Our methodology is unique in considering explicitly the complex nanocomposite structure the material adopts: namely, crystalline domains embedded in a poorly-ordered matrix. The multi-phase model requires unphysical structural rearrangements to fit the data, whereas the single-phase model accounts for the data straightforwardly. Hence the latter provides the more accurate description of the short- and intermediate-range order of ferrihydrite. We discuss how this approach might allow experiment-driven (in)validation of complex models for important nanostructured phases beyond ferrihydrite.
Similar content being viewed by others
Introduction
Ferrihydrite is a nanoparticulate ferric oxyhydroxide of unique importance across a range of fields1: it is widespread in soils and freshwater environments2,3; it forms a core structural component in the Fe-buffering ferritin protein, found in numerous organisms4,5; it is a major component of Fe-containing minerals on Mars6; and it is used in the sequestration of heavy element contaminants7. Structurally, it is known to be a precursor of haematite and goethite8, yet its own three-dimensional atomic structure has remained the subject of intense debate9,10,11,12,13,14. The key difficulties in determining its structure are a combination of a very small particle diameter—giving rise to severe powder diffraction peak broadening—and a high degree of defect incorporation.
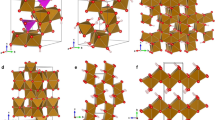
In this respect, ferrihydrite is representative of an important general challenge facing structural science: namely, how might we develop robust protocols for determining the structure of nanoscale materials15,16,17? The conventional—and most straightforward—approach is to approximate nanomaterials as periodic crystals modified by a suitable shape function. This interpretation is implicit in Debye–Sherrer analysis of diffraction peak widths but is also sometimes carried out explicitly via modelling of the pair distribution function (PDF) with appropriate damping functions18,19. This is precisely the approach that has been applied to the problem of ferrihydrite, such that from amongst the variety of structural models proposed over the last fifty years20,21,22, essentially only two competing models remain as the basis for ongoing debate within the community10,23. One is the multi-phase model proposed by Drits et al.23 that contains a mixture of defect-free and defective ferrihydrite nanocrystals together with ‘ultra-dispersed’ haematite (Fig. 1a–c); we refer to this as the ‘MP’ model. The second is the single-phase akdalaite-like model of Michel et al.10,24 (Fig. 1d); we refer to this as the ‘SP’ model. Diffraction and PDF measurements have proven insufficiently discriminating to rule out either model in any definitive sense, although recent experimental and theoretical studies support the case for the SP structure14,25. The difficulty in all comparative studies is that the MP model requires significant simplifications26 to allow its complex composition to be approximated by a single damped periodic structure.
a Representative slices of non-defective and b defective particles in the multiphase (MP) model, viewed along the 〈110〉 direction. White spheres represent Fe atoms, red, O atoms, and blue, water molecules. Both figures are shown in the same style as Fig. 1a in ref. 9 to aid comparison. O anion vacancies can occur in defective particles where all neighbouring Fe atoms are randomly vacant—inclusion of oxygen would be equivalent to the presence of water. c Haematite structure, which forms a third, minority, component of the MP model. d Single-phase (SP) model, where Fe1, Fe2 and Fe3 sites are shown as light grey, brown and black polyhedra, respectively.
Implicit in the interpretation of scattering data in terms of damped periodic models is the assumption that the nanoparticle surface structure is identical to that of the core (or, equivalently, the surface constitutes a sufficiently small volume fraction that it might safely be ignored). In some instances this approximation is justified: nanoparticulate Au is probably the least controversial example27. However, in the case of the most disordered ferrihydrites (so-called ‘2-line’ phases) the structural coherence length is just 2–3 nm28, which requires that half of the atoms in each nanocrystal lie within 3 Å of the surface; significant surface relaxation is expected in such cases29. A cumbersome—though ultimately unavoidable—work-around is to reproduce scattering data from atomistic (‘big box’) rather than periodic (‘small box’) structural models30. Here the concept is to build a realistic nano-scale model of the ferrihydrite structure and then to refine atom positions within this model using an approach, such as reverse Monte Carlo (RMC) refinement31. To date, probably the most comprehensive atomistic reproduction of 6-line ferrihydrite is that reported in ref. 32, where RMC methods were used to refine atom positions within a single nanoparticle of diameter 3.6 nm—incorporating structural defects in a more realistic manner than approximations to a periodic cell can achieve. Even in this atomistic representation, the MP model was heavily simplified because its multiple constituent phases were approximated by a single nanoparticle.
In fact, experiment shows that individual nanoparticle models—whatever their complexity—will never accurately describe the nanostructure of 2-line ferrihydrite. High-resolution transmission electron microscopy (HRTEM) measurements reveal that poorly-defined nanocrystals coexist with an amorphous component (matrix) of a similar chemical composition33. Similar complexity is present in other important iron-containing nanomaterials, such as schwertmannite34 and may arise as a consequence of a complex crystallisation pathway35. Although the amorphous matrix of ferrihydrite may lack long-range order, its constituent atoms cannot be randomly arranged. Consequently, the matrix contributes meaningfully to the PDF at low interatomic separations, even if its signature in the diffraction pattern (i.e., in reciprocal space) is not highly structured. Moreover, the MP model includes multiple nanocrystalline components. Taken together, these considerations mean that the only method by which the SP and MP models might be compared on equal footing is by constructing even larger atomistic models that represent an entire nanocomposite assembly that explicitly includes both nanoparticle and matrix components.
In this study, we address this challenge directly by extending the RMC approach to nanocomposite heterostructures. While RMC methods have long been used to determine the structures of crystalline, amorphous, and nanocrystalline materials36,37,38,39, our methodology is distinct in using a single atomistic model that incorporates at once both nanocrystalline and amorphous components. We build complete atomistic representations of the SP and MP models that are as faithful as possible to the original descriptions laid out in refs. 23,24. Full structural details of the models are given in Supplementary Note 1 and Supplementary Tables 1–3. Our models differ from those of previous studies in that our configurations are an ensemble of several individual nanoparticles, embedded in a structured amorphous, non-random matrix. The structure of each particle follows as faithfully as possible the relevant models described in the literature, without further simplifications. A long-standing criticism of both MP and SP models has been that they do not account at once for both local and long-range features—we assess this directly by using RMC refinements to make perturbative adjustments in atomic positions, fitting simultaneously to real and reciprocal space data. We interrogate the models in terms of quality of fit-to-data, of the physicality of their pairwise correlation functions, and the extent and nature of structural reorganisation introduced in the fitting process. We will show that only the SP model provides a physical representation of the structure of 2-line ferrihydrite, and that the closest unit-cell description is a marginally less distorted variant of the akdalaite model of ref. 24.
Results
Model generation
We begin with a brief description of our approach for generating atomistic representations of ferrihydrite for subsequent RMC analysis; full details are provided in the Supplementary Methods. The nanoparticle and matrix components of the nanocomposite structure are prepared individually before being combined to give the starting RMC model. In all cases we omit H atoms, as required by the correspondingly poor sensitivity in X-ray scattering data.
For the nanoparticle component, we generate each nanoparticle starting from a conventional atomistic configuration of the corresponding phase. The MP model contains spherical nanoparticles of so-called ‘defect-free’ (f-phase, ordered stacking sequence, Fig. 1a) and ‘defective’ (d-phase, disordered stacking sequence, Fig. 1b) ferrihydrite phases together with ultra-dispersed cylindrical nanoparticles of haematite (Fig. 1c). The SP model consists of a single nanoparticle type that is isostructural with akdalaite, Al10O14(OH)2 (Fig. 1d)10,24. We note in passing that an important distinction between the phases present in these models is the absence (MP) or presence (SP) of tetrahedrally-coordinated Fe3+11,40,41,42. In each case a large atomistic configuration is generated, a spherical (ferrihydrite) or cylindrical (haematite) section of appropriate dimensions23 is excised and then surface Fe atoms of this spherical particle removed if under-coordinated. Individual nanoparticles are then positioned and oriented randomly (subject to hard-sphere constraints) within the final box; at this stage we aim for a filling ratio of ~50%, achieved using a hard-sphere Monte Carlo (MC) algorithm. In the case of the MP configuration we also ensure that the correct volume ratio of defect-free, defective, and haematite nanoparticles has been incorporated23.
To prepare the matrix component, we fill a separate configuration (of the same size as the final box) with Fe and O atoms according to the bulk ferrihydrite composition and number density. These atoms are initially placed randomly, but sensible local order is introduced through a MC algorithm that is first driven purely by hard sphere constraints and subsequently by local distance restraints informed by a relevant crystalline phase. The result is a disordered configuration with sensible composition, density, and local Fe and O coordination. The matrix and multi-nanoparticle boxes are then combined, removing from the matrix component any atoms that overlap with nanoparticles.
Ruling out the multi-phase model
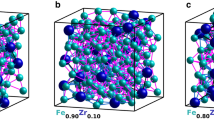
We carried out RMC refinements using these nanocomposite models as our starting configurations. During these refinements, atom positions were adjusted in order to maximise the quality of fit to both X-ray PDF and reciprocal space F(Q) data. A representative atomistic model obtained from these refinements is shown in Fig. 2 and the corresponding fits to data are shown in Fig. 3; full details are given in Supplementary Note 2 and Supplementary Figs. 2–5. What is immediately obvious is that the quality of RMC fit, in both real (PDF) and reciprocal-space (F(Q)) is comparable for both models; certainly the differences in fit are smaller than our uncertainty in the experimental data. Taken at face value, both models appear consistent with the X-ray scattering data; however, by examining the particle restructuring required in order to achieve this fit, we now show that only the SP model accurately describes the structure of ferrihydrite. In Fig. 4a–c, we illustrate the most severe structural reorganisations that occur in representative ferrihydrite nanoparticles of the three different types contained within our RMC models: namely, the single nanoparticle component of the SP model and the d- and f-phases of the MP model. Whereas for the f-phase and the SP model the largest structural reorganisations occur at the nanoparticle/matrix interface (consistent with experiment43,44), our models of the d-phase nanoparticles systematically exhibit large internal reorganisation processes with collective Fe displacements >0.8 Å.
a Nanocomposite simulation box (60 Å)3, with particle and matrix surfaces shown in black and grey, respectively, illustrating its resemblance to the TEM image, shown in d—the enclosed region shows the approximate cubic volume covered by the simulation box. b Simulation box schematic, highlighting the structure of the particles, shown in red, and c the matrix, shown in grey. e A typical particle model, prior to refinement, representative of the circled region in (b). O atoms are coloured red and Fe, white. f Expanded region of (c), emphasising the reasonable atomic connectivity in the matrix structure. g Simulated TEM micrograph, calculated from a 10 Å-thick slice from the RMC-refined model, shown in (h). i Superposition of TEM simulation and atomistic model, highlighting the ordered regions in the simulation. The particle clarity in (g) is highly sensitive to particle orientation, hence some ordered regions, highlighted in (i), are clearer than others.
a RMC fits to reciprocal space data F(Q) and b the PDF, using the D(r) normalisation—see ref. 70 for details. c Individual contributions to the PDF from particle–particle, matrix–matrix, and particle–matrix correlations, shown in the G(r) formalism; G(r) = D(r)∕4πrρ0, where ρ0 is the sample number density. Particle–particle and matrix–matrix correlations are offset by 1.5 and 0.15 units in G(r), respectively, for clarity.
Representative Fe displacement vectors for a the single-phase model, b defective and c non-defective particles in the multiphase model. Only the largest displacements (>0.8 Å) are shown; vector magnitudes are scaled up to emphasise visually the direction of cation movement. The grey wireframes show the initial atomic coordinates. d Histogram of Fe displacements across all particles in the simulation box—frequencies are normalised against the number of cations in each type of particle. ‘Single phase’ and ‘multiphase’ are abbreviated to ‘SP’ and ‘MP’ in the plot legends. e Calculated Fe–O bond valence sums for the nanoparticles prior to RMC refinement, f post-refinement, and g for 4,5, and 6 co-ordinate matrix Fe cations (73% of Fe in multiphase, 64% in single phase), post-refinement. The contributions from tetrahedral and octahedral Fe in the single-phase model are calculated separately in (f). The standard formula \(V=\sum \{\exp [({R}_{0}-{R}_{i})/b]\}\) is used with the literature values b = 0.37, R0 = 1.76 Å, and a maximum Fe–O bond length of 2.6 Å was allowed for the value of Ri.
We quantify this observation in Fig. 4d, where the distribution of Fe reorganisation magnitudes is given for all four nanoparticle types across our ensemble of RMC configurations. The d-phase nanoparticles of the MP model are conspicuous in having a greater proportion of large Fe displacements. The driving force for this reorganisation is partly an incompatibility between the underlying nanoparticle structure and the data, and partly also the presence of short Fe…Fe contacts in the original model. When constructing our RMC starting configurations, it became clear that the rules describing cation distributions in the MP model of ref. 23 are in some respects internally inconsistent; these inconsistencies are obfuscated by a description in terms of conventional unit cells (further discussion is given in Supplementary Note 1). The most significant occurs in the d-phase, where a disordered stacking sequence gives unphysically short Fe…Fe contacts (1.8 Å) whenever equivalent layers occur in succession. A schematic diagram illustrating this point is given in Supplementary Fig. 1.
So we find that the MP model cannot account at once for both PDF and F(Q) data without substantial structural reorganisation; that is to say the MP crystallographic unit-cell description of 2-line ferrihydrite cannot be correct. By contrast, the SP model requires only a relatively subtle distortion to show consistency with the data, which suggests the model provides the more realistic representation of the structure of 2-line ferrihydrite. We have reached this conclusion by building what is (to the best of our knowledge) the first atomistic configuration of the MP model, free of the simplifications that have to date prevented fair and direct interrogation by other approaches.
Nanocomposite model physicality
We proceeded to check for any unphysical local structure in either RMC refinement, in order to assess the efficacy of our large-scale nanocomposite modelling approach. The partial PDFs that describe particle–particle, matrix–matrix, and particle–matrix correlations are illustrated in Fig. 3c; these show varying degrees of structured correlation as a function of distance, and all have a chemically-intuitive form. Particle–particle interactions are most strongly correlated for r ≲ 10 Å and continue to contribute the most structure to the overall PDF over longer distances up to the particle diameter. Structured correlations are only evident within the matrix below 5 Å, showing that local atomic environments are still well-defined in an otherwise apparently-amorphous material. At larger distances, the matrix contribution to the PDF is unstructured and so this component does not compensate for a poorly-fitting particle model by contributing to unreasonable regions of the PDF. We note that the distinction between particle and matrix correlation functions illustrates the need to include a matrix component explicitly when fitting the PDF rather than relying on empirical modifications to the particle–particle correlation functions. In many ways the matrix–particle correlations are qualitatively similar to the matrix–matrix correlations: structure at low-r reflects well-defined chemical order at the particle–matrix interface and the smoothly-continuous behaviour at high-r shows the absence of structured correlations at distances ≳ 5 Å. So there is no evidence that our refined RMC configurations contain any unphysical correlations; we provide a more detailed interpretation of the pairwise correlation functions to support this statement in Supplementary Note 2 and Supplementary Figs. 4–5.
Addressing historical objections to the single-phase model
That RMC refinements based on both SP and MP models give comparable fits to data and correspond to similar particle–particle, matrix–matrix, and particle–matrix correlations answers a key point of contention in the literature. In earlier studies where damped periodic models had been used to interpret X-ray scattering patterns, it was thought that neither the SP nor the MP model could account simultaneously for both real-space and reciprocal-space transforms of the data26. Here we have shown that, by e.g. allowing relaxation at the nanoparticle/matrix interface, the SP model is consistent with the interatomic separations measured in the PDF and also the signature of periodic structural features reflected directly in the diffraction pattern. The same is true of the RMC-refined structure using the MP model particles, although distortions greater than ‘relaxation’ are required, to the extent that the final structure is not representative of the original MP model description.
A further historical objection to the SP model concerns its ability to reproduce chemically sensible Fe bond valence sum (bvs) values24,45. We are able to extract bvs distributions from our RMC configurations and hence address this point directly. In our analysis we define the bvs as \(V=\sum \{\exp [({R}_{0}-{R}_{i})/b]\}\) where standard values b = 0.37, R0 = 1.76 Å are used46. For a given Fe atom, any Fe–O contact < 2.6 Å was used as an Ri value. Figure 4e shows the distribution of Fe bvs values for the three ferrihydrite nanoparticle starting configurations; note that these are essentially delta functions because the nanoparticles are generated based on fixed atom coordinates taken from periodic models. Following refinement, the bvs distributions broaden (Fig. 4f); the widths we observe are entirely consistent with other RMC studies47 and are to be expected for real systems where there are both thermal and configurational fluctuations. It is the midpoint of these distributions that is physically meaningful, and we find that both MP and SP models arrive at bvs values centred around 3.0 Å, as expected. That the Fe bvs values converge on a similar distribution in both MP and SP models—despite the differences in initial bvs distributions—is a strong indication that the data themselves are sensitive to a single robust set of bond valence parameters. Moreover, the bvs distribution for the matrix component also peaks at a physically sensible value ≃3.0, albeit with a greater variance (Fig. 4g).
Restructuring in the single-phase model
Having established that our RMC-refined SP model provides the more physical description of the experimental PDF of ferrihydrite, we sought to extract from our RMC configurations the most succinct structural description of the nanocrystalline component against which we might compare the original akdalaite-based models of refs. 10,24. To this end, we first projected all atomic positions within a single nanoparticle onto a single unit cell, and repeated this calculation for each particle in our RMC box (accounting for differences in particle orientation, of course). For a given nanoparticle we found an entirely reasonable distribution of atomic positions, with no sign of anomalously large displacements. The average atomic positions obtained showed excellent consistency from particle to particle (see Supplementary Fig. 6). And so we could extract a set of averaged RMC-refined atomic coordinates for comparison against the small-box-model values given in ref. 24; these coordinates are compared in Table 1. Further details regarding atomic displacement distributions and consistency checks are given in Supplementary Note 3, Supplementary Table 5, and Supplementary Figs. 6, 7. While the difference in structures is relatively subtle, we found the RMC model to give less distorted Fe coordination geometries (Fig. 5). We quantified this observation using the minimum bounding ellipsoid method, as implemented in the program Pieface48. Here the degree of distortion is related to the asphericity of the smallest ellipsoid that can encompass a given coordination polyhedron. The effect of the RMC fitting is to drive both crystallographically-distinct, six-coordinated Fe sites to adopt more ideal octahedral geometries (a more spherical ellipsoid), whereas the degree of distortion at the tetrahedral Fe site is essentially unchanged from that of the small-box model.
Projection along the c-axis showing the average unit cell coordinates for a the SP starting model (ref. 24) and b our newly-refined RMC refinements. Atom colours follow the scheme of Fig. 1d. Regions of each cell are highlighted to emphasise the decrease in structural distortion that follows RMC refinement. c Quantification of Fe coordination polyhedral distortions, as determined from the tensorial principal axis variances in pieface48, for starting (striped bars) and RMC-refined (filled bars) models. Fe1 and Fe2 are octahedral sites; Fe3 is the tetrahedral site. Error bars indicate the standard uncertainty on the mean variance.
Discussion
The RMC-SP model accounts for the X-ray PDF and F(Q) data, but is it consistent with other measurements of 2-line ferrihydrite? In Fig. 2d, g–i, we compare qualitatively against electron microscopy images not used in the refinement of our RMC model. We find good agreement between images simulated from a representative 10 Å-thick slice of the RMC configuration (Fig. 2g–i) and experiment (Fig. 2d and Supplementary Fig. 8)—lattice fringes and particle outlines are distinguishable from surrounding amorphous content; regions in which there is no clear signature of ordering. Hence our RMC model provides a sensible representation of the structure of 2-line ferrihydrite at both atomic and nanometre scales.
Although constructed from a single nanocrystalline phase, the SP model we develop nevertheless contains three physical components: the ordered nanoparticle interiors, the disordered matrix, and the nanoparticle/matrix interface. The complexity even of this ‘simple’ nanocomposite helps explain some ostensibly contradictory experimental observations. For example, the partitioning of water, hydroxide, and even tetrahedral or octahedral iron is likely to vary amongst these three components, and different experimental probes will show different sensitivities to each component. The intensity of Bragg-like features in X-ray (and neutron) scattering patterns will be sensitive to the composition of the nanoparticle interior and not to that of the matrix. The importance of structural relaxation at nanoparticle boundaries is now increasingly recognised within the field44,49. The interest is motivated by the surface role in ferrihydrite’s geological significance—it sequesters other elements in the natural environment2,50 as well as forming the interface between water pockets and Fe-containing material44,51,52,53,54. Naturally, the X-ray PDF data we have used in our own study are simply not sufficiently sensitive to the location of hydrogen atoms, especially in the presence of strong scatterers such as Fe (as in all other X-ray studies of ferrihydrite24). Nevertheless, our model provides a starting point for subsequent computational determination of the likely partitioning of oxide, hydroxide, and water throughout each of the three nanocomposite components. An obvious target for future studies is the subsequent energetic relaxation of such models, but doing so involves addressing the enormous challenge of extending ab initio methods to large supercell configurations.
Given the paucity of information contained within the scattering functions of disordered and nanocomposite materials, and the enormous number of degrees of freedom available within an RMC refinement, it is unrealistic to expect RMC to arrive at a unique structural ‘solution’ during refinement55,56. The case of ferrihydrite is a fundamentally trickier problem than that of local structure determination in complex crystalline materials, where the presence of an underlying crystal lattice ensures richer information content in scattering data and imposes strong constraints on refinement17. Moreover, nanocomposite materials are inherently non-equilibrium phases, which in turn complicates the application of conventional computational methodologies to structural modelling. What we demonstrate here is that atomistic refinement approaches such as RMC can be used to test proposed models even for structurally complex nanocomposite phases. In the specific case of ferrihydrite we are able to identify an improved unit-cell description of its key nanocrystalline component and characterise the coherence lengthscale for structural correlations at the nanocrystal–matrix interface.
Crucially, the ability to model heterogeneous nanocomposites has significance well beyond the example of ferrihydrite, as important as this system may be. For example, there are closely-related geologically- and biologically-relevant materials for which the approach we develop here is likely to offer significant insight: the structure and transformations of amorphous calcium phosphate, a key precursor in bone formation57,58,59,60; crystallite nucleation in supramolecular gels61; nanodomain evolution in aqueous aerosols62; and the stabilising effects of porous functionalised silica on surrounding media63. Likewise, key components used in functional devices, such as battery cathodes, routinely contain mixtures of amorphous and nanostructured components and are not well described in terms of single-phase approximants64. We anticipate that nanocomposite structure refinement will be particularly important for the many cases where the interface between nanoparticle components—e.g. the amorphous matrix for ferrihydrite—is crucial for material function, since this is precisely the component unaccounted for by conventional multi-phase modelling65.
Methods
Synthesis of 2-line ferrihydrite
Two-line ferrihydrite was synthesised according to the method developed by Schwertmann and Cornell66. We note that the scattering and PDF evaluated as part of this study were published previously in Ref. 67 which includes additional details regarding sample synthesis.
Total scattering data collection and processing
Total scattering X-ray data were collected on powdered dry ferrihydrite at beamline 11-ID-B (90.8 keV, λ = 0.13702 Å) at the Advanced Photon Source, Argonne National Laboratory. Additional details regarding the experimental setup can be found in ref. 67. The data were processed using GUDRUNX,68,69 correcting for background scattering, Compton scattering, multiple scattering and beam attenuation by the sample container, yielding the normalised total scattering function F(Q) and its Fourier transform—the PDF—using the D(r) normalisation with \({Q}_{\max }=22\) Å−1. The formalisms used here for the total scattering functions follow those outlined by Keen70. Owing to the lack of consensus on the accepted ferrihydrite model, the data were normalised differently for the MP and SP models, using the number density and element concentrations that were present in our atomistic models, omitting contributions from hydrogen. However, the different normalisations used resulted in only negligible differences to the data.
Reverse Monte Carlo modelling
Atomistic models for RMC refinement were constructed using bespoke program code—full details are given in the Supplementary Methods. The cubic simulation box, with a = 60 Å, consisted of either nine SP particles or six MP-f, three MP-d and three haematite particles. RMCProfile was used to fit the configuration to the PDF and F(Q) data, simultaneously31. Owing to initial difficulties in fitting the PDF satisfactorily, the low-r region of the PDF was duplicated as an additional, third, dataset, effectively forcing the configurations to fit the shorter-distance local geometry more closely than required for large r. Closest approach constraints of 2.50, 1.64, and 2.50 Å were used for O–O, M–O, and M–M atom pairs, respectively. Pairs of M–O atoms that fell within the range 1.50–2.60 Å in the starting model were constrained to remain within this distance window. Refinement proceeded via random movement of randomly selected atoms, subject to distance-based restraints (see Supplementary Table 4). Moves were accepted if the fit to data improved or accepted within the probability \(P=\exp (-\Delta {\chi }^{2}/2)\) if it worsened. Refinement proceeded for five days, after which no substantial improvement in data fit was observed.
High-resolution transmission electron microscopy and image simulation
TEM specimens were prepared by pipetting small droplets of a fresh ferrihydrite suspension on lacey carbon film-coated 300 mesh Cu grids. The TEM images were obtained using a JEOL JEM 2100, operated at 200 kV. HRTEM images were simulated based on the multislice method using the MacTempas (Total Resolution) software. The diameter of the model nanoparticles was smaller than 60 Å and so the (60 Å)3 box of the RMC-refined model (Fig. 2a) was sliced in 10 Å increments for the multislice calculations. The calculations were performed at an acceleration voltage of 200 kV, spherical abberation of 1.2 mm, and defocus spread of 80 mrad. The thickness was set to 10 Å, i.e. the thickness of a single model slice. Simulated images with defocus values between −600 and +600 Å were compared with the experimental TEM images.
Data availability
The raw data on which this manuscript is based are openly available for download from https://doi.org/10.5287/bodleian:M8GnGvemj. These include the RMC configurations, real- and reciprocal-space fits, and the unit-cell model shown in Fig. 5.
Code availability
The reverse Monte Carlo simulations were performed using RMCProfile, which is freely-available from http://www.rmcprofile.org/. Specific restraints used during the RMC process are given in Supplementary Table 4. All custom code used in this study was developed using widely available algorithms. Copies of the code used can be obtained upon request.
References
Cornell, R.M. & Schwertmann, U. The Iron Oxides: Structure, Properties, Reactions, Occurrences and Uses, 2 edn (Wiley-VCH, Weinheim, Germany, 2003).
Jambor, J. L. & Dutrizac, J. E. Occurence and constitution of natural and synthetic ferrihydrite, a widespread iron oxyhydroxide. Chem. Rev. 98, 2549–2585 (1998).
ThomasArrigo, L. K. et al. Iron and arsenic speciation and distribution in organic flocs from streambeds of an arsenic-enriched peatland. Environ. Sci. Technol. 48, 13218–13228 (2014).
Chasteen, N. D. & Harrison, P. M. Mineralization in ferritin: an efficient means of iron storage. J. Struct. Biol. 126, 182–194 (1999).
Michel, F. M. et al. Reactivity of ferritin and the structure of ferritin-derived ferrihydrite. BBA-Gen. Subjects 1800, 871–885 (2010).
Dehouck, E., McLennan, S. M., Sklute, E. C. & Dyar, M. D. Stability and fate of ferrihydrite during episodes of water/rock interactions on early Mars: an experimental approach. J. Geophys. Res. Planet 122, 358–382 (2017).
Jiang, X. et al. Removal of arsenate by ferrihydrite via surface complexation and surface precipitation. Appl. Surf. Sci. 353, 1087–1094 (2015).
Schwertmann, U., Friedl, J. & Stanjek, H. From Fe(III) ions to ferrihydrite and then to hematite. J. Colloid Interf. Sci. 209, 215–223 (1999).
Manceau, A. Evaluation of the structural model for ferrihydrite derived from real-space modelling of high-energy X-ray diffraction data. Clay Miner. 44, 19–34 (2009).
Michel, F. M. et al. The structure of ferrihydrite, a nanocrystalline material. Science 316, 1726–1729 (2007).
Maillot, F. et al. New insight into the structure of nanocrystalline ferrihydrite: EXAFS evidence for tetrahedrally coordinated iron(III). Geochim. Cosmochim. Ac. 75, 2708–2720 (2011).
Xu, W. et al. Structural water in ferrihydrite and constraints this provides on possible structure models. Am. Mineral. 96, 513–520 (2011).
Peak, D. & Regier, T. Direct observation of tetrahedrally coordinated Fe(III) in ferrihydrite. Environ. Sci. Technol. 46, 3163–3168 (2012).
Chappell, H. F. et al. Structure of naturally hydrated ferrihydrite revealed through neutron diffraction and first-principles modeling. Phys. Rev. Mater. 1, 036002 (2017).
Juhás, P., Cherba, D. M., Duxbury, P. M., Punch, W. F. & Billinge, S. J. L. Ab initio determination of solid-state nanostructure. Nature 440, 655–658 (2006).
Billinge, S. J. L. & Levin, I. The problem with determining atomic structure at the nanoscale. Science 316, 561–565 (2007).
Goodwin, A. L. Opportunities and challenges in understanding complex functional materials. Nat. Commun. 10, 4461 (2019).
Farrow, C. L. & Billinge, S. J. L. Relationship between the atomic pair distribution function and small-angle scattering: implications for modeling of nanoparticles. Acta Crytallogr. A65, 232–239 (2009).
Masadeh, A. S. et al. Quantitative size-dependent structure and strain determination of CdSe nanoparticles using atomic pair distribution function analysis. Phys. Rev. B 76, 115413 (2007).
Towe, K. M. & Bradley, W. F. Mineralogical constitution of colloidal hydrous ferric oxides. J. Colloid Interf. Sci. 24, 384–392 (1967).
Harrison, P. M., Fischbach, F. A., Hoy, T. G. & Haggis, G. H. Ferric oxyhydroxide core of ferritin. Nature 216, 1188–1190 (1967).
Eggleton, R. A. & Fitzpatrick, R. W. New data and a revised structural model for ferrihydrite. Clay. Clay Miner. 36, 111–124 (1988).
Drits, V. A., Sakharov, B. A., Salyn, A. L. & Manceau, A. Structural model for ferrihydrite. Clay Miner. 28, 185–207 (1993).
Michel, F. M. et al. Ordered ferrimagnetic form of ferrihydrite reveals links among structure, composition, and magnetism. Proc. Natl Acad. Sci. USA 107, 2787–2792 (2010).
Sassi, M. & Rosso, K. M. Roles of hydration and magnetism on the structure of ferrihydrite from first principles. ACS Earth Space Chem. 3, 70–78 (2019).
Manceau, A., Skanthakumar, S. & Soderholm, L. PDF analysis of ferrihydrite: Critical assessment of the under-constrained akdalaite model. Am. Mineral. 99, 102–108 (2014).
Page, K. et al. Direct observation of the structure of gold nanoparticles by total scattering powder neutron diffraction. Chem. Phys. Lett. 393, 385–388 (2004).
Janney, D. E., Cowley, J. M. & Buseck, P. R. Transmission electron microscopy of synthetic 2- and 6-line ferrihydrite. Clay. Clay Miner. 48, 111–119 (2000).
Wang, R. M. et al. Layer resolved structural relaxation at the surface of magnetic FePt icosahedral nanoparticles. Phys. Rev. Lett. 100, 017205 (2008).
Egami, T. & Billinge, S. Underneath the Bragg Peaks, 2 edn. (Permagon, Amsterdam, The Netherlands, 2012).
Tucker, M. G., Keen, D. A., Dove, M. T., Goodwin, A. L. & Hui, Q. RMCProfile: Reverse Monte Carlo for polycrystalline materials. J. Phys.: Condens. Matter 19, 335218 (2007).
Gilbert, B. et al. A disordered nanoparticle model for 6-line ferrihydrite. Am. Mineral. 98, 1465–1476 (2013).
Liu, G. et al. Characterization and surface reactivity of ferrihydrite nanoparticles assembled in ferritin. Langmuir 22, 9313–9321 (2006).
French, R. A. et al. The enigmatic iron oxyhydroxysulfate nanomineral schwertmannite: morphology, structure, and composition. Am. Mineral. 97, 1469–1482 (2012).
Das, B. Theoretical study of small iron-oxyhydroxide clusters and formation of ferrihydrite. J. Phys. Chem. A 122, 652–661 (2018).
McGreevy, R. L. & Pusztai, L. Reverse Monte Carlo simulation: a new technique for the determination of disordered structures. Mol. Simul 1, 359–367 (1988).
Keen, D. A. Refining disordered structural models using reverse Monte Carlo methods: application to vitreous silica. Phase Trans. 61, 109–124 (1997).
Tucker, M. G., Dove, M. T. & Keen, D. A. Application of the reverse Monte Carlo method to crystalline materials. J. Appl. Crystallogr. 34, 630–638 (2001).
Petkov, V. et al. Periodicity and atomic ordering in nanosized particles of crystals. J. Phys. Chem. C 112, 8907–8911 (2008).
Carta, D. et al. Structural and magnetic characterization of synthetic ferrihydrite nanoparticles. Mater. Chem. Phys. 113, 349–355 (2009).
Masina, C. J. et al. Structural and magnetic properties of ferrihydrite nanoparticles. RSC Adv. 5, 39643–39650 (2015).
Paktunc, D., Manceau, A. & Dutrizac, J. Incorporation of Ge in ferrihydrite: Implications for the structure of ferrihydrite. Am. Mineral. 98, 848–858 (2013).
Hiemstra, T. & Van Riemsdijk, W. H. A surface structural model for ferrihydrite I: Sites related to primary charge, molar mass, and mass density. Geochim. Cosmochim. Ac. 73, 4423–4436 (2009).
Hiemstra, T. Surface and mineral structure of ferrihydrite. Geochim. Cosmochim. Ac. 105, 316–325 (2013).
Pinney, N., Kubicki, J. D., Middlemiss, D. S., Grey, C. P. & Morgan, D. Density functional theory study of ferrihydrite and related Fe-oxyhydroxides. Chem. Mater. 21, 5727–5742 (2009).
Brese, N. E. & O’Keeffe, M. Bond-valence parameters for solids. Acta Crystallogr. B47, 192–197 (1991).
Diaz-Lopez, M. et al. Local structure and lithium diffusion pathways in Li4Mn2O5 high capacity cathode probed by total scattering and XANES. Chem. Mater. 30, 3060–3070 (2018).
Cumby, J. & Attfield, J. P. Ellipsoidal analysis of coordination polyhedra. Nat. Commun. 8, 14235 (2017).
Hiemstra, T. & Zhao, W. Reactivity of ferrihydrite and ferritin in relation to surface structure, size, and nanoparticle formation studied for phosphate and arsenate. Environ. Sci.: Nano 3, 1265–1279 (2016).
Dyer, J. A., Trivedi, P., Scrivner, N. C. & Sparks, D. L. Surface complexation modeling of zinc sorption onto ferrihydrite. J. Coll. Int. Sci. 270, 56–65 (2004).
Zhao, J., Huggins, F. E., Feng, Z. & Huffman, G. P. Ferrihydrite: surface structure and its effects on phase transformation. Clay. Clay Miner. 42, 737–746 (1994).
Hiemstra, T. Surface structure controlling nanoparticle behavior: magnetism of ferrihydrite, magnetite and maghemite. Environ. Sci.: Nano 5, 752–764 (2018).
Hiemstra, T. Ferrihydrite interaction with silicate and competing oxyanions: geometry and hydrogen bonding of surface species. Geochim. Cosmochim. Ac. 238, 453–476 (2018).
Cismau, A. C., Levard, C., Michel, F. M. & Brown, G. E. Jr Properties of impurity-bearing ferrihydrite II: Insights into the surface structure and composition of pure, Al- and Si-bearing ferrihydrite from Zn(II) sorption experiments and Zn K-edge X-ray absorption spectroscopy. Geochim. Cosmochim. Ac. 119, 46–60 (2013).
McGreevy, R. L. Reverse Monte Carlo modelling. J. Phys.: Condens. Matter 13, R877–R913 (2001).
Biswas, P., Atta-Fynn, R. & Drabold, D. A. Reverse Monte Carlo modeling of amorphous silicon. Phys. Rev. B 69, 195207 (2004).
Posner, A. S. & Betts, F. Synthetic amorphous calcium phosphate and its relation to bone mineral structure. Accounts Chem. Res. 8, 273–281 (1975).
Celotti, G. et al. Crystallinity in apatites: how can a truly disordered fraction be distinguished from nanosize crystalline domains? J. Mater. Sci.: Mater. Med. 17, 1079–1087 (2006).
Mahamid, J. et al. Mapping amorphous calcium phosphate transformation into crystalline mineral from the cell to the bone in zebrafish fin rays. Proc. Natl Acad. Sci. USA 107, 6316–6321 (2010).
Du, L.-W. et al. Structure of clusters and formation of amorphous calcium phosphate and hydroxyapatite: from the perspective of coordination chemistry. Cryst. Growth Des. 13, 3103–3109 (2013).
Yu, R., Lin, N., Yu, W. & Liu, X. Y. Crystal networks in supramolecular gels: formation kinetics and mesoscopic engineering principles. CrystEngComm 17, 7986–8010 (2015).
Hudait, A. & Molinero, V. Ice crystallization in ultrafine water-salt aerosols: nucleation, ice-solution equilibrium, and internal structure. J. Am. Chem. Soc. 136, 8081–8093 (2014).
Puértolas, B. et al. High-temperature stable gold nanoparticle catalysts for application under severe conditions: the role of TiO2 nanodomains in structure and activity. ACS Catal. 5, 1078–1086 (2015).
Grey, C. P. & Dupré, N. NMR studies of cathode materials for lithium-ion rechargeable batteries. Chem. Rev. 104, 4493–4512 (2004).
Sławiński, W. A. Calculation of pair distribution functions for multiphase systems. J. Appl. Cryst. 51, 919–923 (2018).
Schwertmann, U. & Cornell, R.M. Iron Oxides in the Laboratory: Preparation and Characterization, 1 edn. (Wiley-VCH, Weinheim, Germany, 2000).
Michel, F. M. et al. Similarities in 2- and 6-line ferrihydrite based on pair distribution function analysis of X-ray total scattering data. Chem. Mater. 19, 1489–1496 (2007).
McLain, S.E., Bowron, D.T., Hannon, A.C. & Soper, A.K. GUDRUN, a computer program developed for analysis of neutron diffraction data (ISIS Facility, Rutherford Appleton Laboratory, Chilton).
Soper, A. K. & Barney, E. R. Extracting the pair distribution function (PDF) from white beam x-ray total scattering data. J. Appl. Cryst. 44, 714–726 (2011).
Keen, D. A. A comparison of various commonly used correlation functions for describing total scattering. J. Appl. Cryst. 34, 172–177 (2001).
Acknowledgements
N.P.F. and A.L.G. thank the E.R.C. (Grants 279705 and 788144) and E.P.S.R.C. (EP/G004528/2). F.M.M. and K.K. acknowledge the funding support provided by the National Science Foundation through EAR-1451996 and CAREER-1652237, as well as the Virginia Tech National Center for Earth and Environmental Nanotechnology Infrastructure (NanoEarth, NSF Cooperative Agreement 1542100). S.I. acknowledges support from the U.S. Department of Energy (DOE), the DOE BES Geosciences through DE-FG02-06ER15786. This research used resources of the Advanced Photon Source, a U.S. DOE Office of Science User Facility operated for the DOE Office of Science by Argonne National Laboratory under Contract No. DE-AC02-06CH11357. TEM facilities were made available through Virginia Tech’s Institute for Critical Technology and Applied Science Nanoscale Characterization and Fabrication Laboratory (ICTAS-NCFL). We thank Dr Christoper Winkler (ICTAS-NCFL) for assistance with TEM analysis.
Author information
Authors and Affiliations
Contributions
A.L.G. and F.M.M. conceived the study; F.M.M. and K.K. made the samples and collected the total scattering data and TEM images; N.P.F. and M.F.F. modelled and interpreted the data; S.I. carried out the TEM simulations; N.P.F. and A.L.G. wrote the manuscript, with input from all authors.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Funnell, N.P., Fulford, M.F., Inoué, S. et al. Nanocomposite structure of two-line ferrihydrite powder from total scattering. Commun Chem 3, 22 (2020). https://doi.org/10.1038/s42004-020-0269-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42004-020-0269-2
This article is cited by
-
Determination of interactions of ferrihydrite-humic acid-Pb (II) system
Environmental Science and Pollution Research (2022)
-
Adsorption behavior of phosphate on 2-L ferrihydrite adsorbent predicted by partial charge model under varying pH conditions
Korean Journal of Chemical Engineering (2022)
-
Mixed hierarchical local structure in a disordered metal–organic framework
Nature Communications (2021)
-
Transformation of siderite to goethite by humic acid in the natural environment
Communications Chemistry (2020)
-
Direct identification of reaction sites on ferrihydrite
Communications Chemistry (2020)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.