Abstract
Vibrational sum-frequency generation spectroscopy is a powerful method to study the microscopic structure and dynamics of interfacial systems. Here we demonstrate a simple computational approach to calculate the time-dependent, frequency-resolved vibrational sum-frequency generation spectrum (TD-vSFG) of the air-water interface. Using this approach, we show that at the air-water interface, the transition of water molecules with bonded OH modes to free OH modes occurs at a time scale of \(\sim\)3 ps, whereas water molecules with free OH modes rapidly make a transition to a hydrogen-bonded state within \(\sim\)2 ps. Furthermore, we also elucidate the origin of the observed differential dynamics based on the time-dependent evolution of water molecules in the different local solvent environments.
Similar content being viewed by others
Introduction
The air–water interface is of high significance within chemical, physical, and environmental sciences1,2,3. The structure, dynamics, and chemical reactivity at the air–water interface is known to be significantly different from bulk water4,5,6,7,8,9,10. Conventional spectroscopic methods like infrared (IR) and Raman are not surface-specific and thus cannot be used to study the structure and dynamics directly at the interface. With the advent of surface-specific spectroscopic techniques such as vibrational sum-frequency generation (vSFG) spectroscopy, it has become possible to disseminate the contributions of water molecules at the surface from those of the bulk11,12,13. The vSFG technique involves the irradiation of the system with overlapping IR and visible pulses. In case, the IR frequency is resonating with the vibrational frequency of the molecules at the surface, an enhanced vSFG intensity is observed. Moreover, due to the quantum mechanical selection rules of vSFG spectroscopy, the vSFG intensity vanishes for a centrosymmetric system, thus eliminating the contributions from the molecules in the bulk. Ron Shen and coworkers experimentally demonstrated for the first time the applicability of vSFG spectroscopy to study the air–water interface11,12,13. This technique has been further extended to more complex experimental setups like phase-sensitive vSFG, time-resolved vSFG, two-dimensional vSFG (2D-vSFG) to name just a few14,15,16,17,18,19,20,21,22,23,24,25,26,27,28.
These experiments have been supported by several computational studies of the air–water interface29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50. Therein, the vSFG spectrum is computed by the second-order non-linear susceptibility of the system, which is expressed in the terms of the dipole-polarizability (\(\mu -\alpha\)) time-correlation function. Earlier studies have determined the dipole moment and polarizability using empirical maps29,30,41,42,43,44,45. However, very long simulation runs are required for an accurate determination of the (\(\mu -\alpha\)) time-correlation function. Quite recently, a new approach based on the surface-specific velocity–velocity correlation function (ssVVCF) has been proposed to efficiently compute vSFG spectra, which has enabled the determination of vSFG spectra within a few hundred picoseconds47,51. Like IR and Raman spectroscopy, vSFG is also a time-averaged spectroscopic technique. Therefore, different dynamical processes such as ultrafast chemical reactions, vibrational couplings, spectral diffusion, and chemical exchange on interfaces cannot be studied using vSFG spectroscopy. Accordingly, vSFG has been extended into a two-dimensional spectroscopy similar to 2D-IR spectroscopy52. Yet, the theoretical calculation of 2D-vSFG involves computationally expensive calculations of fourth-order polarizations (\({P}^{4}(t)\)), which in turn relies on fourth-order non-linear response functions based on the dipole moment, polarizability, and frequency of the vibrating oscillator45.
In this paper, we demonstrate a simple computational scheme to determine the time-dependent frequency-resolved vSFG spectrum of the air–water interface. Our computational scheme complements the recently reported experimental time-resolved vSFG/2D-SFG techniques20,21,22,23,24,25,26. In particular, we note that the here presented computational method directly implements a pulse sequence proposed by Bonn and coworkers28. This pulse sequence allows us to incorporate the time-dependence and to obtain time-dependent vSFG spectra. As a result, we can analyze the temporal dynamics of the interfacial water molecules without explicitly calculating the higher-order polarization. We use this approach to show that free and bonded OH modes have different timescales of vibrational spectral diffusion. In addition, we also determine the contributions of water molecules in specific orientations with respect to the surface normal to the above-mentioned phenomenon. Our results also support the existence of structural inhomogeneities at the air–water interface53.
Results
Computational time-dependent vSFG method
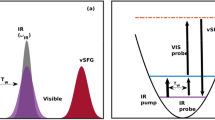
Firstly, we elaborate on the proposed scheme to determine the time-dependent vSFG spectrum of a system. The simplest case of time-dependent spectroscopy is based on the pump-probe pulse sequence as shown in Fig. 1a. In pump-probe spectroscopy, the system is selectively excited based on a broad or narrow width pump pulse followed by the measurement of the signal decay using a probe pulse. Irradiation of the system by the pump pulse leads to the excitation of the system, which gradually reaches an equilibrium state through free induction decay (FID). Further, vSFG experiments involve irradiation of the system by an overlapping IR and visible pulse, which leads to the generation of the vSFG signal as shown in Fig. 1b. Conventional 2D-vSFG spectroscopy permits to study the coherence generated by irradiation of electric fields as a function to time-delay between the applied fields. In our computational scheme, we combine the pulse sequences, as shown in Fig. 1a and b, such that we selectively excite the system using a pump pulse and then determine the vSFG spectrum of the excited molecules. Therefore, the presented approach can also be thought of as the computational implementation of IR-pump vSFG-probe spectroscopy. Mathematically, the vSFG spectrum is given as
where \({\chi }_{{\bf{{abc}}}}^{2}\) is the second-order susceptiblity, whereas \(\alpha\) and \(\mu\) are the polarizbality and dipole moment of the vibrational oscillator. Accordingly, the equation for the calculation of time-dependent vSFG spectrum, as shown in the Fig. 1c, is given by
In the equation mentioned above, we determine the second-order susceptibility of a given vibrational oscillator provided that the oscillator was vibrating at a frequency \(\omega {\prime}\) at time \(t{\prime}\). Further, an explicit time-dependence is generated by continuously varying the value of \({T}_{w}\) as shown in Fig. 1c. Similarly, in the equation mentioned above, \({T}_{w}\) is a parameter. For very large values of \({T}_{w}\ > > \ {t}_{{\mathrm{{corr}}}}\), which is the timescale of vibrational spectral diffusion, Eq. (3) is reduced to conventional time-averaged vSFG. Similarly, for very small values of \({T}_{w} \sim 0\), we obtain the vSFG spectrum within its impulsive limit, where an experimental pump pulse overlaps with the applied IR/Vis pulse. By systematically varying the value of the parameter \({T}_{w}\), we can determine the full time-dependent vSFG spectrum of a given system. In addition, as in real-time pump-probe experiments, we can also vary the value of \(\omega {\prime}\) to any reasonable value and determine the frequency-resolved vSFG of the system. Moreover, the value can be also modified to consider a specific frequency range, such that the small frequency range would correspond to a narrow width pulse excitation, whereas a large frequency range would imply the application of a broadband pump pulse. We note that this scheme requires a priori knowledge of the vibrational frequency of the OH mode. The time-dependent fluctuations in the vibrational frequencies of the OH modes are generally determined using empirical maps29,30,43,44, or a short-time wavelet transform54,55,56. In the present work, we have employed an empirical linear relationship between the hydrogen bond strength and its vibrational frequency, as reported in an earlier work by some of us57, which reads as
The corresponding hydrogen bond strength is obtained from our absolutely localized molecular orbitals based energy decomposition analysis (ALMO-EDA) calculations (see the “Methods” section)58,59. Finally, we have employed the ssVVCF approach to determine the instantaneous fluctuations in the dipole moment and polarisablity, as well as the vSFG spectrum. The \(abc\) components of the vSFG response function is given by
Here, \({r}_{j}^{{\mathrm{{OH}}}}\) and \({\dot{r}}_{j}^{{\mathrm{{OH}}}}\) refers to the intramolecular distance and velocity of a given OH mode, whereas \(Q(\omega )\) is the quantum correction factor60. The latter reads as
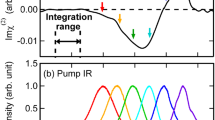
where \(\beta\) is \(1/{k}_{{\mathrm{{B}}}}T\). It is important to emphasize that in the above-mentioned equation, the contributions of several dynamical processes like the intermolecular vibrational energy distribution, ultrafast population relaxation, intermolecular, and intramolecular couplings amongst the water molecules are not incorporated. As a result, in the present work, we specifically investigate the vibrational spectral diffusion of interfacial water molecules using TD-vSFG. Having described a simple scheme to determine the time-dependent vSFG spectrum, we now apply it to determine the vSFG spectrum for different values of \({T}_{w}\) for the bonded and free (non-bonded) OH modes of water molecules. We note that in our present calculations, the intensity of the vSFG peak corresponding to the free OH groups get reduced to zero at \(3756\,{\mathrm{{c{m}}}}^{-1}\). Therefore, we have used this value as a cut-off to classify a particular OH mode as free or hydrogen-bonded OH. In contrast with the experimental vSFG studies, the vSFG peak corresponding to free OH modes is slightly blue-shifted on the frequency axis. However, we note that in our force-field-based simulation study, we have not included the nuclear quantum effects (NQE). The inclusion of NQE not only leads to an overall red-shift of \(\sim\)100 \({\mathrm{{c{m}}}}^{-1}\) within the vibrational frequency distribution, but also an excellent recreation of the non-linear vibrational spectrum51,56. In Fig. 2, we have shown our TD-vSFG spectra for the bonded and free OH groups. The TD-vSFG spectra for the bonded OH modes was calculated for waiting times \({T}_{w}=0,\,0.1,\,0.5,\,1.0,\,2.0,\,2.7\) and \(3.0\) ps, respectively. We note that in the impulsive limit, i.e. for \({T}_{w}=0\) ps, the vSFG spectrum comprises of the negatively peaked region corresponding to the bonded OH modes pointing towards the bulk region of the system. Furthermore, within the initial 100 fs, which is known to be dominated by hindered rotational motion of the water molecules, the vSFG spectrum shows no difference. However, with increasing waiting times, the OH modes are allowed to relax, i.e. break and reform hydrogen bonds. As a result, after 500 fs, the vSFG peak corresponding to the free OH group becomes slowly prominent and by 3 ps the spectrum has nearly attained the time-averaged limit. Accordingly, we infer that the initial non-equilibrium distribution as sampled in the impulsive limit has now averaged to the equilibrium distribution of the bonded and free OH groups. Similarly, we calculated the TD-vSFG spectra of the free OH groups for waiting times \({T}_{w}=0,\ 0.1,\ 0.5,\ 1,\ 2\) and \(4\) ps, respectively. Again, within the impulsive limit, i.e. for \({T}_{w}=0\) ps, the vSFG spectrum exhibits a prominent positive shoulder around 3800 \({\mathrm{{c{m}}}}^{-1}\) corresponding to the free OH groups and that the spectral domain corresponding to the bonded region has negligible intensity. However, within the initial few 100 fs, we observe that the spectral region corresponding to the bonded OH modes starts incrementally gaining intensity. In contrast to the bonded OH modes, free OH modes shows the propensity to rapidly form hydrogen bonds. As a result, these features continue to get more prominent with increasing waiting times as seen for the cases of \({T}_{w}=0.5\) and \(1\) ps, respectively. Moreover, we note that by 2 ps contributions from the bonded OH region have almost saturated, as also seen in the inset of Fig. 2b. Therein, we show the region of the vSFG spectrum corresponding to the bonded OH modes for the waiting times of 2 and 4 ps, respectively. The vSFG spectrum for higher values of \({T}_{w}\) leads to a lowering within the spectral intensity of the free OH modes, though the spectral intensity of the bonded region remains constant. Therefore, we infer that the transition from free to bonded OH modes is complete in <2 ps. Based on the different timescales of transition between the free and bonded OH modes as seen in the TD-vSFG spectrum, we infer the existence of structural inhomogeneities at the air–water interface.
Configurational decomposition of TD-vSFG
The hydrogen bond network at the air–water interface is known to be different from that of the bulk61,62,63. The interface is characterized by the existence of a higher population of free OH modes as compared to the bulk4,7. Based on the orientation of the dipole and OH vectors of water molecules with respect to the surface normal, we have categorized the surface water molecules into five classes as shown in Fig. 3. We note that the dipoles of water molecules corresponding to class III are aligned in-plane with the ai–water interface and are therefore insensitive to the vSFG-probe. The TD-vSFG spectra of the remaining four classes of water molecules are shown in Fig. 4. On that occasion it is important to note that it is generally not possible to disseminate the contributions, as originating from different classes of interfacial water molecules, by means of experimental vSFG measurements. As such, our theoretical TD-vSFG spectra for the different classes of water molecules not only helps to interpret the experimental vSFG spectrum, but also provides an alternative frequency-domain picture of the time-evolution of interfacial water molecules. We interpret the differential dynamics of the free and bonded OH modes based on the frequency-specific contributions of these four classes of water molecules to the vSFG spectra, as well as their timescales of relaxation to the time-averaged vSFG spectrum. In Fig. 4a, TD-vSFG spectra of class I for waiting times \({T}_{w}=0,\ 0.1,\ 0.5,\ 2.0,\ 4.0\) and \(9.0\) ps are shown. The vSFG spectrum within the impulsive limit shows a single sharp peak around 3800 \({\mathrm{{c{m}}}}^{-1}\). However, with increasing waiting time \({T}_{w}\), the broad peak between 3200 and 3800 \({\mathrm{{c{m}}}}^{-1}\) gradually emerges. After ~2 ps the overall features have converged to their time-averaged values, as the negatively valued peak corresponding to \({T}_{w}=2\) ps is only marginally different as compared to the peak for \({T}_{w}=4\) ps. Further, for the very long-time duration, i.e. \({T}_{w}=9\) ps, the obtained spectrum is indistinguishable to the time-averaged vSFG spectrum. Interestingly, the vSFG spectrum for the water molecules of class I are in reasonable agreement with the vSFG spectrum of the free OH modes as shown in Fig. 2b. Evidently, we conclude that the TD-vSFG spectra of the free OH modes and its temporal evolution are mainly governed by the water molecules belonging to class I.
Similarly, the TD-vSFG spectra of water molecules belonging to class II for waiting times \({T}_{w}=0,\ 0.5,\ 2.0,\ 4.0\) and \(9\) ps are shown in Fig. 4b. The water molecules belonging to class II have their dipoles pointed towards the bulk with at least one of the OH modes pointing towards the bulk and the other one aligned at an acute angle with the plane of the air–water interface as shown in Fig. 3. Accordingly, we see that the vSFG spectrum within the impulsive limit has a broad negatively valued peak and a small positively shouldered signal. We find that within the initial 0.5 ps, the positively peaked shoulder around 3800 \({\mathrm{{c{m}}}}^{-1}\) shows a surge in intensity, which gets gradually saturated within nearly 2.0 ps. Based on these findings we infer that the water molecules belonging to this class contribute to the vibrational spectral diffusion of bonded OH modes. The TD-vSFG spectra for water molecules of class IV for waiting times \({T}_{w}=0,\ 0.5,\ 2.5,\ 4.0\) and \(9.0\) ps are shown in Fig. 4c. Water molecules belonging to class IV have both of their OH modes and their dipoles aligned towards the bulk at an acute angle with the surface plane. As a result, the vSFG spectrum for \({T}_{w}=0\) ps is a very broad negatively valued peak over the frequency range of 3400–3900 \({\mathrm{{c{m}}}}^{-1}\). For a short interval after excitation, i.e. within 100 fs, we did not observe any significant change in the overall vSFG spectrum. However, with increasing waiting time \({T}_{w}\) i.e. for 500 fs, the water molecules are undergoing a rearrangement of their hydrogen bond network, which entails that the positively valued peak around 3800 \({\mathrm{{c{m}}}}^{-1}\) starts exhibiting significant vSFG intensity. By 2.5 ps, the free OH peak seems to have reached the time-averaged limit as for the larger waiting times, the overall peak strength remains constant .We note that these molecules have a timescale very similar to the relaxation timescale of bonded OH, as already discussed in Fig. 2a. Accordingly, we infer that the water molecules belonging to class II and IV govern the transition of surface water molecules from the bonded to the free OH state. Lastly, we analyze the time-dependent evolution of water molecules belonging to class V. These water molecules have both of their OH vector and its dipole vector pointed outwards towards the interface, whereas one of the OH modes is free and while the other one is hydrogen bonded. As a result, these water molecules have a vSFG spectrum, which comprises of one broad peak around 3500 \({\mathrm{{c{m}}}}^{-1}\) and one sharp peak around 3800 \({\mathrm{{c{m}}}}^{-1}\) with a positive intensity for both of these peaks. Interestingly, these water molecules have the slowest rate for the transition from their initial state to the equilibrated surface water distribution. As seen in the TD-vSGF spectra for waiting times \({T}_{w}=0,\ 1,\ 4,\ 10\) and \(20\) ps, the vSFG intensity for the broad peak situated around 3500 \({\mathrm{{c{m}}}}^{-1}\) slowly reduces and finally, after 10 ps, makes a transition to the negative region, as in a time-averaged vSFG spectrum. We further note that the transition timescale for this class of water molecules is significantly larger than the spectral diffusion timescale of the surface as well as bulk water molecules. The time-evolution of the vSFG spectrum for the different classes of interfacial water molecules characterizes the timescale at which the a given surface water molecule losses memory on its initial state. However, the convergence of the time-dependent vSFG spectrum to the time-averaged limit requires nearly \({T}_{w}\ > > \ {t}_{{\mathrm{{corr}}}}\), which in general can be safely considered to be a few times the characteristic timescale of the vibrational spectral diffusion. We note that for each class of interfacial water molecules, the vSFG spectra for very long waiting time \({T}_{w}\) are converged and equivalent to the time-averaged vSFG spectrum of the air–water interface. Finally, we conclude that the water molecules belonging to class I contribute to the dynamics of free OH modes, whereas water molecules in class II and IV influence the spectral diffusion of bonded OH modes, while water molecules of V show a very slow vibrational spectral relaxation.
Discussion
To summarize, we have introduced a simple computational approach towards the determination of time-dependent vSFG or IR-pump vSFG-probe spectra of interfacial systems. This method is best described as a computational framework that implements a pump pulse before the conventional vSFG calculation. IR-pump vSFG-probe28 and 2D-vSFG spectroscopy23,24 allows to study the molecular dynamics of chemical species of a non-centrosymmetric system. Nevertheless, a major difference between the two techniques is that 2D-vSFG measures the fourth-order susceptiblity, i.e. \({\chi }^{4}(\omega )\), whereas time-resolved vSFG or IR-pump vSFG-probe spectroscopy collects the \({\chi }^{2}(\omega )\) as a function of applied IR-pump pulse. Another point of difference is that 2D-vSFG spectroscopy involves the generation of a coherent state of vibrational energy levels and that its decay is studied as a function of time-delay. Whereas in IR-pump vSFG-probe spectroscopy, a single IR-pump pulse excites the system and captures the relaxation using a vSFG-probe. Using the IR-pump vSFG-probe method, we have shown the existence of different timescales for the transition between the bonded and free OH modes of the interfacial water molecules. Moreover, we also categorize the surface water molecules into classes based on their preferential orientation at the surface and their contribution towards the vSFG spectrum of the bonded and free OH modes. From application perspective, our approach can be employed to study ultrafast chemical processes such as “on-water” catalysis64,65, chemical exchange and vibrational coupling.
Methods
MD simulations
In the present work, we have performed classical molecular dynamics simulations of 125 water molecules in the canonical NVT ensemble using the flexible q-TIP4P/F water model of Habershon and coworkers at a temperature of 300 K and a density corresponding to a pressure of 1 bar66. The air–water interface was generated by creating a rectangular simulation box of 15.54 Å in the \(x\) and \(y\) directions and 46.60 Å along the \(z\) direction. The system was replicated periodically using the minimum image convention. Short-range interactions were truncated at 8 Å and Ewald summation was employed to determine the long-range electrostatic interactions. Therewith, the system was initially equilibrated using a timestep of 0.1 fs for 20 ps followed by a production run of 500 ps.
ALMO-EDA
Furthermore, ALMO-EDA calculations were performed for all configurations along the trajectory, which were separated by 10 fs. The ALMO-EDA method is a first-principles-based energy decomposition technique that lets you decompose the total interaction energy into different two-body and many-body-based donor–acceptor interactions58,59,67. The total molecular binding energy is given as the sum of the interaction energy of the unrelaxed electron densities on the molecules (\(\Delta {E}_{{\mathrm{{FRZ}}}}\)) and the orbital relaxation energy. The latter is further decomposed into an intramolecular polarization contribution (\(\Delta {E}_{{\mathrm{{POL}}}}\)) that is associated with the deformation of electron clouds on the molecules within their mutual fields, two-body donor–acceptor interactions (\(\Delta {E}_{{\mathrm{{DEL}}}}\)) and a very small amount of higher-order relaxation terms (\(\Delta {E}_{{\mathrm{{HO}}}}\)). Mathematically, the total energy is expressed as the sum of all above-mentioned components as given by
where
These two-body donor–acceptor interactions \(\Delta {E}_{{\mathrm{{D}}}\to {\mathrm{{A}}}}\) are a consequence of the delocalization of electrons from the occupied orbitals of a donor molecule D to the virtual orbitals of an acceptor molecule A. The identification of interfacial water molecules at the air–water system was done using the algorithm for the identification of truly interfacial molecules (ITIM)68,69. The algorithm uses a probe sphere to detect the molecules at the surface. The radius of the probe sphere was set as 2 Å, which has been proven to be a good value for water. A cutoff-based cluster search was also performed using 3.5 Å as a cut-off, which corresponds to the first minimum of the \(O\cdots O\) radial distribution function in liquid water70.
Data availability
The data generated and analyzed during the current study are available from the corresponding author on reasonable request.
References
Ball, P. Life’s Matrix: A Biography of Water (University of California Press, 2001).
Eisenberg, D. S. & Kauzmann, W. The Structure and Properties of Water (Oxford University Press, Oxford, 1969).
Bagchi, B. Water in Biological and Chemical Processes: From Structure and Dynamics to Function (Cambridge University Press, 2013).
Kühne, T. D., Pascal, T. A., Kaxiras, E. & Jung, Y. New insights into the structure of the vapor/water interface from large-scale first-principles simulations. J. Phys. Chem. Lett. 2, 105–113 (2011).
Nagata, Y., Ohto, T., Bonn, M. & Kühne, T. D. Surface tension of ab initio liquid water at the water–air interface. J. Chem. Phys. 144, 204705 (2016).
Karhan, K., Khaliullin, R. Z. & Kühne, T. D. On the role of interfacial hydrogen bonds in "on-water" catalysis. J. Chem. Phys. 141, 22D528 (2014).
Kessler, J. et al. Structure and dynamics of the instantaneous water/vapor interface revisited by path-integral and ab initio molecular dynamics simulations. J. Phys. Chem. B 119, 10079–10086 (2015).
Bakker, H. J. & Skinner, J. L. Vibrational spectroscopy as a probe of structure and dynamics in liquid water. Chem. Rev. 110, 1498–1517 (2010).
Richmond, G. L. Molecular bonding and interactions at aqueous surfaces as probed by vibrational sum frequency spectroscopy. Chem. Rev. 102, 2693–2724 (2002).
Richmond, G. L. Structure and bonding of molecules at aqueous surfaces. Annu. Rev. Phys. Chem. 52, 357–389 (2001).
Du, Q., Superfine, R., Freysz, E. & Shen, Y. R. Vibrational spectroscopy of water at the vapor/water interface. Phys. Rev. Lett. 70, 2313–2316 (1993).
Shen, Y. R. & Ostroverkhov, V. Sum-frequency vibrational spectroscopy on water interfaces: polar orientation of water molecules at interfaces. Chem. Rev. 106, 1140–1154 (2006).
Ostroverkhov, V., Waychunas, G. A. & Shen, Y. R. New information on water interfacial structure revealed by phase-sensitive surface spectroscopy. Phys. Rev. Lett. 94, 046102 (2005).
Verreault, D., Hua, W. & Allen, H. C. From conventional to phase-sensitive vibrational sum frequency generation spectroscopy: probing water organization at aqueous interfaces. J. Phys. Chem. Lett. 20, 3012–3028 (2012).
Hua, W., Verreault, D. & Allen, H. C. Surface prevalence of perchlorate anions at the air/aqueous interface. J. Phys. Chem. Lett. 4, 4231–4236 (2013).
Wei, F. et al. Assembly and relaxation behaviors of phosphatidylethanolamine monolayers investigated by polarization and frequency resolved SFG-VS. Phys. Chem. Chem. Phys. 38, 25114–25122 (2015).
Gonella, G., Lütgebaucks, C., deBeer, A. G. F. & Roke, S. Second harmonic and sum-frequency generation from aqueous interfaces is modulated by interference. J. Phys. Chem. C 120, 9165–9173 (2016).
Roke, S., Kleyn, A. W. & Bonn, M. Time vs. frequency-domain femtosecond surface sum frequency generation. Chem. Phys. Lett. 370, 227–232 (2003).
Samsona, J.-S., Scheua, R., Smolentseva, N., Rick, S. W. & Roke, S. Sum frequency spectroscopy of the hydrophobic nanodroplet/water interface: absence of hydroxyl ion and dangling OH bond signatures. Chem. Phys. Lett. 615, 124–131 (2014).
Backus, E. H. G., Cyran, J. D., Grechko, M., Nagata, Y. & Bonn, M. Time-resolved sum frequency generation spectroscopy: a quantitative comparison between intensity and phase-resolved spectroscopy. J. Phys. Chem. A 122, 2401–2410 (2018).
Cyran, J. D. et al. Molecular hydrophobicity at a macroscopically hydrophilic surface. Proc. Natl Acad. Sci. USA 116, 1520–1525 (2019).
Cyran, J. D., Backus, E. H. G., Nagata, Y. & Bonn, M. Structure from dynamics: vibrational dynamics of interfacial water as a probe of aqueous heterogeneity. J. Phys. Chem. B 122, 3667–3679 (2018).
Bredenbeck, J., Ghosh, A., Nienhuys, H.-K. & Bonn, M. Interface-specific ultrafast two-dimensional vibrational spectroscopy. Acc. Chem. Res. 42, 1332–1342 (2009).
Hsieh, C.-S. et al. Aqueous heterogeneity at the air/water interface revealed by 2D-HD-SFG spectroscopy. Angew. Chem. 53, 8146–8149 (2014).
Hsieh, C.-S. et al. Mechanism of vibrational energy dissipation of free OH groups at the air water interface. Proc. Natl Acad. Sci. USA 110, 18780–18785 (2013).
Zhang, Z., Piatkowski, L., Bakker, H. J. & Bonn, M. Ultrafast vibrational energy transfer at the water/air interface revealed by two-dimensional surface vibrational spectroscopy. Proc. Natl Acad. Sci. USA 3, 888–893 (2011).
Nihonyanagi, S., Yamaguchi, S. & Tahara, T. Ultrafast dynamics at water interfaces studied by vibrational sum frequency generation spectroscopy. Chem. Rev. 16, 10665–10693 (2017).
Bonn, M. et al. Ultrafast energy flow in model biological membranes. New. J. Phys. 9, 390 (2007).
Morita, A. & Hynes, J. T. A theoretical analysis of the sum frequency generation spectrum of the water surface. Chem. Phys. 258, 371–390 (2000).
Morita, A. & Hynes, J. T. A theoretical analysis of the sum frequency generation spectrum of the water surface. II. Time-dependent approach. J. Phys. Chem. B 106, 673–685 (2002).
Ishiyama, T., Imamura, T. & Morita, A. Theoretical studies of structures and vibrational sum frequency generation spectra at aqueous interfaces. Chem. Rev. 114, 8447–8470 (2014).
Morita, A Theory of Sum Frequency Generation Spectroscopy. (Springer: Singapore, 2018).
Wang, L., Ishiyama, T. & Morita, A. Theoretical investigation of c-h vibrational spectroscopy. 1. Modeling of methyl and methylene groups of ethanol with different conformers. J. Phys. Chem. A 121, 6687–6700 (2017).
Raymond, E. A., Tarbuck, T. L. & Richmond, G. L. Isotopic dilution studies of the vapor/water interface as investigated by vibrational sum-frequency spectroscopy. J. Phys. Chem. B 106, 2817–2820 (2002).
Raymond, E. A., Tarbuck, T. L. & Richmond, G. L. Hydrogen bonding interactions at the vapor/water interface as investigated by vibrational sum frequency spectroscopy of HOD/H2O/D2O mixtures and molecular dynamics simulations. J. Phys. Chem. B 107, 546–556 (2003).
Medders, G. R. & Paesani, F. Dissecting the molecular structure of the air/water interface from quantum simulations of the sum-frequency generation spectrum. J. Am. Chem. Soc. 138, 3912–3919 (2016).
Moberg, D. R., Straight, S. C. & Paesani, F. Temperature dependence of the air/water interface revealed by polarization sensitive sum-frequency generation spectroscopy. J. Phys. Chem. B 122, 4356–4365 (2018).
Sun, S. et al. Orientational distribution of free O–H groups of interfacial water is exponential. Phys. Rev. Lett. 121, 246101 (2018).
Sulpizi, M., Salanne, M., Sprik, M. & Gaigeot, M. P. Vibrational sum frequency generation spectroscopy of the water liquid-vapor interface from density functional theory-based molecular dynamics simulations. J. Phys. Chem. Lett. 1, 83–87 (2013).
Khatib, R. & Sulpizi, M. Sum frequency generation spectra from velocity–velocity correlation functions. J. Phys. Chem. Lett. 6, 1310–1314 (2017).
Pieniazek, P. A., Tainter, C. J. & Skinner, J. L. Surface of liquid water: three-body interactions and vibrational sum-frequency spectroscopy. J. Am. Chem. Soc. 133, 10360–10363 (2011).
Li, Y. & Skinner, J. L. IR spectra of water droplets in no man’s land and the location of the liquid–liquid critical point. J. Chem. Phys. 145, 124509 (2016).
Li, Y. & Skinner, J. L. Communication: vibrational sum-frequency spectrum of the air–water interface, revisited. J. Chem. Phys. 145, 031103 (2016).
Pieniazek, P. A., Tainter, C. J. & Skinner, J. L. Interpretation of the water surface vibrational sum-frequency spectrum. J. Chem. Phys. 135, 044701 (2011).
Li, Y., Gruenbaum, S. M. & Skinner, J. L. Slow hydrogen-bond switching dynamics at the water surface revealed by theoretical two-dimensional sum-frequency spectroscopy. Proc. Natl Acad. Sci. USA 110, 1992–1998 (2013).
Skinner, J. L., Pieniazek, P. A. & Gruenbaum, S. M. Vibrational spectroscopy of water at interfaces. Chem. Rev. 45, 93–100 (2011).
Ohto, T., Usui, K., Hasegawa, T., Bonn, M. & Nagata, Y. Toward ab initio molecular dynamics modeling for sum-frequency generation spectra; an efficient algorithm based on surface-specific velocity–velocity correlation function. J. Chem. Phys. 143, 124702 (2015).
Khatib, R. et al. Molecular dynamics simulations of SFG librational modes spectra of water at the water–air interface. J. Phys. Chem. C 120, 18665–18673 (2016).
Nagata, Y. et al. Water bending mode at the water–vapor interface probed by sum-frequency generation spectroscopy: a combined molecular dynamics simulation and experimental study. J. Phys. Chem. Lett. 11, 1872–1877 (2013).
Perakis, F. et al. Vibrational spectroscopy and dynamics of water. Chem. Rev. 116, 7590–7607 (2016).
Kaliannan, N. K. et al. Impact of intermolecular vibrational coupling effects on the sum-frequency generation spectra of the water/air interface. Mol. Phys. https://doi.org/10.1080/00268976.2019.1620358 (2019).
Xiong, W., Laaser, J. E., Mehlenbacher, R. D. & Zanni, M. T. Adding a dimension to the infrared spectra of interfaces using heterodyne detected 2D sum-frequency generation HD 2D SFG spectroscopy. Proc. Natl Acad. Sci. USA 108, 20902–20907 (2011).
VanDerPost, S. T. et al. Strong frequency dependence of vibrational relaxation in bulk and surface water reveals sub-picosecond structural heterogeneity. Nat. Commun. 6, 8384 (2015).
Ojha, D. & Chandra, A. Vibrational echo spectral observables and frequency fluctuations of hydration shell water around a fluoride ion from first principles simulations. J. Chem. Sci. 129, 1069–1080 (2017).
Ojha, D. & Chandra, A. Temperature dependence of the ultrafast vibrational echo spectroscopy of OD modes in liquid water from first principles simulations. Phys. Chem. Chem. Phys. 21, 6485–6498 (2019).
Ojha, D., Henao, A. & Kühne, T. D. Nuclear quantum effects on the vibrational dynamics of liquid water. J. Chem. Phys. 148, 102328 (2018).
Ojha, D., Karhan, K. & Kühne, T. D. On the hydrogen bond strength and vibrational spectroscopy of liquid water. Sci. Rep. 8, 16888 (2018).
Kühne, T. D. & Khaliullin, R. Z. Electronic signature of the instantaneous asymmetry in the first coordination shell of liquid water. Nat. Commun. 4, 1450 (2013).
Khaliullin, R. Z. & Kühne, T. D. Microscopic properties of liquid water from combined ab initio molecular dynamics and energy decomposition studies. Phys. Chem. Chem. Phys. 15, 15746–15766 (2013).
Bader, J. S. & Berne, B. J. Quantum and classical relaxation rates from classical simulations. J. Chem. Phys. 100, 8359–8366 (1994).
Pezzotti, S., Galimberti, D. R. & Gaigeot, M. P. 2D H-bond network as the topmost skin to the air–water interface. J. Phys. Chem. Lett. 8, 3133–3141 (2017).
Pezzotti, S., Serva, A. & Gaigeot, M. P. 2D-HB-Network at the air-water interface: a structural and dynamical characterization by means of ab initio and classical molecular dynamics simulations. J. Chem. Phys. 148, 174701 (2018).
Pezzotti, S., Galimberti, D. R., Shen, Y. R. & Gaigeot, M. P. Structural definition of the BIL and DL: a new universal methodology to rationalize non-linear \({\chi }^{2}\omega\) SFG signals at charged interfaces, including \({\chi }^{2}\omega\) contributions. Phys. Chem. Chem. Phys. 20, 5190–5199 (2018).
Jung, Y. & Marcus, R. A. On the theory of organic catalysis “On Water". J. Am. Chem. Soc. 129, 5492–5502 (2007).
Narayan, S. et al. On Water: unique reactivity of organic compounds in aqueous suspension. Angew. Chem. 117, 3219–3279 (2005).
Habershon, S., Markland, T. E. & Manolopoulos, D. E. Competing quantum effects in the dynamics of a flexible water model. J. Chem. Phys. 131, 24501 (2009).
Elgabarty, H., Khaliullin, R. Z. & Kühne, T. D. Covalency of hydrogen bonds in liquid water can be probed by proton nuclear magnetic resonance experiments. Nat. Commun. 6, 8318 (2015).
Pártay, L. B., Hantal, G., Jedlovszky, P., Vincze, Á. & Horvai, G. A new method for determining the interfacial molecules and characterizing the surface roughness in computer simulations. Application to the liquid–vapor interface of water. J. Comp. Chem. 29, 945–956 (2008).
Sega, M., Hantal, G., Fabian, B. & Jedlovszky, P. Pytim: a python package for the interfacial analysis of molecular simulations. J. Comp. Chem. 39, 2118–2125 (2018).
Kühne, T. D., Krack, M. & Parrinello, M. Static and dynamical properties of liquid water from first principles by a novel Car-Parrinello-like approach. J. Chem. Theory Comput. 5, 235–241 (2009).
Acknowledgements
The authors would like to thank the Gauss Center for Supercomputing (GCS) for providing computing time through the John von Neumann Institute for Computing (NIC) on the GCS share of the supercomputer JURECA at the Jülich Supercomputing Centre (JSC). The generous allocation of computing time on the FPGA-based supercomputer “Noctua” by the Paderborn Center for Parallel Computing (PC\({}^{2}\)) is kindly acknowledged. This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program (grant agreement no. 716142).
Author information
Authors and Affiliations
Contributions
D.O. and T.D.K. conceived the methodology, D.O. and N.K.K. conducted the simulations, D.O. and T.D.K. analyzed the data, D.O. and T.D.K. wrote the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supporting Information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ojha, D., Kaliannan, N.K. & Kühne, T.D. Time-dependent vibrational sum-frequency generation spectroscopy of the air-water interface. Commun Chem 2, 116 (2019). https://doi.org/10.1038/s42004-019-0220-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42004-019-0220-6
This article is cited by
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.