Abstract
Origin of the initial charge separation in optically-excited Ruthenium(II) tris(bidentate) complexes of intrinsic D3 symmetry has remained a disputed issue for decades. Here we measure the femtosecond two-photon absorption (2PA) cross section spectra of [Ru(2,2′-bipyridine)3]2 and [Ru(1,10-phenanthroline)3]2 in a series of solvents with varying polarity and show that for vertical transitions to the lower-energy 1MLCT excited state, the permanent electric dipole moment change is nearly solvent-independent, Δμ = 5.1–6.3 D and 5.3–5.9 D, respectively. Comparison of experimental results with quantum-chemical calculations of complexes in the gas phase, in a polarizable dielectric continuum and in solute-solvent clusters containing up to 18 explicit solvent molecules indicate that the non-vanishing permanent dipole moment change in the nominally double-degenerate E-symmetry state is caused by the solute-solvent interaction twisting the two constituent dipoles out of their original opposite orientation, with average angles matching the experimental two-photon polarization ratio.
Similar content being viewed by others
Introduction
Ruthenium(II) coordination complexes, where the d6 low-spin metal center is bonded to three bidentate ligands, such as 2,2′-bipyridyl (bpy) or 1,10-phenanthroline (phen), have extensive use in photovoltaic cells and other applications that require powerful yet robust electron-transfer photosensitizers1,2,3,4. The utility of Ru(II) complexes arises primarily from their pronounced metal-to-ligand charge-transfer (MLCT) excited states, and their ability to absorb visible light in the singlet manifold and funnel this energy rapidly to the triplet manifold, resulting in a ligand-localized, weakly-bound charge5. However, despite numerous experimental- and theoretical studies indicating that relaxation and solvent dynamics are responsible for separation of charge after photoexcitation in model complexes [Ru(bpy)3]2+ or [Ru(phen)3]2+ 6,7,8,9,10,11,12, no particular mechanism has been identified as responsible for the non-zero permanent dipole moment change in the initial photoexcitation.
According to the underlying D3 symmetry, the permanent electric dipole moment of the free homoleptic complexes necessarily vanishes for all energy levels13,14, as has been confirmed by gas-phase spectroscopic studies15. Even when embedded in a solvent or other condensed dielectric environment, due to the exemplary structural rigidity16,17,18 and fully occupied t2g orbitals on the Ru(II) center19,20, complexes largely retain this D3 symmetry in the ground state and structurally equivalent initially excited state. These inferences are at odds with solvatochromism and electrochromism measurements, which show conclusively that in solution or solid matrix, 1MLCTabsorption involves a substantial change of the permanent electric dipole, Δμ = 5–15 Debye (D)21,22,23,24.
In an effort to resolve this obvious contradiction, we perform two-photon absorption experiments to obtain Δμ for the lowest energy 1MLCT absorption bands in several solvents without assumptions of the local electric field or transition bands involved. The resulting absorption spectra are readily comparable to theoretical calculations, which elucidate, for the first time, a possible mechanism of non-symmetric charge separation in the initial excited state.
Results
Two-photon absorption
Figure 1 shows the femtosecond two-photon absorption (2PA) cross section spectra of deaerated aqueous solutions of [Ru(bpy)3]2+ and [Ru(phen)3]2+ over the laser excitation range, λ2PA = 680–1020 nm, alongside the corresponding one-photon spectrum (λ2PA = 2 ⋅ λ1PA). At shorter-wavelengths, the 2PA spectra display a dominant band that has no 1PA counterpart. In [Ru(bpy)3]2+, this band has maximum cross section, σ2PA = 12 ± 2 GM (1 GM = 10−50 cm4 s photon−1) at λ2PA = 790 nm, with a relatively narrow (~50 nm) symmetric shape. In the case of [Ru(phen)3]2+ the 2PA peak is broader (>100 nm) and notably asymmetric, with increased maximum cross section, σ2PA = 27 ± 4 GM at λ2PA = 740 nm. The 2PA spectra are largely independent of solvent polarity (Supplementary Fig. 1), barring a ~20% variation of the maximum σ2PA (Supplementary Table 1) and few-nm solvent-dependent shifts of the 2PA peak wavelength, discussed in Supplementary Note 1. In [Ru(bpy)3]2+, this shift correlates with solvatochromic shifts reported in the linear absorption spectrum (Supplementary Table 2 and Fig. 2)21, whereas in [Ru(phen)3]2+ this correlation is less obvious (Supplementary Fig. 3), suggesting that the 2PA band in [Ru(bpy)3]2+ is due to a single two-photon allowed transition, while in [Ru(phen)3]2+ more levels may be involved. The notion that the 2PA peak represents a distinct transition from the well-known 1MLCT transitions is corroborated by the measurement of two-photon polarization ratio, Ω = Fcirc/Flin, (Supplementary Fig. 4), which has distinctly different values, Ω ~ 1.15, in the 1MLCT region and, Ω ~ 0.5, in the 2PA band25.
One- and two-photon absorption spectra for ruthenium complexes. One- and two-photon absorption spectra for a [Ru(bpy)3]2+ and b [Ru(phen)3]2+ in H2O. The two-photon absorption cross section (red points) is shown as a function of the illuminating laser wavelength (lower horizontal scale). The corresponding one-photon molar absorption (blue solid lines) is shown at the 1PA wavelength (upper horizontal scale). Inserts show the permanent dipole moment change (black points) evaluated according to Eq. (1) at the long-wavelength side of the 2PA spectrum
Modeling 1MLCT states
At longer-wavelengths, λ2PA > 900 nm, both complexes display a shoulder, σ2PA ~ 6 GM26, with a shape coinciding with the red shoulder of 1MLCT transitions in 1PA spectra. Our next step is to estimate the permanent dipole moment change in the lowest-energy 1MLCT band using the relation between Δμ and two-photon cross section that follows from the two essential states (2ES) model of 2PA27,28:
where σ2PA is the 2PA cross section (in cm4 s), c is the speed of light in vacuum (in cm s−1), h is the Planck constant (in erg s), f = (n2 + 2)/3 is the optical local field correction factor, \(\varepsilon\) is the molar extinction coefficient (in M−1 cm−1), λ1PA is the 1PA transition wavelength (in cm) and NA is the Avogadro constant. The parameter β represents the angle between the Δμ vector and the transition dipole moment vector (μ). While two-level models have been previously applied to ruthenium polypyridyl complexes for the determination of hyperpolarizability29, Eq. (1) is limited to circumstances when only the ground- and final excited state contribute to σ2PA. Linear absorption practically vanishes at wavelengths longer than the 1MLCT transition, and these lower-energy states may be disregarded.
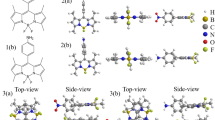
To verify that no higher-energy excited-states act as potential 2PA intermediate states, we pair quadratic response calculations of two-photon transition probabilities for the chromophores in gas-phase using Dalton package30 with calculated one-photon transition energies and oscillator strengths, as well as one-photon transition dipole moment vectors and permanent dipole moment vectors using Gaussian package31 for the chromophores in different environments. Summary of the calculation results for [Ru(bpy)3]2+ are shown in Fig. 2 and Table 1, while results for [Ru(phen)3]2+ are given in the Supplementary Information. In the gas-phase (Fig. 2 first column on the left), one may already note good agreement between calculated and experimental 2PA and 1PA transitions. The one-photon 1MLCT bands are dominated by two double-degenerate E-type energy levels separated by ~0.15 eV. Placing the chromophore in an aqueous dielectric continuum (Fig. 2 center column, also Supplementary Fig. 5 and Supplementary Table 4) lowers energy levels slightly but upholds both the level separation as well as the near-degeneracy of the E states. An explicit H2O-[Ru(bpy)3]2+ cluster (Fig. 2 right column) continues this trend, despite the fact that lower intrinsic symmetry is assumed in the computational method. Even when the number of H2O molecules is increased to 18 or when a different solvent is modeled (Supplementary Tables 5 and 7), the E-level splitting remains small, <140 cm−1, suggesting that the dominant 1MLCT excited states retain their nearly-degenerate character. The robust nature of the E-states is further confirmed from calculations of Natural Transition Orbitals for states 4 and 5 in the gas-phase compared to an explicit H2O-[Ru(bpy)3]2+ cluster-continuum (Supplementary Table 8), which show that the 1MLCT character does not change significantly upon solvation. Notion of E-states remaining close to degenerate is supported by previous infrared, Raman and resonance Raman studies which show that [Ru(bpy)3]2+ only weakly interacts with its host environment17,32.
Energies of the low-lying excited electronic states for [Ru(bpy)3]2+. Dominant 1PA absorbing states are highlighted in cyan, 2PA state is in magenta, compared with aqueous 1PA (blue solid line) and 2PA (red dashed line) spectra. In the gas-phase electronic excitations are rigorously assigned to D3 symmetric states of non-degenerate A1 and A2, or double-degenerate E character
Weak dependence on the environment may be extended to the A1 level, whose transition energy, ~3.1 eV, roughly matches the experimental 2PA band, but whose calculated one-photon oscillator strength practically vanishes. To verify this assignment, we calculate two-photon transition probabilities using Dalton package summarized in Supplementary Table 4. In the case of [Ru(bpy)3]2+, the strongest two-photon transition occurs to a single level identified as the A1 state from gas-phase calculations, while [Ru(phen)3]2+, displays several non-degenerate and double-degenerate excited states that contribute to the 2PA peak. Furthermore, combining the calculated 2PA transition probabilities with Gaussian line shapes using experimentally determined bandwidths of 0.14 and 0.15 eV, for [Ru(bpy)3]2+ and [Ru(phen)3]2+ respectively, gives, σ2PA = 13.4 and 25.3 GM. These theoretical values are in quantitative agreement with our measurements and with previous 2PA estimates for [Ru(bpy)3]2+ by Silverstein et al.32
Success in accurately reproducing the σ2PA of the A1 level lends us confidence for applying the same computational approach to determine which intermediate states contribute most to the observed 2PA peak, and whether a few-state model, such as Eq. (1), can be used to describe 1MLCT excitations in ruthenium complexes. For this, we calculate the two-photon excitation probability while gradually restricting the number of contributing excited states from 20 to the lowest 9 states (Supplementary Note 3 and Table 9). Because excluding higher states leaves the two-photon probability practically unchanged, we may conclude that these contributions are negligible, and observe that the E states located in the 2.5–3.0 eV range (Supplementary Table 10) are the dominant intermediate levels for the 2PA maximum. These results indicate that the 2PA activity of the red shoulder of the 1MLCT band, lying well below the A1 excited state, also has negligible contribution from higher-energy intermediate states, and thus is adequately described by the 2ES model and Eq. (1).
Applying the 2ES model to the observed 2PA polarization ratio, Ω ~ 1.15, results in an average angle between the Δμ and μ dipole vectors of, β ~ 55°, outlined in Supplementary Note 2. This angle is in qualitative agreement with previous estimates22,24 and when used with Eq. (1) yields a dipole moment change, Δμ = 5.4 ± 0.1 D, for aqueous 1MLCTtransitions of both [Ru(bpy)3]2+ and [Ru(phen)3]2+, matching values reported by Kawamoto et al.22 at 452 nm using electroabsorption measurements. Although Kawamoto reports a separate one-photon transition centered at 470 nm with a different Δμ, our results indicate that Δμ remains constant over the broad range, λ1PA = 440−510 nm, shown as black symbols in Fig. 1, indicating a single major transition and further validating the use of the 2ES approximation. Seen in Supplementary Table 1, Δμ is also nearly independent of the solvent polarity, which is very surprising if we consider Δμ to be a result of solvent effects acting on a classical Onsager-type polarizable dipole. However, as the 1MLCT transitions are comprised of two near-degenerate states with nominally antiparallel permanent dipole moments, they may be expected to behave differently than a classical single dipole.
Unlike some nominally centrosymmetric organometallic systems where non-zero permanent dipole moments is caused by spontaneous symmetry-breaking conformations in the ground state33,34,35, the homoleptic Ru(II) complexes are structurally and energetically robust, which precludes conformation-induced lowering of symmetry. Large changes in permanent dipole can also be induced by electronic interaction with non-symmetric environments, provided that the molecular polarizability of the chromophore is different in the ground- and excited state27. Indeed, in a solute-solvent cluster, both chromophores show a non-vanishing permanent ground state dipole moment, as seen in Supplementary Tables 5 and 7. To evaluate what effect induced dipoles have on the 1MLCT excitations, we calculate the permanent dipole moment change for E states in different environments. In the gas-phase (Table 1), the transition dipoles are oriented, α = 90°, with respect to each other (Fig. 3) and have identical absolute values, μ = 1.8 D, which sum to the total absolute transition dipole of 2.5 D. Changes in the permanent dipoles have equal absolute values, Δμ = 2.1 D, but are pointing, as expected, in opposite directions, θ = 180°, such that their total vanishes. In the aqueous continuum, the calculations reveal only minimal deviations from the above picture: the orientations of all vectors remain the same, while the absolute values vary slightly, leading to an increased summary transition dipole moment, 3.3 D, but marginally non-vanishing change in permanent dipole, ~0.9 D. Inserting this total Δμ value into Eq. (1), results in an estimate, σ2PA = 0.2 GM, i.e. much lower than observations in the 1MLCT region. The situation changes, however, when the same calculation is performed with a single water molecule positioned near the [Ru(bpy)3]2+, forming a chromophore-solvent cluster, surrounded by aqueous continuum. While the properties of the transition dipoles remain essentially unchanged, the total absolute permanent dipole change increases dramatically. Most importantly, the relative orientation of the permanent dipole vectors is no longer antiparallel, and their sum no longer cancels. This is shown in the rightmost panel of Fig. 3, where the angle between the individual dipole changes is about θ = 120°. The corresponding estimated 2PA cross section, σ2PA = 3.4 GM, and the angle between summary dipole moments, β = 116° = 64°, are both comparable to experiment. While this estimated cross section is still about a factor of two lower than the observed value, it represents only a single snapshot of possible solvation structures. Models with increased number of explicit water molecules, as well as cluster-continuum models of DMSO and acetonitrile solvents demonstrate that larger cross sections are clearly possible (Supplementary Table 5). These calculations demonstrate that while the magnitude of the individual permanent dipole moments are affected by solvent, it is primarily the relative orientations of the nearly-degenerate pair that allows for large Δμ. Even the addition of toluene, which is too nonpolar to dissolve ruthenium complexes, produced a significant calculated change in the permanent dipole. Thus, the relative orientation of the two permanent dipoles is much more sensitive than a traditional single Onsager-type dipole model and is saturated easily in any solvent, resulting in the constant Δμ observed.
Discussion
The large change in permanent dipole moment observed for [Ru(bpy)3]2+ has been used historically as proof of localization in the initially excited 1MLCT state. However, due to the high symmetry of the complex, it is not certain whether such localization is best described as on a single ligand or delocalized over two equivalent ligands. A report by Tavernelli et al.20 investigated the 1MLCT states of [Ru(bpy)3]2+ in H2O using a LR-TDDFT-QM/MM approach, and found that while excited state orbitals reside on individual bpy ligands, 1MLCT excitation leads to a mixed state of two such orbitals, indicating that the excited electron is initially delocalized over two ligands. Localization was found to rapidly progress to a single ligand coinciding with reorientation of a nearby water molecule; however, electronic absorption measurements, which are essentially instantaneous, should not be affected by even this rapid relaxation. In this regard, the earliest moments described by Tavernelli agree well with our observations of Natural Transition Orbitals of states 4 and 5 in aqueous solution (Supplementary Fig. 8), which each show substantial orbital density on a single ligand. The corresponding changes in permanent dipole moments of these excitations lie oriented at, θ = 120°, as expected for excitations residing on two separate ligands. Notably, a similar excited state depiction was reached by Moret et al.12 who observed that an electron in the triplet MLCT state resides on two ligands throughout most of its lifetime. Even though the triplet state is likely to have a distorted structure compared to the ground and Franck-Condon state, it is becoming apparent that a two-ligand localization model seems to be prominent in localized descriptions of excited [Ru(bpy)3]2+ complexes.
In conclusion, we report the femtosecond two-photon absorption spectra of two nominally D3 symmetric Ruthenium(II) coordination complexes, [Ru(bpy)3]2+ and [Ru(phen)3]2+ in a series of solvents with varying polarity, over the wavelength region corresponding to 1MLCT excitations. We used quantitative agreement between the quantum-chemical calculations of two-photon cross sections and energies for A1 excited state with the experimental spectra to show vanishing contribution from higher-energy intermediate states, which, in turn, allowed us to apply 2ES model of 2PA to determine changes in permanent dipole moment in the lower-energy 1MLCT shoulder. Because in solvent environment the D3 symmetry is most likely only slightly distorted, and because of enhanced polarizability of the nearly double degenerate excited states, we hypothesize that the non-zero summary dipole moment in the vertically-excited state may be a result of solute-solvent electronic interactions that alter the orientation of the permanent dipoles in way that they no longer mutually cancel. These observations are corroborated by the fact that the dipoles are nearly constant in solvents of different polarity and that the two-photon polarization ratio indicates large angle between the permanent- and transition dipoles. Our findings offer, for the first time, a plausible explanation for a long-standing issue of the origin of the initial charge separation and 1MLCT localization in Ru(II) complexes, and may thus contribute to design of materials for various applications from improved photovoltaic cells to solar-powered water splitting systems. In a broader perspective, our findings could lead to a new way of manipulating electrostatic interactions on the molecular level by controlling properties of near-degenerate energy levels.
Methods
Linear spectroscopic measurements
The metal complexes [Ru(bpy)3](PF6)2 (97%, anhydrous) and [Ru(phen)3](Cl)2⋅nH2O (98%), as well as the reference dyes rhodamine 6G (99%), fluorescein (95%) and coumarin 153 (99%) were purchased from Sigma Aldrich and used without purification. The solvents benzonitrile, dichloromethane, dimethyl sulfoxide, ethylene glycol, methanol, and nitrobenzene were purchased from Sigma Aldrich (≥99.9%, HPLC grade) and acetonitrile from Rathburn Chemicals (≥99.9%, HPLC grade), while distilled water was produced in-house. All ruthenium samples used for 2PA were deaerated by bubbling dry nitrogen gas for 10 min and sealed in 1 mm cuvettes (21/Q/1 Starna Cells). UV-visible absorption measurements were recorded for each sample over the 200−800 nm spectral range using a spectrophotometer (UV 3600PLUS, Shimadzu Corp.) with 2 nm band pass slit widths. Ruthenium samples generally had an absorbance of ~1 OD at the 1MLCT maximum.
Two-photon absorption measurements
Two-photon-excited fluorescence (2PEF) measurements were performed using a 1500 Hz pulsed laser (Pharos-SP, Light Conversion) followed by an optical parametric amplifier (Orpheus-HE, Light Conversion) and second harmonic generator (Lyra-SH, Light Conversion) which allowed for wavelength tunability from 315−2600 nm. Pulses had a Gaussian spectral shape (FWHM: 8 ± 2 nm) corresponding to a pulse width of <150 fs. The maximum pulse energy was 0.134 mJ, which could be attenuated by 2 orders of magnitude using a motorized neutral-density variable filter (NDC-100C-2, Thorlabs). A pair of lenses acted as an inverted telescope, such that the beam had a nearly constant ~0.24−1.2 mm FWHM diameter across the sample. A beam splitter was placed before the sample to reflect ~8% of the excitation pulse energy to a pyroelectric reference detector (P4-45, Molectron Detector Inc.). In the case of polarization ratio measurements, a vertical polarizer followed by a λ/4-wave plate (AQWP05M-980, Thorlabs) positioned at either 0° (linear polarization) or 45° (circular polarization) were placed directly in front of the sample, while a rotatable second polarizer after the sample was used to confirm the excitation pulse polarization.
Emission was collected from the sample at 90° and focused into the entrance slit (4 mm slit width) of a grating spectrometer (LOMO MDR-12) set to 610 nm center wavelength with 12 nm bandwidth prior to detection by a photomultiplier tube (9124B, ET Enterprises electron tubes). To further suppress scattered laser light from the sample, a bandpass filter (600 ± 50 nm) was positioned at the spectrometer entrance. Raw voltage signals from the photomultiplier and reference detector were recorded on an oscilloscope (DSOS404A, Keysight) which was synced to the laser repetition rate. Detector pulses were integrated and background subtracted using a LabVIEW program (LabVIEW 2016, National Instruments), which also controlled the variable neutral-density filter and laser wavelength. The 2PEF of each sample (S) was recorded back-to-back with a reference (R) of either Rhodamine 6G, Fluorescein or Coumarin 153. These references have well-characterized 2PA and cross sections (σ)36, allowing for the calculation of sample 2PA cross section via:
where F is the 2PEF signal, C is the concentration, and f is the one-photon excited fluorescence (1PEF) signal of either the sample or reference solutions, performed with identical detection conditions as for 2PEF described above. Absolute cross section measurements were performed at, λ2PA = 800 nm, with corresponding 1PEF exciting the same sample and reference at, λ1PA = 400 nm. Spectral profiles over the range, λ2PA = 680–1040 nm, were scaled to match the absolute cross section at 800 nm.
Computational methods
Full geometry optimization of [Ru(bpy)3]2+ and [Ru(phen)3]2+ at the B3LYP37,38/DGDZVP39,40 level was carried out in the gas-phase and in common solvents including water and DMSO. For the former compound, calculations in acetonitrile and toluene were carried out as well. Vibrational normal mode analysis was used to assess the nature of the stationary points and the lack of imaginary eigenvalues in harmonic vibrational spectra for each optimized structure was confirmed. Solvent effects were included in the framework of the polarized continuum models C-PCM41 and IEF-PCM41,42 as implemented in Gaussian09 package31, for water and organic solvents, respectively. The internally stored values for dielectric constants of respective solvents were used. While unconstrained optimization in the gas phase retained the characteristic D3 symmetry of both complexes, polarized continuum approaches reduced the symmetry to C2 during optimization.
To study the influence of specific solvent interactions on calculated spectral properties, several models of Ru-complex solvent clusters with explicit solvent molecule(s) in the first solvation shell were constructed. The remaining (bulk) solvent effect in these systems was accounted for with the continuum model. Examples of some of the studied solvent cluster-continuum structures of [Ru(bpy)3]2+ are presented in Supplementary Table 6.
According to QM/MM and molecular dynamics simulations by Moret et al.43 the first aqueous solvation shell of [Ru(bpy)3]2+ cation consists of ~15 water molecules within a spherical radius of 6.5 Å, defined as a distance between the ruthenium and oxygen atoms. In the present work, similar tennis ball like patterns of 17−19 explicit water molecules around [Ru(bpy)3]2+ and [Ru(phen)3]2+ were constructed. The optimized Ru-O distances varied within a 5.1–5.8 Å range.
The cluster configurations with 1–2 solvent molecules, initially positioned at the nodal points of solvent shell represented by 17 water cluster model, were carefully selected to provide maximum impact on multiple ligands simultaneously. Three local minima were observed for [Ru(bpy)3]2+ complexes with two explicit water molecules. The differences in water positions designated as A/B/C are rather insignificant, referring to either translation of entire solvent molecule in vicinity of nodal point or the change of the relative orientation of the hydrogen atoms in respect to nearby ligand(s).
It has been shown previously that appropriately tuned range-separated hybrid functional CAM-B3LYP44 with mild coulombic attenuation provides reasonable transition energies in both linear response (LR) and quadratic response (QR) applications, matching and in many cases exceeding the performance of B3LYP functional45. Therefore, the modified CAM-B3LYP was used for all TD-DFT46 calculations. The careful tuning of CAM-B3LYP was carried out to reproduce the experimental 1PA and 2PA absorption maxima wavelengths for [Ru(bpy)3]2+ as exactly as possible. The optimized functional parameters α = 0.03, β = 0.97, and μ = 0.175 were used in the present study.
To characterize the changes in electron density related to particular electronic transitions the dominant natural transition orbitals (NTOs) were calculated and visualized using Gaussian09 and GaussView software packages, shown in Supplementary Table 8.
Computed one-photon transitions
One-photon absorption (1PA) gas-phase and continuum solvation calculations were performed at the mCAM-B3LYP (α = 0.03, β = 0.97, μ = 0.175)//TZP-DKH47,48/6–311G(d,p)49 level using second-order Douglas-Kroll-Hess scalar-relativistic Hamiltonian (DKH-2)50,51,52,53 approach with corresponding TZP basis set for Ru and the 6-311G(d,p) basis set for H, C, and N atoms level using Gaussian09 (G09) package. The default non-equilibrium PCM solvation model was used for inclusion of solvent effects. The excited-state permanent dipoles were calculated from relaxed excited-state electron densities in equilibrium PCM representation using Z-vector method as implemented in G09. While the permanent electric dipole moment (Δμ) calculations are not compatible with DKH-2 approach, the non-relativistic calculations were carried out at mCAM-B3LYP/DGDZVP level. To test the performance of the latter method we compared the calculated gas-phase values of Δμ from G09 mCAM-B3LYP/DGDZVP calculation with the results of similar gas-phase calculations at mCAM-B3LYP (α = 0.03, β = 0.97, μ = 0.175)//TZP-DKH/6–311G(d,p) level using Dalton2015 software suite30. From the data presented in Supplementary Table 3 it is evident that while there are significant differences in transition energies, the values of Δμ predicted by two theoretical methods are rather close. Therefore, we assume that mCAM-B3LYP/DGDZVP method is reasonably suited for Δμ predictions in G09 polarized continuum calculations as well.
Computed two-photon transitions
The gas-phase two-photon absorption (2PA) transition probabilities were obtained by computing the single residue of quadratic response function (QR-DFT) using Dalton2015 package at the mCAM-B3LYP (α = 0.03, β = 0.97, μ = 0.175)//TZP-DKH/6–311G(d,p) level of theory. Due to the software limitations, the symmetry of Ru-complexes was restricted to C2. The transition probabilities were converted to macroscopic cross sections σ2PA via broadening with Gaussian line shapes, which had FWHM of 0.14 eV for [Ru(bpy)3]2+ and 0.15 eV for [Ru(phen)3]2+, determined from decompositions of experimental 1PA and 2PA spectra. Similarly, double residue quadratic response calculations were carried out to estimate transition dipole moments between excited states in [Ru(bpy)3]2+, shown in Supplementary Table 10.
Data availability
All one- and two-photon spectra that support the findings in this study are publicly available online at https://kbfi.ee/mpa. All other data are available from the corresponding author upon reasonable request.
References
Yin, J.-F., Velayudham, M., Bhattacharya, D., Lin, H.-C. & Lu, K.-L. Structure optimization of ruthenium photosensitizers for efficient dye-sensitized solar cells—a goal toward a “bright” future. Coord. Chem. Rev. 256, 3008–3035 (2012).
Stoll, T. et al. Photo-induced redox catalysis for proton reduction to hydrogen with homogeneous molecular systems using rhodium-based catalysts. Coord. Chem. Rev. 304-305, 20–37 (2015).
Huang, H. et al. Highly charged ruthenium(II) polypyridyl complexes as lysosome-localized photosensitizers for two-photon photodynamic therapy. Angew. Chem. Int. Ed. 54, 14049–14052 (2015).
Lemercier, G., Four, M. & Chevreux, S. Two-photon absorption properties of 1,10-phenanthroline-based Ru(II) complexes and related functionalized nanoparticles for potential application in two-photon excitation photodynamic therapy and optical power limiting. Coord. Chem. Rev. 368, 1–12 (2018).
Dongare, P., Myron, B. D., Wang, L., Thompson, D. W. & Meyer, T. J. [Ru(bpy)3]2+* revisited. Is it localized or delocalized? How does it decay? Coord. Chem. Rev. 345, 86–107 (2017).
Stark, C. W. et al. Interligand electron transfer in heteroleptic ruthenium(II) complexes occurs on multiple time scales. J. Phys. Chem. A 119, 4813–4824 (2015).
Henry, W. et al. The early picosecond photophysics of Ru(II) polypyridyl complexes: A tale of two timescales. J. Phys. Chem. A 112, 4537–4544 (2008).
Chergui, M. Ultrafast photophysics of transition metal complexes. Acc. Chem. Res. 48, 801–808 (2015).
Sun, Q., Dereka, B., Vauthey, E., Lawson Daku, L. M. & Hauser, A. Ultrafast transient IR spectroscopy and DFT calculations of ruthenium(II) polypyridyl complexes. Chem. Sci. 8, 223–230 (2017).
Yeh, A. T., Shank, C. V. & McCusker, J. K. Ultrafast electron localization dynamics following photo-induced charge transfer. Science 289, 935–938 (2000).
Webb, M. A., Knorr, F. J. & McHale, J. L. Resonance Raman spectrum of [Ru(bipyridine)3]2+ in water, acetonitrile and their deuterated derivatives: the possible role of solvent in excited-state charge localization. J. Raman Spectrosc. 32, 481–485 (2001).
Moret, M.-E., Tavernelli, I., Chergui, M. & Rothlisberger, U. Electron localization dynamics in the triplet excited state of [Ru(bpy)3]2+ in aqueous solution. Chem. Eur. J. 16, 5889–5894 (2010).
Heully, J.-L., Alary, F. & Boggio-Pasqua, M. Spin-orbit effects on the photophysical properties of \({\mathrm{Ru}}\left( {{\mathrm{bpy}}} \right)_3^{2 + }\). J. Chem. Phys. 131, 184308 (2009).
Alcover-Fortuny, G., Wu, J., Caballol, R. & de Graaf, C. Quantum chemical study of the interligand electron transfer in Ru polypyridyl complexes. J. Phys. Chem. A 122, 1114–1123 (2018).
Xu, S., Smith, J. E. T. & Weber, J. M. The electronic spectrum of cryogenic ruthenium-tris-bipyridine dications in vacuo. J. Chem. Phys. 145, 024304 (2016).
Breu, J., Domel, H. & Norrby, P.-O. Racemic compound formation versus conglomerate formation with [M(bpy)3](PF6)2 (M=Ni, Zn, Ru); Lattice energy minimisations and implications for structure prediction. Eur. J. Inorg. Chem. 2000, 2409–2419 (2000).
Poizat, O. & Sourisseau, C. Infrared, Raman and resonance Raman studies of the \({\mathrm{Ru}}\left( {{\mathrm{2,2}}\prime {\mathrm{ - bpy}}} \right)_3^{2 + }\) cation in its chloride crystal and as an intercalate in the layered MnPS3 compound. J. Phys. Chem. 88, 3007–3014 (1984).
Hoff, D. A., Silva, R. & Rego, L. G. C. Subpicosecond dynamics of metal-to-ligand charge-transfer excited states in solvated [Ru(bpy)3]2+ Complexes. J. Phys. Chem. C. 115, 15617–15626 (2011).
England, J., Scarborough, C. C., Weyhermüller, T., Sproules, S. & Wieghardt, K. Electronic structures of the electron transfer series [M(bpy)3]n, [M(tpy)3]n, and [Fe(tbpy)3]n (M = Fe, Ru; n = 3+, 2+, 1+, 0, 1–): A Mössbauer spectroscopic and DFT study. Eur. J. Inorg. Chem. 2012, 4605–4621 (2012).
Tavernelli, I., Curchod, B. F. & Rothlisberger, U. Nonadiabatic molecular dynamics with solvent effects: A LR-TDDFT QM/MM study of ruthenium(II) tris(bipyridine) in water. Chem. Phys. 391, 101–109 (2011).
Kober, E., Sullivan, B. & Meyer, T. Solvent dependence of metal-to-ligand charge-transfer transitions - Evidence for initial electron localization in MLCT excited-states of 2,2’-bipyridine complexes of ruthenium(II) and osmium(II). Inorg. Chem. 23, 2098–2104 (1984).
Kawamoto, K. et al. Disentangling the 1MLCT transition of [Ru(bpy)3]2+ by Stark absorption spectroscopy. J. Photochem. Photobiol. A-Chem. 353, 618–624 (2018).
Oh, D. H. & Boxer, S. G. Stark effect spectra of \({\mathrm{Ru}}\left( {{\mathrm{diimine}}} \right)_3^{2 + }\) complexes. J. Am. Chem. Soc. 111, 1130–1131 (1989).
Karki, L. & Hupp, J. T. Electroabsorption studies of metal-to-ligand charge transfer in \({\mathrm{Ru}}\left( {{\mathrm{phenanthroline}}} \right)_3^{2 + }\): Evidence for intrinsic charge localization in the initially formed excited state. Inorg. Chem. 36, 3318–3321 (1997).
Callis, P. R. in Topics in Fluorescence Spectroscopy: Volume 5: Nonlinear and Two-Photon-Induced Fluorescence (ed. Lakowicz, J. R.) 1–42 (Springer US, Boston, MA, 2002).
Castellano, F. N., Malak, H., Gryczynski, I. & Lakowicz, J. R. Creation of metal-to-ligand charge transfer excited states with two-photon excitation. Inorg. Chem. 36, 5548–5551 (1997).
Rebane, A. et al. Two-photon voltmeter for measuring a molecular electric field. Angew. Chem. Int. Ed. 54, 7582–7586 (2015).
Rebane, A. et al. Quantitative prediction of two-photon absorption cross section based on linear spectroscopic properties. J. Phys. Chem. C. 112, 7997–8004 (2008).
Vance, F. W. & Hupp, J. T. Probing the symmetry of the nonlinear optic chromophore Ru(trans-4,4′-diethylaminostyryl-2,2′-bipyridine)3 2+ : Insight from polarized hyper-Rayleigh scattering and electroabsorption (Stark) spectroscopy. J. Am. Chem. Soc. 121, 4047–4053 (1999).
Aidas, K. et al. The Dalton quantum chemistry program system: The Dalton program. WIREs Comput. Mol. Sci. 4, 269–284 (2014).
Frisch, M. et al. Gaussian 09, Revision B.01. Gaussian 09, Revision B.01; (Gaussian, Inc.: Wallingford, CT, 2009).
Silverstein, D. W., Milojevich, C. B., Camden, J. P. & Jensen, L. Investigation of linear and nonlinear raman scattering for isotopologues of \({\mathrm{Ru}}\left( {{\mathrm{bpy}}} \right)_3^{2 + }\). J. Phys. Chem. C. 117, 20855–20866 (2013).
Nguyen, K. A., Day, P. N. & Pachter, R. One- and two-photon spectra of platinum acetylide chromophores: a TDDFT study. J. Phys. Chem. A 113, 13943–13952 (2009).
Rebane, A. et al. Symmetry breaking in platinum acetylide chromophores studied by femtosecond two-photon absorption spectroscopy. J. Phys. Chem. A 118, 3749–3759 (2014).
Mikhaylov, A. et al. Spontaneous symmetry breaking facilitates metal-to-ligand charge transfer: A quantitative two-photon absorption study of ferrocene-phenyleneethynylene oligomers. J. Phys. Chem. Lett. 9, 1893–1899 (2018).
de Reguardati, S., Pahapill, J., Mikhailov, A., Stepanenko, Y. & Rebane, A. High-accuracy reference standards for two-photon absorption in the 680−1050 nm wavelength range. Opt. Express 24, 9053–9066 (2016).
Becke, A. D. Density–functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 98, 5648–5652 (1993).
Lee, C., Yang, W. & Parr, R. G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 37, 785–789 (1988).
Godbout, N., Salahub, D. R., Andzelm, J. & Wimmer, E. Optimization of Gaussian-type basis sets for local spin density functional calculations. Part I. boron through neon, optimization technique and validation. Can. J. Chem. 70, 560–571 (1992).
Sosa, C. et al. A local density functional study of the structure and vibrational frequencies of molecular transition-metal compounds. J. Phys. Chem. 96, 6630–6636 (1992).
Cancès, E., Mennucci, B. & Tomasi, J. A new integral equation formalism for the polarizable continuum model: Theoretical background and applications to isotropic and anisotropic dielectrics. J. Chem. Phys. 107, 3032–3041 (1997).
Mennucci, B., Cancès, E. & Tomasi, J. Evaluation of solvent effects in isotropic and anisotropic dielectrics and in ionic solutions with a unified integral equation method: Theoretical bases, computational implementation, and numerical applications. J. Phys. Chem. B 101, 10506–10517 (1997).
Moret, M.-E., Tavernelli, I. & Rothlisberger, U. Combined QM/MM and classical molecular dynamics study of [Ru(bpy)3]2+ in water. J. Phys. Chem. B 113, 7737–7744 (2009).
Yanai, T., Tew, D. P. & Handy, N. C. A new hybrid exchange–correlation functional using the Coulomb-attenuating method (CAM-B3LYP). Chem. Phys. Lett. 393, 51–57 (2004).
Uudsemaa, M., Trummal, A., de Reguardati, S., Callis, P. & Rebane, A. TD-DFT calculations of one- and two-photon absorption in coumarin C153 and prodan: attuning theory to experiment. Phys. Chem. Chem. Phys. 19, 28824–28833 (2017).
Runge, E. & Gross, E. K. U. Density-functional theory for time-dependent systems. Phys. Rev. Lett. 52, 997–1000 (1984).
Jorge, F. E., Canal Neto, A., Camiletti, G. G. & Machado, S. F. Contracted Gaussian basis sets for Douglas–Kroll–Hess calculations: estimating scalar relativistic effects of some atomic and molecular properties. J. Chem. Phys. 130, 064108 (2009).
Campos, C. & Jorge, F. Triple zeta quality basis sets for atoms Rb through Xe: Application in CCSD(T) atomic and molecular property calculations. Mol. Phys. 111, 167–173 (2013).
Frisch, M. J., Pople, J. A. & Binkley, J. S. Self–consistent molecular orbital methods 25. Supplementary functions for Gaussian basis sets. J. Chem. Phys. 80, 3265–3269 (1984).
Douglas, M. & Kroll, N. M. Quantum electrodynamical corrections to the fine structure of helium. Ann. Phys. 82, 89–155 (1974).
Hess, B. A. Applicability of the no-pair equation with free-particle projection operators to atomic and molecular structure calculations. Phys. Rev. A 32, 756–763 (1985).
Hess, B. A. Relativistic electronic-structure calculations employing a two-component no-pair formalism with external-field projection operators. Phys. Rev. A 33, 3742–3748 (1986).
Jansen, G. & Hess, B. A. Revision of the Douglas-Kroll transformation. Phys. Rev. A 39, 6016–6017 (1989).
Acknowledgements
This work was supported by the Ministry of Education and Research, Republic of Estonia (grants MOBJD69, IUT23-9, and IUT23-7) and European Regional Development Fund (project TK134). A.R. acknowledges support from AFOSR grant FA9550-16-1-0189.
Author information
Authors and Affiliations
Contributions
C.S. and A.R. conceived the two-photon absorption experiment. C.S., M.R., M.S. and K.P. performed experimental measurements, with J.P. and A.R. supervising the work. C.S. and A.R. analyzed the experimental results. A.T. and M.U. performed and analyzed computational models. All authors reviewed the paper.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Stark, C.W., Trummal, A., Uudsemaa, M. et al. Solute-solvent electronic interaction is responsible for initial charge separation in ruthenium complexes [Ru(bpy)3]2+ and [Ru(phen)3]2+. Commun Chem 2, 108 (2019). https://doi.org/10.1038/s42004-019-0213-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42004-019-0213-5
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.