Abstract
The conduction and valence band edges (EC and EV) of a material relative to the water redox potential levels are critical factors governing photocatalytic water splitting activity. Here we discuss the large discrepancy in the experimentally measured EC and EV of various transition metal oxides (TMOs) in vacuum and in an aqueous solution. We speculate that the discrepancy stems from the different degree of electron transfer across the surface due to the different environment at the surface of the TMOs in vacuum and water. Accurately modeling the electronic structure at TMO/water interfaces is a significant challenge, however. Using first-principles density functional theory calculations on rutile titanium dioxide and cobalt monoxide model systems, here we identify the optimal approaches to accurately predict the band edge positions in vacuum and water. We then validate the optimized schemes on other TMOs, demonstrating good agreement with experimental measurements in both vacuum and water.
Similar content being viewed by others
Introduction
Valence and conduction band edge alignments relative to the water redox potential levels are critical properties of photocatalytic materials for water splitting, primarily determining the feasibility of the hydrogen and oxygen evolution reactions (HER and OER, respectively) from water splitting under illumination. HER (OER) is known to occur when the EC (EV) is more negative (positive) than the hydrogen evolution potential level, H+/H2 (oxygen evolution potential level, H2O/O2).
Historically, first-principles density functional theory (DFT) studies have been used to predict the environment-dependent band edge positions of various surfaces by investigating the electronic structure of slabs with surfaces in contact with a vacuum layer. This idea is based on the assumption that the band edge positions of a material stay the same before and after contact with the electrolyte, i.e., that the band edges measured in vacuum can represent those in an operating environment. However, this assumption is not always a good one, as the band edges before and after contact with an electrolyte have been shown to be different in many systems1,2,3,4,5,6,7,8,9,10,11,12,13,14.
Recently, a polarization continuum model (PCM)15, an implicit solvation model has been expected to be a technique for understanding solute/solvent interfaces, economically calculating surface energy, reaction barrier, and molecular solvation energies comparable to experimental values. However, the band edge positions calculated in the implicit solvation show little difference from those calculated in vacuum16,17. Furthermore, they have not correctly predicted the band edges measured from flat band potential in water. We suggest that the implicit solvation calculation method fails to reproduce the experimental band edge alignments in an aqueous solution because the model is unable to describe the electron exchange occurring at the realistic surface/water interface.
Wu et al.18 pioneered an explicit solvation method to assess the band edge positions at a material/aqueous solution interface, which successfully reproduces values close to experimental measurements for various materials. Cheng et al.19 and Kharche et al.20 also performed ab initio molecular dynamics (MD) simulations with explicit water to explore the band edge positions in an aqueous solution. However, these materials are primarily non-TMOs, and also paramagnetic, and thus do not have complex magnetic configurations and Hubbard U correction parameters (Ueff). Understanding the effects of explicit solvation on both paramagnetic and magnetic metal oxides is crucial, however, as many magnetic metal oxides including CoO, Co3O4, FeO, Fe2O3, NiO, MnO and Cr2O3, as well as non-magnetic metal oxides such as TiO2, WO3, and others, are potential catalysts for photocatalytic OER, HER, and other aqueous chemical reactions. Currently, there is no general approach for determining which materials require explicit solvation at the first-principles level in order to accurately capture their electronic structure and catalytic properties. Furthermore, a systematic understanding of the roles played by spin polarization and Ueff on the results of calculations of oxides in explicit solvent have yet to be developed.
In this study, we begin to address these issues by using DFT calculations to investigate the band edge positions of two test materials of interest for photocatalytic water splitting, antiferromagnetic CoO and paramagnetic rutile TiO2, in vacuum and in contact with explicit water. Based on the results, we demonstrate that the inclusion of explicit water at the DFT level of accuracy is necessary in order to accurately predict the band edges in an aqueous solution, as well as to fundamentally understand the material/water interface. Moreover, we suggest an optimal explicit solvation calculation approach by focusing on the effect of spin polarization and Ueff values on the band edges of the CoO and rutile TiO2 model systems. Finally, we verify this approach by extending to various other oxide materials of interest for photocatalytic water splitting, including magnetic FeO, NiO, and MnO, as well as non-magnetic anatase TiO2, WO3, and V2O5. In addition to providing a fundamental understanding of these oxide/water interfaces, we expect that the proposed optimized approach will enable more rapid and accurate prediction of the electronic structure and properties of oxide/water interfaces, as well as guide future investigations of other semiconductor/electrolyte systems.
Results
Experimental E C and E V in vacuum and in water
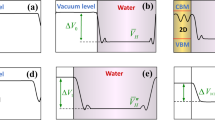
The band edge positions relative to the water redox potential levels are significantly influenced by the material1,2,21, crystal structure22,23, surface characteristics16,24,25,26, and operating environment of a photocatalyst27,28. In the process of the electrochemical potential equilibration between the photocatalyst and the adjacent medium (or electrolyte), electrons transfer across the surface/medium interface. The amount and the direction of the electron transfer is determined by the relative electrochemical potentials of the photocatalyst and the medium, which can be significantly affected by the different surface environments. As a result of the electron transfer process, a depletion layer forms at the surface of the photocatalyst, over which band bending occurs, determining the band edge alignment with the water redox potential levels. The band edge alignments at the surface/medium interface directly influence light absorption, the energies of photogenerated charge carriers, and, eventually, the thermodynamics and kinetics of catalytic reactions at the surfaces. Therefore, in order to properly comprehend the photocatalytic water splitting reactions in an operating environment, it is necessary to understand the aqueous environment-dependent band edge positions of materials, which are different from those in vacuum state as shown in Fig. 1.
Experimentally measured band edge positions of TMOs in vacuum and in water. Experimental EC and EV relative to H+/H2 of CoO, FeO, NiO, MnO, CuO, Cu2O, Co3O4, Cr2O3, TiO2, Ta2O5, WO3, V2O5 measured with ultraviolet photoelectron spectroscopy (UPS) in vacuum state (red filled and open circles)3,4,5,6,7 and measured from flat band potential in an aqueous solution (black filled and open circles)1,2,8,9,10,11,12,13,14 at pH = 1. ‘EC-vacuum’ and ‘EV-vacuum’ in legend indicate the EC and EV measured in vacuum, and ‘EC-water’, ‘EV-water’ denote the EC and EV measured in an aqueous solution. ‘R’ and ‘A’ in parenthesis denote ‘rutile’ and ‘anatase’. The horizontal dashed lines are hydrogen and oxygen evolution potential levels, H+/H2 and H2O/O2
Figure 1 shows the experimental EC and EV of various transition metal oxides (TMOs) as measured in vacuum with UPS (red lines) and in an aqueous solution with flat band potential measurements (black lines). Even at a glance, there is a large change in the band edge positions measured in vacuum and in an aqueous solution for most of these TMOs. This means the surface states as well as their band edges in vacuum are no longer the same as the states in contact with electrolyte, suggesting a significant environmental effect on the band edge positions. Furthermore, examination of Fig. 1 shows that the band edge positions in an aqueous solution relative to the positions in vacuum reflect the intrinsic semiconducting nature of the material. Specifically, n-type semiconducting (or insulating) materials such as Ta2O5, TiO2, WO3 and V2O5, show an upward shift in the band edges in water compared to those in vacuum, which is in agreement with the upward band bending at n-type semiconductor/water interface27,29,30,31. In contrast, CoO, FeO, NiO, MnO, CuO, Cu2O, Co3O4 and Cr2O3, known as p-type semiconductors, exhibit a downward shift in water compared to vacuum, as a result of electron transfer in the process of electrochemical potential equilibrium between the semiconductor and water30,31. These two findings in Fig. 1 imply that the band edge positions (energy states) calculated with a vacuum layer are similar to the bulk state without much perturbation from vacuum17, while the band edges measured in an aqueous solution diverge from the bulk state because of a significant perturbation from water30. Accordingly, the band edges measured in vacuum cannot capture the electron transfer and band bending phenomena occurring at the real material/water interface. To reproduce the band edges in an aqueous environment, we suggest that the solvation effects of water need to be explicitly included in the DFT calculations.
Importance of U eff in band edge prediction
The 3d TMOs show a variety of electronic and magnetic properties, ranging from insulating to metallic or even superconducting behavior, and from Pauli paramagnetism to ferromagnetism or antiferromagnetism. Additionally, these materials can often be tuned from one electronic or magnetic phase to another by varying the temperature, pressure, or doping. These various properties are mainly influenced by 3d orbitals forming d-bands with characteristic effective masses and different strengths of on-site Coulomb interactions. Since these 3d orbitals influence the band gap and the band edge positions32,33, the 3d TMOs also have manifold optical properties or photocatalytic activities depending on the d-band characteristics. In practice, to interpret the diverse phenomena in the 3d TMOs, a Hubbard model34,35 in which the electrons localized on the d-orbitals are subject to an additional on-site Coulomb interaction term (U) and site exchange term (J), has been used. Thus, a Hubbard correction parameter (Ueff = U ─ J) is particularly important to correctly understand the photocatalytic behaviors of various TMOs. Therefore, we herein find an optimal Ueff value (and magnetic configuration) to estimate the EC of TMOs comparable to the experimentally measured values both in vacuum and in an aqueous solution.
E C in vacuum
The band edge positions of a material at the surface/water interface are determined by how the band edges deviate from those in the bulk phase. The deviation comes from the difference between the electrochemical potentials of electrons (i.e., the Fermi level, EF) in the solid and the water. Thus, we examine the EF (referenced to the absolute vacuum level) with respect to the Ueff for TMOs to determine the effect of Ueff on the band edge positions in vacuum.
Figure 2a shows the computed EF relative to vacuum level of TiO2(110) slabs with various surface oxygen stoichiometries and with different Ueff values. The EF is essentially independent of Ueff for a given surface, but varies significantly with the surface stoichiometry. This implies that EC and EV do not change significantly with variation of Ueff, but are sensitive to the surface stoichiometry. As shown in Fig. 2b, there is indeed little change in either EV or EC of rutile TiO2(110) slabs in vacuum as a function of Ueff, while EV, EC, and EF move upward in the energy diagram as the oxygen vacancy concentration is increased. This trend is consistent with excess electrons on the surface due to the oxygen vacancies, which decreases the electron affinity and decreases the work function of the TiO2(110) slab. The decrease in work function with the removal of surface oxygen has also been demonstrated with experimental UPS measurements of rutile TiO236.
Fermi levels and band edges of rutile TiO2(110) in vacuum. a Fermi level (EF) relative to absolute vacuum (E = 0) of O-terminated rutile TiO2(110) with stoichiometric (Stoich), half coverage of O vacancies (Red-0.5), and full coverage of O vacancies (Red-1) surfaces computed with different values of Ueff (no U, 2.5 and 4 eV). b−d EC and EV for the different surfaces computed with different values of Ueff. In panels b─d, EV and EC are relative to absolute vacuum. EC = EV + \(E_{\mathrm{g}}^{{\mathrm{expt}}}\) indicates the value of EC determined by adding the experimental band gap to the computed EV. The experimental value of EC measured for rutile TiO2 in vacuum4 is indicated by the horizontal green line
The calculated band edge positions of the fully oxygen-terminated TiO2(110) slabs are similar to the experimental values when EC is estimated by adding the experimental band gap (\(E_{\mathrm{g}}^{{\mathrm{expt}}}\)) to the DFT-calculated EV (blue triangles in Fig. 2b). Considering that rutile TiO2 prepared at ambient temperature and atmospheric pressure is known to have O-terminated (110) surfaces37,38, the experimentally measured band edge positions of TiO2 seem to arise from the stoichiometric surface. We note that using EC = EV +\(E_{\mathrm{g}}^{{\mathrm{expt}}}\) to determine the EC is reasonable for TiO2 in vacuum because DFT-calculated EV of TiO2 is very similar to the EV obtained from DFT calculations in vacuum19, GW calculations39, QM/MM embedding technique40 as well as the experimental value measured in vacuum with UPS41,42. Therefore, even though DFT calculations fail to precisely predict the EC (or Eg) unlike GW calculations, DFT calculations seem to provide a reasonable EV in vacuum conditions. In addition, Fig. 2b–d show that, for a given surface, the value of EC = EV + \(E_{\mathrm{g}}^{{\mathrm{expt}}}\) is relatively insensitive to the change of the Ueff (Supplementary Fig. 1) while the DFT+U computed value of EC changes more significantly with Ueff, resulting in different Eg (Supplementary Note 1 and Supplementary Fig. 1). The figure also shows that the EV and EC of the stoichiometric TiO2 surface in vacuum are consistent with experimental measurements even when determined from DFT calculations without a Hubbard U correction. Thus, applying Ueff is not necessary for accurately predicting EC of rutile TiO2 in vacuum.
Rock salt CoO is frequently observed to have a magnetic phase in bulk structure43 and nanoparticles44. Also, in most DFT studies of the thermodynamic stability of CoO, the AFM-II phase is more stable than any other magnetic configuration for both bulk and surface structures. However, considering its Néel temperature of 291 K43, we expect that paramagnetic as well as antiferromagnetic phases can be formed for CoO at room temperature. Therefore, we consider a non-magnetic phase as well as an AFM-II phase for the prediction of the band edge positions of CoO in vacuum.
As observed in TiO2(110) slabs in vacuum (Fig. 2a), the EF changes with surface chemistry, but for a given surface, neither spin polarization nor the value of Ueff leads to significant changes, except for the large fluctuation for CoO(100) (Fig. 3a). Therefore, one might expect that the band edge positions are also similar regardless of the spin polarization and Ueff. However, Fig. 3b and c show that the EV and EC change significantly with the use of spin polarization +Ueff, shifting upward more than 2 eV. This significant change suggests that the effects of spin polarization and Ueff on band edge positions in vacuum are in fact very large.
Fermi levels and band edges of various CoO surfaces in vacuum. a Fermi energy levels (EF) relative to absolute vacuum (E = 0) of Co/CoO(111), H*-CoO(111), CoO(100), OH*-CoO(111) and bare CoO(111) slabs computed using DFT with and without spin polarization and/or Ueff = 4.1 eV. b EC and EV computed without spin polarization and without Ueff. c EC and EV computed with the AFM-II phase and Ueff = 4.1 eV. In panels b, c, EV and EC are relative to absolute vacuum. EC = EV + \(E_{\mathrm{g}}^{{\mathrm{expt}}}\) is the EC determined by adding the experimental band gap to the computed EV. The experimental value of EC measured for CoO in vacuum4 is indicated by the horizontal green line
The band edge positions estimated with spin polarization +Ueff (Fig. 3c) have similar values of EC to those estimated by adding the experimental band gap to the computed EV, EC = EV + \(E_{\mathrm{g}}^{{\mathrm{expt}}}\). This is because the DFT-calculated Eg of all CoO surfaces with AFM−II+Ueff = 4.1 eV (2 ─ 2.6 eV) is comparable to the experimental value (2.4 ─ 2.6 eV)8,9.
Among the various surfaces in Fig. 3c, the CoO(100) slab exhibits the EV and EC similar to those measured experimentally. Based on the experimental and theoretical evidence that the CoO(100) facet thermodynamically tends to exist in high vacuum state of ~ 10−10 Torr (~1.315−13 atm, ∆µO = ~ 0.5)17 in EC and EV of CoO were measured via UPS4, we suggest that the EV and EC of CoO in vacuum come from the CoO(100) surface with an AFM-II phase. Also, considering that CoO tends to be cleaved with an exposed (100) plane45, CoO(100) is considered as the most probable surface configuration for CoO.
E C vs. H+/H2 in water
To predict the band edge positions of the CoO and TiO2 surfaces in an aqueous solution, we use an approach similar to the three-step method introduced in ref. 18, which is shown schematically in supplementary Fig. 2. The approach determines the position of the conduction band edge of a material relative to the water reduction potential level, i.e., EC − E(H+/H2), based on the computed energy differences between (1) the conduction band edge and the average Hartree potential of the bulk semiconductor (\(E_{\mathrm{C}}^{{\mathrm{SC}}} - H^{{\mathrm{SC}}}\)); (2) the H+/H2 level and the average Hartree potential of bulk liquid water (\(A^{{\mathrm{H}}_2{\mathrm{O}}} - H^{\left. {{\mathrm{H}}_2{\mathrm{O}}} \right)}\));17,18 and (3) the average Hartree potential in the semiconductor and water regions of the semiconductor-water interface (\(H^{{\mathrm{int}},\;{\mathrm{SC}}} - H^{{\mathrm{int}},{\mathrm{H}}_2{\mathrm{O}}}\)). The values for the first and third steps can potentially be affected by spin polarization and/or Ueff values since the materials contain 3d transition metals. In the following subsections, we discuss the details of the calculations for each step for both CoO and TiO2.
E C ─ H value
Spin polarization and Ueff significantly affect the value of the energy difference between the EC and the average Hartree potential of bulk CoO, \(E_{\mathrm{C}}^{{\mathrm{CoO}}} - H^{{\mathrm{CoO}}}\), as shown in Fig. 4a, changing by almost 4 eV in going from the case with no spin polarization and no Ueff to the case of AFM-II and Ueff = 6 eV. This large change could distort the value of EC vs. H+/H2 at the end of the three-step calculation. Nevertheless, if the value of \(H^{{\mathrm{int}},\;{\mathrm{CoO}}} - H^{{\mathrm{int}},{\mathrm{H}}_2{\mathrm{O}}}\), the potential drop at the CoO/water interface (the value of third step), also changes by the same amount as \(E_{\mathrm{C}}^{{\mathrm{CoO}}} - H^{{\mathrm{CoO}}}\), then EC vs. H+/H2 determined by the relative values of the three steps would be similar, independent of the spin polarization and/or Ueff value. However, this is not the case for CoO and TiO2 as discussed in Section ‘Potential drop at the interface’.
EC-H value of bulk CoO and rutile TiO2. a \(E_{\mathrm{C}}^{{\mathrm{CoO}}} - H^{{\mathrm{CoO}}}\) value (the first step value in the three-step approach18) of bulk CoO with and without spin polarization and various Ueff values. b \(E_{\mathrm{C}}^{{\mathrm{TiO}}_2} - H^{{\mathrm{TiO}}_2}\) of bulk rutile TiO2 with respect to Ueff. Unit of Ueff is eV
As we observed in CoO, the \(E_{\mathrm{C}}^{{\mathrm{TiO}}_2} - H^{{\mathrm{TiO}}_2}\) increases in bulk rutile TiO2, with increasing Ueff (Fig. 4b). With increasing Ueff from 0 to 12 eV, the \(E_{\mathrm{C}}^{{\mathrm{TiO}}_2} - H^{{\mathrm{TiO}}_2}\) increases by ~ 0.9 eV. This increase can potentially distort the EC vs. H+/H2 obtained at the end of the three-step calculation.
Potential drop at the interface
Figure 5b shows plots of the average Hartree potential in the CoO(100) slab/water supercell as a function of distance along the z-axis (Fig. 5a), showing the potential drop at the interface (the value of the third step) with various conditions of spin polarization and/or Ueff values. Only the plot of the Hartree potential computed with no spin polarization +no Ueff (Fig. 5c) shows an ideal stair-like Hartree potential change between the CoO surface and water regions along the distance as observed in ref. 18, while the plots with other conditions diverge from the ideal plot, which implies that there is a huge effect of spin polarization +Ueff on the EC vs. H+/H2 estimated from the three-step calculation. The deviation from the ideal potential change is considered to come from the electric field (or artificial dipole) inside the slab/water supercell generated by the applied spin polarization +Ueff, as explained in Supplementary Fig. 3. With the aspect distorted from the ideal plot, it is difficult to calculate the accurate potential drop at the surface/water interface because two distinct macro-averaged potential levels for CoO slab and water regions are difficult to obtain.
Effects of spin polarization and Ueff on potential drop at CoO(100)/water interface. a Snapshot of the atomic distribution in CoO(100)/water interface supercell. Blue, red, and white circles denote Co, O, and H atoms, respectively. Planar-averaged (denoted ‘(R)’) and its macro-averaged (denoted ‘(A)’) Hartree potentials of the CoO(100)/water interface computed for the structure shown in panel a, along z-axis b with or without spin polarization and/or various Ueff values, c without spin polarization +no Ueff correction, d with AFM-II +no Ueff, e with AFM-II +Ueff = 3 eV. Dotted lines in panels b–e indicate macro-averaged Hartree potentials of the plot calculated with no spin polarization +no Ueff. For comparison, the plot of no spin polarization +no Ueff (no spin−no U, black line) is superimposed in panels d and e. In case of high Ueff values, the amount of distortion is too large to superimpose in panel b. Left of the vertical dotted lines in panels b–e is CoO(100) slab, right is water in CoO/water supercells
However, as Fig. 5b shows, the distortion from the ideal potential drop plot mainly occurs in the water region, considering that the electrostatic potential largely changes by the spin polarization +Ueff in the water rather than in the slab (Supplementary Note 2). The different amount of change is regarded to be from the effect of spin polarization and/or Ueff, intentionally applied to the water region (Supplementary Fig. 3c), different from the adjacent CoO slab which needs the spin polarization and Ueff correction. Also, a close look at the narrow region of the plots close to the interface (Fig. 5c-e), gives us important information; the magnitude of the macro-averaged potential drop at the CoO surface/water interface is similar (\(H^{{\mathrm{int}},{\mathrm{CoO}}} - H^{{\mathrm{int}},{\mathrm{H}}_2{\mathrm{O}}}\) in Fig. 5c-e) or does not change significantly, even though the plots incline by the spin polarization and/or Ueff. This implies that if stair-like Hartree potential-distance plots could be obtained from the calculations with AFM-II and/or Ueff values, i.e., without distortion coming from the applied spin polarization +Ueff correction, the plots may be similar to the ideal potential drop (Fig. 5c). That means again the ideal potential drop at the slab/water interface can be found without consideration of spin polarization and Ueff even for the AFM-II CoO phase. Hence, the EC vs. H+/H2 estimated from the three-step method is expected to be solely affected by the \(E_{\mathrm{C}}^{{\mathrm{CoO}}} - H^{{\mathrm{CoO}}}\), with the ideal potential drop at the interface (Fig. 5c).
As observed at the CoO(100)/water interface, the TiO2(110)/water interface also deviates from the ideal Hartree potential drop plot (obtained with no Hubbard U correction) with the application of Ueff as shown in Fig. 6. The deviation is smaller than at the CoO(100)/water interface. As for CoO(100)/water interface, we also expect that the ideal plot of Hartree potential-distance as well as the \(H^{{\mathrm{int}},{\mathrm{TiO}}_2} - H^{{\mathrm{int}},{\mathrm{H}}_2{\mathrm{O}}}\) value for third step can be calculated without the Ueff. Therefore, Ueff is not needed to obtain the potential drop at the semiconductor/water interface in the explicit solvation calculations for paramagnetic rutile TiO2.
E C vs. H+/H2
Figure 7 shows EC vs. H+/H2 of bulk CoO and CoO surfaces calculated using the three-step approach with various conditions of spin polarization and/or Ueff values, by constraining the potential drop at the interface to the ideal value (Fig. 5c). As can be seen in Fig. 7, the EC vs. H+/H2 is very different depending on spin polarization and/or Ueff values, which shows that the explicit solvation calculation for a magnetic phase is very notorious for the prediction of its band edge positions. Except for the no spin polarization +no Ueff calculation (‘no spin−no U’ in Fig. 5), the estimated EC vs. H+/H2 are far from the realistic range; the bulk CoO calculated with no spin polarization +no Ueff, shows EC vs. H+/H2 comparable to the experimental values of bulk CoO8,9 and CoO micropowders9. In addition, OH*-CoO(111) surface releases EC vs. H+/H2 similar to that of CoO nanoparticles in experiments9. As demonstrated in the previous study17, the presence of the OH*-CoO(111) facet on the CoO nanoparticles is the origin of the upward shifted EC in CoO nanoparticles compared to the bulk CoO.
EC vs. H+/H2 of bulk and CoO surfaces predicted with various explicit solvation conditions. Conduction band edge position (EC) relative to the water reduction potential (H+/H2) of bulk CoO, Co/CoO(111), H*-CoO(111), CoO(100), OH*-CoO(111) and CoO(111) surfaces estimated with three-step method, with fixed value (ideal value) of the potential drop at the CoO/water interface. The water contact with bulk CoO is done by cleaving the relaxed bulk structure perpendicular to (001) plane45. Yellow and orange horizontal lines are the ECs of CoO nanoparticle9 and bulk CoO (or micropowder9) obtained with flat band potential measurements at pH = 7. Unit of U in legend is eV
Considering that Co atoms in the CoO surface in contact with water have been shown experimentally46 and theoretically17 to lose their magnetic moments, it is reasonable to carry out the explicit solvation calculation on the CoO/water interfaces without consideration of spin polarization. The loss of magnetic moment of Co atoms in the CoO surface is regarded to stem from the mixed spin states induced by the charge transfer between the CoO surface and water47. In addition, even though Ueff was applied to the Co atoms in the explicit solvation calculation, the interaction of water with the CoO surface significantly broadens the DOS of the Co 3d orbitals17. This directly suggests that the 3d orbitals are not entirely localized in contact with water, reducing the d-band splitting17,48. The electron delocalization occurs because metal t2g levels of Co atom overlap with the p orbitals of the water, enabling strong orbital mixing, according to previous experimental49 and DFT50 works.
Accordingly, an explicit solvation calculation with no spin polarization +no Ueff is sufficient to capture the realistic CoO/water interfacial structure, the charge transfer between the CoO and water, band bending aspect, and the band edge alignment to water redox potentials, as we demonstrated in this study.
Figure 8 shows EC vs. H+/H2 of bulk TiO2 and TiO2(110) surfaces with various surface oxygen stoichiometry, calculated from the three-step approach. As done for CoO in Fig. 7, we fixed the potential drop at the interface to the ideal value obtained from no Ueff calculation. The bulk TiO2 has the lowest band edge position, while it increases gradually from stoichiometric to half- and full-coverage surface oxygen vacancy TiO2(110) surfaces in sequence. This makes sense because when a neutral oxygen leaves the lattice, excess electrons remain, making the surface negatively charged. This negatively charged surface readily grants the excess electrons to the adjacent water due to the electrochemical potential difference between the surface and water, increasing the degree of upward band bending at the TiO2 (n-type) surface. Accordingly, the EC vs. H+/H2 shifts upwards as the surface becomes more reduced. This trend is in agreement with the change in EC in vacuum (Fig. 2).
EC vs. H+/H2 of bulk and TiO2(110) surfaces predicted with various explicit solvation conditions. Conduction band edge positions (EC) relative to the water reduction potential (H+/H2) of cleaved bulk rutile TiO2 and rutile TiO2(110) surface with full surface oxygen ((110)-stoi), half surface oxygen vacancy ((110)-red-0.5), full surface oxygen vacancy ((110)-red-1) and variation of Ueff (no U, 2.5 and 4 eV) calculated from three-step calculation. For comparison, the experimental value of the EC vs. H+/H2 of rutile TiO2 measured from flat band potential in an aqueous solution of pH = 18 is superimposed in the figure (horizontal orange line). Unit of U in legend is eV
Importantly, the calculation with no Hubbard U correction provides EC vs. H+/H2 of rutile TiO2 closest to the experimental measurement. Therefore, as with CoO, Ueff is not required to evaluate the band edge position of paramagnetic TiO2 in an aqueous solution.
Table 1 summarizes the values of EC and EV relative to the H+/H2 level for rutile TiO2 and CoO model systems calculated with vacuum reference and with the explicit solvation method, together with their experimentally measured values. For simplicity, among DFT-calculated EC and EV of various surfaces under the various conditions that are considered in this study, only conditions showing band edges closest to the experimental values are summarized in the table.
For both rutile TiO2 and CoO, the EC in vacuum can be accurately predicted by adding the experimental band gap to the DFT-computed value of EV relative to the absolute vacuum level (EC = EV + \(E_{\mathrm{g}}^{{\mathrm{expt}}}\)) rather than taking the direct DFT result for EC. This is because the DFT-calculated values of EV for both TiO2 and CoO are accurate comparable to experimental values. Since the calculated EV of rutile TiO2 (110) barely changes with variation of Ueff value (Supplementary Fig. 1), the EC estimated from EV + \(E_{\mathrm{g}}^{{\mathrm{expt}}}\) also does not vary much. Therefore, the Hubbard U correction is unnecessary for the accurate prediction of EC for rutile TiO2, although the Hubbard U correction improves the accuracy of the calculated band gap (Supplementary Fig. 1). However, for CoO, the calculated EC and EV of CoO in vacuum exhibit values closest to the experiment only when the DFT calculation is conducted on CoO(100) surface with spin polarization (AFM-II) +Ueff (Fig. 3). Therefore, EC and EV of TMOs in vacuum can be precisely estimated with the combination of appropriate surface orientation, magnetic ordering configuration, and strength of the on-site Coulomb interaction (Ueff). The optimal conditions are different depending on materials.
However, the EC and EV of bulk rutile TiO2 and CoO model systems in an aqueous solution are in best agreement with experimental measurements when compute without a Hubbard U correction and without spin polarization as can be seen in Table 1. This means that the explicit calculation of the surface/water interface without spin polarization and without Hubbard U correction can capture the realistic electron transfer as well as the band alignment phenomena at the interface of the TiO2 (or CoO)/water without distortion. Therefore, we can expect economical explicit solvation calculation compared to other expensive explicit calculation methods, but accurate prediction of band edge positions comparable to the experiment.
Unlike the vacuum referenced calculation of EC, the EC vs. H+/H2 of rutile TiO2 and CoO model systems in an aqueous solution can be directly assessed from the three-step approach with the explicit water contact. The high accuracy of the EC estimated from the three-step approach with the explicit water contact was also observed from other explicit solvation calculations19,51. This is possible because the explicit solvation involves the real electron transfer across the semiconducting material/water interface, which directly releases EC of the material relative to H+/H2 of water18. Instead, EV can be computed by EV = EC - \(E_{\mathrm{g}}^{{\mathrm{expt}}}\) under the assumption that the EC estimated from water contact calculation is relatively accurate. The EC and EV values predicted with this relationship are closer to the experimental values (regardless of the accuracy of the DFT-computed band gap size), because the main charge transfer is due to fast electron transfer from the polar water molecules to the conduction band of the oxide52,53 regardless of band gap and electron affinity53.
The above optimized conditions for the prediction of band edge positions in vacuum and in an aqueous solution are further validated on FeO, NiO, MnO, anatase TiO2, WO3 and V2O5 as shown in Fig. 9. In all cases, the calculated ECs vs. H+/H2 are comparatively in good agreement with the experimental measurements, except for the vacuum reference calculation of V2O5 and WO3 (not shown in Fig. 9). We expect this discrepancy stems from the inaccurate DFT-estimated EV or from the misunderstanding of the stable surface configurations in the vacuum state. Most importantly, we confirm here again 1) band edges in vacuum are different from those in an aqueous solution both in the experimental measurement and computational study; 2) with optimal conditions with Hubbard U correction or magnetic ordering, which predicts the accurate EV with a vacuum layer, DFT calculations can be used to reproduce the real experimental band edge positions in vacuum regardless of the accuracy of band gap. In most cases, the optimal conditions can be found from the parameters that describe the experimental band gap of bulk phase of a material (Supplementary Fig. 4); 3) the explicit solvation calculations without consideration of on-site Coulomb interaction+ spin polarization can accurately determine the realistic band edges of TMOs in an aqueous solution.
Validation of the optimal parameters for the EC vs. H+/H2 in water. Conduction band edge (EC) positions of CoO, FeO, NiO, MnO, rutile TiO2, anatase TiO2, WO3, V2O5 experimentally measured (open symbol) and calculated with DFT (filled symbol) in vacuum (blue) and in an aqueous solution (red). The band edges of FeO, NiO, MnO, WO3, V2O5 in vacuum are calculated for (001) orientated surface, the band edges of anatase TiO2 in vacuum are computed for (101) surface, with the conditions optimized for bulk phase that can have accurate experimental band gap and magnetic ordering (Supplementary Fig. 4c, d, f). Structural information used for the calculations of all TMOs in this figure is summarized in Supplementary Table 1, and explained in Supplementary Note 1 and Supplementary Fig. 4
Discussion
In conclusion, this study first argues and reveals the large discrepancy in the EV and EC of TMOs experimentally measured in vacuum and in an aqueous solution. To confirm the discrepancy, in the DFT calculations, we find optimal conditions of spin polarization and/or on-site Coulomb interaction parameter (Ueff) for rutile TiO2 and CoO model systems in vacuum and in an aqueous solution, independently; it is demonstrated that for vacuum reference calculation, appropriate Ueff value, magnetic configuration and surface configuration should be identified. Moreover, EC in vacuum estimated from the EV + \(E_{\mathrm{g}}^{{\mathrm{expt}}}\) is closer to the experimentally measured value (UPS measurement in vacuum), independent of the accuracy of band gap. For an explicit solvation method, spin polarization and Hubbard U correction are no longer needed for the best fit to the experimental measurements. Also, the EC in an aqueous solution can be directly predicted with the explicit solvation method, while EV = EC − \(E_{\mathrm{g}}^{{\mathrm{expt}}}\) exhibits a value similar to the experiment in an aqueous solution (flat band potential measurement). It is demonstrated that the optimized parameters and evaluation methods for EC and EV in vacuum calculation and in the explicit water calculation, are in good agreement with the experimental measurements in other TMOs including FeO, NiO, MnO, anatase TiO2, WO3 and V2O5. We elucidated in this study that the explicit solvation calculation should be performed in order to understand the band alignment behavior of a material to water redox level in a real operating environment in which water splitting occurs. With the general DFT calculations of slabs with a vacuum layer, the potential photocatalytic capability for water splitting will never be able to be predicted unless materials intrinsically have similar band edge positions both in vacuum and in an aqueous solution such as TiO2. We strongly believe that our work is a potential milestone in offering the efficient and optimized explicit solvation methods for a variety of TMOs, for the prediction of the band edge positions and even for study of the semiconductor/water interfacial structures and properties.
Methods
Model systems
TiO2 is a promising candidate for photocatalysis. As a result of its abundance, photo-stability, and reasonable activity, it is currently almost the only material suitable for industrial photocatalytic water splitting applications54. In particular, the relatively high photocatalytic activity of TiO2 for HER or OER originates from the ~3 eV band gap and appropriate alignment of the band edges relative to the water redox potentials1,8,10,11. Furthermore, both the band gap and the band edges of TiO2 can be modulated by the formation of surface oxygen vacancies26,36, providing opportunities for optimizing the activity.
CoO nanoparticles, which have a band gap of 2.4–2.6 eV, have been reported to evolve stoichiometric hydrogen and oxygen from water splitting under visible light irradiation even without an external driving potential or a co-catalyst in neutral water9, even though bulk CoO is inactive for photocatalytic water splitting9. The CoO nanoparticles hit the record for the highest solar-to-hydrogen photocatalytic efficiency (~5%) for single-material (i.e., no co-catalysts) nano-particulate photocatalysts. The improvement in the photocatalytic properties of CoO nanoparticles relative to bulk is due to the changes in the band edge positions relative to the water redox potential levels9. Previously, we demonstrated that the optimal band edge positions are a result of the thermodynamically stable facets present on the nanoparticles but not in larger-sized micropowders or bulk-like crystals17.
Bulk structure
Bulk rutile TiO2 was modeled with DFT and DFT + Hubbard U (DFT + U) using VASP55 with projected augmented wave (PAW) pseudopotentials from the VASP database and the generalized gradient approximation (GGA) of Perdew-Burke-Ernzerhof (PBE)56 to describe the exchange-correlation effects (Supplementary Methods). Ueff = 2.5─12 eV were employed for Ti atoms in the DFT + U calculations. An energy cutoff of 600 eV, a Gaussian smearing width of 0.05 eV, and a 6 × 6 × 8 Monkhorst-Pack k-point mesh are used for the structural relaxations of rutile TiO2 until all forces are <0.005 eV Å−1. However, the DFT-relaxed TiO2 bulk phase underestimated the experimental band gap (3 eV5) even with the correction of Ueff (Supplementary Fig. 4a).
Experimentally, bulk CoO crystallizes in the rock salt structure and exhibits type-II antiferromagnetic (AFM-II) spin ordering, in which the magnetic moments of the Co atoms are aligned in parallel within each (111) plane, with antiparallel ordering of adjacent (111) planes43. To model the ground state magnetic ordering and electronic structure of bulk CoO, DFT + U calculations are performed with PAW and GGA-PBE to address the strongly correlated and localized 3d shell of Co with Ueff varied between 1 and 6 eV. An energy cutoff of 800 eV and a 6×6×6 Monkhorst-Pack k-point mesh are used. Atom positions are relaxed until all forces are <0.005 eV Å−1. For the AFM-II phase of bulk CoO with Ueff = 4.1–5 eV, we find a band gap of 2.3–2.66 eV and a lattice constant of 4.26–4.264 Å, in reasonable agreement with the experimental values of 2.4–2.6 eV8,9 and 4.262 Å57,58, respectively (Supplementary Fig. 4b and ref. 17).
Surface structures in vacuum
To study the band edge positions of rutile TiO2 with respect to the absolute vacuum level, we consider symmetric TiO2(110) (1×2) slabs as shown in Supplementary Fig. 5, as the (110) facets of TiO2 have been shown to have the lowest surface free energy37,59,60. Since the surface oxygen stoichiometry is sensitive to the sample preparation conditions in experiment36, which results in the variation of the band edge positions of the surfaces, we consider a range of surface oxygen vacancy concentration from 0, to 0.5, and 1 per 1 × 2 surface unit cell. For the structural relaxations of the slabs, a vacuum layer of ~15 Å and a 8×2×1 Monkhorst-Pack k-point mesh are used (see Supplementary Methods).
The band edge positions of CoO surfaces in vacuum are examined with symmetric supercells of various surface configurations verified to be present under different oxidation conditions, as determined in the previous work:17 metal Co decorated CoO(111) (Co/CoO(111)), fully hydrogenated CoO(111) (H*-CoO(111)), clean CoO(100), and fully hydroxylated CoO(111) (OH*-CoO(111)), together with bare CoO(111) which is unstable for comparison. The computational details are the same as those described in ref. 17. and the structures of CoO surfaces were shown in the SI of ref. 17.
Band edges in explicit liquid water
To predict the conduction band edge position (EC) of a material relative to the water reduction potential level (H+/H2), we carried out the three-step calculation approach of ref. 18. This method is cost efficient compared to other explicit solvation approaches20,61 with similar accuracy, although this approach is sophisticated to calculate. To determine the H+/H2 acceptor level relative to the average Hartree potential in bulk liquid water (second step in the three-step calculation), classical molecular dynamics (MD) simulations are performed at room temperature using the LAMMPS code62 to construct the bulk liquid water structure. The TIP4P/2005 potential63 is employed to describe the atomic configuration and the interaction between water molecules. This TIP4P/2005 potential showed many structural parameters and properties (including density63, thermal expansion coefficient63, diffusivity63, and the structure factor64) comparable to the experimental values, at 298 K. Therefore, the potential is enough to describe liquid water structure at 298 K, even though the TIP4P/2005 potential slightly over-structures liquid water63. 140 H2O molecules are placed in the simulation cell (~11 × 11 × 27 Å3) to mimic the density of liquid water (1 g cm−3) at 298 K and equilibrated within the NVT ensemble for 1000 ps at 298 K17. The temperature was controlled by a Nosé-Hoover thermostat. The H+/H2 acceptor level is determined by substituting an H3O+ for one of the 140 H2O molecules in the optimized bulk liquid water system (H3O+–water), then optimizing the atomic configuration using DFT. Afterwards, the density of states (DOS) of the DFT-optimized H3O+-water is calculated at the Γ k-point with DFT in order to obtain the energy level of the H3O+ ion in water (acceptor level of water) as introduced in refs. 17,18.
The TMO/water interfaces (≈ 10 × 10 × 45 Å3) are explicitly constructed with direct contact of the slabs and liquid water as illustrated in ref. 17. and Supplementary Fig. 6. No preferential orientation of water molecules at the CoO surface/water interface is observed17 from the calculation of orientation of water molecules (angle between water dipole moment vector and the surface normal) after ab initio MD relaxation, without dissociation of water molecules on the CoO surfaces. On the other hand, a few water molecules on rutile TiO2(001) constructed with bulk phase cleaved along (001), are dissociated into OH and H groups and the OH and H groups are adsorbed on the rutile TiO2(001) surface (Supplementary Note 3 and Supplementary Fig. 7). Despite the change in the surface chemistry originated from the water dissociation, the EC vs. H+/H2 barely changes (Supplementary Fig. 8) from that of the as-constructed water/rutile TiO2(001) interface (at t = 0 in the ab initio MD relaxation). Therefore, the EC vs. H+/H2 calculated without further ionic relaxation after the construction of the TMO/water interface supercells, is considered to be able to represent the EC of TMOs obtained after relaxation in water. Thus, the TMO/water supercells are not re-optimized for static DFT calculations. Using static DFT calculations together with various conditions of magnetic configuration or Ueff values, the Hartree potentials of the whole system of the TMO/water interfaces are then obtained as a function of position along the thickness direction (from the slab to the water layer).
Also, as observed in experimental results65,66,67, our ab initio MD calculation of various TiO2/water interfaces (Supplementary Note 4 and Supplementary Fig. 9a−d) showed that water molecules are dissociated on both rutile and anatase TiO2(001) surfaces generated with bulk phase cleaved along (001) (Supplementary Fig. 9a, c), while H2O molecules keep their forms without dissociation on both rutile TiO2(110) and anatase TiO2(101) (Supplementary Fig. 9c, d) that are known to be the most stable among various surfaces. Several H2O molecules (not all H2O molecules) near the surfaces have the preferred orientation with respect to the surface normal, as shown in Supplementary Fig. 9b, d, which are in the same vein as other theoretical calculations68,69,70. Thus, it is considered that the size and the structure of our surface/water interface model are optimal to capture and describe the real interactions of the water-water molecules and the water-surface.
Data Availability
The authors declare that all the other data supporting the findings of this study are available within the article and its supplementary information files and from the first author upon request.
References
Grätzel, M. Photoelectrochemical cells. Nature 414, 338–344 (2001).
Babu, V. J., Vempati, S., Uyar, T. & Ramakrishna, S. Review of one-dimensional and two-dimensional nanostructured materials for hydrogen generation. Phys. Chem. Chem. Phys. 17, 2960–2986 (2015).
Long, M. et al. Efficient photocatalytic degradation of phenol over Co3O4/BiVO4 composite under visible light irradiation. J. Phys. Chem. B 110, 20211–20216 (2006).
Greiner, M. T. et al. Universal energy-level alignment of molecules on metal oxides. Nat. Mater. 11, 76–81 (2012).
Zhang, J., Liu, Z. & Liu, Z. Novel WO3/Sb2S3 heterojunction photocatalyst based on WO3 of different morphologies for enhanced efficiency in photoelectrochemical water splitting. ACS Appl. Mater. Interfaces 8, 9684–9691 (2016).
Gong, H. et al. The synergetic effect of dual co-catalysts on the photocatalytic activity of square-like WO3 with different exposed facets. RSC Adv. 7, 19019–19025 (2017).
Toroker, M. C. et al. First principles scheme to evaluate band edge positions in potential transition metal oxide photocatalysts and photoelectrodes. Phys. Chem. Chem. Phys. 13, 16644–16654 (2011).
Xu, Y. & Schoonen, M. A. A. The absolute energy positions of conduction and valence bands of selected semiconducting minerals. Am. Mineral. 85, 543–556 (2000).
Liao, L. et al. Efficient solar water-splitting using a nanocrystalline CoO photocatalyst. Nat. Nanotechnol. 9, 69–73 (2014).
Li, J. & Wu, N. Semiconductor-based photocatalysts and photoelectrochemical cells for solar fuel generation: a review. Catal. Sci. Technol. 5, 1360–1384 (2015).
Burnside, S., Moser, J.-E., Brooks, K. & Grätzel, M. Nanocrystalline mesoporous strontium titanate as photoelectrode material for photosensitized solar devices: increasing photovoltage through flatband potential engineering. J. Phys. Chem. B 103, 9328–9332 (1999).
Karamé, I. Hydrogenation Ch. 12 (InTech, Rijeka, 2012).
Sivula, K. & van de Krol, R. Semiconducting materials for photoelectrochemical energy conversion. Nat. Rev. Mater. 1, 15010 (2016).
Marszewski, M., Cao, S., Yu, J. & Jaroniec, M. Semiconductor-based photocatalytic CO2 conversion. Mater. Horiz. 2, 261–278 (2015).
Mathew, K., Sundararaman, R., Letchworth-Weaver, K., Arias, T. A. & Hennig, R. G. Implicit solvation model for density-functional study of nanocrystal surfaces and reaction pathways. J. Chem. Phys. 140, 084106 (2014).
Lee, T., Lee, Y., Jang, W. & Soon, A. Understanding the advantage of hexagonal WO3 as an efficient photoanode for solar water splitting: a first-principles perspective. J. Mater. Chem. A 4, 11498–11506 (2016).
Park, K. W. & Kolpak, A. M. Understanding photocatalytic overall water splitting on CoO nanoparticles: effects of facets, surface stoichiometry, and the CoO/water interface. J. Catal. 365, 115–124 (2018).
Wu, Y., Chan, M. K. Y. & Ceder, G. Prediction of semiconductor band edge positions in aqueous environments from first principles. Phys. Rev. B 83, 235301 (2011).
Cheng, J. & Sprik, M. Aligning electronic energy levels at the TiO2/H2O interface. Phys. Rev. B 82, 081406(R) (2010).
Kharche, N., Muckerman, J. T. & Hybertsen, M. S. First-principles approach to calculating energy level alignment at aqueous semiconductor interfaces. Phys. Rev. Lett. 113, 176802 (2014).
Ganguly, A., Anjaneyulu, O., Ojha, K. & Ganguli, A. K. Oxide-based nanostructures for photocatalytic and electrocatalytic applications. CrystEngComm 17, 8978–9001 (2015).
Ping, Y. & Galli, G. Optimizing the band edges of tungsten trioxide for water oxidation: a first-principles study. J. Phys. Chem. C. 118, 6019–6028 (2014).
Kruczynski, L., Gesser, H. D., Turner, C. W. & Speers, E. A. Porous titania glass as a photocatalyst for hydrogen production from water. Nature 291, 399–401 (1981).
Batzill, M. Fundamental aspects of surface engineering of transition metal oxide photocatalysts. Energy Environ. Sci. 4, 3275–3286 (2011).
Yang, S., Prendergast, D. & Neaton, J. B. Tuning semiconductor band edge energies for solar photocatalysis via surface ligand passivation. Nano Lett. 12, 383–388 (2012).
Li, L. et al. Sub-10 nm rutile titanium dioxide nanoparticles for efficient visible-light-driven photocatalytic hydrogen production. Nat. Comm. 6, 5881 (2015).
Beranek, R. Photo)electrochemical methods for the determination of the band edge positions of TiO2-based. Nanomater. Adv. Phys. Chem. 2011, 786759 (2011).
Bolts, J. M. & Wrlghton, M. S. Correlation of photocurrent-voltage curves with flat-band potential for stable photoelectrodes for the photoelectrolysis of water. J. Phys. Chem. 80, 2641–2645 (1976).
Gelderman, K., Lee, L. & Donne, S. W. Flat-Band potential of a semiconductor: using the mott–schottky equation. J. Chem. Educ. 84, 685–688 (2007).
Kibria, M. G. et al. Visible light-driven efficient overall water splitting using p-type metal-nitride nanowire arrays. Nat. comm. 6, 6797 (2015).
Zhang, Z. & Yates, J. T. Jr. Band bending in semiconductors: chemical and physical consequences at surfaces and interfaces. Chem. Rev. 112, 5520–5551 (2012).
Anisimov, V. I., Korotin, M. A. & Kurmaev, E. Z. Band-structure description of Mott insulators (NiO, MnO, FeO, CoO). J. Phys. Condens. Matter 2, 3973–3987 (1990).
Zimmermann, R. et al. Electronic structure of 3d-transition-metal oxides: on-site Coulomb repulsion versus covalency. J. Phys.: Condens. Matter 11, 1657–1682 (1999).
Gutzwiller, M. C. Effect of correlation on the ferromagnetism of transition metals. Phys. Rev. Lett. 10, 159–162 (1963).
Hubbard, J. Electron correlations in narrow energy bands. Proc. R. Soc. A 276, 238–257 (1963).
Borodin, A. & Reichling, M. Characterizing TiO2(110) surface states by their work function. Phys. Chem. Chem. Phys. 13, 15442–15447 (2011).
Ramamoorthy, M., Vanderbilt, D. & King-Smith, R. D. First-principles calculations of the energetics of stoichiometric TiO2 surfaces. Phys. Rev. B 49, 16721–16727 (1994).
Kiejna, A., Pabisiak, T. & Gao, S. W. The energetics and structure of rutile TiO2. J. Phys. Condens. Matter 18, 4207–4217 (2006).
Kang, W. & Hybertsen, M. S. Quasiparticle and optical properties of rutile and anatase TiO2. Phys. Rev. B 82, 085203 (2010).
Scanlon, D. O. et al. Band alignment of rutile and anatase TiO2. Nat. Mater. 12, 798–801 (2013).
Esch, T. R. & Bredow, T. Band positions of Rutile surfaces and the possibility of water splitting. Surf. Sci. 665, 20–27 (2017).
Chung, Y. W., Lo, W. J. & Somorjai, G. A. Low energy electron diffraction and electron spectroscopy studies of the clean (110) and (100) Titanium dioxide (rutile) crystal surfaces. Surf. Sci. 64, 588–602 (1977).
Roth, W. L. Magnetic Structures of MnO, FeO, CoO, and NiO. Phys. Rev. 110, 1333–1341 (1958).
He, X. et al. Phase- and size-dependent optical and magnetic properties of CoO nanoparticles. J. Phys. Chem. C. 119, 9550–9559 (2015).
Petitto, S. C., Marsh, E. M., Carson, G. A. & Langell, M. A. Cobalt oxide surface chemistry: the interaction of CoO(100), Co3O4(110) and Co3O4(111) with oxygen and water. J. Mol. Catal. A: Chem. 281, 49–58 (2008).
Wang, L. et al. Calorimetric study: surface energetics and the magnetic transition in nanocrystalline CoO. Chem. Mater. 16, 5394–5400 (2004).
Aziz, E. F., Lange, K. M., Bonhommeau, S. & Chergui, M. Reply to ‘Dark channel fluorescence…’ and ‘Dips and peaks…’. Nat. Chem. 4, 767–768 (2012).
Smith, B. B. & Nozik, A. J. Study of electron transfer at semiconductor-liquid interfaces addressing the full system electronic structure. Chem. Phys. 205, 47–72 (1996).
Seidel, R. et al. Origin of dark-channel X-ray fluorescence from transition-metal ions in water. J. Am. Chem. Soc. 134, 1600–1605 (2012).
Näslund, L.-Å. et al. Direct evidence of orbital mixing between water and solvated transition-metal ions: an oxygen 1s XAS and DFT study of aqueous systems. J. Phys. Chem. A 107, 6869–6876 (2003).
Cheng, J. & Sprik, M. Alignment of electronic energy levels at electrochemical interfaces. Phys. Chem. Chem. Phys. 14, 11245–11267 (2012).
Nozik, A. J. & Memming, R. Physical chemistry of semiconductor−liquid interfaces. J. Phys. Chem. 100, 13061–13078 (1996).
Chelnokov, E. et al. Electron transfer at oxide/water interfaces induced by ionizing radiation. J. Phys. Chem. C. 118, 7865–7873 (2014).
Hashimoto, K., Irie, H. & Fujishima, A. TiO2 photocatalysis: a historical overview and future prospects. Jpn. J. Appl. Phys. 44, 8269–8285 (2004).
Kresse, G. & Hafner, Ab initio molecular dynamics for liquid metals. J. Phys. Rev. B 47, 558–561 (1993).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Deng, H.-X. et al. Origin of antiferromagnetism in CoO: A density functional theory study. Appl. Phys. Lett. 96, 162508 (2010).
Archer, T., Hanafin, R. & Sanvito, S. Magnetism of CoO polymorphs: density functional theory and Monte Carlo simulations. Phys. Rev. B 78, 014431 (2008).
Diebold, U. Structure and properties of TiO2 surfaces: a brief review. Appl. Phys. A 76, 681–687 (2003).
Hameeuw, K. J., Cantele, G., Ninno, D., Trani, F. & Iadonisi, G. The rutile TiO2(110) surface: obtaining converged structural properties from first-principles calculations. J. Chem. Phys. 124, 024708 (2006).
Pham, T. A., Ping, Y. & Galli, G. Modelling heterogeneous interfaces for solar water splitting. Nat. Mater. 16, 401–408 (2017).
Plimpton, S. Fast Parallel algorithms for short-range molecular. Dyn. J. Comp. Phys. 117, 1–19 (1995).
Abascal, J. L. F. & Vega, C. A general purpose model for the condensed phases of water: TIP4P/2005. J. Chem. Phys. 123, 234505 (2005).
Sedlmeier, F., Horinek, D. & Netz, R. R. Spatial correlations of density and structural fluctuations in liquid water: a comparative simulation study. J. Am. Chem. Soc. 133, 1391–1398 (2011).
Smith, P. B. & Bernasek, S. L. The adsorption of water on TiO2(001). Surf. Sci. 188, 241–254 (1987).
Blomquist, J., Walle, L. E., Uvdal, P., Borg, A. & Sandell, A. Water dissociation on single crystalline anatase TiO2(001) studied by photoelectron spectroscopy. J. Phys. Chem. C. 112, 16616–16621 (2008).
Herman, G. S., Dohnálek, Z., Ruzycki, N. & Diebold, U. Experimental investigation of the interaction of water and methanol with anatase−TiO2(101). J. Phys. Chem. B 107, 2788–2795 (2003).
Fahmi, A. & Minot, C. A theoretical investigation of water adsorption on titanium dioxide surfaces. Surf. Sci. 304, 343–359 (1994).
Vittadini, A., Selloni, A., Rotzinger, F. P. & Grätzel, M. Structure and energetics of water adsorbed at TiO2 anatase 101 and 001 surfaces. Phys. Rev. Lett. 81, 2954–2957 (1998).
Cheng, J. & Sprik, M. Acidity of the aqueous rutile TiO2(110) surface from density functional theory based molecular dynamics. J. Chem. Theory Comput. 6, 880–889 (2010).
Acknowledgements
This work was supported by the Skolkovo Institute of Science and Technology (Skoltech) through the “Center for Research, Education and Innovation for Electrochemical Energy Storage” (contract number 186-MRA) and the KIST project (2E29340). This research used resources of the National Energy Research Scientific Computing Center (NERSC), a DOE Office of Science User Facility supported by the Office of Science of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231.
Author information
Authors and Affiliations
Contributions
K.W. designed the study, performed the computational experiments, analysed the data and wrote the manuscript with assistance and feedback from A.M.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Park, KW., Kolpak, A.M. Optimal methodology for explicit solvation prediction of band edges of transition metal oxide photocatalysts. Commun Chem 2, 79 (2019). https://doi.org/10.1038/s42004-019-0179-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42004-019-0179-3
This article is cited by
-
Absolute band-edge energies are over-emphasized in the design of photoelectrochemical materials
Nature Catalysis (2024)
-
Spontaneously formed gradient chemical compositional structures of niobium doped titanium dioxide nanoparticles enhance ultraviolet- and visible-light photocatalytic performance
Scientific Reports (2021)
-
Explicit solvation effects on low-index Fe surfaces and small particles as adsorbents of Arsenic species: a DFT study
Theoretical Chemistry Accounts (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.