Abstract
Ionic liquid (IL)-water mixtures can exhibit a lower critical solution temperature (LCST) transition, but changes in long-range order and local molecular environment during this transition are not comprehensively understood. Here we show that in IL-H2O LCST mixtures, the IL forms loosely held aggregate structures that grow in size leading up to a critical temperature, whereas the aggregation of a fully miscible aqueous mixture, obtained by minor chemical modification of the anion, decreases with increasing temperature. Radial distribution functions from molecular dynamics simulations support the observation of aggregation phenomena in the IL-H2O mixtures. A local molecular structure of the ions is derived from multi-dimensional NMR experiments in conjunction with reported molecular dynamics simulations. In addition to considerable shifts of water’s hydrogen bonding network in the fully miscible phase, by NMR we observe the anion’s protons response to the intermolecular thermal environment and the intramolecular environment and find that the responses are determined by the sulfonate ionic functional group.
Similar content being viewed by others
Introduction
Room temperature ILs (RTILs) are ionic materials with a melting point below 100 °C due to functional groups introducing steric hindrance and preventing closed packing structures. Owing to their ionic character, ILs have a number of desirable attributes, such as negligible vapor pressure, high ionic conductance, and often high thermal and chemical stability1,2,3,4. The physicochemical properties of ionic liquids can be tailored by chemical modification of the cation and/or anion, leading to a vast number (>1014) of distinct ionic liquid combinations5. This presents an enormous library of ionic liquids to fully explore. To date, much of the fundamental and applied studies have focused on the imidazolium cation-based ILs6,7,8,9. A subclass of ionic liquids undergoes a thermoresponsive liquid–liquid phase transition of either an upper critical solution temperature (UCST) or lower critical solution temperature (LCST). Such thermoresponsive IL-based mixtures have opened up new potential applications such as protein extraction10,11,12, metal ion extraction13, and forward osmosis draw solutes for water purification14,15,16,17,18.
In liquid–liquid mixtures with a LCST transition, a single and miscible phase appears at lower temperatures. However, upon heating above a critical temperature Tc, the single-phase liquid–liquid mixture separates into two immiscible phases. From a thermodynamic view, this behavior is understood in the framework of equation (1), where ΔGmix is the free energy of mixing, ΔHmix is the enthalpy of mixing, and ΔSmix is the entropy of mixing.
At lower temperatures, strong intermolecular interactions, such as hydrogen bonding, lead to a negative enthalpy of mixing and formation of a miscible phase between the two components. These intermolecular interactions are often highly directional and come at an entropic cost. Upon heating above Tc, the entropic term dominates as intermolecular interactions are broken, and the system entropy can increase by phase separation due to increased degrees of freedom from the broken intermolecular interactions19, 20 or if dispersion forces between two like components (A–A) and (B–B) is greater than between unlike components (A–B)21. While this type of behavior has been observed for many polymer-solvent systems, there are fewer cases of small molecule LCST mixtures.
Ionic liquids exhibiting a LCST in aqueous mixtures have been developed by Ohno and coworkers22,23,24,25,26,27,28,29. Their argument for the physicochemical conditions necessary for LCST behavior between an ionic liquid and water mixtures is the balance between the hydrophilic and hydrophobic character of the component positive and negative ions26. If both the anion and cation are too hydrophobic, aqueous mixtures will be immiscible over the whole temperature range, and conversely, if both components are too hydrophilic, aqueous mixtures will remain fully miscible independent of temperature. In studying related protonated tertiary amines, our team has found that is not the total organic content of the molecular ions that drive this phenomena but the proximity of the organic content to the charged center30.
Recent studies have attempted to understand the molecular interactions responsible for the IL-water LCST transition. FT-IR spectroscopic probing of tetrabutylphosphonium [P4444] 4-vinylbenezenesulfonate-water mixtures concluded that the C–H functional groups of the cation responded first to a temperature perturbation, followed by the sulfonate group of the anion. The mechanism proposed that the cation initiates conformational changes (due to greater hydrophobic interaction with water) forming single cation–anion ion pair aggregates due to strong coulombic forces31. A different IL-H2O LCST mixture obtained by replacing the 4-vinylbenezenesulfonate anion with trifluoroacetate ([P4444][CF3COO]) was studied to examine the hydrophilic nature of the ions using 1-propanol probing methodology. The results found that [P4444] showed equally strong hydrophilic and hydrophobic character, whereas the anion exhibited slightly hydrophobic character. The number of water molecules hydrating the cation was 10 times that of the anion and this large hydration shell of the cation results in an unfavorable entropy of mixing32. Cations are known to require greater hydration than anions33, and the largely neutral polarity (neither polar nor non-polar) of the [P4444] further explains why to date many of the observed IL-H2O LCST mixtures are based on quaternary ammonium and phosphonium cations34.
MD simulations demonstrated that the LCST transition of [P6668] and amino acid anions in aqueous solutions occurs by temperature-dependent changes in intermolecular interactions between the anion, cation, and water35. Specifically, the anion’s functional groups, –NH2 and –COOH, are able to form a hydrogen bond to the carboxylate group of another anion. Similar interactions between anions are believed to play a role in the self-assembly of tertiary amine bicarbonates30. With increasing temperature, the anion-water and cation–anion interactions weaken, whereas anion–anion interactions increase, resulting in an LCST transition. Furthermore, radial distribution functions showed no clear interaction of –CH3 groups of one anion to –COO− of another. Consequently, the proposed conclusions only represent a system specific mechanism as it cannot account for the LCST transition of tetralkylphosphonium benzenesulfonate derivatives24, which have no hydrogen bond donor functional groups.
Currently, there exists disagreement in the literature about the molecular interactions responsible for the IL-water LCST transition. In this article, we study the changes in LCST aqueous mixtures of tetrabutylphosphonium 2,4-dimethylbenzene sulfonate [P4444][DMBS] across temperature ranges in both the fully miscible and phase separated regions to obtain further insight in the molecular mechanism of IL-H2O phase separation. The aggregation of ILs is investigated experimentally and theoretically by using the dynamic light scattering method and molecular dynamics simulations, respectively. Multi-dimensional NMR provides an insight into the local molecular structure of the ILs with respect to the views of the intermolecular and intramolecular environment.
Results
Temperature-dependent light scattering of RTIL
Dynamic light scattering (DLS) was used to study the effects of aggregation and changes in long-range order for LCST mixtures. For each experiment, scattering intensity versus delay time was collected, and then analyzed by software to give the distribution versus decay constant occurring by diffusion under Brownian motion. The decay constant, Γ, given by eq. (2), is a function of the diffusion coefficient, Dt, and the scattering vector, q.
The scattering vector is given by eq. (3), where nD is the refractive index of the material, λ is the wavelength and θ is the detection angle.
From the analyzed decay time distribution and known scattering vector, the hydrodynamic diameter, Dh, of the scattering particle can be determined from eq. (4),
where kb is Boltzmann’s constant, η(T) is the viscosity and the Dt is the translational diffusion. Figure 1a shows the results for the particle size distribution versus temperature across the fully miscible region of a 50 wt.% (w/w) mixture of [P4444][DMBS]|H2O. Initially, at temperatures 10 °C below Tc, the solution shows minimal scattering aggregates, meaning the solution is homogenous within the length scale of sensitivity for the DLS apparatus. However, around 30 °C, the solution shows clear correlation with an average scattering size of 3–4 nm, which enlarges with increasing temperature up to 9 nm at 35 °C, just below Tc. A steady increase in water activity (observed vapor pressure relative to the vapor pressure of pure water (aw = p/p0)) suggests that the solute is steadily transitioning from an evenly distributed ideal solute to smaller number of clusters.
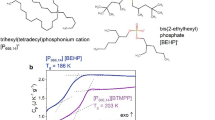
Dynamic light scattering cumulant analysis results for particle size versus temperature. a Particle size versus temperature of [P4444][DMBS]|H2O 50 wt.% over the fully miscible region and phase separated regions of the phase diagram. Phase separation temperature, Tc ca. 36 °C. b Particle size distribution of a [P4444][BnzSO3]|H2O 50 wt.% mixture versus temperature
Plotting the water activity as an observed colligative concentration of osmolality (Equation 5) demonstrates how the effective number of particles in solution are steadily declining as aggregate size grows (Fig. 2). The Osm kg−1 versus temperature plot converges with pure at the critical point 36 °C, just above Tc, which is consistent with limited solubility (<60 mM ideal solute particles) and/or large solute aggregates.
Colligative concentration through the vapor pressure of [P4444][DMBS]|H2O 50 wt.%. See Eq. 5
The aggregate size growth follows DLS measurements of a different LCST aqueous mixture with [P4444][CF3COO], which showed a similar increase in particle size with increasing temperature leading up the critical point36. This observation was also supported by additional experimental techniques and it was assigned to the surfactant free micellar formation by the ionic liquid that swelled in size with increasing temperature until macroscopic phase separation occurred. Aggregation behavior approaching the critical point for [P4444][CF3COO] aqueous mixtures was also observed by density fluctuations from small-angle X-ray scattering (SAXS)37. However, the SAXS study did not support micelle formation i.e., structures consisting of an ordered hydrophilic shell and hydrophobic core36. The authors concluded that the aggregates formed non-distinct ‘fuzzy clusters’ composed of ionic liquid and water molecules37. What appears consistent of IL-water LCST mixtures is the change from a more homogenous mixture (reduced density fluctuations, smaller aggregates) to a more inhomogeneous mixture upon heating up to the Tc and macroscopic phase separation. Thus, the system’s microstructure seems to change gradually with temperature perturbation rather than undergoing a sudden structural change at Tc. This trend was compared against the same test on a chemically similar system not exhibiting a LCST phase transition in water, tetrabutylphosphonium benzenesulfonate [P4444][BnzSO3], and is shown in Fig. 1b. In this system, the 2, 4- methyl positions on the DMBS anion are replaced with hydrogens, yielding benzenesulfonate. Despite the minor chemical change, this system exhibits markedly different behavior. As noted by Ohno24, this mixture remains fully miscible versus temperature rather than undergoing a liquid–liquid phase separation. At lower temperatures, the system reveals scattering aggregates on the order of hundreds of nanometers. The aggregate’s size rapidly reduces an order of magnitude and then more gradually shrinks to tens of nanometers upon further heating. The seemingly inert substitution of methyl groups with hydrogens results in the loss of the LCST transition and opposite aggregation behavior versus temperature as compared to the fully miscible phase of the LCST IL. One possible explanation for the distinct result is that [P4444][BnzSO3] in water forms extended apolar and polar networks, which has been understood to occur in other ionic liquid mixtures38,39,40. In contrast [P4444][DMBS] cannot form extended networks (possibly due to steric disruption) and is relegated to distinct solvated ion pair/pair clustering in water.
Previously unexplored in LCST mixtures are changes in long-range order after phase separation into an aqueous rich and ionic liquid rich phase. In the fully miscible state just below the critical point, the solution formed aggregates on the order of 9 nm. Above Tc, each of the two-phase mixture shows substantial changes in long-range order. The ionic liquid rich phase shows aggregates on the order of 500 nm at 37 °C, just above Tc. The size of aggregates in the IL-rich phase subsequently decrease with increasing temperature to 150 nm at 39 °C and then to 100 nm at 41 °C. The initial 50-fold increase in IL aggregate size going from the miscible phase to IL rich phase would likely arise from the sudden decrease in water concentration and additionally the reduced electrostatic screening from water enabling larger aggregates to form.
The aqueous-rich phase shows nearly an order of magnitude increase scattering diameter of 3000 nm compared to the IL-rich phase just above phase separation. While an increase in aggregate size matches the temperature-dependent exponential particle growth trend in the miscible phase this is also a seemingly counter-intuitive result, as the concentration of ionic liquid is greatly reduced in the aqueous phase. One would expect the aggregate structure to decrease in size with reduced ionic liquid and increased screening between ion pairs from higher water content.
Koga et al. studied the higher order derivatives of the Gibbs energy with regard to the excess enthalpy, and found the LCST IL [P4444][CF3COO] exhibited strong hydrophobic character, especially compared to other ionic liquids not exhibiting a LCST transition in water. The authors proposed that [P4444][CF3COO] acting as an extreme hydrophobe may not dissociate in water-rich regions41. Our observation of large IL aggregates in the water-rich phase supports the author’s proposal, where the hydrophilic IL aggregates rather than dissociate. This decline in aggregate size upon additional heating is similar to the general trend in the fully soluble IL, [P4444][BnzSO3]. Molecular dynamics of the ionic liquid, tetraalkylphosphonium-Bis(oxalato)borate, at very dilute concentrations in water found a ‘loose micelle-like aggregate’ structure with the cation alkyl chains forming a hydrophobic core and hydrophilic shell formed by polar segments of the anion and cation40. However, such a structure cannot be verified by DLS measurements in this work.
Molecular dynamics simulation
Molecular dynamics (MD) simulations were employed to investigate the aggregation trends in the IL-H2O mixtures in response to the temperature for the both [P4444][DMBS] and [P4444][BnzSO3] systems. The radial distribution function (RDF), g(r), is a calculated parameter, which quantifies the spatial correlation between specific atoms, and thus enables detailed understanding of structural features of microscopic ionic liquid systems. The g(r) is defined as the ratio of the local time-averaged number density of specific particles at a given distance, r, from an origin particle to the total average number density of the particles, so then expressed as
where ρn is the total number density of the particles. The mostly charged atom in Supplementary Fig. 3 represents the position of each molecules for the RDF analysis. i.e., the P atoms, S atoms, S atoms, and O atoms, respectively, are taken as reference sites of the [P4444] cation, the [DMBS] anion, the [BnzSO3] anion, and water molecule.
Figure 3 shows the calculated RDF results for [P4444][DMBS]. According to the cation–anion RDF (Fig. 3a), the ion pairs are attracted strongly to each other by means of strong electrostatic interactions. The pronounced peak observed at around 5 Å results from the geometry of the ions. The two simulations for temperatures above Tc display a greater peak height as compared to the that of the lower temperature cases. It is basically counter-intuitive for the more thermal motion of molecules at the higher temperature. This indicates that at higher temperatures ion pairs reside in closer proximity to each other. However, inspection of the two cases in the below Tc range show a remarkable lack of difference. Thus, the apparent temperature dependence of the cation–anion g(r) suggests that the electrostatic interaction is a main driving force responsible for the aggregation in the ionic liquids. As no strong attractive potential exists among ions of the same charge, the cation–cation and anion–anion RDFs must be a consequence of the electrostatic interactions between oppositely charged ions. The cation–cation RDF (Fig. 3b) shows evidence of clustering at above Tc range. Considering the size of the single cation with even butyl chains of around 6 Å, the multiple small peaks between 5 and 10 Å are observed and can be interpreted as all located in the first coordination shell. The many numbers of peaks come from different coordination orientations and mean the ions are loosely tied. The merging of neighboring small peaks at elevated temperature causes a major peak at 7 Å at the two cases above Tc. The peak distance corresponds the summation of the length of a butyl chain in [P4444] and the O–S bond length of sulfonate in [DMBS]. Therefore, the major peak means the ions are compactly tied to each other by the strong electrostatic forces and the ion-pair aggregation is in the dense form of multiple layers of cation–anion shells. The first small peak moving to the larger radius as a temperature change from 10 °C to 20 °C is also consistent with the experimental results (Fig. 1a) at below Tc range. Nevertheless, since the MD simulations were carried out with 80 pairs of ions equilibrated in a simulation box with box lengths less than 10 nm in all dimensions, some experimental results, such as the aggregation on length scales of several thousands of nm, are difficult to be realized in the typical size scale of an MD simulation. For the anion–anion RDF of Fig. 3c, since the [DMBS] anion is a relatively small and flat molecule, which can be located between cations and the aggregation is mainly caused by cation–anion interactions, no clear conclusion can be reached from this. However, the aforementioned trend depending on temperature is not observed at the [P4444][BnzSO3]|H2O mixture without the LCST behavior, as shown in Supplementary Fig. 4a–c. The cation–anion RDF of the 50 wt.% of [P4444][BnzSO3] mixture system shows the opposite trend of a smaller peak height with increasing temperature, which is also consistent with the experimental results of Fig. 1b.
Figure 3d–f presents RDFs with water molecules and also supports the experimental findings of the LCST characteristic. The overall g(r) of all RDFs with water molecules of the two cases above Tc is lower than that of the two below Tc cases, which means there are fewer spaces between ions. The trend is more clearly observed in the ion-water RDFs, and demonstrates the ion-water interactions declines as temperature increases. Hydrogen bonding exists in this ILs|H2O mixture system. The gain or loss of the directional bonding has been used as the most reliable approach to explain the LCST behavior of small molecules42.
In order to gain insight into hydrogen bonding in the IL|H2O mixtures, representative oxygen and hydrogen pair distributions in the [P4444][DMBS] mixture system are presented in Fig. 4. The O–H separation based on the RDFs clearly suggests a simple definition of the hydrogen bonding, as the radius of the first hydrogen atom coordination shell for each oxygen atom, without any further complicated definition. Each occurrence of an O–H approach within 2.45 Å for both pairs in Fig. 4 can be determined as the hydrogen bonding. Applying the definition of O–H separation distance, the number of hydrogen bonds per each oxygen atom in each temperature case was counted and summarized in Fig. 4c. For the [P4444][DMBS] mixture system with the LCST behavior, the degree of hydrogen bonding seems to decrease with increasing temperature. It is known that solutions of 50 wt.% or more contain essentially no free water42. In other words, all water molecules either participate in hydrogen bonding or the formation of hydration shells around the ILs. A lesser degree of hydrogen bonding at the above Tc means more water molecules contribute to the hydration shell of ILs. However, for the [P4444][BnzSO3] mixture system, each oxygen atom is basically involved in more hydrogen bonds compared to the ILs with LCST behavior. As a result, the shortage of water contributing to stable hydration interactions disturbs the mechanism leading to the large IL clusters. The number of hydrogen bonds per oxygen atom in [BnzSO3] anion increases as a function of temperature. The net number of hydrogen bonds (Ow–Hw and OA–Hw) for the mixture display a notable lack of temperature dependence a wide temperature range. Although an additional analysis of angle distribution of water molecules to verify the contribution of dipoles relative to the ions, the dependency of average angle on the temperature is not observed as shown in Supplementary Fig. 5.
Calculated the number of hydrogen bonds for the 50 wt.% ILs|H2O system. a, b RDFs between oxygen and hydrogen for the 50.8 wt.% [P4444][DMBS] ILs|H2O system. a Oxygen of sulfite in anion-Hydrogen in water, b Oxygen in water-Hydrogen in water pairs. Vertical dashed lines denote O–H separation to define hydrogen bonding. c Number of hydrogen bonds as a function of temperature per each oxygen atom for both 50 wt.% of [P4444][DMBS] and [P4444][BnzSO3] with water solution. Error bars present the range of recorded data from MD per 1 ps
Temperature-dependent NMR and IR Spectroscopy of RTIL
1H NMR was used to gain deeper molecular insight into the mechanism of LCST phase transition. Changes in spectral shifts versus temperature were used to monitor and assess intra- and intermolecular interactions in the low temperature fully miscible water-RTIL phase, the high temperature water-rich phase, the high temperature IL-rich phase, and the pure RTIL as a reference sample. Figure 5a shows a 50 wt.% solution of [P4444][DMBS] below and above Tc with Nile Red as a dye to visual identify the two immiscible phases above Tc. Nile Red will be predominately dissolved by the ionic liquid, and therefore remain in the ionic liquid rich phase. Thus, the ionic liquid-rich phase is less dense than the aqueous phase and will reside on top. Control over, which phase is probed, is demonstrated in Fig. 5b. The sampling for in situ temperature-dependent NMR assumes that any initial starting solution within the LCST miscibility gap will result in the same final concentration of IL rich phase and H2O phase for a given temperature above Tc. This assumption is validated from the IL content in the two immiscible phases versus initial concentration measure by Cai et al.14.
Setup and results of the temperature-dependent NMR of RTIL. a 50 wt.% solution of [P4444][DMBS] below and above Tc with Nile Red which is predominately dissolved by the ionic liquid. b Illustrations of controlling which phase is primarily probed above Tc. Green lines indicate ionic liquid rich phase and blue lines indicate aqueous rich phase, yellow dotted line indicates visible separation of the two phases, and black rectangular is the area primarily probed the NMR. c 1H NMR spectra of pure and H2O mixtures of [P4444][DMBS]. Temperature and solution content are indicated with spectra. Note: For the pure ionic liquid, protons E and F overlap. d Temperature dependent proton shifts of a 50 wt.% solution referenced against their position at 25 °C. After phase separation, the IL rich phase is probed. e Similar procedure to d except a 37 wt.% solution used to examine aqueous phase above Tc
Pure [P4444][DMBS] shows negligible ppm shifts versus temperature. The peak structure shows narrowing and resolving of finer structure as motional mobility increases with temperature (Supplementary Fig. 6). Figure 5c compares the spectra of pure [P4444][DMBS] versus a 50 wt.% aqueous solution at 25 °C. Moving from pure IL to an aqueous mixture, the majority of the peak positions remains largely unchanged except for two hydrogen groups. The methylene hydrogen atoms next to the phosphorous cation core (peak F) show a substantial shift upfield of 0.24 ppm. These hydrogens would be more electropositive due to their proximity with cation core, and thus able act as hydrogen bonding acceptors from the water oxygen’s lone pair, resulting in the upfield increase. Hydrogen bonding between water and the methylene group adjacent to the phosphorous core was calculated to exist in [P666(14)][BOB] aqueous mixtures40. In contrast, the anion aromatic peaks B and C shift downfield 0.08 ppm in the presence of water, likely as a result of acting as hydrogen bond acceptors and having electron density pulled away. The aromatic peak A in closest proximity to the sulfonate group does not show any measurable shift in the presence of water.
No meaningful shifts corresponding to the ionic liquid protons are observed over the miscible phase region at 25 < T < 35 °C (Fig. 5d, e). Over the same region, water protons show a linear shift of −0.012 ppm °C−1, a slightly increased rate compared to pure water shift of −0.01 ppm °C−1 43. This linear shifts arises from weakened hydrogen bonds as temperature increases, resulting in increased electron density and shielding44.
Above Tc, water behaves differently in the two immiscible phases (Fig. 5d, e) compared to the miscible phase. The remaining water in the ionic liquid rich phase (right Fig. 5d), on the order of 10–15 wt.%14, moves upfield at a nearly threefold increased rate of −0.038 ppm °C−1, as water’s hydrogen bonds are further weakened. Water in the aqueous phase (Fig. 5e) actually shows an initial shift downfield, likely as a result of water restructuring its extended hydrogen bonded network as the RTIL solute phase separates. Upon further heating, water moves upfield at a rate of −0.01 ppm °C−1, similar to that of bulk water, further indicating that the phases are restructuring to essentially resemble bulk water45. The chemical interpretation of the NMR shifts of the water peak is supported by the behavior of the –OH stretch mode in Raman spectra, shown in Fig. 6. Moving from the fully miscible phase to the ionic liquid-rich phase, there is clear intensity loss in the low frequency region of the –OH stretch in which water is more hydrogen bonding. Similarly, moving to the aqueous phase, an increase in intensity of the same region is observed, and the –OH region more closely resembles pure water.
The ionic liquid protons in the fully miscible phase (T < Tc) showed negligible shifts. In the IL-rich phase (T > Tc), only a few ion protons show minor changes (Fig. 5d). Cation peak F shifts downfield and the anion aromatic peaks, B and C, shift upfield. These are the same peaks that showed the greatest changes when moving from pure to aqueous mixture, however, in the opposite direction.
The IL protons in the H2O-rich phase at T > Tc show very different behavior from the ions in the IL-rich phase (Fig. 5e). Nearly all the IL protons shift downfield with increasing temperature, with aromatic peaks B and C showing the greatest shifts, followed by the Ph–CH3 group E and terminal cation alkyl group I. These downfield shifts can be attributed to increased hydrogen bonding associated with increased water content. Interestingly, the anion’s Ph–H and Ph–CH3 protons A and D nearest the sulfonate group show negligible shifts across the entire temperature range and in all the three phases, whereas protons, in B, C, and E locations show much more sensitivity to temperature and phase change. Such radically different behavior for protons on the anion may indicate that the protons nearest the sulfonate group, A and D are sensitive to the intramolecular environment, whereas those protons furthest from the sulfonate grate, B, C, and E, are sensitive to changes in the intermolecular environment.
Temperature-dependent NMR was previously used to study the LCST behavior of two ionic liquids, ([P4444][SS]) and ([P4446][MC3S]), in aqueous solutions31, 46. We note two important distinctions made in our work versus that in Wu’s studies, namely the use of an external lock and reference in our measures, whereas the D2O signal in the sample was used, and the steps taken to control the phase being probed by the instrument. By referencing the spectrum to chemical shift of tetramethylsilane, known to be largely temperature independent, we are more accurately able to track spectral changes with increasing temperature. This cannot be done using D2O as a reference due to its established temperature-dependent shift. Secondly, efforts to control the phase of probing above the critical temperature when performing in situ measurements on separated phase have important implications for data interpretation. Secondly, the integral area shifts versus temperature, using D2O as a reference, were used to assign the ionic liquid formation of globules after observing a sharp decrease in integral area above Tc. However, we note this observation could arise from probing the aqueous phase above Tc, in which the HOD reference signal would greatly increase relative to IL signal. Thus, we note two important advantages in using an external lock and reference and actively controlling the phase of probing above Tc when studying liquid–liquid phase separations by in situ NMR.
Temperature-dependent and spin-recovery NMR study of LCST RTIL
Temperature-dependent spin-lattice relaxation times (t1) were examined to probe rotational mobility in response to temperature and phase separation. Similar to VT-1H NMR experiments, t1 relaxation changes in low temperature fully miscible water-RTIL phase (T < Tc), and phase separated water-rich phase and IL-rich phases (T > Tc) were measured. All protons showed strictly monoexponential decay. Similar to temperature-dependent chemical shifts, the t1 times of the IL protons show no significant changes versus temperature change in the fully miscible region whereas water’s protons show a continual increased rotational mobility (increased t1) as temperature increases (Fig. 7a, b). After phase separation, water shows markedly different behavior between the IL and aqueous phase. Above Tc, the H2O-rich phase’s water t1 greatly increases towards that of pure water (Fig. 7b). This signal arises from bulk water and thus is not informative of how water is interacting within or in close proximity to the IL nanoparticles observed through dynamic light scattering.
The t1 of residual water in the IL-rich phase (Fig. 7a) shows a continuous decrease with increasing temperature above Tc, indicating a reduced rotational mobility. As temperature increases, water content in the IL-rich phase decreases, resulting in a reduction of IL-water cluster size and/or shortened water chains40. Effectively, water becomes more nanoconfined by the IL, resulting in decreased rotational mobility. Decreased t1 lifetime and the corresponding reduced rotational mobility were previously observed for nanoconfined water in microfluidic devices as a function of volume47.
2D ROSEY NMR measurement
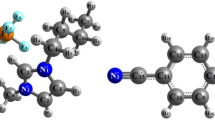
Temperature-dependent 2D ROESY NMR method was used to obtain further information about the structure of individual IL-H2O phases and the mechanism of relevant phase transitions. Cross peaks on 2D ROESY arise from the nuclear Overhauser effect, in which nuclear spin polarization couples to a different nuclear spin through space. Thus, cross peaks represent nuclei correlated through space, approximately up to 0.5 nm, and whose intensities are proportional to the magnitude of magnetization transfer between protons. Figure 8a shows the 2D ROESY spectrum of a 50 wt.% aqueous mixture of [P4444][DMBS]. Initially clear from the spectrum is the large number of proton correlation between the anion and cation protons, thus making determination of structure ordering difficult.
Changes in cross-peak intensities were calculated versus temperature. The cross-peak integrals were obtained from elliptical integration with ranges from the 1D peak integral limits in f1 and f2 dimension for each proton, normalizing to the external DMBS diagonal integral as a reference for comparison across temperature, and then normalizing to the total number of hydrogens contributing to each cross to allow for comparison between cross peaks (i.e., cross-peak D–I, nH = 15). Unfortunately, NOE cross peaks versus temperature reveal no meaningful trends, likely as a result of sensitivity of observing NOE cross peaks to experimental parameters used. This is further exacerbated by the likely change in coupling constant versus temperature. The results of the analysis are shown in Fig. 8b. Comparing various cross-peak intensities reveals a few important trends: (i) anion Ph-meta-H peaks B and C show strong interactions with the terminal cation alkyl chain I, (ii) Ph-ortho-H peak A, the aromatic hydrogen nearest the anionic sulfonate group, shows an interaction with the alpha-methylene group F, nearest the cationic phosphorous core, (iii) Ph-ortho-CH3 group D closest to the anionic sulfonate group shows correlation to the cation’s alpha-methylene group F, whereas the anion’s methyl group furthest from the sulfonate group, Ph-para-CH3 E cross peak with the cation’s alpha-methylene group F is not observed, and (iv) cation–cation and anion–anion cross peaks, especially protons 2–3 carbon neighbors away, show much greater cross-peak intensity than anion–cation cross peaks.
Trends i through iii suggest that the cation is intimate and overlapping contact with the anion. The functional groups ortho to anion’s charged group are correlated with the cations core methylene group alpha to the cations charge center. Functional groups more distant from the charge centers are moving out of the way so the charge centers can make a close approach. This orientation is supported by terminally methyl of the cation butyl group’s interacting with anions meta-hydrogen’s more distant from the anion’s charge center.
The anion–anion and cation–cation cross peaks show greater intensity found in trend iv most likely arises from TOCSY (Total Correlation Spectroscopy) artifacts, despite using pulse sequences to suppress such signals. As such, no conclusion can be drawn from these cross peaks. Observations of anion–cation cross-peak support the structural organization of the anion’s sulfonate group interacting in close proximity to the cation’s core, and the aromatic ring facing outwards from the core.
These results, in conjunction with the large chemical shift of methylene group F upon solvation in water, are in good agreement with modelling structures of [P666(14)]-H2O-[BOB] complexes40. From MD simulations, the pure IL exhibit extended apolar and polar regions from the cation’s alkyl chains and polar segments from the cation core and anion. However, upon the addition of water, the cation and anion showed enhanced spatial correlation forming contact ion pairs with water filling cavities between the ions forming cation–water–anion complexes. In these pairings the negative and polar segments of the anion coordinated with the cation core. These theoretical results align with the results of the ROESY experimental data of our system, which indicates the charged portions of the ions are associating intimately.
Discussion
In summary, we observed a common trend among IL-water LCST mixtures in which the IL forms small aggregates below Tc, which subsequently increase in size upon heating leading up to the critical point. Furthermore, this observation was specific to LCST mixtures i.e., after minor chemical modification of the anion, which led to a fully miscible mixture, the system exhibits long-range order of hundreds on nm, which then decreased in size upon heating. From NMR studies, negligible changes in chemical shifts or rotational mobility of the IL protons over the temperature range encompassing the miscible region were found. The DLS and NMR data reveal the ionic liquids formed aggregates in the aqueous phase rather than undergo major restructuring to fully solvated ions.
We further identified order of magnitude changes in the concentration of the residuals both phases after phase separation (IL in water rich and water in the IL rich). More significant and unexpected changes were observed in the aqueous IL-rich phase that revealed scatters on the micron scale. Currently experimental techniques are unable to elucidate the organizational structure of the aqueous phase.
Methods
IL synthesis
[P4444][DMBS] was prepared by dissolving commercially available tetrabutylphosphonium hydroxide solution (40%) and sodium 2,4-dimethylbenzene sulfonate (slight molar excess) in deionized water and stirring overnight. Note: commercially available tetrabutylphosphonium bromide was initially used, but resulted in cation molar excess after purification. The dissolved mixture was then rinsed three times with dichloromethane to extract the ionic liquid, and further purified with three washings of deionized water. The solvent was removed by rotary evaporation at 70 °C and the ionic liquid was further dried in a vacuum oven for at least 48 h at 100 °C. 1H NMR (500 MHz, Deuterium Oxide) δ 7.78 (d, 1 H), 6.99 (s, 1 H), 6.96 (d, 1 H), 2.60 (s, 3 H), 2.26 (s, 3 H), 2.07–1.98 (m, 8 H), 1.43–1.35 (m, 16 H), 0.89 (t, 12 H).
Dynamic light scattering
Dynamic light scattering experiments were carried out using an ALV-6010/ 200 Multiple Tau Digital Correlator with a 632 nm HeNe laser and a 1 cm cuvette containing a U-shaped channel for external liquid flow enabling temperature-controlled measurements with a water–heater chiller within 0.05 °C. The flow channel prevented 90° scattering detection, so scattered light was collected in a backscatter geometry with a collection angle of 165°. Scans were collected for 90 s and averaged over multiple data acquisitions. Temperature-dependent viscosity of the solutions were measured with a TA Rheometer equipped with a Peltier temperature controller at a 200 rev s−1 shear rate. Temperature-dependent refractive index was measured with an Abbe DR-M2 refractometer at 589 and 680 nm, and extrapolated to 632 nm. (The methods for the viscosity and refractive index are summarized at Supplementary Note 1. The viscosity and refractive results value are presented in Supplementary Figs. 1 and 2, respectively.)
Water activity
Water activity, aw, of solutions and polymeric matrixes was measured via non-contact resistive electrolytic sensor technology on a Novasina LabMaster Standard Water Activity Instrument (range −0.003 to 1.00 aw, with an accuracy of +/−0.003 aw) with Full Temperature Control (0–50 °C, with an accuracy of +/−0.3 °C).
Molecular dynamics simulation
All-atom AMBER force fields for potential energy U were used in the MD simulation of this system.
The first term describes the non-bonded interactions including Van der Waals as the Lennard-Jones 12-6 form and Coulombic forces from atom-centered partial charges. The following terms in the potential energy equation represent, respectively, bonds, angles and torsional interactions. A hybrid bond potential was applied: the Morse potential for the OH bond in water and a harmonic potential for others. The force field parameters of atomistic [P4444] cation and [DMBS] anion were developed in previous works48, 49 and summarized in Supplementary Tables 1–5. A flexible water model50 based on a four-site water model of TIP4P/2005 was employed for water molecules, which depicts well the dynamics and bulk properties of the condensed water. In particular, the flexibility of the OH bond distance and HOH angle enables observation of the structural behavior, which provides this information about directional bonding, e.g., hydrogen bonding. The VdW interaction parameters between unlike atoms were obtained by the Lorentz−Berthelot combining rule. The non-bonded interactions separated by exactly three consecutive bonds (1–4 interactions) were reduced by related scaling factors51, 52, which were optimized as 0.50 for VdW interactions and 0.83 for electrostatic interactions, respectively. Atomic charges were calculated using a web base calculator, AtomicChargeCalculator, via the Electronegativity Equalization Method (EEM)53. The schematic molecular structures and partial charges of the [P4444] cation and [DMBS] anion and water molecule of the flexible TIP4P/2005 water model are presented in Supplementary Fig. 3.
The MD simulation was performed using the LAMMPS package with standard three-dimensional periodic boundary conditions. The non-bonded interactions were cut off at 15 Å while the Ewald summation method was applied to treat the long-range electrostatic interactions. All simulations were carried out at isothermal-isobaric conditions in the Nose-Hoover NPT ensemble with time coupling constants of 25 and 250 fs, respectively. After an initial relaxation with short time steps and an equilibration with long time steps, additional simulations of 12 ns of the ensemble at each temperature were further performed with a fixed time step of 0.25 fs. The atomic trajectories of simulation were recorded with an interval of 1 ps for post-analysis.
For Fig. 3, 80 pairs of [P4444][DMBS] and 1920 water molecules were initially displayed without an overlap, corresponding 50.8 wt.% of ILs in IL|water mixtures. A total of four different temperature cases were performed at atmospheric condition: Two cases of below Tc (10, 20 °C) and two cases of above Tc (50, 60 °C). Temperature conditions far from the measured Tc were selected because the temperature of the liquid states in MD simulation fluctuates by 10 °C up and down. The MD simulation setup for [P4444][BnzSO3] is explained at Supplementary Note 2.
Nuclear magnetic resonance
Variable-temperature 1H Nuclear Magnetic Resonance (VT-NMR) was obtained with a Bruker Avance 500 MHz magnet equipped with a 5 mm PABBO BB/19F-1H/D Z-GRD Z119470/0057 probe head and airflow temperature control within 0.1 °C. All samples were given ample time to equilibrate between temperature changes. Experiments were collected in a coaxial tube, with the inner tube containing DMBS-d6 and tetramethylsilane as the lock and reference, and the outer tube containing the sample54, 55. Aqueous mixtures for NMR experiments used D2O with 5–10 wt.% of H2O to give a comparable HOD intensity to IL signal. Spin-lattice relaxation times (t1) were collected using the inversion recovery method (180-τ-90-acq) with 10–12 geometrically spaced delay times, DS = 2, NS = 8, and 4–5 × t1 times between scans. Nuclear Overhauser Effect (NOEs) were measured using 2D-T-ROESY (Rotating-frame Overhauser Spectroscopy) and the roesyphpp.2 pulse sequence with spectrum width of 8 ppm, 300 ms mixing time, 10 s delay time, 1024 × 256 data points, NS = 8, and DS = 16. Spectra were processed with a sine-square 90° apodization and then phase corrected and baseline subtracted in both dimensions.
Raman spectroscopy
Raman spectroscopy was collected using a Horiba Confocal Raman Microscope with an Ar Ion Laser centered at 488 nm. Laser power levels were verified to be in the linear response regime and low power levels to prevent sample degradation. Samples were sandwiched between glass slides to prevent water evaporation and the temperature was controlled with a temperature-controlled stage connected to a temperature-controlled water bath with 0.1 °C sensitivity.
Data availability
The data supporting the findings of this study are available within the article and its Supplementary Information file or from the corresponding author upon reasonable request.
References
Welton, T. Room-temperature ionic liquids. solvents for synthesis and catalysis. Chem. Rev. 99, 2071–2084 (1999).
Lu, J., Yan, F. & Texter, J. Advanced applications of ionic liquids in polymer science. Prog. Polym. Sci. 34, 431–448 (2009).
Seddon, K. R. Ionic liquids: a taste of the future. Nat. Mater. 2, 363–365 (2003).
Earle, M. J. et al. The distillation and volatility of ionic liquids. Nature 439, 831–834 (2006).
Chiappe, C. & Pieraccini, D. Ionic liquids: solvent properties and organic reactivity. J. Phys. Org. Chem. 18, 275–297 (2005).
Ngo, H. L., LeCompte, K., Hargens, L. & McEwen, A. B. Thermal properties of imidazolium ionic liquids. Thermochim. Acta 357-358, 97–102 (2000).
Dupont, J. & Suarez, P. A. Z. Physico-chemical processes in imidazolium ionic liquids. Phys. Chem. Chem. Phys. 8, 2441–2452 (2006).
Dupont, J., Fonseca, G. S., Umpierre, A. P., Fichtner, P. F. P. & Teixeira, S. R. Transition-metal nanoparticles in imidazolium ionic liquids: recycable catalysts for biphasic hydrogenation reactions. J. Am. Chem. Soc. 124, 4228–4229 (2002).
Mok, Y. et al. Circulatory osmotic desalination driven by a mild temperature gradient based on lower critical solution temperature (LCST) phase transition materials. Phys. Chem. Chem. Phys. 15, 19510–19517 (2013).
Kohno, Y., Saita, S., Murata, K., Nakamura, N. & Ohno, H. Extraction of proteins with temperature sensitive and reversible phase change of ionic liquid/water mixture. Polym. Chem. 2, 862–867 (2011).
Ambadipudi, S., Biernat, J., Riedel, D., Mandelkow, E. & Zweckstetter, M. Liquid–liquid phase separation of the microtubule-binding repeats of the Alzheimer-related protein Tau. Nat. Commun. 8, 275 (2017).
Passos, H., Luís, A., Coutinho, J. A. & Freire, M. G. Thermoreversible (ionic-liquid-based) aqueous biphasic systems. Sci. Rep. 6, 20276 (2016).
Vander Hoogerstraete, T., Onghena, B. & Binnemans, K. Homogeneous liquid–liquid extraction of metal ions with a functionalized ionic liquid. J. Phys. Chem. Lett. 4, 1659–1663 (2013).
Cai, Y. et al. Energy-efficient desalination by forward osmosis using responsive ionic liquid draw solutes. Environ. Sci. Water Res. Tech. 1, 341–347 (2015).
Zhong, Y. et al. Using UCST ionic liquid as a draw solute in forward osmosis to treat high-salinity water. Environ. Sci. Tech. 50, 1039–1045 (2015).
Darvishmanesh, S., Pethica, B. A. & Sundaresan, S. Forward osmosis using draw solutions manifesting liquid-liquid phase separation. Desalination 421, 23–31 (2017).
Nakayama, D. et al. Lower critical solution temperature (LCST) phase separation of glycol ethers for forward osmotic control. Phys. Chem. Chem. Phys. 16, 5319–5325 (2014).
Cai, Y. et al. Towards temperature driven forward osmosis desalination using Semi-IPN hydrogels as reversible draw agents. Water Res. 47, 3773–3781 (2013).
Paricaud, P., Galindo, A. & Jackson, G. Understanding liquid-liquid immiscibility and LCST behaviour in polymer solutions with a Wertheim TPT1 description. Mol. Phys. 101, 2575–2600 (2003).
Kartzmark, E. System triethylamine–water: the equilibrium diagram and some physical properties. Can. J. Chem. 45, 1089–1091 (1967).
Yu, M. & Nishiumi, H. Theory of phase separation in mixtures with lower critical solution temperature. J. Phys. Chem. 96, 842–845 (1992).
Fukumoto, K. & Ohno, H. LCST-type phase changes of a mixture of water and ionic liquids derived from amino acids. Angew. Chem. Int. Ed. 46, 1852–1855 (2007).
Fukaya, Y., Sekikawa, K., Murata, K., Nakamura, N. & Ohno, H. Miscibility and phase behavior of water–dicarboxylic acid type ionic liquid mixed systems. Chem. Commun. 0, 3089–3091 (2007).
Kohno, Y., Arai, H., Saita, S. & Ohno, H. Material design of ionic liquids to show temperature-sensitive LCST-type phase transition after mixing with water. Aust. J. Chem. 64, 1560–1567 (2012).
Kohno, Y. & Ohno, H. Ionic liquid/water mixtures: from hostility to conciliation. Chem. Commun. 48, 7119–7130 (2012).
Kohno, Y. & Ohno, H. Temperature-responsive ionic liquid/water interfaces: relation between hydrophilicity of ions and dynamic phase change. Phys. Chem. Chem. Phys. 14, 5063–5070 (2012).
Ando, T., Kohno, Y., Nakamura, N. & Ohno, H. Introduction of hydrophilic groups onto the ortho-position of benzoate anions induced phase separation of the corresponding ionic liquids with water. Chem. Commun. 49, 10248–10250 (2013).
Fukaya, Y. & Ohno, H. Hydrophobic and polar ionic liquids. Phys. Chem. Chem. Phys. 15, 4066–4072 (2013).
Saita, S., Kohno, Y., Nakamura, N. & Ohno, H. Ionic liquids showing phase separation with water prepared by mixing hydrophilic and polar amino acid ionic liquids. Chem. Commun. 49, 8988–8990 (2013).
McNally, J. S., Wang, X. P., Hoffmann, C. & Wilson, A. D. Self-assembly of molecular ions via like-charge ion interactions and through-space defined organic domains. Chem. Commun. 53, 10934–10937 (2017).
Li, W. & Wu, P. Unusual thermal phase transition behavior of an ionic liquid and poly(ionic liquid) in water with significantly different LCST and dynamic mechanism. Polym. Chem. 5, 5578–5590 (2014).
Morita, T., Miki, K., Nitta, A., Ohgi, H. & Westh, P. Effects of constituent ions of a phosphonium-based ionic liquid on molecular organization of H2O as probed by 1-propanol: tetrabutylphosphonium and trifluoroacetate ions. Phys. Chem. Chem. Phys. 17, 22170–22178 (2015).
Zavitsas, A. A. Properties of water solutions of electrolytes and nonelectrolytes. J. Phys. Chem. B 105, 7805–7817 (2001).
Kohno, Y., Deguchi, Y. & Ohno, H. Ionic liquid-derived charged polymers to show highly thermoresponsive LCST-type transition with water at desired temperatures. Chem. Commun. 48, 11883–11885 (2012).
Zhao, Y., Wang, H., Pei, Y., Liu, Z. & Wang, J. Understanding the mechanism of LCST phase separation of mixed ionic liquids in water by MD simulations. Phys. Chem. Chem. Phys. 18, 23238–23245 (2016).
Wang, R., Leng, W., Gao, Y. & Yu, L. Microemulsion-like aggregation behaviour of an LCST-type ionic liquid in water. RSC Adv. 4, 14055–14062 (2014).
Nitta, A. et al. Density fluctuations in aqueous solution of ionic liquid with lower critical solution temperature: mixture of tetrabutylphosphonium trifluoroacetate and water. Chem. Phys. Lett. 628, 108–112 (2015).
Hayes, R., Warr, G. G. & Atkin, R. Structure and nanostructure in ionic liquids. Chem. Rev. 115, 6357–6426 (2015).
Feng, S. & Voth, G. A. Molecular dynamics simulations of imidazolium-based ionic liquid/water mixtures: alkyl side chain length and anion effects. Fluid Ph. Equilibria 294, 148–156 (2010).
Wang, Y.-L. et al. Atomistic insight into tetraalkylphosphonium-bis(oxalato)borate ionic liquid/water mixtures. I. Local microscopic structure. J. Phys. Chem. B 119, 5251–5264 (2015).
Nitta, A., Morita, T., Nishikawa, K. & Koga, Y. Mixing scheme of an aqueous solution of tetrabutylphosphonium trifluoroacetate in the water-rich region. Phys. Chem. Chem. Phys. 19, 16888–16896 (2017).
Smith, G. D., Bedrov, D. & Borodin, O. Molecular dynamics simulation study of hydrogen bonding in aqueous poly (ethylene oxide) solutions. Phys. Rev. Lett. 85, 5583–5586 (2000).
Ishihara, Y. et al. A precise and fast temperature mapping using water proton chemical shift. Magn. Reson. Med. 34, 814–823 (1995).
Modig, K., Pfrommer, B. G. & Halle, B. Temperature-dependent hydrogen-bond geometry in liquid water. Phys. Rev. Lett. 90, 075502 (2003).
Yaghini, N., Nordstierna, L. & Martinelli, A. Effect of water on the transport properties of protic and aprotic imidazolium ionic liquids–an analysis of self-diffusivity, conductivity, and proton exchange mechanism. Phys. Chem. Chem. Phys. 16, 9266–9275 (2014).
Wang, G. & Wu, P. In-depth study of the phase separation behaviour of a thermoresponsive ionic liquid and a poly(ionic liquid) in concentrated aqueous solution. Soft Matter 11, 5253–5264 (2015).
Tsukahara, T., Hibara, A., Ikeda, Y. & Kitamori, T. NMR study of water molecules confined in extended nanospaces. Angew. Chem. Int. Ed. 46, 1180–1183 (2007).
Zhou, G., Liu, X., Zhang, S., Yu, G. & He, H. A force field for molecular simulation of tetrabutylphosphonium amino acid ionic liquids. J. Phys. Chem. B 111, 7078–7084 (2007).
He, X., Guvench, O., MacKerell, A. D. Jr & Klein, M. L. Atomistic simulation study of linear alkylbenzene sulfonates at the water/air interface. J. Phys. Chem. B 114, 9787–9794 (2010).
González, M. A. & Abascal, J. L. A flexible model for water based on TIP4P/2005. J. Chem. Phys. 135, 224516 (2011).
Cornell, W. D. et al. A second generation force field for the simulation of proteins, nucleic acids, and organic molecules. J. Am. Chem. Soc. 117, 5179–5197 (1995).
Liu, Z., Huang, S. & Wang, W. A refined force field for molecular simulation of imidazolium-based ionic liquids. J. Phys. Chem. B 108, 12978–12989 (2004).
Ionescu, C.-M. et al. AtomicChargeCalculator: interactive web-based calculation of atomic charges in large biomolecular complexes and drug-like molecules. J. Chemin. 7, 50 (2015).
Wilson, A. D. & Stewart, F. F. Structure–function study of tertiary amines as switchable polarity solvents. RSC Adv. 4, 11039–11049 (2014).
Wilson, A. D. & Orme, C. J. Concentration dependent speciation and mass transport properties of switchable polarity solvents. RSC Adv. 5, 7740–7751 (2015).
Acknowledgements
This work was supported by funding from the Assistant Secretary for Energy Efficiency and Renewable Energy, Geothermal Technologies Office of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231 for Lawrence Berkeley National Laboratory. Work at the Molecular Foundry, Lawrence Berkeley National Laboratory, was supported by the Office of Science, Office of Basic Energy Sciences, of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231. Work conducted at Idaho National Laboratories was performed under Contract No. DE-AC07-05ID14517. H.K. gratefully acknowledges financial support from Kwanjeong Educational Foundation. J.F.D. acknowledges the support of Dr. Kevin Wilson and the Director, Office of Energy Research, Office of Basic Energy Sciences, Chemical Sciences, Geosciences, and Biosciences Division of the U.S. Department of Energy. We want to thank Dr. Chih-hao Hsu and Dr. Stephen Whitelam for important discussions and Dr. Sujoy Roy for his provision of equipment necessary to perform dynamic light scattering measurements.
Author information
Authors and Affiliations
Contributions
D.E.S. designed and performed the majority of the experiments and wrote the manuscript. H.K. and J.J.U. carried out the MD simulations and data interpretation, and wrote the manuscript. J.F.D. assisted in performing DLS experiments. A.D.W. carried out water activity measurements, assisted in data interpretation, and writing of the manuscript. R.K. conceived and supervised the project, and assisted in writing the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kang, H., Suich, D.E., Davies, J.F. et al. Molecular insight into the lower critical solution temperature transition of aqueous alkyl phosphonium benzene sulfonates. Commun Chem 2, 51 (2019). https://doi.org/10.1038/s42004-019-0151-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42004-019-0151-2
This article is cited by
-
A review of zero liquid discharge and solvent driven aqueous phase processes for brine treatment
Clean Technologies and Environmental Policy (2024)
-
Combinatorial discovery of small-molecule 1,2,3-triazolium ionic liquids exhibiting lower critical solution temperature phase transition
Scientific Reports (2020)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.