Abstract
There has been extensive research on the sensing of explosive nitroaromatic compounds (NACs) using fluorescent metal-organic frameworks (MOFs). However, ambiguity in the sensing mechanism has hampered the development of efficient explosive sensors. Here we report the synthesis of a hydroxyl-functionalized MOF for rapid and efficient sensing of NACs and examine in detail its fluorescence quenching mechanisms. In chloroform, quenching takes place primarily by exciton migration to the ground-state complex formed between the MOF and the analytes. A combination of hydrogen-bonding interactions and π–π stacking interactions are responsible for fluorescence quenching, and this observation is supported by single-crystal structures. In water, the quenching mechanism shifts toward resonance energy transfer and photo-induced electron transfer, after exciton migration as in chloroform. This study provides insight into florescence-quenching mechanisms for the selective sensing of NACs and reduces the ambiguity regarding the nature of interactions between the MOF and NACs.
Similar content being viewed by others
Introduction
Metal-organic frameworks (MOFs) have been widely used as fluorescence-based sensors for cations, anions, small molecules, explosives, and solvents owing to their pore size variability and easy modulation of the functional moiety for tuning host–guest interactions1,2,3,4. In this regard, there has been continuous research using fluorescent MOFs for the sensing of nitroaromatic compounds (NACs)5,6,7,8, which are considered highly explosive9,10,11,12 and toxic to human and aquatic life13,14,15. However, the development of highly selective and sensitive sensors for explosives still remains a challenge owing to the lack of strong evidence that can unveil the interactions involved in the sensing mechanism.
A fluorescent MOF can be considered as an ensemble of fluorophores that behaves in a different manner than a fluorescent molecule. Energy of an excited fluorophore in an MOF can be rapidly transferred to surrounding fluorophores across the network of the MOF, as the fluorophores in the MOF are periodically arrayed throughout the crystal16,17. In addition, the porosity of MOF provides confined spaces for analytes to be in close proximity with fluorophores, facilitating interactions between them. The interactions in confined spaces may restrict diffusion of the analyte, resulting in different dynamics of the quenching process compared with an analyte dissolved in solvent following collisional quenching processes. Irrespective of the type of quenching mechanism operating, the most important factor for quenching is the distance between fluorophore and the quencher18,19. Hence, the investigation of the interactions operating between fluorophore and the quencher is of outmost importance.
In this paper, we report the synthesis of a new hydroxyl-functionalized indium MOF analogous to MIL-53(Cr)20 for sensing nitro-compounds and their fluorescence quenching mechanisms. To explore the robustness of applicability of the MOF, we chose non-polar (chloroform) and polar (water) solvents and investigated their influences on the sensing mechanism (Fig. 1). In chloroform, quenching takes place mainly by exciton migration (EM) to the ground-state complex (GSC) already formed between the MOF and the analytes. The GSC shows non-emissive behavior owing to photo-induced electron transfer (PET) between the ligand moiety and analyte. Availability of the free hydroxyl moiety of the ligand and the µ2-hydroxyl group of the framework provide extensive hydrogen-bonding interactions with analyte molecules in addition to π–π stacking interactions of the aromatic residue of the ligand in enhancing florescence quenching, which is supported by single-crystal structures for the first time. Conversely, in water at low concentrations, the quenching mechanism shifts to mostly resonance energy transfer (RET) after EM. Further more, at higher concentrations more analyte can diffuse inside, and PET also participates in quenching along with RET. The efficiency of RET originates from the large spectral overlap between MOF emission and 2,4,6-trinitrophenol (TNP) absorption. To the best of our knowledge, the MOF has a quenching constant comparable to the highest values known for MOF-based sensors for TNP in aqueous medium21,22,23,24. This study provides detailed mechanistic insight into the sensing behavior of MOF for analytes, and clarifies the interactions responsible for selectivities of analytes.
Results
Synthesis
Synthesis of (DMF)x(H2O)y@[In(OH)(H2DOBDC)], 1 was carried out by reacting In(NO3)3·xH2O and 2,5-dihydoxy-1,4-benzenedicarboxylic acid (H4DOBDC) in a solution containing N,N-dimethylformamide (DMF) and H2O at 85 °C for 1 d. The as-synthesized 1 has the same network topology as that of the reported pristine MIL-53(Cr) framework (Supplementary Fig. 1 and Supplementary Table 1)20. Activated 1a was prepared by vacuuming (~10−2 torr) the as-synthesized sample, presoaked in acetone at 150 °C for 1 d (Supplementary Figs. 2–6). 1w (1a in water) was prepared by simply soaking as-synthesized 1 in water (Supplementary Figs. 7–9 and Supplementary Table 2). MOF crystals with TNP, 4-nitrophenol (4-NP), 2,6-dinitrotoulene (2,6-DNT), and 2,4-dinitrotoulene (2,4-DNT) in chloroform were successfully prepared by soaking in a saturated solution of the corresponding analyte in CHCl3 (Supplementary Table 3–6). See also Supplementary Data 1–6.
Sensing of NACs
When fluorescence-quenching titrations were performed in the presence of nitro-compounds such as TNP, 2,4-dinitrophenol (2,4-DNP), 4-NP, trinitrophenol (TNT), 2,4-DNT, 2,6-DNT, 4-nitrotoluene (4-NT), 1,3-dinitrobenzene (1,3-DNB), 1,4-dinitrobenzene (1,4-DNB), nitrobenzene (NB), 2,3-dimethyl-2,3-dinitrobutane (DMNB), and nitromethane (NM) in chloroform (Fig. 2a and Supplementary Figs. 10–20), the highest quenching was observed with TNP (93%). When the fluorescence response of 1c (1a in chloroform), with the addition of TNP was plotted according to the Stern-Volmer (SV) (eq. 1), it exhibited a straight line (Fig. 2b), indicating that a single quenching mechanism was operating18,19.
Fluorescence spectra. Fluorescence spectra of the MOF and SV plots with the addition of TNP, a fluorescence spectra showing response on the incremental addition of the solution of TNP (1 mm) in chloroform, b SV plot with the addition of all analytes to 1c, c fluorescence response of 1w upon incremental addition of solution of TNP (1 mm) in water, and d SV plot with the addition of TNP to 1w, where the least-squares fitting line was obtained using data up to the concentration of TNP of 0.045 mm
where I0 is the initial fluorescence intensity (before the addition of analyte), I the fluorescence intensity in the presence of analyte, [A] the molar concentration of analyte, and Ksv the quenching constant (M−1). For TNP, the highest Ksv value (1.65 × 105 M−1) (Fig. 2b and Supplementary Fig. 21) and very low detection limit of 73 ± 15 ppb (Supplementary Note 1, Supplementary Fig. 22a and Supplementary Table 7) were observed.
Excellent stability in water and good quantum yield (0.14) of the MOF are promising for sensing NACs in water. The fluorescence spectra of the MOF in water were also recorded with excitation at 352 nm and monitored in response to the addition of analytes (Fig. 2c and Supplementary Figs. 23–33). The quenching behavior of the nitrophenols in water was the same as the quenching trend in chloroform, whereas other analytes in water behaved differently. The highest quenching efficiency was achieved with TNP, followed by 2,4-DNP and 4-NP upon the addition of 200 µL of 1 mM aqueous solution (Fig. 2c and Supplementary Fig. 34) Quantitative examination of fluorescence quenching efficiency using the SV relationship (described previously) showed the highest efficiency for TNP (Ksv = 8.33 × 104 M−1) when calculated at low analyte concentration with a linear plot (Fig. 2d) and detection limit of 66 ± 8 ppb (Supplementary Note 1 and Supplementary Fig. 22b). At higher concentrations, the plot starts deviating upward from linearity. TNP shows the highest Ksv among the analytes, indicating the selectivity for TNP by the MOF.
GSC and PET
Static quenching is a non-diffusional type of quenching mechanism that results in the quenching of fluorescence by forming a non-fluorescent GSC with an analyte. This type of complex formation is generally accompanied by change in the UV–Vis spectrum of an original fluorophore by a quencher25. To check the possibility of static quenching in chloroform, the absorption spectra of the MOF with and without analytes were measured. The emerging peak at approximately 260 nm in the UV–Vis spectrum of the MOF with TNP in chloroform indicates the formation of a stable GSC (Supplementary Fig. 35).
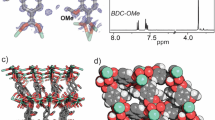
To gain further insight into the interactions leading to complexation of analytes with the MOF, we obtained MOF crystals with the analytes. The crystal structures of MOF with different analytes reveal the crucial roles of both hydrogen-bonding and π–π stacking interactions in forming the GSC, resulting in static quenching (Fig. 3 and Supplementary Figs. 36–41). Since the MOF crystals with TNP shows severe disorder of TNP molecules inside the pores, the exact interactions of TNP with the framework could not be revealed by structure determination. The presence of TNP molecules (approximately a half TNP per H2DOBDC ligand) inside the pore was confirmed by digesting the MOF with acid and analyzing the ratio of TNP and H2DOBDC ligand by using 1H NMR spectroscopy (Supplementary Fig. 42). Further, to have better understanding of interaction of TNP with the framework, the difference Fourier map that shows diffused electron densities inside the pore was plotted using OLEX2 software26 (Fig. 4). Electron-density map suggests that TNP has strong π–π interaction with a ligand moiety. The dense-electron density at the right upper corner indicates the alignment of two nitro groups and one hydroxyl residue of TNP, which may have hydrogen-bonding interactions with the µ2-hydroxyl group ligated to indium metal, whereas its opposite-side nitro group has less-electron density near the statistically disordered ligands in the crystal structure. The deformation/bending of the ligand near the opposite-side nitro group of TNP and perpendicular to the TNP molecule in the framework is owing to steric repulsion between the ligand and the opposite-side nitro group of TNP. Slightly larger dimension of TNP molecule than the pore dimension parallel to the ligand results in the ligand deformation/bending and leads to statistical disordering of the ligands that are not involved in the π–π stacking interaction in the crystal structure. Although we failed obtaining ordered TNP molecules interacting with the framework in the single-crystal structure, the deformation/bending of the ligands is an indication of the presence of strong interactions between TNP and the framework. Stronger interactions between the framework and the analyte via hydrogen-bonding and π–π stacking lead to stronger complexation, which subsequently leads to more efficient quenching. The above results unveil the major role of GSC as a static quenching mechanism.
The framework of the MOF with TNP in chloroform and the difference Fourier map. Electron densities in the solvent pore indicate the presence of TNP and/or solvent CHCl3 molecules near the framework. The two linkers connecting the same two metal ions are the statistically disordered H2dobdc ligands in the crystal structure
The formation of a stronger GSC results in more efficient quenching and this is because of more efficient PET. The energy difference between the lowest occupied molecular orbital (LUMO) of MOF and the LUMO of the analyte is the driving force for the PET process18,19,27, however, poor correlation between the Ksv values in chloroform and the energy differences was observed (Fig. 5a and Supplementary Fig. 43). The energy differences between the LUMO of MOF and the LUMO of the analytes are calculated using the Gaussian 09 package with B3LYP/6–31 G* basis set under the polar continuum of the chloroform medium. On the other hand, when we computationally optimized the geometry of GSC formed between the fluorophore moiety of MOF and analytes, the highest occupied molecular orbital resides only on the fluorophore, whereas the LUMO resides mainly on the analytes (Supplementary Figs. 44–46). This suggests that PET probably operates in chloroform for the quenching of MOF and the efficiency of the PET not only depends on the energy difference between LUMOs of MOF and analyte, but also depends on the overlap of orbitals between the fluorophore and the analyte. The overlap of orbitals that leads efficient PET is better when the complexation between MOF and analyte is stronger. Generally, when a GSC forms between MOF and an analyte, the new complex appears to be non-emmisive, when this complex is photo-excited, the electron of the fluorophore moeity migrates to the LUMO of analyte forming a dark state.
Correlation graphs for comparison in the trend of Ksv values and energy differences between LUMO of the MOF and the LUMOs of the different analytes. Data are reported in a chloroform and b water. c Spectral overlap between the emission spectrum of the MOF and the absorptions of the analytes in water, and d correlation graph for comparing the trend of Ksv values and the overlap integral (J) values for the different analytes in water
To investigate whether the static quenching process also functions in water in the aforementioned manner, ground-state complexation was checked in water. In this case, negligible change was recognized in the UV–Vis spectrum of the MOF with TNP when compared with the UV–Vis spectrum of the MOF, only the convolution of the spectra of the MOF and TNP were noticed (Supplementary Fig. 47). Peak shift or spectral variation in a fluorescence spectrum can also reflect interaction between a fluorophore and an analyte in the ground and excited states5,28. To clarify ground-state complexation of the MOF with analytes the fluorescence spectrum of the MOF in water was first recorded, followed by the incremental addition of analyte. The fluorescence spectra showed red shift (by 15 nm) of the emission peak in the case of TNP (Supplementary Fig. 48a). DNP and NP also showed similar red shifts, but the extents of the shifts were not as significant (Supplementary Figs. 48b and c). These observations indicate weak ground-state complexation between the MOF and the analytes in water.
Failure to obtain crystal structures with ordered analyte molecules inside the pores in water also supports the absence of strong interactions between the MOF and the analytes. Water molecules have higher hydrogen-bond forming affinity with the MOF than the analytes and hamper the formation of strongly bound analyte@MOF complexes.
RET
Dynamic quenching is a diffusion-controlled process and the efficiency of the RET process depends on the degree of spectral overlap integral between donor (fluorophore) emission and acceptor (quencher) absorption along with the quantum efficiency of the fluorophore18,29. As depicted in Supplementary Fig. 49, there is no spectral overlap between the emission of 1c and the absorption of the analyte in chloroform, which rules out the RET process in chloroform.
In the case of water, calculation of the overlap integral of the MOF emission and analyte absorption (Supplementary Table 8) indicates the highest overlap integral value for TNP (Fig. 5c). The graph of quenching efficiency vs. overlap integral value for the analytes revealed a strong linear relationship, indicating increase in quenching efficiency with increase in overlap integral value (Fig. 5d). Furthermore, to check the role of the RET process in quenching, I/I0 was plotted against the overlap integral for TNP, DNP, and NP (Supplementary Figs. 50–52). A linear dependence of the overlap integral with I/I0 for all three analytes was observed, indicating the operation of the RET mechanism in water.
For RET to occur throughout the system, it is essential for the analyte to diffuse into pores of the MOF, as the dimension of the bulk MOF crystals is much larger than the operating range of the RET process. In general, the RET process occurs at 1–5 nm between an energy donor and an energy acceptor. In MOF, the range can be further extended to 50 nm through EM among adjacent fluorophores that are arranged in a periodic manner throughout the framework16,17. However, as the dimension of the MOF crystals (~ 35 µm) is much larger than the maximum operating range of the RET process, most interactions between the fluorophores and the quenchers occur not on the surface but within pores of the MOF. The interactions within pores were validated from the powder X-ray diffraction (PXRD) pattern change in the presence of the analytes. At low concentrations of analytes, no noticeable changes were observed in the PXRD patterns of the MOF (Supplementary Fig. 53). However, when the amount of the analyte was increased, moderate changes in the PXRD patterns were noticed (Supplementary Fig. 54). At higher concentration when the more TNP molecules diffuse inside the pore, the more-effective interaction seems to operate between the MOF and TNP.
In the case of water, RET is mostly operating at low concentration with negligible PET because RET can even operate with far distance. But at higher concentration, when more of analytes diffuse inside the pore and interact with fluorophores, PET also becomes prominent and participate in quenching process. As a result, SV plot deviates from linearity and bends upward at higher concentration (Fig. 2d). Regarding PET there is also a poor correlation between the Ksv values and the energy differences (Fig. 5b). However, when only nitrophenols (TNP, 2,4-DNP, and 4-NP) are considered their Ksv values are in the order TNP > 2,4-DNP > 4-NP, correlating with the order of their energy differences TNP > 2,4-DNP > 4-NP which suggests that PET may also occur in the case of nitrophenols (TNP, 2,4-DNP, and 4-NP). It has been already shown in the description of GSC that the formation of GSC in water is weak, but as the pore dimension is around 10 Å, the analytes are in close proximity to the fluorophore and PET undergoes even in the case of water.
Fluorescence lifetime
Surprisingly, the fluorescence lifetime study of the MOF in chloroform in the presence of TNP showed decrease in the “average” lifetime, which is a typical feature of dynamic quenching (Fig. 6a and Table 1). The result seems to contrast with our anticipation of static quenching because the SV plot is linear as though there were only one type of quenching mechanism, i.e., PET in GSC operating. Careful analysis of the fluorescence decay profiles upon the addition of TNP shows that at least three exponential decay components must be considered to adequately fit the data. From the fit parameters listed in Table 1, it is inferred that acceleration of the average fluorescence decay time does not originate from the reduction of the lifetime of each component but from the increase of the fraction of the fastest relaxing component (τ1) at the expense of the fraction of the slowest relaxing component (τ3). For example, the fraction of the τ3 component case, which is as high as 0.31 in the absence of TNP, decreases upon addition of the analyte and eventually reaches almost zero (a3 = 0.01 at 200 μL addition of 1 mM solution of TNP). Decrease of the τ3 component can be related to the formation of a TNP@MOF complex component, as inferred from the crystal structure. On the other hand, the lifetime reduction of the τ2 component may be owing to change in the environment or in some non-interacting fluorophores. As the framework is flexible, the formation of a TNP@MOF complex with the interacting fluorophores in the MOF can induce slight conformational changes in the remaining uncomplexed fluorophore units, which leads to change in fluorescence lifetime. The combination of these changes leads to overall decrease in the average fluorescence lifetime of the MOF. All the observations made for sensing NACs in chloroform point to the conclusion that the quenching takes place mainly by EM to the GSC already formed between the MOF and the analytes, which is static.
The fluorescence lifetime of the MOF in water remained almost the same even in the presence of the analytes, indicating that the behavior of the quenching process is static (Fig. 6b and Table 1). Even though upward curvature in the SV plot indicates simultaneous operation of static and dynamic quenching processes at higher concentration of analytes, the lifetime study showed that the quenching of NACs in water originates mainly from the static process. The observation contradicts the dynamic nature of RET being responsible for the quenching of NACs in water. The MOF framework can be considered as an ensemble of periodically arrayed fluorophores that behaves differently from a free single fluorophore. MOF has pore space for analytes to penetrate and interact with fluorophores. The analytes interacting with the framework inside the pores have restricted mobility and therefore their diffusion ability is significantly suppressed. As a consequence of slow (or no) diffusion, the fluorescence lifetime of MOFs even in the presence of analytes appears steady and shows apparent static quenching behavior19,25,30. The series of work in this study suggests that to quench NACs in water, the MOF mainly utilizes the RET process at the low concentration of analytes, but at higher concentration RET along with PET (through weak ground-state complexation) participates in quenching mechanism. However, confined environments around the analytes inside the MOF result in the apparent static behavior of both quenching processes: RET and PET (weak ground-state complexation).
Exciton migration
When a fluorophore is excited with polarized light, the emission is depolarized with time as a result of rotational diffusion of the fluorophore. When fluorescence anisotropy, r(t), of the bare ligand H4DOBDC in chloroform was fitted to a single-exponential decay curve, r(t) = r0e−t/τ, the initial fluorescence anisotropy (r0) was obtained to be 0.17 with rotational time constant of ~ 200 ps (Supplementary Fig. 55 and Supplementary Table 9). On the other hand, the r0 value of the MOF was 0.09 with rotational time constant of ~ 150 ps. Because the bulky MOF cannot rotate on ps time scale, the τ value indicates that the fluorescence depolarization occurs through EM among the fluorophores across the network of the MOF within the fluorescence lifetime31. In addition, the lower initial anisotropy value for the MOF than that of the bare fluorophore indicates that a shorter range efficient EM path is also operative on the time scale shorter than the time resolution of our instrument (120 ps). When this EM reaches the fluorophore moiety bound to a TNP molecule (non-fluorescent GSC), the quenching of fluorescence takes place (Supplementary Fig. 56). This overall process leads to amplified quenching (93%) even though the quencher amount is only ~ 20% of the fluorophore. This type of quenching process has also been reported for a covalent-organic framework32.
The results of time-dependent fluorescence anisotropy measurements of the MOF in water suggest that similar EM occurs among arrayed fluorophores across the network of the MOF, as in the case of the MOF in chloroform. The initial fluorescence anisotropy value of the MOF, 0.17, is much smaller than that of the bare H4DOBDC ligand, 0.30 (Supplementary Fig. 57 and Supplementary Table 10). Even though the amount of the quencher is only ~ 7% of the fluorophore, the high quenching efficiency in water supports the assertion that the quenching process occurs via either direct RET between the excited fluorophore and the analyte or EM followed by RET (Supplementary Fig. 58). The sensitivity of the MOF for TNP in water is slightly higher than that in chloroform even though its quenching efficiency is slightly lower in water. Longer operation range of the RET process in water led to the more effective sensing of TNP in water.
Discussion
We synthesized a new fluorescent MIL-53 analog that is stable and flexible in both aqueous and organic solvents. The MOF shows very good sensing ability for NACs, exhibiting the highest efficiency for TNP in both chloroform and water. However, the quenching mechanisms in chloroform and in water are different. In chloroform, quenching takes place mainly by GSC between the MOF and the analyte, which is supported by single-crystal structures for the first time. The GSC shows non-emissive behavior owing to PET from fluorophore ligand moiety to analyte. The crystal structures clarify the importance of both hydrogen-bonding and π–π stacking interactions responsible for GSC. Thus, replacement of the benzene moiety of the ligand by a naphthalene, anthracene, or pyrene moiety for better π–π stacking interaction and introduction of a functional group capable of strong hydrogen-bonding interactions with an analyte will be a powerful approach for further enhancing the sensing efficiency. On the other hand, in a polar–protic solvent (like water) strong hydrogen-bonding ability of solvent hinders ground-state complexation, and therefore quenching occurs through RET and PET (weak ground-state complexation). The efficiency of the RET process can be improved by increasing the overlap integral between MOF emission and analyte absorption. In this regard, it is important to have a MOF with more blue-shifted emission to increase the spectral overlap integral with TNP. In the MOF, amplified quenching was observed regardless of the type of solvent owing to EM among the fluorophores throughout the framework. This study provides new insight into florescence-quenching mechanisms for the selective sensing of analyte and clears the ambiguity regarding the nature of interactions between the MOF and analyte.
Methods
Preparation of MOFs
(DMF)x(H2O)y@[In(OH)(H2DOBDC)], (1), where x and y are numbers of solvent DMF and water molecules, respectively, per formula unit. A mixture of In(NO3)2·xH2O (0.150 g, 0.50 mmol) and H4DOBDC (0.099 g, 0.50 mmol) was dissolved in 10 mL mixed DMF/water solvent (1:1 v/v). The solution in a tightly sealed 25 mL vial was heated at 85 °C for 1 d to form colorless crystals. The crystals harvested were washed using fresh DMF and then air-dried at ambient conditions for an hour. Yield = 0.135 g (81%). Fourier-transform infrared spectroscopy spectrum (KBr, cm–1) of the as-synthesized MOF: 3269 (m), 3062 (w), 2929 (w), 2869 (vw), 2164 (vw), 1658 (s), 1566 (s), 1483 (s), 1452 (s), 1375 (s), 1222 (s), 1116 (m), 1098 (m), 1060 (w), 920 (m), 864 (s), 808 (s), 783 (s), 661 (m). Elemental analysis (EA) was performed using the as-synthesized sample exposed for an hour to ambient conditions before the analysis. EA of (DMF)1.36(H2O)1.14@[(OH)2-MIL-53(In)], C4H4O16In, fw = 537.73 g/mol. Calculated: C, 32.39; H, 3.78; O, 33.92; N, 4.25%. Found: C, 31.81; H, 3.59; O, 33.42; N, 4.81%.
(H2O)x@[In(OH)(H2DOBDC)], (1w). 1w was prepared by simply soaking as-synthesized 1 in water for a week at ambient conditions, changing the water every day.
Preparation of nitrophenol-bound MOFs
Preparation of (TNP)0.5@[In(OH)(H2DOBDC)], (2). Approximately 50 mg of the crystals of 1a was soaked in a saturated solution of TNP in CHCl3. Crystals were collected after 1 day and washed with CHCl3.
Preparation of (4-NP)@[In(OH)(H2DOBDC)] (3), (2,6-DNT)0.5@[In(OH)(H2DOBDC)] (4) and (2,4-DNT)0.5@[In(OH)(H2DOBDC)], (5). Crystals of 3–5 were prepared according to the procedure used for 2, but using 4-NP, 2,6-DNT and 2,4-DNT, respectively, instead of TNP.
Measurement of UV–Vis spectra
In a typical UV–Vis experiment, 0.4 mg or 1.2 mg of 1a (the average crystal dimension of ~ 35 μm) was immersed in a cuvette with 3 mL CHCl3 or H2O, respectively. The mixture was sonicated for 10 min to make a fine suspension. A 0.1 mM NAC solution in CHCl3 or H2O was prepared for each analyte for the measurements. UV–Vis spectra were recorded in the range 250–800 nm.
Steady-state fluorescence measurements
In a typical steady-state fluorescence experiment, 0.4 mg or 1.2 mg of 1a (average crystal dimension of ~ 35 μm) was immersed in a cuvette with 2.5 mL CHCl3 or H2O, respectively. The mixture was sonicated for 10 min to make a fine suspension. The suspension was excited at 352 nm and the fluorescence emission was measured in the range 370–800 nm with incremental addition of analyte solutions (1 mM). The mixture was continuously stirred at constant rate to maintain homogeneity of the suspension.
Time-resolved fluorescence decay and anisotropy measurements
The fluorescence decay profiles were fitted using software provided by PicoQuant Instruments. The fluorescence anisotropies (r) of H4DOBDC and the MOF were investigated under polarized light. The time-dependent fluorescence anisotropy is given by r(t) = [I∥(t) – G·I⊥(t)]/[I∥(t) – 2·G·I⊥(t)], where I∥(t) and I⊥(t) are the time-resolved fluorescence intensities measured in the parallel and perpendicular directions with respect to the excitation and detector polarization, respectively. G-factor is the instrumental sensitivity ratio toward vertically and horizontally polarized light.
Data availability
The X-ray crystallographic coordinates for structures reported in this Article have been deposited at the Cambridge Crystallographic Data Centre (CCDC), under deposition number CCDC 1492751–1492756. These data can be obtained free of charge from The Cambridge Crystallographic Data Centre via www.ccdc.cam.ac.uk/data_request/cif. The remaining data supporting the findings of this study are available within the paper and its supplementary information file.
References
Allendorf, M. D., Bauer, C. A., Bhakta, R. K. & Houk, R. J. T. Luminescent metal–organic frameworks. Chem. Soc. Rev. 38, 1330–1352 (2009).
Cui, Y., Yue, Y., Qian, G. & Chen, B. Luminescent functional metal-organic frameworks. Chem. Rev. 112, 1126–1162 (2012).
Kreno, L. E. et al. Metal-organic framework materials as chemical sensors. Chem. Rev. 112, 1105–1125 (2012).
Lustig, P. W. et al. Metal–organic frameworks: functional luminescent and photonic materials for sensing applications. Chem. Soc. Rev. 46, 3242–3285 (2017).
Lan, A. et al. A luminescent microporous metal–organic framework for the fast and reversible detection of high explosives. Angew. Chem. Int. Ed. 48, 2334–2338 (2009).
Hu, Z., Deibert, B. J. & Li, J. Luminescent metal–organic frameworks for chemical sensing and explosive detection. Chem. Soc. Rev. 43, 5815–5840 (2014).
Zhang, L., Kang, Z., Xin, X. & Sun, D. Metal–organic frameworks based luminescent materials for nitroaromatics sensing. CrystEngComm 18, 193–206 (2016).
Nagarkar, S. S., Desai, A. V. & Ghosh, S. K. Engineering metal–organic frameworks for aqueous phase 2,4,6-trinitrophenol (TNP) sensing. CrystEngComm 18, 2994–3007 (2016).
McQuade, D. T., Pullen, A. E. & Swager, T. M. Conjugated polymer-based chemical sensors. Chem. Rev. 100, 2537–2574 (2000).
Germain, M. E. & Knapp, M. J. Optical explosives detection: from color changes to fluorescence turn-on. Chem. Soc. Rev. 38, 2543–2555 (2009).
Salinas, Y. et al. Optical chemosensors and reagents to detect explosives. Chem. Soc. Rev. 41, 1261–1296 (2012).
Giannoukos, S., Brkic, B., Taylor, S., Marshall, A. & Verbeck, G. F. Chemical sniffing instrumentation for security applications. Chem. Rev. 116, 8146–8172 (2016).
Wollin, K. M. & Dieter, H. H. Toxicological guidelines for monocyclic nitro-, amino- and aminonitroaromatics, nitramines, and nitrate esters in drinking water. Arch. Environ. Contam. Toxicol. 49, 18–26 (2005).
Shen, J. et al. Biodegradation of 2,4,6-trinitrophenol by Rhodococcus sp. isolated from a picric acid-contaminated soil. J. Hazard. Mater. 163, 1199–1206 (2009).
Thorne, P. G. & Jenkins, T. F. A field method for quantifying ammonium picrate and picric acid in soil. Field Anal. Chem. Technol. 1, 165–170 (1997).
Son, H.-J. et al. Light-harvesting and ultrafast energy migration in porphyrin-based metal-organic frameworks. J. Am. Chem. Soc. 135, 862–869 (2013).
Kent, C. A. et al. Light harvesting in microscale metal-organic frameworks by energy migration and interfacial electron transfer quenching. J. Am. Chem. Soc. 133, 12940–12943 (2011).
Lakowicz, J. R. Principles of Florescence Spectroscopy (Springer, Singapore, 331–352, 2010).
Valeur, B. Molecular Fluorescence: Principles and Applications (Wiley, Weinheim, 256–260, 2002).
Serre, C. et al. Very large breathing effect in the first nanoporous chromium(III)-based solids: MIL-53 or CrIII(OH).{O2C-C6H4-CO2}.{HO2C-C6H4-CO2H}x.H2Oy. J. Am. Chem. Soc. 124, 13519–13526 (2002).
Joarder, B., Desai, A. V., Samanta, P., Mukherjee, S. & Ghosh, S. K. Selective and sensitive aqueous-phase detection of 2,4,6-trinitrophenol (TNP) by an amine-functionalized metal–organic framework. Chem. Eur. J. 21, 965–969 (2015).
Mukherjee, S., Desai, A. V., Manna, B., Inamdar, A. I. & Ghosh, S. K. Exploitation of guest accessible aliphatic amine functionality of a metal−organic framework for selective detection of 2,4,6-trinitrophenol (TNP) in water. Cryst. Growth Des. 15, 4627–4634 (2015).
Qin, J. et al. Aqueous- and vapor-phase detection of nitroaromatic explosives by a water-stable fluorescent microporous MOF directed by an ionic liquid. J. Mater. Chem. A 3, 12690–12697 (2015).
Wang, B. et al. Highly stable Zr(IV)-based metal-organic frameworks for the detection and removal of antibiotics and organic explosives in water. J. Am. Chem. Soc. 138, 6204–6216 (2016).
Sanda, S., Parshamoni, S., Biswas, S. & Konar, S. Highly selective detection of palladium and picric acid by a luminescent MOF: a dual functional fluorescent sensor. Chem. Commun. 51, 6576–6579 (2015).
Dolomanov, O. V., Bourhis, L. J., Gildea, R. J., Howard, J. A. K. & Puschmann, H. OLEX2: a complete solution, refinement and analysis program. J. Appl. Cryst. 42, 339–341 (2009).
Pramanik, S., Zheng, C., Zhang, X., Emge, T. J. & Li, J. New microporous metal-organic framework demonstrating unique selectivity for detection of high explosives and aromatic compounds. J. Am. Chem. Soc. 133, 4153–4155 (2011).
Sun, L. et al. A novel (3,3,6)-connected luminescent metal–organic framework for sensing of nitroaromatic explosives. Dalton Trans. 42, 5508–5513 (2013).
Wu, P. & Brand, L. Resonance energy transfer: methods and applications. Anal. Biochem. 218, 1–13 (1994).
Buragohain, A., Yousufuddin, M., Sarma, M. & Biswas, S. 3D luminescent amide-functionalized cadmium tetrazolate framework for selective detection of 2,4,6-trinitrophenol. Cryst. Growth Des. 16, 842–851 (2016).
Zhang, Q. et al. Forster energy transport in metal-organic frameworks is beyond step-by-step hopping. J. Am. Chem. Soc. 138, 5308–5315 (2016).
Dalapati, S. et al. An azine-linked covalent organic framework. J. Am. Chem. Soc. 135, 17310–17313 (2013).
Acknowledgements
This work was supported by NRF (2016R1A5A1009405) through the National Research Foundation of Korea. We acknowledge PAL for beam line use (2017–1st-2D-012 and 2017–3rd-2D-028).
Author information
Authors and Affiliations
Contributions
M.S.L, O.H.K, and A.S. conceived and designed the experiments and co-wrote the paper. A.S. conducted most of the experiments and analyzed data. D.K. solved and analyzed the crystal structures. S.R. and J.H.P conducted the lifetime and anisotropy measurements and analyzed the data. J.S. and G.H.J did the adsorption measurements and analyzed the data. All authors discussed the results and commented on the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Sharma, A., Kim, D., Park, JH. et al. Mechanistic insight into the sensing of nitroaromatic compounds by metal-organic frameworks. Commun Chem 2, 39 (2019). https://doi.org/10.1038/s42004-019-0135-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42004-019-0135-2
This article is cited by
-
Optical properties evaluation on d and f metal ions based dicarboxylic MOFs for pollutant sensing
Bulletin of Materials Science (2023)
-
A Chromo-fluorogenic Probe for Selective Detection of Picric Acid Alongside Its Recovery by Aliphatic Amines and Construction of Molecular Logic Gates
Journal of Fluorescence (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.