Abstract
Density functional theory is central to the study of catalytic processes, but its accuracy is widely debated, and lack of data complicates accuracy estimates. To address these issues, this work explores a simple eight-step process of iron-catalyzed ammonia synthesis. The models’s importance lies in the availability of experimental data and the accessibility of coupled-cluster CCSD(T) calculations, enabling direct assessment of method accuracy for all reaction steps. While many functionals accurately describe the net process N2 + 3H2 → NH3, errors of +100 kJ mol−1 occur in many individual steps for popular functionals such as PBE, RPBE, and B3LYP, which are much worse than commonly assumed. Inclusion of the stoichiometric reaction coefficients reveals major accuracy bottlenecks surprisingly distinct from the N–N dissociation step and dependent on the applied functional. More focus should be directed to these problematic steps in order to improve the accuracy of modeling the catalytic process.
Similar content being viewed by others
Introduction
Chemical catalysis is the central basis for life and at the same time provides the material basis for the modern world1,2,3. Prediction and rational design of chemical reactions require estimates of the involved bond energies with as little error as possible4,5. Kohn-Sham density functional theory (DFT) can describe many chemical processes at relatively good accuracy with modest computational cost and has been successfully applied to both heterogeneous and homogenous catalysis6,7,8,9,10,11,12,13. Recently, the accuracy and reproducibility of DFT has become widely debated, with variable conclusions14,15,16,17,18. Most notably, while different DFT codes are generally precise and hence produce reproducible results15, there is little evidence for the accuracy of DFT applied to each of the individual catalytic steps due to the scarcity of benchmark data.
Many density functionals were developed to reproduce thermochemical data for main-group molecules with simple closed-shell wave functions and for one reaction step at the time19. For such cases, accuracy can be quite high, with errors as small as 10 kJ mol−1 even for closed-shell transition metal systems20. However, the most important catalytic processes commonly involve transition metals with unpaired d-electrons whose treatment depends critically on the type of DFT applied and multiple steps having very distinct changes in electronic structure5,21. Strong double and triple bonds that are often broken during catalysis (e.g., N2, CO, O2) pose an additional challenge to DFT, as the error in electron correlation typically scales with the bond strength22. Despite this, many theoretical studies of transition metal catalysis routinely use a single popular functional such as RPBE or B3LYP for all steps as the basis for conclusions, with assumptions of accuracy largely extrapolated from previous one-step benchmarks23,24,25.
We thus need to understand (i) the benchmarking of full catalytic processes and how errors arise in all individual catalytic steps, (ii) whether performance is determined by specific steps of the processes, i.e., “accuracy bottlenecks”, (iii) to what extent overall accuracy can benefit from cancellation of systematic errors, and (iv) if there are clear performance issues due to the type of DFT used that should be solved. Such assessments are difficult because most available data reflect overall rates and adsorption energies of the full systems26. This prevents mapping the error of a theoretical method to the individual molecular events of the catalytic process.
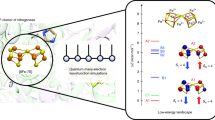
In order to address this problem, this work considers ammonia synthesis from N2 and H2 as a simplified iron-catalyzed reaction, with the net reaction N2 + 3H2 → 2NH3 .27
The model reaction is uniquely defined as the minimal catalytic model where each ligand atom is allowed to bind only one iron atom at a time. The particular advantage of this model benchmark reaction is the availability of experimental thermochemical data and advanced CCSD(T) computations with sufficiently large basis sets to serve as benchmark data. With this model reaction as framework, we can address the four questions raised above by computing the reaction enthalpy of each step using a variety of density functional methods.
Ammonia synthesis was chosen as benchmark as one of the most important and remarkable industrial catalytic processes: ammonia is used as fertilizer to increase crop yields throughout the world to sustain the growing human population28. Industrially, ammonia is produced by the Haber-Bosch process29,30, which was explored by Ertl and co-workers in their Nobel-prize-awarded work31. The process also occurs within nitrogen-fixating bacteria using the nitrogenase enzyme, which contains the remarkable FeMo cofactor32. In the heterogeneous catalytic reaction, dissociation of the extremely strong (945 kJ mol−1) triple N–N bond on the catalyst surface is the rate-determining step of the total reaction33. DFT has been widely used to study this process, and the impact of various approximations is described elsewhere;27,34,35 these approximations generally make predictions very precise (and thus reproducible and useful in trend predictions), but not necessarily accurate15. The fact that the reaction is well-explored makes it particularly suitable for addressing the problem of accuracy dissected into individual catalytic steps.
The present work shows major (+100 kJ mol−1) differences in the computed reaction energies with commonly used functionals. When including the stoichiometric reaction coefficients, the accuracy bottlenecks of the overall catalytic modeling become evident: Other steps than the energy-requiring N–N dissociation become critical to accuracy and the performance of a functional is very dependent on the chemical step studied. Thus, while DFT calculations are generally precise and reproducible15, accuracy is extremely reaction step-dependent and no universal best method exists. This conclusion is not dependent on the accuracy of the benchmark CCSD(T) calculations that may be challenged for some steps since the large variations in DFT outcome prevail regardless of the exact energy of each step. Accordingly, we conclude that studies in theoretical catalysis must necessarily rely on major error cancellation in the reaction steps of interest to become predictive. As a necessary practice, one should therefore always test results using several functionals for the relevant steps of the catalytic process, as performance for one step can be very misleading. On the positive side, the weaknesses of each functional to each type of electronic transformation points to the improvements needed, e.g. in the loosely bound metal hydride states.
Results
Performance of methods for the net reaction
The catalytic model process studied in this work involves eight individual steps, which are electronically highly diverse (reaction 1–8 below):
It is initiated by bonding of N2 and H2 to iron with subsequent cleavage of the bonds into atomic nitrogen and hydrogen, and then gradual formation of ammonia by consecutive hydrogen atom transfer to nitrogen. The optimized geometries for all systems are shown in Supplementary Table 1, and the studied density functionals are listed in Supplementary Table 2. The performance of all methods for the net reaction, which does not involve iron, is shown in Fig. 1 (for detailed electronic energies, see Supplementary Tables 3–5; results are in all cases corrected for zero-point energy, Supplementary Table 6). Many of the methods are accurate, largely because it is a closed-shell reaction of small molecules with no net effect on performance due to the treatment of unpaired electrons. All the methods MP2, CAMB3LYP, CCSD(T), CCSD, PW6B95, M06-2×, B3LYP, and B3LYP* are within chemical accuracy (4 kJ mol−1) for the net process. CCSD(T) includes the essential electron correlation and performs at chemical accuracy, as expected since the applied basis set is saturated within this window of accuracy22,36. The zero-point energy corrections provide most of the correction of the electronic energies to enable comparison to experiment, with a minor additional contribution from thermal enthalpy of ~ RT (~2.5 kJ mol−1) at 298 K. At higher temperature where real processes take place, these corrections become larger but are derived from the same (BP86) frequency calculation representing the geometry optimization and thus do not differentially affect method performance. Thus, errors reported below are primarily due to the methods themselves and not to other approximations applied in the computational treatment.
Figure 1 shows that the hybrid functionals perform decently, as expected. However, the performance of PBE-based functionals, even including the hybrid PBE0, is modest. PBE and its revised version RPBE show errors of 20 and 18 kJ mol−1, respectively, but notably in different directions; i.e., as PBE favors the forward reaction too much, whereas RPBE favors it too little. Figure 1 shows the errors that can be expected when modeling the net energetics of a chemical process where bonds are formed and broken. However, the net reaction tells us little about the catalytic process which involves different steps with large changes in electron correlation; these steps are discussed below.
Benchmark vs. experimental D 0 values
The simple model process (reactions 1–8) enables a direct benchmark of DFT against experimental data for some of the critical bond-breaking and bond-forming steps. Five experimental D0 values for H–H, N–N, Fe–H, Fe–NH3, and NH2–H are available that are relevant to the process. Fig. 2 shows the errors (computed minus experimental) D0 for H–H, N–N, Fe–H, Fe–NH3, and NH2–H for the studied methods (except HF and PWLDA which have large errors off scale; all computed values can be found in Supplementary Table 7 and errors in Supplementary Table 8). The gray dashed lines shows the mean signed error (MSE) for the method, averaged over all five systems, whereas the orange dashed line shows the corresponding mean absolute error (MAE). The methods are ranked according to their MAE. The quantum mechanical gold-standard CCSD(T) agrees well with most of the experimental values, but for Fe-NH3 there is disagreement of 36 kJ mol−1 between experiment and CCSD(T), i.e., one of the numbers is less accurate, and thus both numbers may be considered when evaluating the DFT methods for this particular enthalpy. Major changes in static correlation effects upon ligand dissociation could plausibly cause CCSD(T) to fail, but generally CCSD(T) achieves chemical accuracy with the applied basis set22.
Performance vs. experimental bond strengths. Errors in computed D0 (kJ mol−1) compared to experimental D0 for 20 functionals, and CCSD(T), CCSD, and MP2 at the aug-cc-pV5Z basis set level, corrected for zero-point energies, for five bonds with experimental known D0. Mean signed and absolute errors are shown as dashed gray and orange lines
The HF method produces the clearly largest MAE of 204 kJ mol−1 and a MSE of −204 kJ mol−1 (not shown in Fig. 2; numbers and errors in Supplementary Tables 7 and 8). HF lacks correlation energy in the Löwdin definition and thus underestimates the experimental D0 by more than 200 kJ mol−1 on average for the five bonds, but clearly most for the strong triple bond of N2, as found previously22,36. The local density method PWLDA displays a MAE of 78 kJ mol−1 but with an opposite tendency of strong over-binding (MSE =+78 kJ mol−1) (Supplementary Tables 7/8), which is also well-known and illustrates the original rationale for mixing local DFT and HF exchange in hybrids37. As these extremes illustrate, both the overall accuracy, measured by MAE, and the binding strength, measured by MSE, are important when assessing performance.
The most accurate methods reside to the left of Fig. 2. Given the uncertainty in the benchmark data, the first five methods perform insignificantly different. Among the best methods, one expects to see CCSD(T), which indeed ranks #4. The double-hybrid B2PLYP and the strongly parameterized M06-2X and M06 perform very well for these one-step benchmarks, as does PW6B95. The M06 functionals were developed for good performance on this type of data38 and the test in Fig. 2 confirms their adequacy for studying single bond enthalpies. The optimized exchange O functional by Handy and Cohen39,40 also performs very well regardless of the applied correlation functional (OPBE, OLYP). After these functionals follow hybrid functionals with a HF percentage of 15–25% (from B3LYP* to PBE0).
CCSD cannot compete with hybrid DFT in terms of accuracy, in agreement with previous findings22 and in stark contrast to its high accuracy for closed-shell 2-electron and 4-electron systems16,17. The performance of the GGA functionals PBE41 and revPBE/RPBE (which gives essentially similar results) is of particular interest as they are widely used in theoretical catalysis, including in the study of the Haber-Bosch process27,35,42. PBE performs poorly in direct comparison to experimental data, with considerable over-binding bias (MSE = 22 kJ mol−1 and MAE = 37 kJ mol−1). RPBE and revPBE perform better with a MSE of only 6–7 kJ mol−1, largely removing the overbinding tendency of PBE, but still lacks accuracy across the diverse types of bonds, with MAE = 26 kJ mol−1. Interestingly, the OPBE functional performs markedly better than RPBE for the net reaction.
Performance for iron-catalyzed ammonia synthesis
From the above comparison to experimental D0 values we conclude that CCSD(T) is a suitable benchmark for the steps of the model reaction where experimental data are not available. Accordingly, it is meaningful to study a simple but complete model of iron-catalyzed ammonia synthesis; this model reaction is uniquely defined by the requirement that every ligand can be bound only to one iron atom at the time. While this model of course does not reflect the multi-metal bond types involved in a real catalytic process, it includes the fundamental treatment of all the Fe–N, N–N, H–H, and Fe–H bonds involved in the real process while at the same time being computationally accessible with the costly CCSD(T) methodology that was validated above. This makes the reaction uniquely suited for testing the performance of density functionals where experimental data are scarce or do not entirely reflect the individual steps of the process. Studying several iron atoms and ligand atoms is beyond reach with CCSD(T), and smaller basis sets will lose critical accuracy as shown previously22,43. Accordingly, the described benchmark model reaction may be an important validation tool of DFT methods for the study of iron-based catalysis.
Figure 3 shows the reaction enthalpies of each reaction step 1–8 computed with the studied methods (excluding HF and PWLDA; all numbers are found in Supplementary Tables 9–12). Each step occurs in its relevant stoichiometry for the overall reaction. The benchmark CCSD(T) values are represented by the dashed line. Figure 3 immediately establishes the performance of each functional and identifies weaknesses in each functional specific to each step separately, which is important since these steps are very electronically distinct.
Figure 3 reveals enormous spread in the performance of the studied methods. Even leaving out HF and MP2, which fail massively in most cases, the density functionals spread over hundreds of kJ mol−1 in their estimate of the reaction enthalpy of many steps. The largest variation in performance, and hence the most problematic steps to model, are the central steps 3–6, with estimates varying by more than 500 kJ mol−1. For all steps, the spread in results exceeds 200 kJ mol−1. Step 3, which involves chemisorbed N-N cleavage, produces the largest variation in computational outcome, as one might expect; however step 5 also produces extremely diverse results, as it involves major electronic changes as iron-adsorbed nitrogen and hydrogen combine to form the first N–H bond and free iron. Even for normally well-performing GGA functionals, the errors in the strong, highly correlated bonds such as N2 can exceed 100 kJ mol−1, making these bonds an “accuracy bottleneck” in theoretical catalysis;22 as these steps are combined with other changes in a real catalytic process, results become even more heterogeneous, unfortunately.
Upon closer inspection, the performance of each functional is due to underestimation of some steps and overestimation of other steps. For example, the best performing functional is PBE0 (MAE = 63 kJ mol−1, Supplementary Table 12). In terms of trend prediction vs. CCSD(T) results (Supplementary Figures 1–5), it also has the strongest performance (R2 = 0.92), with many other functionals having R2 ~0.80 ± 0.05 and some (such as the M06 functionals and PWLDA) even lower. Despite its general performance, even PBE0 displays major inconsistencies in its accuracy: It performs excellently for step 1 but underestimates step 2 and 5 considerably (−95 and −133 kJ mol−1), and overestimates step 3 (+136 kJ mol−1). Correspondingly, PBE has particular problems with steps 2, 6, 8, and 1, in order of difficulty. This behavior is, importantly, similar for all the GGA non-hybrids. Thus, one can conclude that the tendencies relate to the treatment of the open shells, and in particular the amount of HF exchange in the functional (25% for PBE0 vs. 0% for PBE and other non-hybrid GGAs).
Figure 4 displays the errors for each reaction step separately. The energy-requiring step of breaking the N-N triple bond is the most difficult for the HF and post-HF methods (HF, MP2, and CCSD) because the HF reference cannot explain the correlation energy of the strongly correlated N-N triple bond. The much-used hybrid PBE0 also has surprisingly large problems with this step. However interestingly, for most other density functionals, steps 2 (orange) and 6 (light green), and to a minor extent steps 1 (light blue) and 8 (brown), are the accuracy bottlenecks of the overall process. Thus, while step 3 (N-N dissociation) is the slowest step of the real process due to the 945 kJ mol−1 bond energy, the critical steps in terms of predictive accuracy (i.e., the “accuracy bottlenecks”) are, remarkable, distinctly other steps. The accuracy-wise critical step 2 is the chemisorption of H2 onto iron to produce Fe-H2 bonds. Step 6 is the more complex breaking of Fe–H and hydrogen abstraction to NH to form NH2. Consistent with Fig. 2, modeling the Fe–H bond is challenging for almost all functionals, probably because the loosely bound hydrides are subject to self-interaction error. Step 8 is the dissociation of the ammonia gas product, which also poses a challenge. These steps are the accuracy bottlenecks that prevent DFT from reaching predictive accuracy, the errors are much more diverse and larger than commonly stated in the literature, and new efforts seem needed to address such “pathological” steps.
Discussion
While the precision of DFT programs is by now well-established15, there is much debate on the accuracy of current DFT in midst of its massive use throughout chemistry16,17,18, partly because accurate benchmark data for complex processes are limited. This study explored the accuracy of DFT for a simple model process of iron-catalyzed ammonia synthesis for which accurate CCSD(T) calculations are feasible and experimental data are available. The main feature is the use of a model reaction for a full catalytic process where the accuracy for individual steps can be directly assessed. Very few model reactions are simple enough to serve as benchmarks while at the same time representing a full catalytic process (many benchmarks exist for individual steps such as bond dissociation energies). This probably explains why the accuracy of an applied functional is not generally addressed in many applications.
Two main limitations can be argued to exist in the present approach: One is the use of CCSD(T) as a benchmark, rather than full CI or multi-reference methods. The other is the simplicity and possible lack of generality of the model reaction. As to the first point, CCSD(T) is considered a golden standard in the field and thus its performance will always be of interest. However, the main results of the work are that the performance of functionals differs massively for many steps, and the performance for each step is also very functional-dependent. These variations will persist regardless of the exact true values of the energies of each step. As to the second point, despite its resemblance to the important Haber-Bosch process, the model process is very simple and specific which can be considered as a necessary sacrifice to achieve benchmark data. The development of additional benchmark models of real catalytic processes should be a main priority of future work as errors will depend on the specific steps of the process studied. However, even if the presence of more metals and compensating interactions in a condense phase will surely reduce errors in larger more realistic models, the tendencies of the functionals will probably persist and reflect methods that overbind and underbind, respectively. Accordingly, the observed large variations in both functional and step performance will also persist. Most steps of the full process are electronically very distinct and thus cover a good portion of the real chemistry of the bonds, except of course for the missing metal-metal modulation on a real surface. The heterogeneous outcome arising from the diversity of electronic-structure changes should be generic to many important catalytic processes involving transition metals with unpaired d-electrons, and as the process is probably not unique in its electronic complexity, the negative results are probably also partly transferable to other open-shell processes.
The difference in accuracy when modeling the overall net reaction and the individual catalytic steps become very clear in this work: For the net reaction N2 + 3H2 → 2NH3, which only involves closed-shell species, many methods are within chemical accuracy (4 kJ mol−1). However, for the individual steps involving complex open-shell electronic configurations, errors commonly exceed several hundred kJ mol−1. Most importantly, the most energy-requiring N–N dissociation step is often not the accuracy bottleneck of modeling the overall process, and different density functionals experience different accuracy bottlenecks. Accordingly, it will be hard to develop simple interpolations that generically reduce DFT errors for transition metal catalysis, as is sometimes possible for organic molecules due to their modularity44. This has negative implications for the accuracy of many studies in theoretical catalysis, which must necessarily rely on extreme error cancellations to become predictive.
The question becomes, how often is DFT really used predictively, and when it is merely used as rationalization of known facts? When does a particular functional work, how predictive is it really, and how far can one rely on e.g., scaling behavior and error cancellation to remedy the major deficiencies in modeling the individual steps which haunt even the best functionals? If only one step of the process is really interesting (e.g., the slowest step) then focus may be put on this step regardless of the major errors for the full cycle. This would need to be explicitly explained and justified. If interest is only in the relative performance vs. a reference catalyst (e.g., for catalyst design) then errors may be substantially reduced, but this has to be shown by a sensitivity test using several functionals. It is very interesting that different functionals have difficulties with different types of electronic transformations. Identification of further accuracy bottlenecks of full, but simple catalytic model reactions as the one in this work should be valuable in future efforts to make DFT accurate enough to predict full catalytic cycles at uniform accuracy.
Methods
Applied software and basis sets
All computations were performed using the Turbomole software, version 7.045. All densities and energies were converged to 10−7 a.u. Geometries were optimized using the BP86 functional, which produces accurate metal-ligand bond lengths (mean absolute errors of ~0.02 Å)46, using the def2-TZVPP basis set47 with polarization functions on all atoms including hydrogen, as is important during this particular process where six hydrogen atoms repeatedly bind to iron and nitrogen. High-quality energies were subsequently computed using def2-QZVPP for iron and aug-cc-pV5Z basis set for N and H48. The large basis set with diffuse functions is required for the electronegative ligand atoms as they contain surplus electron density upon binding to iron, in particular for the loosely bound hydride (M–H−) states. Polarization functions are required for adequate description of differential electron correlation during bonding. The basis set is saturated to within chemical accuracy (4 kJ mol−1) for bond energies, including the strongest, most correlated N–N bond;22 smaller basis than this prevent accurate benchmarking since basis set effects may affect the apparent outcome of the chosen DFT method.
Studied computational methods
To obtain a detailed and general overview of method performance, 25 methods were explored for all eight steps. Four ab initio methods were studied: The Hartree-Fock method (HF), Møller-Plesset second-order perturbation theory (MP2), Coupled-Cluster with single and double excitations included (CCSD), and Coupled-Cluster with the perturbative triple-excitation corrections, CCSD(T), all based on the same HF reference state for each electronic system to ensure consistency. In addition, 21 density functional methods were investigated (Supplementary Table 2; the local PWLDA has been omitted from some figures as the errors are off-scale). They vary in design type and expected performance7,49,50 and thus effectively help to discern the impact of different DFT approximations on the various steps of the process. The HF fraction of hybrids substantially affects computed chemical energies and is thus explicitly stated in Supplementary Table 2. The functionals were studied using their standard keywords or using the xcfun library implemented with Turbomole51. PBE and PBE041 represent non-empirical GGA and hybrid functionals, which are widely used in theoretical catalysis. The revised RPBE functional is also widely used52, as was the similar revPBE53 (both are widely used in the study of surface catalysis). BLYP and the 20% HF-exchange hybrid B3LYP54,55 and its 15% version B3LYP*56 were studied as representative functionals using the LYP correlation functional; B3LYP is the most popular functional in computational chemistry and B3LYP* is reportedly accurate for 3d metals and specifically iron57,58. B3P86 was included to test the change from LYP to another correlation functional, P86. TPSS and TPSSh59,60 represent non-hybrid and hybrid meta functionals; TPSSh was reported to perform well for transition metal chemistry61,62. PWLDA represents the local density approximation (LDA), which uses only the electron density in the description of the energy is fast to compute, and known to over-bind; its performance is very bad and thus not included in the figures for readability but its data can be found in the Supplementary Information. The optimized exchange functional (O) by Handy and Cohen39,40 may provide a more balanced description of d-block chemistry due to its parameterization toward HF energies to reduce the GGA over-binding of metal-ligand bonds and bias towards low-spin states5. To ensure that its effect is robust vs. correlation functional, both OLYP and OPBE were studied. B2PLYP63 was studied as an example of a double hybrid performing well in previous tests of transition metal thermochemistry20,50. The PBEH-3C method was also included for academic interest, although it is designed for structures and frequencies using smaller basis sets64. Finally, the hybrid PW6B9565 and the meta hybrids M06 (with 23% HF exchange) and M06-2× (with 54% HF exchange), and the local meta functional M06-L66 were included as examples of functionals parameterized specifically for broadly accurate thermochemistry.
Electronic states
The used MS values were: Fe (MS = 2); FeH (3/2); FeH2 (2); FeN (½); FeN2 (1) (for FeN2 while MS = 1 is clearly lowest from CCSD(T), MS = 1 and MS = 2 are nearly degenerate with most functionals and thus do not affect their mutual comparison; results with both spin states are shown for comparison in Supplementary Tables 3 and 4); FeNH (2); FeNH2 (3/2); FeNH3 (2); Fe+ (3/2); H (½); N (3/2); NH2 (½). H2, N2, and NH3 are closed-shell systems and were computed as such. In cases where lower-spin open-shell configurations were required, these were carefully optimized starting from higher multiplets and testing for local minima by using several types of start orbitals to derive the lowest possible HF energy, whose orbitals were then used consistently as starting point for all other calculations to ensure full consistency of the electronic states.
Experimental data and corrections applied
Data for the D0 at 298 K of H–H (436 kJ mol−1), N–N (945 kJ mol−1), Fe–NH3 (31 kJ mol−1), NH2–H (450 kJ mol−1) and Fe–H (148/179 kJ mol−1) are available and serve as important benchmark data67. The D0 for Fe–H of 148 kJ mol−1 reported in the Handbook of Chemistry and Physics67 has been revised to 179 kJ mol−1 based on very accurate multi-configurational ab initio methods68. The need for upwards revision of the low FeH value has been previously addressed by others68,69 and thus we used the value 179 kJ mol−1. Dispersion corrections are negligible for these reactions: The largest correction computed by the D3 method70 amounts to −0.76 kJ mol−1 for Fe–N2. For direct comparison to CCSD(T), it suffices to use the non-relativistic benchmark, since relativistic corrections affect CCSD(T) and DFT values to the same extent; thus relativistic corrections were not included; they may potentially contribute up to ~10 kJ mol−1 to the real enthalpy of each step46,49,69.
Data availability
All data required to produce all results of this work (Figs. 1–4) can be found in the supplementary information. Additional raw data are available from the author upon request. xyz coordinates of the systems, details on the applied density functionals, the raw electronic energies computed for all electronic systems and methods and used for constructing the figures, errors for each method, zero-point energy and vibrational and thermal corrections are supplied (Supplementary Tables 1–12), as are linear regression plots of density functional enthalpies vs. CCSD(T) enthalpies (Supplementary Figures 1–5).
References
Que Jr, L. & Tolman, W. B. Biologically inspired oxidation catalysis. Nature 455, 333–340 (2008).
Tasker, S. Z., Standley, E. A. & Jamison, T. F. Recent advances in homogeneous nickel catalysis. Nature 509, 299–309 (2014).
Furuya, T., Kamlet, A. S. & Ritter, T. Catalysis for fluorination and trifluoromethylation. Nature 473, 470–477 (2011).
Bligaard, T. et al. Toward benchmarking in catalysis science: best practices, challenges, and opportunities. ACS Catal. 6, 2590–2602 (2016).
Kepp, K. P. Consistent descriptions of metal–ligand bonds and spin-crossover in inorganic chemistry. Coord. Chem. Rev. 257, 196–209 (2013).
Becke, A. D. Perspective: fifty years of density-functional theory in chemical physics. J. Chem. Phys. 140, 18A301 (2014).
Cramer, C. J. & Truhlar, D. G. Density functional theory for transition metals and transition metal chemistry. Phys. Chem. Chem. Phys. 11, 10757–10816 (2009).
Meunier, B., de Visser, S. P. & Shaik, S. Mechanism of oxidation reactions catalyzed by cytochrome P450 enzymes. Chem. Rev. 104, 3947–3980 (2004).
Ertem, M. Z., Gagliardi, L. & Cramer, C. J. Quantum chemical characterization of the mechanism of an iron-based water oxidation catalyst. Chem. Sci. 3, 1293–1299 (2012).
de Visser, S. P. Propene activation by the oxo-iron active species of taurine/α-ketoglutarate dioxygenase (TauD) enzyme. How does the catalysis compare to heme-enzymes? J. Am. Chem. Soc. 128, 9813–9824 (2006).
Braga, A. A. C., Ujaque, G. & Maseras, F. A. DFT study of the full catalytic cycle of the Suzuki− Miyaura cross-coupling on a model system. Organometallics 25, 3647–3658 (2006).
García-Cuadrado, D., Braga, A. A. C., Maseras, F. & Echavarren, A. M. Proton abstraction mechanism for the palladium-catalyzed intramolecular arylation. J. Am. Chem. Soc. 128, 1066–1067 (2006).
Deubel, D. V., Sundermeyer, J. & Frenking, G. Mechanism of the olefin epoxidation catalyzed by molybdenum diperoxo complexes: Quantum-chemical calculations give an answer to a long-standing question. J. Am. Chem. Soc. 122, 10101–10108 (2000).
Jain, A., Shin, Y. & Persson, K. A. Computational predictions of energy materials using density functional theory. Nat. Rev. Mater. 1, 15004 (2016).
Lejaeghere, K. et al. Reproducibility in density functional theory calculations of solids. Science 351, aad3000 (2016).
Medvedev, M. G., Bushmarinov, I. S., Sun, J., Perdew, J. P. & Lyssenko, K. A. Density functional theory is straying from the path toward the exact functional. Science 355, 49–52 (2017).
Kepp, K. P. Comment on ‘Density functional theory is straying from the path toward the exact functional’. Science 356, 496–497 (2017).
Peverati, R. & Truhlar, D. G. Quest for a universal density functional: the accuracy of density functionals across a broad spectrum of databases in chemistry and physics. Philos. Trans. R. Soc. Lond. A 372, 20120476 (2014).
Bauschlicher, C. W. A comparison of the accuracy of different functionals. Chem. Phys. Lett. 246, 40–44 (1995).
Dohm, S., Hansen, A., Steinmetz, M., Grimme, S. & Checinski, M. P. Comprehensive thermochemical benchmark set of realistic closed-shell metal organic reactions. J. Chem. Theory Comput. 14, 2596–2608 (2018).
Paulsen, H., Schünemann, V. & Wolny, J. A. Progress in electronic structure calculations on spin-crossover complexes. Eur. J. Inorg. Chem. 2013, 628–641 (2013).
Kepp, K. P. Trends in strong chemical bonding in C2, CN, CN–, CO, N2, NO, NO+, and O2. J. Phys. Chem. A 121, 9092–9098 (2017).
Kalek, M. & Himo, F. Mechanism and selectivity of cooperatively catalyzed Meyer–Schuster rearrangement/Tsuji–Trost allylic substitution. Evaluation of synergistic catalysis by means of combined DFT and kinetics simulations. J. Am. Chem. Soc. 139, 10250–10266 (2017).
Ferguson, D. M., Bour, J. R., Canty, A. J., Kampf, J. W. & Sanford, M. S. Stoichiometric and catalytic aryl–perfluoroalkyl coupling at tri-tert-butylphosphine palladium(II) complexes. J. Am. Chem. Soc. 139, 11662–11665 (2017).
Petersen, M. A., van den Berg, J.-A., Ciobîcă, I. M. & van Helden, P. Revisiting CO activation on Co catalysts: impact of step and Kink sites from DFT. ACS Catal. 7, 1984–1992 (2017).
Wellendorff, J. et al. A benchmark database for adsorption bond energies to transition metal surfaces and comparison to selected DFT functionals. Surf. Sci. 640, 36–44 (2015).
Vojvodic, A. et al. Exploring the limits: a low-pressure, low-temperature Haber–Bosch process. Chem. Phys. Lett. 598, 108–112 (2014).
Erisman, J. W., Sutton, M. A., Galloway, J., Klimont, Z. & Winiwarter, W. How a century of ammonia synthesis changed the world. Nat. Geosci. 1, 636 (2008).
Haber, F. Über die synthetische Gewinnung des Ammoniaks. Angew. Chem. 27, 473–477 (1914).
Bosch, C., Mittasch, A., Wolf, H. & Stern, G. Catalytic agent for use in producing ammonia, US1148570 (1915).
Ertl, G. Reactions at surfaces: from atoms to complexity (Nobel Lecture). Angew. Chem. Int. Ed. 47, 3524–3535 (2008).
Burgess, B. K. & Lowe, D. J. Mechanism of molybdenum nitrogenase. Chem. Rev. 96, 2983–3012 (1996).
Emmett, P. H. & Brunauer, S. The adsorption of nitrogen by iron synthetic ammonia catalysts. J. Am. Chem. Soc. 56, 35–41 (1934).
Hellman, A. et al. Predicting catalysis: understanding ammonia synthesis from first-principles calculations. J. Phys. Chem. B 110, 17719–17735 (2006).
Honkala, K. et al. Ammonia synthesis from first-principles calculations. Science 307, 555–558 (2005).
Klopper, W. & Helgaker, T. Extrapolation to the limit of a complete basis set for electronic structure calculations on the N2 molecule. Theor. Chem. Acc. 99, 265–271 (1998).
Becke, A. D. A new mixing of Hartree-Fock and local density-functional theories. J. Chem. Phys. 98, 1372–1377 (1993).
Zhao, Y. & Truhlar, D. G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: two new functionals and systematic testing of four M06-class functionals and 12 other function. Theor. Chem. Acc. 120, 215–241 (2008).
Cohen, A. J. & Handy, N. C. Assessment of exchange correlation functionals. Chem. Phys. Lett. 316, 160–166 (2000).
Handy, N. C. & Cohen, A. J. Left-right correlation energy. Mol. Phys. 99, 403–412 (2001).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865 (1996).
Logadottir, A. et al. The Brønsted–Evans–Polanyi relation and the volcano plot for ammonia synthesis over transition metal catalysts. J. Catal. 197, 229–231 (2001).
Halkier, A. et al. Basis-set convergence in correlated calculations on Ne, N2, and H2O. Chem. Phys. Lett. 286, 243–252 (1998).
Sengupta, A. & Raghavachari, K. Solving the density functional conundrum: elimination of systematic errors to derive accurate reaction enthalpies of complex organic reactions. Org. Lett. 19, 2576–2579 (2017).
Ahlrichs, R., Bär, M., Häser, M., Horn, H. & Kölmel, C. Electronic structure calculations on workstation computers: the program system turbomole. Chem. Phys. Lett. 162, 165–169 (1989).
Jensen, K. P., Roos, B. O. & Ryde, U. Performance of density functionals for first row transition metal systems. J. Chem. Phys. 126, 14103 (2007).
Weigend, F. & Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 7, 3297–3305 (2005).
Dunning, T. H. Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen. J. Chem. Phys. 90, 1007–1023 (1989).
Xu, X., Zhang, W., Tang, M. & Truhlar, D. G. Do practical standard coupled cluster calculations agree better than Kohn-Sham calculations with currently available functionals when compared to the best available experimental data for dissociation energies of bonds to 3d transition metals? J. Chem. Theory Comput. 11, 2036–2052 (2015).
Moltved, K. A. & Kepp, K. P. Chemical bond energies of 3d transition metals studied by density functional theory. J. Chem. Theory Comput. 14, 3479–3492 (2018).
Ekström, U., Visscher, L., Bast, R., Thorvaldsen, A. J. & Ruud, K. Arbitrary-order density functional response theory from automatic differentiation. J. Chem. Theory Comput. 6, 1971–1980 (2010).
Hammer, B., Hansen, L. B. & Nørskov, J. K. Improved adsorption energetics within density-functional theory using revised Perdew-Burke-Ernzerhof functionals. Phys. Rev. B 59, 7413 (1999).
Zhang, Y. & Yang, W. Comment on ‘Generalized gradient approximation made simple’. Phys. Rev. Lett. 80, 890 (1998).
Becke, A. D. Density-functional thermochemistry. III role of exact exchange.J. Chem. Phys. 98, 5648–5652 (1993).
Stephens, P. J., Devlin, F. J., Chabalowski, C. F. & Frisch, M. J. Ab initio calculation of vibrational absorption and circular dichroism spectra using density functional force fields. J. Phys. Chem. 98, 11623–11627 (1994).
Reiher, M., Salomon, O. & Hess, B. A. Reparameterization of hybrid functionals based on energy differences of states of different multiplicity. Theor. Chem. Acc. 107, 48–55 (2001).
Kepp, K. P. Theoretical study of spin crossover in 30 iron complexes. Inorg. Chem. 55, 2717–2727 (2016).
Salomon, O., Reiher, M. & Hess, B. A. Assertion and validation of the performance of the B3LYP* functional for the first transition metal row and the G2 test set. J. Chem. Phys. 117, 4729–4737 (2002).
Tao, J., Perdew, J. P., Staroverov, V. N. & Scuseria, G. E. Climbing the density functional ladder: nonempirical meta generalized gradient approximation designed for molecules and solids. Phys. Rev. Lett. 91, 146401 (2003).
Perdew, J. P., Tao, J., Staroverov, V. N. & Scuseria, G. E. Meta-generalized gradient approximation: explanation of a realistic nonempirical density functional. J. Chem. Phys. 120, 6898–6911 (2004).
Jensen, K. P. Bioinorganic chemistry modeled with the TPSSh density functional. Inorg. Chem. 47, 10357–10365 (2008).
Jensen, K. P. & Ryde, U. Cobalamins uncovered by modern electronic structure calculations. Coord. Chem. Rev. 253, 769–778 (2009).
Grimme, S. Semiempirical hybrid density functional with perturbative second-order correlation. J. Chem. Phys. 124, 34108 (2006).
Grimme, S., Brandenburg, J. G., Bannwarth, C. & Hansen, A. Consistent structures and interactions by density functional theory with small atomic orbital basis sets. J. Chem. Phys. 143, 54107 (2015).
Zhao, Y. & Truhlar, D. G. Design of density functionals that are broadly accurate for thermochemistry, thermochemical kinetics, and nonbonded Interactions. J. Phys. Chem. A 109, 5656–5667 (2005).
Zhao, Y. & Truhlar, D. G. A new local density functional for main-group thermochemistry, transition metal bonding, thermochemical kinetics, and noncovalent interactions. J. Chem. Phys. 125, 194101 (2006).
Rumble, J. CRC Handbook of Chemistry and Physics, 98th Edition. (CRC Press LLC, New York, 2017).
Aoto, Y. A., Batista, deLima, Köhn, A. P., A. & de Oliveira-Filho, A. G. S. How to arrive at accurate benchmark values for transition metal compounds: computation or experiment? J. Chem. Theory Comput. 13, 5291–5316 (2017).
Cheng, L., Gauss, J., Ruscic, B., Armentrout, P. B. & Stanton, J. F. Bond dissociation energies for diatomic molecules containing 3d transition metals: benchmark scalar-relativistic coupled-cluster calculations for 20 molecules. J. Chem. Theory Comput. 13, 1044–1056 (2017).
Grimme, S., Antony, J., Ehrlich, S. & Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 132, 154104 (2010).
Acknowledgements
The Supercomputer Center at Aarhus University in Denmark is gratefully acknowledged for providing the computational resources for this project.
Author information
Authors and Affiliations
Contributions
K.P.K. performed all work associated with this study.
Corresponding author
Ethics declarations
Competing interests
The author declares no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kepp, K.P. Accuracy of theoretical catalysis from a model of iron-catalyzed ammonia synthesis. Commun Chem 1, 63 (2018). https://doi.org/10.1038/s42004-018-0063-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42004-018-0063-6
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.