Abstract
Ultrafast folding proteins have limited cooperativity and thus are excellent models to resolve, via single-molecule experiments, the fleeting molecular events that proteins undergo during folding. Here we report single-molecule atomic force microscopy experiments on gpW, a protein that, in bulk, folds in a few microseconds over a marginal folding barrier (∼1 kBT). Applying pulling forces of only 5 pN, we maintain gpW in quasi-equilibrium near its mechanical unfolding midpoint and detect how it interconverts stochastically between the folded and an extended state. The interconversion pattern is distinctly binary, indicating that, under an external force, gpW (un)folds over a significant free-energy barrier. Using molecular simulations and a theoretical model we rationalize how force induces such barrier in an otherwise downhill free-energy surface. Force-induced folding barriers are likely a general occurrence for ultrafast folding biomolecules studied with single-molecule force spectroscopy.
Similar content being viewed by others
Introduction
Deciphering the mechanisms by which proteins fold has long been one of the central problems in molecular biophysics1,2. This quest has proved challenging, because most single-domain proteins fold slowly via a two-state (i.e., all or none) process3 and atomistic simulations could only access very short timescales4. In this context, downhill folding attracted particular attention with the promise of unveiling details of folding energy landscapes that are hidden in two-state folding5. Downhill folding proteins do not cross significant free-energy barriers and thus exhibit limited cooperativity6, and are among the fastest to fold and unfold7. Their microsecond folding times have been instrumental in bridging the timescale gap between experiment and atomistic molecular dynamics (MD) simulations7,8,9,10,11. The minimal cooperativity of downhill folding has led to methods that distil mechanistic information from conventional ensemble experiments, such as monitoring how thermal denaturation depends on the structural probe12, analyzing heat capacity thermograms in terms of low-dimensional free-energy surfaces13, or estimating free-energy barriers to folding from the curvature of the Eyring plot14.
Whereas many fast-folding proteins share common structural features such as their small size (typically, <45 residues) or primarily helical secondary structure (with the exception of the very small WW domains), the protein gpW is an outlier to these general trends15. gpW has 65 residues and a native α + β structure that consists of two antiparallel α-helices and a single antiparallel two-stranded β-sheet, but it folds and unfolds in only ~4 μs at the denaturation midpoint and exhibits the characteristic features of downhill folding15, including minimally cooperative (un)folding that results in many different patterns at the atomic level when investigated by nuclear magnetic resonance (NMR)16. Both atomistic MD simulations16 and simple statistical mechanics models15,17 agree in classifying gpW as a downhill folder. These properties make this protein an attractive candidate for single-molecule force spectroscopy (smFS) studies, which, to our knowledge, have been previously conducted for just two other ultrafast folders (villin18 and α3D19).
Here we employ an atomic force microscope (AFM) that allows us to make stable measurements at low forces (between 3 and 10 pN) in the constant force mode20,21. Surprisingly, gpW behaves in these experiments as a reversible two-state folder, with distinctly binary, stochastic transitions between the native and an extended state. Detailed analysis of the experiments, coarse-grained MD simulations, and a theoretical model indicate that the pulling force induces a free-energy barrier to the (un)folding of gpW, thus confirming experimentally the scenario of force-induced refolding barriers observed in molecular simulations of RNA22 and predicted for protein unfolding23.
Results
Characterizing the mechanical unfolding midpoint of gpW
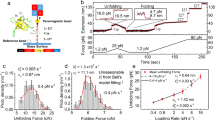
To measure the mechanical unfolding of gpW using the AFM, we designed and expressed a polyprotein construct where gpW was sandwiched between three titin-I91 (formerly termed I27) domains of the human cardiac protein on each side (Fig. 1a). In this construct, the titin-I91 domains serve as molecular fingerprint for AFM trace selection due to their well-characterized unfolding force and contour length24. To determine the mechanical stability of gpW, we performed AFM force-ramp measurements on this construct ramping the force at very slow rates to facilitate the protein’s re-equilibration during the experiment. On our AFM instrument, we could perform these force-ramp experiments at a rate of only 1 pN s−1, starting from pushing the AFM tip against the surface with a 10 pN force (F < 0), gradually moving to the pulling regime, and ending at a final pulling force of 150 pN (F > 0) to also induce the unfolding of the six I91 domains. The recorded traces showed a first broad extension event of ~10–11 nm that takes place at times varying between 10 and 25 s (i.e., 0–15 pN). This event was followed much later on by six, sharp ~24.5 nm unfolding events, the extension expected for each of the I91 titin domains in the polyprotein (Fig. 1b).
GpW unfolds mechanically at small forces. a Schematic of the polyprotein construct (I91)3-gpW-(I91)3. The sample is adsorbed to the gold substrate on one end and to the AFM cantilever on the other. Upon application of a pulling force below 15 pN gpW interconverts between its extended unfolded and native state. b One example of a AFM force-ramp length and force vs. time plot of the gpW construct at a velocity of 1 pN s−1, showing the titin-I91 fingerprint at the end of the trace. Inset shows the hopping pattern of gpW occurring at low forces at the beginning of the trace. c Average length vs. force plot at a force ramp of 1 pN s−1 (29 force-ramp traces) showing the mid-unfolding force of gpW at around 6 pN. Inset shows the derivative of the curve. Propagating baselines lead to an estimated extension for gpW of ∼10.5 nm
Based on the change of extension associated to the isolated first event (~10 nm), we can tentatively assign it to the unfolding of gpW occurring at low forces. Unfolding at low force is expected for a largely α-helical protein that shows marginal stability in ensemble chemical denaturation experiments15. Moreover, a ~10 nm extension is commensurate with the expectation for a worm-like chain (WLC) of 65 residues at these very low forces (see below). Interestingly, this extension event is not a single step such as those observed for the I91 domains. In fact, zooming into the low force region in our traces reveals hopping patterns that are consistent with stochastic series of extension and retraction events (~10–11 nm). Such hopping continues until the cantilever settles at the 10–11 nm extension when the force raises above 15 pN. These observations can be interpreted in terms of multiple folding–unfolding interconversions of gpW taking place at the very low ramping rate of these experiments. The interconversions keep on occurring until the force reaches values high enough to maintain it mechanically unfolded. Past this point the traces remain flat for very long times (>80 s) highlighting the stability of our AFM.
The patterns shown in Fig. 1b indicate that the force is ramped slowly enough so that gpW has time to re-equilibrate. Thus, at each time (force) gpW undergoes unfolding–refolding transitions according to its (un)folding probability at that particular force. The average of many such force-ramp traces reveals the cumulative distribution of the force-induced unfolding probability. Figure 1c shows the average of 29 force-ramp curves similar to that shown in Fig. 1b, and in which we also detected the subsequent mechanical fingerprint of at least 4 I91 domains, in the force regime relevant to gpW unfolding: between 10 pN pushing (F < 0) and 20 pN pulling (F > 0). In this curve, the low- and high-force linear regions (or baselines) represent the mechanical extension of the flexible segments of the polyprotein and the inflection point (i.e., maximum of its derivative) at ~6 pN (see inset to Fig. 1c) indicates the mid-unfolding force of gpW. Propagating the baselines to the mid-unfolding force results in an extension of 10.5 nm for gpW at 6 pN. This extension matches perfectly the prediction for the purely entropic WLC model25 with persistence length ρ~0.8 nm26 and contour length Lc~23.4 nm (gpW has 65 residues and the crystallographic contour length for an amino acid is 0.36 nm): total extension of 11.5 nm − ~1 nm to account for the N–C termini distance in native gpW (derived from the pdb file 2L6Q27) to render a net extension of 10.5 nm. To account for a better WLC approximation of the extension values of gpW, we first derived more force vs. extension values from the average length vs. force plot at a force ramp of 1 pN s−1 (see Fig. 1c). Then we fitted the result to the entropic WLC, modified Marko–Siggia WLC and freely jointed chain model (see Supplementary Note 1, Supplementary Table 1, and Supplementary Figure 1 for further information). In conclusion, the extended WLC analysis confirmed well the predicted mechanical elasticity values of gpW.
Force control of the folding free-energy landscape of gpW
An alternative, more direct way to estimate the mid-unfolding curve is from the (un)folding probabilities (or from the dwell times) measured in experiments at constant force. For an AFM instrument, such measurements are extremely challenging in the very low force regime relevant to gpW unfolding. The spring constant of the Biolever cantilevers that we use is around 5 pN nm−1, which precludes a sufficiently accurate control of the pulling force in a range sufficiently close to the ~6 pN midpoint for gpW. Nevertheless, we could verify shifts in the mechanical unfolding equilibrium of individual gpW molecules using experiments that combine force-ramp and force-clamp AFM measurements (Fig. 2). Particularly, we switched between three applied constant forces in the low force regime (0–15 pN) using slow force-ramp segments (1 pN s−1), followed by a final increasing force ramp (from 1 to 20–100 pN s−1) to quickly unfold the six flanking titin-I91 domains. We used two alternative force routines. In one of these, the force is switched from 5 pN (roughly the midpoint) to 10 pN (mostly unfolded), and then back to 5 pN (Fig. 2a, b). The second routine changes the constant force in steps of 3, 5, and 8 pN (Fig. 2c, d). In both experiments we observe shifts in the equilibrium populations between the native state and a mechanically unfolded state that reflect the tilting of the gpW folding landscape through the application of a pulling force.
Mechanical force modulates the (un)folding equilibrium of gpW. Length and force vs. time plots from experiments were measured using a force sequence of 5 pN–10 pN–5 pN (a, b) and 3 pN–5 pN–8 pN (c, d) (marked by the grey swaths). Insets show the hopping behavior of gpW at higher resolution (b, d). Dashed black lines indicate the extension at each applied force (b, d). The corresponding force vs. time trace indicates the force resolution of the used Biolever AFM cantilever, showing both the digitally filtered force (gray) and unfiltered signal (black)
To interpret the extension data derived from these experiments, we need to consider how the cantilever’s spring constant affects the experimental resolution in force. As it can be seen in Fig. 2b, d, the force fluctuates with a SD of ± 2 pN. The entropic WLC model implemented with the parameters discussed above correlates a 2 pN change in the low force regime (i.e., around 5 pN) with a change in length of 2–3 nm. In this light, the difference in extension of about 3 nm between the 10 and 5 pN segments of Fig. 2a is consistent with the WLC model. In contrast, the unfolding length of gpW during the 3 pN and 5 pN segments of Fig. 2c is very similar, because their force difference falls within the resolution limit of the cantilever (2 × SD or 4 pN). Here we need to mention that we are operating in a force regime that is much lower than in conventional AFM experiments. This limitation combined with the fact that we maintain the force constant for >1 min, make these experiments extremely challenging. Nevertheless, from the experiments shown in Fig. 2, we can phenomenologically conclude that the small applied forces modulate the unfolding behavior of gpW.
Two-state hopping behavior in constant force experiments
On the other hand, the resolution of our AFM should still be good enough to perform force-clamp experiments close to the mechanical midpoint of gpW and analyze in more depth its folding–unfolding behavior. Particularly, we performed force-clamp AFM measurements at 5 pN using an experiment that starts with a force-ramp segment at 1 pN s−1 to reach 5 pN, continues with 20–30 s in which the force is kept constant at 5 pN, and ends with a force-ramp segment that hikes the force at an increasing rate (from 1 to 20 pN s−1). We collected 13 such experimental traces that also showed the mechanical fingerprint for at least fout I91 domains. These traces reveal the distinct patterns of alternating ~10 nm extensions and retractions that indicate the reversible mechanical unfolding–refolding of gpW. We show one such trace in Fig. 3a. Five more traces are superimposed in Supplementary Figure 2 to illustrate the reproducibility of these experiments.
Force-clamp experiments on gpW and lifetime analysis. a A complete force and length vs. time trace from our AFM force-clamp measurements. GpW unfolds and refolds in the 20 s segment held at a constant 5 pN force (marked by a gray swath) and the six I91 domains unfold at the end of the trace. b Detail of the 5 pN segment of the length vs. time trace revealing the hopping pattern of gpW with extensions retractions of ~10.0 nm. The folded state is colored in green and the unfolded state in red, based on the assignment from a hidden Markov model. c Histograms of lengths for the folded and unfolded states at 5 pN and corresponding potential of mean force (dark blue). d Distribution of lifetimes in the folded (green) and unfolded (red) states. In both cases the lifetime histograms were fitted to an exponential distribution (lines)
Zooming into the 5 pN constant force segment of these curves (Fig. 3b) reveals the stochastic binary nature of the gpW folding–unfolding events. To make our observations quantitative, we analyzed all the traces using the PyEMMA software package to generate a hidden Markov model (HMM) from the time series data of measured extensions (see Methods and Supplementary Figure 3). The HMM model analysis supports the definition of two unique states given the timescale separation between the slowest mode (folding/unfolding) and fast dynamical processes (see Supplementary Figure 3c). Using the trajectories assigned with the HMM model, we can produce the histogram of molecular extensions, which shows a distinctly bimodal distribution with one peak at ~0 ± 2 nm (native) and a second peak at ~10 ±3 nm (unfolded) (Fig. 3c). The populations for the unfolded and native states obtained from the length histogram at 5 pN force are nearly equal, confirming that 5 pN is in fact very close to the mechanical denaturation midpoint for gpW (Fig. 3c), as we estimated from the force-ramp experiments (Fig. 1c). We determine the lifetimes of gpW in the native folded and in the mechanically unfolded states from the distribution of dwell times in the HMM model states. These distributions are well fitted to single exponential functions with nearly identical rate constants of 1.9 ± 0.1 s−1 for refolding (red in Figs. 3d) and 1.6 ± 0.1 s−1 for unfolding (green in Fig. 3d), again consistently with ~5 pN being very close to the mid-unfolding force of gpW. These timescales are much slower than the response time of our instrument, which in these experiments is equivalent to the sampling rate since our piezo electric actuator completes the force compensation through the feedback loop in times <1 ms (Supplementary Figure 4). In addition, the response time of the cantilevers we use is in the range of 0.05–1 ms28.
Estimating the free-energy barrier of gpW from experiment
The distribution of molecular extensions shown in Fig. 3c gives us an opportunity to estimate the free-energy barrier by performing a simple Boltzmann inversion to obtain a free-energy surface for the mechanical unfolding of gpW as a function of extension (blue curve in Fig. 3c). This surface has two minima corresponding to the native and partly extended unfolded ensembles separated by a free-energy barrier of ~2.5 kBT. A 2.5 kBT barrier is sufficient to explain the two-state character of the gpW’s mechanical unfolding. However, it is important to note that this estimate corresponds to a lower bound for the actual barrier. This is so because multidimensional free-energy projections onto an order parameter underestimate the barriers, which only approach their true magnitude when the projection represents an optimal reaction coordinate29. In addition, there is experimental broadening of the native and mechanically unfolded minima (and thus a lower apparent barrier on the surface) caused by fluctuations in the overall extension from the cantilever and linker30.
In parallel, we can obtain an upper bound of the actual force-induced barrier by comparing the folding rate we determine at the mid-unfolding force and the folding rate measured previously for untethered gpW using the laser-induced temperature technique15. The folding and unfolding rates at the mid-unfolding force (1.9 and 1.6 s−1) are indeed much slower than the folding and unfolding rates of ~60,000 s−1 measured for untethered gpW at the midpoint temperature (340 K). If we assume that such slowdown is caused solely by an induced folding barrier, we can estimate its magnitude from the ratio of folding rates in the presence, k(F), and the absence of force, k(0), assuming that the pre-exponential in Kramer’s rate expression, k = ko∗exp(−βΔG), is insensitive to the tethering. In such case, the mechanically induced barrier is simply ΔΔG‡ = kBT *ln[k(F)/k(0)]. This naive calculation provides an upper bound to the barrier because it assumes that the entire slowdown is due to the force-induced barrier by ignoring any effect of the cantilever and linker on the dynamics of the tethered protein. From previous T-jump experiments, we can estimate folding and unfolding rates of 19,500 and 27 s−1 at room temperature, respectively, conditions at which gpW folds downhill15. Using this estimate of the folding rate in the absence of force and our measurement of the folding rate at the mid-unfolding force (1.9 s−1) we obtain ΔΔG‡ = kBT *ln[k(F)/k(0)] = 9 kBT. This upper bound is unrealistically high. Recent theoretical work has shown that the dynamic effects of the measuring device on the rates obtained from single-molecule force spectroscopy experiments are only negligible when the underlying process is at least ten times slower than the instrumental response31,32. An in-depth analysis of such instrument-based effects is beyond the scope of this work and will discussed in a follow up publication. Nevertheless, we can anticipate that a fraction of the slowdown we observe for the (un)folding rates of gpW at the mid-unfolding force is likely caused by the cantilever and linker dynamics. What we can safely conclude here is that, at the mid-unfolding force, gpW folds and unfolds by crossing a barrier of at least 2.5 kBT, and that the actual barrier is probably not too far from this value. Regardless of the exact magnitude of the barrier, our smFS experiments demonstrate that under mechanical force gpW folds and unfolds via a two-state mechanism in contrast with its downhill folding behavior in the absence of force. The two-state nature of the process is indeed apparent in several complementary observations that do not depend on the measured timescales: (1) the single exponential distribution of lifetimes; (2) the distribution of molecular extensions; (3) the binary switching patterns observed in the experimental traces; (4) and the results from the HMM model.
Simulations reproduce the force-induced barrier of gpW
To rationalize our experimental results, we performed molecular simulations with a coarse-grained, structure-based model33, which has been used before to describe mechanical unfolding experiments34,35. We parameterized the model with the recently determined three-dimensional structure of gpW27 and ran simulations pulling from the ends of the protein at different forces. When we project the simulation data on the pulling coordinate x (the end-to-end distance), the resulting traces show two-state hopping patterns that bear close resemblance to experiment (Fig. 4a). Simulations in the presence of force lead to a highly extended unfolded state (see Fig. 4b). The difference in extension between the folded and unfolded states in the simulation (~6 nm) is not in quantitative agreement with the experimental value. This discrepancy is likely due to an unrealistically high intrinsic helical propensity in the simulation model, which maintains the two helices fully formed under 6 pN force. However, the general (un)folding behavior is correct in qualitative terms. In Fig. 4c, we show the potential of mean force (PMF) for the projection on the molecular extension (x) in the absence of force and at the simulation mechanical midpoint (6 pN). Comparison of the two PMFs reveals a downhill free-energy landscape in the absence of force and the emergence of a force-induced free-energy barrier that separates the folded and unfolded states at 6 pN. Two-dimensional PMFs obtained by umbrella sampling at different forces (Fig. 4d) show that the pulling coordinate (x) and the folding coordinate (the fraction of native contacts, Q) are correlated even at the lowest forces. Therefore, the downhill character of gpW in the absence of force is inherent to this protein and not an artifact arising from the use of the molecular extension as order parameter for folding in the no-force regime, as it has been reported before for the two-state folder GB135. In the simulations, the barrier induced by force is 5.3 kJ mol−1 (or ~1.7 kBT) for unfolding and 4.8 kJ mol−1 (or ~1.6 kBT) for refolding. These low free-energy barriers observed in the simulations compared with experiments are expected considering that coarse-grained structure-based models generally underestimate the cooperativity of protein folding36. However, within the simplicity of the coarse-grained model, the molecular simulations strongly support the main result derived from our experiments; namely that, starting from a downhill free-energy landscape, the pulling force induces a free-energy barrier that results in binary switching between the native and a partially extended unfolded state in patterns that indicate a two-state description. We obtained similar results in simulations with a phenomenological one-dimensional model specifically developed for mechanical unfolding37 (Supplementary Figure 5). The latter model also permitted to simulate the complex force routines of Fig. 1, which are again in semi-quantitative agreement with experiment.
Coarse-grained structure-based molecular simulations of gpW. a Time series data from a constant force simulation at 6 pN projected on the end-to end distance, x, and the fraction of native contacts, Q. b Blown out segment of the time series on x and representative snapshots corresponding to the folded and unfolded states from the forced-unfolding simulations. c Free-energy profiles for the projection on the end-to end distance (x (nm)) at 0 and 6 pN. d Two-dimensional potentials of mean force on the fraction of native contacts (Q) and the end-to end distance (x) at 0 (left) and 6 pN (right). Top and side plots indicate equilibrium populations for the one-dimensional projections on Q (red) and x (blue). Free energies are expressed in kJ mol−1
The reasonable compliance between experimental results and molecular simulations of single-molecule pulling38 is noteworthy, especially considering the simplified nature of the simulations. Such general agreement gives us license to infer certain mechanistic details from the simulations. The mechanism that emerges is one in which force gradually peels off the two α-helices, starting from the termini. The barrier top is reached at the point in which only the last segment of H1 and the first of H2, together with the loop hinges connecting them to the hairpin, remain in contact (Supplementary Figure 6). When the tertiary contacts between these two structural segments break, the protein unravels; maintaining the helices formed in simulations, and probably with the helices unfolding more prominently in experiments. The mechanical unfolding of the α + β protein gpW is thus very different from that of the all-β CspB, in which the six β-strands unravel one by one stochastically21. Similar mechanistic differences have been found for these two proteins on a recent computational analysis of folding pathways39. It is interesting to note that the mechanical unfolding transition state of gpW that we find here and the thermal unfolding transition state inferred from the folding interaction networks obtained by NMR experiments and MD simulations16 appear to be quite similar. The commonality between the anisotropic unfolding by pulling and thermal denaturation suggests that what makes proteins (un)fold ultrafast, and particularly the relatively large α + β protein gpW15, is their folding occurring via a diffuse mechanism characterized by broad ensembles of parallel microscopic pathways.
Discussion
Here we have determined the mechanical stability of the ultrafast folder gpW using an AFM that operates at very small loads (3–6 pN). When subjected to a constant pulling force that tilts its folding free-energy landscape to the mechanical denaturation midpoint (~5 pN), gpW undergoes remarkably slow interconversions (~2 s−1) between its compact native state and a stretched unfolded ensemble. The stochastic switching patterns of gpW are perfectly amenable to a two-state description, in contrast with the continuum of states that one might expect for a barrierless (downhill) protein.
Over the last years, several studies have reported the detection of conformational transitions of mechanically controlled proteins40,41,42,43. Similar conformational transitions have been reported for another ultrafast folder, the villin headpiece subdomain18. Constant position, equilibrium measurements with an AFM equipped with improved cantilevers have recently unveiled the complex unfolding pathways of bacteriorhodopsins44. However, our results on gpW represent the first example of measurements at quasi-equilibrium of individual protein molecules interconverting between their native and mechanically unfolded states using force-clamp AFM. This was possible because our AFM allows for stable measurements performed at relatively small constant forces, over extended periods of time, with a relatively fast time response, and using simple protein constructs.
Our results highlight the different nature of thermal and mechanical denaturation34, and demonstrate that the scenario of force-induced barriers proposed by Fernandez and colleagues23 does indeed apply to downhill proteins, which lack a free-energy barrier in the absence of force. This scenario is different from cases where small mechanical forces have been observed to increase the transition barrier of barrier limited proteins such as titin45,46. The increase of the transition barrier induced by mechanical forces during protein unfolding is somehow reminiscent to the case of catch bonds47 in cell-adhesion molecules. However, the intrinsic unbinding/unfolding mechanism of catch bonds involves an initial shortening of the molecule(s), so that applying a force increases the barrier. The key to the results in our study likely resides in the polarizing nature of the applied force, which selectively stabilizes highly extended unfolded conformations that would be rarely populated in the absence of force. At low force the unfolded ensemble is kept relatively compact by conformational entropy, but as force increases, the ensemble becomes mechanically compliant by selecting extended conformations over other, more compact, unfolded conformations. As a consequence, the unfolded minimum in the folding free-energy landscape moves farther apart (in terms of end-to-end distance) from the native state so that a force-induced free-energy barrier emerges between the two minima, even if the protein (un)folds downhill in the absence of force.
Methods
Cloning and protein expression
The chimeric polyprotein construct (I91)3-gpW-(I91)3 was designed containing the gpW protein (Top Gene Technologies, Canada) flanked by three Titin-I91 domains on each side using standard DNA manipulation protocols to build the construct inside the pRSET A vector. Each DNA manipulation step needed to add a protein domain consecutively into the plasmid vector was confirmed by DNA sequencing (Parque Científico, Madrid). C41 strand competent cells Escherichia coli were used for protein expression as they are specialized in expressing toxic proteins (Novagen). A gentle cell lysis protocol was used to avoid damage to the expressed polyproteins48. The sample was then purified by high-performance liquid chromatography (Agilent, Santa Clara, CA) in two steps: first using a nickel-affinity HisTrap column (GE Healthcare) and second using a size-exclusion Superdex 200 column (GE Healthcare). Finally, the buffer was changed to the measuring buffer 1 × phosphate-buffered saline (PBS) pH 7.4 using ultrafiltration Amicon 3k filters (Milipore). The final protein concentration was estimated to be around 1 mg ml−1 using a Nanodrop (Thermo Scientific). Then the samples were snap frozen in liquid nitrogen and stored at − 80 °C.
Single-molecule force spectroscopy
All single-molecule force spectroscopy constant force and force-ramp experiments were performed on a force-clamp AFM (Luigs Neumann)49. Biolever cantilevers from Olympus/Bruker were used with a spring constant 3–8 pN nm−1 for all constant force and force-ramp measurements. The spring constant was measured before each experiment using the equipartition theorem within a software built-in procedure. Data were recorded between 0.5 and 4 kHz for the constant force and force-ramp measurements. During combination of force-ramp and constant force experiments, the force was ramped at rate of 1 pN s−1 until reaching the 5 pN constant force (starting from 10 pN pushing F < 0). Then the protein was held for 20–30 s at the constant force before the ramp at 1 pN s−1 was continued until the six Titin-I91 domains were unfold. For the force-clamp experiments with multiple applied constant forces we ramped the polyprotein construct until the desired constant force at a rate of 1 pN s−1. After holding the protein under the constant force for 5–20 s we switched to another force using again a force ramp of 1 pN s−1. After applying all desired constant force segments, we applied a force ramp of 1 pN s−1 until the six Titin-I91 domains were unfolded. To reduce total experimental acquisition time of force-clamp experiments, we ramped at 1 pN s−1 up to reaching 60 pN, and then increased the force rate to 20–100 pN s−1 to quickly reach the high forces required to unfold I91. In the force-ramp experiments the force was ramped at a rate of 1 pN s−1 throughout the whole experiment up to a value of 150 pN (starting from 10 pN pushing F < 0) at which the six Titin-I91 were unfolded.
Experimental conditions
All AFM experiments were carried out at room temperature (~24 °C) in 1 × PBS buffer at pH 7.4. Typically, 40 µl of the protein sample (~µM concentration) was left around 20 min for adsorption on a fresh gold-coated surface (Arrandee). After the adsorption time the sample was then rinsed of the gold surface by 1 × PBS buffer to remove unbounded protein sample just before starting the measurements.
Data analysis with a HMM model
Data from AFM experiments were first screened and analyzed in Igor Pro (Wavemetrics) using the built-in data analysis procedure file and then with Python in-house scripts. First, we shifted all the trajectories so that the native state is centered at x = 0. Then we assigned the trajectories to two states using a HMM model built from the experimental traces with the PyEMMA package50. The procedure involves the generation of a fine-grained Bayesian Markov state model, for which we binned the extension data into 50 microstates. This model was validated using both the convergence of the implied timescales for the slowest relaxation time of the system and a Chapman–Kolmogorov test. From this fine-grained model we constructed a HMM model. The separation of time-scales of ~1 order of magnitude between the slowest mode and the faster modes in the fine-grained model affords a separation into two unique states. Given that we had collected data at two different sampling frequencies, we carried out the analysis of the two datasets separately. Finally, from the assigned trajectories we computed the lifetimes for the folded and unfolded states, and fitted them to a single exponential distribution.
Coarse-grained MD simulations
We used the Karanicolas and Brooks structure-based (i.e., Gō) model33 to run simulations of gpW. Therein, the protein geometry is reduced to the Cα trace and the solvent degrees of freedom are not considered, resulting in a great computational efficiency. The potential energy is calculated as
In Equation 1, Vbond and Vangle are native-centric harmonic terms for bonds and angles, respectively, whereas Vdihedral is based on statistical preferences for torsion angles in the PDB33. The non-bonded contribution is favourable for pairs of residues that are in contact in the reference (i.e., experimental) structure. Two residues i and j are defined to be in contact when any pair of atoms is closer than 5 Angstroms, and their contribution to the energy is
where σij is the distance between the Cα’s of residues i and j in the reference structure, rij is the same distance but in the instantaneous configuration and εij is the strength of the pairwise interaction33. We used the recently determined experimental structure of gpW (PDB id: 2l6q27) as reference. In order to recover a melting temperature comparable to that from the experiments (340 K15) we scaled up the native contacts by 50%.
The molecular simulations were run using a modified version of Gromacs 4.0.551. We propagated the dynamics at a constant temperature of 300 K using a Langevin integrator with a time-step of 10 fs, and a friction constant of 0.2 ps−1. Pulling experiments were simulated using the pull-code from Gromacs by defining pulling groups in the protein ends and pulling in a single dimension at constant force values between 0 and 10 pN. In addition, for the calculation of potentials of mean force, we run umbrella sampling simulations at different force values by imposing umbrella potentials at equally spaced intervals on the fraction of native contacts (Q).
The data from the simulations were projected on different progress variables, including the end-to end extension relevant to the single molecule pulling experiments, and the fraction of native contacts (Q), defined as before52. The results from the umbrella sampling runs at different values of the umbrella coordinate were combined using the weighted histogram analysis method53. From the constant force runs we estimated kinetics by simply imposing a cutoff value for each of the states.
Brownian dynamics on an empirical model
We performed BD simulations following the procedure described before using a naïve representation of the PMF profile23. This potential is written down as the sum of attractive excluded volume interactions given by a Morse potential, an entropic term described by the worm-like chain model of polymer elasticity, and a force-dependent term that reflects the effect of the applied mechanical load on the system. Over this potential, we collected position time series by numerically solving the over-damped Langevin equation, which is a momentum balance given by
Here, D(x) is the diffusion coefficient taken as 100 nm2/s in the folded state and 4000 nm2/s when the protein unfolds (crosses the barrier), and Γ(t) is a thermally fluctuating random force with zero mean and amplitude given by the fluctuation-dissipation theorem, (2Ddt)1/2. The PMF was characterized with an energy barrier of 3 kBT located at 2.7 nm from the native state basin. For the elastic term, we used a persistence length of 0.8 nm and gpW contour length of 23.4 nm.
Data availability
The data that support the findings of this study are available from the corresponding authors upon request.
References
Fersht, A. R. From the first protein structures to our current knowledge of protein folding: delights and scepticisms. Nat. Rev. Mol. Cell Biol. 9, 650–654 (2008).
Dill, K. A. & MacCallum, J. L. The protein-folding problem, 50 years on. Science 338, 1042–1046 (2012).
Jackson, S. E. How do small single-domain proteins fold? Fold. Des. 3, R81–R91 (1998).
Feig, M. & Brooks, C. L. Recent advances in the development and application of implicit solvent models in biomolecule simulations. Curr. Opin. Struct. Biol. 14, 217–224 (2004).
Eaton, W. A. Searching for “downhill scenarios” in protein folding. Proc. Natl Acad. Sci. USA 96, 5897–5899 (1999).
Muñoz, V., Campos, L. A. & Sadqi, M. Limited cooperativity in protein folding. Curr. Opin. Struct. Biol. 36, 58–66 (2016).
Munoz, V. Conformational dynamics and ensembles in protein folding. Annu. Rev. Biophys. Biomol. Struct. 36, 395–412 (2007).
Lindorff-Larsen, K., Piana, S., Dror, R. O. & Shaw, D. E. How fast-folding proteins fold. Science 334, 517–520 (2011).
Gruebele, M., Dave, K. & Sukenik, S. Globular protein folding in vitro and in vivo. Annu. Rev. Biophys. 45, 233–251 (2016).
Liu, Y., Strumpfer, J., Freddolino, P. L., Gruebele, M. & Schulten, K. Structural characterization of lambda-repressor folding from all-atom molecular dynamics simulations. J. Phys. Chem. Lett. 3, 1117–1123 (2012).
Snow, C. D., Nguyen, H., Pande, V. S. & Gruebele, M. Absolute comparison of simulated and experimental protein-folding dynamics. Nature 420, 102–106 (2002).
Sadqi, M., Fushman, D. & Muñoz, V. Atom-by-atom analysis of global downhill protein folding. Nature 442, 317–321 (2006).
Naganathan, A. N., Doshi, U., Fung, A., Sadqi, M. & Munoz, V. Dynamics, energetics, and structure in protein folding. Biochemistry 45, 8466–8475 (2006).
Naganathan, A. N., Doshi, U. & Munoz, V. Protein folding kinetics: barrier effects in chemical and thermal denaturation experiments. J. Am. Chem. Soc. 129, 5673–5682 (2007).
Fung, A., Li, P., Godoy-Ruiz, R., Sanchez-Ruiz, J. M. & Munoz, V. Expanding the realm of ultrafast protein folding: gpW, a midsize natural single-domain with alpha + beta topology that folds downhill. J. Am. Chem. Soc. 130, 7489–7495 (2008).
Sborgi, L. et al. Interaction networks in protein folding via atomic-resolution experiments and long-time-scale molecular dynamics simulations. J. Am. Chem. Soc. 137, 6506–6516 (2015).
Bruscolini, P. & Naganathan, A. N. Quantitative prediction of protein folding behaviors from a simple statistical model. J. Am. Chem. Soc. 133, 5372–5379 (2011).
Žoldák, G., Stigler, J., Pelz, B., Li, H. & Rief, M. Ultrafast folding kinetics and cooperativity of villin headpiece in single-molecule force spectroscopy. Proc. Natl Acad. Sci. USA 110, 18156–18161 (2013).
Walder, R. et al. Rapid characterization of a mechanically labile alpha-helical protein enabled by efficient site-specific bioconjugation. J. Am. Chem. Soc. 139, 9867–9875 (2017).
Perez-Jimenez, R. et al. Probing the effect of force on HIV-1 receptor CD4. ACS Nano 8, 10313–10320 (2014).
Schonfelder, J., Perez-Jimenez, R. & Munoz, V. A simple two-state protein unfolds mechanically via multiple heterogeneous pathways at single-molecule resolution. Nat. Commun. 7, 11777 (2016).
Hyeon, C. & Thirumalai, D. Forced-unfolding and force-quench refolding of RNA hairpins. Biophys. J. 90, 3410–3427 (2006).
Berkovich, R., Garcia-Manyes, S., Klafter, J., Urbakh, M. & Fernandez, J. M. Hopping around an entropic barrier created by force. Biochem. Biophys. Res Commun. 403, 133–137 (2010).
Carrion-Vazquez, M. et al. Mechanical and chemical unfolding of a single protein: a comparison. Proc. Natl Acad. Sci. USA 96, 3694–3699 (1999).
Bustamante, C., Marko, J. F., Siggia, E. D. & Smith, S. Entropic elasticity of lambda-phage DNA. Science 265, 1599 (1994).
Rief, M., Pascual, J., Saraste, M. & Gaub, H. E. Single molecule force spectroscopy of spectrin repeats: low unfolding forces in helix bundles. J. Mol. Biol. 286, 553–561 (1999).
Sborgi, L., Verma, A., Muñoz, V. & de Alba, E. Revisiting the NMR structure of the ultrafast downhill folding protein gpW from bacteriophage λ. PLoS ONE 6, e26409 (2011).
Edwards, D. T. & Perkins, T. T. Optimizing force spectroscopy by modifying commercial cantilevers: improved stability, precision, and temporal resolution. J. Struct. Biol. 197, 13–25 (2017).
Best, R. B. & Hummer, G. Reaction coordinates and rates from transition paths. Proc. Natl Acad. Sci. USA 102, 6732–6737 (2005).
Woodside, M. T. & Block, S. M. Reconstructing folding energy landscapes by single-molecule force spectroscopy. Annu. Rev. Biophys. 43, 19–39 (2014).
Cossio, P., Hummer, G. & Szabo, A. On artifacts in single-molecule force spectroscopy. Proc. Natl Acad. Sci. USA 112, 14248–14253 (2015).
Nam, G. M. & Makarov, D. E. Extracting intrinsic dynamic parameters of biomolecular folding from single‐molecule force spectroscopy experiments. Protein Sci. 25, 123–134 (2016).
Karanicolas, J. & Brooks, C. L. 3rd The origins of asymmetry in the folding transition states of protein L and protein G. Protein Sci. 11, 2351–2361 (2002).
de Sancho, D. & Best, R. B. Reconciling intermediates in mechanical unfolding experiments with two-state protein folding in bulk. J. Phys. Chem. Lett. 7, 3798–3803 (2016).
Dudko, O. K., Graham, T. G. & Best, R. B. Locating the barrier for folding of single molecules under an external force. Phys. Rev. Lett. 107, 208301 (2011).
Eastwood, M. P. & Wolynes, P. G. Role of explicitly cooperative interactions in protein folding funnels: a simulation study. J. Chem. Phys. 114, 4702–4716 (2001).
Berkovich, R., Garcia-Manyes, S., Urbakh, M., Klafter, J. & Fernandez, J. M. Collapse dynamics of single proteins extended by force. Biophys. J. 98, 2692–2701 (2010).
Hyeon, C. & Thirumalai, D. Capturing the essence of folding and functions of biomolecules using coarse-grained models. Nat. Commun. 2, 487 (2011).
Gopi, S. et al. Toward a quantitative description of microscopic pathway heterogeneity in protein folding. Phys. Chem. Chem. Phys. 19, 20891–20903 (2017).
Junker, J. P., Ziegler, F. & Rief, M. Ligand-dependent equilibrium fluctuations of single calmodulin molecules. Science 323, 633 (2009).
Schlierf, M., Berkemeier, F. & Rief, M. Direct observation of active protein folding using lock-in force spectroscopy. Biophys. J. 93, 3989–3998 (2007).
Kim, M. et al. Fast and forceful refolding of stretched alpha-helical solenoid proteins. Biophys. J. 98, 3086–3092 (2010).
Berkemeier, F. et al. Fast-folding alpha-helices as reversible strain absorbers in the muscle protein myomesin. Proc. Natl Acad. Sci. USA 108, 14139–14144 (2011).
Yu, H., Siewny, M. G. W., Edwards, D. T., Sanders, A. W. & Perkins, T. T. Hidden dynamics in the unfolding of individual bacteriorhodopsin proteins. Science 355, 945–950 (2017).
Yuan, G. et al. Elasticity of the transition state leading to an unexpected mechanical stabilization of titin immunoglobulin domains. Angew. Chem. 129, 5582–5585 (2017).
Guo, S. et al. Structural–elastic determination of the force-dependent transition rate of biomolecules. Chem. Sci. 9, 5871–5882 (2018).
Marshall, B. T. et al. Direct observation of catch bonds involving cell-adhesion molecules. Nature 423, 190–193 (2003).
Oroz, J., Hervás, R. & Carrión-Vázquez, M. Unequivocal single-molecule force spectroscopy of proteins by AFM using pFS vectors. Biophys. J. 102, 682–690 (2012).
Popa, I., Kosuri, P., Alegre-Cebollada, J., Garcia-Manyes, S. & Fernandez, J. M. Force dependency of biochemical reactions measured by single-molecule force-clamp spectroscopy. Nat. Protoc. 8, 1261–1276 (2013).
Scherer, M. K. et al. PyEMMA 2: a software package for estimation, validation, and analysis of Markov models. J. Chem. Theory Comput. 11, 5525–5542 (2015).
Hess, B., Kutzner, C., van der Spoel, D. & Lindahl, E. GROMACS 4: algorithms for highly efficient, load-balanced, and scalable molecular simulation. J. Chem. Theory Comput. 4, 435–447 (2008).
Graham, T. G. & Best, R. B. Force-induced change in protein unfolding mechanism: discrete or continuous switch? J. Phys. Chem. B 115, 1546–1561 (2011).
Kumar, S., Rosenberg, J., Bouzida, D., Swendsen, R. & Kollman, P. The weighted histogram analysis method for free-energy calculations on biomolecules. I. The method. J. Comput. Chem. 13, 1011–1021 (1992).
Acknowledgements
D.D.S. and R.B.B. wish to acknowledge Attila Szabo (NIH-NIDDK) for many helpful discussions. This research has been funded in part by the European Research Council (grant ERC-2012-ADG-323059 to V.M.). D.D.S. acknowledges a grant (CTQ2015-65320-R) and Ramón y Cajal contract (RYC-2016- 19590) from the Spanish Ministry of Economy and Competitiveness. R.B. acknowledges the support of the I-CORE Program of the Planning and Budgeting Committee and The Israel Science Foundation (Grant No. 152/11). R.B.B. was supported by the intramural research program of the National Institute of Diabetes and Digestive and Kidney Diseases of the National Institutes of Health. V.M. acknowledges additional support from the W.M. Keck Foundation, the CREST Center for Cellular and Biomolecular Machines (grant NSF-CREST-1547848) and the NSF (grant MCB-1616759). R.P.J. acknowledges support from the Spanish Ministry of Economy and Competitiveness (grant BIO2016-77390-R) and European Commission CIG Marie Curie Reintegration program FP7-PEOPLE-2014.
Author information
Authors and Affiliations
Contributions
J.S. and D.D.S. contributed equally to this work. J.S. performed all experiments and analyzed the data. D.D.S. performed the coarse-grained simulations and analyzed both the experimental and simulation data. R.B.B. contributed materials and analyzed the data. R.B. ran the Langevin simulations. V.M. and R.P.J. conceived the project and supervised the work. All the authors contributed to interpreting the results and writing the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Schönfelder, J., De Sancho, D., Berkovich, R. et al. Reversible two-state folding of the ultrafast protein gpW under mechanical force. Commun Chem 1, 59 (2018). https://doi.org/10.1038/s42004-018-0060-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42004-018-0060-9
This article is cited by
-
Compliant mechanical response of the ultrafast folding protein EnHD under force
Communications Physics (2023)
-
Two energy barriers and a transient intermediate state determine the unfolding and folding dynamics of cold shock protein
Communications Chemistry (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.