Abstract
Many processes taking place in atmospheric aerosol particles are accompanied by changes in the particles’ morphology (size and shape), with potentially significant impact on weather and climate. However, the characterization of dynamic information on particle morphology and position over multiple time scales from microseconds to days under atmospherically relevant conditions has proven very challenging. Here we introduce holographic imaging of unsupported aerosol particles in air that are spatially confined by optical traps. Optical trapping in air allows contact-free observation of aerosol particles under relevant conditions and provides access to extended observation times, while the digital in-line holographic microscope provides six-dimensional spatial maps of particle positions and orientations with maximum spatial resolution in the sub-micron range and a temporal resolution of 240 μs. We demonstrate the broad applicability of our approach for a few examples and discuss its prospects for future aerosol studies, including the study of complex, multi-step phase transitions.
Similar content being viewed by others
Introduction
Aerosol particles undergo many processes that are of great interest for both fundamental and applied research areas. A nonexhaustive list includes optical forces1,2, thermophoresis3, optical binding4,5,6, formation of cloud droplets7, phase transitions8,9,10, coagulation11, evaporation12, photochemistry13,14, reactions with gases or radicals13, ice nucleation15, condensation of molecules on particle surfaces16, and scattering and absorption of light17,18,19. Submicron-sized (both in radius and diameter20) and non-spherical aerosol particles are of particular interest because of their specific properties. Photochemical reactions and evaporation are faster in submicron-sized than in micron-sized particles21,22. Submicron particles have long residence times and high concentrations in the atmosphere, and are thus crucial for atmospheric processes20,23,24. Nonspherical particles, such as desert dust, volcanic ash, soot, and ice particles, act as catalyzers of photochemical reactions13,14,25, cloud condensation nuclei7, and ice nucleation centers15. They also promote alternative pathways of new particle formation14. Due to their high loads in the atmosphere, scattering and absorption of sunlight of these particles also impact the Earth’s radiative forcing26,27.
In this context, size and shape of particles are key properties. Despite their importance, however, their influence on many processes remains poorly understood. Very few experiments are able to record the temporal evolution of particle size and shape in situ in real time. Usual light-scattering or -absorption measurements cannot independently retrieve size and shape without some prior knowledge of these quantities. The issue with conventional light microscopy, such as bright field and dark field methods28, is their fixed imaging plane. This makes the study of particle dynamics virtually impossible because aerosol particles are very mobile even if they are confined in optical traps. As another limiting factor, these methods only provide two-dimensional (2D) images of the particle morphology. Truly three-dimensional (3D) morphologies can be retrieved by imaging particles from different angles, for example, with Fourier ptychography29,30 or optical diffraction tomography31, or by scanning the whole particle volume using confocal imaging32. However, these methods suffer from reduced temporal resolution in the range of milliseconds or seconds because several measurements are required to acquire the whole 3D information. Common to these methods is that they image the incident and the scattered light with an objective onto a camera.
An alternative approach is digital holography (DH), which directly records the interference pattern of incident and scattered light with a camera without any lens or objective. To retrieve an image, the recorded interference pattern, referred to as hologram, is numerically reconstructed using a Kirchhoff–Helmholtz or Fourier transform33,34. The 3D morphology35,36,37 and the 3D position38 of an object is obtained from reconstructions at different image planes. DH is very well suited to image fast moving objects, such as aerosol particles, because the imaged particles only need to be quasi-immobile during the exposure time of each hologram, which typically is several 10 ns for pulsed lasers34 and about 10 μs for continuous lasers39. Even though this has so far only been demonstrated for objects suspended in liquids40,41, DH can also provide movies of the 6D spatial motion of non-spherical objects suspended in air (3D for the position and 3D for the orientation). To date, most of the holographic imaging setups have been used to study objects (such as cells or particles) deposited on a substrate42,43 or suspended in liquids35,39,41,44,45,46. Corresponding investigations of aerosol particles suspended in air are less common and usually limited to particles of several microns in size34,38,47,48,49, likely because aerosol particles are more difficult to image. Central issues with aerosol holography are the fast particle motion in air because of the low damping and the reduced spatial image resolution because of the low refractive index of air.
Here, we report a new holographic setup for the fast imaging of the morphology and the 6D motion of submicron-sized aerosol particles. The setup consists of a holographic microscope and an optical trap to spatially confine aerosol particles in air over extended periods of time. The performance of the new experimental approach is demonstrated for different cases, which include the fast imaging of the morphology and the translation and rotational motion of a peanut-shaped particle, the determination of optical forces that act on a particle from imaging of the particle’s trajectory, and the complex dynamics of an optically bound particle pair.
Results
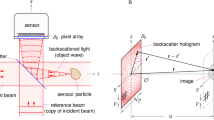
Experimental setup
The experimental setup consists of a digital in-line holographic microscope combined with a counter-propagating optical tweezer (CPT; 532 nm diode laser)22,50,51 for spatial confinement of a single particle or multiple aerosol particles in air (see Methods). Briefly, a digital in-line hologram is the interference pattern of the laser light that illuminates a particle with the light scattered by the particle, which is recorded by a digital camera positioned in the forward direction of the incident laser light33,34. An image of the particle is obtained from the hologram by reconstruction using a Kirchhoff–Helmholtz transform33 (see Methods). The origin of the coordinate system corresponds to the focus of the holography laser beam (406 nm diode laser). The X-axis is defined by the propagation direction of the holography laser, while the Z-axis coincides approximately with the optical axis of the CPT (see Methods). Our short wavelength (406 nm), narrow bandwidth (~0.1 nm) diode laser results in a high longitudinal (X) and lateral (YZ) resolution of 2.95 and 0.77 μm, respectively, as calculated from the formulae presented in33. The high frame rate of the digital camera (max. 4200 per s) allows holographic video microscopy with a time resolutions of 240 μs.
Imaging particle shape and size
Figure 1 and Table 1 demonstrate that the new holographic microscope is capable of providing real-space size and shape of suspended aerosol particles with dimensions in the submicron range. Shown are temporal snapshots of reconstructed holograms for two different types of polystyrene latex particles (PSLs) that are spatially confined by a CPT: a PSL sphere of 450 nm radius in Fig. 1a and a peanut-shaped PSL particle with half-axes of ~0.9 × 0.9 × 1.35 μm3 in Fig. 1b. The reconstructed images clearly reproduce the original particle shapes and nicely show the two partially merged spheres that form the peanut-shaped particle. Background correction and reconstruction of the recorded two-dimensional holograms are explained in Supplementary Figure 1 for the two different particle shapes.
Reconstructed images from measured holograms of a spherical and peanut-shaped particle. a Image of a spherical PSL particle with a radius of a 450 nm. b Image of a peanut-shaped PSL particle with half-axes of ~0.9 × 0.9 × 1.35 μm. The scale bars for a, b represent 1 and 2 μm, respectively. The color code indicates the intensity of the reconstructed image of the particle. The particles are represented by red and yellow colors, while the surrounding air is shown in dark blue color. There is a light blue halo of very low intensity at a distance of ~1–2 μm from the peanut-shaped particle, which arises from an artifact in the holographic reconstruction
Holographic imaging also provides the means of determining characteristic dimensions of individual particles of different morphology. Table 1 summarizes the retrieved radii for PSL spheres of 450 and 800 nm radius, respectively, and the lengths of the half-axes for the peanut-shaped particles. All data agree well with the corresponding supplier data within indicated uncertainties. Furthermore, the data show that the new digital in-line holographic microscope allows one to determine typical particle dimensions with an uncertainty of ±12% reaching far into the submicron range.
Imaging rotation and translation of non-spherical particles
Our holographic imaging setup is not limited to taking single snapshots of shape and size of aerosol particles with submicron dimensions. Its major strength lies in its capability to capture the full six-dimensional motion—three dimensions for translation and three dimensions for rotation—of non-spherical particles with high time resolution. Direct access to time-dependent information about morphology, particle size, and 6D trajectories of suspended aerosol particles opens up the possibility to investigate a multitude of processes in this important size range under atmospherically relevant conditions.
This is exemplified in Fig. 2 for the rotational and translational motion of a peanut-shaped particle that is spatially confined in an offset CPT (Supplementary Figure 2). Fig. 2a shows a few snapshots of the particle motion in the reconstruction plane (parallel to YZ-plane) with low time resolution, while Fig. 2b shows the reconstructed rotational motion in the moving frame for better visualization of the rotational motion. Corresponding videos with high time resolution (240 μs) are provided in Supplementary Movie 1 and Supplementary Movie 2, respectively. At t = 0 ms, the peanut-shaped particle is positioned closer to the focus F2 of the second tweezer (Supplementary Figure 2) and its long axis is largely aligned along the Z-axis (optical axis of the CPT). Over time, the particle translates along the Z-direction while rotating around the Y-axis. At t = 45 ms, the particle is approximately in the middle of the foci of the two tweezers and aligned along the X-axis. Between t = 45 and 77 ms, the particle’s rotation around the Y-axis continues while it moves closer to the focus F1 of the first tweezer.
Imaging of the rotational and translational motion of a peanut-shaped particle in a CPT. a Snapshots of the peanut-shaped particle in the reconstruction plane (parallel to YZ-plane). The time of the snapshots is indicated. b Reconstructed rotational motion in the moving frame based on the experimental data. The rotation angles γ (see Methods) of the peanut-shaped particle for the snapshots shown are 17°, 54°, 60°, 75°, 79°, 82°, 102°, 114°, 118°, 148°, and 172°, respectively. All scale bars represent 8 μm
An offset CPT (Supplementary Figure 2) is required to induce translational and rotational motion. The offset of the foci of the two tweezers in Z-direction by several ten micrometer allows the particle to translate in this direction by about ~40 µm, while still being spatially confined in the trap. The slight offsets of the two tweezers in the XY-plane of a few micrometers induce the rotational motion. With no XY-shift of the beams, the peanut-shaped particle would align along the Z-axis (trapping beam axis), as found for simulations of ellipsoidal dielectric particles in a single-beam tweezer52. We can qualitatively reproduce the motion in Fig. 2 by finite-difference time-domain (FDTD) simulations of optical forces and torques for the peanut-shaped particle in the offset CPT (see Methods and Supplementary Figure 3)53,54. Typical values of calculated torques around the Y-axis are indicated in Supplementary Figure 3 for different times. The calculated torques are in qualitative agreement with the experimentally observed rotational velocity in Supplementary Movie 2. The torque and the rotational velocity are decreasing from t = 0 to 45 ms, when the long axis of the particle is aligned along the X-axis. After the particle has passed this minimum in the torque and the velocity, both increase again and the particle continues rotating in the same direction. Likewise, the calculated optical forces in Z-direction in Supplementary Figure 3 explain the translation of the peanut-shaped particle along the Z-direction observed in the experiment (Supplementary Movie 1). The translational motion also reveals that not all details of the experiment can be reproduced by the idealized simulations. While both the observed acceleration and the calculated forces in Z-direction continuously decrease in value in the time window from 0 to 45 ms, their quantitative behavior does no longer agree at later times. A likely reason for such differences are imperfections in the experimental CPT, which are not reproduced by the idealized offset CPT used for the calculations (Supplementary Figure 2).
External forces from particle trajectories
Figure 3 shows the 3D translational motion of an 800 nm PSL sphere that traverses the CPT (Fig. 3a). In the region of the CPT, the particle’s motion is governed by the external optical forces, which can be quantified from time-dependent holographic imaging of the particle’s trajectory. The CPT is positioned so that the foci F1 and F2 of the two trapping beams do not coincide, but are separated by several ten micrometers along the Z-direction (Fig. 3a). The origin of the coordinate system corresponds to the focus of the holography laser beam. The center-of-mass motion of the particle (Fig. 3b) and the particle’s velocity and acceleration (Supplementary Figure 4) are retrieved from time-resolved holographic images recorded with a time resolution of 240 μs (see Methods). The particle approaches the optical trap with a constant velocity in the XY-plane and zero velocity in Z-direction (Fig. 3a, b and Supplementary Figure 4a). The constant velocity in the XY-plane was created by a constant nitrogen gas stream. At time t ~75 ms, the particle starts to interact with the optical trap. In the trap, the optical forces first accelerate (t ~90–100 ms) and then decelerate (t ~100–110 ms) the particle in Z-direction before it escapes the trap again with constant velocity in the XY-plane and zero velocity in Z-direction due to the nitrogen gas stream (Fig. 3a, b and Supplementary Figure 4). The movie of the particle’s motion provided in Supplementary Movie 3 shows that not only the center-of-mass motion but also the particle’s morphology (sphere) is retrieved in the movie.
Particle motion under the influence of an external optical force. a Sketch of the trajectory (blue trace with arrows) of an 800 nm PSL sphere crossing a CPT (green laser beams). F1 and F2 are the foci of the two laser beams. The arrow on each laser beam indicates their propagation direction. The CPT is slightly tilted with respect to the Z-axis. The origin of the coordinate system corresponds to the focus of the holography laser beam. b Colored dots: Center-of-mass coordinates of the sphere as a function of time. The color code indicates the time. Gray curves: 2D projections on the respective planes. For the sake of clarity, the temporal distance between adjacent coordinate points has been chosen to be 1.2 ms. Note that the time resolution of the holograms is much better (240 μs). c Optical forces in X-direction, Y-direction, and Z-direction as a function of time (see Methods)
Figure 3c shows the retrieved optical forces as the particle traverses the optical trap (see Methods). The particle’s motion along Z-direction is mainly governed by the optical scattering forces of the two counter-propagating laser beams and the viscous drag force. The particle’s motion is overdamped, that is, the optical force and the viscous drag force are very similar. The scattering force of each beam acts in the propagation direction of the respective laser beam and the particle is thus pushed in the direction of the total scattering force of the two counter-propagating beams. Since the particle enters the trap closer to the focus of laser beam 1, the scattering force of beam 1 initially dominates and accelerates the particle towards the center of the trap. The further the particle gets to the trap center, the smaller the total scattering force becomes because the influence of the scattering force of beam 2 increases continuously. From t ~100 ms on, the particle is thus decelerated in Z-direction, and escapes from the trap approximately in the trap center, that is, at t ~110 ms when the total scattering force and thus the velocity in Z-direction is approximately zero. The particle’s velocity in the XY-plane stays almost uniform during the whole process because it is dominated by the influence of the nitrogen gas stream. The optical gradient forces in the XY-plane with a maximum of ~250 fN are weak because the particle is comparatively far away from the two laser foci. They are about a factor of 10 weaker compared with the scattering force in Z-direction (max. ~2670 fN). Nevertheless, Fig. 3c shows that even these small gradient forces can be quantified resulting in a 3D map of the optical forces. We determine a detection limit for the optical forces of ±80 fN corresponding to twice the noise level (~40 fN, Fig. 3c). This example demonstrates how holographic imaging can be exploited to extract temporal 3D maps of external forces acting on a submicron particle.
Dynamics of optically bound particles
The phenomenon of optical binding between different particles in electromagnetic fields is an intriguing manifestation of optical forces55. Optical binding forces arise from the modification of the incident electromagnetic fields by the presence of multiple simultaneously illuminated particles, which can manifest itself in the formation of particle assemblies with extended regular spatial structures and complex dynamical behavior characterized by correlated particle motions. Even though optical binding has attracted increasing attention since its first experimental observation4, it is still not well understood4,5,6,55,56,57,58,59,60,61,62,63. This particularly holds for optical binding of submicron particles in air, for which experimental data are still missing to the best of our knowledge.
Figure 4 exemplifies that fast holographic imaging with high spatial resolution provides the missing experimental tool to access the unexplored area of optical binding of submicron particles. The snapshots provide a glimpse of the complex dynamics of two optically bound 450 nm PSL spheres in an imperfect CPT trap with lateral offsets. All snapshots were reconstructed at the same reconstruction distance with the distance of the particles to the reconstruction plane indicated by the color code: dark red particles are in the reconstruction plane and white particles are behind or in front of the reconstruction plane. The relative motion of the two spheres is characterized by irregular oscillations of their distance combined with an irregular pendular motion, which is roughly orthogonal to the reconstruction plane. The relative distance varies between ~9 and 18 μm, while the out-of-plane motion is <~2 μm. The typical timescale of this relative motion is in the range of a few milliseconds. Furthermore, the particle pair translates as a whole by several micrometers in Z-direction over longer times (120 ms) (Supplementary Figure 5). This correlated motion of the particle pair is observed over a total time of 300 ms. This example shows how holographic imaging opens up the possibility to study the dynamics of optical binding of submicron objects in air in great detail providing the experimental basis for a better understanding of this phenomenon. Access to dynamical 6D (translation and rotation) information for non-spherical particles is a prerequisite for unraveling the influence of optical binding on the rotational motion of particles.
Snapshots of the dynamics of two optically bound 450 nm radius PSL spheres in a CPT. All snapshots were reconstructed at the same reconstruction distance (X = 80 μm). The color code indicates the distance of the particles from the reconstruction plane YZ at X = 80 μm: dark red means that the particles are in the reconstruction plane and white means that the particles are in front of or behind the reconstruction plane. The snapshots visualize both the temporal oscillation of the distance of the two particles and their oscillation in and out of the reconstruction plane. All scale bars represent 4 μm
Discussion
The digital in-line holographic microscope combined with optical traps provides high time (240 μs) and spatial (770 nm) resolution imaging of unsupported, submicron aerosol particles. This opens up new avenues for the study of diverse processes involving aerosol particles under atmospherically relevant condition over extended periods of time. The potential of the new experimental approach to provide unprecedented detailed dynamic information has been demonstrated for various examples ranging from the imaging of the rotational and translational motions of non-spherical, submicron particles to the dynamics of optically bound particles. The comparison with numerical simulations promises new insight into complex phenomena, such as the coupling of rotational and translational motion in optical traps or the dynamics of optically bound particles. Promising applications in atmospheric sciences include the investigation of the dynamics of phase transitions (freezing8,10, efflorescence, and deliquescence9,64) in small aerosol particles which is still not well understood. It has recently become evident that phase transitions in particles are much more complex than previously anticipated and that these processes can happen through multiple, yet unknown pathways50,65,66,67,68. We anticipate that the direct imaging of fast temporal changes in the morphology of particles with the new holographic microscope will prove invaluable for understanding these “non-classical” nucleation phenomena69. This is but an example for the broad applicability of this new experimental tool to many topics in both applied and fundamental particle research.
Methods
Experimental setup
Figure 5 shows a sketch of the experimental setup of the holographic microscope for imaging optically trapped aerosol particles. To trap particles, we use counter-propagating tweezers22,50,51 built from a continuous laser beam (Laser Quantum, OPUS 3 532 nm, typical power: 500 mW). Such dual beam optical traps allow the trapping of submicron and non-spherical particles with comparatively simple optical layouts. The 532 nm continuous laser beam is expanded by a factor of four using a telescope composed of two lenses. A half-wave plate (λ/2) and polarization beamsplitter cube are combined to split the incident beam in two cross-polarized counter-propagating beams with similar power of ~200 mW each (one beam has 5% more power than the other). Each laser beam is then focused into the trapping cell using an aspherical lens (focal length = 56.6 mm at 532 nm). In the current study, we used slightly offset CPTs with foci F1 and F2 separated by several ten micrometers. The total path length of the two CPT beams differ by a few centimeters to ensure that the trapping beams are not interfering with each other (the coherence length of the laser is 7 mm).
Sketch of the experimental setup. a Green lines: Counter-propagating optical tweezer (CPT) for particle trapping with the two arms referred to as CPT beam 1 and beam 2. As explained in the main text (Supplementary Figure 2 and Figure 3), slightly offset CPTs were used in the present work. Blue line: Laser beam for holographic imaging. b Detail of the relative arrangement of the holography and CPT beams. The origin of the coordinate system corresponds to the focus of the holography laser. The X-axis corresponds to the propagation direction of the holography laser. The optical axis of the CPT is slightly tilted with respect to the Z-axis
The holographic microscope measures the interference between the incoming holographic beam (reference beam) and the light scattered by the trapped particles with a fast camera. After background subtraction, each camera image (referred to as raw hologram) is then reconstructed using a Kirchhoff–Helmholtz transform33 (see further below) to retrieve the position and morphology of the observed objects. As explained by Garcia-Sucerquia et al.33, the spatial resolution of the reconstructed images is diffraction-limited if the reference light beam has a narrow bandwidth (~0.1 nm) and is a spherical wave expanding from a point source. The narrow bandwidth light is obtained by reflecting the output of a 406 nm laser diode (MDL-EC-405 nm, continuous wave, typical power <1 mW) off an interference filter (Ondax, ASE-406, bandwidth ≈0.1 nm). The narrow bandwidth light is then coupled into a single mode (SM) fiber with an aspherical lens. The output of the SM fiber is collimated with another lens before being focused with an objective (Mitutoyo ×20, numerical aperture (NA) = 0.42, working-distance = 20 mm). After the focus, the holography beam behaves like a spherical wave expanding from a point source. The focus of the holography beam is positioned 50–300 μm in front of the trapped particles. A larger distance between laser focus and particle provides a larger field of view but a smaller zoom onto the observed particles (the particle will represent a smaller portion of the full image and hence be imaged by fewer pixels). The holograms are measured with a high-speed camera with a maximum temporal resolution of 240 μs (MotionXtra Os 7, 1920 × 1280 pixels, 9.12 μm pixels, up to 4200 full frames/s, 19 μs exposure time for all measurements). A 406 nm optical filter in front of the camera ensures that no scattered light from the trapping beam disturbs the hologram. The calculated lateral (in the YZ-plane) and depth (along X-axis) spatial resolution of the holographic microscope are 0.77 and 2.95 μm, respectively, as calculated from the formulae presented in ref33.
Reconstruction of the holograms
An example for the analysis of the holograms is provided in Supplementary Figure 1. First, the contrast hologram is obtained by subtracting the raw background hologram measured without particle from the raw hologram measured with particle. The contrast hologram is then reconstructed using the Octopus software (v2.0.0, 4deep, Halifax, Canada), which applies a Kirchhoff–Helmholtz transform33. The distance between the focus of the holography laser and the camera sensor (~21.5 mm), the wavelength of the light (406 nm), and the pixel size (9.12 μm) are input parameters for the reconstruction. No other information is required to reconstruct the images, which yield the particles position, orientation, and shape without any a priori knowledge. The proper reconstruction plane, that is, the reconstruction plane between the focus of the holography laser and the camera sensor parallel to the YZ-plane that provides a sharp image of the particle, was found by hand by systematically changing the reconstruction distance (distance between the focus of the holography laser and the reconstructed plane). Inappropriate reconstruction distances result in blurred particle images. The absolute dimensions of the reconstructed image are calculated during the inversion of the contrast hologram. No further calibration is needed for the determination of the particle’s dimension.
Particle position and time derivatives of position
The particle position along the Y-direction and Z-direction are calculated from the dimensions of the image (see above). The center of each reconstructed image corresponds to Y = 0 and Z = 0. The particle position along X-direction corresponds to the reconstruction distance (see above). The first and second time derivatives of the particle position are used to calculate the particle velocity and acceleration, respectively (see Figs. 2–4 and Supplementary Figs. 3–5).
Rotation of the peanut-shaped particle
The rotation angle γ around the Y-axis in Fig. 2 is calculated from Eq. (1):
εR is the ratio of the long axis of the peanut-shaped particle to the diameter of one of the spheres that form the peanut-shaped particle. It is determined from reconstructed images for which the long axis is aligned along the Z-direction. ε0(t) is determined from each reconstructed image recorded at time t as the ratio of the maximum length of the imaged particle to the diameter of one of the spheres that form the peanut-shaped particle. γ is positive for counterclockwise rotations around Y when looking into positive Y-direction and has values 0 ≤ γ ≤ 180°. Hence, s = +1 for 0 ≤ γ ≤ 90° and s = −1 for 90° ≤ γ ≤ 180° in Eq. (1). The first derivative with respect to the rotational angle is used to calculate the rotational velocity.
FDTD calculations of the optical forces and torques
We calculate the optical force \(\overrightarrow {\bf{F}}\) and torque \(\overrightarrow {\mathbf{T}}\) acting on a particle by integrating Maxwell’s stress tensor M over the (closed) surface S of the particle70 as
and
with
where \(\overrightarrow {\mathbf{E}}\) and \(\overrightarrow {\mathbf{H}}\) stand for the electric and magnetic field, respectively, \(q = \left( {\varepsilon _0 {\mathbf{E}} ^2 + \mu _0 {\mathbf{H}} ^2} \right)/2\), ⊗ denotes the dyadic product, \(\overrightarrow {\mathbf{n}}\) stands for the unit normal vector normal to dS at position \(\overrightarrow {\mathbf{r}}\) on the surface S, and \(\overrightarrow {\mathbf{X}}\), \(\overrightarrow {\mathbf{Y}}\), and \(\overrightarrow {\bf{Z}}\) denote the Cartesian unit vectors of the laboratory frame. The <…>t symbol denotes time averaging over the duration of the particle illumination.
We solve Eqs. (2)–(4) with the FDTD method53,54 as implemented in the FDTD Solutions package (see www.lumerical.com for FDTD Solutions, v., Lumerical Solutions, Inc). under the assumption that there is no coherence between the two beams, that is, we obtain the total optical force and torque on the particle as the sum of the forces and torques from two separate FDTD calculations, one for each beam. We note that we use the scalar approximation for describing each Gaussian beam (see www.lumerical.com for FDTD Solutions). We also note that our assumption of no coherence between the beams is well justified, since the two beams have perpendicular polarizations and a path length difference higher than the coherence length of the laser. In our simulations, we use the experimental beam parameters; we further assume that the two beam foci are 100 μm apart and the space between them defines the space in which the particle is optically trapped.
The FDTD approach is exact but also becomes computationally very demanding for the particle sizes of our experiments. Results converged to 1% for a particle with dimensions of a few microns typically require simulation boxes extending to more than ±50λ in the directions perpendicular to the propagation axis and a grid finesse significantly better than λ/100 close to the particle. The solution of the FDTD equations on grids of such size (>108 cells including absorbing boundary conditions) typically took about 20 h using 16 processors sharing 256 GB memory. We expect all results quoted in this work to be accurate within a few percent. We note that the significant computational expense of FDTD calculations has been a severe limiting factor on the density of the calculated points for the case under investigation in this work.
Retrieval of external optical forces
Three forces are considered: the gravitational force \(\overrightarrow {\mathbf{F}} _{\mathrm{g}} = m \cdot \overrightarrow {\mathbf{g}}\) (m is the particle mass and \(\overrightarrow {\mathbf{g}}\) is the gravitational acceleration), the drag force \(\overrightarrow {\mathbf{F}} _{\mathrm{d}}\) calculated from Stokes’s law in Eq. (5), and the optical force \(\overrightarrow {\mathbf{F}}\) calculated from Eq. (6). \(\overrightarrow {\mathbf{F}} _{\mathrm{g}}\) is almost negligible in the particle size range studied. The Brownian motion is not explicitly considered, but appears as noise in the particle velocity and retrieved optical forces.
In Eq. (5), η = 1.82 × 10−5 Pa·s is the surrounding gas viscosity, R is the particle radius, \(\overrightarrow {\mathbf{v}}\) is the velocity of the particle relative to one of the surrounding nitrogen gas stream. To calculate\(\overrightarrow {\mathbf{v}}\), the velocity of the nitrogen gas stream is subtracted from the measured particle velocity. The velocity of the nitrogen gas stream is calculated from the initial velocity of the particle (calculated by averaging the particle velocity from t = 0 to 50 ms) before it interacts with the optical trap. The optical forces \(\overrightarrow {\mathbf{F}}\) (Fig. 3c) are determined from:
where \(\overrightarrow {\mathbf{a}}\) is the particle acceleration (see above and Supplementary Figure 4). The fact that the retrieved optical forces in Fig. 3c are equal to zero before and after the particle interacts with the CPT confirms that the nitrogen gas stream is constant during the whole particle motion.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
References
Bui, A. A. M., Stilgoe, A. B., Nieminen, T. A. & Rubinsztein-Dunlop, H. Calibration of nonspherical particles in optical tweezers using only position measurement. Opt. Lett. 38, 1244–1246 (2013).
Cao, Y., Stilgoe, A. B., Chen, L., Nieminen, T. A. & Rubinsztein-Dunlop, H. Equilibrium orientations and positions of non-spherical particles in optical traps. Opt. Express 20, 12987–12996 (2012).
Zheng, F. Thermophoresis of spherical and non-spherical particles: a review of theories and experiments. Adv. Colloid Interface Sci. 97, 255–278 (2002).
Burns, M. M., Fournier, J.-M. & Golovchenko, J. A. Optical binding. Phys. Rev. Lett. 63, 1233–1236 (1989).
Karásek, V. et al. Long-range one-dimensional longitudinal optical binding. Phys. Rev. Lett. 101, 143601 (2008).
Thanopulos, I., Luckhaus, D. & Signorell, R. Modeling of optical binding of submicron aerosol particles in counterpropagating Bessel beams. Phys. Rev. A. 95, 063813 (2017).
Zhang, R. et al. Variability in morphology, hygroscopicity, and optical properties of soot aerosols during atmospheric processing. Proc. Natl Acad. Sci. USA 105, 10291–10296 (2008).
Vortisch, H. et al. Homogeneous freezing nucleation rates and crystallization dynamics of single levitated sulfuric acid solution droplets. Phys. Chem. Chem. Phys. 2, 1407–1413 (2000).
Colberg, C. A., Krieger, U. K. & Peter, T. Morphological investigations of single levitated H2SO4/NH3/H2O aerosol particles during deliquescence/efflorescence experiments. J. Phys. Chem. A 108, 2700–2709 (2004).
Lu, J. W., Isenor, M., Chasovskikh, E., Stapfer, D. & Signorell, R. Low-temperature Bessel beam trap for single submicrometer aerosol particle studies. Rev. Sci. Instrum. 85, 095107 (2014).
Lee, K. W. & Chen, H. Coagulation rate of polydisperse particles. Aerosol Sci. Technol. 3, 327–334 (1984).
Cammenga, H. K., Schulze, F. W. & Theuerl, W. Vapor pressure and evaporation coefficient of glycerol. J. Chem. Eng. Data 22, 131–134 (1977).
Cwiertny, D. M., Young, M. A. & Grassian, V. H. Chemistry and photochemistry of mineral dust aerosol. Annu. Rev. Phys. Chem. 59, 27–51 (2008).
Dupart, Y. et al. Mineral dust photochemistry induces nucleation events in the presence of SO2. Proc. Natl Acad. Sci. USA 109, 20842–20847 (2012).
Möhler, O. et al. Efficiency of the deposition mode ice nucleation on mineral dust particles. Atmos. Chem. Phys. 6, 3007–3021 (2006).
Laskin, A., Laskin, J. & Nizkorodov, S. A. Chemistry of atmospheric brown carbon. Chem. Rev. 115, 4335–4382 (2015).
Bohren, C. F. & Huffman, D. R. Absorption and Scattering of Light by Small Particles (Wiley, New York, 1983).
Mishchenko, M. I., Travis, L. D. & Lacis, A. A. Scattering, Absorption, and Emission of Light by Small Particles (Cambridge University Press, Cambridge, 2002).
Moosmüller, H., Chakrabarty, R. K. & Arnott, W. P. Aerosol light absorption and its measurement: a review. J. Quant. Spectrosc. Radiat. Transf. 110, 844–878 (2009).
Murphy, D. M. Something in the air. Science 307, 1888–1890 (2005).
Cremer, J. W., Thaler, K. M., Haisch, C. & Signorell, R. Photoacoustics of single laser-trapped nanodroplets for the direct observation of nanofocusing in aerosol photokinetics. Nat. Commun. 7, 10941 (2016).
David, G., Esat, K., Ritsch, I. & Signorell, R. Ultraviolet broadband light-scattering for optically-trapped submicron-sized aerosol particles. Phys. Chem. Chem. Phys. 18, 5477–5485 (2016).
Miles, R. E. H., Carruthers, A. E. & Reid, J. P. Novel optical techniques for measurements of light extinction, scattering and absorption by single aerosol particles. Laser Photon. Rev. 5, 534–552 (2011).
Pruppacher, H. R. & Klett, J. D. Microphysics of Clouds and Precipitation (Wiley Online Library, 1997).
Shemesh, D. & Gerber, R. B. Femtosecond timescale deactivation of electronically excited peroxides at ice surfaces. Mol. Phys. 110, 605–617 (2012).
Kaufman, Y. J., Tanre, D. & Boucher, O. A satellite view of aerosols in the climate system. Nature 419, 215–223 (2002).
IPCC. in Assessment Report of the Intergovernmental Panel on Climate Change [Core Writing] (eds Team, R. K. & Pachauri, L. A.) 151 (IPCC, Geneva, Switzerland, 2014)..
Murphy, D. B. & Davidson, M. W. Fundamentals of Light Microscopy and Electronic Imaging (Wiley, New York, 2012).
Horstmeyer, R., Chung, J., Ou, X., Zheng, G. & Yang, C. Diffraction tomography with Fourier ptychography. Optica 3, 827–835 (2016).
Tian, L. et al. Computational illumination for high-speed in vitro Fourier ptychographic microscopy. Optica 2, 904–911 (2015).
Choi, W. Tomographic phase microscopy and its biological applications. 3D Res. 3, 5 (2012).
Jeong, H.-j, Yoo, H. & Gweon, D. High-speed 3-D measurement with a large field of view based on direct-view confocal microscope with an electrically tunable lens. Opt. Express 24, 3806–3816 (2016).
Garcia-Sucerquia, J. et al. Digital in-line holographic microscopy. Appl. Opt. 45, 836–850 (2006).
Berg, M. J. & Videen, G. Digital holographic imaging of aerosol particles in flight. J. Quant. Spectrosc. Radiat. Transf. 112, 1776–1783 (2011).
Xu, W., Jericho, M., Meinertzhagen, I. & Kreuzer, H. Digital in-line holography for biological applications. Proc. Natl Acad. Sci. USA 98, 11301–11305 (2001).
Kemppinen, O., Heinson, Y. & Berg, M. Quasi-three-dimensional particle imaging with digital holography. Appl. Opt. 56, F53–F60 (2017).
Javidi, B. & Kim, D. Three-dimensional-object recognition by use of single-exposure on-axis digital holography. Opt. Lett. 30, 236–238 (2005).
Prodi, F. et al. Digital holography for observing aerosol particles undergoing Brownian motion in microgravity conditions. Atmos. Res. 82, 379–384 (2006).
Jericho, S. K., Garcia-Sucerquia, J., Xu, W., Jericho, M. H. & Kreuzer, H. J. Submersible digital in-line holographic microscope. Rev. Sci. Instrum. 77, 043706 (2006).
Wang, A. et al. Using the discrete dipole approximation and holographic microscopy to measure rotational dynamics of non-spherical colloidal particles. J. Quant. Spectrosc. Radiat. Transf. 146, 499–509 (2014).
Chiong Cheong, F. & Grier, D. G. Rotational and translational diffusion of copper oxide nanorods measured with holographic video microscopy. Opt. Express 18, 6555–6562 (2010).
Berg, M. J. & Holler, S. Simultaneous holographic imaging and light-scattering pattern measurement of individual microparticles. Opt. Lett. 41, 3363–3366 (2016).
Latychevskaia, T., Gehri, F. & Fink, H.-W. Depth-resolved holographic reconstructions by three-dimensional deconvolution. Opt. Express 18, 22527–22544 (2010).
Merola, F. et al. Simultaneous optical manipulation, 3-D tracking, and imaging of micro-objects by digital holography in microfluidics. IEEE Photonics J. 4, 451–454 (2012).
Merola, F. et al. Digital holography as a method for 3D imaging and estimating the biovolume of motile cells. Lab. Chip. 13, 4512–4516 (2013).
Zakrisson, J., Schedin, S. & Andersson, M. Cell shape identification using digital holographic microscopy. Appl. Opt. 54, 7442–7448 (2015).
Kielar, J. J. et al. Size determination of mixed liquid and frozen water droplets using interferometric out-of-focus imaging. J. Quant. Spectrosc. Radiat. Transf. 178, 108–116 (2016).
Garcia-Sucerquia, J., Alvarez-Palacio, D. C., Jericho, M. H. & Kreuzer, H. J. Comment on “Reconstruction algorithm for high-numerical-aperture holograms with diffraction-limited resolution”. Opt. Lett. 31, 2845–2847 (2006).
Henneberger, J., Fugal, J. P., Stetzer, O. & Lohmann, U. HOLIMO II: a digital holographic instrument for ground-based in situ observations of microphysical properties of mixed-phase clouds. Atmos. Meas. Tech. 6, 2975–2987 (2013).
Esat, K., David, G., Poulkas, T., Shein, M. & Signorell, R. Phase transition dynamics of single optically trapped aqueous potassium carbonate particles. Phys. Chem. Chem. Phys. 20, 11598-11607 (2018).
Li, T., Kheifets, S., Medellin, D. & Raizen, M. G. Measurement of the instantaneous velocity of a Brownian particle. Science 328, 1673–1675 (2010).
Simpson, S. H. & Hanna, S. Computational study of the optical trapping of ellipsoidal particles. Phys. Rev. A 84, 053808 (2011).
Taflove, A. & Hagness, S. C. Computational Electrodynamics: The Finite-Difference Time-Domain Method (Artech House, Norwood, 2005).
Sullivan, D. M. Electromagnetic Simulation Using the FDTD Method (Wiley, New York, 2013).
Dholakia, K. & Zemánek, P. Colloquium: gripped by light: optical binding. Rev. Mod. Phys. 82, 1767–1791 (2010).
Sukhov, S., Douglass, K. M. & Dogariu, A. Dipole–-dipole interaction in random electromagnetic fields. Opt. Lett. 38, 2385–2387 (2013).
Mazilu, M., Rudhall, A., Wright, E. M. & Dholakia, K. An interacting dipole model to explore broadband transverse optical binding. J. Phys. Condens. Matter 24, 464117 (2012).
Thanopulos, I., Luckhaus, D., Preston, T. C. & Signorell, R. Dynamics of submicron aerosol droplets in a robust optical trap formed by multiple Bessel beams. J. Appl. Phys. 115, 154304 (2014).
Summers, M. D., Dear, R. D., Taylor, J. M. & Ritchie, G. A. D. Directed assembly of optically bound matter. Opt. Express 20, 1001–1012 (2012).
Maayani, S., Martin, L. L. & Carmon, T. Optical binding in white light. Opt. Lett. 40, 1818–1821 (2015).
Carruthers, A. E., Reid, J. P. & Orr-Ewing, A. J. Longitudinal optical trapping and sizing of aerosol droplets. Opt. Express 18, 14238–14244 (2010).
Guillon, M., Moine, O. & Stout, B. Longitudinal optical binding of high optical contrast microdroplets in air. Phys. Rev. Lett. 96, 143902 (2006).
Tatarkova, S. A., Carruthers, A. E. & Dholakia, K. One-dimensional optically bound arrays of microscopic particles. Phys. Rev. Lett. 89, 283901 (2002).
Davis, R. D., Lance, S., Gordon, J. A. & Tolbert, M. A. Long working-distance optical trap for in situ analysis of contact-induced phase transformations. Anal. Chem. 87, 6186–6194 (2015).
Lee, S. et al. Multiple pathways of crystal nucleation in an extremely supersaturated aqueous potassium dihydrogen phosphate (KDP) solution droplet. Proc. Natl Acad. Sci. USA 113, 13618–13623 (2016).
Nielsen, M. H., Aloni, S. & De Yoreo, J. J. In situ TEM imaging of CaCO3 nucleation reveals coexistence of direct and indirect pathways. Science 345, 1158–1162 (2014).
Gebauer, D., Kellermeier, M., Gale, J. D., Bergstrom, L. & Colfen, H. Pre-nucleation clusters as solute precursors in crystallisation. Chem. Soc. Rev. 43, 2348–2371 (2014).
Chakraborty, D. & Patey, G. N. Evidence that crystal nucleation in aqueous NaCl solution occurs by the two-step mechanism. Chem. Phys. Lett. 587, 25–29 (2013).
Karthika, S., Radhakrishnan, T. K. & Kalaichelvi, P. A review of classical and nonclassical nucleation theories. Cryst. Growth Des. 16, 6663–6681 (2016).
Jackson, J. D. Classical Electrodynamics (Wiley, New York, 1999).
Acknowledgements
This work was supported by the Swiss National Science Foundation (SNSF grant no. 200020_172472), ETH Zurich and an ETH Career Seed Grant SEED-67 16-1. We thank David Stapfer and Markus Steger from the ETH mechanical and electronic shop for their help.
Author information
Authors and Affiliations
Contributions
R.S. and G.D. conceived the research project. G.D. designed the experimental setup, performed the measurements, and analyzed the data. G.D. and K.E. implemented the experimental setup. I.T. performed the FDTD simulations. G.D. and R.S. wrote the manuscript, on which all authors commented.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
David, G., Esat, K., Thanopulos, I. et al. Digital holography of optically-trapped aerosol particles. Commun Chem 1, 46 (2018). https://doi.org/10.1038/s42004-018-0047-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42004-018-0047-6
This article is cited by
-
Comprehensive deep learning model for 3D color holography
Scientific Reports (2022)
-
Advancing the science of dynamic airborne nanosized particles using Nano-DIHM
Communications Chemistry (2021)
-
Imaging atmospheric aerosol particles from a UAV with digital holography
Scientific Reports (2020)
-
Weighing picogram aerosol droplets with an optical balance
Communications Physics (2020)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.