Abstract
Molecular conductivity is the quantum flow of electrons through a molecule. Since its conception by Aviram and Ratner, molecular conductivity has been realized experimentally in molecules and molecular-scale circuits. Significant challenges, however, remain for its prediction with popular theoretical methods often overpredicting conductance by as much as an order of magnitude. Here we report a current-constrained, electronic structure-based variational principle for molecular conductivity. Unlike existing theories, which set the voltage to compute the current, the current-constrained variational principle determines the voltage from an electronic structure calculation in which the current is added as a constraint. We apply the variational principle to benezenedithiol with gold and nickel leads where it matches experimental values and trends, improving upon previous theory by as much as 1–2 orders of magnitude. The current constraint produces a conducting steady state that includes all many-body effects treatable by the electronic structure calculation.
Similar content being viewed by others
Introduction
Since its theoretical conception in the 1970s1, molecular conductivity has been experimentally realized in the construction of circuit elements such as conductors, diodes, and transistors2,3,4 as well as the exploration of quantum phenomena including Coulomb blockade5 and the Kondo effect6. Theoretical methods for molecular conductivity have been largely constructed using one-electron densities or Greens functions7,8,9,10,11,12,13,14,15,16 as the basic variables with a few employing the full many-electron wavefunction17. Although these methods have been successful in predicting molecular conductivity, limitations exist in their quantitative accuracy from variability in (1) their establishment of voltage through a chemical potential and (2) their treatment of electron correlation in the context of transport. The approximation of the nonequilibrium Greens functions method with density functional theory (NEGFT-DFT) is known to overpredict the current in some benchmark molecules by as much as an order of magnitude18,19,20,21,22,23. Here, we propose a new theory of molecular conductivity that uses a current-constrained variational principle based on two-electron reduced density matrices (2-RDMs) to address these limitations.
The current-constrained variational principle fixes the current as a constraint within the electronic structure calculation. Upon minimization of the energy of the molecule the current constraint naturally mixes ground and excited stationary states to generate the conducting steady state of the molecule. The energy of the steady state, higher than the ground state by the variational principle, defines a response energy of the molecule to the conductance from which the required voltage can be computed. The present approach differs sharply from most existing methods that first define the voltage through a chemical potential and then compute the current. Here we apply the variational principle to computing the molecular conductivity of the benchmark molecule 1,4-benzenedithiol. Although some earlier theoretical studies of benzenedithiol with gold leads have overestimated the current by 1–2 orders of magnitude20,21,24, the present theory matches the experimental conductance of 0.01 G025,26,27,28,29. The theory also predicts that changing the gold lead to a nickel lead increases the conductance by a factor of 2 in agreement with experiment30. We implement the current-constrained variational principle through the direct variational calculation of the 2-RDM31,32,33, which allows us to treat implicitly the correlated ground and excited states of a molecule including correlated many-body effects while circumventing the exponential computational cost of a full configuration interaction calculation34,35,36.
Results
Current-constrained variational principle
The energy of any many-electron molecule or material may be written as a functional of only two electrons
where 2D is the 2-RDM
which is normalized to N(N − 1) with N being the number of electrons and \({}^2\hat K\) the reduced Hamiltonian operator
Each roman number denotes the spin and spatial coordinates of an electron. If the 2-RDM is not constrained to represent at least one N-electron quantum system, minimization of the energy with respect to the 2-RDM generates a ground-state energy that is unrealististically low. This lower bound, however, can be systematically improved through the addition of necessary constraints for the 2-RDM to represent at least one N-electron density matrix, known as N-representability conditions37,38,39. Important, necessary N-representability conditions are the 2-positivity conditions32,33,38 that constrain three forms of the 2-RDM, corresponding to two particles, two holes and a particle-hole pair, to be positive semidefinite
The notation \(M\succcurlyeq 0\) indicates that the matrix (or kernel) M is positive semidefinite. A matrix is positive semidefinite if and only if its eigenvalues are nonnegative. Physically, these three constraints ensure that the probability distributions for two particles, two holes, and a particle-hole pair are nonnegative. Minimization of the energy as a functional of the 2-RDM constrained by these matrix inequalities is a special type of optimization problem known as a semidefinite program32,33,40.
The current-constrained variational principle adds a constraint on the current to the energy optimization within an electronic structure method. In the variational 2-RDM method, the following constraint can be added to the semidefinite program
where 1D is the 1-RDM, \({}^1\hat J\) is the one-electron current operator defined in the Methods, and I is the target current. The 1-RDM depends upon two sets of spin and spatial coordinates 1 and \(\bar 1\), respectively. The two sets of coordinates allow the density matrix to describe not only classical-like probabilities where \(1 = \bar 1\) but also quantum effects like the coherence of the particle between two locations 1 and \(\bar 1\). The symbol Im(M) denotes the imaginary part of the matrix M. Because the current depends on the imaginary part of the 1-RDM, the semidefinite program and the matrices within the program must be generalized to the complex plane (refer to Methods). The modified semidefinite program minimizes the energy over the convex set of two-positive 2-RDMs that support the current I. The optimal 2-RDM supports the current I with the lowest possible energy increase from the energy of the molecule without the current. This response energy is the smallest energy required by the molecule to support the current. Importantly, the steady state of the molecule with conductivity is a complex superposition of ground and excited states. This complex superposition, driven by the competing goals of energy minimization and current constraint feasibility, consistently treats both electron transport and electron correlation within a single correlated electronic structure calculation. The constrained minimization, balancing optimality and feasibility, generates a unique 2-RDM (and current) at the boundary of the set. Because the current arises from a one-body operator (or matrix), the current at the boundary can be decomposed into contributions from each eigenfunction (natural orbital) of the 1-RDM, which can be interpreted as the contributions to the current from different “energy” channels.
The solution of the current-constrained semidefinite program generates a response energy that can be related to the electric field and the voltage. Microscopically, the applied voltage produces an electric field that produces the current through a charge polarization of the molecule. Assuming a uniform electric field, which is reasonable given the size of the leads relative to the molecule, we can compute the voltage V from the electric field strength \(\epsilon\)
where L is the length of the molecule and leads explicitly treated in the calculation. The response energy of the molecule to the electric field can be expressed as a quadratic function of electric field strength
where α is the molecule’s polarizability. Assuming that the response of the molecule to the current is comparable to its response to the electric field, which is reasonable given the microscopic role of the charge polarization in producing the current, we can rearrange Eqs. (8) and (9) to obtain a formula for the voltage
as a function of ΔEcurr, L, and α.
The voltage in Eq. (10) has trends with respect to changes in length, polarizability, and current that are consistent with expectations. The voltage, for example, increases linearly with length L, thereby showing that it is size extensive. A property is size extensive if it scales linearly with system size. Because both the response energy ΔEcurr and the polarization α increase linearly with L, the ratio ΔEcurr/α does not scale with L, and the voltage has a linear dependence on L. Furthermore, as the polarizability of the molecule increases, the voltage decreases, reflecting the microscopic origin of conductivity in charge polarization. Finally, the energy response of the molecule to the current constraint is computed from the solution of the semidefinite program. The energy response can be viewed as arising from a linear but imaginary perturbation in the Hamiltonian owing to the applied current. Because the first-order change in energy vanishes, the linear change in the Hamiltonian generates a second-order change in the energy, scaling quadratically in the current. The square root of the energy response in Eq. (10), therefore, causes the voltage to scale linearly with the current I at low currents. Hence, we observe the emergence of Ohm’s law directly from the variational principle and perturbative arguments.
Application to 1,4-benzenedithiol
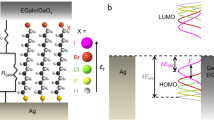
The current-constrained variational principle, implemented in the variational 2-RDM method, was applied to computing the conductance of the 1,4-benzenedithiol molecule, shown schematically in Fig. 1, which has been used extensively to benchmark both experimental25,26,27,28,29 and theoretical studies14,17,20,21,24,41,42,43. For each target current, we computed the response energy by the variational 2-RDM method from which we obtained the voltage by Eq. (10). Calculations were performed for both a gold-atom and a nickel atom lead. Owing to the small size of the molecule a single atom lead is a reasonable, first-order approximation to the atomistic junction between the lead and the molecule. Although the average current across the entire molecule and lead was constrained within the variational calculation, we report the average current confined to the lead, which is the location where the current is experimentally measured. Unlike the current in a classical wire, the quantum-mechanical current has a non-vanishing dispersion about the average because the Hamiltonian operator and the current operator do not typically commute. Computations with the variational 2-RDM method31,32,33 were performed in a finite basis set with a subset of the orbitals, known as active orbitals, being correlated beyond mean field. Additional details including the solution of the complex-valued semidefinite program are provided in the Methods section.
Figure 2a shows the I–V curves from a range of theoretical methods20,21,24 and experiment25 as well as from the variational 2-RDM method (labeled 2-RDM). NEGF-DFT results20,21 are shown from a range of density functionals including PZ, B3LYP, and M06. All three of these methods yield currents that are 1–2 orders of magnitude larger than those from the experiment. It is well-known that DFT with NEGF tends to overpredict the conductance by a significant amount, potentially orders of magnitude18,19,20,21,22. The overprediction has been attributed to several factors including the energetic positioning of the Kohn-Sham orbitals. The current-constrained 2-RDM method, in contrast, yields currents that match the experimental results for the range of available voltages. Although the overprediction of the current by theory has occurred for more than one lead geometry, one cannot exclude that differences between the experimental and theoretical treatments of the leads contribute to the overprediction. Although the 2-RDM and experimental currents appear to be zero in Fig. 2a relative to previous predictions, Fig. 2b displays the base-10 log of the conductance as a function of the voltage, showing that the currents from the 2-RDM method are nonzero and essentially equivalent to those from the experiment. Table 1 compares the computed and measured conductances from several theories and experiments with the conductance from the current-constrained variational 2-RDM method. Although previous theoretical studies overpredict the conductance as discussed above, both the 2-RDM method and the majority of experiments predict a conductance of 0.01 G0 for 1,4-benzenedithiol with gold leads.
Conductivities from theory and experiment. a The I–V curve from the constrained-current variational 2-RDM method (labeled 2-RDM) is compared with the I–V curves for 1,4-benzenedithiol with gold leads from a range of theoretical methods20,21,24 and experiment25. Many of the previous theoretical calculations yield currents that are 1–2 orders of magnitude larger than those from the experiment25; the current-constrained 2-RDM theory, in contrast, yields currents that match the experimental results26,27,28 for the range of available voltages. b Although the 2-RDM and experimental currents appear to be zero in a relative to previous predictions, the graph in b displays the base-10 log of the conductance as a function of the voltage, showing that the currents from the 2-RDM method are nonzero and essentially equivalent to those from the experiment
Chemical substitution has a large role in controlling conductivity in molecular circuit design. Molecular changes can be made not only to the molecule but also to the linkers and the leads. Here, we explore the effect of substituting gold-atom leads with nickel atom leads in 1,4-benzenedithiol. Figure 3 shows the I–V curves of 1,4-benzenedithiol with the gold and nickel leads. Benzenedithiol with the nickel leads is predicted by the 2-RDM method to have approximately twice the conductance of the molecule with the gold leads. This result is consistent with a recent experiment which found that the conductivity was enhanced by a factor of two30.
Conductivities from gold and nickel leads. a The I–V curves of 1,4-benzenedithiol with the gold and nickel leads are compared. b The base-10 log of conductance versus V curves of 1,4-benzenedithiol with the gold and nickel leads are compared. Benzenedithiol with the nickel leads is predicted by the 2-RDM method to have approximately twice the conductance of the molecule with the gold leads, which is consistent with recent experimental observations30
Discussion
The current-constrained variational principle employs a current constraint to produce a steady state for the conductivity in a molecule. The current constraint naturally mixes ground and excited states to produce the steady state. Unlike methods based on scattering theory, this theory of molecular conductivity is more easily interfaced with electronic structure methods to compute electron correlation. Here, we implemented the current-constrained variational principle in the context of variational 2-RDM calculations31,32,33, which can treat strong electron correlation. Application of the theory to the 1,4-benzenedithiol molecule with gold-atom leads improves the conductances from existing theories by 1–2 orders of magnitude20,21,24, matching experimentally measured conductances of 0.01 G025,26,27,28. Because the theory does not set the voltage like other theories for molecular conductivity, it can also be used to compute the conductance of a molecule in the absence of leads, the intrinsic conductance of the molecule. The present work shows that a current-constrained electronic structure theory can effectively treat molecular conductivity without a priori defining a voltage or invoking scattering theory. Although we have employed the variational 2-RDM method, the current-constrained variational principle can in principle be combined with other electronic structure methods. The ability to treat molecular conductivity with the framework of correlated ab initio electronic structure methods like the variational 2-RDM method may open new possibilities for the accurate prediction of molecular conductance and rectification in strongly correlated molecules as well as the study and exploitation of purely quantum effects such as quantum interference15.
Methods
Variational 2-RDM theory
The current-constrained variational principle is implemented through the direct variational calculation of the 2-RDM in a finite basis set31,32,33. The energy is minimized as a functional of the 2-RDM subject to N-representability constraints37,38,39 as well as a current constraint. We employ a necessary set of N-representability constraints known as the two-positivity (or DQG) conditions32,33,38, which constrain three matrix forms of the 2-RDM to be positive semidefinite. Because the constraints relating these forms as well as the current constraint are linear, the minimization is a special form of optimization known as a semidefinite program. A generalization of a linear program, a semidefinite program minimizes a linear function of matrices subject to constraints that the matrices are positive semidefinite as well as linear constraints relating the elements of the matrices32,33. The semidefinite program for the resulting 2-RDM-based optimization is given by
where 2K and 1J are the matrices from the two-electron reduced Hamiltonian operator \({}^2\hat K\) and the one-electron current operator \({}^1\hat J\) in the finite basis set and I is the target current. The elements of the one-electron current matrix 1J are computed from
in which κ is the one-electron coordinate in the direction \(\hat \kappa\) of the current, s denotes the one-electron coordinates of the surface perpendicular to \(\hat \kappa\), L is the length of the molecule, and ϕ p are the real-valued basis set orbitals. An optimization problem that is a semidefinite program has two particularly important properties: (i) it can be solved in polynomial time, and (ii) any local minimum is the global minimum.
Complex-valued semidefinite programming
Once the current is added to the molecule, the 2-RDM becomes Hermitian with its imaginary component containing information about the current. The complex-valued semidefinite program can be solved by mapping it to a real-valued semidefinite program. Just as a complex number can be represented by a real 2 × 2 matrix, a Hermitian matrix M of dimension d × d can be written as a real symmetric matrix S of dimension 2d × 2d44,45:
The restriction that M is positive semidefinite \(M\succcurlyeq 0\) is equivalent to the restriction that S is positive semidefinite \(S\succcurlyeq 0\). With this complex-to-real mapping the semidefinite program is solved for the molecular conductivity by an efficient boundary-point algorithm32 for semidefinite programming.
Complete active-space and basis sets
In the results presented here the variational 2-RDM calculation is performed for a subset of r a orbitals known as the active orbitals. A complete active-space 2-RDM calculation46 has the following steps: (1) initial molecular orbitals are computed from a Hartree-Fock calculation, (2) the active orbitals are correlated through a variational 2-RDM calculation, (3) the active orbitals are mixed with the remaining (inactive) orbitals to lower the energy, and (4) steps two and three are repeated until convergence. In the active-space variational 2-RDM method with 2-positive (DQG) conditions, an \(r_a^6\) variational 2-RDM calculation takes the place of an exponentially scaling \(e^{r_a}\) configuration interaction calculation.
Calculations of 1,4-benzenedithiol with gold and nickel atom leads were performed in an active-space of 16 electrons in 15 orbitals with the orbitals being of π symmetry. The basis set was 6-311G* for sulfur, 6-311G for carbon and hydrogen, and LANL2TZ (with effective core potential (ECP)) for the metals. The length of the molecule in Eq. (16) was set to the dispersion of r in the direction of the applied current in the zero-field limit, which measures the length of the molecule by the extent of its electron cloud. At finite fields the dispersion (length) of the molecule was kept fixed to its zero-field value by an additional constraint in the semidefinite program. This constraint, however, was not found to affect the result significantly, and in most cases it can be neglected.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
References
Aviram, A. & Ratner, M. A. Molecular rectifiers. Chem. Phys. Lett. 29, 277–283 (1974).
Tao, N. J. Electron transport in molecular junctions. Nat. Nanotechnol. 1, 173181 (2006).
Xiang, D., Wang, X., Jia, C., Lee, T. & Guo, X. Molecular-scale electronics: from concept to function. Chem. Rev. 116, 4318–4440 (2016).
Hsu, L.-Y., Jin, B.-Y., Chen, C.-H. & Peng, S.-M. Reaction: new insights into molecular electronics. Chem 3, 378–379 (2017).
Akai-Kasaya, M., Okuaki, Y., Nagano, S., Mitani, T. & Kuwahara, Y. Coulomb blockade in a two-dimensional conductive polymer monolayer. Phys. Rev. Lett. 115, 196801 (2015).
Karolak, M., Jacob, D. & Lichtenstein, A. I. Orbital Kondo effect in cobalt-benzene sandwich molecules. Phys. Rev. Lett. 107, 146604 (2011).
Taylor, J., Guo, H. & Wang, J. Ab initio modeling of quantum transport properties of molecular electronic devices. Phys. Rev. B 63, 245407 (2001).
Damle, P. S., Ghosh, A. W. & Datta, S. Unified description of molecular conduction: from molecules to metallic wires. Phys. Rev. B 64, 201403 (2001).
Di Ventra, M. & Lang, N. D. Transport in nanoscale conductors from first principles. Phys. Rev. B 65, 045402 (2001).
Brandbyge, M., Mozos, J.-L., Ordejón, P., Taylor, J. & Stokbro, K. Density-functional method for nonequilibrium electron transport. Phys. Rev. B 65, 165401 (2002).
Xue, Y. & Ratner, M. A. Microscopic study of electrical transport through individual molecules with metallic contacts. i. band lineup, voltage drop, and high-field transport. Phys. Rev. B 68, 115406 (2003).
Li, X. Q., Luo, J., Yang, Y. G., Cui, P. & Yan, Y. Quantum master-equation approach to quantum transport through mesoscopic systems. Phys. Rev. B 71, 205304 (2005).
Rothman, A. E. & Mazziotti, D. A. Nonequilibrium, steady-state electron transport with N-representable density matrices from the anti-Hermitian contracted Schrödinger equation. J. Chem. Phys. 132, 104112 (2010).
Varga, K. Time-dependent density functional study of transport in molecular junctions. Phys. Rev. B 83, 195130 (2011).
Hsu, L.-Y. & Rabitz, H. Single-molecule phenylacetylene-macrocycle-based optoelectronic switch functioning as a quantum-interference-effect transistor. Phys. Rev. Lett. 109, 186801 (2012).
Goldey, M. B., Brawand, N. P., Voros, M. & Galli, G. Charge transport in nanostructured materials: implementation and verification of constrained density functional theory. J. Chem. Theory Comput. 13, 2581–2590 (2017).
Delaney, P. & Greer, J. C. Correlated electron transport in molecular electronics. Phys. Rev. Lett. 93, 036805 (2004).
Evers, F., Weigend, F. & Koentopp, M. Conductance of molecular wires and transport calculations based on density-functional theory. Phys. Rev. B 69, 235411 (2004).
Quek, S. Y. et al. Amine gold linked single-molecule circuits: experiment and theory. Nano. Lett. 7, 3477–3482 (2007).
Kondo, H., Kino, H., Nara, J., Ozaki, T. & Ohno, T. Contact-structure dependence of transport properties of a single organic molecule between Au electrodes. Phys. Rev. B 73, 235323 (2006).
Hoy, E. P., Mazziotti, D. A. & Seideman, T. Development and application of a 2-electron reduced density matrix approach to electron transport via molecular junctions. J. Chem. Phys. 147, 184110 (2017).
Yamada, A., Feng, Q., Hoskins, A., Fenk, K. D. & Dunietz, B. D. Achieving predictive description of molecular conductance by using a range-separated hybrid functional. Nano. Lett. 16, 6092–6098 (2016).
Shuanglong, L., Nurbawono, A. & Zhang, C. Density functional theory for steady-state nonequilibrium molecular junctions. Sci. Rep. 5, 15386 (2015).
Bratkovsky, A. M. & Kornilovitch, P. E. Effects of gating and contact geometry on current through conjugated molecules covalently bonded to electrodes. Phys. Rev. B 67, 115307 (2003).
Xiao, X., Xu, B. & Tao, N. J. Measurement of single molecule conductance: benzenedithiol and benzenedimethanethiol. Nano. Lett. 4, 267–271 (2004).
Ulrich, J. et al. Variability of conductance in molecular junctions. J. Phys. Chem. B 110, 2462–2466 (2006).
Tsutsui, M., Taniguchi, M. & Kawai, T. Atomistic mechanics and formation mechanism of metalmoleculemetal junctions. Nano. Lett. 9, 2433–2439 (2009).
Tsutsui, M., Teramae, Y., Kurokawa, S. & Sakai, A. High-conductance states of single benzenedithiol molecules. Appl. Phys. Lett. 89, 163111 (2006).
Bruot, C., Hihath, J. & Tao, N. J. Mechanically controlled molecular orbital alignment in single molecule junctions. Nat. Nanotechnol. 7, 35–40 (2012).
Horiguchi, K., Sagisaka, T., Kurokawa, S. & Sakai, A. Electron transport through Ni/1,4-benzenedithiol/Ni single-molecule junctions under magnetic field. J. Appl. Phys. 113, 144313 (2013).
Mazziotti, D. A. Enhanced constraints for accurate lower bounds on many-electron quantum energies from variational two-electron reduced density matrix theory. Phys. Rev. Lett. 117, 153001 (2016).
Mazziotti, D. A. Large-scale semidefinite programming for many-electron quantum mechanics. Phys. Rev. Lett. 106, 083001 (2011).
Mazziotti, D. A. Realization of quantum chemistry without wave functions through first-order semidefinite programming. Phys. Rev. Lett. 93, 213001 (2004).
Schlimgen, A. W., Heaps, C. W. & Mazziotti, D. A. Entangled electrons foil synthesis of elusive low-valent vanadium oxo complex. J. Phys. Chem. Lett. 7, 627–631 (2016).
Valentine, A. J. S., Talapin, D. V. & Mazziotti, D. A. Orbitals, occupation numbers, and band structure of short one-dimensional cadmium telluride polymers. J. Phys. Chem. A 121, 3142–3147 (2017).
Schlimgen, A. W. & Mazziotti, D. A. Static and dynamic electron correlation in the ligand noninnocent oxidation of nickel dithiolates. J. Phys. Chem. A 121, 9377–9384 (2017).
Coleman, A. J. Structure of fermion density matrices. Rev. Mod. Phys. 35, 668–686 (1963).
Mazziotti, D. A. (ed.) (2007) Reduced-Density-Matrix Mechanics: With Application to Many-Electron Atoms and Molecules (Advances in Chemical Physics). 134 (Wiley: New York).
Mazziotti, D. A. Structure of fermionic density matrices: complete N-representability conditions. Phys. Rev. Lett. 108, 263002 (2012).
Vanderberghe, L. & Boyd, S. Semidefinite programming. Siam Rev. 38, 49–96 (1996).
Di Ventra, M., Pantelides, S. T. & Lang, N. D. First principles calculation of transport properties of a molecular device. Phys. Rev. Lett. 84, 979–982 (2000).
Stokbro, K., Taylor, J., Brandbyge, M., Mozos, J.-L. & Ordejn, P. Theoretical study of the nonlinear conductance of di-thiol benzene coupled to Au(111) surfaces via thiol and thiolate bonds. Comput. Mater. Sci. 27, 151–160 (2003).
Smeu, M., Wolkow, R. A. & DiLabio, G. A. Theoretical investigation of electron transport modulation through benzenedithiol by substituent groups. J. Chem. Phys. 129, 034707 (2008).
Goemans, M. X. & Williamson, D. P. Approximation algorithms for max-3-cut and other problems via complex semidefinite programming. J. Comput. Syst. Sci. 68, 442–470 (2004).
Foley, J. J. & Mazziotti, D. A. Measurement-driven reconstruction of many-particle quantum processes by semidefinite programming with application to photosynthetic light harvesting. Phys. Rev. A. 86, 012512 (2012).
Gidofalvi, G. & Mazziotti, D. A. Active-space two-electron reduced-density-matrix method: complete active-space calculations without diagonalization of the N-electron Hamiltonian. J. Chem. Phys. 129, 134108 (2008).
Reed, M. A., Zhou, C., Muller, C. J., Burgin, T. P. & Tour, J. M. Conductance of a molecular junction. Science 278, 252–254 (1997).
Venkataraman, L. et al. Single molecule circuits with well-defined molecular conductance. Nano. Lett. 6, 458–462 (2006).
Acknowledgements
D.A.M. gratefully acknowledges the U.S. Army Research Office (ARO) Grants W911NF-16-C-0030 and W911NF-16-1-0152, the U. S. National Science Foundation Grant CHE-1565638, and the U. S. Air Force Office of Scientific Research Grant FA9550-14-1-0367. D. A. M. also thanks D. R. Herschbach, H. A. Rabitz, and A. R. Mazziotti for their encouragement and support.
Author information
Authors and Affiliations
Contributions
M. S. and D. A. M. conceived of the research and developed the theory. M. S. performed the calculations. M. S. and D. A. M. discussed the data and wrote the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Sajjan, M., Mazziotti, D.A. Current-constrained density-matrix theory to calculate molecular conductivity with increased accuracy. Commun Chem 1, 31 (2018). https://doi.org/10.1038/s42004-018-0030-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42004-018-0030-2
This article is cited by
-
Experimental data from a quantum computer verifies the generalized Pauli exclusion principle
Communications Physics (2019)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.