Abstract
Nitrogen fixing plankton provide nitrogen to fuel marine ecosystems and biogeochemical cycles but the factors that constrain their growth and habitat remain poorly understood. Here we investigate the importance of metabolic specialization in unicellular diazotroph populations, using laboratory experiments and model simulations. In clonal cultures of Crocosphaera watsonii and Cyanothece sp. spiked with 15N2, cellular 15N enrichment developed a bimodal distribution within colonies, indicating that N2 fixation was confined to a subpopulation. In a model of population metabolism, heterogeneous nitrogen (N2) fixation rates substantially reduce the respiration rate required to protect nitrogenase from O2. The energy savings from metabolic specialization is highest at slow growth rates, allowing populations to survive in deeper waters where light is low but nutrients are high. Our results suggest that heterogeneous N2 fixation in colonies of unicellular diazotrophs confers an energetic advantage that expands the ecological niche and may have facilitated the evolution of multicellular diazotrophs.
Similar content being viewed by others
Introduction
Nitrogen (N2) fixing microorganisms (diazotrophs) are critical suppliers of bioavailable nitrogen (N) in the world’s oceans. The N2 fixed by these organisms supports cell growth, but also enters the food web through grazing by zooplankton and excretion of ammonium (\({{{\mathrm{NH}}}}_4^ +\)) or other dissolved nitrogenous compounds1,2,3,4,5. All diazotrophs have a N2 fixing enzyme complex, nitrogenase. Since most nitrogenase enzymes are irreversibly damaged by molecular oxygen6,7, diazotrophs separate photosynthesis and N2 fixation spatially or temporally8,9. Diazotrophs are taxonomically diverse and occupy distinct large-scale habitats9,10,11,12, suggesting there are multiple strategies for managing the energetic demands of photosynthesis, growth, and N2 fixation under a wide range of ocean conditions. However, the links between diverse physiological strategies and the resulting ecological niches and spatial distributions remain poorly understood10,13,14,15.
Crocosphaera watsonii (hereafter Crocosphaera), a marine unicellular diazotroph, is abundant and widespread in tropical and subtropical oceans10,11,16,17, and its areal N2 fixation rate (µmol N m−2 d−1) can be equal to or greater than that of Trichodesmium, a filamentous diazotroph abundant in tropical oceans16,18,19. Due to its strong diel alternation between C and N metabolisms, Crocosphaera is a promising model for investigating cellular C and N physiology17,20,21,22,23. Cyanothece is another well studied unicellular diazotroph. It is closely related to the sequence-defined genus, UCYN-C24,25, which has been observed to supply N to other phytoplankton and contribute to vertical POC (particulate organic carbon) transport26. Intensive studies on Cyanothece physiology make it a model organism to study the physiology of unicellular diazotrophic cyanobacteria27,28.
When exposed to a light:dark cycle, the peak of N2 fixation activity of most unicellular photosynthetic diazotrophs is restricted to the dark period. A similar diel cycle is observed in Crocosphaera20,21,22,29 and Cyanothece27, however, both taxa can be forced to fix N2, if maintained under constant illumination for an extended period23,30,31. This observation led to speculation that its metabolism is heterogeneously distributed among cells in a population14 as observed in Trichodesmium8.
Recent technological advances in the visualization of enriched stable isotopes in individual cells using NanoSIMS enable cell level analyses of N2 fixation activity32,33,34,35,36,37,38. With this technology, high variations in C and N2 fixation activity from in situ “Crocosphaera-like” cell colonies were shown, suggesting heterogeneity of metabolisms17. During the same period of time, similar physiological heterogeneity was observed among the clonal population of Crocosphaera (WH8501)23. These observations lead us to question how widely this heterogeneity applies and how it impacts the cellular energetics and resulting ecological niches.
Here, we investigated physiological heterogeneity among clonal populations of multiple genera of cyanobacteria, Crocosphaera (PS0609A) and Cyanothece (ATCC51142), by quantifying the pattern in N2 fixation and C uptake at the sub-cellular level. Using clonal populations prevents interference from other N fixing organisms, a potential problem noted in the in situ study17 and using different genera and strains of cyanobacteria allows us to evaluate the generality of the pattern. We have also applied multiple statistical methods to quantify the heterogeneity in C and N2 fixation. To analyze the energetics and C consumption of the observed cell-level heterogeneity, we present a model of diazotroph population to simulate the advantage of maintaining both nitrogen fixing and non-N2 fixing cells. We used oceanographic data to predict the implications of metabolically differentiated populations for the ecological niche of unicellular diazotrophs through the photic zone.
Results
Heterogeneity in N enrichment among cells
15N enrichment was variable within a single strain of continuous culture grown Crocosphaera cells (Figs. 1 and 2) and batch culture grown Cyanothece (Fig. 2). Initially, ratios of 13C:12C (=13C/12C) and 15N:14N (=15N/14N) were 8.8 ± 0.5‰ and 3.5 ± 0.1‰, respectively in Crocosphaera harvested at steady state under continuous culture and were 11.0 ± 0.4‰ and 3.6 ± 0.2‰, respectively in Cyanothece harvested at exponential phase under batch culture (Fig. 3 and Supplementary Table 1). After 11 h in the dark, two cells (Fig. 1; white arrows in panel 11D 15N:14N) were more strongly enriched in 15N compared to the other four cells, of which one cell showed the least enrichment (Fig. 1: blue arrow). However, the least 15N enriched cells were actively 13C enriched in the light period (e.g., cells with blue arrow in panel 3L 13C:12C) showing that these cells were alive and metabolically active. The variable 15N enrichment was observed not only under continuous culture but also under exponentially growing batch culture and suggests that heterogeneous 15N2 fixation happens with or without nutrient stress.
Numerals and alphabets in each photo denote time in a photoperiod: 9D and 3 L indicate 9 h in the dark and 3 h in the light, respectively. The colored bars for 12C14N indicate the number of ions collected per pixel, the other colored bars indicate the ratio of 15N: 14N and 13C:12C with the scale factor of ×10,000. White arrows in 15N:14N at 11D show the cells with intensive 15N enrichment, blue arrow shows the cells with less 15N enrichment, pink arrows show 15N hotspots. Scale bars, 5 µm. 12C14N shows the baseline, from which labeling departs in lower panels; 15N:14N shows the fate of newly fixed 15N2, 13C:12C shows newly fixed 13C uptake.
Nitrogen and carbon incorporation by a Crocosphaera and b Cyanothece shown by scatter plot of 15N:14N and 13C:12C in individual cells. Black dot-lines show threshold of 15N and 13C enrichment. c Schematic view of scatter plot. Blue, data obtained during 0D6D; Green, data obtained during 7D-12D; Orange; data obtained 1L-6L; Pink, data obtained 7L-12L. Higher 13C uptake in Crocospharea compared to Cyanothece is likely to reflect higher initial 13C enrichment in the culture for Crocosphaera: 9.7 atm% for Crocosphaera and 1.7 atm% for Cyanothece (see Methods).
a, d Diel change in N2 fixation (15N:14N), b, e diel change in percentage of 15N-enriched cells, c, f diel change in percentage of cells with 15N hotspot in a to c Crocosphaera and d to f Cyanothece. Black and white bars at the bottom of each graph indicate dark and light period, respectively. NO DATA at 4 L in Crocosphaera shows no data was collected.
The 15N2 fixation in the dark was observed based on the temporal changes in cellular 15N:14N ratios in both Crocosphaera and Cyanothece (Fig. 3a, d and Supplementary Table 1). Calculated per-cell 15N enrichment rates, ρ, followed similar trends as the 15N:14N ratio, and increased significantly (p = 0.014 by one-way ANOVA39) in Crocosphaera from 0 fmol N cell−1 h−1 at the start of the dark period to a mean of 17.3 fmol N cell−1 h−1 at 7D, but with a range of 0 fmol N cell−1 h−1 to 37.7 fmol N cell−1 h−1 (Supplementary Table 1b). These values are comparable to those reported in earlier studies (Supplementary Table 2). Cyanothece also showed a similar trend within population heterogeneity; ρ varied from 0 fmol N cell−1 h−1 to 12.7 fmol N cell−1 h−1 across 84 cells at the time of highest mean 15N enrichment (5.54 fmol N cell−1 h−1 at 6D) (Supplementary Table 1b). The 15N:14N ratios measured by NanoSIMS were in good agreement with the ratios measured by mass spectrometer (Supplementary Fig. 1).
The proportion of Crocosphaera cells that incorporated detectable 15N (i.e., cells with 15N:14N exceeding 2 SD above the mean at time 0: 3.8‰ for Crocosphaera, 4.0‰ for Cyanothece) increased from 40 to 75% in the dark, suggesting that at least ~25% of cells did not detectably fix N2 (Fig. 3b, e). Higher variability of 15N enriched cells in Crocosphaera compared to Cyanothece may be the result of low number of observed cells (between 7 to 33 cells at each time point) (Fig. 3b, d). Hotspots of 15N:14N were observed in the dark period. The 15N hotspots started to appear after 5D, and continued to form until the beginning of the light period (2 L), with the peak of 62% at 10D (Fig. 1 and 3c) in Crocosphaera. Similar temporal changes were observed for the proportion of cells with 15N hotspot among total cells in Cyanothece, from 2D to 6 L with a peak at 6D. Therefore, the lack of 15N hotspot in at least ~40% of cells again shows that a large fraction of cells did not detectably fix N2. N2 fixation earlier in the diel cycle in Cyanothece compared to Crocosphaera (Fig. 3) supports previous reports of a peak around 4D in Cyanothece and 9D in Crocosphaera under 12 L:12D cycle21,40.
To quantify the differentiation of rates within each population, we examined the statistical distribution of C and N isotope enrichments among all cells. Intercellular metabolic heterogeneity was defined as the coefficient of variation (CV; ref. 41) in each isotope ratio. The variations in 15N enrichment are observable in cell level 15N:14N ratios, which varied from 3.2‰ to 6.2‰ (4.4 ± 1.0‰, CV = 23.6%) at 6D in Crocosphaera, 3.5‰ to 18.9‰ (8.3‰ ± 4.4‰, CV = 53.8%) at 6D in Cyanothece (Figs. 2 and 3 and Supplementary Table 1). In contrast, 13C uptake (13C:12C ratio) was generally similar across cells, in both 15N-enriched cells and non-enriched cells (Figs. 1 and 2 and Supplementary Table 1). For example, in the 13C:12C ratio of 3 L in Fig. 1, all 14 cells are enriched similarly, with 13C:12C ratios between 7.9‰ and 9.4‰ (8.7‰ ± 0.5‰, CV = 6.2%) in Crocosphaera (Fig. 2). The CV for 15N:14N (23.6 to 31.4% during 6D to 12D, 25.4 to 48.0% during 6 L to 12 L) were greater than those estimated for 13C:12C during 6 L to 12 L (4.8 to 10.6%), suggesting higher heterogeneity in 15N2 fixation compared to 13C fixation. The same trend was observed in Cyanothece (46.4 to 56.2% during 6D to 12D, 45.5 to 48.9% during 6 L to 12 L in 15N:14N, 24.0 to 40.1% in 13C:12C during 6 L to 12 L) (Supplementary Table 1a).
The distribution of isotope ratios among cells reveals qualitatively different enrichment trends for C compared to N, for both Crocosphaera and Cyanothece (Fig. 4). The distribution of 15N:14N reveals two distinct peaks after 12 h, one that remains near the initial ratio and a second that develops at enriched levels of 15N, for both Crocosphaera and Cyanothece (Fig. 4a, b). In contrast, few cells remain at the initial ratio 13C:12C (Fig. 4c, d), and only a single broad peak is evident. To evaluate this bimodality, we calculated the “bimodal separation” (S; ref. 42), a distance between the means of two Gaussian distributions fit to the data (see Methods). The separations of peaks in 15N:14N was consistently larger than for 13C:12C, both for Crocosphaera (S = 1.45 for N, vs. S = 0.42 for C) and for Cyanothece (S = 0.79 for N, vs. S = 0.004 for C). We have also applied the bimodal curve fitted with 15N:14N to 13C:12C with the curve shape maintained (relative relation between two normal distributions and S are maintained); even after the curve is fitted to 13C:12C, the difference between the data and the curve is statistically significant for both diazotrophs (p < 0.001), indicating a significant difference between 15N:14N and 13C:12C.
Frequency distribution of a, b 15N:14N for Crocosphaera and Cyanothece (6 L to 12 L) and c, d 13C:12C for Crocosphaera and Cyanothece (6 L to 12 L), respectively. Red dashed curve is the normal distribution for the initial condition (t = t0) with the special y-axis on the right (that on the left is for other plotted values). Green dashed curve is the normal distribution based on the mean value and standard deviation of the probability density. S, bimodal separation; Dev, deviation from the normal distribution; n, number of samples. Both for Crocosphaera and Cyanothece, S and Dev are larger for 15N:14N, suggesting stronger heterogeneity for N uptake.
To confirm that the distribution of N isotopes develops a bimodal structure indicative of distinct rates among sub-populations, we compared the observed frequency distributions to a single Gaussian distribution with the same mean value and standard deviation (Fig. 4). For 15N:14N, the peak of the normal distribution appears near the local minima between the two peaks of the data (Fig. 4a, b), again indicating strong bimodal separation. In contrast, the normal distribution largely overlaps with the data for 13C:12C (Fig. 4c, d). We computed the deviation (Dev) from the normal distribution by adapting a commonly used form of Chi square (χ2) normalized by the sample number (n) (see Methods). The deviations from a single Gaussian distribution are stronger for 15N:14N than for 13C:12C for both diazotrophs (Dev = 1.97 vs. 0.42 for Crocosphaera and 0.81 vs. 0.33 for Cyanothece). These results qualitatively and quantitatively support stronger heterogeneity in N uptake than for C uptake, indicating a clear separation between N2 fixing cells and non-N2 fixing cells, without a comparable separation of C fixation.
Although Crocosphaera and Cyanothece are generally referred to as free-living unicellular cyanobacteria, they have been reported in colonies of more than two cells17,23 (Fig. 1). In the Crocosphaera culture, 55% of total cells were observed as colonies of 3 to 5 cells in this measurement (Supplementary Fig. 2). Colonial Crocosphaera cells were shown in earlier culture studies23, and an in situ study found that 45 to 85% of Crocosphaera-like cells were observed as colonies of 3 to 242 cells17. Colonial formation of cells might increase the efficiency of excreted \({{{\mathrm{NH}}}}_4^ +\) transfer among cells.
Simulating population heterogeneity of N2 fixation
The strong concentration of newly fixed N in a sub-population of colonial unicellular diazotrophs suggests that localizing the costly process of N2 fixation may confer an advantage to the population as a whole. A large part of the energetic cost of N2 fixation is incurred in the protection of nitrogenase from O2, which is achieved through excess respiration of C (refs. 43,44). We therefore hypothesize that having only a limited proportion of cells to pay the oxygen management cost could reduce community C requirements, potentially leading to overall higher growth.
To evaluate the potential benefits of confining N2 fixation to a sub-population, we used a Cell Flux Model of a N2 fixer44. The model uses a coarse-grained metabolic flux network including core metabolisms of respiration, biosynthesis and N2 fixation, which are constrained by mass, electron and energy balance (Fig. 5) (see Methods for details). We simulate a steady state environment where cells grow at a rate of μ (d−1). To maintain the prescribed rate of growth, energy must be provided by respiration, with distinct rates allocated to N2 fixation and biomass production44,45. In turn, the total respiration rate predicts the intracellular O2 concentrations, for a given diffusivity of O2 across the cell membrane. Additional respiration is added as needed to maintain anoxia inside the cell, thus protecting the nitrogenase enzyme and enabling N2 fixation44. The total carbon consumption rate per cell is computed to satisfy the sum of all 3 demands: biomass growth, N2 fixation, and respiratory protection against O2.
Green space, cytoplasmic space; peach frames, cell membrane layers; circular blobs, chemical compounds; solid arrows, material fluxes; dashed arrows, energy fluxes. C store represents C storage accumulated during the preceding light period, which is used for multiple purposes. The use of C store is represented by solid arrows of different colors by C fluxes and the different energy fluxes from respiration are colored differently; see the list at the bottom. fN represents the fraction of N2 fixing cells; thus that of non-nitrogen-fixing cells becomes 1 − fN. The O2 concentration of N2 fixing cell \([{{{\mathrm{O}}}}_2^{}]_C^N\) is kept small through respiratory protection at the expense of C store. Contrarily, only biosynthetic respiration occurs in non- N2 fixing cells. Excreted, fixed N\(\left( {{{{\mathrm{NH}}}}_4^ + } \right)\) is transferred to non-N2-fixing cells with efficiency of EN; 1 − EN is the fraction of excreted NH4+ lost to the environment. Cells grow at the rate of μ (d−1).
Here we adapted this cellular model44 to represent a heterogeneous colony of cells (the model version named CFM-Colony, with a fraction fN that fix N2, and a remaining fraction 1 − fN, that do not. The two sub-populations share a common medium, allowing N2-fixing cells to transfer fixed nitrogen \(\left( {{{{\mathrm{NH}}}}_4^ + } \right)\) to non- N2-fixing cells. The transfer of newly fixed N is prescribed by an efficiency parameter, EN, with the remaining fraction (1 − EN) of excreted \({{{\mathrm{NH}}}}_4^ +\) being lost from the entire colony.
To quantify the impact of heterogeneous rates of N2 fixation, we compare its population-scale rate of C consumption (denoted CS), to the rate that would apply to a homogeneous population of the same size (denoted \(C_S^0\)). When \(C_S/C_S^0 \, < \, 1\), the colony has lower C consumption with heterogeneous N2 fixation than homogeneous N2 fixation. The rate of N2 fixation by a heterogeneous community, NS, relative to a population with uniform rates, \(N_S^0\) (when fN = 1) can be expressed as follows:
The ratio of C consumption associated with N2 fixation and respiratory protection follows the ratio of N fixation rates by heterogeneous versus homogeneous populations (Eq. 1).
Modeled colonies with N2 fixation confined to a sub-population benefit from a substantial drop in overall C consumption, due to lower community level requirements for respiratory protection of nitrogenase (Fig. 6). For typical Crocosphaera growth rates (μ = 0.2) and a low efficiency of \({{{\mathrm{NH}}}}_4^ +\) transfer (EN = 0.2) C savings amount to ~8 fmol C cell−1 h−1, which is >30% of the C budget of a population with homogeneous rates (Fig. 6a, b). Total C consumption reaches a minimum value at an intermediate value of fN, due to two opposing factors; as fN initially decreases below 1, respiratory protection is reduced. However, as fN decreases, a larger portion of cells must also rely on transferred \({{{\mathrm{NH}}}}_4^ +\), which allows more \({{{\mathrm{NH}}}}_4^ +\) to be dissipated into the environment, requiring higher C consumption to replace it. This effect is represented by (Eq. 1) where increasing fN leads to increasing NS. At an intermediate value of fN, these two factors minimize Cs, and respiratory protection is covered by energetically balanced productive flows of respiration.
a CS for various fN. b \(C_S/C_S^0\) for various fN. c CS for various μ. d \(C_S/C_S^0\) for various μ. For a and c the legend in c shows the colors used for each fluxes; Dark green, biosynthesis; Bright green, respiratory energy production for biosynthesis; Orange, electron donation for N2 fixation; Yellow, respiratory energy production for N2 fixation; Cyan, respiratory protection. See Fig. 5 for more detail where similar colors are used for each C flux. Black solid lines at the top of a and c represent the total C fluxes. Black dotted lines in b and d are for \(C_S/C_S^0 = 1\). fN = 0.5, EN = 0.2, and μ = 0.2 (d−1) unless they are variable on the x-axes. Temperature T = 26 °C and O2 concentration in the environment [O2] = 208 µM, representing saturated concentration at this temperature and salinity of 35ppt81.
The value of fN that maximizes C savings tends to increase with decreasing EN due to increased costs for N2 fixation [Eq. 1] (Fig. 7b). When EN = 0.1, CS (thus \(C_S/C_S^0\)) reaches a minimum at fN ~ 0.56 (Supplementary Fig. 3), a level of heterogeneity similar to that seen in the culture experiments, in which about a half of cells fix N2. This optimum fN also increases with the growth rate µ due to increased energy costs for biomass production and N2 fixation (Fig. 7d). The 2D plot of CS and \(C_S/C_S^0\) for various fN and EN shows that up to 55% of C can be saved at high EN and low fN (Fig. 7a, b). On the other hand, even at EN < 0.1, heterogeneity can still save carbon (Fig. 7b), due to the small cost of N2 fixation relative to respiratory protection44. Considering the fact that C is one of the limiting factors for the growth for diazotrophs28,46,47, heterogeneity of N2 fixation might be an important strategy to increase their growth rates.
a CS for various fN and EN. b \(C_S/C_S^0\) for various fN and EN. c CS for various μ and fN. d \(C_S/C_S^0\) for various μ and fN. In b and d, dashed lines in cyan indicates optimum fN, which gives lowest \(C_S/C_S^0\) for EN and μ, respectively. Dotted lines indicate where \(C_S/C_S^0 = 1\) (note that \(C_S/C_S^0\) is always 1 at fN = 1). Gray zones indicates where N2 fixing capacity cannot sustain the population. fN = 0.5, EN = 0.2, and μ = 0.2 (d−1) unless they are variable on the axes. Temperature T = 26 °C and O2 concentration in the environment [O2] = 208 µM, representing saturated concentration at this temperature and salinity of 35 ppt (ref. 81).
Because unicellular diazotrophs can use \({{{\mathrm{NH}}}}_4^ +\), growth efficiency should be maximized when cells can meet their N demand from \({{{\mathrm{NH}}}}_4^ +\) in the environment, thus saving the considerable cost of N2 fixation (Fig. 6a, c). If cells rely solely on the N2 fixation for their N source, higher growth rate would render respiratory protection negligible, yielding higher growth efficiency. For example, the cell flux model (Fig. 6) predicts that as growth rate increases beyond ~0.28 (d−1), respiratory protection is no longer needed and the growth efficiency reaches its highest level. This occurs at a specific fN where respiratory protection is minimized with minimum loss of N to the environment (CS and \(C_S/C_S^0\) at fN ~ 0.38 in Fig. 6a, b respectively and cyan dashed curve in Fig. 7b).
The amount of C saved by heterogeneous N2 fixation depends only slightly on the poorly known value of EN. This insensitivity is based on the relatively small cost for N2 fixation44. While N2 fixation requires 16 ATP per N2, when EN = 1, the cost is predicted to be low relative to the whole cell energy requirement for biosynthesis since N2 fixation is just one reaction and there are many other pathways where ATP is consumed in the process of biosynthesis. In addition, cost for O2 management is overwhelming. As EN decreases, the cost for N2 fixation increases inversely proportional to EN, but due to the relatively low costs of N2 fixation, the whole cell C costs (thus CS and \(C_S/C_S^0\)) are relatively insensitive to EN.
The energetic advantage of heterogeneous N2 fixation rates increases as growth rates decline (Figs. 6c, d and 7c, d). Slower growth rates reduce the costs of biomass synthesis and N2 fixation, thus making respiratory protection a dominant energetic and C cost (Fig. 6c). Since heterogeneous populations can lower this cost by focusing N2 fixation in a fraction of cells, more C can be saved at lower μ. Over 90% of C can be saved at low μ and low fN (Fig. 7d). On the other hand, when μ > 0.35 (d−1), \(C_S/C_S^0\) can go above 1 (Figs. 6d and 7d) due to high costs for growth and N2 fixation, and N loss to the environment. The growth rates of Crocosphaera compiled from laboratory studies have a mean value of μ < 0.3 (d−1) (ref. 48). In the ocean, nutrients such as iron and phosphorus are generally more limited compared to culture conditions leading to even lower μ. Thus, with a typical growth rate in the ocean, it is likely that population heterogeneity in N2 fixation can save a considerable fraction of population C costs.
Implications for vertical habitat range
Fixed C is required for N2 fixation, respiration and cellular growth, providing energy, electrons and reduced C. In the open subtropical ocean, chlorophyll concentrations typically reach a maximum at the bottom of the photic zone, and the top of the nutricline, ~100 m depth, where both light and nutrients are adequate for growth, albeit at low rates. Below these depths, available light becomes so low that it prevents cells from fixing enough C to be viable (here we define maximum viable depth, MVD). Since heterogeneous N2 fixation reduces the overall C requirement of such populations, it could act to extend their MVD deeper into the nutricline.
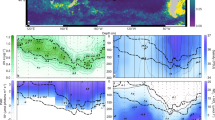
We simulated the depth variation of the growth rate for Crocosphaera populations with homogeneous versus heterogeneous N2 fixation rates (see Methods). The model result shows that MVD of the heterogeneous population is ~ 25 m deeper than that of the homogeneous population (Fig. 8a). This expanded MVD may be important because the available nutrient typically increase with depth and expanding MVD allows Crocosphaera to utilize the higher concentration of the growth-essential nutrient. For example, at the Hawaii Ocean Time-series (HOT) site at 22° 45’N, 158° 00’W (ref. 49), the concentration of phosphate (\({{{\mathrm{PO}}}}_4^{3 - }\): one of the potentially limiting nutrients) increases below ~80 m depth and heterogeneous populations would be able to utilize ~40% higher concentration than homogeneous populations (Fig. 8b). A similar depth profile of \({{{\mathrm{PO}}}}_4^{3 - }\) is observed in the South Pacific Gyre at 25°S, 170°W, where the highest nifH gene concentration of Crocosphaera have also been observed50. Under those conditions, the model predicts heterogeneous population would utilize up to ~90% higher concentration of \({{{\mathrm{PO}}}}_4^{3 - }\) (Supplementary Fig. 4a).
a Light dependent growth rate (µ) of populations of homogeneous (cyan dashed curve: Homo.) and heterogeneous N2 fixation (blue solid curve: Hetero.). b, c observed \({{{\mathrm{PO}}}}_4^{3 - }\) and \({{{\mathrm{NO}}}}_3^ -\) concentrations, respectively, from the Hawaii Ocean Time-series (HOT); 22° 45’N, 158° 00’W (ref. 49). Data are based on 25 years of observations (from 1988 to 2012); red dashed curves represent the averaged values. The red shading represents the difference of the depth where µ becomes zero between the two different populations in a; heterogeneous N2 fixation allows Crocosphaera to utilize higher concentration of \({{{\mathrm{PO}}}}_4^{3 - }\).
In these observations, \({{{\mathrm{NO}}}}_3^ -\) concentrations also increase with depth, which may lead to a partial suppression of N2 fixation (Fig. 8c and Supplementary Fig. 4b). However, the \({{{\mathrm{NO}}}}_3^ -\) concentrations in the expanded vertical niche remain well below what would cause full suppression51,52,53. For example, the concentration of \({{{\mathrm{NO}}}}_3^ -\) at MVD is below 2 µM whereas even 5 µM does not fully suppress N2 fixation of Crocosphaera51,52,53. Since respiratory protection is required regardless of the level of N2 fixation (thus required even when N2 fixation is partially suppressed)54, heterogeneous population would still save C even at depths near the MVD.
Discussion
The results of our laboratory observations demonstrate that unicellular diazotrophic cyanobacteria form colonies in which the key metabolic function of N2 fixation is confined to a distinct subpopulation. Guided by these observations, metabolic modeling shows that this functional specialization may provide an energetic advantage, especially in oligotrophic regions where nutrient availability increases as light diminishes. These findings have important implications for role of metabolic specialization in the evolution of multi-cellularity, and the biogeography of unicellular diazotrophs and their role in biogeochemical cycles. Evaluating these broader implications will require a more complete understanding of the mechanisms and economics of material transfers within colonies, and the environmental factors that influence and sustain them.
Our results suggest that the exchange of newly fixed N within colonies is key to reducing population carbon costs, potentially explaining why the cells are often observed in aggregations (Fig. 1). However, the mechanisms of \({{{\mathrm{NH}}}}_4^ +\) transfer between cells and its overall efficiency (EN) within each colony remain poorly constrained. It is likely that the surface:volume ratio of the cell and the size of aggregated colonies can both influence EN. The diffusivity between the cellular spaces, might be affected by the production of extracellular polymeric substances. Also, the uptake properties of the cells (i.e. the maximum uptake rate and the half saturation constants of \({{{\mathrm{NH}}}}_4^ +\)) influence how effectively they obtain \({{{\mathrm{NH}}}}_4^ +\). For example, if the N is transported with intercellular transporters, EN would decrease considerably. To understand what regulates population heterogeneity of N2 fixation, it may be useful to examine the heterogeneity of N2 fixation under varying growth conditions, including different ambient \({{{\mathrm{NH}}}}_4^ +\) and O2 concentrations. Also, it is possible that N2 fixation is tied to specific phase of the cell cycle, which requires further experiments.
Recent ocean ecological and biogeochemical models simulate various functional groups of diazotrophs including unicellular types55,56, but diazotrophs within the same functional groups are generally represented as a uniform metabolic population. Given the observed bimodality of N2 fixation and its impact on C cost, our study suggests that resolving such heterogeneity and its underlying causes may be essential to simulating the ocean ecosystems and predicting the niche of unicellular diazotrophs. In particular, the dependence of C savings on cellular growth rate would help to test the model predictions for expanded vertical habitat. On the other hand, our model shows that population C savings are relatively insensitive to uncertainties in EN, especially at low growth rate, where the rate of N assimilation becomes small and costs of respiratory protection dominate (Fig. 7c and Supplementary Fig. 5). Thus, while the expansion of vertical niche depends on the growth rate dependence of C savings, it appears robust to uncertainty in N transfer efficiency, EN.
Given the ubiquity of phenotypic heterogeneity57 and inter-cellular cooperation58, metabolic heterogeneity may be a general strategy for maximizing fitness among diazotrophic cyanobacteria. It remains an open question whether filamentous diazotroph Trichodesmium separates N2 fixing cells (diazocytes) and cells responsible for photosynthesis8,59,60,61 or not35,62. If Trichodesmium separates N2 fixation and photosynthesis on cellular level, the observation of heterogeneity of N2 fixation in both Crocosphaera and Cyanothece together with the heterogeneity in N2 fixation in Trichodesmium35 suggest an evolutionary relationship between unicellular and filamentous diazotrophs. However, it remains an open question whether there is connection between heterogeneity in N2 fixation in unicellular diazotrophs and multicellular diazotrophs, as well as whether unicellular or multicellular diazotrophs evolved first in the cyanobacterial lineage63,64,65. The finding that heterogeneity in N2 fixation occurs in both unicellular and multicellular diazotrophs may support the hypothesis that the division of labor is a key factor driving multi cellular cooperation in evolutionary transitions66,67.
Methods
Phytoplankton cultures
A Crocosphaera strain isolated from the surface of the western subtropical Pacific68 was grown in a continuous 1.2 L culture in N-free medium. To closely represent their habitat (the euphotic zones of subtropical gyres), the culture was maintained in a chemostat with a dilution rate 0.20 d−1 (40% of the maximum growth rate), at a temperature of 26 °C, an irradiance of 200 µmol photons m−2 s−1, and a dark:light cycle of 12:12 h (1D to 12D, 1 L to 12 L). The beginning of the dark period was considered time 0 (0D). The N-free medium was prepared from seawater collected from the surface of the western North Pacific Ocean (34°20’N, 138°40’E), enriched with 20 µM of NaH2PO4, f/2 vitamins, and f/2 trace metals69,70. Cyanothece sp. ATCC51142 was grown in a 1.0 L culture in N-free ASP2 medium71 which contains 28.7 µM of K2HPO4, a temperature 26 °C, an irradiance of 400 µmol photons m−2 s−1, and a dark:light cycle of 12:12 h (1D to 12D, 1 L to 12 L) at growth rate (μ) of 0.30 d−1.
15N and 13C uptake
N2 fixation was measured following the method described by Mohr et al.23. Briefly, N-free medium was degassed and rapidly transferred to 125 mL glass bottles with minimal agitation until the maximum volume of the bottles was reached. These were septum-capped and enriched by injecting 1 mL of 15N2 gas (99.8 atom% 15N, lot #11059; SI Science Co., Ltd., Tokyo, Japan) into the 24 vials. Previous study confirmed no contamination of 15\({{{\mathrm{NO}}}}_3^ -\) and 15\({{{\mathrm{NH}}}}_4^ +\) in the 15N2 gas72. To observe 15N and 13C uptake, 0.5 mL of the 15N2-enriched medium was then added to 9.0 mL of Crocosphaera cultures (4.1 × 105 cells mL−1) harvested from the continuous culture in 10 mL serum vials, to a final N2 enrichment of 5.5 atom% and 0.5 mL NaH13CO3 was injected simultaneously to a final enrichment of 9.7 atom%. These vials (n = 24) were sealed with crimp-seal butyl tube closures to eliminate headspace and air bubbles, preventing dilution of 15N2 with atmospheric 14N2. The vials were incubated under the same conditions as previously described and harvested one vial every hour beginning at the start of the dark period (6 PM), and split into three aliquots for NanoSIMS, PON and mass spectrometry, and flow cytometry. Samples prior to isotope injection were also collected and analyzed as time 0. Samples at 4 L were lost. Cells observed under NanoSIMS analysis were from 7 to 37 cells at each time point.
In Cyanothece, 15N and 13C uptake were analyzed as described for Crocosphaera, except for small differences in the source of 15N2 gas (98 atom% 15N, lot# MBBB0968V; Sigma-Aldrich, St. Louis, Missouri, USA), culture volume (4.0 mL of 1.7 × 106 cells mL−1 in 5 mL serum vials), final enrichment (13.6 atom% and 1.7 atom% for 15N and 13C, respectively), sampling frequency (2 h), and the 87 to 220 cells were analyzed per each time point. Contamination of dissolved inorganic nitrogen in N2 was not analyzed in the 15N gas.
NanoSIMS imaging
Cells (1 mL) were fixed in 2.0% w/v glutaraldehyde, and collected using 0.2-µm IsoporeTM GTTP Millipore Membrane filters (Merck Millipore, Billerica, Massachusetts, USA), which were then washed with Milli-Q ultrapure water and stored at −20 °C until further processing. For analysis, samples were sputtered with gold and secondary ions were imaged in 5 or 10 serial images (layers) on a NanoSIMS 50 (Cameca, Gennevilliers, France) to quantify 12C, 13C, 12C14N, and 12C15N in 7 to 220 cells per time point, following earlier studies34,73. Secondary ions were generated by pre-sputtering with a 300 or 500 pA Cs+ beam before scanning a raster of 256 × 256 pixels (10–15 µm2 total raster size) with a 1.7–1.8 pA Cs+ primary beam. Ratios of 15N:14C (inferred from the 12C15N/12C14N) and 13C:12C (13C/12C) are shown in the results (Figs. 1–4, Supplementary Fig. 1 and Supplementary Table 1). The system was tuned for ~9,000 mass resolving power to overcome isobaric interference, and confirmed against isotopic ratios obtained in organic particulates determined by Flash EA elemental analyzer (Thermo Electron Corporation, Waltham, Massachusetts, USA) coupled to a DELTAplus XP mass spectrometer (Thermo Electron Corporation, Waltham, Massachusetts, USA) (Supplementary Fig. 1).
Elemental analysis and mass spectrometry
Cells (8 mL) were collected on Whatman GF/F filters (GE Healthcare UK Ltd., Little Chalfont, Buckinghamshire, United Kingdom) pre-combusted at 450 °C for 6 h, and frozen at −20 °C until further processing. For analysis, filters were dried at 50 °C overnight, exposed to HCl fumes for 2 h, and then dried again. The concentration and isotopic composition of total particulate organic C and N were measured on a Flash EA elemental analyzer (Thermo Electron Corporation, Waltham, Massachusetts, USA) coupled to a DELTAplus XP mass spectrometer (Thermo Electron Corporation, Waltham, Massachusetts, USA). The abundance of 13C and 15N were expressed as δ13C (or δ15N) (‰): δ13C (δ15N) = [(Rsample/Rstandard) −1] * 1000. Lower limit of the detection of the Flash EA elemental analyzer (Thermo Electron Corporation, Waltham, Massachusetts, USA) is 0.005 mg N (Supplementary Table 3).
Flow cytometry
Samples (4.5 mL) were fixed with 0.5% w/v glutaraldehyde, and stored at −80 °C until being counted on a PASIII flow cytometer (Partec GmbH, Münster, Germany) equipped with 10 mW argon ion lasers.
Calculation of carbon and nitrogen uptake rates
Images obtained by NanoSIMS were processed in ImageJ74 following methods described by Popa et al.34. Briefly, the mean isotopic compositions in each cell, delineated by the 12C14N images, were integrated over 5 or 10 serial images, corrected against reference standards, and converted to percentage uptake with a measurement precision of 0.8–1.5%. Cells with a 12C15N:12C14N (15N:14N) ratio exceeding 2 standard deviations above the average at time 0 (at which 15N:14N was 3.8 ‰ for Crocosphaera, 4.0 ‰ for Cyanothece) were considered 15N-enriched. Similarly, cells with a 13C:12C ratio exceeding 2 standard deviations above the mean at time 0 (at which 13C:12C was 9.8 ‰ for Crocosphaera, 11.8 ‰ for Cyanothece) were considered 13C-enriched.
The rate of N2 fixation was defined as the change in % 15N h−1 relative to the initial measurement. Per-cell net N uptake rates (ρ; fmol N cell−1 h−1) were calculated using a method adapted from Popa et al.34, described in [Eq. 2].
where Fxnet is the ratio between 15N in a cell afterΔt and the initial 15N content, and CellQ is the cellular N quota calculated as the sum of particulate organic 15N and 14N normalized to the cell density. As N2 fixation in Crocosphaera occurs only at night21,29, 15N enrichment in the dark (0–12 h) and during light (13–24 h) were treated as N2 fixation and re-uptake of excreted dissolved 15N, respectively.
Statistics and reproducibility
15N:14N ratios were compared by one-way ANOVA39 with 25 time points as factor levels, and individual cells in a sample as independent replicates. Differences were considered significant if p < 0.05. Heterogeneity was defined by the coefficient of variation (CV; ref. 41):
where \({\bar{x}}\) is the mean and σ is the standard deviation among the cells. Normality assumptions were confirmed after logarithmic transformation (p > 0.05 by K-S test, n = 7–37 for Crocosphaera, n = 87–220 for Cyanothece) and residuals had a mean of zero. Dunnett’s T-3 multiple comparisons75 were used to compare background ratios.
To compute the bimodal separation, we first fit the sum of two Gaussian distributions to the histogram42:
where FB(x) is frequency of x, Ai is amplitude, \({\bar{x}}\)i is mean and σi is standard deviation (i = 1 or 2 and \({\bar{x}}\)2 > \({\bar{x}}\)1). We obtain Ai, \({\bar{x}}\)i and σi with Metropolis Algorithm76,77, that minimizes the sum of square error between [Eq. 4] and the histogram. Based on values of \({\bar{x}}\)i and σi, obtained, we calculate the bimodal separation:
To examine the statistical significance of the difference between N and C uptake, we use the curve fitted to 15N:14N, and re-fitted to 13C:12C, by maintaining the original relative relationship between A1 and A2, \({\bar{x}}\)1 and \({\bar{x}}\)2, and σ1 and σ2 and value of S obtained based on 15N:14N of the same diazotroph. The p value is obtained based on the difference between the data of 13C:12C and the fitted curve as a null hypothesis.
To compute the deviation from the normal distribution, we applied the following procedure. If variation in the rate of C or N uptake is randomly distributed among cells of a population with a constant mean rate, we expect the probability density of C and N uptake follows the normal distribution78:
where E(x) is the expected probability density for value x based on the normal distribution, A is the total area of the histogram, σ is the observed standard deviation, and \({\bar{x}}\) is the observed mean value. If the C or N uptake of the population is heterogeneous, we expect stronger deviation from [Eq. 6]; we calculate the deviation from the Chi squared (χ2) statistic79, normalized by the sample number:
where O(x) is observed probability density for the value x. The normalization by n makes results with different sample numbers comparable (here Crocosphaera and Cyanothece).
Reproducibility was confirmed by analyzing 7 to 37 independent Crocosphaera cells, and 87 to 220 independent Cyanothece cells (Supplementary Table 1).
Numerical model of heterogeneous metabolisms
To represent heterogeneous metabolisms within a single clonal population of unicellular diazotrophs, we have modified the Cell Flux Model of diazotrophs44 by simulating two types of cells; N2-fixing and non-N2 fixing (Fig. 5). The model resolves a coarse-grained metabolic flux network based on mass, electron and energy (ATP) balance. These balances quantify stored C use for 3 cellular functions: biosynthesis, electron donation for N2 fixation, and respiration. Respiration can be further classified into three uses; respiration for biosynthesis, for N2 fixation and for respiratory protection (Fig. 5). The model was parameterized for Crocosphaera based on a respiration budget43 by reducing the diffusivity of cell membranes44. We use cellular N of 30 fmol N cell−1 and a diameter of 3μm and temperature of 28 °C to better represent Crocosphaera (strain WH8501) in Großkopf and Laroche43, which gives the diffusivity coefficient of the membrane of 1.51 × 10−5, slightly higher than previously estimated (1.38 × 10−5). To represent Crocosphaera in this study (strain PS0609A) we used a cell diameter of 5 µm (based on Fig. 1 and Sohm et al.80 for a larger size class), a cellular N of 60 fmol cell−1, and the maximum N2 fixation rate of 6.1 fmol cell−1 h−1. To represent the laboratory condition, we applied temperature T = 26 °C and assume saturated O2 concentration [O2] = 208 µM (ref. 81), and μ = 0.20 d−1 (when µ is constant). We have used a uniform growth rate among cells following previous studies82,83,84,85,86.
Application of the model to one dimensional water column
To simulate the light attenuation in the one-dimensional water column, we used Beer’s law:
where I(z) is the light intensity (µmol m−2 s−1) at the depth of z (m), I0 is the light intensity at the surface (µmol m−2 s−1), and k is the extinction coefficient (m−1). To simulate the photosynthesis rate by Crocosphaera, we adapt a commonly used equation with saturating light based on Target theory85,87:
where P(I) is the rate of photosynthesis (fmol C cell−1 h−1) at the light intensity of I, Pmax is the maximum photosynthesis rate (fmol C cell−1 h−1), \(I_0^P\) is the reference light intensity at which P becomes (e − 1)/e. Then, with the Cell Flux Model, we find the growth rate µ (d−1) where CS(µ) = P(I), where we use EN = 0.2 and fN = 0.5 for the population with heterogeneous N2 fixation and fN = 1 for the population with homogeneous N2 fixation. The loss of C to the environment is assumed equal for both of these populations. We consider a simple 12:12 (h) light:dark cycle, at which photosynthesis occurs only during the light period and N2 fixation and respiratory protection occur only during the dark periods. We apply I0 = 1000 and k = 30−1 to resemble observed depth profile of light in the subtropical gyres50,88, and Pmax = 7 and \(I_0^P = 100\) where the simulated maximum growth rate becomes close to the highest side of the observed range48 and MVD of the population of heterogeneous N2 fixation becomes close to 125 (m), below which the nifH copies of Crocosphaera is observed to drop considerably.
Reporting summary
Further information on research design is available in the Nature Research Reporting Summary linked to this article.
Data availability
The data used to generate the graphs presented in the main figures can be found as Supplementary Data 1. All other data that support the findings of this study are available on request from the corresponding author (TM).
Code availability
The model has been written in Python 3 and freely available in Zenodo at https://zenodo.org/record/1251956 (https://doi.org/10.5281/zenodo.1251956).
Change history
07 June 2023
A Correction to this paper has been published: https://doi.org/10.1038/s42003-023-05007-6
References
Montoya, J. P., Carpenter, E. J. & Capone, D. G. Nitrogen fixation and nitrogen isotope abundances in zooplankton of the oligotrophic North Atlantic. Limnol. Oceanogr. 47, 1617–1628 (2002).
Hunt, B. P. V. et al. Contribution and pathways of diazotroph-derived nitrogen to zooplankton during the VAHINE mesocosm experiment in the oligotrophic New Caledonia lagoon. Biogeosciences 13, 3131–3145 (2016).
Horii, S., Takahashi, K., Shiozaki, T., Hashihama, F. & Furuya, K. Stable isotopic evidence for the differential contribution of diazotrophs to the epipelagic grazing food chain in the mid-Pacific Ocean. Glob. Ecol. Biogeogr. 27, 1467–1480 (2018).
Loick-Wilde, N. et al. Nitrogen sources and net growth efficiency of zooplankton in three Amazon River plume food webs. Limnol. Oceanogr. 61, 460–481 (2016).
Kuypers, M. M. M., Marchant, H. K. & Kartal, B. The microbial nitrogen-cycling network. Nat. Rev. Microbiol. 16, 263–276 (2018).
Gallon, J. R. Reconciling the incompatible: N2 fixation and oxygen. N. Phytol. 122, 571–609 (1992).
Fay, P. Oxygen relations of nitrogen-fixation in Cyanobacteria. Microbiol Rev. 56, 340–373 (1992).
Berman-Frank, I. et al. Segregation of nitrogen fixation and oxygenic photosynthesis in the marine Cyanobacterium Trichodesmium. Science 294, 1534–1537 (2001).
Berman-Frank, I., Lundgren, P. & Falkowski, P. Nitrogen fixation and photosynthetic oxygen evolution in cyanobacteria. Res. Microbiol. 154, 157–164 (2003).
Sohm, J. A., Webb, E. A. & Capone, D. G. Emerging patterns of marine nitrogen fixation. Nat. Rev. Microbiol 9, 499–508 (2011).
Moisander, P. H. et al. Unicellular cyanobacterial distributions broaden the oceanic N2 fixation domain. Science 327, 1512–1514 (2010).
Luo, Y. W. et al. Database of diazotrophs in global ocean: abundance, biomass and nitrogen fixation rates. Earth Syst. Sci. Data 4, 47–73 (2012).
Monteiro, F. M., Follows, M. J. & Dutkiewicz, S. Distribution of diverse nitrogen fixers in the global ocean. Glob. Biogeochemical Cycles 24, GB3017 (2010).
Zehr, J. P. Nitrogen fixation by marine cyanobacteria. Trends Microbiol 19, 162–173 (2011).
Zehr, J. P. & Bombar, D. Marine nitrogen fixation: organisms, significance, enigmas, and future directions. In Biological nitrogen fixation (ed. FJ de Bruijn) 857–872 (Wiley, 2015).
Zehr, J. P. et al. Unicellular cyanobacteria fix N2 in the subtropical North Pacific Ocean. Nature 412, 635–638 (2001).
Foster, R. A., Sztejrenszus, S. & Kuypers, M. M. Measuring carbon and N2 fixation in field populations of colonial and free-living unicellular cyanobacteria using nanometer-scale secondary ion mass spectrometry. J. Phycol. 49, 502–516 (2013).
Montoya, J. P. et al. High rates of N2 fixation by unicellular diazotrophs in the oligotrophic Pacific Ocean. Nature 430, 1027–1032 (2004).
Langlois, R. J., Hummer, D. & LaRoche, J. Abundances and distributions of the dominant nifH phylotypes in the Northern Atlantic Ocean. Appl Environ. Microbiol 74, 1922–1931 (2008).
Mohr, W., Intermaggio, M. P. & LaRoche, J. Diel rhythm of nitrogen and carbon metabolism in the unicellular, diazotrophic cyanobacterium Crocosphaera watsonii WH8501. Environ. Microbiol 12, 412–421 (2010).
Dron, A. et al. Light:dark (12:12 h) quantification of carbohydrate fluxes in Crocosphaera watsonii. Aquat. Microb. Ecol. 68, 43–55 (2012).
Masuda, T. et al. Diel regulation of photosynthetic activity in the oceanic unicellular diazotrophic cyanobacterium Crocosphaera watsonii WH8501. Environ. Microbiol. 20, 546–560 (2018).
Mohr, W., Vagner, T., Kuypers, M. M., Ackermann, M. & La Roche, J. Resolution of conflicting signals at the single-cell level in the regulation of cyanobacterial photosynthesis and nitrogen fixation. PLoS ONE 8, e66060 (2013).
Langlois, R. J., LaRoche, J. & Raab, P. A. Diazotrophic diversity and distribution in the tropical and subtropical Atlantic Ocean. Appl. Environ. Microbiol. 71, 7910–7919 (2005).
Foster, R. A. et al. Influence of the Amazon River plume on distributions of free-living and symbiotic cyanobacteria in the western tropical north Atlantic Ocean. Limnol. Oceanogr. 52, 517–532 (2007).
Bonnet, S. et al. Dynamics of N2 fixation and fate of diazotroph-derived nitrogen in a low-nutrient, low-chlorophyll ecosystem: results from the VAHINE mesocosm experiment (New Caledonia). Biogeosciences 13, 2653–2673 (2016).
Reddy, K. J., Haskell, B., Sherman, D. M. & Sherman, L. A. Unicellular, aerobic nitrogen-fixing cyanobacteria of the genus Cyanothece. J. Bacteriol. 175, 1284–1292 (1993).
Červený, J., Sinetova, M. A., Valledor, L., Sherman, L. A. & Nedbal, L. Ultradian metabolic rhythm in the diazotrophic cyanobacterium Cyanothece sp. ATCC 51142. Proc. Natl. Acad. Sci. USA 110, 13210–13215 (2013).
Tuit, C., Waterbury, J. & Ravizzaz, G. Diel variation of molybdenum and iron in marine diazotrophic cyanobacteria. Limnol. Oceanogr. 49, 978–990 (2004).
Colón-López, M., Sherman, D. M. & Sherman, L. A. Transcriptional and translational regulation of nitrogenase in light-dark- and continuous-light grown cultures of the unicellular cyanobacterium Cyanothece sp. strain ATCC 51142. J. Bacteriol. 179, 4319–4327 (1997).
Pennebaker, K., Mackey, K. R. M., Smith, R. M., Williams, S. B. & Zehr, J. P. Diel cycling of DNA staining and nifH gene regulation in the unicellular cyanobacterium Crocosphaera watsonii strain WH 8501 (Cyanophyta). Environ. Microbiol. 12, 1001–1010 (2010).
Wagner, M. Single-cell ecophysiology of microbes as revealed by Raman microspectroscopy or secondary ion mass spectrometry imaging. Annu. Rev. Microbiol. 63, 411–429 (2009).
Musat, N., Foster, R., Vagner, T., Adam, B. & Kuypers, M. M. Detecting metabolic activities in single cells, with emphasis on nanoSIMS. FEMS Microbiol. Rev. 36, 486–511 (2012).
Popa, R. et al. Carbon and nitrogen fixation and metabolite exchange in and between individual cells of Anabaena oscillarioides. ISME J. 1, 354–360 (2007).
Finzi-Hart, J. A. et al. Fixation and fate of C and N in the cyanobacterium Trichodesmium using nanometer-scale secondary ion mass spectrometry. Proc. Natl. Acad. Sci. USA 106, 9931–9931 (2009).
Marchant, H. K., Mohr, W. & Kuypers, M. M. Recent advances in marine N-cycle studies using 15N labeling methods. Curr. Opin. Biotechnol. 41, 53–59 (2016).
Martínez-Pérez, C. et al. The small unicellular diazotrophic symbiont, UCYN-A, is a key player in the marine nitrogen cycle. Nat. Microbiol. 1, 16163 (2016).
Krupke, A. et al. The effect of nutrients on carbon and nitrogen fixation by the UCYN-A–haptophyte symbiosis. ISME J. 9, 1635–1647 (2015).
Iversen, G. R. Analysis of variance. In: International Encyclopedia of Statistical Science (ed. Lovric M.) (Springer, Berlin, Heidelberg, 2011).
Bandyopadhyay, A., Elvitigala, T., Liberton, M. & Pakrasi, H. B. Variations in the rhythms of respiration and nitrogen fixation in members of the unicellular diazotrophic cyanobacterial genus Cyanothece. Plant Physiol. 161, 1334–1346 (2013).
Stȩpniak, C. Coefficient of variation. In: International Encyclopedia of Statistical Science (ed. Lovric M.) (Springer, Berlin, Heidelberg, 2011).
Zhang, C., Mapes, B. E. & Soden, B. J. Bimodality in tropical water vapour. Q. J. R. Meteorological Soc. 129, 2847–2866 (2003).
Großkopf, T. & Laroche, J. Direct and indirect costs of dinitrogen fixation in Crocosphaera watsonii WH8501 and possible implications for the nitrogen cycle. Front. Microbiol. 3, 236 (2012).
Inomura, K., Bragg, J. & Follows, M. J. A quantitative analysis of the direct and indirect costs of nitrogen fixation: a model based on Azotobacter vinelandii. ISME J. 11, 166–175 (2017).
Rittmann, B. E. & McCarty, P. L. Stoichiometry and bacterial energetics. In: Environmental Biotechnology: Principles and Applications. 126–164 (McGraw-Hill, New York, NY, USA, 2001).
Fu, F. X. et al. Interactions between changing pCO2, N2 fixation, and Fe limitation in the marine unicellular cyanobacterium Crocosphaera. Limnol. Oceanogr. 53, 2472–2484 (2008).
Gradoville, M. R., White, A. E. & Letelier, R. M. Physiological response of Crocosphaera watsonii to enhanced and fluctuating carbon dioxide conditions. PLoS ONE 9, e110660 (2014).
Follett, C. L., Dutkiewicz, S., Karl, D. M., Inomura, K. & Follows, M. J. Seasonal resource conditions favor a summertime increase in North Pacific diatom-diazotroph associations. ISME J. 12, 1543–1557 (2018).
Karl, D. M. & Lukas, R. The Hawaii Ocean Time-series (HOT) Program: Background, rationale and field implementation. Deep-Sea Res. 43, 129–156 (1996).
Shiozaki, T. et al. Linkage between dinitrogen fixation and primary production in the oligotrophic South Pacific Ocean. Glob. Biogeochem. Cycles 32, 1028–1044 (2018).
Dekaezemacker, J. & Bonnet, S. Sensitivity of N2 fixation to combined nitrogen forms (NO3− and NH4+) in two strains of the marine diazotroph Crocosphaera watsonii (Cyanobacteria). Mar. Ecol. Prog. Ser. 438, 33–46 (2011).
Knapp, A. N., Dekaezemacker, J., Bonnet, S., Sohm, J. A. & Capone, D. G. Sensitivity of Trichodesmium erythraeum and Crocosphaera watsonii abundance and N2 fixation rates to varying NO3− and PO43− concentrations in batch cultures. Aquat. Microb. Ecol. 66, 223–236 (2012).
Knapp, A. N. The sensitivity of marine N2 fixation to dissolved inorganic nitrogen. Front Microbiol 3, 374 (2012).
Inomura, K., Bragg, J., Riemann, L. & Follows, M. J. A quantitative model of nitrogen fixation in the presence of ammonium. PLoS ONE 13, e0208282 (2018).
Stukel, M. R., Coles, V. J., Brooks, M. T. & Hood, R. R. Top-down, bottom-up and physical controls on diatom-diazotroph assemblage growth in the Amazon River plume. Biogeosciences 11, 3259–3278 (2014).
Dutkiewicz, S. et al. Capturing optically important constituents and properties in a marine biogeochemical and ecosystem model. Biogeosciences 12, 4447–4481 (2015).
Ackermann, M. A functional perspective on phenotypic heterogeneity in microorganisms. Nat. Rev. Microbiol 13, 497–508 (2015).
Celiker, H. & Gore, J. Cellular cooperation: insights from microbes. Trends Cell Biol. 23, 9–15 (2013).
Lin, S., Henze, S., Lundgren, P., Bergman, B. & Carpenter, E. J. Whole-cell immunolocalization of nitrogenase in marine diazotrophic cyanobacteria, Trichodesmium spp. Appl. Environ. Microbiol. 64, 3052–3058 (1998).
Kupper, H., Ferimazova, N., Setlik, I. & Berman-Frank, I. Traffic lights in trichodesmium. Regulation of photosynthesis for nitrogen fixation studied by chlorophyll fluorescence kinetic microscopy. Plant Physiol. 135, 2120–2133 (2004).
Eichner, M. J. et al. Chemical microenvironments and single-cell carbon and nitrogen uptake in field-collected colonies of Trichodesmium under different pCO2. ISME J. 11, 1305–1317 (2017).
Ohki, K. & Taniuchi, Y. Detection of nitrogenase in individual cells of a natural population of Trichodesmium using immunocytochemical methods for fluorescent cells. J. Oceanogr. 65, 427–432 (2009).
Sanchez-Baracaldo, P., Hayes, P. K. & Blank, C. E. Morphological and habitat evolution in the Cyanobacteria using a compartmentalization approach. Geobiology 3, 145–165 (2005).
Hammerschmidt, K., Landan, G., Kümmel Tria, F. D. & Dagan, T. A chronology of multicellularity evolution in cyanobacteria. bioRxiv https://doi.org/10.1101/570788 (2019).
Schirrmeister, B. E., Antonelli, A. & Bagheri, H. C. The origin of multicellularity in cyanobacteria. BMC Evolut. Biol. 11, 45 (2011).
Kirk, D. L. A twelve-step program for evolving multicellularity and a division of labor. BioEssays 27, 299–310 (2005).
Michod, R. E. Evolution of individuality during the transition from unicellular to multicellular life. Proc. Natl. Acad. Sci. USA 104, 8613–8618 (2007).
Masuda, T., Furuya, K., Kodama, T., Takeda, S. & Harrison, P. J. Ammonium uptake and dinitrogen fixation by the unicellular nanocyanobacterium Crocosphaera watsoniiin nitrogen-limited continuous cultures. Limnol. Oceanogr. 58, 2029–2036 (2013).
Guillard, R. R. L. & Ryther, J. H. Studies of marine planktonic diatoms. I. Cyclotella nana Hustedt and Detonula confervacea Cleve. Can. J. Microbiol. 8, 229–239 (1962).
Guillard, R. R. L. Culture of phytoplankton for feeding marine invertebrates. In Culture of Marine Invertebrate Animals (eds Smith W.L. & Chanley M.H) 26–60 (Plenum Press, New York, USA, 1975).
Provasoli, L., McLaughlin, J. J. A. & Droop, M. R. The development of artificial media for marine algae. Arcb. Mikrobiol. 25, 392–428 (1957).
Shiozaki, T. et al. Why is Trichodesmium abundant in the Kuroshio? Biogeosciences 12, 6931–6943 (2015).
Musat, N. et al. A single-cell view on the ecophysiology of anaerobic phototrophic bacteria. Proc. Natl. Acad. Sci. USA 105, 17861–17866 (2008).
Schneider, C. A., Rasband, W. S. & Eliceiri, K. W. NIH Image to ImageJ: 25 years of image analysis. Nat. Methods 9, 671–675 (2012).
Chavez, F. P., Messie, M. & Pennington, J. T. Marine primary production in relation to climate variability and change. Ann. Rev. Mar. Sci. 3, 227–260 (2011).
Metropolis, N., Rosenbluth, A. W., Rosenbluth, M. N., Teller, A. H. & Teller, E. Equation of state calculations by fast computing machines. J. Chem. Phys. 21, 1087–1092 (1953).
Omta, A. W. et al. Extracting phytoplankton physiological traits from batch and chemostat culture data. Limnol. Oceanogr.: Methods 15, 453–466 (2017).
Krishnamoorthy, K. Statistical distributions: an overview. In International Encyclopedia of Statistical Science (ed. Lovric M.) (Springer, Berlin, Heidelberg, 2011).
Wilson, E. B. & Hilferty, M. M. The distribution of chi-square. Proc. Natl. Acad. Sci. USA 17, 684–688 (1931).
Sohm, J. A., Edwards, B. R., Wilson, B. G. & Webb, E. A. Constitutive extracellular polysaccharide (EPS) production by specific isolates of Crocosphaera watsonii. Front Microbiol 2, 229 (2011).
Benson, B. B. & Krause, D. The concentration and isotopic fraction of oxygen dissolved in freshwater and seawater in equilibrium with the atmosphere. Limnol. Oceanogr. 29, 620–632 (1984).
Ågren, G. I. The C:°N:°P stoichiometry of autotrophs - theory and observations. Ecol. Lett. 7, 185–191 (2004).
Pahlow, M. & Oschlies, A. Chain model of phytoplankton P, N and light colimitation. Mar. Ecol. Prog. Ser. 376, 69–83 (2009).
Talmy, D., Blackford, J., Hardman-Mountford, N. J., Dumbrell, A. J. & Geider, R. J. An optimality model of photoadaptation in contrasting aquatic light regimes. Limnol. Oceanogr. 58, 1802–1818 (2013).
Geider, R. J., MacIntyre, H. L. & Kana, T. M. A dynamic regulatory model of phytoplanktonic acclimation to light, nutrients, and temperature. Limnol. Oceanogr. 43, 679–694 (1998).
Ghyoot, C., Flynn, K. J., Mitra, A., Lancelot, C. & Gypens, N. Modeling plankton mixotrophy: a mechanistic model consistent with the Shuter-type biochemical approach. Front. Ecol. Evol. 5, https://doi.org/10.3389/fevo.2017.00078 (2017).
Cullen, J. J. On models of growth and photosynthesis in phytoplankton.Deep Sea Res. 37, 667–683 (1989).
Letelier, R. M., Karl, D. M., Abbott, M. R. & Bidigare, R. R. Light driven seasonal patterns of chlorophyll and nitrate in the lower euphotic zone of the North Pacific Subtropical Gyre. Limnol. Oceanogr. 49, 508–519 (2004).
Acknowledgements
We would like to thank Douglas Campbell for valuable discussions and critical reading of the paper, Michael J. Follows for useful suggestions and Evelyn Lawrenz for her assistance with statistical analyses. This research was financially supported by MEXT grants for Scientific Research on Innovative Areas (24121001, 24121005, K.F.), GAČR (project 16-15467S, O.P.), the Czech Ministry of Education, Youth and Sports (projects LO1416, O.P.), the Simons Foundation (Life Sciences-Simons Postdoctoral Fellowships in Marine Microbial Ecology, Award 544338, K.I.) and the Gordon and Betty Moore Foundation (grant #3775, C.D.).
Author information
Authors and Affiliations
Contributions
T.M. and K.F. designed the experiments and T.M. performed them with help from T.S. T.M. and T.S. analyzed samples with help from N.T. and Y.S. K.I. designed and performed the Cell Flux Model. K.I. and C.D. designed the model application to the water column and K.I. performed the computation. T.M. and K.I. statistically analyzed the data with the advice from C.D. O.P. contributed to the interpretation of findings. T.M. and K.I. prepared the original draft, which is revised by all the co-authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Masuda, T., Inomura, K., Takahata, N. et al. Heterogeneous nitrogen fixation rates confer energetic advantage and expanded ecological niche of unicellular diazotroph populations. Commun Biol 3, 172 (2020). https://doi.org/10.1038/s42003-020-0894-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42003-020-0894-4
This article is cited by
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.