Abstract
Wealth and income are disproportionately distributed among the global population. This has direct consequences on consumption patterns and consumption-based carbon footprints, resulting in carbon inequality. Due to persistent inequality, millions of people still live in poverty today. On the basis of global expenditure data, we compute country- and expenditure-specific per capita carbon footprints with unprecedented details. We show that they can reach several hundred tons of CO2 per year, while the majority of people living below poverty lines have yearly carbon footprints of less than 1 tCO2. Reaching targets under United Nations Sustainable Development Goal 1, lifting more than one billion people out of poverty, leads to only small relative increases in global carbon emissions of 1.6–2.1% or less. Nevertheless, carbon emissions in low- and lower-middle-income countries in sub-Saharan Africa can more than double as an effect of poverty alleviation. To ensure global progress on poverty alleviation without overshooting climate targets, high-emitting countries need to reduce their emissions substantially.
Similar content being viewed by others
Main
Extreme inequality is a major challenge of our time. While global wealth is concentrated among a few individuals1, hundreds of millions still live in extreme poverty, defined by having less than US$1.90 to spend per day2. While international extreme poverty headcounts have been declining steadily, the impacts of the global COVID-19 pandemic might reverse this trend by putting millions of people into poverty3. To tackle this problem, the first of the United Nations (UN) Sustainable Development Goals (SDGs), established in 2015, is to ‘end poverty in all its forms everywhere’.4 Its targets focus on eliminating extreme poverty, as well as halving poverty, defined by national poverty lines, by 2030. Furthermore, the World Bank introduced two additional poverty lines for the global scale, one at US$3.20 per day and one at US$5.50 per day (ref. 5), to address poverty in countries with higher income levels.
In the same year as the SDGs were established, the global community adopted the Paris Climate Agreement and proposed to keep global temperature increase below 2.0 °C or 1.5 °C. This leaves humanity with a limited carbon budget to emit and, thus, requires sizeable reductions of yearly carbon emissions. Currently, not everybody is contributing equally to these emissions. Due to the unequal distribution of wealth and income, there is an unequal distribution of consumption and, in turn, carbon footprints, which cover the carbon emissions caused by the consumption of an individual over the period of one year6. These emissions, too, reveal a picture of extreme ‘carbon inequality’7,8,9,10. Despite a decrease of carbon inequality in recent decades11,12, enormous differences between the global rich and the global poor remain. Moreover, growth of absolute CO2 emissions over the past 25 years was caused mainly by increasing carbon footprints of the top 10% (ref. 9). Hence, carbon inequality is a mirror to extreme income and wealth inequality experienced at a national and global level today.
This leads to the question of whether both global challenges can be addressed at the same time. Can we lift millions of people out of poverty while controlling carbon emissions? Answering this question requires looking behind the scenes and quantifying the intricate connections between consumption and carbon emissions across the world.
To highlight the importance of vastly different contributions to the climate crisis, quantifying carbon inequality is paramount. Consequently, it helps policy makers with establishing fair mitigation policies as well as a just allocation of the remaining carbon budget. Ground-breaking work based on income and expenditure data has been performed on this topic by multiple studies in the past decade7,8,9,11,12,13. Many of these studies distribute nationally aggregated data over population deciles or use highly aggregated expenditure or income groups. By contrast, this research uses outstandingly detailed global expenditure data from the World Bank Consumption Dataset (WBCD), which distinguishes among 201 different expenditure bins in 116 different countries14. Hence, we are able to provide unprecedented detail in the differences in carbon footprints around the world by computing country- and expenditure-specific carbon footprints using an environmentally extended multi-regional input–output (EEMRIO) approach. The carbon footprints include direct as well as indirect CO2 emissions from households, the government sector and investments.
Previous research on the interaction of poverty alleviation and carbon emissions has been performed by ref. 15 using five different expenditure groups and two global poverty lines. However, these five highly aggregated expenditure groups made it impossible to look at country-specific and further international poverty lines. Using highly detailed data and multiple poverty alleviation and eradication scenarios allows us to improve calculations on the impact of poverty alleviation on carbon emissions considerably and include country-specific national poverty lines in the analysis. Moreover, this research is the first to compute carbon footprints of people living in poverty, according to various poverty lines, on a national and global scale. As a result, we can highlight the differences between countries and identify regions where policy action is needed to prevent large increases in carbon emissions due to poverty alleviation. Consequently, this research elucidates to what extent poverty alleviation could conflict with climate change mitigation efforts.
Results
Country- and expenditure-specific carbon footprints ranged between less than 0.01 tCO2 for more than a million people in sub-Saharan countries, such as Madagascar or Burundi, and multiple hundreds of tonnes of CO2 for about 500,000 individuals at the top of the global expenditure spectrum. However, the latter number might be substantially larger, considering that some of the populous of high-income countries, such as Australia, Canada, Japan and the Gulf countries, are missing in the WBCD and that consumption patterns of the very rich are hardly registered16,17. To limit global warming to 1.5 °C or 2.0 °C, per capita carbon footprints need to be in a global target range of about 1.6–2.8 tCO218,19,20. While the global average carbon footprint in 2014 was still higher, at 3.2 tCO2, more than half of the global population had carbon footprints below or within this global target range.
Large differences between and within countries
Average country carbon footprints differ widely between countries (Fig. 1). We found the highest country-average carbon footprints in high-income countries. Above all was Luxembourg, with an average carbon footprint of more than 30 tCO2, followed by the United States with 14.5 tCO2. In turn, sub-Saharan low-income countries had the lowest country-average carbon footprints. More specifically, Madagascar, Malawi, Burkina Faso, Uganda, Ethiopia and Rwanda all had average carbon footprints of less than 0.2 tCO2.
a, National average carbon footprints for 116 countries represented in the WBCD (grey countries are missing from the database and are not included in the analysis). b, Regional average carbon footprints for six regions and three countries. The colouring indicates the average expenditure of the region. A target range of 1.61–2.8 tCO2 for carbon footprints to limit climate warming to 1.5 °C or 2.0 °C is added18,19,20. PPP, purchasing power parity.
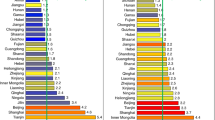
To highlight the differences on the global scale, we grouped countries into six regions while keeping China, India and the United States separate. The regions are Europe, Russia and Central Asia, Latin America, MENAT (Middle East, North Africa and Turkey), sub-Saharan Africa and South and Southeast Asia (including Papua New Guinea and Fiji). The region with the highest average carbon footprint was the United States, followed by Europe, Russia and Central Asia, and China. As seen in Fig. 1, all of them are higher than the target range of global per capita carbon footprints to limit global warming to 1.5 °C or 2.0 °C18,19,20. Latin America and the MENAT region were within this global target range in 2014. However, countries with comparatively higher per capita carbon footprints, such as Argentina and Chile or the Gulf countries, are missing from the analysis. In addition, three regions had lower average carbon footprints than the global target range: India, South and Southeast Asia and sub-Saharan Africa.
Moreover, carbon footprints varied notably within countries and regions. Taking a closer look at population deciles in the analysed countries, we found the highest carbon footprints in the top 10% of the population of Luxembourg, with 76.9 tCO2, followed by the United States with 54.9 tCO2 (Extended Data Fig. 1). Luxembourg’s was also the largest average carbon footprint of a region’s top 10% (Fig. 2). The next highest carbon footprints of the national top 10% can be found mostly in Europe, which results in an average regional carbon footprint of 16.8 tCO2 for the top 10%. By contrast, there were also multiple countries where even the top 10% of the population have carbon footprints below 1 tCO2, for example, in Ethiopia, Uganda and Afghanistan. These carbon footprints are, in turn, lower than the carbon footprints of the bottom 10% in many European and central Asian countries, China and the United States. The carbon footprints of the bottom 10% in most of the sub-Saharan countries were below 0.2 tCO2.
The differences between countries and regions are substantial, especially if one compares western high-income countries with sub-Saharan countries. The carbon inequality is highlighted by comparing the United States, the biggest high-income economy as well as the third most populous country in the world, with Nigeria, the most populous country in Africa and projected to be the third most populous country globally, surpassing the United States by 205021. The carbon footprints of the top 10% in the United States were 40 times higher than the carbon footprints of the top 10% in Nigeria, and more than 500 times higher than the carbon footprints of Nigeria’s bottom 10%.
Unequal carbon footprints across scale
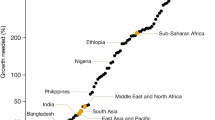
Our results confirm extreme carbon inequality across the world. To visualize this inequality, we divided the global population into the bottom 50%, the middle 40% and the top 10% of carbon emitters7,8,9,15. As shown in Fig. 3, the consumption of the bottom half of global carbon emitters was contributing only one-tenth of global carbon emissions. Meanwhile, the lifestyle of the middle 40% accounted for 43% of global carbon emissions. Consumption of the top 10% was contributing almost half of all emitted CO2. Moreover, Fig. 3 features the global top 1% of carbon emitters. Its expenditure induced about 15% of global CO2 emissions, since the average carbon footprint in the top 1% was more than 75 times higher than that in the bottom 50%.
The uneven distribution of emissions is also visible at the regional and national level; however, it is less pronounced and with clear regional differences. Carbon inequality was lowest in Europe and countries in the region, such as Belarus and Denmark, and highest in Namibia and Papua New Guinea (Supplementary Information). While regional inequality was highest in sub-Saharan Africa, even the average carbon footprint of the top 10% was lower than the global mean (Fig. 2). Only in 32 of the analysed countries and one of the aggregated regions, in Europe, was the consumption of the bottom 50% connected with a larger share of emissions than that of the top 10%. Moreover, in 14 sub-Saharan countries as well as in Papua New Guinea and Fiji, the top 1% were inducing more CO2 emissions than the bottom 50%.
Carbon footprints of people in poverty
Our analysis highlights the low responsibility of the global bottom 50% for CO2 emissions. Many people who are part of the global bottom 50% live in poverty according to international or national thresholds. Across the world, consumption of people living in poverty is associated with an especially small part of carbon emissions. More than a billion represented in the WBCD were living below the extreme poverty line of US$1.90 per day in 2014. Although they accounted for more than one-seventh of the global population, they affected less than 2% of global carbon emissions. Moreover, 37% and 57% of the global population, respectively, lived below the World Bank poverty lines of US$3.20 and US$5.50 per day. They, in turn, induced about 7% and 16% of total emissions. Almost one-fourth of the analysed population lived below national poverty lines. Their consumption contributed slightly less than 6% of global carbon emissions.
In individual countries, the share of people living in poverty varies greatly. In high-income European countries, less than 1% of the population lived on less than US$1.90 per day in 2014. Meanwhile, 31% of the Indian population or 350 million people and more than 100 million people in both Nigeria (67%) and China (9%) were living in extreme poverty (Fig. 4). However, their consumption was linked to only 10%, 39% and 2% of national carbon emissions, respectively. In addition to Nigeria, there are 15 sub-Saharan countries where more than half of the population lived in extreme poverty. These shares further increased for poverty lines of US$3.20 per day and US$5.50 per day. Among countries represented in the WBCD for which ref. 5 determined a national poverty line, Honduras and Burundi had the highest percentage of its population living below the national poverty line, with 74% and 73%, respectively. Although they make up almost three-quarters of the population, their consumption induced less than one-third of their countries’ carbon emissions.
The carbon footprints of people in poverty were mostly below 1 tCO2. People living on less than US$1.90 per day had an average carbon footprint of 0.4 tCO2, about a tenth of the global average carbon footprint. The mean carbon footprint of a person living on less than US$3.20 or US$5.50 per day was only slightly higher at 0.6 tCO2 and 0.9 tCO2, respectively. Again, these values vary widely between countries. While people living on less than US$1.90 per day in Kazakhstan, Mongolia and China had an average carbon footprint of about 1 tCO2, in multiple African countries, the carbon footprint of people living in extreme poverty was less than 0.1 tCO2. This is an effect both of lower expenditures of people living in extreme poverty in Africa and of more carbon emissions induced per dollar spent in these Asian countries (Supplementary Information). Due to the differences between national poverty lines, ranging from US$1.27 per day in Malawi to US$32.39 per day in Luxembourg, carbon footprints of people living in poverty defined by these thresholds varied between more than 5.0 tCO2 in high-income European countries and less than 0.1 tCO2 in low-income countries.
Poverty alleviation and global carbon emissions
To quantify the impact on national and global carbon emissions, we designed seven counterfactual poverty alleviation scenarios. Figure 5 shows the relative increase in emissions and expenditure in each scenario. The scenarios follow the targets of SDG 1 set by the UN in 20154 and use national poverty lines as well as World Bank lending-group poverty lines established by ref. 5. SC1, extreme poverty, is based on SDG 1, target 1.14, and eradicates poverty below the extreme poverty line of US$1.90 per day. SC2, national poverty 1, and SC3, national poverty 2, follow SDG target 1.24 and lift half of the population currently living below national poverty lines above them. While SC2, national poverty 1, shifts 50% of people in every expenditure bin below the national poverty line, SC3, national poverty 2, lifts the half of the population that is already closer to the threshold above it. The latter minimizes additional carbon emissions but results in a highly polarized and undesirable expenditure distribution as the poorest, and hence most vulnerable, are left behind. Scenario SC4, extreme + national poverty 1, combines SC1 with SC2; SC5, extreme + national poverty 2, combines SC1 with SC3. Scenario SC6, $3.20 poverty, and SC7, $5.50 poverty, eradicate poverty below the international poverty lines of US$3.20 and US$5.50 per day, respectively, which are used by the World Bank.
The first five scenarios, following SDG target 1.1 and 1.2 increase global carbon emissions by only 2.1% in the worst case, while relative increases in expenditure are slightly higher. Consequently, this research does not find a clear conflict between SDG targets focused on poverty alleviation, more specifically SDG targets 1.1 and 1.2, and the fight against climate change. Eradicating extreme poverty, modelled in SC1, results in a rise of global carbon emissions of less than 1%. Similarly, reducing the number of people living below national poverty lines (SC2 and SC3) leads to increases of only 1.5% and 0.8%, respectively. Emission increases resulting from achieving both targets at the same time (SC4 and SC5) are lower than the sum of the individual emission increases since national poverty lines can be lower than the extreme poverty line of US$1.90 per day, for example, in China and Nigeria. Achieving the first two targets of SDG 1 would increase the carbon footprints of people shifted out of poverty by about 0.2–0.4 tCO2 on average. Eradicating poverty below US$3.20 per day completely (SC6) and effectively moving about one-third of the global population to higher expenditure bins increases global carbon emissions by less than 5%, far less than the current share of the global top 1%. Going one step further, lifting 3.6 billion people over the poverty line of US$5.50 per day (SC7) increases global emissions by 18%. Even in the latter two scenarios, global expenditure increases stay well below expected increases until 2030 in the shared socioeconomic pathways 1 through 522.
While low- and lower-middle-income countries and, thus, the majority of people living in poverty are well represented in the WBCD, multiple high- and upper-middle-income countries are missing. Their populations would increase total global emissions while adding little to the expected increases of poverty alleviation. Moreover, carbon footprints of the global poor could be higher since the WBCD does not account for energy sources that are not captured by market transactions, such as firewood, which accounts for about 2% of global carbon emissions and is used mainly by low-income populations23. Shifting them to higher expenditure bins could cause a change to energy sources that are already accounted for in the expenditure data of the WBCD. Considering this, as well as recent findings that increasing well-being outcomes for the poorest could decrease energy use24, could lead to negligible increases for SC1 to SC5.
Despite small relative emission increases on the global scale, national emissions, especially in low- and lower-middle-income countries in sub-Saharan Africa, can rise substantially. Eradicating extreme poverty more than doubles emissions in Madagascar. Similarly, eradicating poverty below US$3.20 per day more than doubles national emissions in Niger, Mozambique, the Democratic Republic of Congo and Burundi, all countries with national average carbon footprints below 0.5 tCO2. Raising the threshold to a poverty line of US$5.50 per day results in even higher relative emission increases. In addition, populous countries such as Nigeria contribute notably to the absolute global carbon emission rise. Moreover, some countries in sub-Saharan Africa are projected to experience the largest relative population increases in this century21. Thus, additional emissions due to poverty alleviation could grow in the future, particularly in countries that already show large relative increases, such as Niger or Mozambique. Subsequently, achieving SDG targets could lead to lower population growth in the region25.
Although relative emission increases are largest in sub-Saharan Africa, absolute increases are highest in populous countries, with higher carbon intensities of expenditure, most importantly, India and China. Furthermore, carbon footprints for people shifted out of poverty increase more in countries with high national carbon intensities and coal consumption, such as China and Estonia, while they show only low increases in countries with low carbon intensities, such as Cape Verde and Mauretania. To limit emission increases per person shifted out of poverty, as well as high absolute emission increases, carbon intensity of expenditure needs to be reduced. This can be achieved by switching from fossil fuels to renewable energy sources and by improving energy efficiency26, while considering resulting rebound effects27,28.
The smallest relative emission increases in poverty alleviation scenarios based on international poverty lines are found high-income countries, such as Germany and Denmark. However, achieving SDG target 1.2 in scenarios that lift people above national poverty lines raises absolute emissions, especially in populous countries with higher national poverty lines such as Mexico (US$8.02 per day) and the United States (US$21.70 per day) (ref. 5). Furthermore, scenarios that eradicate extreme poverty and half national poverty headcounts lead to higher absolute emission increases in some high-income countries, such as the United Kingdom (US$21.29 per day) and France (US$24.69 per day), than in more populous, developing countries such as Ethiopia (US$1.80 per day) and Pakistan (US$2.05 per day) (ref. 5). Thus, the focus on developing countries should not divert attention from the need for drastic emission reductions in high-income countries with unsustainable consumption patterns29,30. Above all, the United States shows by far the largest total emission increases in scenarios including national poverty lines. Considering that the United States already has one of the highest national average carbon footprints, mitigation efforts parallel to poverty alleviation are key. Currently, carbon emissions of high-income countries and large economies such as the United States and China are larger than their fair share of the remaining carbon budget would allow31. To stay within the remaining carbon budget, consumption patterns of high emitters need to change drastically18,32, and the global energy transition towards renewable energy sources needs substantial progress26,33.
Discussion
The computed country-average carbon footprints are of the same magnitude as previous international estimations7,8,11,13. As expected, carbon footprints in this research are in general slightly lower than literature values as only CO2 emissions and no other greenhouse gases were considered. The results bolster the findings of ref. 13, that national average carbon footprints increase clearly with rising expenditure and underline the dependence of carbon emissions on expenditure and income levels34. Furthermore, our results confirm extreme global carbon inequality as reported by refs. 7,8,15,9 and surpass energy inequality as reported by ref. 35.
While there have been multiple studies on expenditure-specific carbon footprints in single countries using similar data from expenditure surveys36,37,38,39, global carbon inequality studies with differentiation within individual countries are limited7,8,9,12,15,40. The differentiation into 201 expenditure bins in the WBCD, used in this research, is substantially more detailed than previous studies. Therefore, it provides a new level of insights into consumption-based carbon footprints and carbon inequality at the global, regional and national levels. To uncover the full extent of current inequalities, further drivers such as unequal discursive power6 and unsustainable investments41 need to be highlighted.
Quantifying carbon footprints of people in poverty, which are largely below 1 tCO2, revealed that their per capita contribution to both national and global emissions was remarkably low. To put these results into perspective, the total emissions of the top 1% were in fact bigger than those of the bottom 50%, or those of people living in poverty. Thus, these findings support the plea from ref. 17 that investigating emission patterns of the super rich is key to reducing carbon emissions. Furthermore, it underpins that the affluent class6, as well as high-income countries9, are responsible for an unproportionally large impact on global warming.
Despite the limited emission space left for the global poor, we show that poverty alleviation is still possible with minor increases in global carbon emissions. Higher relative emission increases are to be expected in sub-Saharan Africa. Nevertheless, poverty alleviation in the region is paramount as a substantial percentage of the population lives not only below national poverty lines but also below the extreme poverty line of US$1.90 per day. On top of pursuing SDG target 1.1, eradicating extreme poverty, with the utmost urgency, it is of crucial importance to secure a basic level of well-being for everybody and quantify the resulting environmental impacts, which can be reached with limited energy inputs19,24,42,43. In addition, large emission reductions are required in high-income and high-emitting countries, which could see further emission increases as a result of lifting people above national poverty lines. As some carbon budget allocation approaches indicate a negative future budget for regions such as the United States and the European Union44,45, financial transfers from high-income regions46,47 to sub-Saharan Africa in exchange for carbon mitigation or reduced increases could be beneficial for all involved parties.
Methods
To analyse global carbon inequality, we computed country- and expenditure-specific carbon footprints using detailed expenditure data linked with an EEMRIO analysis. Subsequently, we apply multiple poverty alleviation scenarios to determine impacts on carbon emissions.
EEMRIO analysis
The input–output approach has been widely used for economic, environmental and societal analysis of economic structures48. Country- and expenditure-specific per capita carbon footprints along the supply chain of the consumed goods and services can be calculated using the MRIO framework, despite highly aggregated and imperfect datasets49. EEMRIO analysis has been applied in numerous studies to analyse environmental impacts of consumption and trade. A particularly common application is the computation of environmental footprints, such as ecological footprints and water footprints50, greenhouse gas and biodiversity footprints51, or carbon emissions and carbon footprints13,14,34,52. In addition, multiple studies have looked at the interconnections of income, inequality and carbon emissions by using the EEMRIO approach8,15,53,54.
The EEMRIO approach uses an MRIO table, which consists of the inter-regional trade between m sectors in n countries. The data are collected in matrix \(Z\left( {\left( {mn} \right) \times \left( {mn} \right)} \right)\), consisting of elements \(z_{ij}^{rs}\) as the inter-regional trade of sector i in region r into sector j in region s. Furthermore, it contains country-specific final demand vectors in matrix \(F\left( {\left( {mn} \right) \times \left( {tn} \right)} \right.\) for t different categories.
The elements on the final demand matrix F are \(f\thinspace_i^{rs,\tau }\) for final demand in region s for sector i of country r in final demand category τ. First, the total output of each sector in each region is computed and stored in a column vector \(x\left( {\left( {mn} \right) \times 1} \right)\), with elements \(x_j^S\) as the total output of sector j in region s. Subsequently, the \(A\left( {\left( {mn} \right) \times \left( {mn} \right)} \right)\) matrix is calculated with equation (1). It consists of elements \(a_{ij}^{rs}\), representing the technological production mix and efficiency.
The underlying formula of the MRIO framework can be simplified into:
Here, the Leontief inverse (I – A)−1 consists of the identity matrix I and the A matrix. Moreover, an aggregated final demand vector \(\bf{f}\left( {\left( {mn} \right) \times 1} \right) = \left( {\bf{f}\thinspace_i^r} \right)\) is used:
For multiple final demand vectors gathered in a final demand matrix F, equation (2) turns into equation (4).
Here, \(X\left( {\left( {mn} \right) \times \left( {tn} \right)} \right)\) represents a matrix of total output vectors \(\bf{\chi} ^{s,\tau }\) induced by the final demand vectors fs,τ in F.
To account for environmental impacts such as consumption-based CO2 emissions in this research, the MRIO framework can be extended by pre-multiplying the total output x with CO2 coefficients. CO2 emission data are stored in a vector \(\bf{\gamma} \left( {\left( {mn} \right) \times 1} \right)\) with elements \(\gamma _j^s\), which represent total CO2 emissions from sector s in region j. CO2 coefficients \(c_j^s\), in a column vector \(\bf{c}\left( {\left( {mn} \right) \times 1} \right)\), are created by dividing total CO2 emissions by the total output x:
Vector c is diagonalized into a matrix \(\hat c\left( {\left( {mn} \right) \times \left( {mn} \right)} \right)\). By pre-multiplying the total output matrix X with the diagonalized matrix \(\hat c\), a matrix of consumption-based CO2 emissions \(E\left( {\left( {mn} \right) \times \left( {tn} \right)} \right)\) can be computed (see equation (6)). The elements of matrix E, \(e_i^{rs,\tau }\), represent the consumption-based CO2 emissions induced by final demand fs,τ in sector r in region i.
Data
This research is based on a detailed expenditure dataset for the year 2011 from the WBCD14. The dataset was constructed by the World Bank from expenditure survey raw data and contains 116 countries and almost 90% of the global population. Multiple countries are missing from the dataset and, thus, are not included in the analysis. For every country in the WBCD, 201 expenditure bins and the corresponding population share are provided. The lowest expenditure bin represents expenditure of less than US$201150 PPP (in the following, US$2011 PPP is indicated by US$) per year, while people in the highest expenditure bin spend more than US$951,689 per year. For each bin, the expenditure for 33 different sectors of goods and services is listed. This detailed dataset provides the opportunity to compute per capita carbon footprints for each expenditure bin in each country represented in the WBCD. However, in some countries, the WBCD did not register people in every bin, resulting in empty bins at the bottom and top end of the expenditure spectrum. This can lead to underestimating national carbon inequalities (for example, in China) as extremes are missing. The most recent database of the Global Trade Analysis Project (GTAP 10)55 is used in addition to the WBCD to perform the EEMRIO analysis for computing the carbon footprints. As the most detailed and most recent version available, the GTAP 10 dataset in purchaser’s price on the world economy of 2014 was chosen, and WBCD data from 2011 were adjusted to prices of 2014. GTAP 10 contains information about 121 individual countries and 20 aggregate regions. For every country and region, the economy is divided into 65 economic sectors. The MRIO table, thus, shows the interconnection of 9,165 sectors, covering the world’s economy55. The GTAP 10 dataset has been chosen for the EEMRIO due to its high resolution on developing countries all over the world, matching the large number of developing countries in the WBCD.
The database contains the MRIO table. The essential part of the MRIO table is a square matrix of 9,165 times 9,165 entries with rows and columns for each economic sector in each region represented in GTAP 10. Each row in the input–output matrix represents the sales in million US$2014 of one economic sector in a region to all the other economic sectors in every region of the database. A column of the matrix, by comparison, corresponds to all the purchases in million US$2014 of an economic sector from every other sector of every region. As a result, the matrix combines all the intersectoral transactions of the world economy. In addition to the matrix of intersectoral transactions, the MRIO table of GTAP 10 shows 423 final demand vectors. The final demand vectors in GTAP 10 represent the purchases undertaken as investments, the purchases by households and the purchases of the government sector of every region in the database. Moreover, GTAP 10 contains a dataset of region-specific MtCO2 emissions for every economic sector as well as for direct household emissions in every region.
Matching the WBCD to GTAP 10
To compute country- and expenditure-bin-specific per capita carbon footprints, we matched the expenditure represented in the WBCD with GTAP 10 household final demand vectors. Most countries in the WBCD are also present as individual countries in GTAP 10. Hence, the WBCD data can easily be matched with the household final demand vector of the country. However, some countries of the WBCD are part of aggregated regions in the GTAP 10 dataset. To match WBCD data of these countries with household final demand vectors of GTAP 10, we scaled down the aggregated regions to country level. As the dataset does not contain detailed economic data on the individual countries in the aggregated regions, we used population data from the year 201421 to scale down household final demand vectors, assuming that the economies of countries in one aggregate region are similar in their purchases and sales. This is done by dividing the population of the country by the overall population of the aggregate region, resulting in population ratios of the country in relation to the region. Subsequently, the household final demand vector of the aggregate region is multiplied with the calculated population ratio and thereby scaled down to the country level.
Moreover, the population data in the WBCD are updated to 2014 by using UN population statistics. The UN population data for every country in the WBCD are attributed to the different expenditure bins on the basis of the population shares of each bin in the original dataset. Furthermore, to match the most recent MRIO table provided by GTAP 10, for the year 2014, the WBCD expenditure data are inflated to 2014 using aggregated consumer price indices from the World Bank56.
Bridging the WBCD to GTAP 10
After matching WBCD countries to the corresponding countries and regions in GTAP 10, we bridged the expenditure data of the former to the household final demand vectors of the latter. Therefore, a bridging matrix that links the expenditure in each of the 33 sectors of goods and services of the WBCD to the corresponding 65 economic sectors of GTAP 10 is constructed for every country individually. The bridging process follows the methodology of ref. 38. First, total expenditure of a WBCD country is computed by multiplying the expenditure share of each sector in each bin with the number of people in the expenditure bin and the mean expenditure of the bin. Second, GTAP 10 household final demand vectors, containing 65 times 141 entries per vector, are aggregated for the 65 economic sectors by summing the values of household final demand for each of the sectors. The total country expenditures, containing the expenditure in US$2014 of the population of one country in each of the 33 goods and services, are then bridged to the total household final demand vectors, containing household final demand in each of the 65 economic sectors. More specifically, the RAS approach was used to bridge WBCD to GTAP 10 data. The RAS approach, or biproportional balancing technique, is used to update and balance input–output data. The approach uses a diagonal matrix R to manipulate rows and a second diagonal matrix S to manipulate columns57.
The initial bridging matrix B0 contains 33 columns and 65 rows with ones whenever a sector from the WBCD corresponds to a GTAP 10 sector and zeros otherwise. For multiples of the 33 goods and services sectors in the WBCD, there is more than one corresponding sector available in GTAP 10. The RAS method then uses an iteration procedure to arrive at a bridging matrix B, which bridges WBCD expenditure to GTAP 10 household final demand vectors, avoiding any double counting. In the following, the bridging is described for one of the 116 WBCD countries. The iteration of the RAS approach follows equation (7) and equation (8) in n iteration steps:
Vector R is defined in equation (9), and vector S is defined in equation (10):
R0 represents the total household final demand vector for the country and S0 the total country expenditure vector. The indices i and j represent the goods and services sectors in the WBCD and the economic sectors in GTAP 10, respectively. The iteration for the bridging matrix B stops at n = 500. Subsequently, the bridging matrix B is normalized, transposed and corrected for empty rows, which occur because of missing expenditure in individual sectors of the WBCD.
The total expenditure vector of the WBCD is multiplied by the final bridging matrix B to get the preliminary bridged WBCD expenditure in 65 GTAP 10 sectors:
As the sum of household final demand vectors R0 in GTAP 10 and the sum of the bridged total expenditure vectors \(S_{{\mathrm{pre}}}^0\) from the WBCD are not equal for the corresponding countries, the difference in each of the 65 economic sectors is bridged back into the 33 sectors of the WBCD using the just determined bridging matrix B:
The difference for each sector, from vector D33, is allocated to the different expenditure bins of a country on the basis of the share of expenditure that the expenditure bin contributes to the total expenditure in the respective sector. The matched expenditure data \(E_{kl}^m\) from the WBCD are calculated by correcting the original expenditure data \(E_{kl}^0\) using the corresponding share of D33:
For each sector l in each expenditure bin k, the share of the difference D33 is added to the original value. The share is determined by multiplying the difference in sector \(D_l^{33}\) by the share of total expenditure that the bin k represents, \(s_k = \mathop {\sum }\limits_{l = 1}^{33} E_{kl}^0/\mathop {\sum }\limits_{k = 1}^{201} \mathop {\sum }\limits_{l = 1}^{33} E_{kl}^0\), as well as by the ratio of the share of sectoral expenditure in the bin, \(r_{kl} = E_{kl}^0/\mathop {\sum}\nolimits_{l = 1}^{33} {E_{kl}^0}\), over the total ratio of the expenditure of the sector l in the country, \(r_l = \mathop {\sum}\nolimits_{k = 1}^{201} {E_{kl}^0/\mathop {\sum}\nolimits_{k = 1}^{201} {\mathop {\sum}\nolimits_{l = 1}^{33} {E_{kl}^0} } }\). If there is no expenditure in a certain sector l registered in the original dataset, but the value in the corresponding GTAP 10 sector is nonzero, equation (14) is simplified to:
In the final step of the bridging process, the matched expenditure sets, including the added difference of every bin in every country, are bridged using the bridging matrix B for the country. To divide the bridged expenditure data of the different expenditure bins over the 65 sectors in the 141 regions, the regional shares of the household final demand in each economic sector need to be calculated. The regional shares pmn are computed by dividing the household final demand \(f_{mn}^{{{{\mathrm{Hou}}}}}\) value of a sector m in a country n by the total household final demand value of that sector:
Subsequently, we multiplied the bridged expenditure data of every sector in every expenditure bin by the regional shares pmn to determine the final bridged and matched expenditure data. The matching and bridging process guarantees that the bridged expenditure of a country in the WBCD and the corresponding value of the household final demand vector in each of the 65 economic sectors and 141 regions of GTAP 10 are identical at the end of the process. This is important to ensure that the MRIO table is balanced before the EEMRIO analysis is performed.
Carbon footprint analysis
To determine country- and expenditure-specific carbon footprints, first, we calculated the final demand vectors for specific countries and specific expenditure bins as described in the bridging process and divided them by the population in the expenditure bin to get per capita final demand vectors. In a second step, using the EEMRIO approach, we computed the carbon emissions corresponding to the household per capita final demand vectors of each expenditure bin. The results are vectors \(\bf{e}^{s,{{{\mathrm{Hou}}}},\beta }\), for region s, the household final demand category (Hou) and expenditure bin β. These vectors represent the carbon emissions induced by the expenditure of one person in expenditure bin β living in country s. By summing the elements of the vector \(\bf{e}^{s,{{{\mathrm{Hou}}}},\beta }\), the per capita household carbon footprint \({\mathrm{CF}}^{s,{{{\mathrm{Hou}}}},\beta }\) for expenditure bin β in country s is computed. As country-specific carbon intensities are fixed per sector, we are not able to distinguish individual carbon intensities for expenditure groups. This could lead to underestimating carbon emissions associated with low expenditures and overestimating emissions induced by high expenditures since purchasing a twice-as-expensive version of the same product does not always induce twice as many emissions.
In addition to household carbon footprints, emissions from the governmental sector and investments are considered in this analysis, following the methodology of ref. 15. While more recent approaches endogenize investments into the intermediate input matrix Z (ref. 58), we compute carbon footprints separately and sum them in the end. We assume that higher household spending corresponds with higher investments in a sector. Due to lack of data, we make the same assumption for governmental spending, although this relationship is ambiguous. While people with higher expenditures are more likely to benefit from governmental expenditure on transport infrastructure, such as roads, they are less likely to use other public institutions, such as public healthcare. To determine the respective carbon footprints, final demand vectors for country s are taken from the GTAP 10 dataset for investments \(\bf{f}\thinspace^{s,{{{\mathrm{Inv}}}}}\) and the governmental sector fs,Gov. In addition, a share vector \(\bf{\sigma} ^{s,\beta }\left( {9,165 \times 1} \right)\)is computed, which represents the share that each expenditure bin β contributes to the total household expenditure in country s for every economic sector in every region in GTAP 10. The emission vectors \(\bf{e}^{s,{{{\mathrm{Inv}}}}}\) and \(\bf{e}^{s,{{{\mathrm{Gov}}}}}\) are diagonalized into \(\hat e^{s,{{{\mathrm{Inv}}}}}\)and \(\hat e^{s,{{{\mathrm{Gov}}}}}\). Subsequently, they are multiplied with the corresponding share vector, as shown in equation (17) and equation (18) to receive bin-specific carbon emission vectors \(\bf{e}^{s,{{{\mathrm{Gov}}}},\beta }\)and \(\bf{e}^{s,{{{\mathrm{Inv}}}},\beta }\).
The expenditure-bin emission vectors are summed and divided by the population in the respective bin to receive the per capita carbon footprints induced by government spending and investments CFs,Gov,β and CFs,Inv,β.
The carbon footprints computed so far cover the indirect emissions induced by final demand from households, the government and investments. Moreover, a sizeable amount of CO2 is released directly by households from energy sources used mostly for cooking, for heating and as fuel for vehicles. Hence, the direct part of the carbon footprint is computed additionally. The GTAP 10 dataset distinguishes direct household carbon emissions from four sources: natural gas (usage, transmission and distribution), oil, coal and petroleum products. However, emissions from firewood and biomass are missing from the database and, thus, not included in the analysis. For each country, the sum of carbon emissions from natural gas usage, transmission and distribution are distributed to the expenditure bins by using the share that each expenditure bin contributes to the total country expenditure in the WBCD sector of gas manufacture and distribution. This is based on the assumption that the direct household emissions are proportional to the expenditure in this sector. The same procedure is applied to emissions from coal, oil and petroleum products, using expenditure-bin shares of the country expenditure in the WBCD sector for petroleum and coal products. Subsequently, the respective expenditure-bin direct household carbon emissions are divided by the population in the expenditure bin, resulting in the direct household carbon footprint for natural gas, CFs,Gas,β, and coal, oil and petroleum products, CFs,COP,β.
In the last step, we sum the five carbon footprints induced by household expenditure, government spending, investment and direct household emissions.
Equation (19), thus, gives the total per capita carbon footprint CFs,β for expenditure bin β in country s, considering direct and indirect emissions induced by expenditure.
Poverty alleviation scenarios
To calculate the effect of poverty alleviation on carbon emissions, we created seven scenarios. The scenarios follow SDG targets 1.1 and 1.2 set by the UN in 20154 and use national poverty lines as well as World Bank lending-group poverty lines established by ref. 5. We use the updated extreme poverty line of US$1.90 (ref. 2). People are lifted out of poverty in a static, one-time shift from lower expenditure bins to higher expenditure bins in the WBCD to explore the effects of varying expenditure distributions and increased total expenditure. This counterfactual approach focuses on expenditure as one of the multiple dimensions of poverty and does not attempt to account for impacts of poverty alleviation in other dimensions59 or the dynamic of poverty alleviation processes in reality. We transferred international, national and lending-group poverty lines used in the scenarios from per-day thresholds to per-year thresholds and inflated them to US$201456. A detailed description of the scenarios can be found in the Supplementary Information.
Reporting Summary
Further information on research design is available in the Nature Research Reporting Summary linked to this article.
Data availability
Global MRIO tables and carbon emissions were retrieved from the GTAP database, version 10 (https://www.gtap.agecon.purdue.edu/). Poverty lines can be obtained from ref. 5. Expenditure data were collected from the World Bank (https://data.worldbank.org/). Please contact the corresponding authors for more details.
Code availability
Code developed for data processing in MATLAB, Python and R is available in the Supplementary Information.
References
Time to Care (Oxfam, 2020); https://www.oxfam.org/research/time-care
Ferreira, F. H. G. et al. A global count of the extreme poor in 2012: data issues, methodology and initial results. J. Econ. Inequal. 14, 141–172 (2016).
Projected Poverty Impacts of COVID-19 (Coronavirus) (World Bank, 2020); http://pubdocs.worldbank.org/en/461601591649316722/Projected-poverty-impacts-of-COVID-19.pdf
Transforming Our World: The 2030 Agenda for Sustainable Development (UN, 2015); https://sdgs.un.org/2030agenda
Jolliffe, D. & Prydz, E. B. Estimating international poverty lines from comparable national thresholds. J. Econ. Inequal. 14, 185–198 (2016).
Wiedmann, T., Lenzen, M., Keyßer, L. T. & Steinberger, J. K. Scientists’ warning on affluence. Nat. Commun. 11, 3107 (2020).
Chancel, L. & Piketty, T. Carbon and Inequality: From Kyoto to Paris (Paris School of Economics, 2015); https://doi.org/10.13140/RG.2.1.3536.0082
Hubacek, K. et al. Global carbon inequality. Energy Ecol. Environ. 2, 361–369 (2017).
The Carbon Inequality Era (Oxfam, 2020).
Emissions Gap Report 2020 (UN, 2020); https://www.unep.org/interactive/emissions-gap-report/2020/
Lawrence, S., Liu, Q. & Yakovenko, V. M. Global inequality in energy consumption from 1980 to 2010. Entropy 15, 5565–5579 (2013).
Semieniuk, G. & Yakovenko, V. M. Historical evolution of global inequality in carbon emissions and footprints versus redistributive scenarios. J. Clean. Prod. 264, 121420 (2020).
Hertwich, E. G. & Peters, G. P. Carbon footprint of nations: a global, trade-linked analysis. Environ. Sci. Technol. 43, 6414–6420 (2009).
Zhong, H., Feng, K., Sun, L., Cheng, L. & Hubacek, K. Household carbon and energy inequality in Latin American and Caribbean countries. J. Environ. Manage. 273, 110979 (2020).
Hubacek, K., Baiocchi, G., Feng, K. & Patwardhan, A. Poverty eradication in a carbon constrained world. Nat. Commun. 8, 912 (2017).
Barros, B. & Wilk, R. The outsized carbon footprints of the super-rich. Sustain. Sci. Pract. Policy 17, 316–322 (2021).
Otto, I. M., Kim, K. M., Dubrovsky, N. & Lucht, W. Shift the focus from the super-poor to the super-rich. Nat. Clim. Change 9, 82–84 (2019).
Ivanova, D. et al. Quantifying the potential for climate change mitigation of consumption options. Environ. Res. Lett. 15, 093001 (2020).
O’Neill, D. W., Fanning, A. L., Lamb, W. F. & Steinberger, J. K. A good life for all within planetary boundaries. Nat. Sustain. 1, 88–95 (2018).
Tukker, A. et al. Environmental and resource footprints in a global context: Europe’s structural deficit in resource endowments. Glob. Environ. Change 40, 171–181 (2016).
World Population Prospects 2019 (UN, 2019); https://population.un.org/wpp/Publications/Files/WPP2019_Volume-I_Comprehensive-Tables.pdf
Crespo Cuaresma, J. Income projections for climate change research: a framework based on human capital dynamics. Glob. Environ. Change 42, 226–236 (2017).
Bailis, R., Drigo, R., Ghilardi, A. & Masera, O. The carbon footprint of traditional woodfuels. Nat. Clim. Change 5, 266–272 (2015).
Baltruszewicz, M. et al. Household final energy footprints in Nepal, Vietnam and Zambia: composition, inequality and links to well-being. Environ. Res. Lett. 16, 025011 (2021).
Abel, G. J., Barakat, B., Kc, S. & Lutz, W. Meeting the sustainable development goals leads to lower world population growth. Proc. Natl Acad. Sci. USA 113, 14294–14299 (2016).
Gielen, D. et al. The role of renewable energy in the global energy transformation. Energy Strategy Rev. 24, 38–50 (2019).
Fouquet, R. Long-run demand for energy services: income and price elasticities over two hundred years. Rev. Environ. Econ. Policy 8, 186–207 (2014).
Fouquet, R. Lessons from energy history for climate policy: technological change, demand and economic development. Energy Res. Soc. Sci. 22, 79–93 (2016).
Steinberger, J. K., Lamb, W. F. & Sakai, M. Your money or your life? The carbon-development paradox. Environ. Res. Lett. 15, 44016 (2020).
Dubois, G. et al. It starts at home? Climate policies targeting household consumption and behavioral decisions are key to low-carbon futures. Energy Res. Soc. Sci. 52, 144–158 (2019).
Lucas, P. L., Wilting, H. C., Hof, A. F. & Vuuren, D. P. Van Allocating planetary boundaries to large economies: distributional consequences of alternative perspectives on distributive fairness. Glob. Environ. Change 60, 102017 (2020).
Creutzig, F. et al. Towards demand-side solutions for mitigating climate change. Nat. Clim. Change 8, 268–271 (2018).
Owusu, P. A. & Asumadu-Sarkodie, S. A review of renewable energy sources, sustainability issues and climate change mitigation. Cogent Eng. 3, 1167990 (2016).
Ivanova, D. et al. Mapping the carbon footprint of EU regions. Environ. Res. Lett. 12, 054013 (2017).
Oswald, Y., Owen, A. & Steinberger, J. K. Large inequality in international and intranational energy footprints between income groups and across consumption categories. Nat. Energy 5, 231–239 (2020).
Ala-Mantila, S., Heinonen, J. & Junnila, S. Relationship between urbanization, direct and indirect greenhouse gas emissions, and expenditures: a multivariate analysis. Ecol. Econ. 104, 129–139 (2014).
Duarte, R., Mainar, A. & Sánchez-Chóliz, J. Social groups and CO2 emissions in Spanish households. Energy Policy 44, 441–450 (2012).
Hardadi, G., Buchholz, A. & Pauliuk, S. Implications of the distribution of German household environmental footprints across income groups for integrating environmental and social policy design. J. Ind. Ecol. https://doi.org/10.1111/jiec.13045 (2020).
Steen-Olsen, K., Wood, R. & Hertwich, E. G. The carbon footprint of Norwegian household consumption 1999–2012. J. Ind. Ecol. 20, 582–592 (2016).
Chakravarty, S. et al. Sharing global CO2 emission reductions among one billion high emitters. Proc. Natl Acad. Sci. USA 106, 11884–11888 (2009).
Ceddia, M. G. The super-rich and cropland expansion via direct investments in agriculture. Nat. Sustain. 3, 312–318 (2020).
Millward-Hopkins, J., Steinberger, J. K., Rao, N. D. & Oswald, Y. Providing decent living with minimum energy: a global scenario. Glob. Environ. Change 65, 102168 (2020).
Rao, N. D., Min, J. & Mastrucci, A. Energy requirements for decent living in India, Brazil and South Africa. Nat. Energy 4, 1025–1032 (2019).
Pan, X., Teng, F. & Wang, G. Sharing emission space at an equitable basis: allocation scheme based on the equal cumulative emission per capita principle. Appl. Energy 113, 1810–1818 (2014).
van den Berg, N. J. et al. Implications of various effort-sharing approaches for national carbon budgets and emission pathways. Climatic Change 162, 1805–1822 (2020).
Cameron, C. et al. Policy trade-offs between climate mitigation and clean cook-stove access in South Asia. Nat. Energy 1, 15010 (2016).
Jakob, M., Steckel, J. C., Flachsland, C. & Baumstark, L. Climate finance for developing country mitigation: blessing or curse? Clim. Dev. 7, 1–15 (2015).
Lave, L. B. Using input–output analysis to estimate economy-wide discharges. Environ. Sci. Technol. 29, 420A–426A (1995).
Wiedmann, T. A review of recent multi-region input–output models used for consumption-based emission and resource accounting. Ecol. Econ. 69, 211–222 (2009).
Ewing, B. R. et al. Integrating ecological and water footprint accounting in a multi-regional input–output framework. Ecol. Indic. 23, 1–8 (2012).
Wilting, H. C., Schipper, A. M., Ivanova, O., Ivanova, D. & Huijbregts, M. A. J. Subnational greenhouse gas and land-based biodiversity footprints in the European Union. J. Ind. Ecol. https://doi.org/10.1111/jiec.13042 (2020).
Brizga, J., Feng, K. & Hubacek, K. Household carbon footprints in the Baltic States: a global multi-regional input–output analysis from 1995 to 2011. Appl. Energy 189, 780–788 (2017).
Bolea, L., Duarte, R. & Sánchez-Chóliz, J. Exploring carbon emissions and international inequality in a globalized world: a multiregional-multisectoral perspective. Resour. Conserv. Recycl. 152, 104516 (2020).
Han, M., Lao, J., Yao, Q., Zhang, B. & Meng, J. Carbon inequality and economic development across the Belt and Road regions. J. Environ. Manage. 262, 110250 (2020).
Aguiar, A., Chepeliev, M., Corong, E. L., McDougall, R. & van der Mensbrugghe, D. The GTAP data base: version 10. J. Glob. Econ. Anal. 4, 1–27 (2019).
Consumer Price Index (World Bank, 2020).
Miller, R. E. & Blair, P. D. Input–Output Analysis: Foundations and Extensions (Cambridge Univ. Press, 2009).
Södersten, C. J. H., Wood, R. & Hertwich, E. G. Endogenizing capital in MRIO models: the implications for consumption-based accounting. Environ. Sci. Technol. 52, 13250–13259 (2018).
Rao, N. D., Riahi, K. & Grubler, A. Climate impacts of poverty eradication. Nat. Clim. Change 4, 749–751 (2014).
Acknowledgements
We thank O. Dupriez for providing the raw dataset of the WBCD. This study was supported by the National Natural Science Foundation of China (72174111, H.Z.), the Shandong Natural Science Foundation of China (ZR2021MG013, H.Z.) and the Major Program of National Social Science Foundation of China (no. 21ZDA065, H.Z.).
Author information
Authors and Affiliations
Contributions
K.H., Y.S. and B.B. conceptualized and designed the study with crucial inputs from K.F. and H.Z. K.F. and H.Z. provided the expenditure and MRIO databases. B.B. performed the calculations and prepared the manuscript. B.B., K.H. and Y.S. contributed to writing the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Sustainability thanks Gilang Hardadi, Joel Millward-Hopkins and Victor Yakovenko for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data
Extended Data Fig. 1 Per capita carbon footprints (CF) for each decile of national populations.
Per capita carbon footprints (CF) for each decile of national populations. The colouring indicates the average expenditure of the country.
Supplementary information
Supplementary Information
Supplementary Information and Figs. 1–12.
Supplementary Table 1
Supplementary tables for national, regional and global carbon footprints, as well as poverty analysis and poverty alleviation scenarios
Supplementary Software 1
Supplementary Python code for bridging the WBCD to GTAP 10, steps 1 and 3.
Supplementary Software 2
Supplementary MATLAB code for bridging the WBCD to GTAP 10, step 2.
Supplementary Software 3
Supplementary MATLAB code for running the EEMRIO analysis.
Supplementary Software 4
Supplementary MATLAB function for running the EEMRIO analysis.
Supplementary Software 5
Supplementary R code for the poverty alleviation scenario analysis.
Rights and permissions
About this article
Cite this article
Bruckner, B., Hubacek, K., Shan, Y. et al. Impacts of poverty alleviation on national and global carbon emissions. Nat Sustain 5, 311–320 (2022). https://doi.org/10.1038/s41893-021-00842-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41893-021-00842-z
This article is cited by
-
The potential of wealth taxation to address the triple climate inequality crisis
Nature Climate Change (2024)
-
Revisiting Copenhagen climate mitigation targets
Nature Climate Change (2024)
-
Accessing the impact of poverty age groupings on carbon neutrality targets: scenarios from developing Sub Sahara African countries
Environmental Science and Pollution Research (2024)
-
Achieving the 1.5 °C goal with equitable mitigation in Latin American countries
Mitigation and Adaptation Strategies for Global Change (2024)
-
Is there a Green Dividend of National Redistribution?
The Journal of Economic Inequality (2024)