Introduction

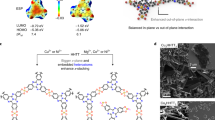
The quantum behavior of an electron moving in a two-dimensional lattice exposed to a magnetic field is a fundamental problem of solid-state physics that has been studied deeply in the 70s. By plotting for the first time the allowed energies of the electrons and varying the magnetic field, Douglas Hofstadter found the stunning form of a graph that consists of duplicates of itself, embedded infinitely deeply, and that encodes nature in such a complex but equally self-similar manner1. This so-called Hofstadter butterfly (HB), which is shown in Fig. 1a and b, emerges from the commensurability of the magnetic and the lattice lengths when constraining a free electron onto a lattice. This effect has fascinated theoretical physicists and mathematicians over many decades2,3,4,5,6,7,8,9,10 and connects the mathematical concept of fractals with the world of physics by encoding the most exotic behaviors of quantum mechanics and topology, namely the quantum Hall effect and conductance quantization in 2D materials11,12,13,14. However, the minimal magnetic field strength, Bp, for resolving HBs depends inversely on the plaquette area Ap of a lattice closed loop, such as a hexagon in a honeycomb lattice,

$${B}_{{{{\rm{p}}}}}=\frac{{\Phi }_{0}}{{A}_{{{{\rm{p}}}}}}.$$
(1)

where, \({\Phi }_{0}=\frac{h}{2e}\) is the magnetic flux quantum. The HB repeats itself infinitely with a period of Bp. For graphene, for instance, Bp is around 78 kT, making it inaccessible for experimental validation. Hence, the HB has served since its discovery as a physical playground of mainly theoretical interest but with no direct observation. However, in the last three decades experimental verification of the HB via artificial lattices with very large unit cells, such as moiré lattices or 2D electron gas lattices, has turned this once-theoretical issue into an active field in experimental solid-state physics nowadays15,16,17,18,19,20,21,22,23,24,25,26. It was only the escamotage of artificial lattices, like moiré patterns, resulting in large plaquette areas which enabled the first indirect experimental demonstration of HB through magnetotransport measurements.

Fig. 1: From covalent organic frameworks to a measurable Hofstadter butterflies.
figure 1

a, b Application of a magnetic field to a square (honeycomb) lattice with a plaquette area Ap, marked as light green, leads to the fractal HB pattern with a period of Bp. c From left to right: the lattice formation of COF-5 from its tritopic (red) and linear (blue) molecular building blocks. Applying a perpendicular magnetic field to a COF leads to a HB resolved at small magnetic fields Bp. d Relation between the magnetic field to resolve a full HB Bp and the area of a plaquette according to Eq. (1). The dashed black line indicates twice the highest continuous magnetic field achievable to this date44. The orange points represent experimentally known COFs with square, tetragonal and honeycomb lattices collected from the CURATED-COFs database (for details on the curation, see Supplementary Note 1)57. The black triangles indicate graphene and the three COFs investigated in this study whose structures are shown.

Full size image

Two-dimensional covalent organic frameworks (2D COFs), however, have not yet been at the center of such investigations and we can show that they indeed could be the first single-layered material to directly observe HBs. COFs are crystalline covalently bound organic polymers that have first been successfully synthesized in 200527. The crystalline polymers are constructed from organic building block molecules attached to each other in a regular fashion which creates a periodic and often porous structure as depicted in Fig. 1c. Due to the many available types of precursor molecules, various different structures with tunable properties are possible. As a result, COFs have gained ever since a lot of attention in the polymer and solid-state community.

Many COFs are layered materials, similar to the graphene sheets in graphite, but experimental methods have been refined to create few-layer and indeed monolayer 2D COFs28,29,30,31,32,33,34,35. These are based on simpler lattice types, like honeycomb or hexagonal lattices, with usually very large unit cells. This would lead to a lower magnetic field required for the experimental validation of the HB. Additionally, it has been shown how in these materials the lattice topology itself mediates electronic and mechanical properties36,37. Moreover, recent investigations of topological effects in 2D COFs showed their potential as topological materials38,39,40,41,42,43. All of this makes 2D COFs interesting materials for the exploration of fractality, quantum effects and finally finding a HB at experimentally viable magnetic fields.

In Fig. 1d, the dependency of Bp on the plaquette area Ap is depicted, including known 2D COFs with honeycomb, tetragonal or square lattice structure. This shows that several COFs already exist where the HB can be measured to a great extent with experimentally achievable magnetic fields. We chose 91 T as comparison, which is twice the highest achievable continuous magnetic field (2 ⋅ 45.5 T = 91 T 44), as the HB is symmetric in the magnetic field and consequently only half of its spectrum needs to be measured. Additionally, a greater complexity and a richer phenomenon of the HB is expected due to COFs rich pore hierarchy. The HB for three different exemplary 2D COFs (shown in Fig. 1d) are calculated in the following: complex hierarchical patterns and fractal HBs can be observed at measurable magnetic fields.

Results

Embedded Hofstadter butterflies

Figure 2 shows the well-known COF-5 with its three different plaquette types marked as I to III. COF-5 is the first synthesized and one of the most studied COF which has, just like graphene, a honeycomb lattice as shown in Fig. 2b27. As the HB repeats itself with a period of Bp, we search for a reoccurring pattern in the calculated spectrum. In Fig. 2c, one can see such a pattern with a period of approximately 240 kT. This spectrum, however, does not resemble the HB of an equivalent honeycomb lattice (Fig. 1b) and its period is very large. A zoom into the spectrum, as shown in Fig. 2d, indicate more complex patterns and a further zoom in Fig. 2e reveals astonishingly a HB that is equivalent of the one of graphene, but only at 528.7 T. This corresponds to the Bp of the lattice plaquette I according to equation (1). To avoid confusion in the following discussion, we will call the patterns that resemble the HB of simple lattices specifically ‘HB’ and the rest of the spectrum generally ‘butterfly spectrum’.

Fig. 2: Hierarchical periodic spectra for COF-5.
figure 2

a Structure of COF-5 including annotations for the largest to the smallest plaquettes (I–III). b Extended 2D structure of the honeycomb lattice of COF-5 with indicated applied magnetic field. c Butterfly spectrum from 0 to 240 kT. d Butterfly spectrum from 0 to 5000 T. e Honeycomb HB from 0 to 530 T. The intensity of the DOS in the butterfly spectra is depicted in a logarithmic scale although the colorbar was omitted for clarity.

Full size image

How can we understand the formation of different patterns on the various scales of magnetic fields? As seen in Fig. 2c, the butterfly spectrum contains many different ‘bands’ that change with the magnetic field. We will call those ‘ribbons’ to give a clear distinction to bands in band-structure plots. This complexity arises due to the numerous electronic states that COFs have compared to simple lattices.

A zoom closer to some of the ribbons in Fig. 2d, shows that each ribbon itself contains many smaller complex features that sometimes overlap and interfere with each other and create new patterns.

A comparison with the band structure in Supplementary Fig. 2 reveals that some ribbons are based on a band-structure equivalent of a simple honeycomb lattice, while others are more similar to the one of a kagome-lattice. It is known that COF-5 has kagome-characteristic bands45. The resulting butterfly spectrum of these kagome-like bands is similarly distorted as the one of a simple kagome-lattice HB6. Furthermore, a comparison of the band structure and HBs of all studied COFs in this manuscript is shown in Supplementary Fig. 5. The final zoom in Fig. 2e into the isolated ribbon at around −6.9 eV shows the honeycomb HB. This shows that the lattice type itself dictates the electronic structure and topological effects. A key difference to the HB in a simple honeycomb lattice is that HB in COF-5 is strictly speaking not repeating itself, but is distorted for higher magnetic fields due to the superposition of different periodicities.

Hierarchical patterns in 2D COFs

But why do we see a periodic pattern at ~240 kT in Fig. 2c for COF-5? This value does not coincide with any of the Bp values of the three plaquette types I to III in COF-5 labeled in Fig. 2a: the honeycomb lattice plaquette I, the benzene ring II and the boronic ester based five-membered ring III, with periodicities Bp of 528.7 T, 81.06 kT, and 121.9 kT, respectively. As the latter two periods have approximately a common denominator, a new periodic pattern with a bigger period at ~240 kT ( ≈ 2 ⋅ 121.9 kT ≈ 3 ⋅ 81 kT) is visible.

To better understand the influence of multiple plaquette types on the butterfly spectrum, we next investigate a COF with four different plaquettes. This COF is based on Phthalocyanine as shown in Fig. 3a and has a square lattice. It has been shown in previous studies that this COF has interesting topological properties, although usually investigated including a metal-center40,42,43. In Fig. 3a, we depict the four different kinds of plaquettes marked as I to IV: square lattice plaquette that arises from the fused Phthalocyanines units I, the pore inside of a Phthalocyanine unit II, the benzene ring III and the pyrole five-membered ring IV. In Fig. 3d, we can see that similar to COF-5, there is an overlap of the periodicities of III (81.18 kT) and IV (121.6 kT) that leads to a new combined pattern with a period of ~240 kT.

Fig. 3: Different periodicities in the butterfly spectrum shown in the example of Phthalocyanine-COF.
figure 3

a Structure of the Phthalocyanine-COF including annotations for the largest to the smallest plaquettes (I–IV). b Extended 2D structure of Phthalocyanine-COF including an indicated applied magnetic field. c HB from 0 to 3600 T. d Butterfly spectrum from 0 to 245 kT. The solid green lines indicate the periodicity generated by plaquette IV (121.6 kT), the dashed red line by plaquette III (81.18 kT), and the dotted gray line by plaquette II (16.92 kT). The intensity of the DOS in the butterfly spectra is depicted in a logarithmic scale although the colorbar was omitted for clarity.

Full size image

The spectrum shows that there are patterns with different periods which are marked in the figure. For better visualization of the repeating patterns, a wider magnetic field range of the butterfly spectrum plotted in Supplementary Fig. 3. When zooming into one of the ribbons in Fig. 3d, we see as expected a HB in Fig. 3c that resembles the one of a square lattice (compare to Fig. 1a), which further shows how lattice types guides topological effects like the HB. But since the period of II is only around five times larger than I, the oscillation of II distrorts the HB in Fig. 3c. From this we can see that the closer the scales of periodicities of different plaquettes are, the more they influence each other and the more distorted the HB is.

We would like to point out that the fractality and the actual HB is only created by the lattice plaquette, i.e. the biggest plaquette. The other plaquettes are only responsible for additional periodicity, but not for fractality, as shown in Supplementary Fig. 4.

Towards a measurable HB in 2D COFs

The COFs investigated so far do not have large enough unit cells to create a periodicity Bp that would be measurable in today’s experiments. Hence, a COF with larger pores is required. One COF (COF-122) exists already that is close to the required unit cell size46. However, as parts of this COF have many rotational degrees of freedom and is hence not flat, it is in our opinion not suitable for a flat monolayer material. For this reason, we propose a COF that is based on the recently reported class of Starphene molecules which are triangular molecules of fused benzene rings47. When connected, a highly porous COF with a honeycomb lattice would result which we call Starphene-COF, as shown in Fig. 4a and b. This theoretical COF also is a fully conjugated system which should lead to a good conductivity. In the Starphene-COF, there are only two plaquette types: the honeycomb lattice plaquette I and the benzene-rings II. This leads to a period of 133.8 T for the lattice plaquette I and a period of approximately 78.68 kT for the benzene ring (II). The full butterfly spectrum up to 80 kT is depicted in Fig. 4d. In Fig. 4c, we zoom in to the magnetic field range of the smaller period and see that a HB arises that looks similar to the one of a simple honeycomb lattice in Fig. 1b. Since Bp is only 133.8 T, the HB of the Starphene-COF would be accessible to a great extent by available magnetic fields, possibly solving the quest for direct experimental verification of the HB in a single-layer 2D material in the future.

Fig. 4: Towards a measurable HB in 2D COFs with the Starphene-COF.
figure 4

a Structure of the Starphene-COF. b Extended 2D structure of the honeycomb lattice of the Starphene-COF including an indicated applied magnetic field. c HB from 0 to 134 T. The green overlay indicates the range in which the spectrum would be measurable according to the highest achievable magnetic field of 45.5 T44. d Butterfly spectrum from 0 to 80 kT. The intensity of the DOS is depicted in a logarithmic scale although the colorbar was omitted for clarity.

Full size image

The butterfly spectrum in Fig. 4d also has some interesting properties similar to a related class of materials, graphene antidot lattices (GALs) which is graphene with periodic holes. In GALs, a typical graphene HB pattern still emerges, even though it becomes less distinct the bigger the holes in the lattice becomes. The Starphene-COF can be seen as an edge case of such a GAL, in the sense of a porous graphene which has the biggest possible hole for its repeating unit. Another feature that is known from GALs is that the band gap is being quenched with increasing magnetic field, which can be seen for the Starphene-COF at around 6 kT at 0 eV in Fig. 4d48.

During the preparation of the manuscript, a COF with a very large pore was reported49. We show in Supplementary Fig. 1 the corresponding HB that is resolved at 122.6 T, which is even lower than our proposed Starphene-COF. This demonstrates how the rapid advances in synthesis can provide systems to experimentally measure the HB in the near future.

Discussion

We have shown that 2D COFs are promising materials for the direct experimental verification of the Hofstadter butterfly in pure 2D materials and that there are additional hierarchical patterns that are not present in HBs of simple lattices. This work might turn this merely-theoretical issue from the 70s into an active experimental research activity nowadays and trigger the race for the first direct measurement. We found equivalents of simple lattice HB inside the complex and beautiful butterfly spectra of 2D COFs. Moreover, hierarchical structures and periodicities can be found within these spectra, due to the various pore types inside a single COF-structure, opening dimensions for more physical discoveries. Furthermore, we showed that for 2D COFs with large unit cells the magnetic field to measure a HB is small enough to be experimentally viable. 2D COFs can provide the ideal playground for the investigation of such fundamental quantum effects and the recent advances in single-layer synthesis of 2D COFs will lead in the foreseeable future to the direct observation of the Hofstadter butterfly in a single-layer 2D material.

Methods

Calculation of the HB

A tight-binding hamiltonian was constructed from the Slater-Koster parametrization which is used in Density Functional based Tight Binding. The parameters include tabulated distance-dependent orbital-orbital interactions and respective on-site energies50. Here, the matsci parametrization with on-site energies for the angular momentum p for the given atom and ppπ hopping parameters51. The hopping was assigned according to the respective distance between the atoms. To simplify the model and the energy-spectrum, only nearest neighbor interactions were considered. With the help of the Atomic Simulation Environment (ASE) package52, the geometry and hamiltonian were imported into the pybinding code with which all further calculations were performed53. For the geometry, only a strict 2D system was used, meaning the z-coordinates were discarded. The influence of a perpendicular magnetic field on the 2D structure was approximated with the Peierls-substitution54:

$${t}_{{{{\rm{nm}}}}}\to {t}_{{{{\rm{nm}}}}}{{{{\rm{e}}}}}^{i\frac{2\pi }{{\Phi }_{0}}\int\nolimits_{n}^{m}{{{{\bf{A}}}}}_{nm}{{{\rm{d}}}}{{{\bf{l}}}}}$$
(2)

with tnm as the hopping-parameter or off-diagonal elements for nearest neighbor sites n and m, Φ0 as the magnetic flux quantum, Anm as the magnetic vector potential with a chosen gauge of A(x, y, z) = (By, 0, 0). The electronic density of states (DOS) for the structures with an applied perpendicular magnetic field was calculated with the in pybinding integrated Kernel Polynomial Method (KPM). In the KPM, the DOS is calculated by reconstruction from the KPM moments which are evaluated in a stochastic fashion55. The DOS was evaluated for a 50 × 50 supercell and 3 random vectors for the stochastic calculation of KPM moments. Sweeping through a magnetic field range and plotting the DOS for each magnetic field, results in the shown butterfly spectra. The energy scale was centered with respect to the the minimum and maximum energy value of the butterfly spectrum. This convention for the energy scale was chosen instead Fermi level centering because the TB model only includes ppπ orbitals and their occupation for more complex systems (like the Phthalocyanine-COF or COF-5) cannot be derived directly from the TB model.

Optimization of COF structures

The 2D COF-structures where obtained from optimization with Density Functional based Tight Binding calculations with the code DFTB+56. The optimization was carried out at the Γ point with a maximum force component of 1e-06 of the conjugate gradient algorithm. A tolerance of 1e-08 for the self consistent cycles was chosen. As Slater-Koster parameters, the matsci parameter set was used51.