Abstract
To date, quantum communication widely relies on attenuated lasers for secret key generation. In future quantum networks, fundamental limitations resulting from their probabilistic photon distribution must be overcome by using deterministic quantum light sources. Confined excitons in monolayers of transition metal dichalcogenides (TMDCs) constitute an emerging type of emitter for quantum light generation. These atomically thin solid-state sources show appealing prospects for large-scale and low-cost device integration, meeting the demands of quantum information technologies. Here, we pioneer the practical suitability of TMDC devices in quantum communication. We employ a WSe2 monolayer single-photon source to emulate the BB84 protocol in a quantum key distribution (QKD) setup and achieve click rates of up to 66.95 kHz and antibunching values down to 0.034—a performance competitive with QKD experiments using semiconductor quantum dots or color centers in diamond. Our work opens the route towards wider applications of quantum information technologies using TMDC single-photon sources.
Similar content being viewed by others
Introduction
Quantum information technologies rely on the availability of high-performance sources emitting flying qubits1. Due to the challenges in the fabrication of practical quantum light sources emitting single- and entangled-photon states on-demand, implementations using faint lasers, or weak coherent pulses (WCPs), took the lead in the design and development of practical quantum communication systems. The invention of decoy-state protocols mitigated severe security loopholes related to the Poissonian photon statistics2,3, but at the cost of additional protocol overhead. Solid-state quantum light sources4, on the other hand, offer deterministic operation in combination with engineered device functionalities, showing up prospects to overcome fundamental limitations of probabilistic sources. Semiconductor quantum dots5,6 and color centers in diamond7 are currently the main candidates among quantum emitters in the solid state. However, monolayers of transition metal dichalcogenides (TMDCs) encounter increasing interest, due to the ease and flexibility in engineering their photonic properties and their straightforward integration in photonic devices8,9,10,11. Single-photon emission from trapped excitons in atomically thin crystals was initially confirmed in monolayers of WSe212,13,14,15,16 and later complemented using WS217, MoS218, MoSe219, and MoTe220. In addition, correlated pair emission from the biexciton–exciton radiative cascade was experimentally shown in WSe221, outlining the possibility to generate entangled-photon pairs. From a technological viewpoint, TMDC-based quantum light sources feature interesting advantages over other solid-state implementations: a relatively simple and low-cost fabrication, the tailoring of the excitonic properties via multi-stacking of monolayers22, giant susceptibility to external strain23, and a deterministic control on the spatial position of the quantum emitters24,25, even in optical cavities10. In addition, TMDC-based single-photon sources cover all three telecom windows centered around 850, 1300, and 1550 nm20, including wavelengths compatible with atomic transitions used for quantum memories26. The first telecom window, addressed in this work, is particularly suited for free-space optical communication scenarios, including air-to-ground links using airplanes27 or satellites28. Despite the immense progress seen in this field over the last decade29, applications of TMDC quantum emitters in quantum information remained elusive so far. Here, we realize a bright single-photon source based on a strain-engineered WSe2 monolayer and demonstrate the feasibility of quantum key distribution (QKD) via the BB84 protocol30. We evaluate the single-photon purity, or g(2)(0), the quantum bit error ratio (QBER), as well as the secret key rates expected in full implementations of QKD and explore routines to optimize the achievable performance in terms of tolerable losses. A comparative analysis reveals that our atomically thin single-photon source is readily competitive with QKD experiments using semiconductor quantum dots and color centers in diamond.
Results
Experimental QKD setup
The QKD setup used in our experiments is illustrated in Fig. 1a. The transmitter (Alice) contains the single-photon source. For the source implementation, we followed a strategy detailed in ref. 31, based on a strain-engineered WSe2 monolayer device containing localized quantum emitters (see Methods section “TMDC monolayer device” for details on the sample). The emission of a single emitter is collected in a confocal setup using spectral and spatial filtering via interference filters and coupling to a single-mode (SM) optical fiber. The preparation of single photons in four different polarization states for the BB84 protocol is implemented in a fiber polarization controller in combination with a Glan–Thompson prism. The key parameters relevant for QKD are determined by preparing the polarization states in sequential measurement runs. The flying qubits are then sent to the receiver module (Bob) via a short free-space link, either in a back-to-back configuration, i.e., without additional loss, or including a variable attenuator for emulating transmission losses. The receiver (Bob) comprises a four-state polarization decoder with passive basis choice and silicon-based single-photon detectors. Here, photons in the BB84-states are decoded in four different output channels (see Methods section “QKD receiver” for details on the experimental setup).
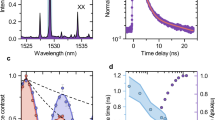
a The transmitter (Alice) comprises a strain-engineered WSe2 monolayer inside a closed-cycle cryocooler, a diode laser with variable repetition rate, dielectric filters, and an optical fiber together with a polarizer for adjusting the polarization states. Alice sends single-photon pulses with fixed polarization (H, V, D, A) to the receiver (Bob). Inside the quantum channel, losses can be introduced using a variable attenuator. Bob comprises a four-state polarization analyzer based on bulk polarization optics. b Emission spectra of the WSe2 monolayer sample recorded at different locations in the setup: before (blue) and after (orange) spectral filtering and coupling to the SM fiber. The selected quantum emitter emits at a wavelength of 807 nm. c Second-order autocorrelation histograms of the triggered quantum emitter at clock rates of 2.5, 5.0, and 10.0 MHz. The autocorrelation is evaluated from the events registered at all four receiver channels.
QKD performance
To evaluate the performance of the source in our QKD setup, we select a localized WSe2 emitter featuring a single, bright emission line at 807.3 nm. Figure 1b displays spectra of the selected emitter recorded before (blue) and after (orange) spectro-spatial filtering and coupling to the SM fiber under triggered optical excitation at 5.0 MHz. Here, the observed asymmetric line shape (0.6 nm full width at half-maximum at saturation) most likely results from spectral diffusion31 in combination with efficient coupling to acoustic phonons32. To evaluate the single-photon purity of the flying qubits employed in the quantum channel of our QKD setup, we extract the second-order intensity autocorrelation g(2)(τ) by correlating the detected photon events at all four output channels in the Bob module. The corresponding g(2)(τ) histograms recorded at saturation of the quantum emitter are depicted in Fig. 1c for different clock rates of 2.5, 5.0, and 10.0 MHz. All three histograms clearly reveal a high single-photon purity with strongly suppressed coincidences around zero-time delay. The corresponding antibunching values g(2)(0), extracted by integrating the raw coincidences over a full repetition period, are 0.16 (2.5 MHz), 0.17 (5.0 MHz), and 0.25 (10.0 MHz) measured at saturation. Here, the noticeable increase in the integrated g(2)(0) at the highest clock rate arises from the overlap of the correlation peaks neighboring the one at zero delay (c.f., further below for a detailed discussion on limiting factors and a comparison to the literature). For the following studies, we choose a clock rate of 5.0 MHz as the optimal trade-off for our experiments.
Next, we investigate how the optical pumping conditions of the quantum emitter influence the performance in QKD. Figure 2a shows the click rate (total signal from all four channels) detected at the receiver in a back-to-back configuration, i.e., negligible losses in the quantum channel, together with the corresponding g(2)(0) of the single-photon source as a function of the pumping strength. In this experiment, we utilize the receiver module itself for characterizing our source. Note, that in full implementations, Alice must monitor the source also on her side. This can be implemented by using a tap-coupler or a polarizing beamsplitter in front of the encoding electro-optical modulator, which splits a fraction of the single-photon pulses for monitoring the source during transmission. Without the in situ monitoring of the source, security loopholes can arise, e.g., due to underestimation of multiphoton events. We observe an almost monotonic increase in the click rate up to (66.95 ± 1.07) kHz at saturation pump power (Psat) corresponding to a brightness of the single-photon source under pulsed excitation of (2.9 ± 0.3)% in the SM fiber. Under continuous wave excitation, we observe a maximum count rate of 530 kHz, corresponding to a single-photon flux of (1.15 ± 0.23) MHz in the SM fiber (see Methods section “Estimating the source brightness and spectral background contribution” for details on the efficiency estimate). For QKD applications, the important parameter to extract is the mean photon number per pulse into the quantum channel μ. With the transmission ηBob = 0.56 of the receiver module, including the transmission of the optics and detector efficiencies, we achieve maximum values of up to μ = 0.024. In a full implementation including an electro-optical modulator, with typical insertion losses of 3 dB for fiber-based and 1 dB for free-space implementations, the overall losses will be slightly higher, resulting in lower values of μ. The antibunching value shows a more complex dependence. Under weak pumping, g(2)(0) first decreases with increasing excitation power to a minimum value of 0.127 ± 0.002 at 0.37Psat. Further increasing the pumping strength, g(2)(0) shows a moderate increase up to 0.172. While the decrease of g(2)(0) at weak pumping is attributed to an improved signal-to-noise ratio, its increase at stronger pumping results from noticeable spectral contributions of residual emission lines close to the selected emitter (cf. Fig. 1b, inset), which are not perfectly rejected by the spectro-spatial filter used on Alice’s side. The additional dip at 1.5Psat might indicate different decay paths or pumping into different energy levels of the localized quantum emitter. The contribution of the spectral background to g(2)(0) is estimated to 0.040 at 0.37Psat, partly explaining the deviation from an ideal single-photon source (see ref. 33 and see Methods section “Estimating the source brightness and spectral background contribution” for details). Using temporal filtering as a post process, g(2)(0) can be reduced down to 0.034 ± 0.002 for an acceptance time window width of 24 ns (see Supplementary Fig. 4). This value compares favorably with the lowest antibunching values of g(2)(0) = 0.058 ± 0.003 reported to date for TMDC-based quantum emitters under pulsed optical excitation at comparable wavelength20. In the following, we intentionally neither apply background corrections nor fitting routines to the g(2)(0) values; this is important for QKD applications, where both signal and background photons contribute to the overall key. An underestimation of the g(2)(0) leads to an underestimation of the multiphoton pulses in the quantum channel (see also Methods section “Key rate calculations” for details) which in turn results in an information leak to an attacker. Even if using temporal filtering to optimize the performance of our QKD setup further below, we use the full g(2)(0) value as the worst-case assumption. To exploit the positive effect of temporal filtering on the g(2)(0), Alice has to apply the temporal filter already on her side, e.g., by using an additional electro-optical intensity modulator before the quantum channel (see ref. 34 for a detailed discussion). This reduces the multiphoton pulses in the quantum channel and makes them no longer accessible to an attacker. For our setup, the additional losses of a modulator would not be compensated by the reduction of multiphoton pulses (see Supplementary Fig. 5).
a Excitation power resolved series of the click rate and g(2)(0). The source reaches saturation at 52.5 μW. Solid lines are a guide to the eye. Error bars are the standard deviations. b Input–Output characterization of Bob for extraction of the QBER. The detection rates in kHz observed at each channel are stated and additionally encoded in the field’s opacity. c Rate-loss diagram considering the experimental data from a. Although the g(2)(0) is not at the minimum at saturation, the achievable distance and secret key rate for each distance has its maximum at saturation. d Real-time security monitoring over exemplary time of 1.5 h (P = 0.43Psat, H-input polarization). The QBER is calculated from all registered events. In full implementations using only subsets for an estimation, this value might be higher. Antibunching g(2)(0) of the single-photon source evaluated by correlating all registered events in non-overlapping blocks for 10 s (blue) and 100 s (orange) accumulation time (exemplary g(2)(τ) histograms shown as insets). See Supplementary Fig. 6 for details on the accumulation time.
To estimate the QBER achievable in our QKD setup, the fiber-coupled single-photon pulses are sequentially prepared using a static linear polarizer (see Methods section “QKD transmitter”) set to horizontal (H), vertical (V), diagonal (D), or antidiagonal (A) polarization. The pulses are recorded at the receivers’s four detection channels. The resulting experimental data are summarized in Fig. 2b in a 4 × 4 matrix with each entry corresponding to the event rate in the respective measurement configuration (see Supplementary Fig. 1 for the full-time-resolved data underlying this illustration). The working principle of the polarization decoder results in prominent diagonal elements, i.e., for a given input state, almost all photons are detected in the respective channel of the corresponding basis, whereas a probabilistic projection is observed in the conjugate basis. Erroneous detection events at the wrong channel within one basis, e.g., events detected in the V-channel for H-input, are much less probable and cause the finite QBER to be considered in the security analysis in the following. In our QKD analysis, mainly two sources contribute to the errors: Background events resulting from residual stray light plus dark counts of the four detectors (80 Hz in total) and optical imperfections inside the receiver. Additional deviations from an ideal setup are detection efficiency mismatches between channels, which need to be considered in full implementations35. From the experimental data in Fig. 2b, we extract a QBER of only 0.52%. This value gives a lower bound for full implementations as it describes the limit the receiver optics set to the overall QBER. In full QKD implementations, additional errors are expected due to imperfections in the polarization preparation using electro-optical modulators. These are typically in the range of 1%. In the following, we apply the lower bound found in our characterization. Based on the previous parameter analysis, we can extrapolate the secret key rate expected in full implementations of QKD as a function of tolerable losses. To this end we evaluate the secret key rate S∞ in the asymptotic limit, i.e., assuming an infinitely long key, by following the formalism presented in ref. 36 using an upper bound for the multiphoton contribution as in ref. 37 (cf. Methods section “Key rate calculation” for details). Note, that in full implementations, a finite state preparation quality needs to be considered as discussed in ref. 38. While being negligible in our QKD testbed (due to the use of a linear polarizer), this effect becomes relevant in the case of a dynamic state preparation using electro-optical modulators, which limit the state preparation quality (see Supplementary Fig. 2 and corresponding discussions for details on the effects of using electro-optical modulators). The resulting rate-loss dependencies of our QKD experiment are displayed in Fig. 2c as a function of the pumping strength. While each curve follows a linear trend (in logarithmic scaling) at low to moderate losses, a multi-exponential drop is observed in the high-loss regime determining the well-known distance limit in point-to-point quantum communication39,40. At a low excitation power of 0.05Psat the maximally achievable tolerable loss is limited to 13.82 dB. Although g(2)(0) increases at strong pumping (cf. Fig. 2a), we find the largest secret key rate and maximally achievable tolerable loss of 20.14 dB inside the transmission link to be expected at saturation of our quantum emitter (see Fig. 2c). Note, that in our QKD testbed the increase in g(2)(0), which in turn results in a larger multiphoton emission probability, is overcompensated by an increase in μ, resulting in larger detection rates at higher pump strength. For practical implementations in quantum information, the temporal stability of the employed single-photon source is an important characteristic and many QKD protocols benefit from monitoring the security parameters in real time to certify its security. Time traces of the key parameters of our fiber-coupled atomically thin single-photon source, recorded during a measurement period of 1.5 h, are presented in Fig. 2d. Here, the click rate, the QBER, and the g(2)(0) value are depicted together with their corresponding probability distribution (cf. right panel). Photon flux and QBER are stable over time with average values of (36.5 ± 0.9) kHz and (0.69 ± 0.06)%, respectively. The same holds true for the antibunching with an average value of g(2)(0) = 0.14, shown for two different accumulation times of 10 s (blue) and 100 s (orange), resulting in standard deviations of 0.015 and 0.006, respectively (see Supplementary Fig. 6 for details on the accumulation time). In the following section, the performance of our system will be optimized and compared with other technologies (see Table 1).
Optimization and benchmarking
For the operation of practical QKD systems, the optimization of parameters entering the secret key rate (e.g., intensities, acceptance time windows) is a crucial step in gaining optimal performance for a given link scenario41. This becomes important in communication scenarios that are affected by time-dependent variations, as e.g., the link transmission in free-space optical settings between stationary42 or moving platforms27,28. Here, the transmission losses inside the quantum channel can drastically vary due to the weather conditions or the transmitter-receiver distance. In the following, we explore temporal filtering, to optimize the performance of our single-photon QKD setup. As mentioned in the previous section, detector dark counts as well as imperfections of polarization optics contribute to the overall QBER. While the detector noise is uncorrelated in time, erroneous detection events due to optical imperfections are correlated with the clock rate of our experiment. Hence, the contribution of detector noise can be efficiently reduced by narrowing the temporal acceptance window on the receiver side, resulting in lower QBERs—ideally down to the limit of QBER = 0.42% of our present setup. As the applied temporal filter will also reduce the detection events available for key distillation, there is an optimal trade-off between QBER and sifted key for which the secret key can be maximized for a given channel loss (see Supplementary Fig. 3 for details). Due to the asymmetric temporal shape of the single-photon pulses, it is beneficial to vary both the width Δt and the center tc of the acceptance time window as seen in Fig. 3a. Here, the asymptotic secret key rate S∞(Δt, tc), simulated from the experimental data in Fig. 2d, is depicted in heatmaps corresponding to four different loss scenarios in the quantum channel of 0, 12, 18, and 22 dB (see Methods section “Parameter optimization” for details). Note, that the loss budget stated here is only the contribution of the transmission channel to the overall losses, i.e., the loss from the last optical element on Alice’ side to the first trusted optical element on Bob’s side. The loss of the receiver module is added for during the calculation of the secret key rate. The optimal parameter settings for the temporal acceptance window, resulting in the largest possible secret key rate, are marked by blue circles in the heatmaps together with the resulting single-photon pulse in the respective lower panels. While the gain achieved via the 2D temporal filtering is small in the low-loss regime, the improved signal-to-noise ratio results in clear advantages at higher losses. This is clearly seen from the extrapolated rate-loss dependencies in Fig. 3b, comparing the non-optimized (dotted line) with the optimized (solid line) case, with the secret key rate S∞(Δt, tc) being optimized for each individual loss. Three regimes can be distinguished: While in the low-loss regime (green), the gain achieved via temporal filtering is marginal, the optimization leads to an improved S∞(Δt, tc) in the intermediate-loss regime (yellow) between 4 dB and 19.08 dB, where the upper limit corresponds to the maximally tolerable loss in the non-optimized case. In the high-loss regime (red), secure communication is only possible if a parameter optimization is applied. Overall, this routine allows us to extend the maximally tolerable transmission loss by 3.51 dB to 22.59 dB using the optimal settings for the temporal filter width Δt and center tc. Assuming a free-space optical communication link at clear-sky weather conditions (0.06 dB/km–0.08 dB/km atmospheric loss at 785 nm42, neglecting beam spread), this corresponds to an extension of the achievable communication distance by 43.9 km.
a Expected secret key rate fraction S∞(Δt, tc) as a function of the acceptance time window Δt and tc. From the experimental results in back-to-back configuration (0 dB loss in the quantum channel) at 0.43Psat and fixed g(2)(0) = 0.134, three different loss scenarios are simulated. Blue circles mark the optimal parameter sets resulting in a maximal secret key rate. b Rate-loss diagram comparing the non-optimized secret key rate (compare Fig. 2c) and optimized case. For each individual loss, the secret key rate was optimized according to (a). Open circles correspond to experimental results using a variable attenuator in the quantum channel.
To put our results into perspective, we compare our results with previous QKD experiments using non-classical light sources. As summarized in a recent review article43, several proof-of-principle experiments using semiconductor quantum dots for single-photon (e.g., refs. 44,45,46,47) or entanglement-based48,49 QKD as well as color centers in diamond for single-photon QKD (e.g., refs. 50,51) have been reported to date, covering all three telecom windows and different levels of device integration. Recently, also quantum emitters in hexagonal boron nitride (hBN)52 as well as molecules of polyaromatic hydrocarbons53 were considered and evaluated for their application in QKD, including an implementation of the B92 protocol54 using an hBN-based SPS55. For our following comparison, we restrict ourselves to the state-of-the-art of BB84-QKD: the pioneering work by Waks et al.44, which reported the largest secret key rate for quantum dot-based QKD to date, Leifgen et al.51, evaluating nitrogen- and silicon-vacancy centers in diamond for QKD, and Takemoto et al.47 with the longest distance achieved for SPS-based QKD so far (c.f. Table 1 for the parameter sets). The rate-loss dependencies of these reports, together with our present work, are presented in Fig. 4. The single-photon QKD experiment using quantum dots by Waks et al.44 realized at an operation wavelength of 877 nm reported the largest secret key rate to date, the experiment of Takemoto et al.47 reports the highest tolerable losses. The work of Leifgen et al.51 represents the current state-of-the art for QKD implementations with color centers in diamond. The comparison with our present work reveals that our simple WSe2-based single-photon source is already competitive with state-of-the-art QKD experiments in terms of the expected secure bits per pulse and, if optimization routines are applied, also in terms of the tolerable losses, which exceed the values achieved in ref. 44 and are close to the once in ref. 47. The mean photon number per pulse inside the quantum channel even clearly surpasses the performance of previous single-photon QKD experiments, which we attribute mainly to the use of a more efficient spectral filtering of the single photons. Straightforward improvements include the integration of TMDC monolayers in microcavities9,10 to reduce the radiative lifetime and increase the photon extraction efficiency. While the Purcell enhancement allows for smaller duty cycles, resulting in improved signal-to-noise ratios, the increased extraction efficiency directly translates to higher values of μ. Both effects combined will lead to significant improvements in the achievable tolerable losses. Implementing already moderate improvements in the performance of the TMDC-based single-photon source (see Fig. 4, dashed gray line: μ = 0.05, g(2)(0) = 0.05, and 10 Hz dark count rate), we anticipate maximally tolerable losses in the quantum channel exceeding 25 dB to become possible. This loss budget brings free-space optical links between the Canary Islands42 or even satellite-to-ground QKD within reach28.
Rate-loss diagram considering our experimental data from Table 1 and the parameters from previous QKD experiments using semiconductor quantum dots (QD)44,47, and nitrogen-vacancy (NV) centers in diamond51 (see Methods section “Parameter optimization” for details on the key rate calculation). The black curves show the expected performance of our WSe2-based source without (dashed line) and with (full line) optimization via temporal filtering. Implementing moderate improvements to our source (gray dashed line), tolerable losses exceeding 25 dB become possible, bringing satellite links within reach28.
Discussion
We demonstrated the feasibility of quantum communication using an atomically thin single-photon source based on a strain-engineered WSe2 monolayer. Implemented in a QKD setup emulating the BB84 protocol, the atomically thin TMDC single-photon source shows a performance superior to previous QKD experiments using solid-state non-classical light sources, opening the route for low-cost large-scale applications in quantum information. Utilizing directly fiber-pigtailed TMDC devices in combination with compact Stirling cryocoolers, user-friendly plug&play quantum light sources will be developed, following our recent demonstration for QD-based devices56. Further advances in material engineering might even bring room temperature operation within reach57. Future real-world QKD applications using highly integrated TMDC-based single-photon sources, will employ fast electro-optical modulator fed by quantum random number generators for polarization-state preparation, enabling secure communication between distant and moving platforms via free-space-optical links. In this context, also finite key-size effects need to be taken into account—a task for which recent work in the field promises substantial improvements over previous work58. Considering advanced implementations in quantum communication but also photonic quantum computing, important milestones to achieve will be the demonstration of high photon-indistinguishability of single and between multiple remote TMDC single-photon sources11.
Methods
TMDC monolayer device
The TMDC sample used in this work comprises a strain-engineered monolayer of WSe2 providing localized quantum emitters for single-photon generation. The sample is fabricated by mechanical exfoliation of sheets of WSe2 transferred to a nano-structured metallic surface, resulting from the deposition of 200 nm of silver on a 600-μm-thick sapphire substrate capped with 10 nm of chromium. The resulting surface contains silver nanoparticles of varying size, which induce wrinkles in the overlying WSe2 acting as strain centers for the excitonic emission. For a detailed characterization of this type of sample, we refer the interested reader to ref. 31.
QKD transmitter
At the heart of the transmitter (Alice), the strain-engineered WSe2 monolayer device is mounted inside a closed-cycle cryocooler (attoDRY800 by Attocube Systems AG) cooled down to 4.2 K including an aspheric lens for collecting the emission of single quantum emitters with a numerical aperture of 0.77. The quantum emitters are optically triggered using a SM fiber-coupled pulsed diode laser (LDH-P-650 by PicoQuant GmbH) with variable repetition rate emitting at 660 nm, which is directed to the sample via a 90:10 beamsplitter. The 90% port of the latter is used to collect the sample luminescence. Spectral filtering of a single emission line of a quantum emitter at the long-wavelength tale of the inhomogeneously broadened ensemble is achieved by two long-pass (LP) filters (cut-on wavelengths: 750 nm and 800 nm), before the emission is coupled to a single-mode (SM) optical fiber (type 780HP, 5 μm core diameter, NA = 0.13) with an aspheric lens (18-mm focal length). Noteworthy, here the use of LP filters (instead of a grating spectrometer) in combination with the additional spatial filtering via the SM fiber enables us to achieve a low-loss optical setup. For preparing single-photon pulses in the four different polarization states required for emulating the BB84 protocol, a fiber-based polarization controller in combination with a Glan–Thompson prism is used. Note, while full implementations of QKD require a dynamic modulation of the polarization states (e.g., via electro-optical modulators), we statically prepare the polarization states in sequential measurement runs in the QKD system used in this proof-of-concept work. This allows us to determine all key parameters for QKD and their limits.
QKD receiver
The polarization qubits prepared at the transmitter are then sent to the receiver module (Bob) via a short free-space link, either in a back-to-back configuration, i.e., without additional loss, or including a variable attenuator (absorptive neutral density filters) for emulating transmission losses. Bob comprises a four-state polarization decoder with passive basis choice designed for operation in the wavelength range 720–980 nm. The measurement bases are chosen by a nonpolarizing 50:50 beamsplitter cube. The final discrimination of the polarization state is realized with polarizing beamsplitters, one of them has an additional half-wave plate in front to project incoming photons from the diagonal/antidiagonal basis to the beamsplitter axes. Each of the four output ports has a fiber collimator with attached optical multimode fiber (FG050LGA, 15 m) connected with single-photon counting modules (COUNT-T100-FC, Laser Components GmbH) having a mean efficiency of 80% at 810 nm, 500 ps timing resolution and 20 Hz dark count rate. The stream of detection events is registered and digitized by a time-to-digital converter (quTAG, qutools GmbH) and synchronized with the excitation laser. More details can be found in ref. 34. Characterizing the polarization decoder with our single-photon source, we determine the QBER for each detection channel individually (QBERH = 0.57%, QBERV = 0.42%, QBERD = 0.84%, and QBERA = 0.26%) resulting in an average QBER of 0.52%. For the key rate calculations, we assumed the worst case of QBERD = 0.84%.
Estimating the source brightness and spectral background contribution
To estimate the single-photon flux our WSe2 emits into the SM fiber on Alice’s side, we analyzed the transmission of our QKD setup. The efficiency of the receiver module Bob including the detector efficiencies and optics’ transmission is (56 ± 5)% with additional losses in the polarizer, fiber, and mating sleeves. This results in a transmission of our setup of (46 ± 9)% from the SM fiber to the detectors. The total detection rate of up to (66.95 ± 1.07) kHz thus corresponds to a single-photon flux in SM fiber of (146 ± 29) kHz or a brightness of the SM fiber-coupled single-photon source of (2.9 ± 0.3)% under pulsed excitation at 5 MHz. Under continuous wave excitation we observe a maximum count rate of 530 kHz at saturation of the quantum emitter corresponding to (1.15 ± 0.23) MHz in the SM fiber. To explore limiting effects to the single-photon purity of our source, we account for residual background contributions in the observed spectra. Assuming an uncorrelated background, the expected autocorrelation function can be expressed via \({g}_{b}^{\left(2\right)}(0)=1+{\rho }^{2}\left[{g}_{{{{\rm{emitter}}}}}^{(2)}\left(0\right)-1\right]\), where \(\rho =S/\left(S+B\right)\) is the ratio of signal S to background B and \({g}_{{{{\rm{emitter}}}}}^{(2)}\left(0\right)\) is the single-photon purity of the emitter itself33. Extracting ρ = 0.97 from the inset in Fig. 1b and assuming \({g}_{{{{\rm{emitter}}}}}^{(2)}\left(0\right)=0\), results in a limit of \({g}_{b}^{\left(2\right)}\left(0\right)=0.040\pm 0.003\) solely due to the spectral background, partly explaining the nonideal single-photon purity. The estimate of the spectral background is in good agreement with the temporally filtered value of \({g}^{(2)}\left(0\right)=0.034\pm 0.002\), where residual laser emission is rejected.
Key rate calculations
Using the formalism presented in the ref. 36 the so-called GLLP rate, named after the authors Gottesman, Lo, Lütkenhaus, and Preskill, reads
Here, Ssift is the sifted key rate and \(A=\left({p}_{{{{\rm{click}}}}}-{p}_{{{{\rm{m}}}}}\right)/{p}_{{{{\rm{click}}}}}\) is the single-photon detection probability. The latter is a function of the multiphoton emission probability pm and overall click probability pclick ≈ μ ⋅ T ⋅ ηBob + pdc, with the channel transmission T, the transmission of the Bob module ηBob including detector efficiencies, and the dark count probability pdc. The QBER is denoted with e, \(h\left(e\right)\) the binary Shannon-entropy, and fEC is the error correction efficiency. The factor A is a correction for the finite pm of practical quantum light sources. One possible way to estimate pm in an experiment is the second-order autocorrelation giving an upper bound of pm = μ2g(2)(0)/237. The factor μ stands for the mean photon number per pulse inside the quantum channel and corresponds to the overall efficiency of Alice in the case of sub-Poissonian light sources. From the click rates measured at our receiver in back-to-back configuration and the transmission of Bob ηBob = 0.56, we determine the mean photon number per pulse into the quantum channel μ in our experiment. From μ and g(2)(0) it is then straightforward to extract pm. While we use neutral density filters to measure the parameters for estimating the secret key rate in Fig. 3b, the simulated rate-loss graphs in Figs. 2c and 3b are obtained by using the dependence of pclick on the channel transmission.
Parameter optimization
Using the formalism presented in ref. 34, we optimized the acceptance time window of detection events. By reducing the acceptance time window, the dark count probability pdc decreases proportionally. At the same time, the number of accepted detection events and hence the click rate is reduced. The reduction of the available key material does not shrink proportionally to the acceptance window size Δt but follows the arrival time probability distribution of the emitter. This distribution is asymmetrical due to the slow exponential decay of the spontaneous emission compared to the fast excitation. It is not enough to vary the acceptance window size Δt around the maximum of the distribution. By additionally varying the center tc one can cover all possible acceptance time windows. In Fig. 3a, we used a subset of 136 s (sifted block of 5 Mbit) of the measurement in Fig. 2d and evaluated the timestamps for each acceptance time window individually to obtain a 2D heat-map depicting the (normalized) secret key rate depending on Δt and tc. We use 50 by 50 equal steps (minimum Δt = 4 ns). The QBER and sifted key faction are varied, g(2)(0) = 0.134 is fixed to its unfiltered value. Finally, we simulate the rate-loss dependency using the parameter pclick as mentioned above. In this fashion the optimized rate-loss graph in Fig. 4 is simulated with 2D optimization for each loss regime individually.
Data availability
The data that support the plots within this paper and other findings of this study are available from the corresponding author upon reasonable request.
References
Kimble, H. J. The quantum internet. Nature 453, 1023–1030 (2008).
Wang, X.-B. Beating the photon-number-splitting attack in practical quantum cryptography. Phys. Rev. Lett. 94, 230503 (2005).
Ma, X., Qi, B., Zhao, Y. & Lo, H.-K. Practical decoy state for quantum key distribution. Phys. Rev. A 72, 012326 (2005).
Aharonovich, I., Englund, D. & Toth, M. Solid-state single-photon emitters. Nat. Photonics 10, 631–641 (2016).
Michler, P. et al. A quantum dot single-photon turnstile device. Science 290, 2282–2285 (2000).
Tomm, N. et al. A bright and fast source of coherent single photons. Nat. Nanotechnol. 16, 399–403 (2021).
Hensen, B. et al. Loophole-free Bell inequality violation using electron spins separated by 1.3 kilometres. Nature 526, 682–686 (2015).
Mak, K. F. & Shan, J. Photonics and optoelectronics of 2D semiconductor transition metal dichalcogenides. Nat. Photonics 10, 216–226 (2016).
Luo, Y. et al. Deterministic coupling of site-controlled quantum emitters in monolayer WSe2 to plasmonic nanocavities. Nat. Nanotechnol. 13, 1137–1142 (2018).
Iff, O. et al. Purcell-enhanced single photon source based on a deterministically placed WSe2 monolayer quantum dot in a circular Bragg grating cavity. Nano Lett. 21, 4715–4720 (2021).
Turunen, M. et al. Quantum photonics with layered 2D materials. Nat. Rev. Phys 4, 219–236 (2022).
Tonndorf, P. et al. Single-photon emission from localized excitons in an atomically thin semiconductor. Optica 2, 347–352 (2015).
He, Y.-M. et al. Single quantum emitters in monolayer semiconductors. Nat. Nanotechnol. 10, 497–502 (2015).
Srivastava, A. et al. Optically active quantum dots in monolayer WSe2. Nat. Nanotechnol. 10, 491–496 (2015).
Chakraborty, C., Kinnischtzke, L., Goodfellow, K. M., Beams, R. & Vamivakas, A. N. Voltage-controlled quantum light from an atomically thin semiconductor. Nat. Nanotechnol. 10, 507–511 (2015).
Koperski, M. et al. Single photon emitters in exfoliated WSe2 structures. Nat. Nanotechnol. 10, 503–506 (2015).
Palacios-Berraquero, C. et al. Atomically thin quantum light-emitting diodes. Nat. Commun. 7, 12978 (2016).
Barthelmi, K. et al. Atomistic defects as single-photon emitters in atomically thin MoS2. Appl. Phys. Lett. 117, 070501 (2020).
Yu, L. et al. Site-controlled quantum emitters in monolayer MoSe2. Nano Lett. 21, 2376–2381 (2021).
Zhao, H., Pettes, M. T., Zheng, Y. & Htoon, H. Site-controlled telecom-wavelength single-photon emitters in atomically-thin MoTe2. Nat. Commun. 12, 6753 (2021).
He, Y.-M. et al. Cascaded emission of single photons from the biexciton in monolayered WSe2. Nat. Commun. 7, 13409 (2016).
Novoselov, K. S., Mishchenko, A., Carvalho, A. & Neto, A. H. C. 2D materials and van der Waals heterostructures. Science 353, aac9439 (2016).
Iff, O. et al. Strain-tunable single photon sources in WSe2 monolayers. Nano Lett. 19, 6931–6936 (2019).
Branny, A., Kumar, S., Proux, R. & Gerardot, B. D. Deterministic strain-induced arrays of quantum emitters in a two-dimensional semiconductor. Nat. Commun. 8, 15053 (2017).
Palacios-Berraquero, C. et al. Large-scale quantum-emitter arrays in atomically thin semiconductors. Nat. Commun. 8, 15093 (2017).
Chou, C.-W. et al. Functional quantum nodes for entanglement distribution over scalable quantum networks. Science 316, 1316–1320 (2007).
Nauerth, S. et al. Air-to-ground quantum communication. Nat. Photonics 7, 382–386 (2013).
Liao, S.-K. et al. Satellite-to-ground quantum key distribution. Nature 549, 43–47 (2017).
Liu, X. & Hersam, M. C. 2D materials for quantum information science. Nat. Rev. Mater. 4, 669–684 (2019).
Bennett, C. H. & Brassard, G. Quantum cryptography: Public key distribution and coin tossing. In Proceedings of IEEE International Conference on Computers, Systems, and Signal Processing, 175 (IEEE, 1984).
Tripathi, L. N. et al. Spontaneous emission enhancement in strain-induced WSe2 monolayer-based quantum light sources on metallic surfaces. ACS Photonics 5, 1919–1926 (2018).
He, Y.-M., Höfling, S. & Schneider, C. Phonon induced line broadening and population of the dark exciton in a deeply trapped localized emitter in monolayer WSe2. Opt. Express 24, 8066–8073 (2016).
Brouri, R., Beveratos, A., Poizat, J.-P. & Grangier, P. Photon antibunching in the fluorescence of individual color centers in diamond. Opt. Lett. 25, 1294–1296 (2000).
Kupko, T. et al. Tools for the performance optimization of single-photon quantum key distribution. npj Quantum Inf. 6, 29 (2020).
Lydersen, L. & Skaar, J. Security of quantum key distribution with bit and basis dependent detector flaws. Quantum Info. Comput. 10, 60–76 (2010).
Gottesman, D., Lo, H.-K., Lütkenhaus, N. & Preskill, J. Security of quantum key distribution with imperfect devices. Quantum Info. Comput. 4, 325–360 (2004).
Waks, E., Santori, C. & Yamamoto, Y. Security aspects of quantum key distribution with sub-Poisson light. Phys. Rev. A 66, 042315 (2002).
Tomamichel, M., Lim, C. C. W., Gisin, N. & Renner, R. Tight finite-key analysis for quantum cryptography. Nat. Commun. 3, 634 (2012).
Takeoka, M., Guha, S. & Wilde, M. M. Fundamental rate-loss tradeoff for optical quantum key distribution. Nat. Commun. 5, 5235 (2014).
Pirandola, S., Laurenza, R., Ottaviani, C. & Banchi, L. Fundamental limits of repeaterless quantum communications. Nat. Commun. 8, 15043 (2017).
Wang, W. & Lo, H.-K. Machine learning for optimal parameter prediction in quantum key distribution. Phys. Rev. A 100, 062334 (2019).
Ursin, R. et al. Entanglement-based quantum communication over 144 km. Nature Phys. 3, 481–486 (2007).
Vajner, D. A., Rickert, L., Gao, T., Kaymazlar, K. & Heindel, T. Quantum communication using semiconductor quantum dots. Adv. Quantum Technol. 5, 2100116 (2022).
Waks, E. et al. Quantum cryptography with a photon turnstile. Nature 420, 762–762 (2002).
Intallura, P. M. et al. Quantum communication using single photons from a semiconductor quantum dot emitting at a telecommunication wavelength. J. Opt. A: Pure Appl. Opt. 11, 054005 (2009).
Heindel, T. et al. Quantum key distribution using quantum dot single-photon emitting diodes in the red and near infrared spectral range. New J. Phys. 14, 083001 (2012).
Takemoto, K. et al. Quantum key distribution over 120 km using ultrahigh purity single-photon source and superconducting single-photon detectors. Sci. Rep. 5, 14383 (2015).
Basset, F. B. et al. Quantum key distribution with entangled photons generated on demand by a quantum dot. Sci. Adv. 7, eabe6379 (2021).
Schimpf, C. et al. Quantum cryptography with highly entangled photons from semiconductor quantum dots. Sci. Adv. 7, eabe8905 (2021).
Beveratos, A. et al. Single photon quantum cryptography. Phys. Rev. Lett. 89, 187901 (2002).
Leifgen, M. et al. Evaluation of nitrogen- and silicon-vacancy defect centres as single photon sources in quantum key distribution. New J. Phys. 16, 023021 (2014).
Zeng, H. Z. J. et al. Integrated room temperature single-photon source for quantum key distribution. Opt. Lett. 47, 1673–1676 (2022).
Murtaza, G. et al. Efficient room-temperature molecular single-photon sources for quantum key distribution. Preprint at https://arxiv.org/abs/2202.12635 (2022).
Bennett, C. H. Quantum cryptography using any two nonorthogonal states. Phys. Rev. Lett. 68, 3121 (1992).
Samaner, Ç., Paçal, S., Mutlu, G., Uyaník, K. & Ateş, S. Free-space quantum key distribution with single photons from defects in hexagonal boron nitride. Adv. Quantum Technol. 5, 2200059 (2022).
Gao, T. et al. A quantum key distribution testbed using a plug&play telecom-wavelength single-photon source. Appl. Phys. Rev. 9, 011412 (2022).
Luo, Y., Liu, N., Li, X., Hone, J. C. & Strauf, S. Single photon emission in WSe2 up to 160 K by quantum yield control. 2D Mater. 6, 035017 (2019).
Morrison, C. L. et al. Single-emitter quantum key distribution over 175 km of fiber with optimised finite key rates. Preprint at https://arxiv.org/abs/2209.03394 (2022).
Acknowledgements
We acknowledge financial support by the German Federal Ministry of Education and Research (BMBF) via the project “QuSecure” (Grant No. 13N14876) within the funding program Photonic Research Germany, the BMBF joint project “tubLAN Q.0” (Grant No. 16KISQ087K), and by the Einstein Foundation via the Einstein Research Unit “Quantum Devices”. C.S. gratefully acknowledges funding by the European Research Council via the project “unlimit-2D” (ERC project 679288). C.A.S. acknowledges the support from the Comunidad de Madrid fund “Atraccion de Talento, Mod. 1”, Ref. 2020-T1/IND-19785. The authors are grateful for helpful discussions as well as infrastructural support by Stephan Reitzenstein and technical assistance by Oliver Iff.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Contributions
T.G. designed and built the QKD setup and the evaluation software used for the experiments. T.G. and M.v.H. operated the single-photon source, which was provided by C.A.S. and C.S. T.G. performed the experiments and analyzed the data. T.G. and T.H. wrote the manuscript with input from all authors. T.H. conceived the experiment and supervised the project.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Gao, T., von Helversen, M., Antón-Solanas, C. et al. Atomically-thin single-photon sources for quantum communication. npj 2D Mater Appl 7, 4 (2023). https://doi.org/10.1038/s41699-023-00366-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41699-023-00366-4
This article is cited by
-
Predicting quantum emitter fluctuations with time-series forecasting models
Scientific Reports (2024)
-
Tailoring polarization in WSe2 quantum emitters through deterministic strain engineering
npj 2D Materials and Applications (2024)
-
The Roadmap of 2D Materials and Devices Toward Chips
Nano-Micro Letters (2024)
-
Single-emitter quantum key distribution over 175 km of fibre with optimised finite key rates
Nature Communications (2023)
-
Layered materials as a platform for quantum technologies
Nature Nanotechnology (2023)