Abstract
Hysteretic friction behavior has been observed on varied 2D nanofilms. However, no unanimous conclusion has yet been drawn on to the exact mechanism or relative contribution of each mechanism to the observed behavior. Here we report on hysteretic friction behavior of supported atomically thin nanofilms studied using atomic force microscopy (AFM) experiments and molecular dynamics (MD) simulations. Load dependent friction measurements were conducted on unheated and heated samples of graphene, h-BN, and MoS2 supported by silica substrates. Two diverging friction trends are reported: the unheated samples showed higher friction during unloading than during loading, and the heated samples showed a reversed hysteresis. Further, the friction force increased sub-linearly with normal force for heated samples, compared with unheated samples. Tapping mode AFM suggested that the interaction strength of the substrate was increased with heating. Roughened substrates in the MD simulations that mimicked strong/weak interaction forces reproduced the experimental observations and revealed that the evolution of real contact area in different interface interaction situation caused the diverging behaviors. Surface roughness and interaction strength were found to be the key parameters for controlling the out-of-plane deformation of atomically thin nanofilms.
Similar content being viewed by others
Introduction
Owing to their two-dimensional (2D) planar structure and strong in-plane covalent bonding, 2D nanofilms such as graphene, h-BN, and MoS2, exhibit ultra-high mechanical strength and intrinsically low interfacial friction that can, in some cases, reach vanishing low/superlubritic friction coefficients1,2,3. Thus, 2D nanofilm-based lubricants are poised to make significant impact both as solid lubricants on their own or as boundary friction modifiers in oil-based lubricants4,5,6. Focusing on their application as novel solid lubricants, the intrinsic attraction or adhesive properties of 2D nanofilms to solids has been shown to be a significant factor in determining their lubricating properties7,8. More specifically, the substrate-nanofilm interaction has endowed these nanofilms with various unique frictional characteristics that macroscopic film does not possess, such as thickness-dependent friction7, adhesion-dependent negative friction coefficient9, non-uniform interface interaction tuned friction10 and load-dependent friction hysteresis11. While these observations have been made, a unifying lubrication mechanism or some method of determining the relative contributions of the various proposed friction reducing mechanisms proposed for 2D nanofilms has not yet been discovered.
Major progress in understanding the lubrication mechanisms of 2D nanofilms has been achieved using atomic force microscopy (AFM)12. In particular, the variation of friction with applied load in AFM experiments has shown a non-conventional behavior8,9,11,13 compared with the expected trends predicted by contact mechanics theory14. In such cases, 2D nanofilms often exhibit linear increases in friction with applied load8,11, as well as friction hysteresis8,9,11,13,15, where the applied normal force was increased and then decreased and the friction force was not the same for a given load during either segment of the experiment. Such results indicate that many experimental conditions, such as environment, sliding history, surface preparation, etc., may influence the results obtained from experiments, and thus the developed lubrication theories. Currently, there are two mechanisms that have been proposed to explain the observed hysteresis in load dependent friction measurements: the puckering effect7,11,16; and surface contamination, such as the capillary formation from ambient humidity, temperature, and chemical contamination8,9,13,15,17. Friction hysteresis was first reported for graphene on copper by ref. 11. It was suggested that the relatively weak adhesion between graphene and copper foil substrate compared with stronger adhesive forces between the tip and the graphene caused the graphene to pucker and inhibited the puckered graphene from fully relaxing during unloading. This suggested that there was also a hysteresis in the contact area during a loading-unloading cycle results in the hysteresis in friction, which was supported by the work of ref. 9. This proposed mechanism was well-received as it is based on one of the lubrication mechanisms proposed for layer dependent friction on 2D nanofilms7. Deng et al. found that when the tip slid against the graphite surface, the topmost graphene layer could even delaminate from the graphite due to a weaker adhesion interface, which resulted in a significant increase in friction as the applied normal load was decreased9. However, Ye et al. found that the puckering of the graphene film was less correlated to the friction hysteresis, but rather with the shape that the water molecules formed between the tip and graphene which dominated the friction hysteretic behavior13. The role of water was confirmed by Gong et al.’s experiment and simulation, where graphene was found to exhibit higher friction hysteresis in high humidity conditions, and the hysteresis was not observed under dry conditions8. However, Zhang et al. found that changing the humidity had limited influence on hysteresis, while the environmental contaminants between the tip and graphene surface tuned the adhesion force of graphene/tip, thus leading to different friction hysteretic behaviors17. Additionally, according to the recent paper of Gong et al., after the surface contamination and water molecules were removed from the graphene sample using the ultra-high vacuum (UHV) AFM, the friction hysteretic was still observed until high temperature annealing of the sample was conducted15. As only a small amount of water/contamination may be present on freshly prepared surfaces that were subjected to low temperature heating and UHV conditions, friction hysteresis may also be an intrinsic property of the nanofilm covered surface itself.
Although several hypotheses have been proposed regarding the origin of friction hysteresis for supported 2D nanofilms, no unanimous conclusion has yet been drawn on to the exact mechanism or relative contribution of each mechanism to the observed behavior11,13,15,17. Herein, we re-examine the friction hysteretic behavior of three different material combinations of supported 2D nanofilms prepared through mechanical exfoliation, including graphene/Silica, MoS2/Silica, and h-BN/Silica. In each case, we prepare the samples with or without a heating step during mechanical exfoliation process, which resulted in an increase of the 2D nanofilm/substrate interfacial adhesion on the heated samples. Load dependent friction measurements revealed that the unheated and heated samples had two distinct different friction hysteretic behaviors, which were correlated with the interface interaction between 2D nanofilm and substrate. MD simulation was then performed on 2D nanofilm/substrate system with different interface interaction, confirming the observed results in experiments and also providing atomistic mechanisms of friction reduction for these materials.
Results
Characterization of the interfacial interaction between graphene/substrate
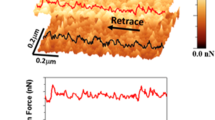
To study the hysteretic behavior of 2D nanofilms, two different graphene/Silica samples were prepared using the mechanical exfoliation method, as shown in Fig. 1a18. In the first set of samples, the graphene was exfoliated onto the silica substrate without any heat treatment in ambient environment. In the second set of samples, the graphene/Silica/scotch tape was heated to ~100 °C for 10 min before exfoliation and removal of the scotch tape19. Figure 1b–d shows topographic images of unheated and heated graphene samples and the corresponding height profiles. The thickness of each layer is approximately 0.335 nm (close to the theoretical thickness of graphene), regardless of the sample tested. This result suggests that limited water molecules were intercalated between graphene and substrate and between graphene layers in either sample20. Additionally, bubbling from intercalated water between the graphene and the substrate was not observed in either sample despite the ambient humidity of the laboratory environment. The scanning areas and the corresponding friction force images of the surfaces of the unheated and heated graphene samples are shown in Supplementary Fig. 1, where the surfaces of the supported graphene were unaffected by heating the sample at first glance: both samples appear contaminant free and similar decreases in the friction forces were observed between the substrate and graphene, as well as when the number of layers of graphene covering the substrate is increased. Previous work17,21,22 has suggested that periodic stripes having a spacing of 4.3 ± 0.2 nm should be observed when environmental adsorbates are present. Supplementary Fig. 2 shows that such a structure is not present on the graphene sample, suggesting that the influence of environmental adsorbates can be neglected here.
a A schematic diagram showing the mechanical exfoliation preparation steps of graphene. The silica substrate (with graphite decorated tape) was heated on a hot plate in air at ~100 °C for 10 min for the heated graphene sample. b–d Topographic images of unheated and heated graphene samples and the corresponding height profiles (below). The white dashed lines in the topographic images indicate the location of the height profiles (below), as well as the labels along the line indicate the number of graphene layers covering the silica substrate.
AFM tapping mode imaging was employed to determine the interfacial adhesion of graphene/Silica samples. The phase signal variation over the graphene samples was acquired, providing a map of effective stiffness of the sample surface and serve as an indicator of the contact state of the embedded interface23,24,25,26. The phase variation is illustrated in Fig. 2a, where a lower phase value indicates a lower contact stiffness and thus weaker interface strength between the graphene and substrate27,28,29. Figure 2b–e shows phase images acquired on several regions of different samples, having varying graphene thickness above the substrate. In each image, the silica substrate was also imaged as a reference point for the phase value. Using the value of the phase for the silica substrate to normalize the results, which was in fact very close to the same value in both samples, the variation in phase over the number of graphene layers covering the substrate could be examined. Figure 2f shows the phase and stiffness difference between the silica substrate and each of the different layers of graphene identified. There was a significantly larger decrease to more negative values in phase for the unheated sample compared with the heated sample, suggesting a sharp decrease in the graphene/Silica adhesive interaction19,30. In both samples, there was a layer-dependent variation of phase difference: a monotonic decrease to more negative values in phase was observed as the number of layers increased for both heated and unheated samples. Additionally, there was a layer-dependent variation of phase difference for both heated and unheated samples: a monotonic decrease to more negative values in phase was observed as the number of layers increased, suggesting that the adhesive interaction of the graphene with the substrate decreased as more graphene layers were added31,32.
a A schematic diagram showing the correlation between the phase signal and the local bonding state of the graphene/substrate interface. Phase images of b, c heated and d, e unheated graphene samples. The numbers within the images indicate the layer number. f The phase difference and the stiffness difference between substrate and graphene for unheated and heated samples. The error bars in f indicate the standard deviation in the average phase value.
Hysteretic friction behavior of graphene
Load dependent friction measurements were then conducted on the unheated and heated graphene/Silica samples to investigate the friction hysteretic behavior. In these measurements, the applied normal force was increased from ~0 nN applied load to a maximum value and then decreased to zero. Images of the surface were acquired at a constant normal force while simultaneously acquiring the lateral force in the forward and reverse scan directions. Before discussing the results on graphene, load dependent friction measurements were conducted on the silica substrates for reference. Supplementary Fig. 3a shows that the friction forces measured on the silica substrate were not strongly impacted by heating the sample. While a direct comparison of the friction forces measured on the silica substrate is difficult to make, resulting from possible changes in the tip size/chemistry and the alignment of the laser/sensor between samples, neither sample exhibited significant friction hysteresis and the slope of the friction force versus normal force curves were very similar between both samples.
Figure 3a, b shows the load dependent friction measurements acquired on the graphene covered regions on the unheated and heated samples, respectively. The friction measured on the graphene covered areas were far lower than those measured on the silica substrate (Supplementary Fig. 3). In both samples, the friction forces were observed to decrease with the number of layers of graphene as expected7. However, the layer-dependent friction behavior on unheated and heated graphene samples were different. For the unheated sample, since the interface between graphene and the substrate was weak, the friction of unheated graphene showed obvious layer-dependence, which was often observed on 2D nanofilms. For the heated sample, due to the improvement of the interface strength, the layer-dependence was greatly suppressed, where the fiction on bilayer was almost the same as that on trilayer, especially below the applied normal force of 30 nN. Previous works showed a similar phenomenon, where the friction strengthening was disappeared on heated graphene due to the heating process strengthening the interface strength between graphene and the underlaying substrate15. Therefore, besides the phase difference in Fig. 2, the analysis on the layer-dependent friction behaviors further convinced us that the heating process did increase the interface strength between graphene and substrate19. Comparing the friction on like coverage of graphene shows that the friction forces were much higher on the unheated samples than on heated samples. The variations in friction force versus normal force during loading were nonlinear for both samples, but their curvatures were different. For the unheated sample, the slope in the variation in friction force versus normal force, i.e., friction coefficient, increased with increasing normal force, while for the heated sample, the friction coefficient decrease with increasing normal force. The load-dependent friction coefficient was most evident on monolayer, which was most sensitive to interface interaction7.
A second difference between the heated and unheated samples is the friction hysteretic behavior. In Fig. 3a, we see that the unheated sample demonstrated friction forces that were higher during unloading than during loading regardless of the layer number. This is in contrast to the friction forces shown in Fig. 3b for the heated sample, where the friction forces were lower during unloading than loading. Additionally, the amount of hysteresis depended on the coverage of graphene: a greater amount of hysteresis was observed for fewer (e.g., one) layers on the unheated sample than for a higher number (e.g., three) layers. Therefore, the diverging hysteretic behavior suggests that the lubrication mechanism is not the same for the two samples resulting from the different interface interaction between graphene and the substrate. It is noted that the same measurements were conducted for smaller ranges in normal force (Supplementary Fig. 4), confirming that the hysteresis was not a result of tip wear.
Hysteretic friction behavior for other 2D nanofilms
To explore the universality of the diverging hysteretic behavior for other supported 2D nanofilms, the same heating treatments were performed for exfoliated MoS2 and h-BN samples. Figure 4 shows the topographic images and friction images of the four samples, where the monolayer regions can be readily distinguished. The load dependence of friction on the monolayer region of the four samples are shown in Fig. 4c, f, i, l. The friction behavior of the MoS2 and h-BN samples was similar to that of the graphene samples. First, the friction on unheated samples was always larger than that on the heated samples. Second, the same nonlinear variation of the friction force and the normal-force-dependent friction coefficient was observed on MoS2 and h-BN samples, where the unheated samples always showed a higher friction coefficient under higher normal force, while the friction coefficient of heated samples exhibited the reverse trend. Third, the same diverging hysteretic behavior for heated versus unheated samples for each nanofilm material was observed. For the unheated sample with relatively weak interface interaction, the friction forces were higher during unloading than loading, and for the heated sample with stronger interface interaction, the hysteretic behavior was reversed. It is noted that the overall friction on monolayer MoS2 is much larger than that on monolayer graphene, and the overall friction on monolayer h-BN is slight smaller than that on monolayer graphene, which agrees well with previous results of friction published on these materials33. Thus, we confirmed that the diverging hysteretic behavior on supported 2D nanofilms is universal property of 2D materials, which is modulated by the interface interaction.
Topographic images of a unheated MoS2, d heated MoS2, g unheated h-BN and j heated h-BN samples and the corresponding height profiles (inset). Friction images of b unheated MoS2, e heated MoS2, h unheated h-BN and k heated h-BN samples. The white dashed square indicates the scanning area in the friction measurements. The load dependence of friction on c unheated MoS2, f heated MoS2, i unheated h-BN and l heated h-BN samples. The error bars in c, f, i, and l indicate the standard deviation in the mean friction force.
MD simulations of hysteretic friction
To further understand the underlying mechanism determining the normal-force-dependent friction coefficient and the diverging hysteretic behavior observed on heated and unheated 2D materials, MD simulations of the friction occurring between a silicon-supported graphene layer and a silicon tip were performed. As shown in Fig. 5a two simulations were conducted both having a silicon substrate with an average surface roughness of 0.3 nm over a 20 × 20 nm2 surface. The two simulations had different interaction strengths, one with a low interaction strength and another with a higher interaction strength, mimicking the adhesive strength change in experiments that resulted from the two heat treatments. Unsurprisingly, the graphene layer conformed better to the substrate with the higher interaction strength than the substrate with the lower interaction strength. While the apparent change in surface roughness is visible in Fig. 5a, AFM measurements of the surface topography in Fig. 1a of the unheated (weak interaction strength) and heated (strong interaction strength) did not show a conclusive change in surface roughness resulting from the error associated with characterizing surface roughness (average roughness, Ra, of the heated and unheated monolayer graphene sample was 0.1211 nm and 0.1208 nm, respectively): e.g., a change of less than 1% in average surface roughness over the scan area is difficult to measure with certainty. Despite the absence of change, the average surface roughness measured over the 5 × 5 μm2 scan frame was comparable to that used in the MD simulations.
a Snapshots of the tip sliding on the roughened substrate supported graphene for the two cases examined taken during loading at 10 nN applied load. b Load dependent friction curve obtained from MD simulations for the low and high interaction cases. c Strain map of graphene in the (top) loading and (bottom) unloading periods at 10 nN applied load for the two cases examined. d The number of contacting atoms between the sliding tip and the graphene film during loading and unloading measurements for the two cases.
Figure 5b shows that the simulation with the high interaction energy simulation showed the same friction hysteresis as the heated sample from experiments, whereas the simulation with the low interaction energy has the same friction hysteresis as the unheated sample from experiments. The consistency between the simulation and the experimental results and the literature on the adhesive properties of heated/unheated samples suggests that examination of the sliding interface may provide further understanding of how the structure of the contact is impacted by the surface roughness, interaction energy, and graphene overlayer. We also suggest that the curvature of the friction versus normal force in Fig. 5b for the high/low interaction energy substrates follows the same trend as the experimental measurements in Figs. 3 and 4. However, with the number of loads examined in the simulations, this curvature change linked to the experimental results, which had significantly more data points, is slightly less obvious.
Discussion
The proposed mechanisms for layer dependent friction on 2D materials, as well as for observed friction hysteresis, include the pucker-effect7, enhancement of interaction between tip-sample atoms (quality of the contact)16, water meniscus13, deformation of confined liquid layers, and electron-phonon coupling34. In this case here, we observe two different friction hysteretic behaviors from a change in substrate interaction. As we have not examined velocity dependent friction in the experiments, and the MD simulations did not include water or other medium on the surface, we focus rather on understanding the current friction results within the the first two proposed mechanisms. In the pucker-effect, an increase in contact area between the tip and the 2D material that is dependent on sliding history and load was previously reported11. Figure 5d shows the number of atoms contacting between the tip and the graphene film in the load dependent friction measurements shown in Fig. 5b. Here, the number of contacting atoms follows the trend in hysteresis: in the low interaction substrate, the number of atoms in contact during unloading is less for the same normal force value as was observed in loading. The opposite is true for the higher interaction force. However, the low interaction force shows a dramatic decrease in the number of contacting atoms during unloading compared with the smaller increase in contacting atoms during the unloading simulations in the high interaction substrate case.
A closer examination of the contact state was performed to further understand the link between contact size, quality, and friction. We characterized the in-plane stresses and strains created in the graphene layer as the tip slid across the substrate. Figure 5c shows that larger area of highly strained atoms is observed at the same load/sliding history for the low graphene-substrate interaction than in the high graphene-substrate interaction simulation. This is a result of more gaped regions between graphene and the rough substrate with low graphene-substrate interaction, as the graphene was less adhered to the surface variations of the underlying substrate. The higher strain/less adherent graphene resulted in a higher effective contact area between the sliding tip and the substrate in the low graphene-substrate interaction simulations, and thus resulted in the observed higher friction. In addition, with the lower graphene-substrate interaction, the effective contact is smaller during loading than unloading, resulted in a lower friction during loading than unloading, However, the opposite trend was observed for the high graphene-substrate interaction. To better interpret the impact of amount of strain in the graphene nanofilm, a histogram of the strains in the contacting area between the tip and graphene was created, shown in Supplementary Fig. 5. This histogram shows a change in the average/center value of the strain as well as a significant change in the width of the distribution of the strain values for the two surface interactions. At 10 nN applied load, larger number of high compressive strain atoms (more atoms were resisting the motion of sliding) was observed during unloading than that during loading for low interaction case, which also contributed to the higher friction forces observed during unloading compared with loading. However, for high interaction case, a different trend was observed that larger number of atoms at contact experienced tensile strain during unloading. Meanwhile, the strain becomes more narrowly distributed around 0% during unloading for the high interaction case.
In several previous works, similar simulations have been performed where no friction hysteresis has been observed in the MD simulations8,13,35,36. In the simulations contained within this study, the presence of hysteretic friction is a result of the minor roughness of the substrate, compared to the previous studies that were constructed only with atomic-scale roughness. This roughness allows for small portions of the graphene film to be detached and adhere less to the substrates, particularly in valleys of roughness of the substrate that the graphene smoothen. It is in these regions that the interaction between graphene and the tip can be sufficiently higher than between graphene and the substrate, that a pucker can begin to form. Thus, the small amount roughness is required for the formation of a pucker, or an increase in the contact area of the tip and the substrate. The interaction strength between the graphene and the substrate then controls how much this layer can lift off the substrate during sliding, as well as how well it conforms to the surface roughness of the substrate. The observation of variation in the number of atoms in contact between the tip and sample/the contact area in Fig. 5d directly follows the hysteretic behavior observed in experiments, providing a simulation that replicates the observed data contained within this manuscript, as well as that suggested in ref. 11. It is noted that, the tip-sample interaction can be affected by the tip material, surface contaminants, and possible intercalated liquid molecules between tip and sample17,20,37,38. However, we used the tips of the same kind in all friction experiments and the ambient conditions were barley changed. Thus, the influence of the tip-sample interaction on the frictional hysteresis behavior was not specifically investigated here with the tip-sample interaction also fixed in all MD simulations. And finally, the change in strain in the graphene layer suggests that the contact quality, suggested in ref. 16, is indeed important to the observed friction and hysteretic behavior of 2D materials. The formation of the pucker and subsequent alignment of graphene-tip atoms to favorable positions during sliding allows for the build-up of strain in the 2D material as the tip slides. However, the surface roughness and the interaction strength between the tip and substrate are two critical parameters that control the amount of strain that can be built-up in the 2D material, which has been missing from the literature on the friction behavior of 2D materials and the proposed friction mechanism for 2D materials. Thus, the combination of out-of-plane stiffness, the adhesive interaction between the graphene/2D material and the substrate, and the alignment of the tip and 2D material atoms is required for interpreting the friction mechanism of 2D materials.
In summary, friction hysteretic behaviors of supported atomically thin nanofilms were studied using experiments and MD simulations. Load dependent friction measurements were conducted on the unheated and heated 2D nanofilm/Silica samples. Two diverging friction hysteretic behaviors were found, where the unheated sample demonstrates friction forces that were higher during unloading than during loading, while the hysteresis of heated sample was reversed. Meanwhile, two distinct evolving behaviors of the normal-force-dependent friction coefficient were found, where the unheated/heated sample had an increasing/decreasing friction coefficient during loading. The phase images of two different samples obtained by AFM tapping mode indicated that the heating process during the mechanical exfoliation preparation strengthened the interface interaction between 2D material and the substrate, which can potentially affect the frictional behaviors. MD simulations were performed on the 2D nanofilm attached on a rough substrate with weak and strong interface interaction, where the normal-force-dependent friction coefficient and the diverging friction hysteretic behaviors were reproduced. The evolution of the real contact area in different interface interaction situation is responsible for these unique behaviors. The increased interaction strength between the graphene and the substrate that occurred through heating resulted in a gradual decrease in contact area between the tip and sample during sliding, compared with the unheated sample where the contact area increased during sliding. Further, the surface roughness of the substrate beyond atomic scale roughness is necessary for the formation of a pucker and the hysteretic behavior observed in the load dependent friction measurements. This increased roughness allowed for the flexible graphene/2D lubricant to lift off and change its contact configuration with the sliding AFM tip. The essential role of the interface interaction in the 2D nanofilm/substrate system revealed in this paper provides a knob for tuning the friction behaviors of supported 2D materials.
Methods
Sample preparation
Graphene, MoS2, and h-BN samples were prepared through the mechanical exfoliation method1,18,19. Silicon wafers with a 300 nm thermally grown oxide (Silicon Valley Microelectronics, Inc.) were used as the substrate. Cleaved pieces were cleaned by ultrasonicating the silica pieces in acetone and subsequently in ethanol. Graphite, MoS2, and h-BN flakes (2D Semiconductors, Inc.) were pressed against scotch tape repeatedly. For the unheated sample, the 2D nanofilm was directly transferred onto the silica substrate. For the heated sample, instead of immediately removing the tape to complete the exfoliation, the substrate with the 2D nanofilm attached tape was heated for 10 min at ~100 °C in air on a hot plate with the temperature of the hot plate surface monitored using an infrared thermometer. The effect of chemical reaction during the heating process was not considered here. First, the samples were heated at 100 °C. According to previous research, these three 2D materials have great chemical stability for temperatures below of ~500 °C (graphene), ~325 °C (MoS2) and ~840 °C (h-BN)39,40,41. Second, it takes days to weeks for these three 2D materials to react with water or oxygen42, but in our experiments, the samples were only heated for 10 min. Third, unlike the directly exposed 2D material, the mechanical exfoliation was performed after heating process, which means the 2D nanofilm was protected by the thick island on it during the heating process19.
Sample measurements
A MFP3D AFM (Asylum Research) was employed to perform the friction, topography, adhesion and phase measurements in ambient conditions (20–25 °C, relative humidity 10%). In contact mode friction measurements, silicon tips (Nanosensors PPP-CONT) were used and the normal and lateral force constants were calibrated by the Sader method43 and the diamagnetic lateral force calibration technique44, respectively. More specifically, the thermal resonance of the first normal oscillatory mode was used, along with the cantilever plan-view dimensions (length and width) to determine the normal bending stiffness of the cantilever. The stiffness of tips used in experiments ranged from 0.25 to 0.35 N/m. A force distance curve was acquired before friction measurements, as shown in Supplementary Fig. 6. The linear voltage response of the position sensitive detector (PSD) to the normal displacement of the sample was determined by calculating the slope of a linear fit to the force distance curve, allowing for the conversion of force to distance. The diamagnetic lateral force calibration then allowed for a determination of the lateral (PSD) sensitivity, or conversion factor from volts to distance, in reference to the normal sensitivity44. Zero applied normal force was determined as the bending signal measured by the PSD when the tip was far from the sample. Lateral forces are the instantaneous twisting forces recorded during a contact mode scan. The friction force was determined by calculating the half difference of the trace and retrace lateral forces in a single line. All friction measurements which were obtained under a scanning rate of 2 Hz. The scanning area was 2 × 2 μm for graphene/Silica samples and was 1 × 1 μm for MoS2/Silica and h-BN/Silica samples. The reported mean friction forces in friction force versus normal force measurements were determined by averaging the friction forces over the areas of interest. Tapping mode imaging was performed also using silicon tip, but one with a higher stiffness of 29.5 N/m (Nanaosensors PPP-NCL). The phase difference reported is the phase lag between the cantilever excitation piezo and the measured oscillation of the cantilever. The contact stiffness difference (Δk) can be calculated based on the measured phase difference (ϕ) with the equation: \(\Delta k={k}_{n}\sin (\phi )\frac{{A}_{0}}{{A}_{sample}}\), where the kn is the stiffness of cantilever, A0 and Asample are the cantilever deflection amplitudes when the cantilever is out of and in contact with the sample, where \(\frac{{A}_{0}}{{A}_{sample}}\) is close to 1 in the experiments28.
Molecular dynamics simulations
A fully atomistic model was developed to mimic the experimental measurements, which consisted of an apex of an AFM tip that was scanned over a substrate of graphene covering a rough silicon substrate. The in-plane dimensions of the substrate was 20 × 20 nm2. The simulation box has periodic boundary condition in x and y direction and non-periodic in z direction. The rough silicon substrate was modeled as amorphous silicon45 having a RMS roughnesses of 0.3 nm. The three bottom layers of atoms in the model substrates were fixed in place throughout the simulation. The model hemispherical tip apex was constructed of silicon and had radius of 2.5 nm, illustrated in Supplementary Fig. 7. The three topmost atomic layers of the tip were treated as a rigid body that was subject to a range of external normal loads varying from 0 to 40 nN. The tip was also connected to a support through a harmonic spring that moved laterally at a constant speed of 1 m/s. A complete friction loop obtained through a forward and backward scan. The sliding distance was 8 nm in both forward and backward scan. A full load dependent simulation consisted of multiple continuous forward and back scan loops. The load increased by 10 nN from 0 nN in each scan loop and reached to a maximum of 40 nN, then load decreased by 10 nN in the following loops. The harmonic spring had stiffness of 8 N/m in the horizontal directions, but did not resist motion in the vertical direction (normal to the graphene surface)46. A Langevin thermostat was applied to the free atoms in the system to maintain a temperature of 300K. The inter-atomic interactions within the tip/substrate and graphene layers were described via Tersoff47 and the Adaptive Intermolecular Reactive Empirical Bond Order (AIREBO) potential48, respectively. The long range interactions between tip and substrate were modeled using the Lennard-Jones (LJ) potential with parameters obtained from the standard mixing rules49,50. To explore the effect of heated substrate with stronger adhesion, we also ran simulations with an artificially strong substrate-graphene interaction strength (εSi−C = 0.01406 eV, doubled interaction strength compared to original interaction). The simulations were performed using the LAMMPS simulation software51.
Data availability
The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.
Code availability
The code generated during the current study are available from the corresponding author on reasonable request.
References
Geim, A. K. & Novoselov, K. S. The rise of graphene. Nat. Mater. 6, 183–191 (2007).
Zhang, S. et al. Tuning friction to a superlubric state via in-plane straining. Proc. Natl Acad. Sci. 116, 24452–24456 (2019).
Yuan, J., Yang, R. & Zhang, G. Structural superlubricity in 2D van der Waals heterojunctions. Nanotechnology 33, https://doi.org/10.1088/1361-6528/ac1197 (2022).
Berman, D., Erdemir, A. & Sumant, A. V. Graphene: A new emerging lubricant. Mater. Today 17, 31–42 (2014).
Zhang, S., Ma, T., Erdemir, A. & Li, Q. Tribology of two-dimensional materials: From mechanisms to modulating strategies. Mater. Today 26, 67–86 (2019).
Berman, D., Erdemir, A. & Sumant, A. V. Approaches for Achieving Superlubricity in Two-Dimensional Materials. ACS Nano 12, 2122–2137 (2018).
Lee, C. et al. Frictional characteristics of atomically thin sheets. Science 328, 76–80 (2010).
Gong, P., Ye, Z., Yuan, L. & Egberts, P. Evaluation of wetting transparency and surface energy of pristine and aged graphene through nanoscale friction. Carbon 132, 749–759 (2018).
Deng, Z., Smolyanitsky, A., Li, Q., Feng, X.-Q. & Cannara, R. J. Adhesion-dependent negative friction coefficient on chemically modified graphite at the nanoscale. Nat. Mater. 11, 1032–1037 (2012).
Zhang, S. et al. Dual-scale stick-slip friction on graphene/h- bn moiré superlattice structure. Phys. Rev. Lett. 128, 226101 (2022).
Egberts, P., Han, G. H., Liu, X.-Z., Johnson, A. T. C. & Carpick, R. W. Frictional behavior of atomically-thin sheets: hexagonal-shaped graphene islands grown on copper by chemical vapor deposition. ACS Nano 8, 5010–5021 (2014).
Bennewitz, R. Friction force microscopy. Mater. Today 8, 42–48 (2005).
Ye, Z. et al. Load-dependent friction hysteresis on graphene. ACS Nano 10, 5161–5168 (2016).
Carpick, R. W., Ogletree, D. F. & Salmeron, M. A general equation for fitting contact area and friction vs load measurements. J. Colloid Interface Sci. 211, 395– 400 (1999).
Gong, P. & Egberts, P. Influence of heating on the measured friction behavior of graphene evaluated under ultra-high vacuum conditions. Appl. Phys. Lett. 119, 063102 (2021).
Li, S. et al. The evolving quality of frictional contact with graphene. Nature 539, 541–545 (2016).
Zhang, D., Zhang, Y., Li, Q. & Dong, M. Origin of friction hysteresis on monolayer graphene. Friction 10, 573–582 (2022).
Geim, A. K. Graphene: status and prospects. Science 324, 1530–1534 (2009).
Huang, Y. et al. Reliable exfoliation of large-area high-quality flakes of graphene and other two-dimensional materials. ACS Nano 9, 10612–10620 (2015).
Arif, T., Colas, G. & Filleter, T. Effect of humidity and water intercalation on the tribological behavior of graphene and graphene oxide. ACS Appl. Mater. Interfaces 10, 22537–22544 (2018).
He, G., Muser, M. H. & Robbins, M. O. Adsorbed layers and the origin of static friction. Science 284, 1650–1652 (1999).
Gallagher, P. et al. Switchable friction enabled by nanoscale self-assembly on graphene. Nat. Commun. 7, 1–7 (2016).
Gajewski, K. et al. Microscale surface potential gradient disturbances observed in bilayer graphene. Appl. Surf. Sci. 510, 145504 (2020).
Zheng, F. et al. Critical stable length in wrinkles of two-dimensional materials. ACS Nano 14, 2137–2144 (2020).
Magonov, S., Elings, V. & Whangbo, M.-H. Phase imaging and stiffness in tapping-mode atomic force microscopy. Surf. Sci. 375, L385–L391 (1997).
Stark, M., Möller, C., Müller, D. J. & Guckenberger, R. From images to interactions: High-resolution phase imaging in tapping-mode atomic force microscopy. Biophys. J. 80, 3009–3018 (2001).
Xu, C. et al. Revisiting frictional characteristics of graphene: Effect of in-plane straining. ACS Appl. Mater. Interfaces 14, 41571–41576 (2022).
Nalam, P. C., Gosvami, N. N., Caporizzo, M. A., Composto, R. J. & Carpick, R. W. Nano-rheology of hydrogels using direct drive force modulation atomic force microscopy. Soft Matter 11, 8165–8178 (2015).
Xu, C. et al. Abnormal raman characteristics of graphene originating from contact interface inhomogeneity. ACS Appl. Mater. Interfaces 13, 22040–22046 (2021).
Peng, L., Qisui, W., Xi, L. & Chaocan, Z. Investigation of the states of water and OH groups on the surface of silica. Colloids Surf. Physicochem. Eng. Aspects 334, 112–115 (2009).
Li, T. & Zhang, Z. Snap-through instability of graphene on substrates. Nanoscale Res. Lett. 5, 169–173 (2010).
Aitken, Z. H. & Huang, R. Effects of mismatch strain and substrate surface corrugation on morphology of supported monolayer graphene. J. Appl. Phys. 107, 1–10 (2010).
Vazirisereshk, M. R. et al. Origin of nanoscale friction contrast between supported graphene, MoS2, and a Graphene/MoS2 heterostructure. Nano Lett. 19, 5496–5505 (2019).
Filleter, T. et al. Friction and dissipation in epitaxial graphene films. Phys. Rev. Lett. 102, 086102 (2009).
Ye, Z., Tang, C., Dong, Y. & Martini, A. Role of wrinkle height in friction variation with number of graphene layers. J. Appl. Phys. 112, 116102 (2012).
Ye, Z. & Martini, A. Atomistic simulation of the load dependence of nanoscale friction on suspended and supported graphene. Langmuir 30, 14707–14711 (2014).
Lazar, P. et al. Quantification of the interaction forces between metals and graphene by quantum chemical calculations and dynamic force measurements under ambient conditions. ACS Nano 7, 1646–1651 (2013).
Baboukani, B. S., Pitkar, A., Ye, Z. & Nalam, P. C. Load-dependent friction hysteresis for graphitic surfaces in n-hexadecane. Adv. Mater. Interfaces 9, 2201249 (2022).
Nan, H. Y. et al. The thermal stability of graphene in air investigated by raman spectroscopy. J. Raman Spectrosc. 44, 1018–1021 (2013).
Zhou, H. et al. Thickness-dependent patterning of mos2 sheets with well-oriented triangular pits by heating in air. Nano Res. 6, 703–711 (2013).
Li, L. H., Cervenka, J., Watanabe, K., Taniguchi, T. & Chen, Y. Strong oxidation resistance of atomically thin boron nitride nanosheets. ACS Nano 8, 1457–1462 (2014).
Wang, X., Sun, Y. & Liu, K. Chemical and structural stability of 2d layered materials. 2D Mater. 6, 042001 (2019).
Sader, J. E., Chon, J. W. M. & Mulvaney, P. Calibration of rectangular atomic force microscope cantilevers. Rev. Sci. Instrum. 70, 3967 (1999).
Li, Q., Kim, K. S. & Rydberg, A. Lateral force calibration of an atomic force microscope with a diamagnetic levitation spring system. Rev. Sci. Instrum. 77, 1–13 (2006).
Dong, Y. Effects of substrate roughness and electron–phonon coupling on thickness-dependent friction of graphene. J. Phys. D Appl. Phys. 47, 055305 (2014).
Dong, Y., Li, Q. & Martini, A. Molecular dynamics simulation of atomic friction: A review and guide. J. Vac. Sci. Technol. A 31, 030801 (2013).
Tersoff, J. Empirical interatomic potential for silicon with improved elastic properties. Phys. Rev. B 38, 9902 (1988).
Stuart, S. J., Tutein, A. B. & Harrison, J. A. A reactive potential for hydrocarbons with intermolecular interactions. J. Chem. Phys. 112, 6472 (2000).
Lorentz, H. Ueber die anwendung des satzes vom virial in der kinetischen theorie der gase. Annalen der Physik 248, 127–136 (1881).
Berthelot, D. Sur le mélange des gaz. Compt. Rendus 126, 1703–1706 (1898).
Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 117, 1–19 (1995).
Acknowledgements
The authors would like to acknowledge funding from the Natural Sciences and Engineering Research Council (NSERC) of Canada Discovery Grants Program (Grant Number RGPIN-2020-04545) and Research Tools and Instruments (RTI). The authors would also like to thank Dr. Shuai Zhang and Prof. Qunyang Li for providing the diamagnetic lever calibration device. C.X. would also like to acknowledge financial support from the University of Calgary Eyes High Postdoctoral Match-Funding Program.
Author information
Authors and Affiliations
Contributions
The manuscript was written and revised by C.X., Z.Y., and P.E. C.X. was responsible for conducting the experiments, analyzing the experimental data, and preparing the first draft of the manuscript. Z.Y. was responsible for conducting and analyzing the molecular dynamics simulations. P.E. was responsible for obtaining the funding the support the experimental research.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Xu, C., Ye, Z. & Egberts, P. Friction hysteretic behavior of supported atomically thin nanofilms. npj 2D Mater Appl 7, 1 (2023). https://doi.org/10.1038/s41699-022-00363-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41699-022-00363-z
This article is cited by
-
Machine-learning structural reconstructions for accelerated point defect calculations
npj Computational Materials (2024)