Abstract
Semiconducting two-dimensional materials with chemical formula MoSi2X4 (X = N, P, or As) are studied by means of atomistic ground- and excited-state first-principles simulations. Full-fledged quasi-particle bandstructures within the G0W0 approach substantially correct the electronic bandgaps previously obtained with hybrid-functional density functional theory and highlight the absence of lateral valleys close in energy to the conduction band minimum. By solving the Bethe–Salpeter equation, we show that the optical properties are dominated by strongly bound excitons with the absorbance and maximum short-circuit current densities of MoSi2P4 and MoSi2As4 comparable to those of transition metal dichalcogenides. Due to the presence of the outer SiX layers, the exciton binding energies are smaller than those generally found for transition metal dichalcogenides. Long radiative lifetimes of bright excitons, over 10 ns at room temperature for MoSi2As4, and the absence of band-nesting are very promising for application in efficient ultra-thin optoelectronic devices.
Similar content being viewed by others
Introduction
Atomically thin two-dimensional (2D) materials are nowadays the subject of intense fundamental and technological research1,2,3,4,5,6. Due to the reduced dimensionality and the weak dielectric screening, their opto-electronic response, even at room temperature, is dominated by strongly bound electron-hole pairs, called excitons7. Among a plethora of semiconducting 2D materials, the family of group VI transition metal dichalcogenides (TMDs) is most attractive for very high absorbance and optical bandgaps ranging from the visible to the near-infrared region of the electromagnetic spectrum8,9. TMDs thus are promising candidates for next generation opto-electronic and photonic devices, such as photovoltaic solar cells10,11, photodetectors12,13, and light-emitting diodes14. However, the opto-electronic performance of TMDs is affected by spin and momentum-forbidden dark excitons. The former originate from the strong spin-orbit coupling at the K and K′ points15,16, the latter are mainly due to the presence of lateral valleys at the Λ (or Q) point, midway between the Γ and K points of the Brillouin zone17. Their energy ordering relative to the bright direct K-K excitons has a profound impact on the photoluminescence efficiency. A spin-forbidden dark exciton as lowest-energy state, as in WS2, and finite momentum excitons energetically close to the bright exciton, as in MoS2, introduce additional non-radiative decay channels that hamper the photoluminescence quantum yield17.
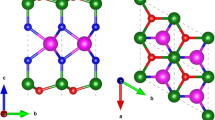
The 2D semiconducting material MoSi2N4 recently has been synthesized by chemical vapor deposition18. It has a layered structure with P\(\overline{6}\)m2 space group, in which an inner MoN2 layer is coordinated to two outer SiN layers, compare Fig. 1. It exhibits an indirect band gap, a high strength (66 GPa), and remarkable ambient stability. Theoretical calculations based on the deformation potential approach predict high intrinsic electron and hole mobilities of 270 cm2 V−1s−1 and 1200 cm2 V−1s−1, respectively18,19, which result in a high on/off ratio of 4000 at 77 K in a back-gated field-effect transistor. The carrier type and bandgap of MoSi2N4 can be easily manipulated by doping20. Interestingly, other 2D materials with the general formula MoSi2X4 and the same structure as MoSi2N4 can be obtained by elemental substitution and exhibit versatile properties21. The indirect bandgap becomes direct after replacing the N atoms by P or As atoms22,23. The absence of inversion symmetry in the structure of MoSi2X4 allows for valley polarization by optical pumping with circularly polarized light22,24, making the materials suitable for application in spintronics and valleytronics21. Several members of the family exhibit high piezoelectric coefficients and are predicted to show high lattice thermal conductivity, comparable with Cu25.
Despite the appeal of the materials, theoretical investigations in the literature have focused on the electronic and optical properties22,26,27 mainly within the limited density functional theory (DFT) approach. It is known that DFT fails at properly predicting both the electronic bandgap of semiconductors and the light absorption spectra. In particular, DFT intrinsically misses the excitonic features that are essential in low-dimensional materials. For this reason, in this work, we study MoSi2X4 (X = N, P, or As) employing state-of-the-art many-body perturbation theory techniques, to disclose the excitonic nature of the optical properties, which inevitably must be taken into account to provide thorough insights into the basic properties of these materials and reliable guidance to future experimental works.
Results and discussion
Structure and electronic properties
Figure 1 shows the relaxed atomic structures of MoSi2N4, MoSi2P4, and MoSi2As4. Their optimized lattice constants are 2.91, 3.47, and 3.62 Å, respectively, in agreement with previous reports18,27. The PBE and G0W0 band structures are reported in Fig. 2. We confirm that MoSi2N4 is an indirect bandgap semiconductor both at the PBE and G0W0 levels, with the valence band maximum (VBM) located at the Γ point and the conduction band minimum (CBM) located at the K point. Both the valence and conduction band edges are split due to spin-orbit coupling and lack of inversion symmetry. The valence band edge at the K point shows a splitting of 158 (141) meV at the G0W0 (PBE) level, while the conduction band edge shows a much smaller splitting of 10 (3) meV. The G0W0 bandgap is 2.79 eV, i.e., 1.02 eV larger than the PBE bandgap. The direct gap at the K point is 2.96 eV, i.e., 0.18 eV larger than the indirect bandgap. In MoSi2P4 and MoSi2As4 the bandgaps turn direct with the VBM shifting to the K point. The splittings at the VBM and CBM are much larger than for MoSi2N4, specifically, 158 (139) and 14 (4) meV for MoSi2P4 and 203 (181) and 28 (16) meV for MoSi2As4 at the G0W0 (PBE) level due to the heavier masses of P and As. The G0W0 bandgap is 1.17 eV for MoSi2P4 and 1.01 eV for MoSi2As4. As a comparison, the HSE06 hybrid functional27 underestimates the direct bandgap with respect to the G0W0 bandgap by about 0.35 eV for MoSi2P4 and MoSi2As4 and by 0.65 eV for MoSi2N4. This fact has sizeable implications on the optical properties of the materials. It is worth mentioning that the G0W0 bandgaps of MoSi2X4 are inversely proportional to the atomic number of the X element, as explained by the decreasing electronegativity.
Figure 2 also displays a first significant difference from traditional TMDs. The absence of lateral valleys (e.g., the Λ valleys in TMDs) along the Γ-K high-symmetry direction. Due to the absence of Λ valleys close in energy to the K valleys, excitons have fewer non-radiative recombination channels in MoSi2X4 than in TMDs, hinting at a less suppressed quantum yield and high efficiencies in optoelectronic devices. It recently has been proven that non-radiative recombination channels can be efficiently suppressed in TMDs by electrostatic doping28 and strain29. We anticipate that the same approaches can be applied to further enhance the quantum yield of MoSi2X4 (X = N, P, or As).
Optical properties
In the upper panels of Fig. 3 we report the absorption spectra computed at the BSE level. The absorption onset falls in the visible region for MoSi2N4, at 2.31 eV, and in the near infrared region at 0.77 and 0.71 eV for MoSi2P4 and MoSi2As4, respectively. The overlap of the absorption spectra with the incident AM1.5G solar flux Φs(ω) (shaded gray region in Fig. 3), while limited for MoSi2N4, is larger for MoSi2P4 and MoSi2As4. To quantify the theoretical efficiency of the absorption of solar light we compute the maximum short-circuit current density as \({J}_{{{{\rm{sc}}}}}^{\max }=e\int \,d\omega A(\omega ){\Phi }_{s}(\omega ),\) where A(ω) is the absorbance11. The value of \({J}_{{{{\rm{sc}}}}}^{\max }\) is only 0.7 mA/cm2 in the case of MoSi2N4, while MoSi2P4 and MoSi2As4 exhibit large values of 3.6 and 4.5 mA/cm2, respectively, because of the lower absorption onset. These values are comparable with well-studied TMDs30, such as MoS2 (3.9 mA/cm2) and MoSe2 (4.6 mA/cm2), indicating great potential of MoSi2X4 in photovoltaic applications.
Exciton fine structure
Selected absorption peaks A, B, \(\widetilde{{{{\rm{B}}}}}\), and C are marked in the upper panels of Fig. 3, with the electronic transitions taking place at the k-points correspondingly highlighted in the lower panels. Similarly to TMDs, peaks A and B are due to well-defined excitons with contributions from transitions at the K and K’ points, reflecting the band splitting induced by the spin-orbit coupling. As shown in more detail for MoSi2P4 in Fig. 4a–c, excitons A and B originate from the allowed transitions between same-spin bands, namely VBM → CBM for exciton A and VBM−1 → CBM+1 for exciton B. The binding energy of exciton A is 0.68 eV in MoSi2N4 and 0.44 eV in both MoSi2P4 and MoSi2As4, i.e., smaller than the binding energy of the lowest-energy bright exciton of a MoS2 monolayer, estimated to be larger than 0.70 eV at the same level of theory31,32. Excitons A and B in the case of MoSi2N4 are located at 2.31 and 2.45 eV, respectively, in agreement with the experimental values (2.21 and 2.35 eV)18. The 0.1 eV blueshift of the computed exciton energies with respect to the experimental values can be attributed to three main effects that were not included in the calculations: the presence of a substrate, which has been shown to reduce the optical gap of single-layer TMDs by up to 0.1 eV33,34, temperature effects, which already at 0 K cause a redshift of 75 meV in single-layer MoS2 due to zero-point renormalization35, and tensile strain, which has a strong impact on the band structure of MoSi2N4 already at small magnitudes (see Supplementary Fig. 4).
G0W0 bandstructure of a MoSi2P4 and d MoSi2N4 with weights of the single-particle transitions giving rise to excitons A, B, \(\widetilde{{{{\rm{B}}}}}\), and C (Fig. 3). In b and c we report details of the CBM(+1) and VBM(−1), respectively, around the K point.
Spin-forbidden transitions between opposite-spin bands at the K and K′ points give rise to the dark exciton AD with zero dipole moment for in-plane light polarization. Above peaks A and B, it is possible to identify in Fig. 3 several peaks with lower intensities. As a representative, we select a peak \(\widetilde{{{{\rm{B}}}}}\), which is due to VBM−1 → CBM+1 transitions (as peak B) taking place near the K and K’ points (Fig. 4). These transitions are slightly more energetic and less intense, as they occur only in the vicinity of the high-symmetry K and K′ points.
Finally, we find in Fig. 3 an intense absorption peak at higher energy, well above the G0W0 direct bandgap, which originates from direct transitions (VBM → CBM) within the Brillouin zone (lower panels of Fig. 3). We mark it as C to suggest a possible analogy with the intense peaks that are found in TMDs and are mainly given by similar transitions at k-points intermediate between Γ and K. In the case of the TMDs these transitions take place in regions of the Brillouin zone where the valence and conduction bands are almost parallel, i.e., ‘nested’36. In such conditions, photo-generated electrons and holes relax with opposite momenta to their closest band extrema, i.e., to the Λ valley and Γ hill, respectively. Hence, photo-generated carriers remain separated in momentum space, and the quantum yield drops significantly37. This does not happen for MoSi2P4 and MoSi2As4 according to Fig. 4, since no lateral valley is interposed between the transitions and the band extrema at the K and K’ points. In Fig. 5 we show a schematic of the electron-hole relaxation mechanisms in (a) MoS2 and (b) MoSi2P4. In MoS2 the excited electrons from peak C quickly relax via intraband scattering to the Λ valley between the Γ and K points (dashed red arrow). Simultaneously, the excited holes relax to the Γ hill (blue dashed arrow). Once relaxed, the charge carriers can follow phonon-mediated radiative recombination (dot-dashed green arrow), or non-radiative recombination, or phonon scattering to the K and K′ points (dotted red and blue arrows). Only a relatively small fraction of the photo-excited carriers reaches the K and K′ points and recombines radiatively, with moderate yield37. In the cases of MoSi2P4 and MoSi2As4, see Fig. 5b, the photo-generated electrons and holes are statistically favored to quickly relax to the closest K or K’ points, via interband scattering (red and blue dashed arrows). It is not possible to fully exclude relaxation paths leading holes to the Γ hill, however they are disfavored by the longer interband scattering chain.
Band nesting in TMDs results in a large enhancement of the joint density of states (jDOS) and, in turn, in an increased absorbance. In MoSi2P4 and MoSi2As4 the large intensity of peak C can be similarly traced back to the jDOS, see Fig. 6a. However, this enhancement is not related to band nesting, see Fig. 4, but rather to the reduced curvature of the valence and conduction bands in the region where the electronic transitions contributing to peak C occur. In MoSi2N4 the intense peak C is mainly due to contributions from electronic transitions in the vicinity of K/K’, as well as at Γ (see the lower panels of Figs. 3 and 4d). The band structure of MoSi2N4 shows flat conduction and valence bands around Γ, which enhance the jDOS and, consequently, the intensity, see Fig. 6b. This feature is absent in MoSi2P4 and MoSi2As4.
As mentioned, the energetic ordering of excitons AD and A is crucial for the optoelectronic performance. We have verified that in our calculations the bright-dark splitting \(\Delta \equiv {E}_{{{{\rm{A}}}}}-{E}_{{{{{\rm{A}}}}}_{{{{\rm{D}}}}}}\) is converged within 2 meV (see Supplementary Fig. 2c). It is important to notice that, while in the case of MoSi2N4 the dark exciton AD is the lowest-energy state, with a bright-dark splitting Δ = 9 meV, the ordering is reversed in the cases of MoSi2P4 and of MoSi2As4, where we have Δ = −3 and −13 meV, respectively (lower panels of Fig. 3). This is the result of interplay between the splitting of the conduction band due to the spin-orbit coupling and the exchange interaction between the electron and hole in the exciton32,38. Indeed, in all three studied materials the band splitting provides a negative contribution to Δ, since the opposite-spin bands involved in exciton AD are the VBM and CBM+1, implying that the electronic transitions contributing to exciton A (VBM → CBM) are less energetic than those contributing to exciton AD. On the contrary, the exchange interaction always contributes positively to Δ, lowering the energy of the dark exciton with respect to the bright exciton. The contribution of the exchange interaction to Δ is found to be between 12 meV (MoSi2P4) and 18 meV (MoSi2N4), being large enough to overcome the band splitting due to the spin-orbit coupling only in the case of MoSi2N4 (positive Δ). The negative Δ implies that MoSi2P4 and MoSi2As4 will show an enhanced quantum yield at low temperatures, unlike TMDs such as WS2, WSe239, and MoS240,41. In the case of MoSi2As4, due to the large Δ = −13 meV, the quantum yield is expected to be only moderately suppressed even at room temperature, unlike MoSe2 with Δ = −1 meV16,42. The energetic ordering of the excitons and bright-dark splitting represent the second main specificity of the materials under consideration with respect to traditional TMDs.
The lower panels of Fig. 3 also give the intrinsic radiative lifetimes of excitons A and B at 0 K, \({\tau }_{{{{\rm{A}}}},{{{\rm{B}}}}}^{0}\), which all fall in the range of tenths of ps, in line with the values obtained for 2D TMDs43. As shown in Refs. 43,44,45, in a 2D material the finite temperature radiative lifetime 〈τX〉(T) of exciton X is proportional to \({k}_{{{{\rm{B}}}}}T{M}_{{{{\rm{X}}}}}^{* }/{E}_{{{{\rm{X}}}}}^{2}\), where \({M}_{{{{\rm{X}}}}}^{* }\) and EX are the effective mass and energy of the exciton at zero momentum, respectively. We report in Table 1 the effective masses of the electrons, holes, and excitons, together with the finite temperature exciton radiative lifetimes calculated at T = 4 and 300 K.
The values obtained for MoSi2N4 are slightly larger than those of MoS2, MoSe2, and WSe246. Conversely, the values obtained for MoSi2P4 and MoSi2As4 are about two orders of magnitude larger. This is primarily due to the combination of low energy (EA,B < 1 eV) and high effective mass of the excitons, which enhances the temperature-dependent factor in 〈τ〉(T). Long radiative lifetimes are often associated with exciton localization due to defects or strain, as observed for TMD monolayers and bilayers47,48, or with interlayer excitons in 2D van der Waals heterostructures of TMDs49,50,51.
We plot in Fig. 7 the square moduli of the wavefunctions of excitons A, B, \(\widetilde{{{{\rm{B}}}}}\), and C of MoSi2P4. Corresponding results for MoSi2N4 and MoSi2As4 are reported in Supplementary Figs. 5 and 6, respectively. The hole (white diamond) is kept fixed where the valence band edge has the highest probability density. In all cases, excitons A and B both have a circular shape around the hole. The Bohr radii of excitons A and B are estimated to be, respectively, aA = 1.79 nm and aB = 1.76 nm in MoSi2P4, 0.98 nm and 0.96 nm in MoSi2N4, and 1.65 nm and 1.64 nm in MoSi2As4, in line with the values found in TMDs52,53,54. Exciton \(\widetilde{{{{\rm{B}}}}}\) is more delocalized, and exciton C spreads along the zigzag direction. The side views in Fig. 7 show that excitons A, B, and \(\widetilde{{{{\rm{B}}}}}\) are concentrated on the inner MoSi2 layer, whereas exciton C extends to the outer SiP layers. Exciton C shows a similar delocalization in MoSi2As4, while it does not extend to the outer SiN layers in MoSi2N4.
Exciton-exciton annihilation (strong exciton Auger recombination) is a key technological bottleneck to obtain high quantum yield in TMDs, and the less localized C exciton may enhance the annihilation rate by increasing the annihilation radius55,56,57. Lee et al.58 have employed ultra-flat Au substrates with atomically controlled h-BN spacers to suppress the exciton-exciton interaction and improve the quantum yield of TMDs by an order of magnitude. In MoSi2X4 layers, due to the contribution of the excitons in the inner MoX2 layer, the outer SiX layers can act as the h-BN spacers. Thus, chemical vapor deposition of MoSi2X4 on a metallic substrate may directly lead to highly efficient optoelectronic devices.
We provide a state-of-the-art study of the electronic and optical properties of 2D MoSi2X4 based on many-body perturbation theory. The G0W0 approximation overcomes the drawbacks of DFT, being superior to hybrid-functionals, to achieve reliable electronic band structures and bandgaps. The bandgap of MoSi2N4 is indirect, while the bandgaps of MoSi2P4 and MoSi2As4 are direct at the K point with a bandgap value of around 1 eV. Unlike traditional TMDs, they have no lateral valleys close in energy to the CBM. By solving the Bethe-Salpeter equation, we obtain absorption spectra displaying excitonic features. The absorption onset falls into the visible region for MoSi2N4, and into the near-infrared region for MoSi2P4 and MoSi2As4, resulting, together with a strong light-carrier coupling, in a significant absorption of the solar flux and in maximum short-circuit current densities comparable to those of TMDs. The analysis of the exciton fine-structure reveals a crucial interplay between the band splitting induced by the spin-orbit coupling and the exchange interaction within the exciton, which results in a bright lowest-energy exciton for both MoSi2P4 and MoSi2As4. The negative bright-dark splitting is particularly large (−13 meV) for MoSi2As4. Our detailed analysis suggests that the materials under investigation provide remarkable quantum yields, especially MoSi2As4. Absence of lateral valleys, negative bright-dark splitting, and long exciton radiative lifetime give rise to high performance optoelectronic materials.
Methods
We perform DFT calculations within the plane-wave expansion using the Quantum Espresso package59. The gradient-corrected Perdew–Burke–Ernzerhof (PBE) functional60 is employed together with fully relativistic norm-conserving pseudopotentials61 that account for the spin-orbit coupling. We consider as semicore states the Mo 4s and 4p orbitals, as well as the As 3d orbitals. Convergence is achieved with an 80 Ry kinetic energy cutoff and a uniform 24 × 24 × 1 Monkhorst-Pack k-point mesh62. A 15 Å vacuum region along the c-direction, the direction perpendicular to the layer plane, is introduced to ensure decoupling of periodic replicas. The structure relaxation is assumed to have reached convergence when the maximum component of the residual ionic forces is smaller than 10−8 Ry/Bohr.
Building up on the obtained DFT results, we perform many-body perturbation theory calculations within the G0W0 approximation using the Yambo code63,64. A box cutoff along the c-direction is applied to the bare Coulomb potential. The inverse dielectric matrix, \({\varepsilon }_{{{{\bf{G}}}}{{{\bf{G}}}}^{\prime} }^{-1}\), is obtained within the plasmon-pole approximation64. We adopt the quasiparticle bandgap value at the K point as convergence parameter and fix a convergence threshold of 50 meV. Following this criterion, we employ a 36 × 36 × 1 k-point mesh, 300 bands and a 10 Ry cutoff for the G vectors in \({\varepsilon }_{{{{\bf{G}}}}{{{\bf{G}}}}^{\prime} }^{-1}\) and 240 bands for the computation of the correlation self-energy. In order to speed up the convergence with respect to empty states we adopted the technique described in Ref. 65 as implemented in the Yambo code64.
The quasiparticle band structures are then used to build and solve the Bethe-Salpeter equation on a 36 × 36 × 1 k-point mesh, including eight valence and ten conduction bands in the excitonic Hamiltonian (compare the Supplementary Information).
Data availability
The data supporting the findings of this study are available within the article.
Code availability
No custom code is used.
References
Novoselov, K. S. et al. Two-dimensional atomic crystals. Proc. Natl Acad. Sci. USA 102, 10451–10453 (2005).
Geim, A. K. & Grigorieva, I. V. Van der Waals heterostructures. Nature 499, 419–425 (2013).
Bhimanapati, G. R. et al. Recent advances in two-dimensional materials beyond graphene. ACS Nano 9, 11509–11539 (2015).
Tan, T., Jiang, X., Wang, C., Yao, B. & Zhang, H. 2d material optoelectronics for information functional device applications: status and challenges. Adv. Sci. 7, 2000058 (2020).
Kang, S. et al. 2d semiconducting materials for electronic and optoelectronic applications: potential and challenge. 2D Mater. 7, 022003 (2020).
Bernardi, M., Ataca, C., Palummo, M. & Grossman, J. Electronic properties of two-dimensional layered materials. Nanophotonics 6, 479–493 (2016).
Zheng, X. & Zhang, X. Excitons in two-dimensional materials. In Thirumalai, J. & Pokutnyi, S. I. (eds.) Advances in Condensed-Matter and Materials Physics, chap. 2 (IntechOpen, Rijeka, 2020).
Rasmussen, F. A. & Thygesen, K. S. Computational 2d materials database: Electronic structure of transition-metal dichalcogenides and oxides. J. Phys. Chem. C 119, 13169–13183 (2015).
Manzeli, S., Ovchinnikov, D., Pasquier, D., Yazyev, O. V. & Kis, A. 2d transition metal dichalcogenides. Nat. Rev. Mater. 2, 17033 (2017).
Nassiri Nazif, K. et al. High-specific-power flexible transition metal dichalcogenide solar cells. Nat. Commun. 12, 7034 (2021).
Bastonero, L., Cicero, G., Palummo, M. & Re Fiorentin, M. Boosted solar light absorbance in PdS2/PtS2 vertical heterostructures for ultrathin photovoltaic devices. ACS Appl. Mater. Interfaces 13, 43615–43621 (2021).
Zha, J. et al. Infrared photodetectors based on 2d materials and nanophotonics. Adv. Funct. Mater. 32, 2111970 (2022).
Taffelli, A., Diré, S., Quaranta, A. & Pancheri, L. MoS2 based photodetectors: a review. Sensors 21, 2758 (2021).
Wang, C., Yang, F. & Gao, Y. The highly-efficient light-emitting diodes based on transition metal dichalcogenides: from architecture to performance. Nanoscale Adv. 2, 4323–4340 (2020).
Mueller, T. & Malic, E. Exciton physics and device application of two-dimensional transition metal dichalcogenide semiconductors. npj 2D Mater. Appl. 2, 29 (2018).
Robert, C. et al. Measurement of the spin-forbidden dark excitons in MoS2 and MoSe2 monolayers. Nat. Commun. 11, 4037 (2020).
Malic, E. et al. Dark excitons in transition metal dichalcogenides. Phys. Rev. Mater. 2, 014002 (2018).
Hong, Y.-L. et al. Chemical vapor deposition of layered two-dimensional MoSi2N4 materials. Science 369, 670–674 (2020).
Jian, C.-C., Ma, X., Zhang, J. & Yong, X. Strained MoSi2N4 monolayers with excellent solar energy absorption and carrier transport properties. J. Phys. Chem. C 125, 15185–15193 (2021).
Abdelati, M. A., Maarouf, A. A. & Fadlallah, M. M. Substitutional transition metal doping in MoSi2N4 monolayer: structural, electronic and magnetic properties. Phys. Chem. Chem. Phys. 24, 3035–3042 (2022).
Wang, L. et al. Intercalated architecture of MA2Z4 family layered van der Waals materials with emerging topological, magnetic and superconducting properties. Nat. Commun. 12, 2361 (2021).
Li, S. et al. Valley-dependent properties of monolayer MoSi2N4, WSi2N4, and MoSi2As4. Phys. Rev. B 102, 235435 (2020).
Yao, H. et al. Novel two-dimensional layered MoSi2Z4 (Z = P, As): New promising optoelectronic materials. Nanomaterials 11, 559 (2021).
Yang, C., Song, Z., Sun, X. & Lu, J. Valley pseudospin in monolayer MoSi2N4 and MoSi2As4. Phys. Rev. B 103, 035308 (2021).
Mortazavi, B. et al. Exceptional piezoelectricity, high thermal conductivity and stiffness and promising photocatalysis in two-dimensional MoSi2N4 family confirmed by first-principles. Nano Energy 82, 105716 (2021).
Nguyen, C., Hoang, N. V., Phuc, H. V., Sin, A. Y. & Nguyen, C. V. Two-dimensional boron phosphide/MoGe2N4 van der Waals heterostructure: A promising tunable optoelectronic material. J. Phys. Chem. Lett. 12, 5076–5084 (2021).
Ai, H. et al. Theoretical evidence of the spin-valley coupling and valley polarization in two-dimensional MoSi2X4 (X = N, P, and As). Phys. Chem. Chem. Phys. 23, 3144–3151 (2021).
Lien, D.-H. et al. Electrical suppression of all nonradiative recombination pathways in monolayer semiconductors. Science 364, 468–471 (2019).
Kim, H., Uddin, S. Z., Higashitarumizu, N., Rabani, E. & Javey, A. Inhibited nonradiative decay at all exciton densities in monolayer semiconductors. Science 373, 448–452 (2021).
Bernardi, M., Palummo, M. & Grossman, J. C. Extraordinary sunlight absorption and one nanometer thick photovoltaics using two-dimensional monolayer materials. Nano Lett. 13, 3664–3670 (2013).
Qiu, D. Y., da Jornada, F. H. & Louie, S. G. Optical spectrum of MoS2: Many-body effects and diversity of exciton states. Phys. Rev. Lett. 111, 216805 (2013).
Marsili, M., Molina-Sánchez, A., Palummo, M., Sangalli, D. & Marini, A. Spinorial formulation of the GW-BSE equations and spin properties of excitons in two-dimensional transition metal dichalcogenides. Phys. Rev. B 103, 155152 (2021).
Cho, Y. & Berkelbach, T. C. Environmentally sensitive theory of electronic and optical transitions in atomically thin semiconductors. Phys. Rev. B 97, 041409 (2018).
Trolle, M. L., Pedersen, T. G. & Véniard, V. Model dielectric function for 2d semiconductors including substrate screening. Sci. Rep. 7, 39844 (2017).
Molina-Sánchez, A., Palummo, M., Marini, A. & Wirtz, L. Temperature-dependent excitonic effects in the optical properties of single-layer MoS2. Phys. Rev. B 93, 155435 (2016).
Carvalho, A., Ribeiro, R. M. & Castro Neto, A. H. Band nesting and the optical response of two-dimensional semiconducting transition metal dichalcogenides. Phys. Rev. B 88, 115205 (2013).
Kozawa, D. et al. Photocarrier relaxation pathway in two-dimensional semiconducting transition metal dichalcogenides. Nat. Commun. 5, 4543 (2014).
Echeverry, J. P., Urbaszek, B., Amand, T., Marie, X. & Gerber, I. C. Splitting between bright and dark excitons in transition metal dichalcogenide monolayers. Phys. Rev. B 93, 121107 (2016).
Wang, G. et al. In-plane propagation of light in transition metal dichalcogenide monolayers: optical selection rules. Phys. Rev. Lett. 119, 047401 (2017).
Molina-Sánchez, A., Sangalli, D., Hummer, K., Marini, A. & Wirtz, L. Effect of spin-orbit interaction on the optical spectra of single-layer, double-layer, and bulk MoS2. Phys. Rev. B 88, 045412 (2013).
Molas, M. R. et al. Brightening of dark excitons in monolayers of semiconducting transition metal dichalcogenides. 2D Mater. 4, 021003 (2017).
Lu, Z. et al. Magnetic field mixing and splitting of bright and dark excitons in monolayer MoSe2. 2D Mater. 7, 015017 (2019).
Palummo, M., Bernardi, M. & Grossman, J. C. Exciton radiative lifetimes in two-dimensional transition metal dichalcogenides. Nano Lett. 15, 2794–2800 (2015).
Chen, H.-Y., Palummo, M., Sangalli, D. & Bernardi, M. Theory and ab initio computation of the anisotropic light emission in monolayer transition metal dichalcogenides. Nano Lett. 18, 3839–3843 (2018).
Chen, H.-Y., Jhalani, V. A., Palummo, M. & Bernardi, M. Ab initio calculations of exciton radiative lifetimes in bulk crystals, nanostructures, and molecules. Phys. Rev. B 100, 075135 (2019).
Robert, C. et al. Exciton radiative lifetime in transition metal dichalcogenide monolayers. Phys. Rev. B 93, 205423 (2016).
Tongay, S. et al. Defects activated photoluminescence in two-dimensional semiconductors: interplay between bound, charged and free excitons. Sci. Rep. 3, 2657 (2013).
Linhart, L. et al. Localized intervalley defect excitons as single-photon emitters in WSe2. Phys. Rev. Lett. 123, 146401 (2019).
Kim, J. et al. Observation of ultralong valley lifetime in WSe2/MoS2 heterostructures. Sci. Adv. 3, e1700518 (2017).
Jauregui, L. A. et al. Electrical control of interlayer exciton dynamics in atomically thin heterostructures. Science 366, 870–875 (2019).
Unuchek, D. et al. Room-temperature electrical control of exciton flux in a van der Waals heterostructure. Nature 560, 340–344 (2018).
Zhang, C., Wang, H., Chan, W., Manolatou, C. & Rana, F. Absorption of light by excitons and trions in monolayers of metal dichalcogenide MoS2: Experiments and theory. Phys. Rev. B 89, 205436 (2014).
Berkelbach, T. C., Hybertsen, M. S. & Reichman, D. R. Theory of neutral and charged excitons in monolayer transition metal dichalcogenides. Phys. Rev. B 88, 045318 (2013).
Dong, S. et al. Direct measurement of key exciton properties: Energy, dynamics, and spatial distribution of the wave function. Nat. Sci. 1, e10010 (2021).
Mouri, S. et al. Nonlinear photoluminescence in atomically thin layered WSe2 arising from diffusion-assisted exciton-exciton annihilation. Phys. Rev. B 90, 155449 (2014).
Hoshi, Y. et al. Suppression of exciton-exciton annihilation in tungsten disulfide monolayers encapsulated by hexagonal boron nitrides. Phys. Rev. B 95, 241403 (2017).
Erkensten, D., Brem, S. & Malic, E. Exciton-exciton interaction in transition metal dichalcogenide monolayers and van der Waals heterostructures. Phys. Rev. B 103, 045426 (2021).
Lee, Y. et al. Boosting quantum yields in two-dimensional semiconductors via proximal metal plates. Nat. Commun. 12, 7095 (2021).
Giannozzi, P. et al. QUANTUM ESPRESSO: a modular and open-source software project for quantum simulations of materials. J. Phys.: Condens. Matter 21, 395502 (2009).
Perdew, J. P., Burke, K. & Wang, Y. Generalized gradient approximation for the exchange-correlation hole of a many-electron system. Phys. Rev. B 54, 16533–16539 (1996).
van Setten, M. J. et al. The pseudodojo: training and grading a 85 element optimized norm-conserving pseudopotential table. Comput. Phys. Commun. 226, 39–54 (2018).
Monkhorst, H. J. & Pack, J. D. Special points for Brillouin-zone integrations. Phys. Rev. B 13, 5188–5192 (1976).
Marini, A., Hogan, C., Grüning, M. & Varsano, D. Yambo: an ab initio tool for excited state calculations. Comput. Phys. Commun. 180, 1392–1403 (2009).
Sangalli, D. et al. Many-body perturbation theory calculations using the Yambo code. J. Phys.: Condens. Matter 31, 325902 (2019).
Bruneval, F. & Gonze, X. Accurate GW self-energies in a plane-wave basis using only a few empty states: towards large systems. Phys. Rev. B 78, 085125 (2008).
Acknowledgements
M.S. and U.S. acknowledge the King Abdullah University of Science and Technology (KAUST) for funding the research reported in this publication. M.S. thanks Dr. Huabing Shu and Dr. Zhiyong Zhu for helpful discussions. M.R.F. and M.P. acknowledge CINECA for high-performance computing resources under the Iscra-B initiative. M.P. acknowledges funding from Tor Vergata University through the TESLA project and INFN through the TIME2QUEST project.
Author information
Authors and Affiliations
Contributions
M.S. executed the calculations under the guidance of M.P. M.R.F. and M.S. drafted the manuscript and prepared the figures. All authors contributed to the evaluation of the results and contributed to the final version of the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Sun, M., Re Fiorentin, M., Schwingenschlögl, U. et al. Excitons and light-emission in semiconducting MoSi2X4 two-dimensional materials. npj 2D Mater Appl 6, 81 (2022). https://doi.org/10.1038/s41699-022-00355-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41699-022-00355-z
This article is cited by
-
A new family of septuple-layer 2D materials of MoSi2N4-like crystals
Nature Reviews Physics (2024)
-
The effect of X-atom (X = B, C, N, and O) doping and vacancy defect on the electronic and magnetic properties of binary antimonene-phosphorene nanoribbon: a first-principle investigation
Applied Physics A (2024)