Introduction

Manipulation and creation of electronic states near the Fermi level in materials offers a powerful approach toward engineering properties and functionalities relevant to device applications. In particular, features of electronic structure of special and fundamental interests are linearly dispersive electronic bands forming conical structures called Dirac cones. A zero effective mass for the fermions near the Dirac point and the Berry phase variation around the cone can foster unusual electronic and optical response functions and extraordinary transport properties1,2,3,4,5,6. However, clean Dirac-cone structures such as those found in graphene without other intervening states near the Fermi level are quite rare. Systematic search and exploration of candidate materials and artificially assembled composite systems hosting such Dirac-cone features with little warping or nonlinear distortion over wide energy and momentum ranges have been critical developmental areas for the materials community7,8,9,10,11. Selenium (Se), the material chosen for modifying the electronic band structure of bilayer graphene in the present work, is itself a candidate material in the bulk limit for hosting Weyl fermions (Dirac fermions without spin degeneracy)12. Furthermore, it is a photoconductor widely employed for the xerographic process13 and is a component in the prototypical topological insulator Bi2Se3, which supports topological Dirac surface states14,15,16. Nevertheless, pure Se is unstable in vacuum due to its high vapor pressure; for this very reason, there have been few studies involving pure Se in the bulk or thin-film limits.

The discovery reported herein of a distinct Dirac cone at the zone center when Se molecules are gently adsorbed on bilayer graphene at very low temperatures is quite unexpected. While cloning of Dirac cones in graphene via heterostructure moiré modulation and bilayer twisting is well-documented, the electronic structures in these systems are generally quite complex17,18. Cloning of Dirac cone in few-layer graphene systems has also been reported for intercalation or adsorption of various metals, resulting in \(\left( {\sqrt 3 \times \sqrt 3 } \right)R30^ \circ\) lattices19,20,21,22,23. However, the bonding between the metal atoms and the graphene layers is strong and can lead to substantial modifications of the atomic structure. In contrast, our case epitomizes simplicity and offers a fresh perspective on electronic structure modification. The Se-graphene interaction is expected to be of the very weak van der Waals type. Thus, the electronic structure of the Se-graphene composite system should be essentially a spatially decoupled combination of the graphene and Se electronic states. Graphene alone has no electronic states at the zone center for energies near the Fermi level. Both free and physisorbed Se molecules have a large electronic gap at the Fermi level between the highest occupied molecular orbital (HOMO) states and the lowest unoccupied molecular orbital (LUMO) states. Consequently, Se-derived electronic states cannot be directly involved in the Fermiology of the Se/bilayer graphene system. Therefore, the Dirac cone at the zone center induced by Se adsorption exemplifies a case of emergent electronic band structure.

Results and discussion

Experimental band structure and Dirac-cone cloning

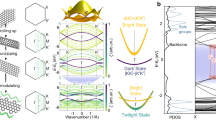
Figure 1a and b display band maps obtained by angle-resolved photoemission spectroscopy (ARPES) using 40.81-eV photons from a helium discharge lamp; the sample was bilayer graphene (BLG) prepared on a 6H-SiC(0001) surface, which during the measurement was maintained at 20 K after saturation adsorption of Se vapor at the same temperature. For comparison, Fig. 1c and d show ARPES maps of the same sample after the sample temperature was raised to 30 K to desorb the Se. Evidently, the adsorption of Se at 20 K creates a Dirac cone at the zone center, but otherwise, the ARPES maps for the two cases are virtually similar. The observed ARPES bands are summarized in Fig. 1e and f, where the blue and green curves indicate bands due to BLG and SiC(0001), respectively, based upon prior experimental and theoretical studies24,25,26,27,28. The red curves identify the Se-induced electronic structure, which is dominated by the emergent Dirac cone at the zone center. For the clean BLG surface, there are actually two closely-spaced Dirac cones centered at the Brillouin zone corner \({{{\bar{\mathrm K}}}}\) point due to bilayer splitting24,25,26,27,28. However, with a photon energy of 40.81 eV used for the band mapping, the lower Dirac cone dominates the ARPES map near the \({{{\bar{\mathrm K}}}}\) point (see Supplementary Note 2 and Supplementary Fig. 2). Additionally, the ARPES cross sections for the two branches of the lower Dirac cone are quite different, leading to marked left-right intensity asymmetry27,28,29. The Se-induced Dirac cone at the zone center, by contrast, is left-right symmetric in intensity (see Supplementary Note 3 and Supplementary Fig. 3), and yet, its dispersion relation replicates exactly that of the graphene Dirac cones at the zone corners. This intensity symmetrization arises because the clone at the zone center is a hybrid offspring of the graphene Dirac cones symmetrically located at the hexagonal zone corners.

Fig. 1: Band structure measurements.
figure 1

a ARPES map of Se-covered BLG near the zone center taken at 20 K, showing a cloned Dirac cone. b Same ARPES map with an adjusted intensity scale over extended energy and momentum ranges. c, d ARPES maps from the same sample warmed up to 30 K, indicating the absence of the cloned Dirac cone. e, f Band structure for the Se-covered BLG with the band origins indicated.

Full size image

The appearance and disappearance of the Dirac cone at the zone center, correlated with the adsorption and desorption of Se at 20 K and 30 K, respectively, are reversible and repeatable (see Supplementary Note 4 and Supplementary Fig. 4). The adsorption at 20 K was carried out with the sample exposed to a background Se vapor in a growth chamber maintained at room temperature with its wall partially coated with Se by prior Se evaporation from an effusion cell; the adsorption at 20 K saturated in about ten minutes. The very low desorption temperature of 30 K confirms that the adsorption of Se is of the very weak van der Waals type. Attempts to acquire reflection high-energy electron diffraction (RHEED) patterns from the Se-saturated sample at 20 K were unsuccessful because the incident electron beam removed the adsorbed Se immediately, as evidenced by the same RHEED pattern as that obtained from the clean BLG surface. The removal of Se was also confirmed by ARPES band mappings. These observations confirm the delicate nature of the Se adlayer.

Available thermodynamic data show that Se vapor at room temperature consists of a mixture of Sen molecules, with n = 2–830. The largest of these molecules, Se8, should have the largest van der Waals adsorption energy and is the most likely candidate for Se adsorption by fractionation in our case. This reasoning is confirmed via ARPES measurements conducted at larger binding energies. Figure 2a, b shows ARPES maps for the clean BLG surface and the Se-covered BLG surface at 30 K and 20 K, respectively. Several prominent nondispersive bands in the 20-K map that are absent in the 30-K map can be attributed to the molecular orbitals of adsorbed Se8. Figure 2c presents first-principles theoretical band dispersions for a \(\left( {2\sqrt 3 \times 2\sqrt 3 } \right)R30^\circ\) adlayer of Se8 on a BLG surface; the adsorption geometry involving a buckled Se8 molecular structure was determined by energy minimization and is indicated schematically in Fig. 2d. The red and green colors for the bands in Fig. 2c indicate the Se s- and p-orbital contributions, respectively, while the gray color indicates the C orbital contributions from the BLG substrate. The calculated Se bands are nearly dispersionless because Se8 molecules are well-separated on the surface. The experiment and theory agree fairly well with each other, though the sp-gap of Se is somewhat smaller in the experiment. The upper p-bands are very weak in the ARPES map but can be made readily visible (Fig. 2e) by “forceful addition” of Se on the surface via rapid evaporation of Se from a heated Se effusion cell onto the already Se-saturated surface at 20 K. The amount of Se added would correspond to a 10-Å film from a thickness monitor reading. Since the Dirac-cone feature from the BLG substrate is still visible in the ARPES map, the actual amount of Se addition could be less than 10 Å due to a less-than-unity sticking probability. Furthermore, the added Se might form clusters or aggregates instead of a uniform film. The observed Se bands for the original Se-saturated sample at 20 K shift downward slightly with the forceful addition of Se based on a comparison of Fig. 2b, e, which can be attributed to chemical shifts arising from a different solid-state environment for Se.

Fig. 2: Nondispersive bands from molecular Se8 and structural model.
figure 2

a ARPES map along \(\overline {{\Gamma }} \overline {{{\mathrm{K}}}}\) from a clean BLG at 30 K. b Similar ARPES map of Se-covered BLG maintained at 20 K. c Theoretical band structure for a \(\left( {2\sqrt 3 \times 2\sqrt 3 } \right)R30^\circ\) Se8 adlayer on a BLG surface. The green and red curves indicate bands derived from Se p- and s-orbitals, respectively. d Adsorption geometry for Se8 on BLG from calculations. e ARPES map from a Se-saturated surface at 20 K further deposited with 10 Å of Se. f Same calculation as c for a side-by-side comparison with e.

Full size image

Identification of Se8 as the adsorbed species is consistent with a prior scanning tunneling microscopy (STM) study31 of a Au(111) surface covered by Se deposition followed by thermal annealing to 200 °C; STM images taken at 78 K show a well-ordered lattice of Se molecules consisting of 8 Se atoms in a square ring-like structure. Since the bonding between Au and Se is strong, the detailed molecular morphology of the adsorbed Se (especially after thermal annealing) is likely different from our case, but the 8-member unit structure is consistent with the assignment of Se8 as the adsorption species during deposition in vacuum in our work.

Selenium adsorption and film growth

The forceful addition of Se on the Se-saturated sample at 20 K does not happen at low Se deposition rates of ~0.3 Å/min (~0.1 monolayer/min). A detailed view of the process of Se addition up to 10 Å with a higher Se evaporation rate at ~1 Å/min is shown in Fig. 3a. The Se-induced Dirac cone at the zone center gradually disappears, while the upper Se p-bands become more visible. Heating the sample to 30 K after the additional deposition of 10 Å of Se at 20 K does not return the sample to the clean state after a 12-hour wait (see Supplementary Note 5 and Supplementary Fig. 5). The same approach of forceful addition also works with the sample maintained at 30 K (Fig. 3b); however, there is no Se-induced Dirac cone at the outset, and the lower graphene bands remain visible. Additional measurements confirm that the results generally depend on the deposition rate and processing history; this behavior is consistent with a first-order phase transition between solid and vapor phase Se, and the growth is thus governed by nucleation under kinetic constraints32.

Fig. 3: Coverage-dependent ARPES maps upon forceful addition of Se.
figure 3

a ARPES maps taken with the sample maintained at 20 K. b ARPES maps taken with the sample maintained at 30 K.

Full size image

Se adlayer geometry and antiphase domains

To address the central question of how gentle Se adsorption at 20 K gives rise to a Dirac cone at the zone center, we have considered various structural models involving Se adatoms or Sen admolecules (see Supplementary Note 6–8 and Supplementary Figs. 6–8). A \(\left( {\sqrt 3 \times \sqrt 3 } \right)R30^\circ\) or \(\left( {3 \times 3} \right)\) arrangement of Se adatoms would create a clone of the Dirac cone at the zone center by superlattice modulation of the crystal potential, which folds the \({{{\bar{\mathrm K}}}}\) points back to the \({{{\bar{\mathrm \Gamma }}}}\) point (Fig. 4a)33,34,35. The \(\left( {3 \times 3} \right)\) structure can be ruled out as it would give rise to additional band folding not observed experimentally. In any case, such adatom models are ruled out by first-principles simulations; the chemical bonding of the Se adatom to the graphene substrate results in just a few dispersive adatom-substrate hybridized bands that are inconsistent with the observed many flat molecular bands (see Supplementary Fig. 6). Also, the very weak adsorption of Sen molecules onto the BLG surface cannot possibly cause the molecules to break into individual adatoms. A more reasonable model is a layer of van der Waals bonded Sen molecules. If these molecules are well-separated on the BLG surface, the molecular orbitals should form flat bands. Calculations show that small n values yield too few flat bands compared to experiment (see Supplementary Fig. 7). The best match to the experimental results is found for n = 8 (Fig. 2d), which is consistent with the expectation based on fractionation adsorption discussed above.

Fig. 4: Cloning of Dirac cones by band folding.
figure 4

a Brillouin zones (blue lines) for \(\left( {\sqrt 3 \times \sqrt 3 } \right)R30^\circ\), \(\left( {3 \times 3} \right)\), and \(\left( {2\sqrt 3 \times 2\sqrt 3 } \right)R30^\circ\)adlayers. The red lines indicate the \(\left( {1 \times 1} \right)\) zone of BLG. Green dots indicate folded zone centers; these, plus the one at the \({{{\bar{\mathrm \Gamma }}}}\) point, should each host a clone of the Dirac cones. Green circles also indicate folded zone centers but with a zero scattering amplitudes due to antiphase cancellation; no clones are expected for these. b Antiphase domain model. The gray honeycomb grid represents the top graphene layer on the BLG surface. Thin and thick blue grids indicate the \(\left( {\sqrt 3 \times \sqrt 3 } \right)R30^\circ\) and \(\left( {2\sqrt 3 \times 2\sqrt 3 } \right)R30^\circ\) lattices, respectively. The four rhombi labeled A, B, C, and D are \(\left( {2\sqrt 3 \times 2\sqrt 3 } \right)R30^\circ\) unit cells related by half-unit-cell antiphase translations.

Full size image

For the sample saturated with Se adsorption at 20 K, the structure must be a closely packed layer without continuous three-dimensional buildup. A \(\left( {\sqrt 3 \times \sqrt 3 } \right)R30^\circ\) array of Se8 would give rise to a Dirac cone at the zone center with no other clones within the first zone, but the Se8 molecule is too large to physically fit into a \(\left( {\sqrt 3 \times \sqrt 3 } \right)R30^\circ\) unit cell (Fig. 2d). The intermolecular spacing becomes more favorable for a \(\left( {3 \times 3} \right)\) configuration, but it is still a bit too small. Theoretical simulations show non-negligible overlap of the molecular orbitals from neighboring Se8 molecules, resulting in noticeable Se-band dispersions (see Supplementary Fig. 8). A \(\left( {2\sqrt 3 \times 2\sqrt 3 } \right)R30^\circ\)configuration offers the closest packing possible compatible with flat bands. This configuration, after energy minimization, is adopted for generating the band structures in Fig. 2, which agree well with the experiment. However, the size of the Brillouin zone for the \(\left( {2\sqrt 3 \times 2\sqrt 3 } \right)R30^\circ\) configuration is one-half of that for the \(\left( {\sqrt 3 \times \sqrt 3 } \right)R30^\circ\) configuration; additional clones of the Dirac cone should arise at the folded zone centers (indicated by green circles in Fig. 4a), but there is no evidence for these in the data.

The lack of additional clones for the \(\left( {2\sqrt 3 \times 2\sqrt 3 } \right)R30^\circ\) configuration can be understood as a result of random nucleation and domain growth that leads to the coexistence of antiphase domains related by half-unit cell slips (or glides). With the unit cell vectors of \(\left( {2\sqrt 3 \times 2\sqrt 3 } \right)R30^\circ\) denoted by \({{{\mathbf{a}}}}_1\) and \({{{\mathbf{a}}}}_2\) (Fig. 4b), a domain can be translated by \({{{\mathbf{a}}}}_1/2\), \({{{\mathbf{a}}}}_2/2\), and \(\left( {{{{\mathbf{a}}}}_1 + {{{\mathbf{a}}}}_2} \right)/2\) to create three additional symmetry-inequivalent but energetically equivalent domains. The geometrical relationship between the four symmetry-distinct antiphase domain unit cells, A–D, is illustrated in Fig. 4b. A real space model for random nucleation followed by growth and domain wall formation is shown in Fig. 5; the particular domain boundary shown corresponds to one between domains A and C (or between B and D). Across the domain boundary, the two structures are related by a translation of \({{{\mathbf{a}}}}_2/2\), and the two structures are energetically equivalent. Random nucleation leads to equal populations of all possible domains.

Fig. 5: Growth and domain formation.
figure 5

a Random adsorption of Se8 molecules on energetically equivalent sites on the BLG surface to form nuclei for growth. b Growth of \(\left( {2\sqrt 3 \times 2\sqrt 3 } \right)R30^\circ\) domains. c Domain boundary formation. This boundary corresponds to one between domains A and C (or between B and D) as defined in Fig. 4.

Full size image

With the reciprocal unit vectors denoted by \({{{\mathbf{b}}}}_1\) and \({{{\mathbf{b}}}}_2\), the structure factors of the crystal potential associated with odd multiples of \({{{\mathbf{b}}}}_1\) (\({{{\mathbf{b}}}}_2\)) cancel separately for the A/B and C/D (A/C and B/D) pairs. Explicitly, the total scattering amplitude A is given by a sum of the scattering amplitudes from the four different domain types \(A_\zeta\) (ζ = 1–4)

$$A \propto \mathop {\sum}\limits_\zeta {A_\zeta } \propto \mathop {\sum}\limits_\zeta {\exp \left( { - i \cdot {{{\mathbf{K}}}} \cdot {{{\mathbf{t}}}}_\zeta } \right)}$$
(1)

where \({{{\mathbf{K}}}} = m{{{\mathbf{b}}}}_1 + n{{{\mathbf{b}}}}_2\), with m and n being integers, is a reciprocal lattice vector. The four domain types are related by half-unit cell translations given by \({{{\mathbf{t}}}}_\zeta = 0,{{{\mathbf{a}}}}_1/2,{{{\mathbf{a}}}}_2/2,{{{\mathrm{ and }}}}\left( {{{{\mathbf{a}}}}_1 + {{{\mathbf{a}}}}_2} \right)/2\) for ζ = 1–4, respectively. The phase factor \(\exp \left( { - i \cdot {{{\mathbf{K}}}} \cdot {{{\mathbf{t}}}}_\zeta } \right)\) in Eq. (1) is thus either +1 or –1 depending on whether m and n are even or odd. It is straightforward to show that A is nonzero only if both m and n are even. This effectively doubles the reciprocal unit cell size, and the band folding for the \(\left( {2\sqrt 3 \times 2\sqrt 3 } \right)R30^\circ\) structure, with antiphase-domain cancellation, becomes the same as that for the \(\left( {\sqrt 3 \times \sqrt 3 } \right)R30^\circ\) structure. See Supplementary Note 9 for a more detailed derivation.

Cloning of Dirac cones allows the creation of useful electronic features near the Fermi level. The discovery of a neat Dirac cone at the zone center in the present case was a surprise but is now understood in terms of fractionation molecular adsorption, steric constraints on layer forming, and antiphase domain structures related to growth kinetics; the observed flat molecular band features are confirmed by first-principles calculations. Our results broaden the perspective for designing and engineering electronic features, including the utilization of gentle physical adsorption of large molecules. While an adsorbed Se8 layer may seem delicate for applications, it is conceivable that a robust overlayer or capping layer added on top by deposition may well preserve the electronic features of interest at the interface (a cloned Dirac cone), thus pointing to a way to integrate the system into functional architectures.

Methods

Experimental details

Substrates of 6H-SiC(0001) were annealed to 1300 °C to form a BLG-terminated surface; the process was monitored by RHEED and verified by ARPES. Deposition of Se was performed with the sample exposed to a background Se pressure in a growth chamber maintained at room temperature or by direct evaporation from a heated Se effusion cell for higher deposition rates. Band mapping by ARPES was performed using a Scienta R4000 analyzer and a monochromatized Scienta-Omicron VUV5K helium discharge lamp operating at 40.81 eV as the light source.

Computational details

Theoretical calculations of the adsorption geometry and electronic structure were performed using the Vienna Ab initio Simulation Package (VASP)36. The projected augmented wave method37 and generalized gradient approximation (GGA) functional of Perdew-Burke-Ernzerhof form (PBE)38 were employed using a supercell geometry with a 25-Å vacuum gap and a cutoff energy of 500 eV. All structures were relaxed, and the energy and force convergence limits were set to 1.0 × 10–6 eV and 0.001 eV/Å, respectively. The Monkhorst-Pack scheme was adopted for Brillouin zone sampling over a 9 × 9 × 1 grid for structural relaxation and a 15×15×1 grid for band structure calculations39. Van der Waals corrections in the DFT-D2, DFT-D3, and vdw-DF2 frameworks were included to account for the long-range dispersion interaction40,41,42. The band structures shown in Fig. 2 were computed using the D2 functional. Results based on the D3 and DF2 functionals are similar with some variations in band energies up to ~0.7 eV; the differences are an indication of the calculations’ precision (see Supplementary Note 10 and Supplementary Fig. 9).