Abstract
Long-term stable excitons, bound pairs of electrons and holes, in van der Waals materials were found to be handled at room temperature, paving the way to develop optoelectronic/photonic devices for future high-speed communication technology. To miniaturize and integrate such functions to achieve highly efficient excitonic devices, understanding and manipulation of exciton dynamics in the nanoscale structures is absolutely essential. Since the spatial resolution of the optical techniques, which have been mainly used in the research of this field, is limited to μm to several tens of nm, the introduction of new technology is strongly desired. Here, we demonstrate a method to probe and visualize neutral excitons using the laser-combined multiprobe scanning tunneling microscopy (STM) system. Ultrafast dynamics of excitons in the nanostructures produced in an in-plane WS2/WSe2 heterostructure, such as dynamics in the ps region of many-body effects under high density and spatial variation in the effect of local defects on lifetime, was successfully revealed with a spatial resolution of 1 nm order. This method is expected to accelerate research on exciton dynamics and the development of applications directly based on the experimental results of nanoscale.
Similar content being viewed by others
Introduction
To develop the high speed (terabits per second) optical communication technology, which has become indispensable in modern society, the development of information transmission methods that do not use charge transfer with large transmission losses is essential. Thus, the use of excitons, electrically neutral quasi-particles formed by bound electrons and holes, has attracted considerable attention. However, the binding energy of excitons generated in a conventional three-dimensional semiconductor is in the range of meV to 10 meV orders, and excitons are easily dissociated at room temperature. Therefore, such devices can be realized only in a low-temperature environment, which has been the most important problem to be solved for the application of excitons1.
In recent years, transition metal dichalcogenides (TMDCs), which are two-dimensional materials in the form of atomic layers, have been attracting considerable attention because of their high carrier mobility, clear bandgap, and strong light-matter interactions2. In particular, excitons generated in TMDCs by light irradiation have high binding energy (up to 100 meV order) due to the confinement effect derived from the two-dimensional structure and the reduced screening effect3. Therefore, two-dimensional excitons exist stably even at room temperature4 and can move long distance in the atomic layer. Furthermore, exciton resonance causes strong emission and absorption at the same wavelength, which makes spatial energy transfer via photons easy and is particularly promising for application in photonic integrated circuit materials5.
However, the optical properties are strongly dependent on the exciton structure. Multibody effects such as the exciton-exciton annihilation (EEA) process through collisions also appear strongly6. In addition, for example, exciton funneling is caused by the narrowing of the bandgap due to in-plane stress7,8. The experimental results correspond well with the theoretical calculations. However, when actually making a device, various local distortions and defects are formed, and each of them has a different effect on the dynamics of excitons.
Since the exciton radius is on the order of 1 nm9, it is necessary to clarify its dynamics on the nm scale to understand and utilize its characteristics. Despite that, so far, research on exciton dynamics has mainly been actively carried out by photoluminescence (PL)10, pump-probe methods11, photoelectron emission microscopy12 and scanning near-field optical microscope13. With such measurement methods, the spatial resolution is limited to μm to several tens of nm, and it is difficult to evaluate the local exciton dynamics while observing the nanoscale structure on the order of 1 nm.
Scanning tunneling microscopy (STM) has the atomic-level spatial resolution, and recently, a high temporal resolution has also been given14,15,16, making STM one of the promising techniques for the purpose. However, since tunnel current is the probe of STM, neutral excitons have never been considered to be a target.
Here, we demonstrate a method to probe and visualize neutral exciton dynamics using laser-combined STM. Ultrafast dynamics of excitons in the nanostructures produced in atomically thin materials, such as dynamics in the ps region of many-body effects under high density and the spatial variation in the effect of ripples and grain boundaries (GBs) on lifetime, was successfully revealed with a spatial resolution of 1 nm order.
Results and discussion
Laser-combined STM system for probing exciton dynamics
Excitons are dissociated by an electric field. In STM, the bias voltage applied between the probe and the sample causes the electric field immediately below the STM tip in the area of several nanometers. Therefore, by dissociating excitons using this electric field, it becomes possible to realize the visualization of neutral excitons with a spatial resolution higher than that of optical methods (Fig. 1a, b).
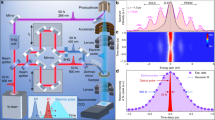
a Time-resolved STM (TR-STM) setup for measuring carrier dynamics in TMDCs. b Band structure showing the mechanism to detect excitons by STM. The direction of the band bending depends on the bias voltage applied between the STM tip and the sample. c Schematic structure of the time-resolved-multiprobe STM system we have developed. BS beam splitter, PBS polarized beam splitter, OPO optical parametric oscillator, FR Faraday rotator, EOM electro-optical modulation element (see Supplementary Fig. 1 for details).
Figure 1c shows the time-resolved multiprobe STM (TR-MP-STM) we have developed. Since STM requires the conductivity of the sample, it is difficult to measure a small sample placed on an insulator substrate with a single probe. In multiprobe STM (MP-STM), by using two contact AFM probes as electrodes, measurement can be performed without pretreatment, such as electrode fabrication, and the gate voltage can be adjusted along with the voltage between the source and the drain, enabling measurement in the operating environment. In this experiment, we used the STM mechanism with a new modulation technique as a probe to measure the dynamics of excitons at the nanoscale and visualize them two-dimensionally (see Methods and Supplementary Fig. 1).
Sample preparation for nanoscale analysis and measurement setup
To evaluate multibody effects such as the EEA process through collisions, the effect of the nanoscale potential, and the spatial resolution of the system, as a sample, a single-layer WS2/WSe2 in-plane heterostructure island was prepared on a SiO2/p-Si (SiO2 thickness: 285 nm) substrate by chemical vapor deposition17. After growing a threefold-symmetric WS2 structure, a WSe2 structure was grown around it, by controlling the growth conditions18. Triangular-shaped structures, indicating the existence of second-layer islands19, were not observed over the area chosen for experiments. Similarly to the technique reported in a previous paper20, the areas used for measurements were cleaned by scanning the STM tip to remove adsorbents.
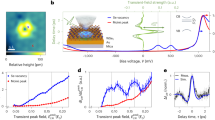
Figure 2a shows an optical microscope image of the sample and a schematic illustration of the structure of the area surrounded by the square frame in the image. As shown in the schematic diagram, an island with a structure having an angular change of ~7.6° in the middle of the WS2/WSe2 interface was selected. This angular change is thought to be due to the confluence of islands that grew in different plane directions during the growth of WS2. The existence of a GB was confirmed, as shown by the red line in the figure. (see Supplementary Fig. 2 for more detail). Using this GB, detailed experiments were conducted to study the effects of such local structures on exciton dynamics.
a Optical microscope image of the sample setup, and a schematic illustration of the sample showing the structure of the area surrounded by the square frame in the optical image. After growing a threefold-symmetric WS2 structure, a WSe2 structure is grown around it18. In the schematic illustration, the Au electrode on WS2 is transparent. The pale-yellow areas above and below the Au electrodes are Au thin films of different thicknesses. The left and right sides of the SiO2/Si regions are shadows due to the Au thin films on the outside. b Schematic of the measurement setup. c, STM topography image acquired at the WSe2/WS2 heterointerface, which position is shown in a with a green square. d Line profiles along AB and CD in c. The ripple structure is clearly shown in the WS2 area. e Fluorescence spectrum measured in each region of WSe2 and WS2 (excitation wavelength 532 nm, spot diameter 2 μm, excitation power 2.5 mW). Measured positions are marked in a with a red (WSe2) and a blue (WS2) circles, respectively. The spectrum for WS2 (blue curve) can be divided into two peaks (pink and light blue curves) with different intensity by fitting.
Reflecting the ambipolar field effect transistor (FET) characteristics of the WS2/WSe2 structure, it is an off state when the gate-source voltage is 0 V under the dark condition. Since excitons are unstable in conventional three-dimensional semiconductors such as GaAs, the dynamics of photoexcited carriers were measured by observing the current change due to photoexcitation. However, in TMDCs, since excitons are stable, it is necessary to separate their dynamics from those in dark current upon photoexcitation. In addition, to prevent complexity due to the presence of trions, etc., the measurement was performed under a gate-source voltage of 0 V, resulting in almost no free carriers. In the presence of free carriers, the band bending is reduced due to the effect of surface photovoltage, and the material bandgap should appear in I-V curves. However, as shown in Supplementary Fig. 3, such phenomena were not observed, supporting that the effect of free carriers are not dominant in this case.
Figure 2c, d respectively show the STM topography image acquired at the WS2/WSe2 heterointerface and the line profile along AB and CD in the image. The WSe2 region is relatively flat with a height roughness of ~0.3 nm, which corresponds to the roughness of the SiO2/Si substrate. On the other hand, ripple structures with various amplitudes in the range of 0.3–1.2 nm were observed in the WS2 region. It has been reported that such ripple structures are spontaneously/artificially formed in a TMDC single layer21,22 (see Methods). It has also been reported that the modulation of the electronic state structure by stress greatly affects the excitonic characteristics23,24.
First, to confirm the state of the sample, the fluorescence spectrum was measured in each region of WS2/WSe2 as shown in Fig. 2e. As a result of Lorentz function fitting, the peak center and full width at half maximum (FWHM) were obtained to be 1.74 and 0.085 eV for WSe2 (black line), and 1.97 and 0.10 eV for WS2 (blue line), respectively. The peak center positions were roughly in agreement with previously reported results25. The fluorescence intensity of WS2 was about eight times higher than that of WSe2. On the SiO2 substrate, the dielectric constant of the sample fluctuates due to substrate roughness and the impurity distribution. Excitons gather at the local minimum potential area generated by the interaction with the substrate. Therefore, at higher density regions, EEA in the non-radiative process is actively generated, suppressing PL26.
In the WSe2 area, WSe2 contacts the substrate over the entire interface, but in the WS2 area, the contact points are reduced due to the ripple structure. Therefore, WSe2 has a greater influence from the substrate, and PL is greatly suppressed. These are in good agreement with the observed difference in PL intensity27. Since such ripples spatially modulate the stress, the bandgap should be modulated accordingly. We also carried out fitting analysis on the PL spectra. As shown in Fig. 2e, the WSe2 signal remained in one peak, which directly shows the effect of trions is not dominant, while the WS2 signal was separated into two peaks (pink and light blue). Considering each peak as a signal from the suspended and contact areas, the results correspond well with the previous ones27. The energy position of the contact component (pink peak) depends on the effect of the substrate. So far, exciton manipulation and PL enhancement by using a relatively large ripple structure of μm order created mechanically have been proposed28. Therefore, in this experiment, the PL enhancement in WS2 may occur even with ripples on the order of 10 nm22. However, it is difficult to detect complex exciton dynamics in nanostructures with a high spatial resolution by optical methods, which is an important new possibility of our method.
Analytical model of exciton measurement by MP-STM
First, we investigate the mechanism of exciton dissociation with a high binding energy by the electric field generated by the bias voltage applied between the STM tip and the sample (see Supplementary Fig. 3 and its explanations). In a weak electric field, the photocurrent is determined by the dissociation rate of the densest ground-state excitons29,30. Therefore, it is expected that the origin of the tunnel current It can be explained by the mechanism of excitons dissociation under the STM tip. We assumed the following simple model:
Here N (t) is the exciton density at a certain time t, Γ(t) is the exciton dissociation rate, tpass is the time required for excitons to pass through the region under the STM tip where the electric field is applied, S is the dissociation probability (see Methods). One-dimensionally, tpass can be considered to be tpass = w/v, where v is the average exciton velocity and w is the width of the region in the sample where the electric field is applied by the STM tip. Also, v can be derived from the following equation for the diffusion coefficient D31:
Here, τ is the momentum scattering time, which is ~ 100 fs at 80 K31. D is affected by various factors (board, temperature, exciton density, etc.). Calculation, using D = 0.5 cm2/s for WSe2/hBN under weak excitation by continuous light32, gives v ~ 3.16 × 104 m/s.
On the other hand, to obtain w, an evaluation using GBs in the WS2 region was performed. Figure 3a shows an STM topographic image and images of currents Is and Id flowing into the source and drain electrodes on the sample, respectively (Vs = −6 V, Iset = 5 pA). Figure 3b shows a schematic diagram of the relationship between the STM tip position and the current obtained at the source and drain electrodes. Assuming that the GB region consists of a thin, one-dimensional, high-resistance structure, when the distance between the STM tip and the GB is sufficiently large, the photocarriers that separate immediately below the STM tip flow to only one of the easily accessible electrodes. In contrast, when the STM tip approaches the GB, a strong electric field induced by the STM tip is applied over the GB region. Therefore, even when the STM tip is on the source (drain) electrode side of the GB, exciton dissociation occurs on the GB, and the drain (source) current is detected.
a STM topographic image and images of currents Is and Id flowing into of the source and drain electrodes on the sample (Vs = −6 V, Iset = 5 pA), respectively. Each image consists of 128 horizontal line scans. The light spot size was about 20 μm and the area was illuminated almost entirely. No apparent overlayers with a triangular shape were not observed in the illuminated area. Red triangles indicate the left side edge. See Supplementary Fig. 2 about the GB structures. b Schematic diagram of the relationship between the STM tip position and the current obtained at the source and drain electrodes. c Steplike change and the spatial derivative obtained from the plot of Is in a. The values were averaged over a ±15 nm area from the interface. d, e Electric field and exciton binding energy dependences of S for WS2 and WSe2, respectively. f Cross-sections along the broken lines shown in d (Eb = 0.28 eV) and e (Eb = 0.31 eV).
In the STM topographic image shown in Fig. 3a, the GB appears to be wide, but as can be seen from the Is and Id images, the amount of current clearly changes on the right side, indicating that the right edge has a high resistance and becomes the turning point. The three images in Fig. 3a were obtained by 128 horizontal line scans of the STM tip from bottom to top. Figure 3c shows the cross-section (steplike dashed line) obtained from the Is image in Fig. 3a and its spatial derivative (red line). To obtain the cross-section, we averaged the vales of 128 lines with the following manner. The right edge of the GB, turning point, is not straight but has a zigzag shape as shown in the Is image. Therefore, the 128 lines were first adjusted so that the locations with Is = 2.8 pA, which almost correspond to the flexion point of each line around the edge, matched each other. Then, the values of Is for the 128 lines were averaged to obtain the cross-section shown in Fig. 3c.
As a result of estimating the transition width, an FWHM of 2.5 nm was obtained, indicating that the spatial resolution of our system is in the 1 nm order. tpass ~80 fs was obtained as the time required for excitons to pass through this region with a velocity of v ~ 3.16 × 104 m/s.
To obtain the exciton dissociation rate Γ, we referred to the dissociation rate of ground-state excitons under a weak in-plane electric field (<50 V/μm) obtained by Høgni et al. using weak-field asymptotic theory29. When a TMDC membrane is sandwiched by dielectrics placed on its top and bottom, the binding energy of excitons is changed by dielectric screening. The relationship between Γ and the binding energy of excitons is as follows.
Here μ is the reduced mass of excitons, which was taken from ref. 33. ε = (εa + εb)/2 is the average relative permittivity of the upper side (εa) and lower side (εb) of the TMDC membrane. W0 depends on the in-plane electric field and is called the field factor, Eb is the scaled binding energy of a ground-state exciton, and E is the in-plane electric field. g0, called the asymptotic coefficient, is derived from an unperturbed ground state at the distance of infinity. The exciton binding energy and the electric field dependences of S (=(1 − exp (−Γ tpass)), derived from Eqs. (1) to (3) using tpass ~80 fs and Γ, calculated for WSe2 and WS2 are shown in Fig. 3d, e, respectively.
Exciton dissociation tends to be more difficult in WS2 than in WSe2, higher electric field is necessary for the former to dissociate the excitons with the same binding energy, as shown in Fig. 3d, e, which is considered to be due to the sensitivity of the material dependence of g0 in Eq. (3). Therefore, it changes sensitively with the material (see Supplementary Fig. 4 for details).
Assuming ε = 2.4 (εa = 1 as vacuum, εb = 3.8 as SiO2), the binding energies Eb of the excitons of WSe2 and WS2 are obtained as 0.28 eV and 0.31 eV29, respectively. Figure 3f shows cross-sections along the broken lines shown in Fig. 3d, e corresponding to those values. From the intersections of the broken lines and the horizontal axis in the figure, the threshold electric fields are obtained as 35 (WSe2) and 40 MV/m (WS2). These values are in good agreement with those in the previous paper30. Assuming that these electric fields are applied to the region directly under the STM tip (~2.5/2 = 1.25 nm from Fig. 3c), the threshold voltages for dissociating excitons on the nanoscale are directly analyzed as ~44 mV (WSe2) and ~50 mV (WS2), respectively.
Confirmation of EEA process by TR-MP-STM measurement
Next, to investigate exciton dynamics in detail, time-resolved measurement was performed using the optical pump-probe MP-STM system shown in Fig. 1 and Supplementary Fig. 1. First, it was investigated whether the EEA effect could be measured as the process of decay of excitons. The measurement was performed on the WSe2 side, which was not affected by the ripple structure and showed a strong EEA effect.
Figure 4a shows schematic illustrations of the EEA dynamics. In this sample and the temperature condition, the exciton lifetime due to direct recombination is of ns order3. Therefore, to suppress the effect of long-lived components on the time-resolved spectrum, for example, the process by which residual excitons are further excited34, experiments were conducted with the laser repetition rate of frep = 1 MHz here. The measurement conditions were Vs = +6 V and Iset = 1 pA, and, as shown in Fig. 4b, the measurement was performed for ~160 ps while changing the light intensity (6, 12, and 24 μJ/cm2). It is known that dynamics due to the EEA process shown in Fig. 4a6,26 are produced in this time scale, namely, rapidly changing components were observed on the ps scale, corresponding to the EEA process measured by the optical pump-probe method.
a Schematic illustrations of exciton-exciton annihilation dynamics. b TR-MP-STM signals obtained in the WSe2 region for the fluences of 6, 12, and 24 μJ/cm2. Vs = +6 V, Iset = 1 pA, and frep = 1 MHz. c Mapping of S for changes in exciton density and exciton binding energy. d Cross sections along the three lines in c. The measurements were performed at the same place as the PL measurement, indicated by the red triangle in Fig. 2a. The heterostructure interface was not exposed to light.
Since TR-STM combined with the optical pump-probe method uses the absorption bleaching mechanism, the average current decreases with decreasing delay time35. Therefore, in this setup, as the delay time approaches zero, the time-resolved signal
is expected to increase in the negative direction. However, as shown in Fig. 4b, the obtained time-resolved signal ΔI increased in the positive direction as the delay time approached zero. To understand the results, a new mechanism is required to explain the increase in ΔI with decreasing delay time, and the higher exciton density, different from the absorption bleaching mechanism.
One possibility is to consider the following two points in this case: (1) The effect of absorption bleaching is not so large. (2) The probability of dissociation depends on the density of excitons and has a threshold. As a result, I (td) decreases with td (see Supplementary Fig. 5 for details). It has been reported that the binding energy of excitons is reduced by the screening effect of the excitons themselves photogenerated in a single-layer WS2 sample36. On the other hand, the value of S derived from Eq. (1) also increases significantly with decreasing exciton binding energy. Using the relationship between the change in exciton binding energy with changing exciton density36, the change in S with changing binding energy shown in Fig. 3d can be expressed as shown in Fig. 4c. Figure 4d shows the relationship along the three lines in Fig. 4c. As the exciton density increases, S increases non-linearly, and when the delay time is short and the instantaneous exciton density is large, a larger current due to exciton dissociation can be obtained. The exciton density shown here is in good agreement with the order of the excitation intensity used in this experiment.
We analyze the experimental results by the EEA mechanism26,37,38. The rate equation can be written as
where, N (t) is the exciton density, N(0) = N0, γ is the EEA rate, and τ is the exciton recombination lifetime.
For times shorter than τ, Eq. (6) can be written as
giving
In the region of t << τ, the exponential decay appears as a straight line. Therefore, we introduced the following function and analyzed the signals shown in Fig. 4b (td > 2 ps was considered here).
By fitting the spectra for 6, 12, 24 μJ/cm2 in Fig. 4b with parameters A, B, and C, t0 was obtained as 14.6 ± 1.0, 10.8 ± 0.5, and 4.58 ± 0.29 ps, respectively. On the other hand, the light absorption rate of WSe2 at a wavelength of 600 nm was estimated to be ~3% was applied39. Thus, N0 was obtained as 5.5 × 1011, 1.1 × 1012, and 2.2 × 1012 cm−2 for light intensities of 6, 12, and 24 μJ/cm2, respectively. It has been reported that the ps-scale EEA process predominates in the exciton density range of 1011–1013 cm−2 in a TMDC atomic layer on a thermally oxidized SiO2 substrate26. Using these values, γ was determined to be 0.10 ± 0.02 cm2s−1, in good agreement with 0.12 cm2s−1 obtained by the time-resolved PL of WS2/SiO226.
This is the first ever detection of exciton dynamics using the mechanism of exciton dissociation in the nm order region below the STM tip using TR-MP-STM. The spatial resolution of the time-resolved STM (~2.5 nm) greatly exceeds that of conventional ultrahigh-speed time-resolved measurement methods such as the optical pump-probe method11, time-resolved PL10, time-resolved PEEM12, and scanning near-field optical microscope13 methods (several tens of nm).
Time-resolved STM measurement on ripple structure
It was shown that the dynamics of the EEA process in the high-density state, which is the characteristic of exciton dynamics in low-dimensional systems, can be measured by TR-MP-STM. Next, to show the high usefulness of this method, TR-MP-STM measurements were performed on the nanostructures, ripples and GBs, which are characteristic of this sample.
Figure 5a shows a schematic diagram of the nanoscale ripple structure observed in Fig. 2c. Figure 5b shows an STM image taken over a ripple area in WS2 (top figure), and the time-resolved signals acquired at the corresponding tip positions with a color scale (bottom figure). While the STM tip was moved one-dimensionally across the ripple, it was stopped every 2.6 nm, and a delay time scan was performed five times for 2 ns to obtain the time-resolved spectrum at each STM tip position. The STM conditions were Vs = −3.5 V and Iset = 40 pA.
a Schematic of nanoscale ripple structure observed in Fig. 2c. Vs = −3.5 V, Iset = 40 pA, frep = 80 MHz, fluence 13 μJ/cm2 and center wavelength 633 nm. b STM image taken over a ripple area in WS2 and the time-resolved signal acquired at the corresponding tip position on a color scale. c TR-MP-STM signal obtained along the red and blue lines in b. d Cross section along the green line in the STM image (upper figure in b), and the variation in the time constant for the corresponding position (lower figure in b). e Schematic diagram of the principle of spatially changing exciton dynamics. The error bars in d are the errors obtained with the fitting shown in c.
Figure 5c shows the data obtained at typical points shown by the red (top area) and blue (bottom area) dashed lines in Fig. 5b. In the time scale larger than 100 ps, the EEA process due to the high-density state immediately after excitation is approximately completed, and the recombination relaxations of thermalized exciton and exciton migration mainly occur. In fact, single-component exponential fittings matched the data well in this region, and the lifetimes were 2.41 ± 0.12 and 0.50 ± 0.01 ns for the top and bottom regions, respectively. The drive limit of the mechanical delay stage of our present system is 2 ns. In this experiment, we reduced the light intensity by 1/100 compared to that used in ref. 40 to reduce the free carriers’ influence and investigate the excitons’ dynamics. Therefore, to increase the signal-to-noise ratio, we introduced a new modulation method instead of thinning out the pulsed light using a Pockels cell as in the case of the previous paper (details are shown in Supplementary Fig. 1). Although fitting looks good, we need to use another approach, including the previous method40, when discussing longer lifetimes in more detail. Since that is not the case here, we leave this issue for future works.
Figure 5d shows the cross section along the green line in the STM image in Fig. 5b and the relaxation time constant obtained at each location. If the fitting error exceeded 50% of the extracted value, it was removed from the data. It was clarified that the top region of the ripple structure has a long lifetime of ns order, and the bottom region has a short lifetime of 100 ps order. In addition, the exciton lifetime tended to be particularly long in the top region of the ripples with a small width and height appearing at x < 42 nm.
Next, the origin of these phenomena will be discussed. Figure 5e shows a schematic diagram of the principle of spatially changing exciton dynamics. There are three possible effects of the substrate. (1) Fluctuations in exciton density: Excitons accumulate where the bandgap is locally reduced by the roughness of the substrate26. (2) Screening: The radius of excitons increases, thereby increasing the distance over which two excitons interact41. (3) Interaction of the substrate with phonons42. (1) and (2) affect the fast decay component due to the EEA effect. In fact, as shown in Fig. 5c, the EEA effect can be seen even in the low current (low density) region at the bottom (blue line). On the other hand, the slow decay component after the EEA effect has decreased is expected to have a shorter lifetime if the effect of (3) is present. This was confirmed as being due to the difference in lifetime measured at the top and bottom locations of the ripple.
From the viewpoint of STM measurement, it is considered that the binding energy of excitons becomes smaller, and dissociation due to an electric field becomes easier. Therefore, the measured current becomes larger in the bottom region. In fact, consistent results were obtained (Supplementary Fig. 6).
Furthermore, the exciton lifetime depends on the size of the ripple, as shown in Fig. 5d, as described above. The reason for the long exciton lifetimes in the top region of the ripples with small width and height is considered to be as follows. The following equation expresses the maximum accumulated stress for a ripple28.
Here, σ is Poisson’s ratio (WS2: 0.18), t is the film thickness, h is the ripple height, and λ is the ripple width. The maximum stress is inversely proportional to the ripple width. In addition, it has been reported that the band structure changes from a direct to an indirect transition type43. Smaller ripples may have a longer lifetime owing to similar effects.
TR-MP-STM measurement at a grain boundary
The effect of defect levels existing in the GBs was investigated. The defects in GBs are considered to enhance the recombination over a region of about 5 nm from the GB44,45. This phenomenon cannot be confirmed with the resolution of PL (~several tens of nm), and we attempted to confirm it with TR-MP-STM. In the region of WS2 containing a GB shown in Fig. 3a, TR-MP-STM maps were obtained for delay times of 1, 10, 100, 500, 1000, and 1950 ps together with a topographic image of the region with frep of 80 MHz. 1950 ps is the limit of the delay time of our system used here. The results are shown in Fig. 6a, where the values in the image obtained for 1950 ps was subtracted from the other images.
a STM image corresponding to the area shown in Fig. 3a and TR-MP-STM measurement results obtained over the surface for the delay times of 1, 10, 100, 500, 1000, and 1950 ps. 1950 ps is the limit of the delay time of our system used here. Here, the values in the image obtained for 1950 ps was subtracted from the other images. The measurement conditions were Vs = −3 V, Iset = 10 pA, fluence 13 μJ/cm2 and center wavelength 633 nm, and the excitation energy was adjusted to the peak of the exciton resonance spectrum of WS2. b TR-MP-STM spectra obtained in the white square shown in a. x indicates the distance from the boundary. The 56 spectra for each x were averaged. Lifetimes obtained by fitting are shown in each figure. c Lifetime as a function of x. As can be seen in Fig. 3a, Id was measured when the probe was in the area to the right of the right GB edge. Therefore, to reduce the influence of the structures in GB, this measurement was performed on the right side of the GB edge. The error bars in b are the standard deviation of the 56-point values in the y direction at each x point in the white square shown in a. The error bars in c are the fitting errors obtained in b.
The time-resolved measurements in Fig. 6a were performed over the entire surface in the figure at each pixel of 2 nm (x-direction) × 0.3 nm (y-direction). In the area surrounded by the white square around the boundary of 10 nm (x-direction from the boundary) × 16.8 nm (y-direction), 5 (=10/2) × 56 (=16.8/0.3) time-resolved spectra were measured for x = 0, 2, 4, 6, and 8 nm. The 56 spectra for each x were averaged, and the results are shown in Fig. 6b. Fitting was performed by a single exponential function using all the data before averaging.
As shown in Fig. 6a, the obtained time-resolved signal was not uniform, and fluctuations were observed on a scale of about 10 nm. This is because the exciton binding energy changes non-uniformly with the change in the dielectric constant, which is related to the roughness of SiO2 used as the substrate and the residual impurities induced by the resist treatment. Figure 6c summarizes the results shown in Fig. 6b. The lifetime changes over the 8 nm, with the spatial resolution of 1 nm order, was observed, for the first time. Similar effects of GB have been reported in previous papers44,46. The defects in GBs are considered to enhance exciton recombination over a region of about 5 nm from the GBs. The band structure was observed to be modulated continuously over ~5 nm around a grain boundary (GB). As can be seen in Fig. 3a, Id was measured when the probe was in the area to the right of the right GB edge. Therefore, to reduce the influence of such structures in GB, the measurements were performed on the right side of the GB edge.
There is another possibility in the present case. The effect of the ripple structure was confirmed, as shown in Fig. 5. Since the edge of the GB is zigzag and disordered, the modulation of the ripple structure may have an influence on the exciton dynamics (see Supplementary Fig. 2 for more details). To analyze that, we measured the cross-sections around the GB edge, which is summarized in Supplementary Fig. 7. As the results show, the ripple structure is distorted near the GB, supporting its effect on the lifetime of the excitons. Since the GB edge has a disordered structure with a narrow width, it was difficult to stably measure I-V curves under laser irradiation in the 10 nm region. To clarify the mechanism in more detail, further study is needed, which we would like to leave for a future work.
We have developed a time-resolved multiprobe STM (TR-MP-STM) method by combining multiprobe STM with a new delay time modulation approach of pump-probe optics. First, we clarified the principle of STM measurement to probe neutral excitons. Then, using this system, we succeeded in evaluating the spatiotemporal dynamics of excitons in nanostructures such as ripples and GBs in monoatomic-layer semiconductors with a spatial resolution of 1 nm order. In the WSe2 region, the rate of the EEA process induced by collisions between excitons was determined to be 0.10 ± 0.02 cm2s−1. Subsequently, exciton dynamics in the nanoscale ripple structures was revealed. It was also directly observed that the exciton dynamics is modulated by local defects. Exciton recombination lifetime changed near a GB over a region about 8 nm, which agreed well with the modulation of the ripple structure near the GB edge.
This method is expected to accelerate research on exciton dynamics and the development of applications directly based on the analysis of experimental results of nanoscale.
Methods
Newly developed delay time modulation method
A schematic diagram of the TR-MP-STM system is shown in Supplementary Fig. 1a. The wavelength of Ti: sapphire laser pulse (pulse time width ~150 fs, wavelength 830 nm, repetition rate 80 MHz) is converted by an optical parametric oscillator (OPO) (~400 fs, 633 nm). The beamline is divided into two by an unpolarized half mirror, and a delay time scan of up to ~2 ns can be performed by a mechanical delay stage mounted on one of the optical paths (Path 1). In the other optical path (Path 2), an EOM and a Faraday rotator are used to change the polarization. Delay-time modulation is achieved by switching between two optical paths (Path 2-1, Path 2-2). Supplementary Fig. 1b shows the principle of new delay time modulation shown in the blue shaded area in Supplementary Fig. 1a. The newly developed MPSTM part for time-resolved measurement also has its own novel structure (See Supplementary information for more details).
Explanation of Eq. (1)
While excitons pass through the electric field (t = 0 − tpass), they are dissociated and measured as tunnel current. Since the dissociation rate is Γ, the rate equation at which n excitons in the electric field dissociate is shown as dn/dt = −Γ·n, and the probability that one exciton dissociates during tpass becomes (1 − exp (−Γ·tpass)). Therefore, the tunnel current It obtained by dissociating the N excitons diffused immediately below the probe every second is proportional to N · S = N · (1 − exp (−Γ·tpass)).
Multiprobe STM for time-resolved measurement
As shown on the left of Fig. 1a and Supplementary Fig. 1a, an optical zoom lens was placed on the multiprobe measuring unit40,47. This system can mount up to four STM/AFM probes, and the position of the probe tip can be determined with μm accuracy by observing the optical image using a CCD camera. Therefore, it is possible to access the desired location of the isolated two-dimensional sample on the insulating substrate and perform STM/AFM measurement. In addition, a half mirror is installed inside the zoom lens, and the laser can be focused at the desired position on the sample through the objective lens, making it an ideal system for TR-STM measurements. To easily perform preliminary experiments such as STM observation and light-modulated scanning tunneling spectroscopy (LM-STS) measurement48, the optical path can be switched by the flip mirror in front of the zoom lens so that continuous laser light is used instead of pulsed light.
In this experiment, instead of using AFM probes in direct contact with the sample as before40, two Au electrodes were prepared on the sample. Then, two Pt-coated conductive cantilevers (spring constant 0.2 Nm−1) were mechanically brought into contact with the Au electrode and used to apply the sample bias voltage Vs. In this state, one STM tip was made approach the sample and performed various measurements. In addition, to combine STM with photoexcitation, we developed a holder with an elaborate structure to prevent the measured part from being in the shadow of the probe. The time-resolved signal ΔI was detected by a lock-in amplifier using the periodic change in the voltage used for EOM modulation as a reference. All experiments were performed under ultrahigh vacuum (~10−7 Pa) at a temperature of 85 K.
Besides, the time-resolved data are obtained immediately below the STM tip because excitons are dissociated by the bias voltage applied between the STM tip and sample. Since STM has an atomic-level resolution, we can observe and examine the area we choose for experiments before measurement. In the ripple measurement in Fig. 5, for example, excitons are confined to each region. Therefore, the result of the time-resolved measurement is obtained without the influence from the adjacent structure.
Origin of ripple structure in WSe2 region
The stress generated at the heterointerface in the WSe2/WS2 plane due to the lattice constant mismatch should generate tensile stress on WS2, which does not correspond to this ripple structure49. It has been reported that a ripple structure was formed when the GBs in single-layer MoS2 on a sapphire substrate were irradiated with light. However, in that case, the ripple period coincided with the step period of the substrate, and the interaction between the MoS2 layer and the substrate step was considered to be the cause22. On the other hand, in this case, the substrate was SiO2/Si and unrelated to the step period. According to a previous report of calculation, the ripple structure is formed spontaneously50, which have occurred in this study, However, the details of its formation are beyond the scope of this paper.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
References
Grosso, G. et al. Excitonic switches operating at around 100K. Nat. Photonics 3, 577–580 (2009).
Britnell, L. et al. Strong light-matter interactions in heterostructures of atomically thin films. Science 340, 1311–1314 (2013).
Robert, C. et al. Exciton radiative lifetime in transition metal dichalcogenide monolayers. Phys. Rev. B 93, 205423 (2016).
Wang, G. et al. Colloquium: excitons in atomically thin transition metal dichalcogenides. Rev. Mod. Phys. 90, 021001 (2018).
Zhu, Z. et al. Excitonic resonant emission-absorption of surface plasmons in transition metal dichalcogenides for chip-level electronic-photonic integrated circuits. ACS Photonics 3, 869–874 (2016).
Kumar, N. et al. Exciton-exciton annihilation in MoSe2 monolayers. Phys. Rev. B 89, 125427 (2014).
Cordovilla Leon, D. F., Li, Z., Jang, S. W., Cheng, C.-H. & Deotare, P. B. Exciton transport in strained monolayer WSe2. Appl. Phys. Lett. 113, 252101 (2018).
Moon, H. et al. Dynamic exciton funneling by local strain control in a monolayer semiconductor. Nano Lett. 20, 6791–6797 (2020).
Qiu, D. Y., da Jornada, F. H. & Louie, S. G. Optical spectrum of MoS2: many-body effects and diversity of exciton states. Phys. Rev. Lett. 111, 216805 (2013).
Kulig, M. et al. Exciton diffusion and Halo effects in monolayer semiconductors. Phys. Rev. Lett. 120, 207401 (2018).
Cui, Q., Ceballos, F., Kumar, N. & Zhao, H. Transient absorption microscopy of monolayer and bulk WSe2. ACS Nano 8, 2970–2976 (2014).
Wang, L., Xu, C., Li, M. Y., Li, L. J. & Loh, Z. H. Unraveling spatially heterogeneous ultrafast carrier dynamics of single-layer WSe2 by femtosecond time-resolved photoemission electron microscopy. Nano Lett. 18, 5172–5178 (2018).
Plankl, M. et al. Subcycle contact-free nanoscopy of ultrafast interlayer transport in atomically thin heterostructures. Nat. Photonics 15, 594–600 (2021).
Terada, Y., Yoshida, S., Takeuchi, O. & Shigekawa, H. Real-space imaging of transient carrier dynamics by nanoscale pump–probe microscopy. Nat. Photonics 4, 869–874 (2010).
Yoshida, S. et al. Probing ultrafast spin dynamics with optical pump-probe scanning tunnelling microscopy. Nat. Nanotechnol. 9, 588–593 (2014).
Yoshida, S. et al. Terahertz scanning tunneling microscopy for visualizing ultrafast electron motion in nanoscale potential variations. ACS Photonics 8, 315–323 (2021).
Li, S. et al. Halide-assisted atmospheric pressure growth of large WSe2 and WS2 monolayer crystals. Appl. Mater. Today 1, 60–66 (2015).
Wada, N. et al. Efficient and chiral electroluminescence from in‐plane heterostructure of transition metal dichalcogenide monolayers. Adv. Funct. Mater. https://doi.org/10.1002/adfm.202203602 (2022).
Kobayashi, Y. et al. Continuous heteroepitaxy of two-dimensional heterostructures based on layered chalcogenides. ACS Nano 13, 7527–7535 (2019).
Chen, S. et al. Tip-based cleaning and smoothing improves performance in monolayer MoS2 devices. ACS Omega 6, 4013–4021 (2021).
Luo, S. et al. Formation of ripples in atomically thin MoS2 and local strain engineering of electrostatic properties. Nanotechnology 26, 105705 (2015).
Liu, H. & Chi, D. Dispersive growth and laser-induced rippling of large-area singlelayer MoS2 nanosheets by CVD on c-plane sapphire substrate. Sci. Rep. 5, 11756 (2015).
Dhakal, K. P. et al. Local strain induced band gap modulation and photoluminescence enhancement of multilayer transition metal dichalcogenides. Chem. Mater. 29, 5124–5133 (2017).
Lee, J. et al. Switchable, tunable, and directable exciton funneling in periodically wrinkled WS2. Nano Lett. 21, 43–50 (2021).
Zhao, W. et al. Evolution of electronic structure in atomically thin sheets of WS2 and WSe2. ACS Nano 7, 791–797 (2013).
Hoshi, Y. et al. Suppression of exciton-exciton annihilation in tungsten disulfide monolayers encapsulated by hexagonal boron nitrides. Phys. Rev. B 95, 241403 (2017).
Yu, Y. et al. Engineering substrate interactions for high luminescence efficiency of transition-metal dichalcogenide monolayers. Adv. Funct. Mater. 26, 4733–4739 (2016).
Castellanos-Gomez, A. et al. Local strain engineering in atomically thin MoS2. Nano Lett. 13, 5361–5366 (2013).
Kamban, H. C. & Pedersen, T. G. Field-induced dissociation of two-dimensional excitons in transition metal dichalcogenides. Phys. Rev. B 100, 045307 (2019).
Massicotte, M. et al. Dissociation of two-dimensional excitons in monolayer WSe2. Nat. Commun. 9, 1633 (2018).
Glazov, M. M. Quantum interference effect on exciton transport in monolayer semiconductors. Phys. Rev. Lett. 124, 166802 (2020).
Wagner, K. et al. Nonclassical exciton diffusion in monolayer WSe2. Phys. Rev. Lett. 127, 076801 (2021).
Olsen, T., Latini, S., Rasmussen, F. & Thygesen, K. S. Simple screened hydrogen model of excitons in two-dimensional materials. Phys. Rev. Lett. 116, 056401 (2016).
Shang, J. et al. Observation of excitonic fine structure in a 2D transition-metal dichalcogenide semiconductor. ACS Nano 9, 647–655 (2015).
Yokota, M. et al. Bases for time-resolved probing of transient carrier dynamics by optical pump-probe scanning tunneling microscopy. Nanoscale 5, 9170–9175 (2013).
Cunningham, P. D., Hanbicki, A. T., McCreary, K. M. & Jonker, B. T. Photoinduced bandgap renormalization and exciton binding energy reduction in WS2. ACS Nano 11, 12601–12608 (2017).
Suna, A. Kinematics of exciton-exciton annihilation in molecular crystals. Phys. Rev. B 1, 1716–1739 (1970).
Sun, D. et al. Observation of rapid exciton–exciton annihilation in monolayer molybdenum disulfide. Nano Lett. 14, 5625–5629 (2014).
Li, Y. et al. Measurement of the optical dielectric function of monolayer transition-metal dichalcogenides: MoS2,MoSe2,WS2,and WSe2. Phys. Rev. B 90, 205422 (2014).
Mogi, H. et al. Development of laser-combined scanning multiprobe spectroscopy and application to analysis of WSe2/MoSe2 in-plane heterostructure. Appl. Phys. Express 12, 045002 (2019).
Stier, A. V., Wilson, N. P., Clark, G., Xu, X. & Crooker, S. A. Probing the influence of dielectric environment on excitons in monolayer WSe2: insight from high magnetic fields. Nano Lett. 16, 7054–7060 (2016).
Nie, Z. et al. Tailoring exciton dynamics of monolayer transition metal dichalcogenides by interfacial electron-phonon coupling. Commun. Phys. 2, 103 (2019).
Wang, Y. et al. Strain-induced direct–indirect bandgap transition and phonon modulation in monolayer WS2. Nano Res. 8, 2562–2572 (2015).
Liu, X., Balla, I., Bergeron, H. & Hersam, M. C. Point defects and grain boundaries in rotationally commensurate MoS2 on epitaxial graphene. J. Phys. Chem. C 120, 20798–20805 (2016).
Su, W., Kumar, N., Shu, H., Lancry, O. & Chaigneau, M. In situ visualization of optoelectronic behavior of grain boundaries in monolayer WSe2 at the nanoscale. J. Phys. Chem. C 125, 26883–26891 (2021).
Huang, Y. L. et al. Bandgap tunability at single-layer molybdenum disulphide grain boundaries. Nat. Commun. 6, 6298 (2015).
Mogi, H. et al. Ultimate high conductivity of multilayer graphene examined by multiprobe scanning tunneling potentiometry on artificially grown high-quality graphite thin film. ACS Appl. Electron. Mater. 1, 1762–1771 (2019).
Takeuchi, O. et al. Microscopic description of the current–voltage characteristics of a bulk-heterojunction organic solar cell under illumination. Appl. Phys. Express 7, 021602 (2014).
Xie, S. et al. Coherent, atomically thin transition-metal dichalcogenide superlattices with engineered strain. Science 359, 1131–1136 (2018).
Mirõ, P., Ghorbani-Asl, M. & Heine, T. Spontaneous ripple formation in MoS2 monolayers: Electronic structure and transport effects. Adv. Mater. 25, 5473–5475 (2013).
Acknowledgements
We acknowledge the financial supports of a Grant-in-Aid for Scientific Research from Japan Society for the Promotion of Science (17H06088, 20H00341), Japan Core Research Evolutional Science and Technology (CREST) (JPMJCR1875, JPMJCR16F3), and JST, PRESTO (JPMJPR22AA), Japan.
Author information
Authors and Affiliations
Contributions
H.M. developed the system, and took data with R.K., R.M., and J.W. N.W. and Y.M. prepared samples. Y.A., S.Y., and O.T. provided technical advice. H.S. organized and supervised the project and edited the paper with H.M.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Mogi, H., Arashida, Y., Kikuchi, R. et al. Ultrafast nanoscale exciton dynamics via laser-combined scanning tunneling microscopy in atomically thin materials. npj 2D Mater Appl 6, 72 (2022). https://doi.org/10.1038/s41699-022-00345-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41699-022-00345-1
This article is cited by
-
Dynamical control of nanoscale light-matter interactions in low-dimensional quantum materials
Light: Science & Applications (2024)
-
Externally-triggerable optical pump-probe scanning tunneling microscopy with a time resolution of tens-picosecond
Scientific Reports (2023)