Abstract
Contacting two-dimensional (2D) semiconductors with van der Waals semimetals significantly reduces the contact resistance and Fermi level pinning due to defect-free interfaces. However, depending on the band alignment, a Schottky barrier remains. Here we study the evolution of the valence and conduction band edges in pristine and heavily vanadium (0.44%), i.e., p-type, doped epitaxial WSe2 on quasi-freestanding graphene (QFEG) on silicon carbide as a function of thickness. We find that with increasing number of layers the Fermi level of the doped WSe2 gets pinned at the highest dopant level for three or more monolayers. This implies a charge depletion region of about 1.6 nm. Consequently, V dopants in the first and second WSe2 layer on QFEG/SiC are ionized (negatively charged) whereas they are charge neutral beyond the second layer.
Similar content being viewed by others
Introduction
Layered two-dimensional (2D) transition metal dichalcogenide (TMDC) semiconductors are promising beyond silicon materials owing to their attractive optoelectronic properties1,2,3,4 and weak inter-layer coupling that overcomes vital engineering challenges of bulk materials regarding heteromaterial integration and miniaturization. Among potential applications for 2D-TMDCs are stacked nanosheet field effect transistors,5,6 lateral heterojuction diodes7,8,9,10, or photodetectors11,12, which all require high-quality 2D-TMDCs with tunable electronic properties. Hence, huge effort is devoted to establish high-quality scalable production13, controlled doping14,15,16,17,18,19,20,21,22, and optimized electronic contacts23,24,25,26,27,28,29.
In recent years, epitaxial growth of wafer-scale substitutionally doped semiconducting 2D-TMDCs such as MoS2, WS2, and WSe2 has been successfully established using metalorganic chemical vapor deposition (MOCVD). Doping with nonisovalent transition metals such as V21 and Nb30 or Re18,31 and Mn32 yielded the expected p-type or n-type behavior, respectively, but it was noted that dopant ionization energies are significantly higher in the monolayer limit due to strong defect state localization33. Moreover, for metal-TMDC contacts, Fermi level pinning because of metal–induced gap states (MIGS) at the interface or due to disorder-order induced gap states, which originate from vacancies or substitutional defects, reduce the tunability of the Schottky barrier height and results in high contact resistance, thus limiting device performance24,27,28,34,35,36,37. Van der Waals semimetals like graphene or graphite greatly suppress the formation of MIGS owing to their low density of states at the Fermi level while at the same time reducing interface disorder through the absence of dangling bonds.
Here we investigate the layer-dependent valence and conduction band onsets of a prototypical semimetal–TMDC contact formed between multilayer WSe2 grown on quasi-freestanding epitaxial graphene on 6H-SiC(0001) (QFEG/SiC) (Fig. 1a, b). By means of scanning tunneling microscopy and spectroscopy (STM/S) we compare the band onset evolution from 1 to 7 monolayers (ML) between p-type V-doped (0.44%, 4.7 ⋅ 1012 cm−2) and nominally undoped WSe2. For the V-doped WSe2 we find that the Fermi level is pinned to the defect state energy from 3 ML on, whereas the Fermi level resides in the band gap in the mono- and bilayer case, suggesting a charge depletion region of around 1.6 nm.
a Top view of the atomic structure of a single WSe2 layer. b Top: Schematic of multi-layered WSe2 grown on top of QFEG/SiC(0001) viewed from the side. Bottom: Illustration of the band alignment of multi-layered V-doped WSe2 on top of QFEG. WD denotes the depletion depth. c, d Large-scale STM image (VB = 1.6 V) of multilayer undoped (c) and V-doped (d) WSe2. The number of WSe2 layers are labelled on both images. e, f Height profiles of undoped (e) and V-doped (f) WSe2 taken along the lines depicted in the respective STM image. Each step in the height profile is around 0.65 nm and corresponds to a change of 1 ML.
Results and discussion
Layer-dependent STS of undoped WSe2
Figure 1c, d show large-scale STM topography images of undoped and V-doped WSe2 samples grown on QFEG/SiC. For both samples multilayer WSe2 regions can be found. After identifying the QFEG and single-layered WSe2 by their distinct STS fingerprints, we determine the number of WSe2 ML by counting the number of discrete steps of 0.65 nm height, as depicted in the height-profiles shown in Fig. 1e, f.
Figure 2 summarizes the layer-dependent STM/STS results obtained for undoped WSe2. As exemplarily shown in the STM image of 1 ML of undoped WSe2 in Fig. 2a, the dominant type of defect that we observe occurs with a density below 0.02% and is identified as molybdenum atoms that substituted W38. As depicted in Fig. 1b, the local density of states of 1 ML undoped WSe2 revealed by STS exhibits distinct valence and conduction band edges with the Fermi level (at zero sample bias VB) close to the center of the 2.34 eV band gap. The layer dependence of the valence and conduction band edges and of the band gap for undoped WSe2 is shown in Fig. 2b, c. Independent of the number of layers, the Fermi level is close to the center of the band gap for undoped WSe2. With increasing number of layers, both, the conduction and the valence band edge of undoped WSe2 move symmetrically toward the Fermi energy, hence lowering the band gap for thicker films due to inter-layer hybridization. The evolution of the band gap with the number of layers is qualitatively in good agreement with previous reports39,40,41.
a STM image of undoped monolayer WSe2 at VB = 1.4 V. b Layer dependent STS signal of undoped WSe2. c The experimentally determined conduction band edge, valence band edge, and band gap of undoped WSe2 as a function of layer count (markers). The experimental data in (c) is fitted with the tight binding model presented in the text (dashed lines). d The energy of each plateau identified in the STS of undoped WSe2 plotted versus the corresponding number of hole band edge n in the quantum well model.
When examining the layer dependent STS data of undoped WSe2 in more detail, we find that for more than 1 ML WSe2 additional steps in the local density of states of the valence band can be seen (Fig. 2b). Such steps are indicative of a staggered DOS as expected for a 2D system42. Hence, our data suggest that every additional layer of WSe2 introduces another electron subband in the valence band spectrum. This behavior has recently also been observed in transport experiments by Takeyama et al.43 and can be described by a tight binding model of weakly coupled 2D quantum wells. Thereby, the weak van der Waals inter-layer coupling is introduced by an inter-layer electron (hole) hopping term te(h). The resulting energies of the nth subband edge is given by: \({E}_{{{{\rm{e(h)}}}}}^{n}={E}_{{{{\rm{e(h)}}}}}-2{t}_{{{{\rm{e(h)}}}}}cos(\frac{n\pi }{N+1})\) where Ee(h) are the conduction (valence) band edges of 1 ML WSe2 and N is the number of layers44. In Fig. 2d, we plot the width of the identified energy plateaus E\({}_{{{{\rm{h}}}}}^{n}\) for 1–7 ML of undoped WSe2. Fitting the quantum well model to the layer dependence of the valence band edge, conduction band edge, and band gap in Fig. 2c, we estimate Eh = −1.05 ± 0.02 eV, Ee = 1.30 ± 0.03 eV, th = 0.29 ± 0.02 eV and te = 0.21 ± 0.02 eV. The derived values for the hopping parameters coincide very well with those reported by Ruiz-Tijerina et al.45 for WSe2 in their k ⋅ p tight binding model theoretically investigating the intersubband transitions.
Layer-dependent STS of vanadium-doped WSe2
After having established that undoped WSe2 exhibits the expected layer-dependence, we focus on V-doped WSe2. In Fig. 3, STM images for different numbers of layers of V-doped WSe2 are shown. When comparing the high-resolution STM images of 1 ML of undoped (Fig. 2a) and 1 ML of V-doped (Fig. 3a) WSe2 taken at positive bias voltage, we observe a high density of localized circular depressions in the STM topography for V-doped WSe2. We identify these depressions as V dopants, because their density of about 0.44% is more than an order of magnitude higher than the density of all impurities observed for undoped WSe2 and both, the STM and STS signatures, coincide with the one we previously reported for V atoms substituting W21. In Fig. 3b–i, the layer-dependent appearance of the V dopants is presented. At negative VB, V dopants in the topmost layer appear as circular protrusions, independent of the number of WSe2 layers. At positive VB on the other hand, the contrast changes from a circular (dark) depression for 1 ML and 2 ML, to a hexagonal (bright) orbital shape from 3 ML and beyond.
a–i STM images of 1 ML (a), 2 ML (b, c), 3 ML (d, e), 5 ML (f, g), and 7 ML (h, i) V-doped WSe2. The blue markers indicate the positions at which the dI/dV spectra shown in Fig. 4a, b have been recorded. VB is indicated in the top right corner in each STM image.
In Fig. 4, we analyze the layer-dependent progression of the local electronic states of the V dopants. We perform STS centered on the V dopants that are in the topmost layer of n-layered WSe2 for n = {1, 2, ..., 7} and compare the results to STS of n-layered undoped and V-doped WSe2 that are recorded as far from vanadium substituents as possible given the high dopant density. The STS results for V-doped WSe2 are shown in Fig. 4a. While the band gap is also narrowing for increasing number of layers, the shift of the band edges is highly asymmetric. Whereas the conduction band onset stays roughly at the same energy, the valence band onset shifts from −1.18 V (1 ML) to −0.12 V (3ML) and converges to ~0 V for larger number of layers. On individual V dopants (Fig. 4b) we observe additional electronic states above the valence band edge as reported in Ref. 21 confirming their p-type character. Like the valence band maximum (VBM) of V-doped WSe2, the localized dopant states progressively shift toward the Fermi level, where they get pinned for 3ML and thicker samples. At the same time, the difference between the highest occupied defect state and the VBM gets smaller, indicating a weakening of the defect state binding energy. The comparison of the layer-dependent band edge evolution and band gap for V-doped WSe2 and undoped WSe2 is summarized in Fig. 4c, d.
a, b STS recorded for 1–3 ML of V-doped WSe2 (a) and of V dopants (b) in the topmost WSe2 layer (blue). The gray lines display the 1 ML data for comparison. The black arrows indicate the positions of the valence and conduction band edges for V-doped WSe2 and of the localized dopant state and the conduction band edge for V dopants. c, d Layer-dependence of conduction and valence band edge (c) and band gap (d) for undoped WSe2 (red), V-doped WSe2 (light blue), and V dopants (dark blue), respectively.
Layer-dependent Schottky contact
The pinning of the valence band edge of V-doped WSe2 can be understood as a Schottky contact where the p-type dopants in the depletion region of two ML are ionized, i.e., negatively charged. For three or more ML, the charge transition level is just below zero bias voltage, hence when scanning the charge–neutral V dopants with negative bias voltage, thus probing the electronic states below the Fermi level, they exhibit the same STM signature as the negatively charged V dopants in the first and second layer V-WSe2 (Fig. 3a, b, d, f, h). However, when probing the V dopants in the third or higher V-WSe2 layer they appear charge–neutral.
At the graphene/TMDC interface, the position of the Fermi level with respect to the TMDC bands is determined by the work function and is essentially the same for doped and undoped WSe2 samples. In the bulk limit, the Fermi level assumes the intrinsic value in the center of the band gap for the undoped TMDC, whereas it gets pinned at the dopant state for the V-doped TMDC, respectively. Here we quantify over how many TMDC layers this transition is happening corresponding to the depletion depth of the Schottky contact. We find that the depletion depth for the technologically relevant 2D–3D interface of layered 0.44% V-doped WSe2 on QFEG/SiC to be between 2 ML and 3 ML, which is between 1.3 nm and 1.95 nm.
In summary, we identified a distinct layer dependence of the electronic structure of pristine and p-type V-doped WSe2 on a QFEG/SiC substrate using STM/S. For pristine WSe2, the band gap narrows symmetrically, with the Fermi level fixed to the center of the band gap. Moreover, we find that each additional WSe2 layer introduces an extra subband in the valence band spectrum. The progression of the conduction and valence band edge for 0.44% V-doped multilayer WSe2 on the other hand exhibits a prototypical Schottky contact behavior. While for monolayer V-doped WSe2 the Fermi level resides close to the center of the band gap, it gets pinned to the highest dopant state upon exceeding 2 ML, corresponding to a depletion depth of about 1.6 nm.
Methods
MOCVD growth of undoped and V-doped WSe2 films
The undoped and V-doped WSe2 samples were synthesized in a custom-designed vertical cold wall gas-source CVD reactor as reported previously in Refs. 17,46. Tungsten hexacarbonyl (W(CO)6) (99.99%, Sigma-Aldrich), hydrogen selenide (H2Se) (99.99%, Matheson), and vanadium (V(C5H5)2) (sublimed, 95% Strem Chemicals) were used as metal, chalcogen, and dopant precursors, respectively, in a 100% H2 ambient.
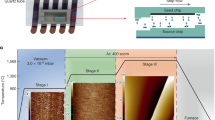
The metal and dopant precursors are kept inside stainless-steel bubblers where temperature and pressure are constantly maintained at 25 °C and 970 mbar, and 40 °C and 970 mbar, respectively. H2Se is supplied from a separate gas manifold. All three precursors are introduced from separate lines to prevent intermixing before reaching the reactor inlet. The growth of undoped and V-doped WSe2 followed the three-step growth reported in Ref. 47, which consists of a nucleation, a ripening, and a lateral growth stage on c-plane sapphire (Cryscore Optoelectronic LTd, 99.95%. ). At all three stages, the growth temperature, pressure, and H2Se flow rate were kept constantly at 800 °C, 930 mbar, and 7 sccm.
For the growth of undoped WSe2, the metal precursor is inserted with a flow rate of 20 sccm for 2 min during the nucleation phase. At the ripening stage, the W(CO)6 flow is switched off and the formed nuclei are annealed in H2Se for 10 min. During the lateral growth phase, W(CO)6 is re-introduced with a constant flow of 4.5 sccm.
For the growth of V-doped WSe2, V(C5H5)2 was additionally inserted simultaneously with W(CO)6 during the nucleation phase with a flow of 60 sccm and with a flow of 5 sccm during the lateral growth phase. The vanadium density was deduced from STM measurements.
Scanning probe microscopy
Undoped and V-doped WSe2 were prepared ex situ on QFEG on SiC substrates followed by a final 450 °C anneal in ultrahigh vacuum. The measurements were performed with a commercial LT STM from Scienta Omicron operated at 5 K and at pressures below 2 ⋅ 10−10 mbar. The tungsten tip was prepared on a clean Au(111) surface (sputtering: 10 min, Ar+, 1 kV; annealing: 10 min, 450 °C) and confirmed to be metallic. STM topographic measurements were taken in constant current mode with the bias voltage given with respect to the sample. STS measurements were recorded using a lock-in amplifier at 860 Hz and a modulation amplitude of 10 mV. The band gap was determined as described in Ref. 48 by fitting the valence and conduction band edge and the band gap intensities of the logarithmic STS data with a line.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Code availability
Upon request, authors will make available any previously unreported computer code or algorithm used to generate results that are reported in the paper and central to its main claims.
References
Kim, S. J., Choi, K., Lee, B., Kim, Y. & Hong, B. H. Materials for Flexible, Stretchable Electronics: Graphene and 2D Materials. Annu. Rev. Mater. Res. 45, 63–84 (2015).
Chhowalla, M., Jena, D. & Zhang, H. Two-dimensional semiconductors for transistors. Nat. Rev. Mater. 1, 1–15 (2016).
Manzeli, S., Ovchinnikov, D., Pasquier, D., Yazyev, O. V. & Kis, A. 2D transition metal dichalcogenides. Nat. Rev. Mater. 2, 1–15 (2017).
Kang, S. et al. 2D semiconducting materials for electronic and optoelectronic applications: potential and challenge. 2D Mater. 7, 022003 (2020).
Radisavljevic, B., Radenovic, A., Brivio, J., Giacometti, V. & Kis, A. Single-layer MoS2 transistors. Nat. Nanotechnol. 6, 147–150 (2011).
Sebastian, A., Pendurthi, R., Choudhury, T. H., Redwing, J. M. & Das, S. Benchmarking monolayer MoS2 and WS2 field-effect transistors. Nat. Commun. 12, 693 (2021).
Duan, X. et al. Lateral epitaxial growth of two-dimensional layered semiconductor heterojunctions. Nat. Nanotechnol. 9, 1024–1030 (2014).
Gong, Y. et al. Two-step growth of two-dimensional WSe2/MoSe2 heterostructures. Nano Lett. 15, 6135–6141 (2015).
Sahoo, P. K., Memaran, S., Xin, Y., Balicas, L. & Gutiérrez, H. R. One-pot growth of two-dimensional lateral heterostructures via sequential edge-epitaxy. Nature 553, 63–67 (2018).
Utama, M. I. B. et al. A dielectric-defined lateral heterojunction in a monolayer semiconductor. Nat. Electron. 2, 60–65 (2019).
Lopez-Sanchez, O., Lembke, D., Kayci, M., Radenovic, A. & Kis, A. Ultrasensitive photodetectors based on monolayer MoS2. Nat. Nanotechnol. 8, 497–501 (2013).
Jayachandran, D. et al. A low-power biomimetic collision detector based on an in-memory molybdenum disulfide photodetector. Nat. Electron. 3, 646–655 (2020).
Kang, K. et al. High-mobility three-atom-thick semiconducting films with wafer-scale homogeneity. Nature 520, 656–660 (2015).
Habib, M. et al. Ferromagnetism in CVT grown tungsten diselenide single crystals with nickel doping. Nanotechnology 29, 115701 (2018).
Yang, L. et al. Ta Doping Enhanced Room-Temperature Ferromagnetism in 2D Semiconducting MoTe2 Nanosheets. Adv. Electron. Mater. 5, 1900552 (2019).
Chu, D. & Kim, E. K. Hole conduction of tungsten diselenide crystalline transistors by niobium dopant. Adv. Electron. Mater. 5, 1800695 (2019).
Kozhakhmetov, A. et al. Scalable BEOL compatible 2D tungsten diselenide. 2D Mater. 7, 015029 (2019).
Kozhakhmetov, A. et al. Scalable Substitutional Re-Doping and its Impact on the Optical and Electronic Properties of Tungsten Diselenide. Adv. Mater. 32, 2005159 (2020).
Yun, S. J. et al. Ferromagnetic Order at Room Temperature in Monolayer WSe2 Semiconductor via Vanadium Dopant. Adv. Sci. 7, 1903076 (2020).
Li, S. et al. Tunable Doping of Rhenium and Vanadium into Transition Metal Dichalcogenides for Two-Dimensional Electronics. Adv. Sci. 8, 2004438 (2021).
Kozhakhmetov, A. et al. Controllable p-type doping of 2d WSe2 via vanadium substitution. Adv. Funct. Mater. 31, 2105252 (2021).
Lin, Y.-C., Torsi, R., Geohegan, D. B., Robinson, J. A. & Xiao, K. Controllable Thin-Film Approaches for Doping and Alloying Transition Metal Dichalcogenides Monolayers. Adv. Sci. 8, 2004249 (2021).
Allain, A., Kang, J., Banerjee, K. & Kis, A. Electrical contacts to two-dimensional semiconductors. Nat. Mater. 14, 1195–1205 (2015).
Retamal, J. R. D., Periyanagounder, D., Ke, J.-J., Tsai, M.-L. & He, J.-H. Charge carrier injection and transport engineering in two-dimensional transition metal dichalcogenides. Chem. Sci. 9, 7727–7745 (2018).
Liu, Y. et al. Approaching the schottky-mott limit in van der waals metal-semiconductor junctions. Nature 557, 696–700 (2018).
Went, C. M. et al. A new metal transfer process for van der waals contacts to vertical schottky-junction transition metal dichalcogenide photovoltaics. Sci. Adv. 5, eaax6061 (2019).
Zhang, X. et al. Near-ideal van der Waals rectifiers based on all-two-dimensional Schottky junctions. Nat. Commun. 12, 1522 (2021).
Park, S. et al. The Schottky-Mott rule expanded for two-dimensional semiconductors: Influence of substrate dielectric screening. ACS Nano 15, 14794–14803 (2021).
Kwon, G. et al. Interaction- and defect-free van der waals contacts between metals and two-dimensional semiconductors. Nat. Electron. 5, 241–247 (2022).
Zhang, K. et al. Tuning transport and chemical sensitivity via niobium doping of synthetic MoS2. Adv. Mater. Interfac. 7, 2000856 (2020).
Zhang, K. et al. Tuning the electronic and photonic properties of monolayer mos2 via in situ rhenium substitutional doping. Adv. Funct. Mater. 28, 1706950 (2018).
Zhang, K. et al. Manganese doping of monolayer MoS2: the substrate is critical. Nano Lett. 15, 6586–6591 (2015).
Zhu, G.-J., Xu, Y.-G., Gong, X.-G., Yang, J.-H. & Yakobson, B. I. Dimensionality-inhibited chemical doping in two-dimensional semiconductors: The phosphorene and MoS2 from charge-correction method. Nano Lett. 21, 6711–6717 (2021).
Sotthewes, K. et al. Universal fermi-level pinning in transition-metal dichalcogenides. J. Phys. Chem. C 123, 5411–5420 (2019).
Shen, P.-C. et al. Ultralow contact resistance between semimetal and monolayer semiconductors. Nature 593, 211–217 (2021).
Rhodes, D., Chae, S. H., Ribeiro-Palau, R. & Hone, J. Disorder in van der Waals heterostructures of 2D materials. Nat. Mater. 18, 541–549 (2019).
Liu, X., Choi, M. S., Hwang, E., Yoo, W. J. & Sun, J. Fermi level pinning dependent 2D semiconductor devices: challenges and prospects. Adv. Mater. https://doi.org/10.1002/adma.202108425 (2021).
Schuler, B. et al. How Substitutional Point Defects in Two-Dimensional WS2 Induce Charge Localization, Spin-Orbit Splitting, and Strain. ACS Nano 13, 10520–10534 (2019).
Prakash, A. & Appenzeller, J. Bandgap Extraction and Device Analysis of Ionic Liquid Gated WSe2 Schottky Barrier Transistors. ACS Nano 11, 1626–1632 (2017).
Nguyen, P. V. et al. Visualizing electrostatic gating effects in two-dimensional heterostructures. Nature 572, 220–223 (2019).
Kim, H.-g. & Choi, H. J. Thickness dependence of work function, ionization energy, and electron affinity of Mo and W dichalcogenides from DFT and GW calculations. Phys. Rev. B 103, 085404 (2021).
Kittel, C. Introduction to solid state physics. 8th edn (Wiley, 2005).
Takeyama, K. et al. Resonant tunneling due to van der waals quantum-well states of few-layers WSe2 in WSe2/h-BN/p+-MoS2 junction. Nano Lett. 21, 3929–3934 (2021).
Chaves, A. et al. Bandgap engineering of two-dimensional semiconductor materials. npj 2D Mater. Appl. 4, 1–21 (2020).
Ruiz-Tijerina, D. A., Danovich, M., Yelgel, C., Zólyomi, V. & Fal’ko, V. I. Hybrid k ⋅ p tight-binding model for subbands and infrared intersubband optics in few-layer films of transition-metal dichalcogenides: MoS2, MoSe2, WS2, and WSe2. Phys. Rev. B 98, 035411 (2018).
Liu, B. et al. Chemical Vapor Deposition Growth of Monolayer WSe2 with Tunable Device Characteristics and Growth Mechanism Study. ACS Nano 9, 6119–6127 (2015).
Zhang, X. et al. Diffusion-Controlled Epitaxy of Large Area Coalesced WSe2 Monolayers on Sapphire. Nano Lett. 18, 1049–1056 (2018).
Tang, S. et al. Quantum spin Hall state in monolayer 1T’-WTe2. Nat. Phys. 13, 683–687 (2017).
Acknowledgements
S.S. acknowledges funding from the Swiss National Science Foundation under the project numbers 159690 and 195133. A.K. and J.A.R. acknowledge Intel through the Semiconductor Research Corporation (SRC) Task 2746 and the Penn State 2D Crystal Consortium Materials Innovation Platform (2DCC-MIP) under NSF cooperative agreement DMR-1539916 for financial support. B.S. appreciates funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program (Grant agreement No. 948243).
Author information
Authors and Affiliations
Contributions
B.S. conceived the project. C.D. prepared the QFEG/SiC substrates and A.K. grew the undoped and V-doped WSe2 samples, both under the supervision of J.A.R. S.S., and B.S. performed the STM experiments. S.S., B.S., and O.G. analyzed the STM experiments. S.S. and B.S. wrote the paper with inputs from all co-authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Stolz, S., Kozhakhmetov, A., Dong, C. et al. Layer-dependent Schottky contact at van der Waals interfaces: V-doped WSe2 on graphene. npj 2D Mater Appl 6, 66 (2022). https://doi.org/10.1038/s41699-022-00342-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41699-022-00342-4