Abstract
Greater stability of low-dimensional halide perovskites as opposed to their three-dimensional counterparts, alongside their high extinction coefficient and thus excellent emission properties, have made them popular candidates for optoelectronic applications. Topological edges are found in two-dimensional perovskites that show distinct electronic properties. In this work, using Kelvin Probe Force Microscopy, performed on butylammonium lead bromide (BA2PbBr4) single crystals with optical bandgap of ~413 nm, we elucidate the electronic response of the edges and their potential impact on photodetector devices. We show that the charge-carriers are accumulated at the edges, increasing with the edge height. Wavelength-dependent surface photovoltage (SPV) measurements reveal that multiple sub-bandgap states exist in BA2PbBr4. As the edge height increases, the SPV amplitude at the edges reduces slightly more as compared to the adjacent regions, known as terraces, indicating relatively less reduction in band-bending at the surface due possibly to increased de-population of electrons from sub-bandgap states in the upper bandgap half. The existence of sub-bandgap states is further confirmed by the observation of below-bandgap emission (absorption) peaks characterised by spectral photoluminescence and photothermal deflection spectroscopy measurements. Finally, we fabricated a photodetector using a millimetre size BA2PbBr4 single crystal. Noticeable broadband photodetection response was observed in the sub-bandgap regions under green and red illumination, which is attributed to the existence of sub-bandgap states. Our observations suggest edge-height dependence of charge-carrier behaviour in BA2PbBr4 single crystals, a potential pathway that can be exploited for efficient broadband photodetector fabrication.
Similar content being viewed by others
Introduction
Low-dimensional hybrid perovskites, including the single-crystal two-dimensional (2D) structures, have attracted huge interest due to their enhanced crystallinity1, improved photostability2, and moisture stability3,4 as compared to their three-dimensional (3D) counterparts. The general formula of Ruddlesden–Popper layered perovskites is (RNH3)2(CH3HN3)n−1MnX3n+1, where R is an organic moiety, M is a divalent cation, X is single or a mixture of halide anions, and n is the number of [MX6]4− sheets between organic layers5. The inorganic [MX6]4− sheet is sandwiched between two insulating organic layers, which interact with the adjacent organic layer through van der Waals force. Since the thickness of the [MX6]4− sheet is much smaller than the value of de Broglie wavelength of carriers, strong quantum confinement and quantum size effects exist6. A resultant unique quantum well like structure of 2D perovskites contributes to the formation of strongly bound exciton and enhanced photon absorption7. Hence, 2D perovskites exhibit different optical properties compared to 3D ones.
A unique characteristic of 2D family of perovskites is the presence of the topological edge effect. Numerous reports have focused on investigating and understanding the origin and the effect of these edges. It was reported that the bound electron-hole pairs are dissociated through the relatively lower energy states residing at the crystal edges8. The formation of edge states with lower emission energies triggered by moisture has been examined and it was found that carriers with longer lifetimes were transported readily through edge states, resulting in high conductivity at the edge states9. Edge states have been associated with perovskite degradation, which could be stabilised using phosphine oxides10. The impact of different alkylammonium iodide treatment on crystal edges in (BA)2(MA)n-1PbnI3n+1 (BA: butylammonium, MA: methylammonium) was investigated using spectral photoluminescence (PL) and confocal PL. It was realised that crystal edges are related to local loss of BA cations and can be reduced by the addition of BA cations11. The edge states properties could vary depending on the height of the edge, hence examining 2D perovskites at the nanoscale in a spatially resolved mode is required. Scanning probe microscopy techniques are useful in this regard12,13,14. Wang et al. studied the electrical properties of edge states in 2D BA2PbI415 and quasi-2D (BA)2(MA)n−1PbnI3n+116 through conductive atomic force microscopy and found distinctively different electrical conductivity at the edges compared to the terrace regions.
Two-dimensional and quasi-2D perovskites have been deployed as the active layer in various optoelectronic devices, such as photodetectors. Interestingly, wavelength-dependent photocurrent creation in (BA)2(MA)n–1PbnI3n+1-based quasi-2D photodetector was reported under sub-bandgap illumination from 630 to 800 nm at room temperature17. Tan et al. deployed BA2PbBr4 for photodetector fabrication and reported photocurrent generation under sub-bandgap illumination (from 460 to 510 nm) at room temperature5, indicating the possibility of broadband photodetector fabrication. However, it was not clear whether distinct edges with different heights in 2D perovskite reported previously contribute to this sub-bandgap photocurrent response.
Here, we investigate the effect of edge height in 2D single crystal of BA2PbBr4 on its electronic properties at nanoscale. We visualised distinct contact potential differences (CPD) of different edge heights using Kelvin Probe Force Microscopy (KPFM). An increase in work function with an increase in edge height was observed, indicating that charges are accumulated at the edge states. Furthermore, surface photovoltage (SPV) measurement under sub-bandgap illumination was performed to assess the wavelength-dependent properties of the edge states. It was noticed that BA2PbBr4 exhibits photovoltage response at low-energy incident photons, as well as edge-height-dependent SPV response, where the latter could be attributed to the different number of sub-bandgap states as the edge height changes. The presence of multiple emission (absorption) peaks in the PL (absorption) spectrum below the optical bandgap is in line with the existence of sub-bandgap states observed in KPFM results. Finally, we fabricated photodetectors based on BA2PbBr4 single crystals, which shows clear photocurrent at energies far below the bandgap, due potentially to the sub-bandgap states’ contribution.
Results and discussion
Crystallinity and surface properties of BA2PbBr4
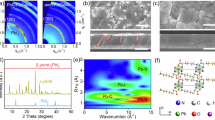
The BA2PbBr4 single crystals were fabricated using expressed synthesis procedure18, described in the Experimental Section. Figure 1a inset shows an example optical image of the transparent single crystal. Based on the optical images in Supplementary Fig. 1, the surface of the as-grown BA2PbBr4 single-crystal exhibits irregular features. To avoid unexpected effects from potential contaminants on the as-grown sample, exfoliated samples (using scotch tape19), shown in Supplementary Fig. 1, are used throughout this work, unless otherwise stated. Scanning electron microscope (SEM) image of BA2PbBr4 is given in Supplementary Fig. 2, illustrating the layered nature of the single crystal. To assess potential changes in the microstructural configuration after exfoliation, high-resolution transmission electron microscopy was conducted. As shown in Supplementary Fig. 3, the interplanar distances of 5.98, 5.92, 4.23, and 4.18 Å were obtained for the exfoliated sample, which corresponds to \(\left( {\bar 1\bar 10} \right)\), (110), \(\left( {0\bar 20} \right)\), and (200) planes, respectively. These values agree with simulated data reported in the literature18, indicating minimal crystal structure change after exfoliation.
a XRD pattern of exfoliated BA2PbBr4. The insert is an optical image of the BA2PbBr4 single crystal. b Schematic of the crystal structure (Ruddlesden–Popper) of BA2PbBr4 based on XRD patterns. c AFM topography image of an exfoliated BA2PbBr4 single crystal. d Pole figure for (008) plane. ND (θ), RD (Φ), TD (Ψ) represent normal direction, rolling direction, and transverse direction, respectively. The (008) direction (2θ = 25.7 °) was the surface-normal direction. XPS spectra of the exfoliated BA2PbBr4 sample for e Br 3d, f Pb 4f, g C 1s, and h N 1s, respectively.
To confirm the crystallinity of the exfoliated single crystal, X-ray diffraction (XRD) measurement is performed (see Fig. 1a). XRD patterns of the exfoliated BA2PbBr4 show a typical peak pattern that indicates (00l) planes in BA2PbBr420,21. From the XRD results, the d-spacing value for (002) was calculated to be 13.8 Å, which is the interplanar spacing between inorganic Pb-I octahedra sheets shown in Fig. 1b. In addition, the crystal structure of BA2PbBr4 was determined by using single-crystal XRD. As shown in Supplementary Fig. 4 and Supplementary Table 1, BA2PbBr4 crystal has lattice parameters a = 8.3476 Å, b = 8.2209 Å, and c = 27.555 Å. The height of the layer measured by atomic force microscopy (AFM) in Fig. 1c is in a good agreement with the c-axis lattice parameter of the BA2PbBr4 unit cell. Further insight into the crystallinity of the sample was attained through conducting a pole figure measurement, depicted in Fig. 1d. There were no peaks with orientation in any direction other than the central peak of (008). This result implies that the preferred crystallinity of exfoliated BA2PbBr4 crystal was in the (00l) direction.
Figures 1e, h illustrates the X-ray photoelectron spectroscopy (XPS) data, probing Br 3d, Pb 4f, C 1s, and N 1s elements on the surface of the exfoliated BA2PbBr4 single crystal. In the Br 3d spectrum (Fig. 1e), peaks are observed at 69.4 eV (Br 3d3/2) and 68.3 eV (Br 3d5/2), which correspond to the presence of Br− anions22. In the Pb 4f spectrum (Fig. 1f), there are two main peaks at 143.4 eV (Pb 4f5/2) and 138.5 eV (Pb 4f7/2), stemming from Pb2+ cations. The spin-orbit split between Pb 4f5/2 and Pb 4f7/2 states is 4.8 eV→4.9 eV, which is close to the reported values23. Furthermore, two minor peaks were located at 141.3 and 136.6 eV, related to the presence of metallic lead (Pb0)24. From Supplementary Tables 2 and 3, the element ratio of Br/Pb is around 4.3, even though the theoretical ratio of Br/Pb should be 4. In general, the existence of low amount of metallic Pb0 could be formed for perovskite during the irradiation with X-ray25, which could result in subtle change of chemical composition. In addition to reason related to external factor, we speculate that a low amount of metallic Pb0 may be attributed to the relatively small loss of short chain length organic cation; long-chain organic amines have been shown to result in comparable amounts of Pb0 and Pb2+ due to difference in volatile properties26. In C 1s spectrum (Fig. 1g), there are two peaks located at 286.1 eV and 284.7 eV. The specific peak at 284.7 eV in the C 1s spectrum and the distinguished peak at 401.6 eV in the N 1s spectrum (Fig. 1h) could be assigned to C-NH3+ in the BA cations27. From the XRD and XPS results, we confirm that the synthesised BA2PbBr4 single crystal has high degree of crystallinity with a low amount of metallic Pb0.
Edge height effect in BA2PbBr4
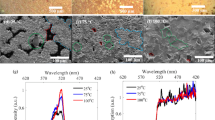
The above results provided insight regarding the bulk crystal quality of the BA2PbBr4 perovskite samples and surface chemistry. Considering that the crystal edges of 2D perovskite single crystals randomly form both during crystallisation28 and by exfoliation29, we then investigate the electronic properties of the BA2PbBr4 surface at the nanoscale using KPFM measurements. A schematic of the measurement setup is presented in Fig. 2a. Figure 2b, c show topography images acquired at two different locations of the same sample. From Fig. 2b, c, it was noticed that edges with various heights are formed within BA2PbBr4. To investigate the work function change of the edges as the heigh varies, KPFM measurement was conducted in the dark on the exfoliated BA2PbBr4. The CPD images, given in Fig. 2d, e, show distinct CPD values at the edges compared to the neighbouring regions, known as terraces. Considering that the c-axis lattice parameter of our BA2PbBr4 is 27.6 Å, concluded from the XRD and AFM measurements, the measured edge height can be converted into the number of stacked monolayers (see Supplementary Fig. 5 and the associated Supplementary Note 1). Figure 2f plots the distribution of CPD values as a function of edge heights extracted from Fig. 2d, e. As the edge height increases the value of CPD increases too and seems to eventually reach a plateau.
a Schematic of the KPFM measurement setup. b and c Topography images of an exfoliated BA2PbBr4 single crystal measured at two different locations on the same sample, and d and e are the corresponding CPD images, respectively. f Distribution of CPD variation, work function, and charge density as a function of the edge height. CPD variation at terrace positions adjacent to the different edge heights is presented (grey diamonds) for comparison. The solid lines are a fit to the data using an exponential function or linear function. g Energy band diagram illustrating the impact of edge height on the Fermi level (EF,e) position obtained from KPFM. Ef,e: the Fermi level of edge, Ef,t: the Fermi level of terraces, Evac: vacuum level; EC: conduction band edge; EV: valence band edge. EC and EV were determined from complementary UPS and UV–Vis measurements.
It has been reported that defect ionisation energy in 2D materials depends on the dimension and the number of stacked layers30,31. It reduces as the number of layers is increased owing to increased screening effect, however, this reduction in ionisation energy is not proportional to the number of layers and can start to plateau after reaching certain number of layers, hence the accumulation of holes at the edges is not in a linear fashion.
To confirm that these CPD changes originate from the edge height change, we compared the CPD values of the terraces representing the flat regions adjacent to the edges and that of the edges with different heights (see Supplementary Fig. 6). In general, higher CPD values were observed at the edges than in the terrace regions. Furthermore, CPD line profiles clearly show that the CPD values at the edges increase as their height increases, whereas CPD at terrace regions remain almost unchanged regardless of the neighbouring edge height shown in Fig. 2f. These results corroborate the previous observation that the reported CPD variation in Fig. 2g mostly depends on the edge height and is independent of the terraces.
We used a highly ordered pyrolytic graphite as a reference sample to calibrate the work function of the probe tip of the KPFM measurement setup (see Supplementary Fig. 7). This allowed subsequent calculation of the work function of the perovskite samples upon a change in the edge height. The details related to converting CPD values to work function are provided in the Experimental Section. A schematic of how the edge height affects the work function is shown in the energy diagram of Fig. 2h. It is noted that an increase in CPD values at the edges upon increase in the height corresponds to an increase in the work function, whereas the insignificant change of CPD values at the terrace regions indicates no detectable spatial variation of the work function there. For instance, the work function of the edge with the height of 171 nm (62 stacked monolayers) can reach 5.06 eV compared to an edge height of 11 nm (4 stacked monolayers) with a work function of 4.98 eV. It is noteworthy that the work function calculated from KPFM is slightly different from that of the Ultraviolet Photoelectron Spectroscopy (UPS) measurement (Supplementary Fig. 8). The work function of ~5.11 eV obtained from UPS measurement, averaged over an area of around 200 to 900 µm2 (ref. 32), is lower than KPFM measurement, where the later provides localised information at nanometre scale33. Altogether, it seems that a large number of holes are accumulated at the edge states compared to the terraces, and as a result, the EF shifts towards lower values, approaching the valence band edge.
Surface photovoltage spectra measurement
Using KPFM measurements under external illumination, SPV, illumination-induced change in surface potential, can be determined. The difference between CPD measured under illumination and CPD measured in the dark gives SPV34,35:
The polarity of the sample surface can be determined by the sign of the SPV. In the case of a p-type (n-type) sample, negative (positive) SPV values are realised, consistent with a decrease (an increase) in CPD under illumination or an increase (a decrease) in sample surface work function35. This is due to the associated downward (upward) band-bending at the surfaces, respectively, leading to different photo-generated charge-carrier re-distribution within the space-charge region and towards the sample bulk. In addition, SPV spectroscopy using illumination with photon energies lower than the bandgap energy can reveal the existence of sub-bandgap states (e.g., defect states with energies here denoted by Esg) on the surface of the semiconductor with below-bandgap transitions.
The SPV map under 450 nm laser excitation associated with the topography image of Fig. 3a was calculated and is presented in Fig. 3b. Negative SPV values were observed under illumination regardless of the edge height, implying the p-type nature of the sample34,35. The change in SPV values as a function of illumination wavelength across two edge regions denoted by P1 (edge height of ~150 nm) and P2 (edge height of ~45 nm) are summarised in Fig. 3c. The associated SPV images measured under monochromatic light ranging from 1.75 eV (750 nm) to 2.75 eV (450 nm), all being sub-bandgap illumination, are provided in Supplementary Fig. 9. Interestingly, negative SPV values were observed under all these lower than optical bandgap photoexcitation conditions indicating the presence of sub-bandgap states (at least) on the surface. The terraces in the vicinity of P1 and P2 lines showed similar SPV values within uncertainty upon sub-bandgap photoexcitation, which is in agreement with the finding of CPD measurement in the dark (Fig. 3). However, the amplitude of SPV was reduced in both terraces and edges as the incident photo energy decreased (i.e., longer wavelength). One possible reason could be reduction in defect absorption cross-section at longer wavelength (see Supplementary Fig. 11). Another possible explanation is a decrease in the number of sub-bandgap states that interact with longer wavelength. Under almost all the photoexcitation wavelengths more negative SPV values were detected for the edge region across the P2 line with lower edge height as compared to the edge region across the P1 line with higher edge height (Fig. 3c), whereas terraces show the largest amplitude of SPV (most negative) compared to edges regardless of the height.
a Topography and b the corresponding SPV image (subtracted CPD images acquired in the dark from that of under 450 nm illumination). c SPV signal change as a function of incident photon energy for two different regions of edges and terraces marked with the red and black lines in panel a and b denoted by P1 and P2, respectively. Energy band diagram change under sub-bandgap illumination in case of d low edge height (e.g., P2) and e high edge height (e.g., P1). Etip: work function of the tip; Esg: energy level of sub-bandgap states.
Charge-carrier transition mechanisms involved in sub-bandgap illumination could be through either population of the states with electrons, de-population of the states from electrons, or both. Electrons can transit from the valance band, EV, to sub-bandgap states, Esg, which is equivalent to hole transitions to EV (population with electrons, or excitation of trapped holes). As a consequence, the created holes in the valence band can move towards the bulk, the downward band-bending—of a p-type sample—reduces as the negative surface charge is increased (see Supplementary Fig. 10a), contributing to an increase in SPV amplitude. Alternately, electron transitions could be promoted from Esg to the conduction band, EC (i.e., de-population of trapped electrons), shown in Supplementary Fig. 10b, resulting in increased band-bending35,36,37. In this latter case, in the absence of electric field-driven movement of electrons towards the bulk, other driving forces are needed for the carriers to diffuse away from the surface so that the transition contributes to SPV. The SPV amplitude at the lower edge height (P2 line) is larger than that at higher edge height (P1 line). This indicates that the band-bending at the surface for the lower edge height has reduced more and becomes more negatively charged compared to that of P1 line with higher edge height. Figures 3d, e shows possible energy diagram change of the lower edge height (P2 line) and higher edge height (P1 line) upon sub-bandgap photoexcitation. As shown in Fig. 3d, there is relatively lower number of generated electrons from Esg in lower edge height (P2 line), resulting in dominantly reduced band-bending at surface. On the other hand, number of transited electrons from Esg in higher edge height increased (P1 line), implying that relatively increased band-bending at the surface in Fig. 3e.
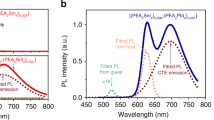
The presence of sub-bandgap states demonstrated through KPFM measurements is further supported by the multiple sub-bandgap transitions observed in the absorption spectrum measured on an as-grown stand-alone single-crystal flake using photothermal deflection spectroscopy (PDS) (see Supplementary Fig. 11). The sample used for the absorption spectrum measurement was not exfoliated so to avoid complications associated with interference of the substrate signal, hence PDS signal was purely from the single-crystal flake of BA2PbBr4. Multiple sub-bandgap transitions are observed, including two relatively broad ones (at ~1200 and ~600 nm) that add up to approximately the bandgap energy of BA2PbBr4, which may indicate potential transitions from valence band to a defect band as well as from the same defect band to the conduction band (this, however, requires further investigation). The low-energy sub-bandgap PL peak emissions (see Supplementary Fig. 12) also represent existence of sub-bandgap states. Defect-induced PL had been previously reported for single-crystal flakes of PEA2PbI438,39,40.
BA2PbBr4-based photodetector
In order to investigate the effects of sub-bandgap states on device performance, photodetectors with the lateral structure of Au/BA2PbBr4 single crystal/Au were fabricated and tested as shown in Fig. 4a. Different illumination light sources with wavelengths of 447 nm (blue), 515 nm (green), and 634 nm (red) at 1 mW cm−2 were used. The resultant wavelength-dependent current–voltage curves of the device are as provided in Fig. 4b. The device responded to all the wavelengths and photocurrent could be measured. Especially, the device showed the highest photocurrent response under blue light illumination. From the photocurrent and dark current characteristics of the device, the parameters of the photodetector were calculated (see Experimental Section).
a Schematic illustration of BA2PbBr4 photodetector. The insert photo is an optical image of the device. b The current–voltage curves of the photodetector measured in the dark and under various monochromatic lights; R, G, B represent the incident lights of red (634 nm), green (515 nm), and blue (447 nm). Light intensity-dependent performance of BA2PbBr4 photodetector under red, green, and blue illumination at 5 V bias voltage: c photocurrent density, d responsivity (R), and e detectivity (D*).
A photocurrent of 2.1 × 10−10 A was measured under 447 nm, at 1 mW cm−2 illumination intensity at 2 V, giving an ON/OFF ratio of 13.87. These results are consistent with previously reported results by Tan et al., showing distinct photocurrent responses between 460 to 640 nm5. Contrary to previous literature5, our photodetector device produced measurable photocurrent under the illumination of 515 and 634 nm at 1 mW cm−2, which were far below the bandgap of BA2PbBr4, even though the ON/OFF ratio at 2 V were relatively low, 1.665 and 1.607, respectively. The calculated performance parameters, including EQE, responsivity, and detectivity, were summarised in Table 1. It is noted that since the optical absorption coefficient significantly reduces at energies lower than the bandgap energy, the photo responses here are considerably low. Nonetheless, these results confirm the existence of sub-bandgap states within the bandgap, where photons with below-bandgap energy are absorbed and the photocurrent is derived from these states with the external biases41. In addition, the device that stored in Ar-filled glovebox for over 7 months is still working shown in Supplementary Fig. 13 and related parameters of device are summarised in Supplementary Table 4. Therefore, the superior long-term stability of device is evident in these results.
To understand the relationship between the device performance and the edges, we conducted the time-resolved photoluminescence (TRPL) of the sample. As shown in Supplementary Fig. 14 and Supplementary Table 5, the TR-PL at 415 nm, representing the PL of terrace decays slightly faster than the PL at 437 nm representing the sub-gab states, originated by edge. This reveals that the charge-carrier recombination at the edge is slower (1.05 → 1.34 ns), which can attribute to the efficient charge transport through the edge. It indicates that the long-lived charge-carriers attribute to the high current density in device performance. Moreover, conductive AFM (c-AFM) was implemented to confirm the relationship of the photocurrent according to edge height. As shown in Supplementary Fig. 15a,b, we investigate two different edge height positions labelled by position 1 (~26 nm) and position 2 (~54 nm). The obtained current is significantly small with the range of pico-ampere (pA) under a DC bias voltage of 10 V due to the intrinsic insulating properties of BA2PbBr4. Nonetheless, as shown in Supplementary Fig. 15c, the line profiles of topography and current from these two positions labelled by 1 and 2 show current variation is much prominent at position 2 (0.8 pA) compared to that at position 1 (0.69 pA). Given that wavelength of used light LED has almost below-bandgap, different current variation with regards to edge height may be attributed to different amounts of sub-bandgap states42,43. In addition, considering that responsivity is related to carrier generation rate and carrier lifetime44, increased carrier lifetime or enhanced photo carrier generation is required to increased responsivity of photodetector. Thus, it is believed that increased carrier lifetime at edge provided by TRPL and enhanced sub-bandgap induced hot carrier with increase edge height from c-AFM can elucidate effect on responsivity of photodetector.
We also performed light intensity-dependent photo-response measurement with the BA2PbBr4 single-crystal photodetector device. Figure 4c shows the photocurrent density obtained under the blue, green, and red-light illumination at 5 V bias voltage with the light intensity ranges from 0.5 μW cm−2 to 1 mW cm−2. Significant photocurrent response to all light intensities was observed when the device was operated under blue illumination, which also shows a substantial increase under higher light intensity. On the other hand, under red and green illumination, relatively low photocurrent was measured with intensities below 0.1 mW cm−2, so there is no big difference between red and green illumination. The photocurrent density started to show obvious growth when the light intensity was above 0.1 mW cm−2, and green illumination excites a higher photocurrent than red illumination.
In Fig. 4d, e, light intensity-dependent photo-response characteristics of R and D* under the blue, green, and red-light illumination at 5 V bias voltage are shown. As more carrier recombination is expected to happen under high light intensity, R and D* values all decrease with increased light intensity, following the photoconductor behaviour. It is obvious that the 2D single-crystal photodetector shows the best performance under blue illumination within the whole light intensity region, while under red and green illumination the photodetector shows similar performance. At higher light intensity, the performance gap under different wavelengths becomes larger, indicating the charge recombination has a greater effect on device performance under red and green illumination as fewer carriers can be excited to the sub-bandgap states. The highest R and D* were achieved to be 0.381 mA W−1 and 9.01 × 1010 Jones respectively, under 447 nm illumination with the light intensity of 0.5 μW cm−2 at 5 V bias. These results suggest the great potential of BA2PbBr4 single-crystal photodetectors with a wide detection range extended to the below-bandgap region.
In conclusion, we implemented KPFM measurements to investigate the edge effect in 2D BA2PbBr4. In the dark condition, CPD values at the edges are significantly increased by increasing height of the edge, while that of the terraces remains unchanged. These distinct increase in CPD values with edge height indicate a different extent of increase in work function, hence charge accumulation at the different edge heights. In addition, we utilised SPV spectra measurement in KPFM under sub-bandgap illumination to investigate wavelength-dependent intrinsic properties of BA2PbBr4. It was revealed that BA2PbBr4 consists of sub-bandgap states. The reduced SPV amplitudes were observed at the edges with larger heights as well as with respect to terraces. It is proposed that increased de-population of electrons from sub-bandgap states in the upper bandgap half as the edge height increases can be a potential underlying mechanism, resulting in relatively lower extent of reduction in band-bending at the surface to confirm the presence of sub-bandgap states within BA2PbBr4, we performed spectral PL and PDS measurements. These results indicate that there are sub-bandgap states in addition to the two direct bandgaps. Combing the spectral SPV, PL, and PDS measurement results, it is likely that more sub-bandgap states are present in the case of thicker edge heights. Lastly, we fabricated BA2PbBr4 photoreactor devices and employed red (634 nm), green (515 nm), and blue (447 nm) light shone on the devices to confirm the effect of sub-bandgap states in BA2PbBr4. Remarkable broadband photodetection response was detected in the sub-bandgap regions (under green and red illumination) due to the existence of sub-bandgap states. Although the precise control of edge height in 2D or quasi 2D perovskite crystals still needs to be investigated to take advantage of their properties, our observations of the edge height-dependent carrier behaviour in BA2PbBr4 single crystals provides insights for their deployment in broadband photodetectors.
Methods
Synthesis
1 M of PbBr2 (98%, Sigma-Aldrich) was dissolved in 5 mL of HBr aqueous solution (48 wt. % in H2O, Sigma-Aldrich) at 90 °C with constant stirring until completely dissolving. In a separate vial, 10 mmol of butylamine (99.5%, Sigma-Aldrich) was added into 5 mL of HBr aqueous solution drop by drop in an ice water bath with constant stirring. The resultant BABr solution was added to the PbBr2-HBr solution. The precursor was heated to 100 °C in an oil bath with constant stirring and kept at 100 °C for 15 min before it was gradually cooled to room temperature. The cooling process was in stable and uninterrupted condition. After 2 h, the crystallisation was completed. The thin white plate-like crystals were filtered and washed with acetone for several times and dried in a vacuum oven at 60 °C overnight.
Characterisation
Scanning electron microscopy (SEM)
The cross-sectional image was obtained using a Field Emission Scanning Electron Microscope (FE-SEM, JEOL JSM-7100F) with a hot (Schottky) electron gun.
Optical microscopy
Olympus BX61 Microscope Digital camera was utilised for obtaining optical microscopy images.
Ultraviolet–visible (UV–visible) spectroscopy
Ultraviolet–visible absorption spectra for BA2PbBr4 single crystals were collected using a Model V650 from Jasco with accessory ISV-722.
To calculate the Tauc plot, the Kubelka–Munk function was utilised.
where R is reflectance.
The Tauc plot of (f(R)*hυ)2 verse (hυ) was used for determining direct bandgap45,46,47.
Photothermal deflection spectroscopy (PDS)
Photothermal deflection spectroscopy (PDS) is a highly sensitive metrology technique, typically able to measure optical absorption at levels up to 1000x lower than conventional spectrophotometers. With PDS, monochromatic pump light is focused on a sample immersed in an inert liquid. Heat generated by the absorbed light transfers to the liquid, creating a thermally induced refractive index gradient, which is probed by a laser aligned parallel to the sample surface. Modulating the pump light at a frequency in the range of 1–10 Hz results in periodic deflection of the probe laser due to the refractive index change. This deflection is proportional to the amount of light absorbed by the sample.
For these measurements, the pump light source was a monochromator with a Xe arc lamp, modulated by an optical chopper at 4.5 Hz. Bandwidths of 4, 8, and 16 nm in the UV, visible, and NIR, were achieved. The output slit was imaged onto the sample, resulting in a spectral irradiance at the sample in the range of 9 mW nm−1 cm−2. For the probe beam, a 635 nm laser was weakly focused to yield a beam waist at the coincidence point of the pump and probe. A sensor, synchronised to the chopper wheel, monitored the position of the laser. Scanning the monochromator over the 250–1500 nm range produced the spectral data shown in this work.
The PDS spectrum in arbitrary units was then scaled at 335 nm to the absorptivity spectrum (i.e., 1-reflectivity-transmission) obtained from the UV–Vis spectrophotometer measured using Lambda 1050, Perkin Elmer.
Spectral photoluminescence (PL) measurement
Photoluminescence measurements were performed at 8 K using a closed cycle compressed helium cryostat (CTI Cryogenics/RG Hansen and Associates) under vacuum. Samples were excited using a 375 nm diode laser (Coherent, CUBE 375–16 C) focused to a 100 µm diameter spot. The emission was collected using a 4-f optical imaging arrangement and coupled to a 27 cm focal length spectrometer (J/B SPEX 270 M) with a thermoelectrically cooled photomultiplier (Amherst, M4100) mounted at the exit aperture. The spectrally resolved signal was recorded using a lock-in amplifier and optical chopper (Stanford Research Systems, SR510).
Time-resolved photoluminescence (TRPL) measurement
The photoluminescence spectra and decay curves were acquired on a FluoTime 300 (PicoQuant GmbH) using a PicoHarp 300 as time-correlated single photon counting setup (TCSPC) and a pulsed laser diode with an excitation wavelength of 405 nm (LDH-P-C-405, PicoQuant GmbH). The repetition rate of the diode was 4 MHz. We measured two different spots of three individual samples, thus the extracted charge-carrier lifetime values are the average values of 6 measurements at each PL peak point (415 and 437 nm). Here the TRPL decay was fit by the stretched exponential decay and the mean charge-carrier lifetime was calculated via stretch parameter and Gamma function48
where the stretch parameter 0 < β < 1, and the charge-carrier mean lifetime is given by,
where the Γ is Gamma function. For the accurate calculation, the instrument response function (IRF) was obtained and used for the fitting process.
Kelvin probe force microscopy (KPFM)
All measurement for AFM and KPFM was implemented using AFM equipment (AIST-NT smartSPM1000) under N2 condition at room temperature. Before the measurement, unexpected contaminants on the surface of the sample were cleaned with N2 blowing. Contact potential difference (CPD) maps were obtained in the amplitude modulation mode with a scan rate of 1 Hz by using Au-coated conductive probes (HA_HR/Au from TipsNano, force constant k is ~13 N m−1, the resonance frequency of ~230 kHz).
To calculate the work function of the sample, CPD is defined as the difference of work function between the tip and the sample. The related equation for CPD can be represented as below49:
where Φtip and Φsample are the work function of the tip and sample surface, respectively, and e is the elementary charge50. Au-coated tip was calibrated with highly oriented pyrolytic graphite (HOPG) in Supplementary Fig. 7 and the absolute work function at the edge of BA2PbBr4 was calculated by51:
where ΦHOPG = 4.65 eV52, CPDsample and CPDHOPG are measured CPD of the sample and HOPG, respectively.
In terms of SPV measurement, an external illumination source from Ytterbium fibre laser (FemtoPower 1060, NKT Photonics Inc.) with a pulse width of <200 fs, a high-repetition-rate of 80 MHz, and bend with of 25 nm were utilised. The laser beam entered a short-pass filter (FESH0750) with a spot size of 9.54 um2 and it was applied to the sample at an angle of 30° to the surface to prevent unintentional shading from the probe shown in Supplementary Fig. 16. The wavelength and intensity of the illumination source could be adjusted. For comparing SPV results with wavelength, we set 3.97 × 1021 cm−2 s−1 photon flux before SPV measurement. Laser light with a wavelength of 1300 nm was used to monitor the deflection of the AFM beam, removing the possibility of its absorption by the measured sample.
Calculation of charge density from KPFM results
In order to calculate charge density, we used the equation surface charge and potential difference based on a simple parallel capacitor model53,54,55.
where εo is vacuum permittivity, ε is the sample permittivity, d is distance between tip and surface of the sample, ΔVdc is applied AC voltage for measuring KPFM, Φtip and Φsample are work function of tip and sample, respectively. e is the elementary charge. The equation between height and CPD can be extracted from our experimental results \(\left( {{{{\mathrm{CPD}}}} = {{{\mathrm{exp}}}}\left[ {6.2 - \frac{{3.1}}{{\left( {{{{\mathrm{edge}}}}\;{{{\mathrm{height}}}} + 96} \right)}}} \right]} \right)\).ε is used 27.4 according to literature56.
Conductive AFM (c-AFM)
Conductive AFM (c-AFM) was carried out using an atomic force microscope (Park system NX10) in the air using Pt-coated Si tip (HQ:NSC35/pt) under white LED with illumination of 1200 lux as shown in Supplementary Fig. 17.
X-ray diffraction for 2 theta and pole figure maps
X-ray diffraction patterns were obtained by using a PANalytical Xpert Materials Research diffractometer system with a Cu Kα radiation source (λ = 1.5405 Å) at 45 kV and 40 mA.
The crystallographic orientation was investigated utilising X-ray diffraction (XRD) using Cu-Kα radiation with λ = 1.5405 Å at an operating voltage of 35 kV and current of 40 mA. A receiving slit of 3–8 mm2 was applied to measure the (008) pole figure with background subtraction. The defocused errors and pole figures were corrected and calculated, respectively, using the texture analysis software X’pert Texture from PANalytical B.V version 1.1a
Single-crystal XRD
The single-crystal data of BA2PbBr4 crystal has been collected by the Bruker D8 Quest instrument at room temperature using the Mo radiation source (λ = 0.71073 Å). The data has been processed by the Bruker SAINT software package (APEX3). The structure was solved by an intrinsic phasing method (SHELXT) and refined using the Olex2 software.
High-resolution transmission electron microscopy (HR-TEM)
TEM sample preparation
The mechanical exfoliation of BA2PbBr4 was conducted in ambient air using scotch tape. Tapes with exfoliated BA2PbBr4 were put in a vial with chlorobenzene. The vial was sonicated for 10 min to detach exfoliated BA2PbBr4 from scotch tape. After removing the scotch tape, ~20 µl of the suspension was dropped on a holey carbon grid and placed in a fume hood for at least 15 min to evaporate any remaining solvent from the TEM grid.
TEM measurement
HRTEM was implemented by using JEOL JEM-F200 with an accelerating voltage of 200 kV equipped with a Gatan Oneview Camera. Owing to the beam sensitivity of the BA2PbBr4 film, the microscope was aligned on a region of bare carbon, and the image was taken immediately after the sample is moved into view.
Determine FFT pattern
FFT patterns from HRTEM images were obtained with Gatan Microscopy Suite 3 software. To confirm crystal planes and orientation FFTs were compared with diffraction patterns 57simulated with JEMS v4.10131 using crystallographic information file (.cif) from previous literature was utilised18.
Ultraviolet photoelectron spectroscopy (UPS) and X-ray photoelectron spectroscopy (XPS)
UPS was implemented by using (ESCALAB250Xi, Thermo Scientific). The He I (21.2 eV) emission was used as a UV source and the helium pressure in the chamber during analysis was about 2 × 10−9 mbar. The work function (WF) from UPS spectra was determined from incident photon energy hv = 21.2 eV, Ecutoff and Eonset. In terms of XPS measurement, ESCALAB250Xi, Thermo Scientific with Al Kα X-ray source was used and obtained the binding energies were calibrated by C 1s (284.8 eV).
Photodetector characterisation
To fabricate the later-structure photodetector, 80 nm gold electrodes were thermally evaporated on the BA2PbBr4 single crystal. All the I–V curves were measured at room temperature in the ambient atmosphere with an Autolab electrochemical station (Multi Autolab M204) and a probe station. The light source was from a LED light with different wavelengths of R (634 nm), G (515 nm), B (447 nm) at 1 mW cm−2. And the active area of device is 8.85 mm2.
The used equation to determine parameters of photodetector devices are58,59:
where Iph and Id are current under illumination and dark, respectively; Pin is incident light intensity; R is responsibility; A is active area; hν indicates that the energy of photon; e is the elementary charge (1.60 × 10−19 C). D* is detectivity expressed in the Jones unit.
Data availability
The raw data generated during and/or analysed during the current study are available from the corresponding author on reasonable request.
References
Liao, Y. et al. Highly oriented low-dimensional Tin halide perovskites with enhanced stability and photovoltaic performance. J. Am. Chem. Soc. 139, 6693–6699 (2017).
Coriolano, A. et al. Improved photostability in fluorinated 2D perovskite single crystals. Nanomaterials 11, 465 (2021).
Zhang, Q. et al. Improved moisture stability of 2D hybrid perovskite (HOOC–CH2–NH3)2PbI4 by dehydration condensation between organic components. ACS Appl. Energy Mater. 1, 2502–2511 (2018).
Smith, I. C., Hoke, E. T., Solis-Ibarra, D., McGehee, M. D. & Karunadasa, H. I. A layered hybrid perovskite solar-cell absorber with enhanced moisture stability. Angew. Chem. Int. Ed. 53, 11232–11235 (2014).
Tan, Z. et al. Two-dimensional (C4H9NH3)2PbBr4 perovskite crystals for high-performance photodetector. J. Am. Chem. Soc. 138, 16612–16615 (2016).
Zhu, X. et al. Vapor-fumigation for record efficiency two-dimensional perovskite solar cells with superior stability. Energy Environ. Sci. 11, 3349–3357 (2018).
Hong, X., Ishihara, T. & Nurmikko, A. V. Dielectric confinement effect on excitons in PbI4-based layered semiconductors. Phys. Rev. B 45, 6961–6964 (1992).
Blancon, J. C. et al. Extremely efficient internal exciton dissociation through edge states in layered 2D perovskites. Science 355, 1288 (2017).
Shi, E. et al. Extrinsic and dynamic edge states of two-dimensional lead halide perovskites. ACS Nano 13, 1635–1644 (2019).
Na Quan, L. et al. Edge stabilization in reduced-dimensional perovskites. Nat. Commun. 11, 170 (2020).
Zhao, C., Tian, W., Leng, J., Zhao, Y. & Jin, S. Controlling the property of edges in layered 2D perovskite single crystals. J. Phys. Chem. Lett. 10, 3950–3954 (2019).
Kazakova, O., Panchal, V. & Burnett, T. L. Epitaxial Graphene and graphene–based devices studied by electrical scanning probe microscopy. Crystals 3, 191–233 (2013).
Pearce, R. et al. On the differing sensitivity to chemical gating of single and double layer epitaxial graphene explored using scanning kelvin probe microscopy. ACS Nano 7, 4647–4656 (2013).
Ziegler, D. et al. Variations in the work function of doped single- and few-layer graphene assessed by Kelvin probe force microscopy and density functional theory. Phys. Rev. B 83, 235434 (2011).
Wang, K. et al. Distinct conducting layer edge states in two-dimensional (2D) halide perovskite. Sci. Adv. 5, eaau3241 (2019).
Wang, K. et al. Nature of terrace edge states (TES) in lower-dimensional halide perovskite. J. Mater. Chem. A 8, 7659–7670 (2020).
Hossain, R. F., Min, M., Ma, L.-C., Sakri, S. R. & Kaul, A. B. Carrier photodynamics in 2D perovskites with solution-processed silver and graphene contacts for bendable optoelectronics. NPJ 2D Mater. Appl. 5, 34 (2021).
Sheikh, T. & Nag, A. Mn doping in centimeter-sized layered 2D butylammonium lead bromide (BA2PbBr4) single crystals and their optical properties. J. Phys. Chem. C. 123, 9420–9427 (2019).
Dhanabalan, B. et al. Simple fabrication of layered halide perovskite platelets and enhanced photoluminescence from mechanically exfoliated flakes. Nanoscale 11, 8334–8342 (2019).
Yu, D. et al. Two-dimensional halide perovskite as β-ray scintillator for nuclear radiation monitoring. Nat. Commun. 11, 3395 (2020).
Nie, L., Ke, X. & Sui, M. Microstructural study of two-dimensional organic-inorganic hybrid perovskite nanosheet degradation under illumination. Nanomaterials 9, 722 (2019).
Liu, M. et al. Aluminum-doped cesium lead bromide perovskite nanocrystals with stable blue photoluminescence used for display backlight. Adv. Sci. 4, 1700335 (2017).
Gonzalez-Carrero, S., Espallargas, G. M., Galian, R. E. & Pérez-Prieto, J. Blue-luminescent organic lead bromide perovskites: highly dispersible and photostable materials. J. Mater. Chem. A 3, 14039–14045 (2015).
Syafutra, H. et al. Surface degradation mechanism on CH3NH3PbBr3 hybrid perovskite single crystal by a grazing E-beam irradiation. Nanomaterials 10, 1253 (2020).
McGettrick, J. D. et al. Sources of Pb(0) artefacts during XPS analysis of lead halide perovskites. Mater. Lett. 251, 98–101 (2019).
Hofstetter, Y. J. et al. Vacuum-induced degradation of 2D perovskites. Front. Chem. 8, 66 (2020).
Zhou, Q. et al. High-performance perovskite solar cells with enhanced environmental stability based on a (p-FC6H4C2H4NH3)2[PbI4] capping layer. Adv. Energy Mater. 9, 1802595 (2019).
Liu, Y. et al. Surface-tension-controlled crystallization for high-quality 2D perovskite single crystals for ultrahigh photodetection. Matter 1, 465–480 (2019).
Li, J. et al. Fabrication of single phase 2D homologous perovskite microplates by mechanical exfoliation. 2D Mater. 5, 021001 (2018).
Zhu, G.-J., Xu, Y.-G., Gong, X.-G., Yang, J.-H. & Yakobson, B. I. Dimensionality-inhibited chemical doping in two-dimensional semiconductors: the phosphorene and MoS2 from charge-correction method. Nano Lett. 21, 6711–6717 (2021).
Wang, D. & Sundararaman, R. Layer dependence of defect charge transition levels in two-dimensional materials. Phys. Rev. B 101, 054103 (2020).
Cole, K. M., Kirk, D. W. & Thorpe, S. J. Co(OH)2 powder characterized by X-ray photoelectron spectroscopy (XPS) and ultraviolet photoelectron spectroscopy (UPS). Surf. Sci. Spectra 27, 024013 (2020).
Luo, D., Sun, H. & Li, Y. In Surface Science Tools for Nanomaterials Characterization. (ed. Kumar, C. S. S. R.) 117–158 (Springer Berlin Heidelberg, 2015).
Chen, R., Zhu, J., An, H., Fan, F. & Li, C. Unravelling charge separation via surface built-in electric fields within single particulate photocatalysts. Faraday Discuss. 198, 473–479 (2017).
Chen, R., Fan, F., Dittrich, T. & Li, C. Imaging photogenerated charge carriers on surfaces and interfaces of photocatalysts with surface photovoltage microscopy. Chem. Soc. Rev. 47, 8238–8262 (2018).
Kronik, L. & Shapira, Y. Surface photovoltage spectroscopy of semiconductor structures: at the crossroads of physics, chemistry and electrical engineering. Surf. Interface Anal. 31, 954–965 (2001).
Ma, W. et al. Surface photovoltage inversion and photocatalytic properties of PbI2 microcrystals under sub-bandgap illumination. J. Mater. Sci. 52, 9696–9708 (2017).
Tekelenburg, E. K., Kahmann, S., Kamminga, M. E., Blake, G. R. & Loi, M. A. Elucidating the structure and photophysics of layered perovskites through cation fluorination. Adv. Opti. Mater. 9, 2001647 (2021).
Kahmann, S., Tekelenburg, E. K., Duim, H., Kamminga, M. E. & Loi, M. A. Extrinsic nature of the broad photoluminescence in lead iodide-based Ruddlesden–Popper perovskites. Nat. Commun. 11, 2344 (2020).
Do, T. T. H., Granados del Águila, A., Xing, J., Liu, S. & Xiong, Q. Direct and indirect exciton transitions in two-dimensional lead halide perovskite semiconductors. J. Chem. Phys. 153, 064705 (2020).
Lin, Q., Armin, A., Burn, P. L. & Meredith, P. Near infrared photodetectors based on sub-gap absorption in organohalide perovskite single crystals. Laser Photonics Rev. 10, 1047–1053 (2016).
Chen, R.-S. et al. Photoconductivities in monocrystalline layered V2O5 nanowires grown by physical vapor deposition. Nanoscale Res. Lett. 8, 443 (2013).
Huang, H. M. et al. Photoconductivity in single AlN nanowires by subband gap excitation. Appl. Phys. Lett. 96, 062104 (2010).
Ganguly, S., Tang, X., Yoo, S.-S., Guyot-Sionnest, P. & Ghosh, A. W. Extrinsic voltage control of effective carrier lifetime in polycrystalline PbSe mid-wave IR photodetectors for increased detectivity. AIP Adv. 10, 095117 (2020).
Sarfraz, A. & Hasanain, S. K. Size dependence of magnetic and optical properties of Co3O4 nanoparticles. Acta Phys. Polonica A 125, 139–144 (2014).
Island, J. O. et al. Electronics and optoelectronics of quasi-1D layered transition metal trichalcogenides. 2D Mater. 4, 022003 (2017).
Goodall, J. B. M. et al. Optical and photocatalytic behaviours of nanoparticles in the Ti–Zn–O binary system. RSC Adv. 4, 31799–31809 (2014).
Habisreutinger, S. N., Wenger, B., Snaith, H. J. & Nicholas, R. J. Dopant-free planar n–i–p perovskite solar cells with steady-state efficiencies exceeding 18%. ACS Energy Lett. 2, 622–628 (2017).
Rosenwaks, Y., Shikler, R., Glatzel, T. & Sadewasser, S. Kelvin probe force microscopy of semiconductor surface defects. Phys. Rev. B 70, 085320 (2004).
Melitz, W., Shen, J., Kummel, A. C. & Lee, S. Kelvin probe force microscopy and its application. Surf. Sci. Rep. 66, 1–27 (2011).
Weber, S. A., Memesa, M., Berger, R., Butt, H. J. & Gutmann, J. S. Electrical scanning probe microscopy of an integrated blocking layer. J. Nanosci. Nanotechnol. 10, 6840–6844 (2010).
Sankaran, K. J. et al. Laser-patternable graphene field emitters for plasma displays. Nanomaterials 9, 1493 (2019).
Horowitz, Y. & Asscher, M. Low energy charged particles interacting with amorphous solid water layers. J. Chem. Phys. 136, 134701 (2012).
Lin, S. & Wang, Z. L. Scanning triboelectric nanogenerator as a nanoscale probe for measuring local surface charge density on a dielectric film. Appl. Phys. Lett. 118, 193901 (2021).
Xu, J. et al. Charge transfer of single laser crystallized intrinsic and phosphorus-doped Si-nanocrystals visualized by Kelvin probe force microscopy. J. Appl. Phys. 116, 134309 (2014).
Wang, S. et al. Wafer-sized 2D perovskite single crystal thin films for UV photodetectors. J. Mater. Chem. C. 9, 6498–6506 (2021).
Stadelmann, P. A. EMS-a software package for electron diffraction analysis and HREM image simulation in materials science. Ultramicroscopy 21, 131–145 (1987).
Choi, E. Y. et al. Synthesis and characterization of a wide bandgap polymer based on a weak donor-weak acceptor structure for dual applications in organic solar cells and organic photodetectors. Org. Electron. 46, 173–182 (2017).
Wang, J., Han, J., Chen, X. & Wang, X. Design strategies for two-dimensional material photodetectors to enhance device performance. InfoMat 1, 33–53 (2019).
Acknowledgements
J.S. acknowledges support by the Australian Research Council through Discovery Grants and the ARC Centre of Excellence in Future Low Energy Electronics Technologies (FLEET). The authors acknowledge the technical assistance of the surface analysis laboratory, Solid State & Elemental Analysis Unit (SSEAU), and the facilities of Microscopy Australia at the Electron Microscope Unit (EMU) within the Mark Wainwright Analytical Centre (MWAC), University of New South Wales (UNSW). Arman Mahboubi Soufiani acknowledges the funding support from ACAP (RG193402-I). J.L. acknowledges the support by the Korea Institute of Energy Technology Evaluation and Planning (KETEP) grant funded by the Ministry of Trade, Industry & Energy (MOTIE) of the Republic of Korea (no. 20203040010320).
Author information
Authors and Affiliations
Contributions
E.C. wrote original draft and conducted overall characterisation part of this research. Y.Z. wrote original draft and performed the experiments related to photodetector section. A.M.S. discussed the KPFM and SPV results and contributed to its data analysis and interpretation as well as to the overall writing of the manuscript. M.L. conducted c-AFM measurement and contributed to analysis of c-AFM results. R.F.W. contributed to data curation and analysis for TEM. M.E.P. measured PDS. P.J.R. conducted and analysed PL results. W.L. measured TRPL and analysed TRPL results. J.S. provided resources for conducting experiments and reviewed paper. J.L. analysed TRPL results and reviewed revised manuscript. J.-H.Y. reviewed and edited paper and supervised overall research. J.S.Y. conceived concept of this research and supervised overall experiments.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Choi, E., Zhang, Y., Soufiani, A.M. et al. Exploration of sub-bandgap states in 2D halide perovskite single-crystal photodetector. npj 2D Mater Appl 6, 43 (2022). https://doi.org/10.1038/s41699-022-00317-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41699-022-00317-5