Abstract
The interfacial shear coupling (ISC) governs the relative in-plane deformations of layered two-dimensional (2D) van der Waals (vdW) materials, which is significant for both the fundamental theory of solid mechanics and the stability design of 2D devices. Here we study the representative ISC of 2D vdW stacks using bilayer graphene (BLG) and isotope-labeled Raman spectroscopy. The results show that under uniaxial tensile strain, the ISC between two graphene layers evolves sequentially with bonding, sliding and debonding process, and the corresponding interfacial shear strength is inversely proportional to the sample size. Molecular dynamics (MD) simulations demonstrate the origin of this inverse proportionality as stronger interlayer vdW interaction induced by the edge lattices and atoms of BLG that have more degrees of freedom. These results not only provide new fundamental insights into the multiscale interpretation of macroscopic interfacial shear properties of 2D vdW stacks but also have great potential in guiding the design of graphene-based composite materials and flexible 2D electronics.
Similar content being viewed by others
Introduction
The assembly of two-dimensional (2D) materials into vertical van der Waals (vdW) stacks has opened new avenues for fundamental scientific studies in the past decade1,2,3, and the interfacial vdW interaction has been extensively recognized as playing the most critical role in determining the innovative properties of these stacks4,5,6. Besides most previous work that has focused on the electronic properties, the mechanical coupling between the layers of 2D vdW stacks is also important in governing their structural integrity (durability) and mechano-electronic performances7,8. Especially, considering that an atomic-thick vdW stack often has the same type of deformation under a macroscopic load, it is of great significance to study the relative in-plane deformations of all its layers, that is, the shear deformation and the corresponding interfacial shear strength (ISS) of the stack, governed by the interfacial shear coupling (ISC) between its layers.
The key to studying the ISC of a 2D stack is to obtain the strain/stress information of each layer. Unlike measuring the adhesion energy between 2D layers by nanoindentation using the 2D material-wrapped atomic force microscope tip9, there are two bottlenecks in observing the in-plane deformation of each layer experimentally. One is to build 2D stacks with ultraclean vdW interfaces with as few impurities and defects as possible, and the other is to develop a reliable strain measurement technique with high accuracy, which can distinguish the signal from each layer even in a homogenous vdW stack.
In recent years, Raman spectroscopy has been widely used for strain measurement in 2D materials by the shift of their spectral peaks, owing to that it can relate the lattice elongation of a crystal with its spectral feedback10,11,12,13,14,15,16. However, when this technique is used for a homogeneous 2D stack, even consisting of only two layers, their Raman signals will totally overlap. Considering the width of a spectral peak, the accurate strains of the two layers cannot be obtained until the peak from one layer is shifted “out” from that of the other layer by a large enough strain difference (Supplementary Fig. 1). Taking bilayer graphene (BLG) as an example, the full-width-at-half-maximum (FWHM) of Raman G peak for one layer is approximately 15 cm–1 and its shifting rate by strain is ~30 cm–1 %−1 15, only a strain difference larger than 0.5% in the two layers can differentiate the overlapped G peaks, otherwise, peak decomposition and line fitting using nondeterministic and subjective parameters have to be adopted17,18,19.
Inspired by the success of using isotope to study the growth mechanism and doping level of graphene20,21,22, here we study the interlayer shear coupling of BLG by isotope-labeled Raman spectroscopy. The results show that under uniaxial tensile strain, the ISC between two graphene layers evolves sequentially with the bonding, sliding and debonding process, and the ISS of BLG is inversely proportional to the sample size. Molecular dynamics (MD) simulations demonstrate the origin of this inverse proportionality as stronger interlayer vdW interactions from the edge lattices and atoms of 2D materials that have more degrees of freedom.
Results and discussion
Realization and resolution of strain in each layer of BLG
Raman spectroscopy has been intensely used to quantitatively assess the strain in graphene owing to its high sensitivity in detecting lattice-related phonon energy variations10,11. In a typical Raman spectrum of graphene, the G peak that originates from the first-order scattering process of doubly degenerate E2g phonons at the center of the Brillouin zone is usually chosen for strain measurement. As the uniaxial strain increases, this peak shifts to lower wavenumbers (i.e., redshifts) and splits into two subpeaks, namely, G– and G+, then the well-established model can be adopted to calculate the strain components in graphene
Where εll and εtt are strains parallel and perpendicular to the tensile direction, respectively, \(\omega _{\text{G}}^{0}\) represents the G peak position of unstrained graphene, \(\Delta \omega _G^ +\) and \(\Delta \omega _G^ -\) are the shifts of G+ and G– subpeaks relative to \(\omega _G^0\), respectively, and constants γ = 1.99 and β = 0.9910.
Because Raman spectra are the fingerprints of atom vibrations, when the mass of atoms in a material changes, the positions of its Raman peaks also change. For graphene formed by 12C and 13C isotopes, their Raman peak positions satisfy the relationship
where ω12 and ω13 are the positions of Raman peaks with the same origin for 12C and 13C graphene, respectively. The G peaks of unstrained 12C and 13C graphene are at ~1580 and ~1525 cm–1, respectively, and their 2D peaks that correspond to the second-order scattering of phonons are at ~2680 and ~2575 cm–1, respectively. Therefore, if the different layers in BLG are labeled by 12C and 13C isotopes, the Raman signals from them can be effectively distinguished (Fig. 1a), as we previously demonstrated23. For the G peaks that are usually used as the strain indicator, they are differentiated for 55–60 cm–1 in a Raman spectrum, capable enough of probing the strains in each layer independently.
a Overlapped and differentiated Raman peaks from BLG composed of identical and isotope carbon atoms, respectively. b Schematic of the experimental setup for the shear property measurement of BLG by Raman spectroscopy. c OM image of a BLG island transferred on the formvar/PDMS substrate. d A typical Raman spectrum of AB-stacked 12C/13C BLG, compared with that of AB-stacked 12C/12C BLG. e Raman G peaks evolution of AB-stacked 12C/13C BLG with increased PDMS tensile strain. Scale bar in c: 5 μm.
The construction of an ultraclean vdW interface is another crucial factor in accurately analyzing the mechanical coupling between 2D layers. Previous studies have used layer-by-layer wet transfer to build the stacks18,19, but it introduces impurities and brings errors to the results. In contrast, Chemical vapor deposition (CVD) -synthesized BLG has natural and better-defined interface for quantitative characterization. By carefully adjusting the H2 to CH4 flow ratio during CVD, we obtain large BLG islands with regular hexagonal shapes and zigzag edges24,25, as shown in preliminary optical microscopy (OM) and scanning electron microscopy (SEM) characterizations of the synthesized samples (Supplementary Fig. 2). It is noteworthy that the smaller adlayer is grown underneath the first layer after CVD process24,26,27, after transfer they are flipped, so that the adlayer is on top and the first layer attaches to the flexible substrate. This pyramid stack (Fig. 1b) has been proven as the most efficient structure to transfer stress between graphene layers28. In our experiments, the lateral size of the top graphene layers range from 30 to 90 μm, and that of the bottom layers are larger than 5 mm, ensuring the location of the former within the uniform strain region of the latter, according to the Saint-Venant’s principle29. In this work, we focus on the analysis of AB-stacked BLG (AB-BLG), in which the projection of half of the atoms in the top layer is at the carbon-ring center of the bottom layer, as illustrated in the OM image (Fig. 1c). AB-stacked 12C/13C BLG islands are selected via their broad Raman 2D peaks, which are at ~2640 cm–1 and merged by eight subpeaks27 (Fig. 1d). In-situ Raman measurements on these isotope-labeled BLG were conducted during the stretching of flexible substrates, and a typical G peak evolution of the 12C bottom layer and the 13C top layer is shown in Fig. 1e. Apparently, both peaks redshift and split into two subpeaks (12G+ and 12G–, 13G+ and 13G–), demonstrating that uniaxial tension occurs in both graphene layers through the stress transfer at the vdW interfaces of the substrate/bottom graphene and the bottom/top graphene.
ISS calculation based on strain evolution of two layers
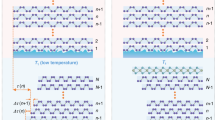
We present the evolutions of εll (the strain along the tensile direction) at the central regions of the top and bottom layers for a 36-μm AB-BLG with increased substrate strain (Fig. 2a). The strain values are obtained from Eq. (1) based on the 12C and 13C Raman G peak shifts. Besides the pre-stretching and strain relaxation, the top (blue dot) and bottom (red dot) graphene layers exhibit three sequential stages of strain characteristics as substrate stretches. During the first stage, the strains in both layers gradually increase with the same value, indicating that they have the same tensile deformation. When the substrate is stretched to a certain extent and the shear strain arose from the vdW interaction between top and bottom layers reaches the maximum, the BLG evolves into the second stage, in which the strain in the bottom layer continues to increase but slows down its rate, whereas the strain in the top layer maintains unchanged. At this stage, sliding of the top layer on the bottom layer occurs. Finally, the strains in the top and bottom graphene layers decrease dramatically, implying the fact that the vdW interaction cannot afford the relative shear deformation between the layers and substrate any longer and the interface is failed. Considering that we focus on the study of the ISS that is defined as the starting point of the interlayer failure13, i.e. the interface of the edge region starts to fail, we choose to only measure the regular strain distributions at the bond stage. Although the Raman result of the center region shows two more processes of sliding and decoupling here, they both occur after the failure of the edge regions, so that is negligible in the discussion here.
a Strain evolution of the top and bottom layers for an AB-BLG with substrate stretching. b, c Strain distributions along the tensile direction in the top and bottom graphene layers, respectively. d Calculated ISS of BLG as a function of its top layer size. The ultimate ISS value is fitted from the inverse proportionality of the data and indicates the ISS governed purely by vdW interaction for an infinite-sized BLG.
By scanning the Raman spectra of the BLG island along the tensile direction, we plot its εll distributions of the top and bottom layers under different substrate strains, respectively, normalized by the top layer size. The actual size of the top layer is 30 μm (Supplementary Fig. 3). The strain distributions in the top layer have a plateau-like shape, and the plateau height gradually increases with increased substrate strain, but the strains at both edges remain zero. On the contrary, the strain distributions in the bottom layer have a complementary basin-like shape, where its minimum strain is nearly the same as the maximum strain of the top layer, and the maximum strains in the bottom layer appear at its two edges (Fig. 2b, c, and Supplementary Fig. 4).
The fitted solid lines for the data (see Supplementary Note 1) demonstrate that the strain distributions in both graphene layers are consistent with the shear-lag model13, and the ISS of AB-stacked BLG that describes the strength of its vdW shear coupling can be obtained by
where τc is the ISS, E is the Young’s modulus of graphene that is assumed as 350 N m−1, εc is the maximum strain in the top graphene layer, and L is the lateral size of the top layer along the tensile direction.
A series of experiments were conducted using BLG with different sizes, and the results showed that the size of the top layer plays a crucial role in the ISS of BLG, i.e., the ISS exhibits an apparent inverse proportionality with the size (Fig. 2d). In solid mechanics, ISS is a significant constant for bulk materials and represents the maximum affordable stress during the shearing deformation, and based on the definition, it equals the internal stress per area averaged from the sum of interfacial vdW interactions. With the assumption deduced from Fig. 2d that the edge of the top graphene layer has a much stronger vdW interaction with the bottom layer, we attribute the origin of this inverse proportionality of ISS to the different vdW interactions in the edge and terrace regions of BLG (Supplementary Fig. 5). Based on this assumption, the experimental data in Fig. 2d can be well-fitted by a first-order inversely proportional function. Moreover, according to the fitted line, ultimate ISS of 0.015 MPa can be obtained in an extreme case where the size of the top graphene layer is infinitely large, which represents the ISS of AB-stacked BLG caused only by vdW interactions between the layer terraces. This value is comparable to that of 0.04 MPa reported in a previous literature17, and the difference is reasonably understandable considering that the sample in the literature is not infinitely large. The ISS of BLG with different sizes may have reference significance for the mechanical properties of graphene-based composite materials.
Edge effect analysis from MD simulation
To understand the ISC of AB-stacked BLG, MD simulations were carried out using the large-scale atomic/molecular massively parallel simulator (LAMMPS)30. A two-layer graphene sheet with a large bottom layer (red) and a small top layer (blue) is placed on an infinite substrate (yellow) to avoid wrinkles in graphene (Supplementary Fig. 6). The widely-used adaptive intermolecular reactive empirical bond order (AIREBO) potential31 is employed to describe the C-C in-plane atomic interactions in each graphene layer, the Kolmogorov and Crespi (KC) potential32 is used to describe the interlayer vdW interaction between the graphene layers, and the Lennard-Jones (LJ) potential is adopted for the vdW interaction description between the substrate and the bottom graphene layer33. For all simulations, the substrate is regarded as rigid, and uniaxial tensile displacements are directly applied to the edges of the bottom graphene layer.
The simulated εll distributions in the two layers of a strained BLG show plateau- and basin-like shapes that are consistent with the experimental results. For a 36.9-nm-long BLG, its top and bottom graphene layers are strongly bonded to deform simultaneously, with the maximum strains of 0.73% for the former and 0.77% for the latter (Fig. 3a, b, and Supplementary Fig. 7). To further investigate the influence of edges on the ISC, more MD simulations of BLG with the top layer size of 30.0, 51.6 and 65.4 nm were conducted and their top layer εll distributions are calculated. When the top layer of BLG is stretched to the maximum strain, the interlayer shear forces between the layers reach the maximum as well. The maximum strain to bond the layers in BLG increases nonlinearly with the BLG size and eventually reaches ~0.8% (Fig. 3c). If we define the region with strain less than 90% of the maximum strain as the edge-affected region, its lengths for 30.0-, 36.9-, 51.6-, and 65.4-nm-long BLG are 13.8, 17.2, 20.6, and 21 nm, respectively. The 51.6-nm-long BLG has the threshold length for this edge-affected region, and when the size of BLG is larger, the influence of edges over the sheet becomes smaller. As a direct consequence of the edge effect, the maximum value of calculated interlayer shear force decreases with the size of BLG increasing (Fig. 3d), confirming the inverse proportionality of ISS in our experiments.
To further reveal the atomic mechanism underlying the edge effect, we studied the interlayer energy distributions of BLG along the tensile direction with different strains (Fig. 4a). The energy increase caused by the applied force is mainly concentrated in the edge region, which is also a manifestation of the stronger van der Waals interaction. The magnified top view of the edge region in simulated BLG is presented for more details (Fig. 4d). When BLG is unstrained, its top and bottom layers exhibit an AB stack. When the uniaxial tensile strain increases, the interlayer dislocations in BLG gradually occur and evolve. Interestingly, the stacked atoms in both layers move relatively in both directions that are parallel and perpendicular to the applied force, as illustrated by the blue and red hexagons that represent the top and bottom graphene lattices, respectively (the central and left edge regions are shown in Supplementary Fig. 8). More careful investigations into the simulated graphene layers suggest that the interlayer dislocation is a relative rotation between the two graphene layers (Supplementary Fig. 9) and such rotation is clearly due to the lack of material’s dimension and can be considered as a dimensional effect, thus we suspect that the higher interlayer energy at the edge is due to the rotated dislocation in the edge region. Based on this view, a simplified MD model was constructed in which the bottom graphene layer is fixed and the top layer is rotated along the clockwise direction (Fig. 4b). The interlayer energy increment as a function of the rotation angle between the layers is calculated (Fig. 4c), exhibiting an exponential increase even with a slight change of the rotation angle. Moreover, the interfacial interactions between the outermost edge atoms of the top graphene layer and the bottom graphene layer are stronger than those between the other regions through a slightly shorter vdW distance34, because these atoms are not terminated by other carbon atoms and have higher degrees of freedom, as shown in the cross-section view of the edge morphology of BLG (the inset of Fig. 4d). This enhanced interlayer interaction for edge atoms will also contribute to the edge effect in BLG especially when the graphene size is small. Furthermore, many critical issues that determine the application performance of the 2D vdW stacks, especially in graphene-based composite materials and flexible electronic devices, depending on the understanding of the interfacial load transfer and their optimization that are also supported by the experimental data.
a Interlayer energy distribution of BLG under different applied strains. b Schematic of simulated rotated BLG. c Energy increment as rotation angle varies in BLG. d Top and side views of the right edge region for simulated BLG and the variation of interlayer dislocation in a top view with increasing strain. The blue and red hexagons represent the top and bottom graphene lattices, respectively.
In conclusion, we study the ISC of AB-BLG with the naturally grown interface and one layer substituted by 13C isotope using Raman spectroscopy, and explore the origin of ISC through MD simulations. Under uniaxial tension, the two layers of BLG show three sequential stages: simultaneous deformation, top layer sliding and the failure of the interface. Moreover, the obtained ISS exhibits an inverse proportionality on the size of BLG. Checking against the present MD simulations, it shows that the inverse proportionality is originated from the rotated interlayer dislocations and atoms with shorter vdW distances in the edge region, which contributes higher interlayer energy to the interface. We believe that these results not only provide new fundamental insights into the multiscale interpretation of macroscopic interfacial shear properties of 2D vdW stacks but also have great potential in guiding the design of graphene-based composite materials and flexible 2D electronics.
Methods
BLG synthesis
13C-isotope-labeled BLG was synthesized by the CVD method on Cu24. A commercially-available Cu foil (#46365, Alfa Aesar China Chemical Co., Ltd.) was firstly cleaned and annealed at 1060 °C in an atmosphere of 300 standard cubic centimeter per minute (sccm) H2 and then 10 sccm O2, followed by introducing 12CH4 into the growth chamber for 1 to 1.5 h. Then 12CH4 was stopped and evacuated, and 13CH4 was introduced for another 1 to 1.5 h. Finally, the growth chamber was cooled to room temperature without stopping the gases, and characterizations of OM (Olympus BXFM-ILHS, Olympus Co., Ltd), SEM (5KV, S-3400 I, Hitachi Co., Ltd) were conducted for the quality evaluation of synthesized graphene.
BLG transfer
BLG islands with two layers formed by different isotopes were selected and transferred for tensile experiments using formvar-coated PDMS substrates as we reported previously15. A thin layer of formvar (1 wt.% in chloroform) was dip-coated onto the surface of graphene, then a 0.7-mm-thick PDMS (Sylgard 184 elastomer Kit, Dow Corning, USA) film with a much larger size was closely attached onto the formvar surface. After removing the Cu substrate by aqueous 1 M FeCl3, the sandwiched graphene/formvar/PDMS sample was rinsed and cut into a 16 mm × 5 mm piece for strain loading.
Strain measurement
A homemade tensile testing machine modified from a micrometer-equipped multiaxis stage (MAX313D, ThorLabs, Inc.) was used to stretch the sample uniaxially at 1.5 μm s–1, corresponding to a tensile strain rate of 0.0175% s–1 for PDMS. The strain in graphene is measured by micro-Raman spectroscopy (LabRAM HR Evolution, Horiba Co., Ltd.) using a laser with an excitation wavelength of 532 nm. A long-focal-depth 50× objective lens with NA = 0.95 and a standard grating of 1800 grooves mm−1 were used for signal collection, and the polarization of the incident light was kept perpendicular to the tensile direction. The diameter of the laser spot was estimated as 1 μm, and the spectral resolution is approximately 0.5 cm–1. Here the laser power is 1.25 mW, and its thermal effects can be neglected (Supplementary Fig. 10). The obtained Raman spectra were analyzed using LabSpec6 software.
Data availability
All data needed to evaluate the conclusions in the paper are included in the paper and/or the Supplementary Materials. Additional data related to this paper may be requested from the authors.
References
Novoselov, K. S., Mishchenko, A., Carvalho, A. & Castro Neto, A. H. 2D materials and van der Waals heterostructures. Science 353, aac9439 (2016).
Liu, Y. et al. Van der Waals heterostructures and devices. Nat. Rev. Mater. 1, 16042 (2016).
Liu, Y., Huang, Y. & Duan, X. Van der Waals integration before and beyond two-dimensional materials. Nature 567, 323–333 (2019).
Cao, Y. et al. Correlated insulator behaviour at half-filling in magic-angle graphene superlattices. Nature 556, 80–84 (2018).
Burch, K. S., Mandrus, D. & Park, J.-G. Magnetism in two-dimensional van der Waals materials. Nature 563, 47–52 (2018).
Zhang, Y. et al. Direct observation of a widely tunable bandgap in bilayer graphene. Nature 459, 820–823 (2009).
He, Y. et al. Strain-Induced Electronic Structure Changes in Stacked van der Waals Heterostructures. Nano Lett. 16, 3314–3320 (2016).
Gao, Y. et al. Elastic coupling between layers in two-dimensional materials. Nat. Mater. 14, 714–720 (2015).
Li, B. et al. Probing van der Waals interactions at two-dimensional heterointerfaces. Nat. Nanotechnol. 14, 567–572 (2019).
Mohiuddin, T. M. G. et al. Uniaxial strain in graphene by Raman spectroscopy: G peak splitting, Grüneisen parameters, and sample orientation. Phys. Rev. B 79, 205433 (2009).
Huang, M. et al. Phonon softening and crystallographic orientation of strained graphene studied by Raman spectroscopy. Proc. Natl Acad. Sci. USA. 106, 7304–7308 (2009).
Yu, T. et al. Raman mapping investigation of graphene on transparent flexible substrate: The strain effect. J. Phys. Chem. C. 112, 12602–12605 (2008).
Jiang, T., Huang, R. & Zhu, Y. Interfacial sliding and buckling of monolayer graphene on a stretchable substrate. Adv. Funct. Mater. 24, 396–402 (2014).
Frank, O. et al. Compression behavior of single-layer graphenes. ACS Nano 4, 3131–3138 (2010).
Wang, Y. L. et al. Domain-boundary independency of Raman spectra for strained graphene at strong interfaces. Carbon 134, 37–42 (2018).
Wang, Y., Cong, C., Qiu, C. & Yu, T. Raman spectroscopy study of lattice vibration and crystallographic orientation of monolayer MoS2 under uniaxial strain. Small 9, 2857–2861 (2013).
Wang, G. et al. Measuring interlayer shear stress in bilayer graphene. Phys. Rev., Lett. 119, 036101 (2017).
Dou, W. et al. Interfacial mechanical properties of double-layer graphene with consideration of the effect of stacking mode. ACS Appl. Mater. Interfaces 10, 44941–44949 (2018).
Androulidakis, C., Koukaras, E. N., Paterakis, G., Trakakis, G. & Galiotis, C. Tunable macroscale structural superlubricity in two-layer graphene via strain engineering. Nat. Commun. 11, 1595 (2020).
Li, X., Cai, W., Colombo, L. & Ruoff, R. S. Evolution of graphene growth on Ni and Cu by carbon isotope labeling. Nano Lett. 9, 4268–4272 (2009).
Kalbac, M. et al. Raman spectroscopy and in Situ Raman spectroelectrochemistry of bilayer C-12/C-13 graphene. Nano Lett. 11, 1957–1963 (2011).
Frank, O., Dresselhaus, M. S. & Kalbac, M. Raman spectroscopy and in Situ Raman spectroelectrochemistry of isotopically engineered graphene systems. Acc. Chem. Res 48, 111–118 (2015).
Liu, J. et al. Inherent strains in chemical-vapor-deposited bilayer graphene on Cu. Carbon 184, 109–114 (2021).
Liu, J. et al. Sequential growth and twisted stacking of chemical-vapor-deposited graphene. Nanoscale Adv. 3, 983–990 (2021).
Zhao, P. et al. The role of hydrogen in oxygen-assisted chemical vapor deposition growth of millimeter-sized graphene single crystals. Nanoscale 8, 7646–7653 (2016).
Li, Q. et al. Growth of adlayer graphene on Cu studied by carbon isotope labeling. Nano Lett. 13, 486–490 (2013).
Fang, W. et al. Rapid identification of stacking orientation in isotopically labeled chemical-vapor grown bilayer graphene by Raman spectroscopy. Nano Lett. 13, 1541–1548 (2013).
Sgouros, A. P. et al. Efficient mechanical stress transfer in multilayer graphene with a ladder-like architecture. ACS Appl. Mater. Interfaces 13, 4473–4484 (2021).
Saint-Venant, A. D. Memoire Sur La Torsion Des Prismes (Mem. Sav. Acad. Sci. Press, Paris, 1856).
Plimpton, S. Fast parallel algorithms for short-range molecular-dynamics. J. Comput. Phys. 117, 1–19 (1995).
Stuart, S. J., Tutein, A. B. & Harrison, J. A. A reactive potential for hydrocarbons with intermolecular interactions. J. Chem. Phys. 112, 6472–6486 (2000).
Kolmogorov, A. N. & Crespi, V. H. Registry-dependent interlayer potential for graphitic systems. Phys. Rev. B 71, 235415 (2005).
Dong, S., Zhu, C., Chen, Y. & Zhao, J. Buckling behaviors of metal nanowires encapsulating carbon nanotubes by considering surface/interface effects from a refined beam model. Carbon 141, 348–362 (2019).
van Wijk, M. M., Dienwiebel, M., Frenken, J. W. M. & Fasolino, A. Superlubric to stick-slip sliding of incommensurate graphene flakes on graphite. Phys. Rev. B 88, 235423 (2013).
Acknowledgements
This work was financially supported by the National Natural Science Foundation of China (11872330).
Author information
Authors and Affiliations
Contributions
J.L.: conceptualization, data curation, formal analysis, methodology, writing–original draft. C.Z.: formal analysis, data curation, software. Z.Z.: methodology, visualization. Q.R.: software, visualization. X.Z.: methodology. Y.Z.: methodology. Y.J.: methodology. W.Q.: methodology. H.W.: funding acquisition, supervision. J.Z.: writing – review & editing, supervision. P.Z.: conceptualization, writing – review & editing, supervision.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Liu, J., Zhu, C., Zhang, Z. et al. Interlayer shear coupling in bilayer graphene. npj 2D Mater Appl 6, 38 (2022). https://doi.org/10.1038/s41699-022-00314-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41699-022-00314-8