Abstract
van der Waals solids are ideal platforms for the discovery of new states of matter and emergent properties under external stimuli. Under pressure, complex chalcogenides like MPS3 (M = Mn, Ni, Co, V) host sliding and structural transitions, insulator-to-metal transitions, the possibility of an orbitally-selective Mott state, piezochromism, and superconductivity. In this work, we bring together diamond anvil cell techniques, infrared and Raman scattering spectroscopies, and X-ray diffraction with a detailed symmetry analysis and first-principles calculations to uncover a series of high-pressure phases in NiPS3. Remarkably, we find five different states of matter between ambient conditions and 39 GPa—quite different than in the other MPS3 materials. Even more strikingly, infrared spectroscopy and X-ray diffraction combined with a symmetry analysis reveal both metallicity and loss of the inversion center above ~23 GPa suggesting that NiPS3 may be a polar metal with a P3m1 space group under these conditions and P1 symmetry under maximum compression. In addition to identifying a candidate polar metal ripe for further inquiry, we suggest that pressure may tune other complex chalcogenides into this elusive state.
Similar content being viewed by others
Introduction
Structural phase transitions in complex chalcogenides are attracting considerable attention as drivers of exciting new states of matter with the potential to host emergent properties. As demonstrated in FePS3 as well as the Mn and V analogs, external stimuli such as pressure (and likely strain) induce a layer-sliding transition and systematic bandgap reduction followed by a volume collapse to the metallic state at room temperature1,2,3,4,5,6,7,8,9. A similar progression might be anticipated to take place in NiPS36,10,11,12,13, but even the most cursory inspection shows that this is not the case. Instead, this system hosts an entire series of structural phase transitions and associated symmetry progressions of mysterious origin. Compression thus gives rise to several new states of matter in the MPS3’s (M = Mn, Ni, Co, V)—each with properties that can be deterministically controlled. As demonstrated in FePS3 and CrSiTe3, a low-temperature structural phase transition triggers superconductivity as well2,14. Whether this is the case in NiPS3 is not yet apparent, but it is already clear that this system has a rich set of symmetry progressions12 as well as metallic11,12,15 and relaxation behavior15 making it an intriguing platform for deeper study. The recent discoveries of light-induced metallicity16 and intercalation-controlled magnetism17 provide complementary pathways for property regulation, although the structural aspects of these processes are under-explored.
In order to unravel these complexities, we combined high-pressure vibrational spectroscopies and X-ray diffraction with an extensive symmetry analysis and first-principles calculations of phase stability, lattice dynamics, and structure to explore the symmetry progression in NiPS3. Analysis of the infrared absorption and Raman scattering response reveals that pressure drives a series of structural phase transitions from C2/m → \(P\bar{3}\,\) → \(P\bar{3}m1\,\) → a polar phase above ~23 GPa where inversion symmetry is lost. At the same time, NiPS3 becomes metallic as evidenced by the development of a Drude in the infrared which screens the phonons. X-ray diffraction reveals a P3m1 space group under these conditions, so in addition to becoming metallic, the system breaks inversion symmetry. NiPS3 remains a polar metal in the two highest pressure states, which X-ray diffraction suggests are P3 and P1, respectively. This complicated symmetry progression and the development of a possible polar metallic phase draws a clear distinction between NiPS3 and its structural siblings like MnPS3, FePS3, and V0.9PS3 and signifies unique underlying physics. We discuss the unprecedented number of distinct states of matter in the symmetry progression in terms of stability and stacking sequences as well as the structure-property relationships in the MPS3 family of materials. The latter is key to understanding prospects for physical and chemical tuning as well as tailoring properties hosted by the ultra-low symmetry phases in these systems.
Results and discussion
Local lattice distortions and symmetry progression under pressure
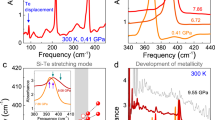
Figure 1 summarizes the vibrational response of NiPS3 under compression at room temperature. Based upon a C2/m structure at ambient conditions [Supplementary Fig. 2, of the Supplementary information], we anticipate 12 infrared-active modes (5Au + 7Bu) and 15 Raman-active modes (8Ag + 7Bg)10,18,19. Overall, the vibrational properties are in good agreement with this symmetry analysis and our first-principles lattice dynamics calculations with the exception of (i) an infrared-active Bu mode near 450 cm−1 and (ii) a Raman-active lattice mode near 110 cm−1, probably due to low oscillator strengths12,20,21. NiPS3 displays several structural phase transitions with increasing pressure. We identify the critical pressures (Pc’s) by the appearance or disappearance of peaks, splittings or combinations, and frequency shifts as discussed below22. Within our investigated range, we find three critical pressures (Pc’s) and four different phases—the last of which is a polar metal. Clearly, NiPS3 is much more complex than the Mn and Fe analogs4,6,9. The mode assignments, symmetries, and displacement patterns of NiPS3 are summarized in Supplementary Tables 1 and 2 of the Supplementary information.
a–d Close-up view of the infrared absorption and frequency vs. pressure plots. e–h Close-up view of the Raman scattering response and frequency vs. pressure plots. Spectra for the ambient pressure (AP) phase are shown in gray; those for the high-pressure phases (HP-I, HP-II, and HP-III) are shown in teal, green, and black, respectively. Closed and open circles represent two independent runs. Note that infrared spectra in the HP-III phase do not appear in our measurements because the phonons are screened by the metallic response. The critical pressures (PC’s) separate the high-pressure phases and are indicated with dashed vertical gray lines.
The C2/m → HP-I transition at 9 GPa is challenging to unravel because there is spectroscopic evidence for both increasing and decreasing symmetry. This suggests that the initial and final space groups do not have a simple group ↔ subgroup relationship across Pc1. Let’s begin by considering the evidence for increasing symmetry. Two different 2 → 1 peak condensations take place near 260 and 570 cm−1 [Fig. 1e-h]. We assign these Raman-active modes as in-plane antisymmetric bends and stretches of the P2S\({}_{6}^{4-}\) dimer units, respectively20,23. This means that in addition to the mirror planes, axial glides, inversion centers, two-fold rotations, and the two-fold screw axes that characterize the C2/m space group, the system gains additional symmetry elements across Pc1 = 9 GPa. Examination of C2/m group ↔ supergroup relationships in Supplementary Fig. 1 provides several candidates for this intermediate phase including \(P\bar{3}1m\), \(P\bar{3}m1\), and Cmmm. We can distinguish between these different space groups by realizing that a reduction in out-of-plane motion of the phosphorous-dimer atoms (560 cm−1) and changes in Ni positions (255 cm−1) combined with a decrease in monoclinic angle4,12 establish new mirror planes, axial glides, two-fold rotations, and two-fold screw axes in the ab-plane. Taken together, these findings support a \(P\bar{3}1m\) space group. Vibrational spectroscopy also contains evidence for symmetry breaking across the 9 GPa transition, and the loss of these specific symmetry elements has to be taken into account in order to identify the space group of HP-I. Symmetry reduction is, of course, signaled by the appearance of new peaks. The rise of the out-of-phase intralayer Ni translational mode in the Raman scattering response near 120 cm−1 across Pc1 is a beautiful example of this effect [Fig. 1e, f]. A second example involves the infrared-active out-of-plane antisymmetric PS3-bending modes near 280 cm−1 [Fig. 1a, b]. The key is to unravel how these modes correspond to the symmetry elements that are lost across Pc1. We do this by considering the relevant mode displacement patterns and how they impact different symmetry elements. These include some of the newly established symmetry elements of \(P\bar{3}1m\) such as axial glide planes, two-fold rotations, and two-fold screw axes. Candidate subgroups include P31m, \(P\bar{3}\), and P312. Moreover, while many symmetry elements are lost here, the inversion center remains intact and is very robust under compression. Furthermore, we do not see a large increase in the overall number of peaks in the spectra. It is also important to note that the infrared and Raman spectra are never equivalent, thus providing additional evidence for retention of the inversion center. Of the three candidate subgroups of \(P\bar{3}1m\), only \(P\bar{3}\) retains the inversion center. We therefore assign the 9 GPa structural phase transition as C2/m → \(P\bar{3}\). As shown in Supplementary Fig. 4, X-ray diffraction is consistent with this result.
There is another structural phase transition at Pc2 = 16 GPa. Increasing symmetry from \(P\bar{3}\) → HP-II, group theory provides five space group candidates: \(P\bar{3}1m\), P6/m, P63/m, \(P\bar{3}c1\), and \(P\bar{3}m1\). \(R\bar{3}\) was also considered because it is seen in similar materials including α-RuCl3 and CrSTe3, although these materials are spectroscopically quite different with an overall fewer number of vibrational modes and likely inconsistent with our data24,25. We can remove some of the candidates from this list almost immediately. From a comparison with the intermediate space group from the \(C2/m\to P\bar{3}\) transition, changes in the spectra indicate that NiPS3 does not revisit \(P\bar{3}1m\). Without any evidence for six-fold symmetry, the material does not appear to increase symmetry to either P6/m or P63/m. We are therefore left to select between \(P\bar{3}c1\) and \(P\bar{3}m1\). In order to discriminate between these two space groups, we examine experimental evidence in Fig. 1a, b alongside an analysis of the space group-specific symmetry elements in Supplementary Table 3, of the Supplementary information. While the Raman-active vibrational modes change smoothly across Pc2, the infrared response is much more revealing and useful. We focus on the Au infrared-active mode at 189 cm−1. The displacement pattern of this mode consists of in-plane Ni translations within the layer and out-of-plane S motions. The disappearance of this mode at Pc2 signals increased symmetry in HP-II [Fig. 1a, b]. More specifically, the loss of this motion indicates the development of additional axial glides and mirror planes along the c-axis as well as two-fold rotations and screw axes in the ab-plane. The addition of these symmetry elements is consistent with \(P\bar{3}m1\). While two-fold rotations and screw axes are expected to develop in \(P\bar{3}c1\) as well, diagonal glide planes are also anticipated. There is, however, no evidence for diagonal glide plane formation in HP-II. The smooth behavior of the out-of-plane S motion of the Bu mode at 194 cm−1 is also inconsistent with significant new interlayer interactions across Pc2 = 16 GPa. These findings are in line with our high-pressure X-ray diffraction which refines to \(P\bar{3}m1\) above 16 GPa [Supplementary Fig. 4, of the Supplementary information]. The sequence of pressure-induced transitions thus far is C2/m → \(P\bar{3}\,\) → \(P\bar{3}m1\).
NiPS3 has an additional structural phase transition at Pc3 = 23 GPa. As we argue below, the space group progression across this transition (from HP-II to HP-III) is \(P\bar{3}m1\,\) → P3m1. Unfortunately, the spectra in Fig. 1 provide no mode splittings or frequency shifts across Pc3 that can be used to unravel the next step in the symmetry progression. This does not mean, however, that the data are not of any use. The Raman-active modes in Fig. 1 harden continuously across Pc3 and remain unaffected by the pressure-driven transition. This indicates that there are no changes in local structure emanating from even-symmetry displacements and that subgroups involving such distortions can be eliminated from consideration. We next turn our attention to the infrared response in order to consider the possible role of odd-symmetry distortions. Unfortunately, the development of a Drude screens the behavior of the infrared-active phonons above 23 GPa. Thus, while the infrared response establishes metallicity (albiet at a slightly lower pressure than that from transport work)12,15, it does not provide any information on the behavior of the infrared-active phonons above 23 GPa.
Figure 2 displays the infrared reflectance of NiPS3 under compression. The overall level rises significantly with increasing pressure, consistent with developing metalicity. The latter also screens the infrared-active P–S stretching mode near 590 cm−1, in line with the discussion above. This metallicity is consistent with the middle-infrared spectra of Ma et al.12, and in combination with the loss of the inversion center (established by X-ray scatting, discussed below) suggests that NiPS3 may be a polar metal at pressures above 23 GPa. Along with metallicity, polar metals require a continuous second-order structural transition, the loss of an inversion center, and the development of a unique polar axis26. Screening of long-range Coulombic forces and elimination of polar moment ordering makes this state of matter quite uncommon. Very few polar metals have been experimentally realized. Examples include LiOsO3, Cd2Re2O7, the Td phases of MoTe2 and WTe2, and antiperovskite Hg3Te2X227,28,29,30,31,32. Although the size of any polarization and whether it is ferroelectric (switchable) or pyroelectric (not switchable) are unexplored, the possibility of ferroelectricity in the metallic state of a chalcogenide like NiPS3 opens the door to many intriguing opportunities for studying this intriguing state of matter. Furthermore, if the polar metal state can be stabilized under low pressures or strain, there will be applications in nanoelectronics since these effects take place at room temperature.
a Reflectance of NiPS3 as a function of frequency showing the development of metallicity under pressure. Dashed lines omit the well-known diamond signature and guide the eye. b Close-up view of the 590 cm−1 P-S stretch which is increasingly screened by the Drude under pressure, consistent with the development of metallicity. The metallicity develops gradually, in line with transport results12,15 and consistent with a infrared-active second-order transition. This implies that a group-subgroup symmetry analysis is reasonable. c Calculated displacement pattern of the P-S stretching mode. Phosphorus and sulfur centers are purple and yellow, respectively. Black arrows indicate both direction and magnitude of the distortion.
A subgroup analysis for \(P\bar{3}m1\) suggests several possible pathways by which symmetry in NiPS3 can be reduced. As before, some can be immediately eliminated. For instance, the spectroscopic results are different from the ambient pressure phase and HP-I, indicating that HP-III does not possess C2/m symmetry or revisit \(P\bar{3}\). To differentiate between the remaining two space groups, P3m1 and P321, we bring our spectroscopic findings together with X-ray diffraction as discussed below. Importantly, both of these candidate space groups are polar and lack an inversion center.
Establishing loss of the inversion center above 23 GPa by X-ray scattering
Figure 3a displays the X-ray diffraction profile of NiPS3 as a function of pressure at room temperature. Similar to the vibrational properties work, we identify the PC’s by the appearance/disappearance of various resonances as well as changes in peak position and splitting. The critical pressures extracted from the X-ray diffraction studies are in excellent agreement with those obtained from the infrared absorption and Raman scattering measurements. The phases are again labeled from ambient pressure (AP) through the various high-pressure phases (HP-I to HP-V). Figure 3b, c displays diffraction images recorded at 13 and 24 GPa, in high-pressure phases HP-I and HP-III, respectively. These images indicate that NiPS3 remains single-crystal-like across the full series of structural transitions up to 39 GPa [Supplementary Fig. 4, of the Supplementary information]. One of the challenges that arise from the experimental configuration and angle of incidence is that we do not collect all of the diffraction peaks. This issue prevents a full refinement of the high-pressure structures. On the other hand, there are usually enough peaks to distinguish between symmetry candidates. We therefore carried out the least-squares fitting of the lattice constants [Table 1] to investigate the symmetries suggested by vibrational spectroscopy. The space groups are labeled accordingly in Fig. 3.
a Integrated X-ray diffraction profiles under pressure. The appearance of X-ray diffraction peaks at the given angle are indicated, alongside dashed lines to guide the eye. Critical pressures, dividing individual pressure phases, are indicated by solid blue horizontal lines. The space groups of individual high-pressure phases are labeled. The asterisk (*) and plus (+) marks correspond to the diffraction response from NaCl in B1-type structure (below 30 GPa) and B2-type (above 30 GPa)46. b, c The X-ray diffraction images on the detector for HP-I (13 GPa) and HP-III (24 GPa). The peaks from NiPS3 are enclosed with squares alongside the hkl indices for each phase. The gray labels in c indicate the diffraction from HP-II. The Bragg diffraction from the diamond anvils is masked with red circles.
To complement our spectroscopic work, we performed high-pressure X-ray diffraction measurements between 0 and 39 GPa and carried out detailed refinements of each phase that were compared with minimum energy calculations. We discuss the analysis of HP-III as an illustration of this process. As a reminder, infrared spectroscopy reveals that this phase is metallic [Fig. 2]. The predicted space group candidates are P3m1 and P321. Both of these space group candidates fit similarly well to the X-ray data based upon the values of their lattice constants [Table 1]. For example, the peaks at 2Θ = 4.8°, 8.3°, 14.5°, and 14.8° correspond to (h, k, l) = (1,0,0), (1,1,0), (3,0,0), and (3,0,1), respectively [Fig. 3c]. We discovered, however, that P321 does not retain the hexagonal structure centered around the P2S\({}_{6}^{4-}\) dimer, suggesting P3m1 as the most probable space group for HP-III. A schematic structure of this phase is provided in Supplementary Fig. 5 of the Supplementary information. The sequence of transitions under pressure is therefore C2/m → \(P\bar{3}\,\) → \(P\bar{3}m1\,\) → P3m1.
We carried out a similar analysis for all of the phases from AP to HP-V. Although perfect fits are not always obtained [Table 1], the extracted space groups from AP to HP-III are in excellent agreement with the spectroscopic results. The data also suggest that the symmetry of NiPS3 continues to decrease with increasing pressure [Fig. 3 and Supplementary Fig. 4]. With evidence for symmetries lower than P3m1 under additional compression, we anticipate the space groups for HP-IV and HP-V to be P3 and P1 respectively. In principle, P1 should have a larger electric polarization than either P3m1 or P3.
Evidence for the series of pressure-induced transitions from ab initio calculations
In order to provide insight into the structural transitions and lattice dynamics of NiPS3, we carried out a combinatorial search of all possible stacking sequences up to and including three-layer periodicity followed by first-principles density functional theory calculations including on-site Coulomb repulsion, magnetism, and van der Waals correction. Three potential candidates were identified: (i) the well-known bulk C2/m structure with staggered phosphorus dimers where each layer slips by a/3 along the monoclinic a-axis, (ii) the trigonal \(P\bar{3}\) structure with three-layer periodicity along the c-axis, and (iii) the triclinic P1 structure, the lowest symmetry space group with the same c-axis periodicity as \(P\bar{3}\). Note that the suggested intermediate high-pressure space groups \(P\bar{3}m1\) and P3m1 could not be accommodated within our model crystal structures. We also mention in passing that sticking between adjacent NiPS3 layers, reported in ref. 12 but unobserved in our current calculations, can be reproduced only when the on-site Coulomb repulsion and magnetism are ignored. It is our experience that neglecting the Coulomb repulsion and magnetism in MnPS3 and NiPS3 leads to substantial underestimation of the lattice parameters as well11. Further computational detail is available in the Methods section.
Figure 4a displays enthalpy versus pressure for the three candidate structures mentioned above. At ambient conditions, the C2/m phase is energetically stable—consistent with the experiment. The other two structures are slightly less favorable with energies that are 3–4 meV higher. We find that the enthalpies of both P1 and \(P\bar{3}\) drop below that of the C2/m phase near 4 GPa. The critical pressure varies significantly depending upon the choice of the U parameter and the type of van der Waals correction. That said, we do not find evidence for a \(P\bar{3}\) ground state up to 20 GPa. The origin of this fast stabilization of the P1 phase is unclear at this time and is under study now. Note that the calculated enthalpy difference between C2/m, \(P\bar{3}\), and P1 is less than 20 meV per formula unit even up to 20 GPa, smaller than the energy scale of thermal fluctuations at room temperature (≈30 meV). The incorporation of temperature effects in the lattice dynamics calculations may stabilize \(P\bar{3}\) in the intermediate pressure range. By contrast, enthalpy differences between competing phases in MnPS39 and FePS38 are greater than 50 meV per formula unit. The small enthalpy difference between competing structural phases along with a narrower van der Waals gap20 may be the origin of the sluggish15 and complicated set of pressure-induced structural phase transitions in NiPS3. Finally we note in passing that the \(P\bar{3}1m\)-type stacking which is reported to occur in the high-pressure regimes of MnPS39, FePS34,7,8, and V0.9PS35 is not stabilized in NiPS3, and in our first-principles calculations, it becomes increasingly unfavorable under pressure. At 20 GPa, the relative enthalpy of the \(P\bar{3}1m\) phase with respect to C2/m reaches between 30 and 60 meV per formula unit—depending on the type of magnetism and exchange-correlation functionals employed (not shown). Figure 4b, c displays a comparison of calculated and experimental infrared- and Raman-active mode frequencies as a function of pressure. Overall, the computed frequencies are in excellent agreement with our experimental results. The measured infrared response, for instance, reveals a gradual change in slope of the {A, B}u modes close to 230 cm−1 near 12 GPa. Based on our computed phonon frequencies, we can understand this structure as the merging of {A, B}u modes (blue and violet lines) into an Eu doublet (orange solid line beyond 8 GPa); this merge takes place with a 10 cm−1 red shift. In addition, the experimental infrared response shows the sudden appearance of a peak around 280 cm−1 beyond 12 GPa, which matches well with the theoretical orange line and can be identified as another Eu mode. The agreement between computational and experimental findings is less evident in the Raman data due to the overall density of modes [Fig. 4c], but we comment that merging the two separate modes near 280 cm−1 close to 8 GPa, possibly the Ag and Bg modes, into a single Eg doublet can account for our results.
a Relative enthalpies of the \(P\bar{3}\) and P1 phases with respect to C2/m. b, c Comparison between frequencies of computed and experimental b infrared and c Raman modes. For clarity, Au/g (blue) and Bu/g (violet) modes from the C2/m phase and Eu/g (orange) modes from the \(P\bar{3}\) phase are selected for display. The experimental frequencies are overlaid in open circles (cyan). The experimental frequencies were shifted from the theoretical data by 5 and 8 cm−1 in panels b and c, respectively, to overlap the theoretical curves. Frequencies from the C2/m (\(P\bar{3}\)) phase are depicted as solid (dashed) lines below 8 GPa and dashed (solid) lines above 8 GPa.
Overall, our theoretical results are reasonably consistent with the experimental observations. The theory correctly predicts C2/m as the ambient pressure phase as well as a structural transition from C2/m to \(P\bar{3}\). It also identifies P1 as the final state. There are also, unfortunately, some inconsistencies. These include: (i) X-ray and spectroscopic measurements show the P1 phase should appear beyond 30 GPa, whereas theory always favors P1 over \(P\bar{3}\), (ii) the c-axis periodicites of the \(P\bar{3}\) structure are different, with computational structures tending to prefer more complex stacking patterns for \(P\bar{3}\). and (iii) we do not identify \(P\bar{3}m1\) and P3m1 space groups as low energy candidates in the intermediate pressure range—despite their identification in the experiment. These discrepancies may have their origins in our model structures which do not contain components of in-plane-symmetry lowering and the resulting multiplications of in-plane periodicity.
Finally, it is worth mentioning that the behavior of NiPS3 is vastly different from MnPS3, FePS3, and V0.9PS3 under pressure where structural and insulator-metal transitions drive the formation of phosphorous chains along the layer-normal direction4,5,9. We speculate that (i) charge-transfer involving Ni2+33,34 may disfavor phosphorous ion participation in the insulator-metal transition thereby preventing the simple \(P\bar{3}1m\)-type stacking observed in the Mn, Fe, and V analogs, and (ii) the much narrower van der Waals gap in NiPS320, possibly originating from partially filled eg orbitals and the consequent stronger inter-plane interactions11, may prevent layers from sliding easily to form the more familiar stacking patterns. Taken together, these mechanisms may contribute to more complex stacking patterns of the Ni honeycomb layers as well as local lattice distortions within the layers.
Possible polar metallicity in NiPS3, other complex chalcogenides, and the two-dimensional limit
The unique symmetry progression in NiPS3 under compression provides an opportunity to explore a variety of different states of matter not present in other members of the MPS3 family of materials. By combining high-pressure vibrational spectroscopies and X-ray diffraction with an extensive symmetry analysis and first-principles calculations, we show that this system displays a series of five different structures from C2/m at ambient conditions to P1 above 35 GPa. Strikingly, NiPS3 appears to be a polar metal above ~23 GPa due to the development of metallicity (evidenced by a Drude in the infrared that screens the phonons) and loss of the center of inversion (established by a combined symmetry and structural analysis). Whether this phase is ferroelectric (switchable) or pyroelectric (not switchable) is not yet clear; future work will surely address this question. Although of contemporary interest, polar metals are uncommon and currently not well understood. Physical systems are in short supply due to the need to overcome the innate opposition between metallicity and the presence of polar moments27,30,32. The most common way to overcome these competitive effects is with a unique polar axis26,35. The latter is often a result of an anisotropic crystal environment, can be induced through the application of external stimuli: pressure, strain, and magnetic field. Such a mechanism is possible in NiPS3 if the unique polar axis is along with c. In any case, the discovery of a candidate physical manifestation of this elusive state of matter is useful and important, offering a real system on which to carry out experiments and test predictions. Additionally, exploring the opposite effect of pressure by dimensionality-lowering layer exfoliation20 or thin-film growth may reveal unprecedented states of matter36, considering that strong spin-orbital-lattice coupling33,34 and interlayer interactions11 in NiPS3 may result in a complicated interplay in the two-dimensional limit. We anticipate that our findings will inspire further exploration of NiPS3 and a search for polar metallicity in other complex chalcogenides.
Methods
Crystal growth and loading of the diamond anvil cell
NiPS3 single crystals were prepared by chemical vapor transport techniques as described previously37. In order to fulfill the need to access high pressures alongside the requirement for the necessary throughput for the experiments, various diamond culets and gasket sizes were employed. Typically, single-crystal samples were loaded into a symmetric diamond anvil cell with 300 μm anvils using a stainless steel gasket with a thickness on the order of 50 μm and a 100 μm hole along with a pressure medium and an annealed ruby ball. Type IIas and ultra-low fluorescence diamonds were employed for infrared absorption and Raman scattering, respectively. Signal response for each measurement was maximized for the excitations of interest. Depending on the measurement, a quasi-hydrostatic pressure environment was obtained using KBr (Raman and middle-infrared) or petroleum jelly (far-infrared) as a pressure-transmitting medium. Fluorescence from the R1 peak of the ruby ball was used for pressure determination38. Similarly, we loaded single-crystalline NiPS3, NaCl pressure-transmitting medium, and ruby chips for pressure calibration38 into a diamond anvil cell for X-ray diffraction measurements. In the present X-ray diffraction measurement, the single crystals were loaded with the ab-plane parallel to the diamond face. A pre-compressed NaCl flake was placed underneath the sample. This pressure-transmitting medium assured that the pressure distribution across the sample was as homogeneous as possible.
Spectroscopic measurements
High-pressure infrared measurements were carried out in both transmittance and reflectance mode over the 50–8000 cm−1 frequency range with a resolution of 2 or 4 cm−1 for far and middle-infrared, respectively. A helium-cooled bolometer was employed in the far-infrared. Raman scattering for NiPS3 was performed in a back-scattering geometry using a green laser (λexcit = 532 nm; ≈ 1 mW power) and a 1200 g/mm grating, with 30 second integration times, averaged three times at each pressure. Compression was reversible within our sensitivity. These experiments were performed at the 22-IR-1 beamline at the National Synchrotron Light Source II at Brookhaven National Laboratory. All data were collected at room temperature. The critical pressures were determined from splittings, combinations, and inflection points in the mode frequency vs. pressure plots in conjunction with our X-ray analysis.
X-ray diffraction measurements
High-pressure X-ray diffraction measurements were performed at 16-ID-B at the Advanced Photon Source, Argonne National Laboratory. The wavelength of the X-ray beam was 0.4066 Å, and the beam spot size was 10 μm in diameter for all measurements. Diffraction data were collected on a flat panel detector array (Dectris Pilatus 1M-F, pixel size: 172 × 172 μm) in the forward scattering geometry at room temperature. For two-dimensional X-ray diffraction data reduction, Dioptas was used39. Samples were single-crystal-like up to the highest pressure. Measurements were performed with the X-ray beam perpendicular to the ab-plane, in this manner X-ray diffraction peaks for the restricted hkl indices were obtained. To maximize the number of reflections from the single crystal, data was recorded by rotating the cell about the vertical axis (by ±10 degrees). This process is illustrated in Supplementary Fig. 5, in the Supplementary information.
Symmetry analysis
We point out that a group-subgroup analysis is valid only for a second-order phase transition. That is why we did more than move up and down the subgroup/supergroup symmetry tree—even though we suspect that the transitions of interest here are second order. For instance, we tested a number of space groups that have been seen in another van der Waals materials such as Cmmm and \(R\bar{3}\). And we tested them in terms of calculating their energies relative to other candidates under those conditions, trying to relax the structure to one with a suitable match to the experiment, and comparing the calculated lattice dynamics of that candidate structure to our measured results.
First-principles calculations
Density functional theory calculations were carried out using projector-augmented-wave (PAW) method as implemented in Vienna ab initio Simulation Package (vasp)40,41. Perdew-Burke-Ernzerhof generalized gradient approximation was chosen as the exchange-correlation functional42. On-site Coulomb repulsion and van der Waals interactions were incorporated via the choice of a rotationally-invariant flavor of DFT+U formalism43 and optB86b functional, respectively44. The total energy of each magnetic structure is calculated by assuming Néel-type antiferomagnetic order. A non-shifted Γ centered 9 × 9 × 4 k-mesh was used to sample Brillouin zone. For all self-consistent calculations, plane-wave energy cutoff and energy convergence criterion were set to 500 and 10−8 eV, respectively. Internal atomic coordinates of NiPS3 were relaxed until Hellmann-Feynman force on each atom satisfies convergence criteria, 10−4 eV/Å. To compute infrared and Raman-active modes of vibration, we employed the phonopy code interfaced with vasp45. The mode decomposed phonon frequencies were calculated as a function of pressure to compare with the experimental phonon frequencies.
Data availability
The datasets generated and/or analyzed during the present study are available from the corresponding author on reasonable request.
Code availability
The Vienna ab initio Simulation Package (vasp, Ver. 5.4, see https://www.vasp.at) and Wien2k (Ver. 2019, see http://www.wien2k.at) are commercial codes, while DFT+embedded DMFT Functional code (see http://hauleweb.rutgers.edu/tutorials/) is an open-source one which runs on top of the Wien2k package.
References
Wang, Y. et al. Pressure-driven cooperative spin-crossover, large-volume collapse, and semiconductor-to-metal transition in manganese(II) honeycomb lattices. J. Am. Chem. Soc. 138, 15751–15757 (2016).
Wang, Y. et al. Emergent superconductivity in an iron-based honeycomb lattice initiated by pressure-driven spin-crossover. Nat. Commun. 9, 1914 (2018).
Tsurubayashi, M. et al. Metal-insulator transition in Mott-insulator FePS3. AIP Adv. 8, 101307 (2018).
Haines, C. et al. Pressure-induced electronic and structural phase evolution in the van der Waals compound FePS3. Phys. Rev. Lett. 121, 266801 (2018).
Coak, M. J. et al. Isostructural Mott transition in 2D honeycomb antiferromagnet V0.9 PS3. npj Quantum Mater. 4, 38 (2019).
Coak, M. J. et al. Tuning dimensionality in van-der-Waals antiferromagnetic Mott insulators TM PS3. J. Phys. Condens. Matter 32, 124003 (2019).
Coak, M. J. et al. Emergent magnetic phases in pressure-tuned van der Waals antiferromagnet FePS3. Phys. Rev. X 11, 011024 (2021).
Zheng, Y., Jiang, X.-x, Xue, X.-x, Dai, J. & Feng, Y. Ab initio, study of pressure-driven phase transition in FePS3 and FePSe3. Phys. Rev. B 100, 174102 (2019).
Harms, N. C. et al. Piezochromism in the magnetic chalcogenide MnPS3. npj Quantum Mater. 5, 56 (2020).
Kim, K. et al. Suppression of magnetic ordering in XXZ-type antiferromagnetic monoloyer NiPS3. Nat. Commun. 10, 345 (2019).
Kim, H.-S., Haule, K. & Vanderbilt, D. Mott metal-insulator transitions in pressurized layered trichalcogenides. Phys. Rev. Lett. 123, 236401 (2019).
Ma, X. et al. Dimensional crossover tuned by pressure in the layered magnetic NiPS3. Sci. China Phys. Mech 64, 297011 (2021).
Wildes, A. R. et al. Magnetic structure of the quasi-two-dimensional antiferromagnet NiPS3. Phys. Rev. B 92, 224408 (2015).
Cai, W. et al. Pressure-induced superconductivity and structural transition in ferromagnetic CrSiTe3. Phys. Rev. B 102, 144525 (2020).
Matsuoka, T. et al. Pressure-induced insulator-metal transition in two-dimensional Mott insulator NiPS3. J. Phys. Soc. Jpn 90, 124076 (2021).
Belvin, B. et al. Exiton-driven antiferromagnetic metal in a correlated van der Waals insulator. Nat. Commun. 12, 4837 (2021).
Tezze, D. et al. Tuning the magnetic properties of NiPS3 through organic-ion intercalation. Nanoscale 14, 1165 (2022).
Bernasconi, M. et al. Lattice dynamics of layered M PX3 (M = Mn,Fe,Ni,Zn; X = S,Se) compounds. Phys. Rev. B 38, 12089 (1988).
Evarestov, R. A. & Kuzmin, A. Origin of pressure-induced insulator-to-metal transition in the van der Waals compound FePS3 from first-principles calculations. J. Comput. Chem. 41, 1337–1344 (2020).
Neal, S. N. et al. Symmetry crossover in layered M PS3 complexes (M = Mn, Fe, Ni) via near-field infrared spectroscopy. Phys. Rev. B 102, 085408 (2020).
Kuo, C.-T. et al. Exfoliation and Raman spectroscopic fingerprint of few-layer NiPS3 van der Waals crystals. Sci. Rep. 6, 20904 (2016).
Clune, A. J. et al. Developing the pressure-temperature-magnetic field phase diagram of multiferroic [(CH3)NH2]Mn(HCOO)3. Inorg. Chem. 59, 10083–10090 (2020).
Sourisseau, C., Forgerit, J. P., & Mathey, Y. Vibrational study of the [P 2 S\({}_{6}^{4-}\) layered compounds (M = Fe, Co, Ni, In2/3), and their inetercalates with [Co(η5 -C5 H5)\({}_{6}^{4-}\)] cations. J. Solid State Chem. 49, 134–149 (1983).
Reschke, S. et al. Electronic and phonon excitations in α -RuCl3. Phys. Rev. B 96, 165120 (2017).
Casto, L. D. et al. Strong spin-lattice coupling in CrSiTe3. APL Mater. 3, 041515 (2015).
Anderson, P. W. & Blount, E. I. Symmetry considerations on Martensitic transformations: “ferroelectric” metals? Phys. Rev. Lett. 14, 217 (1965).
Shi, Y. et al. A ferroelectric-like structural transition in a metal. Nat. Mater. 12, 1024–1027 (2013).
Sergienko, I. A. et al. Metallic “ferroelectricity” in the pyrochlore Cd2 Re2 O7. Phys. Rev. Lett. 92, 065501 (2004).
Sakai, H. et al. Critical enhancement of thermopower in a chemically tuned polar semimetal MoTe2. Sci. Adv. 2, e1601378 (2016).
Sharma, P. et al. A room-temperature ferroelectric semimetal. Sci. Adv. 5, eaax5080 (2019).
Volkov, P. A. & Chandra, P. Multiband quantum criticality of polar metals. Phys. Rev. Lett. 124, 237601 (2020).
Cai, W. et al. Pressure-induced ferroelectric-like transition creates a polar metal in defect antiperovskites Hg3 Te2 X2 (X = Cl,Br). Nat. Commun. 12, 1509 (2021).
Kim, S. Y. et al. Charge-spin correlation in van der Waals antiferromagnet NiPS3. Phys. Rev. Lett. 120, 136402 (2018).
Kang, S. et al. Coherent many-body exciton in van der Waals antiferromagnet NiPS3. Nature 583, 785–789 (2020).
Zhou, W.X. & Ariando, A. Review on ferroelectric/polar metals. Jpn. J. Appl. Phys 59, SI0802 (2020).
Lane, C. & Zhu, J.-X. Thickness dependence of electronic structure and optical properties of a correlated van der Waals antiferromagnetic NiPS3 thin film. Phys. Rev. B 102, 075124 (2020).
Nitsche, R. & Wild, P. Crystal growth of metal-phosphorus-sulfur compounds by vapor transport. Mater. Res. Bull. 5, 419–424 (1970).
Mao, H. K., Xu, J. & Bell, P. M. Calibration of the ruby pressure gauge to 800 kbar under quasi-hydrostatic conditions. J. Geophys. Res. 91, 4673–4676 (1986).
Prescher, C. & Prakapenka, V. B. DIOPTAS : a program for reduction of two-dimensional X-ray diffraction data and data exploration. High Press Res. 35, 223–230 (2015).
Kresse, G. & Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 47, 558(r) (1993).
Kresse, G. & Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169 (1996).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865 (1996).
Dudarev, S. L., Botton, G. A., Savrasov, S. Y., Humphreys, C. J. & Sutton, A. P. Electron-energy-loss spectra and the structural stability of nickel oxide: an LSDA.U study. Phys. Rev. B 57, 1505 (1998).
Klimeš, J., Bowler, D. R. & Michaelides, A. Van der Waals density functionals applied to solids. Phys. Rev. B 83, 195131 (2011).
Togo, A. & Tanaka, I. First principles phonon calculations in materials science. Scr. Mater. 108, 1–5 (2015).
Bassett, W. A., Takahashi, T., Mao, H.-K. & Weaver, J. S. Pressure-induced phase transformation in NaCl. J. Appl. Phys. 39, 319–325 (1968).
Acknowledgements
Research at the University of Tennessee is supported by the U.S. Department of Energy, Office of Basic Energy Sciences, Materials Science Division under award DE-FG02-01ER45885 (J.L.M.). D.M. acknowledges support from the Gordon and Betty Moore Foundation’s EPiQS Initiative, Grant GBMF9069. Work at the National Synchrotron Light Source II at Brookhaven National Laboratory was funded by the Department of Energy (DE-AC98-06CH10886). Use of the 22-IR-1 beamline is supported by COMPRES, the Consortium for Materials Properties Research in Earth Sciences, under NSF Cooperative Agreement EAR 1606856 and CDAC (DE-NA0003975). S.S. and H.-S.K. acknowledge support from the Korea Research Fellow (KRF) Program and the Basic Science Research Program through the National Research Foundation of Korea funded by the Ministry of Education (NRF-2019H1D3A1A01102984 and NRF-2020R1C1C1005900), and also the support of computational resources including technical assistance from the National Supercomputing Center of Korea (Grant No. KSC-2021-CRE-0222). E.F. and H.B.C. acknowledge the support from the U.S. Department of Energy (DOE), Early Career Research Program Award KC0402020, under Contract DE-AC05-00OR22725.
Author information
Authors and Affiliations
Contributions
This project was developed by J.L.M., H.-S.K., and N.C.H. Crystal growth and sample characterization were carried out by A.H. with guidance from D.M. The spectroscopic measurements were performed by N.C.H., A.J.C., K.A.S., Z.L., and J.L.M. The X-ray measurements were carried out by T.M., E.F., J.S., and H.C. First-principles calculations were performed by S.S. with guidance from H.-S.K. The manuscript was written by N.C.H., T.M., S.S., H.-S.K., and J.L.M. All authors commented on the final document.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Harms, N.C., Matsuoka, T., Samanta, S. et al. Symmetry progression and possible polar metallicity in NiPS3 under pressure. npj 2D Mater Appl 6, 40 (2022). https://doi.org/10.1038/s41699-022-00313-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41699-022-00313-9
This article is cited by
-
Nickel phosphorous trisulfide: A ternary 2D material with an ultra-low coefficient of friction
Friction (2024)
-
Insulator–metal transition in CrSiTe3 triggered by structural distortion under pressure
npj 2D Materials and Applications (2023)