Introduction

The need for improved performance, greater throughput and higher integration density has pushed the scaling boundaries of the complementary metal-oxide-semiconductor (CMOS) technology. With the rise in artificial intelligence (AI), even this has proved to be insufficient in implementing machine learning (ML) and other generic neural algorithms on existing hardware architectures1,2. Additionally, the processing of AI algorithms on the edge devices needs to simultaneously address issues such as privacy, security, cost, latency, and bandwidth3. Therefore, the implementation of such algorithms on the hardware requires highly energy-efficient and massively parallel architectures with low latency and memory requirements. Achieving these parameters with CMOS technology utilizing traditional von-Neumann architectures is challenging because of communication and memory bottleneck along with non-linear effects that traditional designs suffer from4,5.

However, the implementation of ML algorithms using analog CMOS design techniques can offer a significant improvement in system performance parameters6,7. The analog implementation allows designers to utilize full MOS device physics; hence the architecture can be optimized down to transistor level. But, the analog implementation comes with its own challenges such as the designed circuits are sensitive to device mismatch and non-linear effects8. This makes it difficult to design analog circuits in state-of-the-art technology nodes. On the contrary, one could design systems that utilize these shortcomings (i.e., mismatch, non-linearity) as an advantage rather than engineering out the design9,10,11,12,13,14,15.

Additional degradation in conventional system design comes from the fact that today’s systems are increasingly dependent on memory technologies such as random-access-memory and Flash. These memories are essentially based on the charge storage mechanism, resulting in degradation of performance, reliability, and noise margin in lower technology nodes. To overcome the von-Neumaan bottleneck, several emerging memory devices are being explored where the data can be processed in situ within the memory by exploiting the physical principles of resistive switching (RS). While the transition metal-oxide (TMO) based resistive RAM (RRAM) technology is nearing commercialization, the recent time has witnessed a surge of experimental demonstrations of 2D material-based RRAM. These 2D RAMs can overcome the vertical scaling limit of TMO RRAMs since the remarkable RS is demonstrated even at monolayer16. The fundamental mechanism of RS in 2D RRAM appears to be different17,18, and thus it may outperform the TMO RRAM in terms of operating speed and power. In addition, we show that the state-currents expand multiple orders of magnitude (from sub-nano Ampere to milli Ampere) in 2D RAM, which is, to our best knowledge, not yet reported for any TMO based RRAM.

Here, we propose the use of a hybrid architecture based on extreme learning machine (ELM algorithm) for edge computing by integrating existing CMOS technology with emerging memristive technologies made of two-dimensional (2D) materials. The result is a hybrid architectural framework (Fig. 1a) that can surpass the current technological limitations while offering outstanding advancements in overall system performance. Our system utilizes the non-linearity offered by the CMOS circuit and the inherent device mismatch along with minimum transistor count to offer efficient design in terms of area and power. We show the system performance for generic classification applications such as audio, image, and other real-time datasets.

Fig. 1: CMOS-memristor hybrid architecture framework.
figure 1

a Hybrid LRF-ELM classification architecture which can be used for high input dimensional data such as image and audio spectrogram. b System architecture showing CMOS encoder chip and Memristor decoder chip along its functional sub-blocks.

Full size image

Results

Hybrid system architecture

The proposed architecture consists of a CMOS Encoder chip followed by the Memristor Decoder chip, as shown in Fig. 1b. These two units work in tandem yet being isolated from one another. The CMOS Encoder chip consists of an ELM encoder, a row-select encode unit, a bias generator unit, and a control unit. The core of the proposed architecture employs local receptive fields-based extreme learning machine (LRF-ELM) algorithm (Fig. 1a). LRF-ELM19 is a variant of the ELM algorithm where the weights between input and hidden layer are local and random20. The only trainable weights are the output weights, which can be learned using the least square method for a given classification or regression task. The output function of the ELM for a generalized single layer feed-forward topology is given by19,20:

$$F(x_j) = \mathop {\sum }\limits_{i = 1}^L w_i \cdot G\left( {a_j,b_i,x_j} \right), \, j = 1, \ldots , \ldots ,N$$
(1)

where \(w_i \in {\mathbb{R}}^M\) is the weight connecting the \(i^{\rm{th}}\) hidden node to \(M\) target nodes, \(a_j \in {\mathbb{R}}^n\) and \(b_i \in \mathbb{R}\) are the are random and fixed parameters of \(i^{\rm{th}}\) hidden node, \(x_j \in {\mathbb{R}}^n\) belongs to any \(N\) arbitrary distinct sample input and \(G\left( \cdot \right)\) is a non-linear continuous function.

For the non-linear function being a Gaussian kernel, \(G\left( \cdot \right)\) can be written as:

$$G\left( {a_j,b_i,x_j} \right) = e^{\left( { - b_i||x_j - a_j||^2} \right)}$$
(2)

where \(a_j\;{{{\mathrm{and}}}}\;b_i\) are the random and fixed parameters of \(i^{\rm{th}}\) Gaussian node arising from device mismatch. For an arbitrary distinct sample, \(x_j \in {\mathbb{R}}^n\) is the \(j^{\rm{th}}\) sample input vector and \(t \in {\mathbb{R}}^M\) is the target vector, the output function corresponding to \(j^{\rm{th}}\) sample input can be written as:

$$F\left( {x_j} \right) = h_j\cdot W$$
(3)

Where \(\left\{ {h_j} \right\}_{j = 1}^N \in {\mathbb{R}}^{1 \times L}\) is the hidden layer output vector for any \(N^{\rm{th}}\) arbitrary sample input and \(W \in {\mathbb{R}}^{L \times M}\) is the output weight matrix. The output layer weight matrix \(W\) is then be analytically calculated using modified quantization aware stochastic gradient descent (SGD) learning algorithm explained in detail in “Quantization aware learning for LRF-ELM”.

Figure 1a shows the network level architecture of the hybrid LRF-ELM network used in our framework for a generic case of one target node\(({T \in {\mathbb{R}}^{N \times 1}})\). The same architecture can also be generalized for multiple target nodes. The output weight vector for \(j^{\rm{th}}\) training sample, \(m^{\rm{th}}\) output node and \(L\) hidden nodes and can then be written as \(w_m = [{w_{1m},w_{2m,........,}w_{Lm}}]\). For the case of 4 target node \(( {T \in {\mathbb{R}}^{N \times 4}})\), the input and the hidden layer of the LRF-ELM network shown in Fig. 1a form the ELM encoder unit in the CMOS-Memristor chip in Fig. 1b. The output of this ELM encoder (a row of matrix \(H\)) is passed as an input to the row-select encode unit. Depending on the select signal \(\left( {Sel \, < \, 0:n \, > } \right)\), the output of hidden node is passed to the Memristor Decoder chip. The Memristor Decoder chip consists of a row-select decode, a memristor crossbar array and a mixed-signal interface unit. The weight matrix \(W\) is implemented using a memristor crossbar array made of 2D materials, as shown in the Memristor Decoder chip of Fig. 1b. Each output node of the LRF-ELM network in Fig. 1a is a differential pair integrator21 (DPI) whose array is implemented in the mixed-signal interface unit of the Memristor Decoder chip. We designed the CMOS Encoder chip in a 180 nm technology node, and post-layout simulations with hidden node parasitics were carried out to verify the results. CMOS circuit non-linearity was captured during training and inferencing, and weights were stored in memristors as the quantized conductance states. The main advantages of the proposed framework are: (1) the framework is tolerant to device variability and utilizes inherent MOS device mismatch as random weights to its advantage, hence get away with any memory storage requirement for the first layer weights; (2) the architecture is robust to process variations and therefore can be designed to much lower CMOS technology node, leading to further improvement in system performance parameters; (3) the overall energy consumption of the proposed system is very low; thus, a good candidate for edge computing applications; (4) in the proposed hybrid system, the CMOS Encoder Chip and the Memristor Decoder Chip are two significant parts of the ELM framework, and each part can be optimized separately. This arrangement enables to explore other types of emerging memories just by replacing the decoder chip, without affecting the overall system; (5) the memristor array performs multiply and accumulate (MAC) operation between the higher-dimensional input feature map and the stored quantized weights on a time-multiplexed basis; (6) the LRF-ELM framework for real-time dataset classification uses 9D Gaussian CMOS circuit operating in the subthreshold regime. The circuit, therefore, offers the desired non-linearity with minimum transistor count, hence, offering a low area and low power; and (7) the framework offers a substitute for digital memory with the multi-state memristive device, thus could save energy and area footprint.

Quantization aware learning for LRF-ELM

The classification network was trained off-chip using modified quantization aware SGD learning22. To incorporate the variability in each state (total 26 states) arising due to device to device and cycle to cycle variations, we included the statistical device variabilities \(\left\{ {\sigma _k} \right\}_{k \,=\, 1}^{26}\) as a parameter while training the algorithm. Here, we have used quantization aware SGD algorithm rather than batch gradient descent and modified it to incorporate statistical variability while training. The algorithm is described below with the dimensions of the parameters. Algorithm 1 shows the modified SGD based learning. The algorithm takes into account the quantization error arising due to the mapping of learned weight to the closest available memristor states along with the statistical variability present in the memristor device. In each learning iteration, the function \(f\left( \cdot \right)\) assigns each element of the intermittent weight matrix\(\left( {\tilde w_{lm}} \right)\) to one of the closest available memristor state \(\left( {s_{\rm{{mean}}_{k}}} \right)\). Here,\(\left\{ {S_{\rm{{mean}}}} \right\}^{1 \times 26}\) and \(\left\{ \sigma \right\}^{1 \times 26}\) are the mean and the variance vectors obtained from the memristor data matrix \(\left( {M_{\rm{{Data}}}} \right)\) (explained in detail in Supplementary Fig. 1 and Supplementary Note 1). Thereafter, each element of the quantized weight vector \(w_{lm}^Q\) is defined as a random number picked from the Gaussian distributions with mean as \(s_{{\rm{mean}}_{k}}\) and variance corresponding to that mean as \(\sigma _k\). Here,

M Target class matrix for N training samples:\(\left\{ T \right\}^{N \times M} = \left( {\begin{array}{*{20}{c}} {t_{11}} & \ldots & {t_{1M}} \\ \vdots & \ddots & \vdots \\ {t_{N1}} & \cdots & {t_{NM}} \end{array}} \right)\);

Intermittent output weight matrix for L hidden nodes:\(\left\{ {\tilde W} \right\}^{L \times M} = \left( {\begin{array}{*{20}{c}} {\tilde w_{11}} & \ldots & {\tilde w_{1M}} \\ \vdots & \ddots & \vdots \\ {\tilde w_{L1}} & \cdots & {\tilde w_{LM}} \end{array}} \right)\);

Quantized output weight matrix for L hidden nodes:\(\left\{ {W^Q} \right\}^{L \times M} = \left( {\begin{array}{*{20}{c}} {w_{11}^Q} & \ldots & {w_{1M}^Q} \\ \vdots & \ddots & \vdots \\ {w_{L1}^Q} & \cdots & {w_{LM}^Q} \end{array}} \right)\);

A row of Target class matrix corresponding to an input sample: \(\left\{ {t_j} \right\}_{j = 1}^N \in {\mathbb{R}}^{1 \times M}\);

Mean vector and mean of each state: \(\left\{ {S_{\rm{{mean}}}} \right\}^{1 \times 26} = \left[ {s_{\rm{{mean}}_1},s_{\rm{{mean}}_2}, \cdots \cdots ,s_{\rm{{mean}}_{26}}} \right]\);\(\left\{ {s_{\rm{{mean}}_k}} \right\}_{k = 1}^{26} \in {\mathbb{R}}^{1 \times 1}\);

Variance vector and variance of each state: \(\left\{ \sigma \right\}^{1 \times 26} = \left[ {\sigma _1,\sigma _2, \cdots \cdots ,\sigma _{26}} \right]\);\(\sigma \in {\Bbb R}^{1 \times 26}\);\(\alpha \in {\Bbb R}\);\(\left\{ {h_j} \right\}_{j = 1}^N \in {\Bbb R}^{1 \times L}\);

Algorithm 1

Quantization aware stochastic gradient descent learning for hybrid LRF-ELM

CMOS encoder chip (ELM encoder unit)

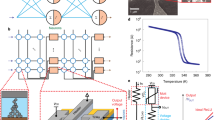
The LRF-ELM19 architecture overcomes the high-dimensionality problem by assigning the sparse connection between input and hidden nodes, as shown in Fig. 1a. For a particular feature input, the value of weights for LRF of all the hidden nodes is the same. Each input node corresponds to a local receptive field generated by taking windows of dimension \(3 \times 3\) and shifting by the stride of two. For the input matrix of dimension \(31 \times 51\), a total of 375 input nodes will be obtained. The output layer has time-multiplexed all-to-all connectivity with the hidden layer through a row-select encode, a row-select decode, and a memristor array. In an LRF-ELM architecture, the output of each hidden node depends on the different combinations of input nodes. This enables the learning of local correlations more appropriately and is invariant to small translations and rotations. We use a Gaussian function as a hidden node in our architecture, which is implemented using subthreshold MOS circuits23,24,25. Each hidden node in Fig. 1a implements a 9D Gaussian circuit for LRF-ELM network. These Gaussian circuits were implemented by cascading one-dimensional (1D) Gaussian cells sequentially in an N-P-N-P fashion, where N and P are NMOS and PMOS cells, respectively.

Figure 2a shows the block level architecture of a 9D Gaussian cell (one hidden node) formed by cascading N and P-type Gaussian cells, which allows the circuit to work at a lower swing and reduces settling time. Figure 2b shows the structure of a single NP Gaussian cell made by cascading an N-type and a P-type cell, and Fig. 2c, d illustrate the CMOS architecture of the N-type and P-type Gaussian cells, which closely approximate to Gaussian characteristics. The output current equation of the Gaussian cell for \(j^{\rm{th}}\) input sample and \(i^{\rm{th}}\) feature input as shown in Fig. 2c is given by24,25:

$$I_{\rm{{out1}}} = \frac{{\tilde I_{\rm{{bias}}}}}{2}{\rm{sech}}^2\left( {\frac{{x_{ji} - a_{ji}}}{{2\eta U_T}}} \right)$$
(4)

where \(\tilde I_{\rm{{bias}}}\) is the bias input current, \(x_{ji}\) is a feature input, \(a_{ji}\) is the random offset emerges due to device mismatch and \(V_x\) is a constant voltage. The DC characteristic plots of Iout2 and Iout1 shown in Fig. 2c always satisfy the constrain given by \(I_{\rm{{out1}}} + I_{\rm{{out2}}} = \tilde I_{\rm{{bias}}}\). A similar equation can be obtained for\(I_{\rm{{out4}}}\). On approximating, (4) closely resembles the Gaussian function in (5)24,25 and can be rewritten as:

$$g\left( {a_{ji},b_i,x_{ji}} \right) \simeq C_1e^{\left( { - b_i||x_{ji} - a_{ji}||^2} \right)}$$
(5)

Where \(C_1\) is a constant and \(b_i\) is a Gaussian kernel parameter obtained by scaling the input voltages. By cascading 9 of such 1D Gaussian structures, a nine-dimensional (9D) Gaussian cell can be obtained, whose equation is approximated by:

$$G\left( {a_j,b_i,x_j} \right) \simeq C_2\mathop {\prod }\limits_{i = 1}^9 g\left( {a_{ji},b_i,x_{ji}} \right)$$
(6)

Where \(a_j \in {\Bbb R}^9\) and \(x_j \in {\Bbb R}^9\) Fig. 2a shows the block diagram for the implementation of (6) for 9D Gaussian cell.

Fig. 2: Hidden layer neuron block and its equivalent MOS architecture.
figure 2

a Block diagram representation of a hidden node implementing 9D Gaussian cell using 2D NP Gaussian cells. b Block level representation of a generic 2D NP Gaussian cell made by cascading N and P-type Gaussian cells and current mirrors. c MOS structure of P-type Gaussian cell. d MOS structure of N-type Gaussian cell. e Layout of a single hidden layer node in Fig. 2a implementing 9D Gaussian cell using 180 nm CMOS TSMC technology.

Full size image

CMOS encoder chip (row-select encode and control unit)

In LRF-ELM, the number of hidden nodes depends on the size of the input feature map to capture local correlations, the input feature dimension, the strides for convolution, and the accuracy desired by the application. For instance, the hidden nodes count required for digit recognition can be significantly lower than digit classification. In all the cases, the output pin count in the CMOS chip cannot be scaled in proportion to the number of hidden nodes. To overcome this challenge, we designed a row-select encode unit whose detailed explanations are mentioned in Supplementary Fig. 2 and Supplementary Note 2, respectively. The circuit utilizes cascode analog multiplexers26 designed using transmission gate. It can be noted that the number of cascoded multiplexer circuits inside the row-select encode unit is equal to the number of outputs in CMOS Encoder chip. The control unit consists of a voltage bias generator and a scan chain flip-flop; the scan chain flip-flop controls the select line of the row-select encoder in the CMOS chip and the row-select decode of the memristor chip. This helps in time-multiplexing the output of the hidden node to the memristor crossbar array. At each clock edge, \(n^\prime\) rows are connected to the row-select decode unit of the memristor chip. The control unit simultaneously provides the timing control pulse voltage \({\rm{Out}}\_{\rm{Pulse}}\) in Fig. 1b to the DPI21 circuit in the memristor chip. It can further be noted that the pulse width of the \({\rm{Out}}\_{\rm{Pulse}}\) is kept such that the capacitor in the DPI does not reach its saturation level until all the hidden nodes are scanned through select inputs.

Memristor decoder chip (memristor crossbar)

The learned weights between the hidden node and the output node were programmed in the memristor crossbar array, where each memristor device can have multiple quantized conductance states. Memristor crossbar performs MAC operation between the hidden nodes output voltage and memristor conductance. It also decodes the input feature from the hidden layer to a higher-dimensional space. The hidden node voltages\(\left( {h_1, \ldots \ldots ,h_L} \right)\) in the LRF-ELM network of Fig. 1a are passed through the row-select encode unit of the CMOS chip to row-select decode unit of the memristor chip on a time-multiplexed basis. The row selection timing is precisely controlled using the timing control block of the CMOS chip. These voltages are then passed as an input to the memristor crossbar where each memristor device is programmed to one of the 26 possible states corresponding to 26 pre-trained conductive states. Each column’s output in a memristor crossbar is stored as a charge in a capacitor of a DPI integrator circuit21 (Fig. 1b). At each time step, the capacitor (C in Fig. 1a) in the DPI array keeps on integrating the output from the memristor crossbar array till the complete hidden nodes are scanned for particular data inputs. The final results are then obtained by comparing the voltages at the DPI output nodes.

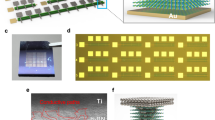
The crossbar array of memristors has been fabricated using chemical vapor deposited (CVD) multilayer hexagonal boron nitride (h-BN) as RS medium27, which was sandwiched by Au electrodes (see “Methods” and Fig. 3a). These devices exhibit non-volatile bipolar RS at low currents down to ~2 pA in high resistive state and ~10 nA in low resistive state, as shown in Fig. 3b. The device-to-device variability of the electrical properties of these devices is low. As an example, Fig. 3c shows the distribution of the set and reset voltages (VSET and VRESET) for 16 devices; the coefficient of variance (CV) is calculated as the mean value (µ) divided by the standard distribution (σ), and the values reported are 6.2% for VSET and 12.4% for VRESET. The value of CV of VSET and VRESET is calculated for every single device (see Fig. 3d, f) and for an accumulated number of devices (see Fig. 3e, g), when using current limitations of 1 µA (pink spheres) and 1 mA (blue/red spheres), and these values are compared with the values reported in the literature (which is mainly focused on cycle-to-cycle variability, although some studies reporting device-to-device variability have also been reported)28,29,30,31,32,33,34,35,36,37,38,39,40. The amount of data presented is much superior to that reported in any other study and shows a realistic picture of the real cycle-to-cycle and device-to-device variability, which is amongst the lowest in both cases. Compared to memristors made of traditional metal oxides (which are the reference in this field), the use of h-BN is beneficial because it allows better control of the potentiation process; while the potentiation in most metal oxides is only controllable at high currents and it shows an erratic trend (the currents go up in some pulses and down in others, with an overall upward trend)41,42,43,44, the potentiation in h-BN memristors is controllable even in the sub-microampere regime, and it shows a very smooth trend45 (refer Fig. 3j). The reason is that the conductance modulation in CVD-grown multilayer h-BN takes place in few-atoms-wide native defects that are surrounded by highly stable crystalline 2D layered h-BN; thus, ionic migration takes place in a very confinement volume and cannot propagate laterally46, allowing to control it more accurately. The Au/h-BN/Au devices here presented exhibited more than 26 stable conductance states47 starting at 10 nS (i.e., the lowest conductance, see Fig. 3d), something very challenging to achieve when using standard memristors made of TMO. The lateral size of the memristors used in the crossbar array is 5 µm × 5 µm, although good miniaturization has been demonstrated using 150 nm × 200 nm cross-point devices48 and nanodot devices with a radius of ~25 nm47, exhibiting excellent potential for high integration density. The fact that only scalable methods have been used during this process facilitates the integration of the proposed setup in the semiconductor fabrication line46.

Fig. 3: Memristive crossbar array.
figure 3

a SEM image of a 10 × 10 crossbar array of metal/h-BN/metal memristors. The scale bar is 40 µm. b I–V curves measured in one of the memristors in a when programmed using ICC = 1 µA, demonstrating the presence of stable bipolar RS. c Statistical analysis of the VSET and VRESET for a population of 16 devices. d, f Comparison of coefficient of variation (CV) of VSET and VRESET of all our h-BN memristors (respectively) with the values reported in previous publications. The Cv is calculated from different devices and is ordered from smaller to higher. e, g Change of CV of VSET and VRESET (respectively) with increasing population of tested devices. For example, the value of CV for n memristors indicates the cumulative CV for a population of n memristors. h Current signal measured when applying sequences of pulsed voltage stresses, demonstrating analog transitions between different conductance states (up: amplitude 5.8 V, duration 1 ms and interval 1 ms; middle: amplitude 5.8 V, duration 500 µs and interval 500 µs; bottom: amplitude 4 V, duration 20 ms and interval 25 ms). i Cumulative probability plot of the currents registered during a constant voltage stress at 0.1 V for 100 s, at 26 different current levels during the potentiation of the Au/h-BN/Au device. In all cases the current is stable. More stable states may be registered if the reading is carried out at other resistance levels.

Full size image

Memristor decoder chip (row-select decode unit and mixed interface circuit)

The output of the CMOS chip is passed to the row-select decode unit of the memristor chip. Depending on the select signal \(\left( {Sel \, < \, 0:n\, > } \right)\) in the row-select decode block, the outputs are routed to the memristor crossbar array. The row-select decode is a network of CMOS pass transistors and charge-based switching gates. The block architecture and detailed explanation are presented in Supplementary Fig. 3 and Supplementary Note 3, respectively. It can be noted that the select lines of the row-select decode unit in memristor chip and the row-select encode in CMOS chip are synchronized with the clock edge of the control-and-timing unit, and the number of analog pass transistors is equal to the number of outputs coming from the CMOS Encoder chip. The mixed interface circuit (Fig. 1b) of the output nodes consists of an array of current mode log-domain DPI synapses working in the subthreshold regime. The output response (\(I_{Y1}\)) of one DPI circuit receiving a cumulative input current \(\left( {I_{o1}} \right)\) from all the memristors in a column of a crossbar and arriving at t0 while ending at t1 is given by21:

$$I_{Y1}(t) = \frac{{I_{\rm{{gain}}}I_{o1}}}{{I_\tau }}\left( {1 - e^{\frac{{ - (t - t_0)}}{\tau }}} \right) + I_{Y1}(t_0)e^{\frac{{ - (t - t_0)}}{\tau }}$$
(7)

for the charging pulse period, and:

$$I_{Y1}(t) = I_{Y1}(t_1)e^{\frac{{ - (t - t_1)}}{\tau }}$$
(8)

for the discharge pulse; \(I_{Y1}(t_0)\) and \(I_{Y1}(t_1)\) represent the initial condition at \(t_0\) and \(t_1\) respectively, and \(I_{\rm{{gain}}} = I_0e^{ - \left( {\frac{{( {\left| {V_g - V_{DD}} \right|})}}{{\eta U_T}}} \right)}\) represents the virtual p-type subthreshold current, \(\eta\) is the sub-threshold slope factor and \(U_T\) is the thermal voltage. At each clock edge, when the row-select encode and row-select decode switches their select inputs \(\left( {Sel \,<\, 0:n\, > } \right)\), the resultant DPI current (\(I_{Yj},j \in (1:4)\)) starts falling. This fall is accumulated till the output of each hidden node is scanned by the row-select encode and row-select decode. The outputs of the mixed-signal interface unit are then compared with a pre-defined threshold value. Above and below the threshold value, the outputs are classified as one and zero, respectively, which are then used to identify which class the dataset belongs. It is noted that the capacitor \(\left( C \right)\) and voltages \(V_g\),\(V_\tau\) and \(V_W\) are set such that the output does not saturates while discharging even when all the rows are scanned. The integration time period (here charging and discharging time of C) is kept proportional to the switching time of the select inputs \(\left( {Sel \, < \, 0:n \, > } \right)\). Here, the settling time of the circuit and the operating frequency of the flip-flop decide the clock frequency and hence indirectly control the integration time period through the \({\rm{Out}}\_{\rm{Pulse}}\).

System performance analysis

Device mismatch poses a major challenge in analog circuit design8. Several methods are proposed to overcome this issue as it affects system performance in one way or another. The proposed framework utilizes inherent device mismatch for implementing random weights between input and hidden nodes. Figure 2a shows one of the hidden nodes of an LRF-ELM architecture of Fig. 1a implementing 9D Gaussian cell. Device mismatch between each transistor in a 9D Gaussian cell (hidden node) adds randomness to these offset voltages \(a_j\) shown in (5) and (6). Figure 4a shows the output current characteristic plot at each N and P Gaussian cell output port in a 9D Gaussian architecture shown in Fig. 2a. The characteristic plots are obtained when two inputs \(x_{j1}\) and \(x_{j2}\) in Fig. 2a are varied simultaneously from 0 to 1.8 volts, while other inputs are assigned a constant fixed voltage. One can analyze the variation in the non-linear Gaussian curve when inputs are varied. It can also be seen that the available output range for maintaining this non-linearity should be preferably kept between 0.8 to 1.6 V. Hence, all the inputs were normalized in this range before being applied to the classification network. It can further be noted that this range can be tuned by changing the aspect ratio of transistors. We choose the aspect ratio of NMOS and PMOS as 2 to satisfy minimum power and area constraints. Figure 4b shows the output current plot when \(V_{\rm{{bias}}}\) (corresponds to current \(I_{\rm{{bias}}}\) in Fig. 2b) is varied from 0 to 1.8 V and all the input is kept constant and fixed. This \(V_{\rm{{bias}}}\) acts as a tunable hyperparameter for adjusting the current amplitude and non-linearity characteristics in the design. Figure 4c shows the change in the output current amplitude of 9D Gaussian cells for 200 hidden neurons due to process, device mismatch, and gain variation. It can be seen that the output current varies for input voltages according to a log-normal distribution due to the exponential relationship between the voltage and the current of a transistor in the subthreshold region. This is a significant source of non-linearity to random offset voltage \(a_{ji}\) in the Gaussian cell.

Fig. 4: Gaussian non-linearity and mismatch characteristic curve.
figure 4

a Output current characteristic plot at the output of each N and P-type Gaussian cell shown in Fig. 2a when two inputs \(x_{j1}\) and \(x_{j2}\) are varied simultaneously from 0 to 1.8 volts and other inputs \((x_{j3} - x_{j9})\) are fixed constants. b Plot of output current at the output of 1D Gaussian cell (\(I_{\rm{{out1}}}\) in Fig. 2c, d) when Vbias is varied from 0 to 1.8 V and all other inputs in a 9D Gaussian cell is kept constant. c Variation in output current amplitude of 200 hidden neurons exhibiting a log-normal distribution for fixed input voltages due to process, mismatch and gain.

Full size image

Framework testing and dataset

A generic ELM network (fully connected) is deemed suitable for classification and recognition of low dimensionality datasets but possess hardware challenges for datasets having high feature dimension because of significant increase in hardware complexity. We tested the proposed hybrid LRF-ELM framework for both classification and recognition results on high-dimensional audio and image datasets. For classification, we utilized environmental sound classification (ECS-50) dataset49 and free-spoken-digit (FSDD) dataset50. Pre-processing and feature extraction was done offline using cascade of asymmetric resonators-inner hair cell (CAR-IHC) cochlear model51. The extracted feature (cochleogram) was then passed to the LRF-ELM network for classification. The size of the extracted feature dimension (cochleogram matrix) was \(31 \times 51\) for ECS-50 dataset and \(47 \times 51\) for FSDD datasets. This feature matrix size was optimized to properly capture all the relevant feature in the respective datasets. Table 1 shows the classification results for ESC-5049 and FSDD50 datasets. For ESC-50 dataset, classification was performed on pre-processed data samples (where each data point is a cochleogram matrix of 1-s audio signal). Dataset for ESC-50 was created by combining 200 data samples each from 5 different classes belonging to different groups where each group belongs to different class categories such as animal, natural landscape, human non-speech, interior domestic, and exterior urban sounds. Speaker recognition was performed on FSDD dataset where average accuracy for various speakers was shown in Table 1 for 2000 pre-processed datapoints of 1-s each.

Table 1 Classification result for the audio dataset in LRF-ELM network.
Full size table

We also tested the framework for the image classification task. For this, we utilized semeion digit recognition dataset52 from the UCI repository. The input image dimension was scaled to \(12 \times 13\) and passed to LRF-ELM network for classification. Table 2 shows the digit recognition accuracy on semeion dataset.

Table 2 Classification result for image dataset in LRF-ELM network.
Full size table

Additionally, we also tested the system for lower-dimensional datasets less than 9 features so that we can directly use standard ELM framework rather than using LRF-ELM technique. The system was trained offline using quantization aware SGD algorithm22.

For low dimensional sensory feature signals, we utilized an activity recognition system based on multi-sensor data fusion (AReM) dataset52 from University of California Irvine repository with multivariate, sequential, and time-series characteristics. Four activities, namely walking, standing, lying, and sitting, were used from the dataset for classification. We normalized the input features between the non-linearity voltage range of the Gaussian kernel obtained for the fixed bias voltage Vbias. This was then passed to a fully connected pre-trained ELM network. The classification results were obtained for DPI output array. We also showed the classification for other real-time datasets such as Breast Cancer, Ionosphere and Haberman52. Table 3 summarizes the classification accuracy of the framework on these datasets.

Table 3 Classification results for lower-dimensional dataset in a fully connected ELM network.
Full size table

In all the above cases, the number of hidden nodes \(L\), were kept ~10 times53 of the input features \(\left( {K \times 10} \right)\). Floating accuracy in Tables 1–3 denote the classification accuracy when full precision weights between hidden nodes and output were used. Quantized accuracy shows the accuracy when the weights were mapped to the nearest available 26 stable memristor conductance states. CMOS power consumption per computation for a single hidden node for a supply voltage of 0.95 V was found to be 7.8 µW (detailed explanation of energy efficiency is presented in Supplementary Note 4 and Supplementary Note 5).

Discussion

This paper proposes the design of a hybrid edge computing system utilizing emerging 2D materials along with existing CMOS technology. The proposed system integrates best of both process; the area and energy efficiency of 2D materials and the scalability and power efficiency of the existing CMOS process. We utilized a beyond conventional near-memory approach where 2D memristor crossbar array is used as the multi-state analog memory, thus overcoming the problem of area and memory wall in CMOS. The designed system is generic enough to be used in several applications such as audio detection, speech, and non-speech detection, image classification, and other edge computing tasks where latency, power, and area are severely constrained. We showed the fabrication of a crossbar memristors array using multilayer h-BN as dielectric that exhibits analog bipolar RS in >96% of devices. Analysis related to the operating frequency, throughput, and power consumption are presented in Supplementary Fig. 4, and their description in Supplementary Note 4 and Supplementary Note 5, respectively. Furthermore, the isolation among CMOS Encoder chip and Memristor Decoder chip allows us to explore other memory technologies, such as Phase Change Memory and RRAM. Thus, the proposed low-power framework with good classification results makes our system suitable for resource-constrained edge devices.

Methods

Simulation

Post-Layout CMOS circuit analyses were executed on Cisco Hyperflex HX420c with 72 Intel Xeon processing cores in parallel with 32 GB swap memory and 240 GB random-access memory. Cadence IC 6.18 with Spectre 18 was used along with Virtuoso Layout GXL for inferencing each dataset with a turn-around time of ~2 weeks for each model.

Fabrication of memristors’ crossbar arrays

The fabrication of crossbar arrays of memristor follows three steps from the bottom electrode, middle dielectric layer, and top electrode. First, the matrix of Au bottom electrodes is patterned via photolithography (mask aligner from SUSS MicroTec, model MJB4) and electron beam evaporation (Kurt J. Lesker, model PVD75) on a 300 nm SiO2/Si substrate. Each pattern consists of 5 µm wide metal wires connecting large metal pads (~104 μm in size) for better probe station tip engagement. Second, for the dielectric layer, ~6 nm thick CVD h-BN sheets transferred (from its growth substrate, i.e., Cu foil) on the matrix of bottom electrodes via standard wet transfer method, in which FeCl3 water-based solution is used as the copper substrate etcher and PMMA is used as the polymer scaffold54. Third, a matrix of Au top electrodes was patterned and deposited with the same recipe as the first step, except that the pattern was aligned to form a cross-point junction with the bottom electrodes. The cross-point regions between the wires define the active area of each memristor, which are 5 µm × 5 µm. The growth process of the h-BN sheet is described in depth in reference27.

Device characterization

The structure and surface morphology of the crossbar arrays is analyzed by scanning electron microscopy (SEM, from Carl Zeiss, model Supra 55). The electrical information is collected by semiconductor device analyzer (from Keysight, model B1500) connected with probe station (from Cascade Microtech company, model M150). We use the waveform generator/fast measurement unit (WGFMU) connected for pulsed voltage stress application and simultaneous current recording. For all electrical measurements, the stress tip is always applied to the top electrode, while the ground tip is always applied to the bottom electrode.