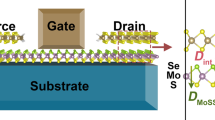
Abstract
Utilizing a two-dimensional material in an electronic device as channel layer inevitably involves the formation of contacts with metallic electrodes. As these contacts can dramatically affect the behavior of the device, we study the electronic properties of monolayer Janus MoSSe in contact with different metallic electrodes by first-principles calculations, focusing on the differences in the characteristics of contacts with the two sides of MoSSe. In particular, we demonstrate that the Fermi level pinning is different for the two sides of MoSSe, with the magnitude resembling that of MoS2 or MoSe2, while both sides can form Ohmic contacts with common electrode materials without any further adaptation, which is an outstanding advantage over MoS2 and MoSe2.
Similar content being viewed by others
Introduction
A Schottky contact between a semiconductor and a metal can be characterized by the Schottky barrier height (SBH), that is, the energy barrier that must be overcome by charge carriers to cross the contact. A sizable SBH would reduce the injection efficiency and therefore compromise the device performance1. Consequently, the choice of an adequate electrode material to realize a small SBH is essential2. Regulation of the SBH by varying the work function of the electrode often is hindered by Fermi level pinning due to metal-induced gap states (particularly originating from dangling bonds)3 and defect-induced gap states4. In the case of Fermi level pinning the Schottky–Mott rule is violated and the transport across the contact is greatly suppressed. The effect of Fermi level pinning turns out to be reduced at weakly interacting van der Waals contacts5,6.
Two-dimensional MoS2 suffers from high resistance at contacts with usual metallic electrodes (sizable SBH and Fermi level pinning)7. Countermeasures include the introduction of point defects in MoS28,9, the reduction of the electrode thickness10, and the utilization of two-dimensional metals as electrodes11,12. Interestingly, introduction of an insulating buffer layer can induce an interface dipole that reduces the SBH, but regrettably this gives rise to an additional tunnel barrier13,14,15. We propose to overcome this issue by applying a material with an intrinsic dipole to achieve the same effect while avoiding the additional tunnel barrier.
The two-dimensional Janus transition metal dichalcogenide MoSSe was first prepared in 2017 by substituting the S atoms on one side of MoS2 with Se atoms16. Similar to MoS2, its band gap and carrier mobility feature a distinct thickness dependence17,18, while the intrinsic dipole of MoSSe (the structural symmetry of MoS2 is broken) strongly modifies the electronic properties19,20,21. A number of theoretical studies have concluded that MoSSe performs well in gas sensing22,23, photocatalytic water splitting24,25,26, field-effect transistors27, and solar cells28. On the other hand, application of MoSSe as channel layer in electronic or photoelectric devices requires insights into the contacts with metallic electrodes29,30,31,32, as the achieved device efficiency will strongly depend on the characteristics of these contacts33. In the present work, we therefore study the contacts of Janus MoSSe with the potential electrode materials Al, Ti, Cu, Mo, Ag, and Au, considering both the S and Se sides of MoSSe. Al, Ti, Cu, Ag, and Au are chosen as they are common experimental electrode materials for MoS234,35,36,37,38 and Mo as it is predicted to provide suitable contact properties39. We find that the weak interaction at the contacts paves the way to Ohmic behavior without any further adaptation, indicating that MoSSe is a highly promising candidate for the channel layer of electronic devices.
Results
First-principles calculations
We consider contacts of both the S and Se sides of MoSSe with a variety of metals (Al, Ti, Cu, Mo, Ag, and Au) and refer to them as the SeMoS/metal and SMoSe/metal contacts, respectively, see Fig. 1. We obtain for MoSSe a lattice constant of 3.25 Å and a dipole moment of 0.21 Debye, which agrees well with previous reports40,41. We define the contact binding energy as Eb = (EMoSSe + Emetal ‒ Econtact)/N, where EMoSSe, Emetal, and Econtact are the total energies of the isolated MoSSe, isolated metal, and combined system, respectively, and N is the number of S or Se atoms forming the contact. We find that the S side always leads to stronger binding than the Se side, especially for the contacts with Ti and Mo (Fig. 2a). Not surprisingly, the contact distance d (distance between the average atomic positions in the atomic layers forming the contact) correlates well with the binding energy (Fig. 2b). Bader charge analysis reveals for each metal a charge transfer Δq to MoSSe, slightly more for the S than the Se side due to the stronger binding (Fig. 2c). Only for Au the charge transfer is almost zero (and in the opposite direction for the Se side). The enhanced charge transfers obtained for Ti and Mo agree with the enhanced contact binding energies in these cases. To evaluate the effect of the charge transfer on the induced dipole moment, we study the quantity D = (Dcontact ‒ DMoSSe)/N, where Dcontact and DMoSSe are the dipole moments of the combined system and isolated MoSSe, respectively, and N is the number of S or Se atoms forming the contact. A positive value means that the induced dipole moment points from the metal to MoSSe. For Al, Ti, Mo, and Ag we obtain positive values, which are larger for the S than the Se side except for Mo (Fig. 2d). For Au the values are negative, i.e., the induced dipole moments point from MoSSe to the metal. Notably, for the SMoSe/Cu and SeMoS/Ag contacts the induced dipole moments are almost zero.
Being a key parameter of a semiconductor-metal contact, the SBH is derived from weighted electronic band structures separating the contributions of MoSSe and the metal electrode (Fig. 3). We obtain Ohmic contacts (negative SBH) for Al, Ti, Mo, and Ag in contact with both sides of MoSSe, in contrast to MoS2 and MoSe239,42. A SeMoS-dominated (parabolic) band crosses the Fermi level close to the Γ point in the cases of the SeMoS/Al and SeMoS/Ag contacts, while the band crossing the Fermi level on the path F–K shows distinct hybridization between states of SeMoS and the metal. A similar hybridized band is present in the cases of the SMoSe/Al and SMoSe/Ag contacts. We find generally enhanced hybridization at the contacts involving Ti and Mo, which reflects the previously discussed strong binding. Theoretically, MoS2 (MoSe2) is predicted to form with Mo (Ti) an n-type Schottky contact with Φn = 0.13 eV (0.1 eV)39,42. Experimentally, the SBH can be reduced to 0.05 eV in the case of monolayer MoS2 in contact with Ti11 and to 0.06 eV in the case of tri-layer MoS2 in contact with Al36. We obtain for the SeMoS/Au (SMoSe/Au) contact n-type Schottky characteristics with Φn = 0.06 (0.40) eV and Φp = 0.91 (0.78) eV. Finally, for Cu the situation is more complex, as we obtain an Ohmic SeMoS/Cu contact and an n-type Schottky SMoSe/Cu contact with Φn = 0.11 eV and Φp = 0.33 eV. In general, contacts with the S side turn out to be advantageous over contacts with the Se side of MoSSe: They are more likely to be Ohmic and achieve lower Φn (Φp) in the case of n-type (p-type) Schottky characteristics.
While an Ohmic contact without Schottky barrier results in favorable transport performance, the tunnel barrier induced by the van der Waals gap due to absence of chemical interaction between the two-dimensional semiconductor and bulk metal also requires attention (Fig. 4a). The tunnel barrier is characterized by the width wTB and height ΦTB (potential barrier that an electron must overcome on its way from the metal to MoSSe). Let Φgap and Φmin denote the maximum of the tunnel barrier and the maximum effective potential on the MoSSe side of the contact. By definition, the barrier height is ΦTB = Φgap ‒ ΦMoSSe and the barrier width refers to an effective potential of ΦMoSSe. Lower barrier width and height enhance the electron injection (bottom left corner of Fig. 4b). We find three groups of contacts: group 1 promises the best performance (Ti and Mo), group 2 is intermediate (Cu and SMoSe/Ag), and group 3 suffers from unfavorable tunnel barriers.
We obtain lower work functions for contacts with the S than the Se side of MoSSe, and for each contact the Fermi level is close to the conduction band edge (EC) of pristine MoSSe (Fig. 5a). The interface dipole due to the Janus structure enables this suitable band alignment as compared to MoS2 and MoSe2. In the case of Au (higher work function than the other metals) the interface dipole is not sufficient to remove the Schottky barrier, which is consistent with our previous discussion that the charge transfer between Au and MoSSe is almost zero. The question remains whether the creation of an Ohmic contact is due to the interface dipole or whether the Fermi level pinning is weaker in the case of MoSSe (i.e., the SBH can be regulated by the work function of the metal, Wmetal). Since the Schottky–Mott rule Φn = Wmetal ‒ χ, with χ being the electron affinity of the semiconductor, does no longer apply, we study the Fermi level pinning by calculating S = dΦn/dWmetal, where S = 0 represents strong pinning and S = 1 represents a contact without pinning. Due to defects, the theoretical value generally overestimates the experimental result7,43. Linear fitting results in S = 0.28 for contacts with the S side and S = 0.50 for contacts with the Se side of MoSSe (Fig. 5b, c). Therefore, the Fermi level pinning is weaker for the Se than the S side, which is consistent with our previous discussion that the contact binding energy is smaller for the Se than the S side, highlighting the prevalent effect of the terminating atomic layer. Importantly, our values of S for contacts with the S and Se sides of MoSSe resemble those reported for MoS2 (S = 0.26)7 and MoSe2 (S = 0.67)42, respectively, implying that the breaking of the structural symmetry and consequent introduction of a dipole moment are essential for the formation of Ohmic contacts.
Discussion
By studying the interaction between monolayer Janus MoSSe and common electrode materials, using first-principles calculations, we discover that the asymmetric structure of MoSSe enables the creation of Ohmic contacts, for both terminations (S and Se sides). The Ohmic contacts, which are desirable from the perspective of electronic device applications, are attributed to the interface dipole formed when MoSSe is in contact with a metal with sufficiently low work function. At the same time, the symmetry breaking results in weaker Fermi level pinning for the Se (0.28) than the S (0.50) side. We find that Ti performs best among the studied metals to contact MoSSe, for both terminations, as not only an Ohmic contact is formed, but also the tunnel barrier is lower than 7 eV. Our results suggest that MoSSe is a promising replacement for MoS2 as channel material in electronic devices, and we identify suitable electrode materials to contact MoSSe.
Methods
First-principles calculations
All calculations are performed with the Vienna ab initio simulation package (plane-wave cutoff of 500 eV)44. The optB88-vdW functional is used45, as it provides a reliable description of the van der Waals interaction in layered materials46. The convergence criteria are set to 10−5 eV for the total energy and 0.01 eV/Å for the maximal residual force. A very fine Monkhorst-Pack k-sampling with a separation of 0.015–0.020 Å−1 between grid points is employed. A simulation model is built for the energetically favorable surface of each metal47, using for the in-plane lattice constant the bulk value of the metal. The lattice mismatch to MoSSe is minimized by choosing individual matching patterns. More specifically, we attach a 2 × 2 × 1 supercell of (111) Al, Ag, or Au to a √3 × √3 × 1 supercell of MoSSe, a 2 × 2 × 1 supercell of (001) Ti to a √3 × √3 × 1 supercell of MoSSe, a √7 × √7 × 1 supercell of (111) Cu to a 2 × 2 × 1 supercell of MoSSe, and a 2 × 2 × 1 supercell of (111) Mo to a √7 × √7 × 1 supercell of MoSSe. This results in lattice mismatches of 1.7%, 4.7%, 4.0%, 3.4%, 2.4%, and 2.4% to Al, Ti, Cu, Mo, Ag, and Au, respectively. For the metals a thickness of six (12 in the case of MoSSe/Mo) atomic layers is adopted, with the outward four (eight in the case of MoSSe/Mo) fixed in the structure relaxation. A vacuum layer of 15 Å thickness ensures in each simulation model that there is no artificial interaction between periodic images in the out-of-plane direction.
Data availability
No datasets were generated or analyzed in the current study.
References
Tung, R. T. The physics and chemistry of the Schottky barrier height. Appl. Phys. Rev. 1, 011304 (2014).
Li, Y. et al. Tunable interlayer coupling and Schottky barrier in graphene and Janus MoSSe heterostructures by applying an external field. Phys. Chem. Chem. Phys. 20, 24109–24116 (2018).
Bardeen, J. Surface states and rectification at a metal semiconductor contact. Phys. Rev. 71, 717–727 (1947).
Hasegawa, H. & Sawada, T. On the electrical properties of compound semiconductors interfaces in metal/insulator/semiconductor structures and the possible origin of interface states. Thin Solid Films 103, 119–140 (1983).
Liu, Y. et al. Approaching the Schottky-Mott limit in Van Der Waals metal-semiconductor junctions. Nature 557, 696–700 (2018).
Shen, T., Ren, J.-C., Liu, X., Li, S. & Liu, W. Van Der Waals stacking induced transition from Schottky to Ohmic contact: 2D metals on multilayer InSe. J. Am. Chem. Soc. 141, 3110–3115 (2019).
Kim, C. et al. Fermi level pinning at electrical metal contacts of monolayer molybdenum dichalcogenides. ACS Nano 11, 1588–1596 (2017).
Bampoulis, P. et al. Defect dominated charge transport and Fermi level pinning in MoS2/metal contact. ACS Appl. Mater. Interfaces 9, 19278–19286 (2017).
Chee, S.-S., Lee, J.-H., Lee, K. & Ham, M.-H. Defect-assisted contact property enhancement in molybdenum disulfide monolayer. ACS Appl. Mater. Interfaces 12, 4129–4134 (2020).
Wang, Y. et al. Van der Waals contacts between three-dimensional metal and two-dimensional semiconductors. Nature 568, 70–74 (2019).
Bertolazzi, S., Krasnozhon, D. & Kis, A. Nanvolatile memory cells based on MoS2/graphene heterostructures. ACS Nano 4, 3246–3252 (2013).
Pierucci, D. et al. Band alignment and minigaps in monolayer MoS2-graphene van der Waals heterostructures. Nano Lett. 16, 4045–4061 (2016).
Chuang, S. et al. MoS2 p-Type transistors and diodes enable by high work function MoOx contact. Nano Lett. 14, 1337–1342 (2014).
Farmanbar, M. & Brocks, G. Ohmic contact to 2D semiconductors through van der Waals bonding. Adv. Electron. Mater. 2, 1500405 (2016).
Su, J., Feng, L., Zheng, W. & Liu, Z. Controlling the electronic and geometric structures of 2D insertions to realize high performance metal/insertion-MoS2 sandwich interfaces. Nanoscale 9, 7429–7441 (2017).
Lu, A. Y. et al. Janus monolayers of transition metal dichalcogenides. Nat. Nanotechnol. 12, 744–749 (2017).
Yin, W. J. et al. Tunable dipole and carrier mobility for a few layer Janus MoSSe structure. J. Mater. Chem. C. 6, 1693–1700 (2018).
Xia, C. et al. Universality of electronic characteristics and photocatalyst applications in the two-dimensional Janus transition metal dichalcogenides. Phys. Rev. B 98, 165424 (2018).
Li, F., Wei, W., Zhao, P., Huang, B. & Dai, Y. Electronic and optical properties of pristine and vertical and lateral heterostructures of Janus MoSSe and WSSe. J. Phys. Chem. Lett. 8, 5959–5965 (2017).
Palsgaard, M. et al. Stacked Janus device concepts: abrupt pn-junctions and cross-plane channels. Nano Lett. 18, 7275–7281 (2018).
Riss-Jensen, A. C., Deilmann, T., Olsen, T. & Thygesen, K. S. Classifying the electronic and optical properties of Janus monolayers. ACS Nano 13, 13354–13364 (2019).
Jin, C. et al. A Janus MoSSe monolayer: a superior and strain-sensitive gas sensing material. J. Mater. Chem. A 7, 1099–1106 (2019).
Chaurasiya, R. & Dixit, A. Defect engineered MoSSe Janus monolayer as a promising two-dimensional material for NO2 and NO gas sensing. Appl. Surf. Sci. 490, 204–219 (2019).
Guan, Z., Ni, S. & Hu, S. Tunable electronic and optical properties of monolayer and multilayer Janus MoSSe and a photocatalyst for solar water splitting: a first-principles study. J. Phys. Chem. C. 122, 6209–6216 (2018).
Ma, X., Wu, X., Wang, H. & Wang, Y. A Janus MoSSe monolayer: a potential wide solar spectrum water-splitting photocatalyst with a low carrier recombination rate. J. Mater. Chem. A 6, 2295–2301 (2018).
Yin, W. et al. Role of intrinsic dipole on photocatalytic water splitting for Janus MoSSe/nitrides heterostructure: a first-principles study. Prog. Nat. Sci. 29, 335–340 (2019).
Tang, X. et al. Distorted Janus transition metal dichalcogenides: stable two-dimensional materials with sizable band gap and ultrahigh carrier mobility. J. Phys. Chem. C. 122, 19153–19160 (2018).
Idrees, M. et al. Optoelectronic and solar cell applications of Janus monolayers and their Van Der Waals heterostructures. Phys. Chem. Chem. Phys. 21, 18612–18621 (2019).
Gong, C., Colombo, L., Wallace, R. M. & Cho, K. The unusual mechanism of partial Fermi level pinning at metal-MoS2 interfaces. Nano Lett. 14, 1714–1720 (2014).
Pan, Y. et al. Monolayer phosphorene-metal contacts. Chem. Mater. 28, 2100–2109 (2016).
Yang, Z. et al. A Fermi-level-pinning-free 1D electrical contact at the intrinsic 2D MoS2-metal junction. Adv. Mater. 31, 1808231 (2019).
Liu, J. et al. Asymmtric Schottky contacts in Van Der Waals metal-semiconductor-metal structures based on two-dimensional Janus materials. Research 2020, 6727524 (2020).
Allain, A., Kang, J., Banerjee, K. & Kis, A. Electrical contacts to two-dimensional semiconductors. Nat. Mater. 14, 1195–1205 (2015).
Yuan, H. et al. Influence of metal-MoS2 interface on MoS2 transistor performance: comparison of Ag and Ti contacts. ACS Appl. Mater. Interfaces 7, 1180–1187 (2015).
Abraham, M. & Mohney, S. E. Annealed Ag contact to MoS2 field-effect transistors. J. Appl. Phys. 112, 115306 (2017).
Kwon, J. et al. Thickness-dependent Schottky barrier height of MoS2 field-effect transistors. Nanoscale 9, 6151–6157 (2017).
Kim, G.-S. et al. Schottky barrier height engineering for electrical contacts of multilayered MoS2 transistors with reduction of metal-induced gap states. ACS Nano 12, 6292–6300 (2018).
Andrews, K., Bowman, A., Rijal, U., Chen, P.-Y. & Zhou, Z. Improved contacts and device performance in MoS2 transistors using a 2D semiconductor interlayer. ACS Nano 14, 6232–6241 (2020).
Kang, J., Liu, W., Sarkar, D., Jena, D. & Banerjee, K. Computational study of metal contacts to monolayer transition-metal dichalcogenide semiconductors. Phys. Rev. X 4, 031005 (2014).
Ma, X., Wu, X., Wang, H. & Wang, Y. A Janus MoSSe monolayer: a potential wide solar-spectrum water-splitting photocatalyst with a low carrier recombination rate. J. Mater. Chem. A 6, 2295–2301 (2018).
Zhao, N. & Schwingenschlögl, U. Transition from Schottky to Ohmic contacts in Janus MoSSe/germanene heterostructures. Nanoscale 12, 11448–11454 (2020).
Huang, L., Li, B., Zhong, M., Wei, Z. & Li, J. Tunable Schottky barrier at MoSe2/metal interfaces with a buffer layer. J. Phys. Chem. C. 121, 9305–9311 (2017).
Fang, Q. et al. Junction-configuration-dependent interfacial electronic states of a monolayer MoS2/metal contact. J. Mater. Chem. C. 7, 3607–3616 (2019).
Kress, G. & Joubert, J. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758–1775 (1999).
Thonhauser, T. et al. Van der Waals density functional: self-consistent potential and the nature of the Van der Waals. Phys. Rev. B 76, 125112 (2007).
Bjӧrkman, T. Testing several recent Van Der Waals density functionals for layered structures. J. Chem. Phys. 141, 074708 (2014).
Skriver, H. L. & Rosengaard, N. M. Surface energy and work function of elemental metals. Phys. Rev. B 46, 7157–7168 (1992).
Acknowledgements
The research reported in this publication was supported by funding from King Abdullah University of Science and Technology (KAUST).
Author information
Authors and Affiliations
Contributions
N.Z. executed the calculations. N.Z. and U.S. interpreted the data and wrote the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Zhao, N., Schwingenschlögl, U. Dipole-induced Ohmic contacts between monolayer Janus MoSSe and bulk metals. npj 2D Mater Appl 5, 72 (2021). https://doi.org/10.1038/s41699-021-00253-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41699-021-00253-w