Abstract
MoSe2–WSe2 heterostructures host strongly bound interlayer excitons (IXs), which exhibit bright photoluminescence (PL) when the twist angle is near 0° or 60°. Over the past several years, there have been numerous reports on the optical response of these heterostructures but no unifying model to understand the dynamics of IXs and their temperature dependence. Here we perform a comprehensive study of the temperature, excitation power, and time-dependent PL of IXs. We observe a significant decrease in PL intensity above a transition temperature that we attribute to a transition from localized to delocalized IXs. Astoundingly, we find a simple inverse relationship between the IX PL energy and the transition temperature, which exhibits opposite power-dependent behaviors for near 0° and 60° samples. We conclude that this temperature dependence is a result of IX–IX exchange interactions, whose effect is suppressed by the moiré potential trapping IXs at low temperature.
Similar content being viewed by others
Introduction
The interlayer excitons (IXs) of MoSe2–WSe2 heterostructures comprise an electron in the MoSe2 layer bound to a hole in the WSe2 layer (depicted in Fig. 1a). These IXs have been the subject of intense research in recent years1,2,3,4,5,6,7,8,9,10,11,12,13,14,15; however, a fundamental observation of the IX, the strongly temperature-dependent photoluminescence (PL) intensity, has been largely unexplained. It is known that heterostructures with near 0° (R-type) and near 60° (H-type) twist angle between layers host optically bright IXs due to the alignment of the electron and hole in crystal momentum space4, where both the spin-singlet and spin-triplet IXs become bright with distinct optical selection rules16. Here the singlet (triplet) corresponds to the IX configuration with opposite (the same) electron and hole spin orientations. Previous reports on IX dynamics have attributed the temperature dependence of the IX to extrinsic disorder potentials3,16,17,18,19, but many of these studies were performed on non-hexagonal boron nitride (non-hBN)-encapsulated samples with large disorder. The recent reports on trapping IXs at moiré potentials motivate a new exploration of IX dynamics in the context of the moiré-trapped IXs6,7,10,12,20,21.
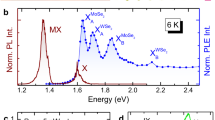
a Cartoon depiction of hBN-encapsulated MoSe2–WSe2 heterostructure showing an IX composed of an electron and hole in opposite layers. b, c Example PL spectra of R(H)-type IX at two different temperatures for fixed excitation power 56 µW (74 µW). The left insets depict a top view of the real-space alignment. The right insets show the alignment of the valleys in momentum space. d Spectrally integrated PL of R- and H-type heterostructures as a function of temperature, showing temperature-dependent transitions at 40 and 30 K, respectively, marked by larger circles. e Energy-dependent transition temperature for five different samples. The R and H subscripts label the sample number, labeled in order of increasing IX energy, where the a and b subscripts denote two disconnected sample regions of the same device. T’ labels the lower energy triplet’ peak, and T labels the higher energy triplet peak. The IX center energy varies with temperature and excitation power, the transition temperature is plotted for each power, and the solid dot marks the transition temperature for the highest excitation power. f Cartoon of IX trapped in moiré potential (Vmoiré) below a transition temperature (Tc). Excitation wavelength is 670 nm, and the confocal collection diameter is 1 µm.
Results
Contrasting R- and H-type heterostructures
In this article, we investigate the physics of IXs in five different hBN-encapsulated MoSe2–WSe2 heterostructures (two R-type and three H-type) by performing temperature, excitation power, and time-resolved PL measurements. The insets of Fig. 1b, c show the real-space and momentum-space band alignments of the layers. In R(H)-type heterostructures, the ±K MoSe2 conduction band nearly aligns with the ±K (\(\mp\)K) WSe2 valence band in momentum space.
Our first observation is that both R- and H-type heterostructures show a >20-fold decrease in PL intensity with increasing temperature from 1.6 to ~80 K (Fig. 1b, c). Figure 1d shows an example of the spectrally integrated IX PL intensity as a function of temperature for a representative R- and H-type sample (see “Methods” for integration procedure). We note that R-type samples show a single dominant singlet IX peak at low temperature and power, which broadens with increasing temperature and power to higher energy (Fig. 1b). At powers up to ~500 µW, our H-type samples show two peaks (for example, 1.37 and 1.4 eV at 1.6 K in Fig. 1c). We assign the 1.4 eV peak to the triplet IXs as previously reported16,22. The nature of the 1.37 eV peak is not completely understood, but its power, polarization dependence, and g-factor are similar to that of the 1.4 eV triplet (See Supplementary Fig. 1 and Supplementary Table 1). We therefore refer to the 1.37 eV peak as the triplet’, which may originate from IXs localized to lower-energy moiré sites7. We note that other recent works have observed a similar peak near ~1.35–1.37 eV in H-type samples22,23,24. We note that at powers <500 nW and temperatures <10 K we observe narrow (~200 µeV) IX emission lines consistent with Seyler et al.6, which are inhomogeneously broadened (see Supplementary Fig. 1).
Power-dependent transition temperature
Our second observation is that this transition temperature is excitation power dependent (as shown in Fig. 1e). To elucidate these effects, we performed a systematic investigation of the PL intensity by varying the excitation power for each temperature measured. For each excitation power, we extract a transition temperature, defined as the temperature at which the spectrally integrated IX PL counts are reduced by a half. We emphasize that, while previous works have explored the IX temperature6,17,23 dependence, our systematic approach on five different samples allows us to observe a previously obscured and striking feature: the IX transition temperature is inversely related to the IX energy (Fig. 1e).
Figure 1e shows the power-dependent transition temperature for five different samples. Because the IX center energy varies with temperature and excitation power, we plot the transition temperature for each power used (~0.01–144 µW), and the solid dot marks the transition temperature for the highest excitation power. Figure 1e shows two important features: (1) the transition temperature increases with decreasing IX energy, and (2) the R- and H-type samples show the opposite power dependence. Further analysis of the IX center energy and linewidth as a function of power and temperature is shown in Supplementary Figs. 2 and 3.
The energy-dependent transition temperature can be explained by the trapping of IXs to moiré potentials below a transition temperature (Tc), depicted in Fig. 1f. IXs are localized to moiré traps21 at T < Tc. At the transition temperature (T = Tc), thermal energy is sufficient to scatter the IX out of the moiré traps, but the exact value of Tc is dependent on the IX energy of the sample. That is, the lower the IX energy, the more the thermal energy is required to free the IX from the moiré trap. For T > Tc, the IXs are free of the moiré traps, and the strong dipole–dipole interaction between IXs results in the density-dependent expansion of the IX cloud4, scattering the IX out of the collection spot where the density is high. This results in an effective nonradiative decay of the collected IX PL and a decrease in the integrated PL intensity and lifetime. We note that previous studies in non-encapsulated MoSe2–WSe2 heterostructures4,17 typically exhibit (low power) linewidths on the order of 50 meV, and different samples exhibit ~80 meV of variation in the IX center energy, which can be attributed to disorder arising from the interactions with the substrate. More recently hBN-encapsulated MoSe2–WSe2 heterostructures have been reported that exhibit significantly narrower IX linewidths on the order of 5–10 meV25,26,27, which were attributed to the ultra-flat hBN substrate and cleaner transition metal dichalcogenide (TMD) heterostructures. Here we investigate hBN-encapsulated samples, allowing us to measure the intrinsic IX energy more accurately. We also note that the energies of the two different structure types (R-type vs. H-type) are consistent with the theoretical prediction that R-type heterostructures have a deeper moiré-trapping potential than H-type heterostructures7,10. We attribute the variation between the different structures of the same type (i.e., the two different R-type samples and three different H-type samples) to variations in doping and small built-in electric fields that shift the IX energy4,9,22,26. Supplementary Fig. 4 shows spatially resolved PL spectra that has relatively small ~1 meV variation in IX center energy.
Figure 1e also shows that the R-type structures exhibit a decrease in transition temperature for increasing excitation power, whereas the H-type structures exhibit an increase in transition temperature for increasing power. To elucidate this effect, we consider the power- and temperature-dependent IX PL maps, for example, R- and H-type heterostructures, as shown in the insets of Fig. 2a, b. In both cases, the PL is strongest at low temperature and high power; however, Fig. 2a, b show that the transition temperature decreases for the R-type and increases for the H-type as the excitation power is increased. For the H-type samples, which show two PL peaks, we fit each spectrum with two Voigt functions to calculate the two peak areas independently. Figure 2b shows the transition temperature for the low (~1.355 eV) peak of the sample H3. The transition temperature of the high-energy 1.39 eV peak also increases with increasing power and is shown in Supplementary Fig. 5. The measurements were repeated on all five samples, whose data are shown in Supplementary Fig. 5 and are consistent with the qualitative behaviors shown in Fig. 2a, b. We note that a previous report on the temperature dependence of H-type samples showed that the relative PL intensity of the singlet to the triplet increases with temperature16.
a, b Transition temperature as a function of excitation power for an R(H)-type sample, which decreases (increases) with increasing power. The insets show the full temperature- and power-dependent integrated IX PL maps. c, d Temperature- and lifetime-dependent integrated IX PL map for an R(H)-type sample. The insets show the results of a biexponential fit for each temperature. The short lifetime t1 is on order of 200 ns (12 ns) for R(H)-type samples at low temperature. In both cases, the lifetime decreases with increasing temperature. The long lifetime t2 component is on order of 900 ns (300 ns) and is relatively constant with temperature.
Time-resolved photoluminescence
In order to explore this qualitatively different power dependence between R- and H- type samples, we performed time-resolved PL spectroscopy on the samples (see Supplementary Fig. 6). Figure 2c, d show the temperature and lifetime dependence of PL. The time-dependent PL is fit with a biexponential for each temperature whose time constants (t1 and t2) are plotted in the insets of Fig. 2c, d. The R(H)-type shows a short lifetime component t1 on the order of 200 ns (12 ns) at low temperature, which decreases near the high-power transition temperatures (40 and 33 K, respectively). We attribute this fast decay component to the scattering time of IXs out of the moiré potential. The longer lifetime for the R-type structures is consistent with the lower IX energy and deeper confinement potential. Both structures exhibit a long lifetime component (t2) on the order of 300–800 ns that does not vary significantly with temperature (second insets of Fig. 2c, d). The long lifetime component is attributed to the intrinsic radiative and nonradiative decay. We emphasize the primary finding that, at high temperature, the lifetime decreases while the integrated IX PL intensity also decreases, which is due to the activation of a new nonradiative decay channel, i.e., the scattering of the IX outside of the collection spot when they are no longer localized to moiré potentials.
Low-temperature power-dependent photoluminescence
In order to understand the opposite power-dependent transition behaviors for R- and H-type structures, we investigated the low-temperature (1.6 K) power dependence of the IX (Fig. 3). The IXs in our experiment are generated through the laser excitation of the intralayer excitons followed by the ultrafast interlayer charge transfer. It has been shown that the interlayer charge transfer largely conserves the spin of the electron/hole, thus the formed IXs in both R- and H-type structures should be dominated by the intravalley or intervalley spin singlet (see Supplementary Note 1). In the R-type structure, depicted in Fig. 3, the dominant IX species is the lowest energy intravalley singlet, composed of an electron and hole of opposite spin in the same valley. Figure 3b shows (normalized) low- and high-power PL spectra of an R-type structure at low temperature (1.6 K). At 400 nW excitation, a Lorentzian fit to the PL spectrum yields a full width at half maximum of ~8 meV, which is consistent with other recent reports22,25,26,27. At high power, the IX lineshape broadens asymmetrically to higher energy, which is shown in Fig. 3c, d for two different R-type samples. We attribute this broadening to the filling of higher-energy IX states that are localized to the moiré traps. This effect is more prominent for the R-type due the deeper moiré potential7, which is again consistent with the observed lower IX energy for R-type structures which can also host higher energy IX states that are filled at higher IX density.
a Energy diagram of IXs in R-type heterostructures showing the ±K valley conduction band of the MoSe2 nearly aligning with the ±K valley valence band of the WSe2. The solid arrow depicts the spin of the electrons, the split arrow depicts the spin of the holes, and the K subscripts label the layer. One of the optically bright intravalley singlet transitions is shown in blue between the +K valley of both MoSe2 and WSe2 (i.e., +KW to +KM). b Example of normalized R-type PL spectra at low and high excitation powers. c, d Power-dependent PL spectra for two different R-type samples show the onset of a high energy shoulder with increasing power. e Energy diagram of IXs in H-type heterostructures showing the ±K valley conduction band of the MoSe2 nearly aligning with the \(\mp\)K valley valence band of the WSe2. The lowest energy direct transition is an intravalley triplet (yellow), composed of an electron and hole of the same spin in the same valley. The red arrow depicts the intervalley singlet transition. f Example of normalized H-type PL spectra at low and high excitation powers. g, h Power-dependent PL spectra for two different H-type samples. T = 1.6 K for all measurements.
Figure 3e depicts the band diagram for the H-type structures, where the lowest energy direct transition is the intravalley triplet, composed of an electron and hole of the same spin in the same valley (yellow transition in Fig. 3e). Since the formed IXs should be mostly in the singlet configuration, IXs in H-type structures should be dominated by the lowest energy intervalley singlet, composed of an electron and hole with opposite spin in opposite valleys (depicted as the red transition in Fig. 3a, e). Figure 3f shows the (normalized) low- and high-power PL spectra of an H-type structure, where we attribute the ~1.37 and ~1.39 eV peaks to the triplet’ and triplet IX. We note that the H-type structures also exhibit a higher energy intravalley singlet16,22,26, composed of an electron and hole in the same valley with the same spin. At very high powers (~1 mW), we observe the emergence of the intravalley singlet peak near 1.425 eV (see Supplementary Fig. 1). The intravalley singlet is not observed in our low-power measurements and is not required to explain our primary results.
IX–IX exchange interaction
Finally, we consider a model that explains the different power-dependent transition behaviors for R- and H-type structures (i.e., the insets of Fig. 2a, b). This difference can be understood by considering the effect of the scattering from dark intervalley IXs to bright intravalley IXs (see Fig. 4). In both structures, optical injection leads to the preferential formation of singlet IXs (see Supplementary Note 1). For R-type samples, the low-energy singlet is a bright intravalley singlet as depicted in Fig. 3a, whereas for H-type samples, the low-energy singlet is a dark intervalley singlet as depicted in Fig. 3e.
In Supplementary Note 2, we present a model that reproduces our experimental observations for both R- and H-type samples. The model is based on the IX–IX exchange interaction between pairs of IXs at neighboring moiré sites (see Supplementary Figs. 8 and 9). In both cases, the scattering is important particularly at higher excitation power and higher temperatures where the IX wavefunction is more delocalized and IX–IX exchange interactions can mediate the scattering process between intervalley IXs and intravalley IXs4. In both cases, the IX–IX exchange interaction can scatter singlets to triplets, but since singlets are bright in R-type and dark in H-type samples, this exchange scattering has opposite effects on the PL intensity. In R-type samples, a pair of bright intravalley singlet IXs can scatter to a pair of dark intervalley triplet IXs, which then serves as an additional PL decay channel at high power or high temperature (see Fig. 4a).
On the other hand, for H-type (Fig. 4b), the lowest energy intervalley singlet is a dark state. Scattering from the dark intervalley singlet to the bright intravalley triplet increases the PL intensity. Therefore, the increase of the transition temperature for increasing excitation power (Fig. 2b) is unique to H-type structures and is a consequence of the high density of dark intervalley singlets. At high temperature and excitation power, the dark intervalley singlet can serve as a reservoir of IXs that then scatter into bright intravalley triplets. Supplementary Fig. 10 shows theoretical PL intensity as a function of temperature for R- and H-type samples whose power dependence matches our experimental result.
Discussion
In summary, we have systematically investigated the effect stacking type on IXs in MoSe2–WSe2 heterostructures. We show that the IX energy is inversely related to a temperature-dependent transition of the IX PL intensity for both R- and H-type structures. We attribute this transition to the trapping of IXs to moiré potentials at low temperature, which also results in an increase of the IX lifetime. Finally, we explain the importance of the IX–IX exchange interaction on the power dependence of the transition. Our work has important consequences for future studies of IXs in TMD heterostructures, because it explains the intrinsic temperature dependence of IXs, which was not previously understood. We also show that R- and H-type structures have opposite behaviors around this transition that make the identification of heterostructure type important for the interpretation of past and future works.
Methods
Sample fabrication
MoSe2, WSe2, and hBN flakes were exfoliated from bulk crystals onto Si/SiO2 wafers using Scotch tape. Layer thickness was measured by optical contrast, atomic force microscopy, and PL. The heterostructures were assembled using the polymer-based dry transfer method28. We used thick (>20 nm) bottom hBN to ensure the highest heterostructure quality. Polarization-resolved second-harmonic generation was29,30 used to align monolayers of MoSe2 and WSe2 near 0° or 60°. The R- and H-type heterostructures were distinguished by performing low-temperature and low-power Zeeman splitting measurements on the moiré excitons following the work of Seyler et al. (Supplementary Table 1 and Supplementary Fig. 1)6.
Optical experiments
Temperature-dependent PL measurements were performed in an optical cryostat by exciting the sample with a 670 nm vertically polarized continuous wave (CW) diode laser focused to a diffraction limited spot with a 0.81 NA objective. We used a confocal pinhole to specifically collect IX emission from the ~1 µm excitation spot. The PL spectra were detected with a grating spectrometer and cooled charge-coupled device camera.
To analyze the transition temperature, we spectrally integrate the PL in two different ways. In the samples with only one dominant peak, we integrated over a range of ~100 meV centered on the peak in order to define the transition temperature, whereas for the H-type samples that exhibit triplet’ and triplet peaks, which have a resonance near 1.36 and 1.39 eV, respectively, at low temperature, we fit two Voigt profiles to each spectrum and used the area for each peak, determined by the fit, to calculate the transition temperature. For each power, the transition temperature was calculated as the temperature when the integrated area was half of the value at 1.6 K. The center energies plotted in Fig. 1e were then determined by fitting to spectrum at the transition temperature for each power. The temperature-dependent data were recorded from a single thermal cycle. However, the measurements for several samples were repeated for different thermal cycles and produced the same results.
The time-resolved PL measurements were performed using a time-correlated single photon counting technique. The samples were excited with 20–30 ns square pulses generated by optically gating a 720 nm CW laser with an acousto-optic modulator. The PL was spectrally filtered using a single grating spectrometer and detected with a single photon avalanche detector and Picoharp picosecond event timer (see Supplementary Fig. 6).
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Code availability
Upon request, authors will make available any previously unreported computer code or algorithm used to generate results that are reported in the paper and central to its main claims.
References
Rivera, P. et al. Observation of long-lived interlayer excitons in monolayer MoSe2-WSe2 heterostructures. Nat. Commun. 6, 6242 (2015).
Schaibley, J. R. et al. Directional interlayer spin-valley transfer in two-dimensional heterostructures. Nat. Commun. 7, 13747 (2016).
Schaibley, J. R. et al. Valleytronics in 2D materials. Nat. Rev. Mater. 1, 16055 (2016).
Rivera, P. et al. Valley-polarized exciton dynamics in a 2D semiconductor heterostructure. Science 351, 688–691 (2016).
Ross, J. S. et al. Interlayer exciton optoelectronics in a 2D heterostructure p-n junction. Nano Lett. 17, 638–643 (2017).
Seyler, K. L. et al. Signatures of moiré-trapped valley excitons in MoSe2/WSe2 heterobilayers. Nature 567, 66–70 (2019).
Yu, H. et al. Moiré excitons: from programmable quantum emitter arrays to spin-orbit–coupled artificial lattices. Sci. Adv. 3, e1701696 (2017).
Yu, H., Cui, X., Xu, X. & Yao, W. Valley excitons in two-dimensional semiconductors. Natl Sci. Rev. 2, 57–70 (2015).
Rivera, P. et al. Interlayer valley excitons in heterobilayers of transition metal dichalcogenides. Nat. Nanotechnol. 13, 1004–1015 (2018).
Tran, K. et al. Evidence for moiré excitons in van der Waals heterostructures. Nature 567, 71–75 (2019).
Mak, K. F. & Shan, J. Opportunities and challenges of interlayer exciton control and manipulation. Nat. Nanotechnol. 13, 974–976 (2018).
Wu, F., Lovorn, T. & Macdonald, A. H. Theory of optical absorption by interlayer excitons in transition metal dichalcogenide heterobilayers. Phys. Rev. B 97, 035306 (2018).
Sigl, L. et al. Condensation signatures of photogenerated interlayer excitons in a van der Waals heterostack. Phys. Rev. Res. 2, 042044 (2020).
Choi, J. et al. Twist angle dependent interlayer exciton lifetimes in van der waals heterostructures. Phys. Rev. Lett. 126, 047401 (2020).
Woźniak, T., Faria Junior, P. E., Seifert, G., Chaves, A. & Kunstmann, J. Exciton g factors of van der Waals heterostructures from first-principles calculations. Phys. Rev. B 101, 235408 (2020).
Zhang, L. et al. Highly valley-polarized singlet and triplet interlayer excitons in van der Waals heterostructure. Phys. Rev. B 100, 041402 (2019).
Nagler, P. et al. Interlayer exciton dynamics in a dichalcogenide monolayer heterostructure. 2D Mater. 4, 025112 (2017).
Xiao, D. et al. Coupled spin and valley physics in monolayers of MoS2 and other group-VI dichalcogenides. Phys. Rev. Lett. 108, 196802 (2012).
Yu, H., Liu, G., Bin & Yao, W. Brightened spin-triplet interlayer excitons and optical selection rules in van der Waals heterobilayers. 2D Mater. 5, 035031 (2018).
Jin, C. et al. Observation of moiré excitons in WSe2/WS2 heterostructure superlattices. Nature 567, 76–80 (2019).
Choi, J. et al. Moiré potential impedes interlayer exciton diffusion in van der Waals heterostructures. Sci. Adv. 6, 8866–8889 (2020).
Joe, A. Y. et al. Electrically controlled emission from singlet and triplet exciton species in atomically thin light-emitting diodes. Phys. Rev. B 103, 161411 (2021).
Li, Z. et al. Interlayer exciton transport in MoSe2/WSe2 heterostructures. ACS Nano 15, 1539–1547 (2021).
Brotons-Gisbert, M. et al. Moire-trapped interlayer trions in a charge-tunable WSe2/MoSe2 heterobilayer. Preprint at https://arxiv.org/abs/2101.07747 (2021).
Ciarrocchi, A. et al. Polarization switching and electrical control of interlayer excitons in two-dimensional van der Waals heterostructures. Nat. Photonics 13, 131–136 (2019).
Jauregui, L. A. et al. Electrical control of interlayer exciton dynamics in atomically thin heterostructures. Science 366, 870–875 (2019).
Unuchek, D. et al. Valley-polarized exciton currents in a van der Waals heterostructure. Nat. Nanotechnol. 14, 1104–1109 (2019).
Zomer, P. J., Guimarães, M. H. D., Brant, J. C., Tombros, N. & Van Wees, B. J. Fast pick up technique for high quality heterostructures of bilayer graphene and hexagonal boron nitride. Appl. Phys. Lett. 105, 013101 (2014).
Kumar, N. et al. Second harmonic microscopy of monolayer MoS2. Phys. Rev. B 87, 161403(R) (2013).
Malard, L. M., Alencar, T. V., Barboza, A. P. M., Mak, K. F. & De Paula, A. M. Observation of intense second harmonic generation from MoS2 atomic crystals. Phys. Rev. B 87, 201401 (2013).
Acknowledgements
We thank Matthew Klein for assistance with developing the optical set-up. Also, we acknowledge useful discussions with Rolf Binder and Allan MacDonald. This work is mainly supported by the National Science Foundation (Grant Nos. DMR-1838378 and DMR-2054572). D.G.M. acknowledges support from the Gordon and Betty Moore Foundation’s EPiQS Initiative, Grant GBMF9069. K.W. and T.T. acknowledge support from the Elemental Strategy Initiative conducted by the MEXT, Japan, Grant No. JPMXP0112101001, JSPS KAKENHI Grant No. JP20H00354, and the CREST (JPMJCR15F3), JST. J.R.S. acknowledges support from AFOSR (Grant Nos. FA9550-17-1-0215, FA9550-18-1-0390, and FA9550-20-1-0217) and the National Science Foundation Grant. No. ECCS-1708562. B.J.L. acknowledges support from the National Science Foundation under Grant No. ECCS-1607911 and Army Research Office under Grant no. W911NF-18-1-0420. H.Y. acknowledges support by the Department of Science and Technology of Guangdong Province in China (2019QN01X061).
Author information
Authors and Affiliations
Contributions
J.R.S. and B.J.L. conceived and supervised the project. F.M. fabricated the structures and performed the experiments, assisted by D.N.S., B.H.B., M.K., C.M., I.I., A.A., and S.R. F.M. and C.M. analyzed the data with input from J.R.S. and B.J.L. M.R.K. and D.G.M. provided and characterized the bulk MoSe2 and WSe2 crystals. T.T. and K.W. provided hBN crystals. H.Y. provided theoretical support in interpreting the results. F.M., J.R.S., B.J.L., and H.Y. wrote the paper with input from O.L.A.M. All authors discussed the results.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Mahdikhanysarvejahany, F., Shanks, D.N., Muccianti, C. et al. Temperature dependent moiré trapping of interlayer excitons in MoSe2-WSe2 heterostructures. npj 2D Mater Appl 5, 67 (2021). https://doi.org/10.1038/s41699-021-00248-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41699-021-00248-7
This article is cited by
-
Localisation-to-delocalisation transition of moiré excitons in WSe2/MoSe2 heterostructures
Nature Communications (2024)
-
Twistronics and moiré excitonic physics in van der Waals heterostructures
Frontiers of Physics (2024)
-
Thermally induced atomic reconstruction into fully commensurate structures of transition metal dichalcogenide layers
Nature Materials (2023)
-
Exploring the regulatory effect of stacked layers on moiré excitons in twisted WSe2/WSe2/WSe2 homotrilayer
Nano Research (2023)
-
Unveiling strain-enhanced moiré exciton localization in twisted van der Waals homostructures
Nano Research (2023)