Abstract
Silver (Ag) and graphene (Gr) inks have been engineered to serve as efficient electrical contacts for solution-processed two-dimensional (2D) organo-halide (CH3(CH2)3NH3)2(CH3NH3)n−1PbnI3n+1 (n = 4) layered perovskites, where all inkjet-printed heterostructure photodetectors (PDs) were fabricated on polyimide (PI) substrates. To date, limited studies exist that compare multiple contacts to enable high-performance engineered contacts to 2D perovskites. Moreover, of these few reports, such studies have examined contacts deposited using vapor-based techniques that are time-consuming and require expensive, specialized deposition equipment. In this work, we report on the inkjet printed, direct contact study of solution-processed, 2D perovskite-based PDs formed on flexible PI substrates. Solution processing offers a cost-effective, expedient route for inkjet printing Gr and Ag using a dispersion chemistry developed in this work that is compatible with the underlying 2D perovskite layer to construct the PDs. The wavelength λ-dependent photocurrent Ip peaked at λ ~ 630 nm for both PDs, consistent with the bandgap Eg ~ 1.96 eV for our semiconducting 2D perovskite absorber layer. The external quantum efficiency was determined to be 103% for Ag-perovskite PDs, where strain-dependent bending tests were also conducted to reveal the opto-mechanical modulation of the photocurrent in our devices.
Similar content being viewed by others
Introduction
Organic–inorganic hybrid perovskites described by the formula ABX3 (A = CH3NH3+; B = Pb2+ or Sn2+; and X = Cl−, I−, Br−) have recently emerged as attractive materials for solar energy conversion1,2,3 and various optoelectronic applications4,5. These hybrid perovskites have remarkable optoelectronic properties, such as long carrier lifetimes (~102–103 ns), high absorption coefficient, high light yield (~9000 photons/MeV), large exciton binding energy (~360 meV), high carrier mobility, a wide spectral absorption range up to ~800 nm, long carrier diffusion lengths (~1 μm), and low charge carrier recombination rates6,7,8. Such properties have positioned these materials for various devices, such as solar cells9,10, light-emitting diodes11, and photodetectors (PDs)12,13. In just a few years, researchers have found ways to increase the power conversion efficiency of single junction perovskite solar cells to over ~25.5%, making it the fastest advancing photovoltaic technology to date10. Alongside solar cells, PDs have also attracted significant attention and are finding their way into niche applications, such as optical communications for defense, environmental monitoring, chemical/biological sensing, and space exploration14,15.
As an optoelectronic device, a PD converts incoming light into a detectable electrical signal through the generation of charge carriers. It is highly desirable that a PD operate at low-power levels, and at the same time exhibit a high photoresponsivity R and detectivity D with a fast response, and a high ratio of photocurrent-to-dark current, i.e., the ON/OFF ratio. The drawback of commercially available PDs based on materials such as SiC, Si, InGaAs, ZnO16,17,18 is their relatively narrow spectral response within the ultra-violet, visible, and infrared regimes, respectively. The hybrid two-dimensional (2D) perovskites when used in PDs have advantages over commercially available PDs, since they exhibit a wide dynamic range given their lower defect densities and tunable bandgaps. External quantum efficiency (EQE) also tends to be impressive over a wide spectral regime19. For example, 2D (EDBE)PbCl4 hybrid perovskite (EDBE = 2,2′-(ethylenedioxy)bis(ethylammonium)) has found its way in X-ray detection, likely to replace currently available materials for scintillators, due largely, to the absence of deep traps and a minimal density of shallow trap states within the detector; here thermal artifacts are also nulled-out due to the large exciton binding energy of 2D (EDBE)PbCl420. The absorption coefficient of the 2D perovskites is also found to be very intimately tied to the direct bandgap nature of the electronic transitions occurring in not only 2D perovskites, but also 3D perovskites12. These characteristics strongly suggest that the 2D perovskites are ideal candidates for PDs, particularly since their stability appears to be superior to that of conventional 3D perovskites12.
In this paper, 2D (CH3(CH2)3NH3)2(CH3NH3)n−1PbnI3n+1 family of perovskite compounds (n = 4) was synthesized using the Ruddlesden–Popper (RP) method19,21,22, which is one of the most common techniques used for the synthesis of 2D perovskites. Previously, a homologous series of RP perovskite phases with the generic formula (CH3(CH2)3NH3)2(CH3NH3)n−1PbnI3n+1 (n = 1–7) were synthesized by Ruddlesden and Popper19 using butylammonium as the organic spacer, where the number of layers was adjusted by the ratio between the lead source, the methylammonium iodide (MAI), and the butylamine precursor solutions. As eluded to earlier, the potential of 2D perovskites lies in their enormous structural tunability, which allows flexibility to tailor optoelectronic properties toward a desired application23,24. For example, Aharon and Etgar24 synthesized highly luminescent MAPbX3 quantum dots, where the Eg varied from ~1.90 to 2.26 eV as the cation X was changed from I− to Br−. In particular, n, which is the number of octahedra sheets sandwiched between two organic interlayers, strongly determines the major features of the resulting 2D perovskite, such as bandgap, exciton binding energy, and photoluminescence properties23.
One of the key parameters to achieving optimal device performance with reference to transduction of incoming light-to-electricity lies in the ability to control charge carrier flow. The electrical contact between the electrode and the active absorber material is known to play a decisive role in influencing carrier transport25. However, fundamental challenges related to contacts often limit the ultimate performance and potential of semiconductors broadly speaking for electronics and optoelectronics, and semiconducting 2D perovskites are no exception. A Schottky barrier ΦB between the metal and semiconductor often arises, including in transition metal dichalcogenides (TMDCs) based devices26,27; the TMDCs are a broader class of inorganic layered materials28,29,30, just like hybrid organo-halide 2D perovskites where a weak van der Waals interaction serves as the glue between layers. Schottky barriers significantly limit the injection of charge carriers from the semiconducting transport channel region to the external circuit. Lin et al.31 conducted a carrier transport study in single-crystalline CH3NH3PbBr3 perovskites with ΦB of ~170, 380, and 470 meV for Au, Pt, and Ti electrodes, respectively, where low-power sputtering was used for metal contact deposition. Guo et al.32 also presented a simulation model of graphene and other metallic van der Waals solids contacting 2D halide perovskite sheets (C4H9NH3)2PbX4 (X = Cl, Br, and I) for field-effect transistors. To date, the few studies that compare multiple contacts to 2D perovskites have exclusively relied on vapor-based techniques31,32. However, vapor-based techniques are very expensive, time-consuming, and require specialized equipment for the metal contact deposition.
In this report, we provide prototypical demonstrations of inkjet printed, solution-processed electrical contacts to inkjet-printed 2D perovskites formed on flexible substrates. Our devices were constructed with the 2D perovskite serving as the optical absorber layer in a PD platform. The metal contacts explored here include inkjet-printed graphene (Gr) with work function ϕGr ~ 4.5 eV, and inkjet-printed silver (Ag) with work function ϕAg ~ 4.26 eV, where efficient carrier injection from the 2D perovskite to the external contacts at the metal–semiconductor (MS) interface is validated through temperature T-dependent and wavelength λ-dependent optoelectronic transport measurements of the photocurrent Ip; from these measurements ΦB was then extracted. Besides material characterization conducted on our 2D (CH3(CH2)3NH3)2(CH3NH3)n−1PbnI3n+1 (n = 4) formulations using techniques such as x-ray diffraction (XRD), including at low-grazing angles (θ = 2.5°–12°), and scanning electron microscopy (SEM), the device figures of merit, such as R and D, ON/OFF ratio, τrise and τfall, EQE were calculated for both the Gr and the Ag-contacted PDs. Additionally, the λ-dependent Ip and strain-dependent bending measurements were also performed. Our promising results, particularly with Ag contacts, confirm the excellent potential of inkjet-printed 2D perovskites for enabling high-performance PDs on flexible substrates using scalable, additive manufacturing production routes for flexible electronics and solar cells in the future.
Results and discussion
Material analysis
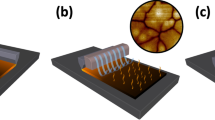
In order to construct our devices using the additive manufacturing process of inkjet printing, first, the Gr and Ag inks were formulated using isopropyl alcohol (IPA, 2-propanol) solvent. This is an atypical choice of solvent for inkjet printing, but this choice was necessitated by the constraints of post-processing the underlying 2D perovskite layer upon which the contact layer was printed. Since the perovskite layer degrades at T > 100 °C33, low-boiling point solvents used to disperse the 2D metal inks as the contact layer to the underlying perovskite provide the needed advantage during the annealing step to restrict annealing T to <100 °C. Specifics of the ink formulation steps and the optimized inkjet printing parameters used for printing the perovskite and the contact layers are provided in the “Methods” section. Figure 1 illustrates the complete process flow from a to d. Shown in Fig. 1a, the ink formulation procedure for the 2D perovskite is outlined on the left, while the Gr/Ag ink dispersion chemistry is shown on the right. The inks were formulated using magnetic stirring for the perovskite formulation in dimethylformamide (DMF) (left) and for the Gr/Ag formulation was in IPA using ultrasonication (right). The bottom-left inset in Fig. 1a represents the crystalline structure of the synthesized 2D perovskite (BA)2(MA)3Pb4I13, where the BA represents n-butylamine (CH3(CH2)3NH2), and MA is the methylammonium (CH3NH3). The inkjet printing sequence for the heterostructure device architecture is depicted in b, while in c the annealing conditions are shown with the specific temperature constraints. Depicted in Fig. 1d is the final inkjet-printed heterostructure device with the Gr-perovskite and Ag-perovskite shown on the top and bottom, respectively. Figure 1b shows the construction of the inkjet-printed heterostructure perovskite (yellow dispersion) and the Gr/Ag metal contact layer (blue dispersion) devices. Precautionary measures were needed in printing the Gr/Ag dispersions in low-boiling point solvents such as IPA, to overcome nozzle clogging issues, where a mandatory nozzle cleaning sequence was necessary since the IPA in the Gr/Ag ink dries out quickly. Details on the nozzle cleaning procedure for the Gr/Ag ink is explained in greater detail within the “Methods” section. In Fig. 1c, annealing of the perovskite and Gr/Ag layers was performed in both cases at 100 °C for 30 min at ambient, where the perovskite layer was annealed first right after printing and then it was placed back into the platen to print the Gr/Ag layers and annealed subsequently. The annealing is critical to drive off entrapped solvents to yield a dense film for realizing high-integrity electronic devices on polyimide (PI) substrates. Our demonstration of successfully printing IPA-based ink dispersions widens the portfolio of other intriguing temperature-sensitive materials that would otherwise be excluded from the portfolio of flexible electronics materials. Finally, Fig. 1d represents the optical micrograph of the inkjet-printed flexible Gr-perovskite and Ag-perovskite heterostructure PDs on flexible PI substrates with printed Gr (top) and Ag (bottom) contacts, with the perovskite layer beneath the metal contacts.
A complete process flow is shown in this figure that provides a pictorial representation of the ink formulation features in (a), inkjet printing in (b), annealing in (c), and micrographs of fabricated devices in (d). In (a), the perovskite (left) and Gr/Ag inks (right) were formulated using magnetic stirring and ultrasonication, respectively. The details of the ink formulations are explained in the “Methods” section. The bottom-left inset in (a) depicts the crystalline structure of (BA)2(MA)3Pb4I13, a family of n = 4 2D perovskite compounds, where the BA represents n-butylamine (CH3(CH2)3NH2), and MA is the methylammonium (CH3NH3). b inkjet printing of the formulated perovskite (yellow ink) and Gr/Ag (blue ink), to form our heterostructure flexible PD device. Frequent nozzle cleaning is necessary for the Gr/Ag ink as the IPA present in the Gr/Ag ink dries out fast. c Annealing of the perovskite and Gr/Ag layers was performed in both cases at 100 °C for 30 min at ambient, where the perovskite layer was annealed first right after printing and then it was placed back into the platen to print the Gr/Ag layers and an additional annealing step was subsequently conducted. d Optical micrograph of the inkjet-printed flexible Gr-perovskite and Ag-perovskite heterostructure PD devices on flexible PI substrates with printed Gr (top) and Ag (bottom) contacts, where the metal contacts were printed on top of the underlying 2D perovskite layer.
Charge carrier transport in a perovskite PD is closely influenced by the crystallographic structure and morphology of the photoactive absorber layer to determine device performance34. Upon the synthesis of the 2D (CH3(CH2)3NH3)2(CH3NH3)3Pb4I13 (exact synthesis procedures are outlined in the “Methods” section), XRD of the inkjet-printed perovskite film was performed at room temperature using the Rigaku Ultima III Diffractometer, as shown in Fig. 2a. The sample was a ~15 mm2 perovskite pattern printed on top of the PI substrate, as shown in the top-left inset of Fig. 2a. The XRD technique characteristically captures the features of the unit cell crystalline lattice by revealing the specific reflections for the 2D (CH3(CH2)3NH3)2(CH3NH3)3Pb4I13 perovskite film formed using the RP synthesis approach19,21. The XRD spectra for the 2D perovskite film displays the typical peaks occurring at 2θ = 13.84° assigned to the (CH3(CH2)3NH3)2(CH3NH3)3Pb4I13 (111) crystallographic planes21. Additionally, the 2θ peaks at 27.23° and 28.31° are assigned to the (0k0) and (202) crystallographic plane, while the (111) and (202) reflections reveal the vertical growth morphology of the 2D perovskite with respect to the substrate plane22. The top-right inset in Fig. 2a shows the low-grazing angle XRD spectra of the same inkjet-printed film taken from 2θ = 2.5° up to 12°. The low-grazing angle XRD reveals the number of layers present in the 2D perovskite35, and is evident from the top-right inset of Fig. 2a, five distinct reflections for 2θ < 14° are identified, which occur at ~3.4°, 4.5°, 6.7°, 8.9°, and 10°; this is indicative of the number of PbI3 octahedra present in each layer of the 2D perovskite crystal. Although our synthesized 2D perovskite was experimentally designed to have four layers (i.e., n = 4) according to the RP synthesis approach, the low-grazing XRD spectra suggests that there may be an additional layer within the compound, which nonetheless is still a 2D perovskite19,21,35, though impurities may also cause this. Ruddlesden and Popper19 also indexed an additional peak in their XRD scan for 2D (CH3(CH2)3NH3)2(CH3NH3)n−1PbnI3n+1 (n = 6), which included some 3D n = ∞ phases and other lower RP phases, whereas in n = 7, small amounts of n = 5 and n = 6 co-crystallize. Nonetheless, the key focus of this paper is the breakthrough studies on solution-processed electrical contacts that are compatible with inkjet-printed heterostructure perovskites for PDs on flexible substrates.
a The XRD spectra of inkjet-printed 2D perovskite films on SiO2/Si substrates. The 2θ peaks at 13.84° and 28.31° are assigned to the (CH3(CH2)3NH3)2(CH3NH3)3Pb4I13 (111) and (202) crystallographic planes, respectively. The top-right inset shows low-grazing angle XRD data, that depicts five distinct reflections at ~3.4°, 4.5°, 6.7°, 8.9°, and 10° for 2θ < 14° which is indicative of the number of 2D perovskite layers in the compound. The top-left inset displays the optical microscopy image of the printed perovskite sample on top of the PI substrate over an area ~15 mm2 used for the XRD analysis. b SEM image of an inkjet-printed perovskite heterostructure PD on a Si substrate. The inset shows the magnified view of the microfibular structure of the inkjet-printed 2D perovskites structure, which significantly increases film roughness and yields a very high photoluminescence38. c SEM image at 52° tilt angle of the printed Gr-perovskite PD on a Si substrate, where the right inset displays the Gr-perovskite lateral MS junction.
The inkjet-printed films were imaged using an SEM, as shown by the micrographs in Fig. 2b, c, where the heterostructure PDs were printed on a rigid Si substrate which obviated the need for a conductive coating during SEM imaging. The formation of microfibers within the printed film is clearly evident from this micrograph in Fig. 2b and its inset. This characteristic microfibular morphology has been seen in a number of prior studies36,37,38. Wang et al.38 reported that a higher PbI2 to MAI ratio (>PbI2(0.8): MA(1)) in the precursor leads to the formation of microfibers within the film, which significantly increases film roughness and yields a very high photoluminescence. In addition, they validated that MAPbI3 resulting from lower PbI2 to MAI ratios (<PbI2(0.6): MA(1)) do not exhibit the typical photoluminescence and absorption peaks38. Figure 2c illustrates the 52° tilted top view of the heterostructure PD, where the Gr contacts are apparent on top of the perovskite layer, while its inset on the right displays the magnified view of the printed surface, revealing the embedded network of microfibers and the lateral view of the Gr-perovskite interface.
Electrical transport comparison with Gr and Ag contacts
After completing the material characterization analysis on the synthesized 2D perovskites and fabricating the inkjet-printed PDs, we then proceeded with the electronic and optoelectronic transport measurements at cryogenic temperatures T from ~4 to 350 K using the Lakeshore CRX-4K probe stage and a broadband light source. To compare the Gr and Ag contacts, a systematic study was performed on the inkjet-printed PDs, where a broadband light source was used to illuminate the devices as they were held in vacuum (~10−6 Torr). As mentioned previously, the Gr and Ag contacts are used in this study and both PDs are fabricated using similar conditions for the ink formulation, printing passes, jetting voltage, and annealing temperature, so that a comparative analysis between the two metal contacts is possible. Figure 3a illustrates the distinct T-dependent current (I)–voltage (V) Characteristic observed for bias voltages ranging from −40 to +40 V at 10.75 mW/cm2 for the Gr-perovskite PD. On the other hand, Fig. 3b displays the T-dependent I–V for the Ag-perovskite PD at similar conditions. For both PDs, some nonlinearity in the I–V was observed for T ranging from ~4 to 300 K, and the response appeared to be more Ohmic at T ~350 K. A sudden rise in the photocurrent Ip was observed with respect to T, for both PDs and the results are plotted in Fig. 3c, showing the Ip is increasing as T increases at a fixed light intensity F of ~10.75 mW/cm2. At low T, the electrons are localized within their atomic cores, and as T increases, they gain sufficient energy to move from the valence band into the conduction band, forcing Ip to increase as T increases. In Fig. 3c, the Ip rises with T from ~4 to 350 K, particularly at higher T, for both PDs at a fixed bias voltage of ~40 V. While printing both PDs, the number of printing passes and distance between the metal electrodes were kept constant, so relative comparisons in Ip can be made. At 4 K, Ip(4K) ~4.0 and 3.4 nA, while at 300 K, Ip(300K) ~14 and 10 nA, for Ag-perovskite and Gr-perovskite, respectively, as summarized in Table 1. The dark current Id was found to be ~1 pA for both PDs and was T independent, which was measured by turning the broadband light source off. The inset in Fig. 3c shows the Ip behavior over a narrower range from ~4 up to 200 K. At T > 4 K and T > 50 K, the Ip started decreasing until reaching the transition temperature Ttransition ~ 150 and 170 K for Ag-perovskite and Gr-perovskite PDs, respectively; the Ip started to increase rapidly beyond Ttransation. This dip at Ttransation has also been observed in prior reports, where the orthorhombic-to-tetragonal phase transition occurring in 2D perovskites between ~150 and 200 K is noted as the primary cause39. Incidentally, Weller et al.39 established that in CH3NH3PbI3, a low-T orthorhombic-to-tetragonal phase transition is evident at ~165 K, whereas the high-T transition from tetragonal-to-cubic takes place at ~327 K. In the orthorhombic phase (T ~ 4 K < T < 170 K), where all of the lattice parameters a, b, and c are unequal (a ≠ b ≠ c), a dimensional stress in the unit cell is induced as it transitions to the tetragonal phase, where two of the lattice parameters a and b are equivalent (a = b ≠ c). From the T-dependent I–V of both PDs, the devices contacted with the Ag electrodes clearly showed Ip to be greater for T > 250 K due to the increased collection of photocarriers compared to the Gr contacts. This also supports the Schottky barrier analysis data, which is discussed shortly in reference to Fig. 3f.
The I–V characteristics of a Gr-perovskite and b Ag-perovskite heterostructure PDs with T ranging from ~4 to 350 K at F ~ 10.75 mW/cm2. c The T-dependent Ip change of Gr-perovskite and Ag-perovskite PDs for T ranging from ~4 to 350 K. The inset displays the Ip behavior for T ranging from ~4 to 200 K, where the Ttransition was observed at ~150 and 170 K for Gr-perovskite and Ag-perovskite PDs, respectively, which is likely due to the orthorhombic-to-tetragonal phase transition occurring within the perovskite. The Arrhenius plot of ln(Ip/T3/2) versus 1000/T at bias voltages ranging from 0.4 to 4 V for d Gr-perovskite and e Ag-perovskite PDs. f The Schottky barrier height ΦB as a function of voltage for the Gr-perovskite and Ag-perovskite PDs. At 0 V, the ΦB was found to be ~920 and 712 meV for Gr-perovskite and Ag-perovskite PDs, respectively, in the T regime from ~100 to 150 K.
To compare the charge transport characteristics of our 2D perovskite with Gr and Ag contacts, the Schottky barrier height ΦB was calculated using T-dependent transport data. Figure 3d, e shows the ln(Ip/T3/2) versus 1000/T Arrhenius plot for various V ranging from 0.4 to 4 V for the Gr-perovskite and Ag-perovskite PDs, respectively. The ΦB was extracted from the forward-bias fit for T ~50–300 K using the ideal Schottky diode formula:
where If is defined as forward-bias current, and Is the saturation current that is given by:
here A is the Richardson constant, ω is the contact area of the metal–perovskite junction, q is the electron charge (~1.602 × 10−19 C), Vf is the forward-bias voltage, and kB is the Boltzmann constant (~8.617 × 10−5 eV/K). Since our 2D perovskite falls in the 2D materials family, the Ip is defined by the 2D thermionic emission equation below40, which employs the reduced power law for a 2D transport channel according to:
here A* is the 2D equivalent Richardson constant, n is the ideality factor, and V is the bias voltage. The ΦB was extracted from the ln(Ip/T3/2) versus 1000/T Arrhenius plot in the T regime from ~100 to 150 K through the linear fit y = a + bx, where b is the slope and a is the y-intercept. Figure 3f displays the change in ΦB with increasing bias voltage. It is observed that at 0.4 V, the ΦB decreased more than half of its initial value at 0 bias voltage and almost saturates above 1 V for both PDs. At 0 V, the ΦB was found to be ~920 and 712 meV for Gr-perovskite and Ag-perovskite, respectively, in the T regime from ~ 50 to 100 K. Table 1 summarizes the ΦB of our inkjet-printed perovskite with Gr and Ag contacts. For our synthesized perovskite, the experimental value of ΦB was compared with the theoretical equivalent, where ΦB (theoretical) was determined using:
The calculated theoretical ΦB values were determined to be ~680 and 440 meV for Gr-perovskite and Ag-perovskite interfaces, respectively, where the work function ϕ of Gr and Ag are ϕGr = 4.5 eV and ϕAg = 4.26 eV, respectively, and the perovskite electron affinity χ ~ 3.82 eV41. The difference between the theoretical ΦB of the two contact metals is \(\Delta _{\Phi _B}\)(theoretical) = ΦB (Gr) − ΦB (Ag) = 680 − 440 meV = 240 meV, whereas at a 0 V bias voltage, the difference between the experimental ΦB values is \(\Delta _{\Phi _B}\)(experimental) = ΦB (Gr) − ΦB (Ag) = 920 − 712 meV = 208 meV, which closely matches \(\Delta _{\Phi _B}\)(theoretical). In both the theoretical and experimental cases, ΦB for Ag was found to be lower than that of the Gr contact. This is in alignment with the higher Ip observed in our Ag-contacted 2D perovskite devices, in contrast to the Gr contacted devices. Limited prior studies exist on contacts to 2D perovskites using evaporation-assisted metal contact deposition31, where ΦB was found to be ~170, 380, and 470 meV for Au, Pt, and Ti electrodes, respectively. Our all inkjet-printed electrical contacts yield a facile, reliable, and more cost-effective route to form electrical contacts to 2D perovskites, which resulted in ΦB ~ 712 meV for the MS junction interface with Ag-perovskite. This work shows the important steps toward the analysis of the Schottky barrier between inkjet-printed Gr and Ag contacts to 2D perovskites, which should pave the way for their future applications in optoelectronics and photovoltaics.
To fully characterize the performance of our inkjet-printed PDs, their figures of merit were computed, such as R, D, EQE, ON/OFF ratio, and wavelength λ-dependent transport, as shown by the data in Fig. 4a–d. Figure 4a provides the dependence of R as a function of light intensity F for both Gr- and Ag-contacted PDs at T ~ 300 K and biased at 40 V. Here, the R is determined using:
with Jph as the photocurrent density in A/cm2 and F as the light intensity in W/cm2. From Fig. 4a, the R was calculated to be ~0.27 and 0.53 A/W for the Gr-perovskite and Ag-perovskite PDs, respectively, at F ~ 5.24 μW/cm2 (0.00524 mW/cm2) and a decrease is noted at higher F for both PDs. Similarly, at T ~ 300 K, the inset in Fig. 4a shows the corresponding D as a function of F for both PDs at 40 V, where the D is tabulated using:
a R as a function of F, where the highest R was found to be ~0.27 and 0.53 A/W at F ~ 5.24 μW/cm2 (0.00524 mW/cm2) for Gr-perovskite and Ag-perovskite PDs, respectively. The inset shows D as a function of F, where D was calculated to be ~1.55 × 1013 Jones and 3.24 × 1013 Jones for Gr-perovskite and Ag-perovskite, respectively. b The EQE as a function of T (~4–350 K). The EQE increases considerably with increasing T, and at room temperature, EQE was determined to be ~78% and 103% for the Gr-perovskite and Ag-perovskite PDs, respectively. The inset shows the EQE as a function of F for both PDs. c ON/OFF ratio comparison for both PDs at T ~ 4–350 K. At ~300 K, the ON/OFF ratios were ~2 × 103 and 3.4 × 103 for Gr-perovskite and Ag-perovskite PDs, respectively. d The Ip as a function of λ for the Gr-perovskite PD, while the inset shows the corresponding Ip versus λ for the Ag-Perovskite PD at T ~ 200, 300, and 350 K.
here D is measured in cm Hz1/2 W−1(Jones), ω is the effective area (~0.0048 cm2) between the metal contacts, R is the responsivity, and Id is the dark current (~4 pA) in Amps. At 300 K and F ~ 5.24 μW/cm2 (0.00524 mW/cm2), D was calculated to be ~1.55 × 1013 Jones and 3.24 × 1013 Jones for the Gr-perovskite and Ag-perovskite PDs, respectively. It is seen that for the Ag-perovskite PD, both the R and D are 2X higher compared to the Gr-perovskite PDs. Table 1 summarizes the R and D of our inkjet-printed perovskite with Gr and Ag contacts. The R for Ag-perovskite is higher compared to other heterostructure PDs, where the perovskite was contacted with thermally evaporated Au and ITO42,43. In particular, the Au/CH3NH3PbI3/ITO44 and CH3NH3PbI3/Au42 PDs showed R ~ 0.036 and 0.037 A/W, respectively, whereas Au/CH3NH3PbI3 nanonet PD demonstrated higher R ~ 10.33 A/W43; interestingly the CH3NH3PbI3 nanonets were created by using monolayer colloidal crystal templates. Additionally, 3D perovskites with Au contacts45,46 also showed lower R and D compared to our Ag-perovskite PDs. Other combinations of electrode–absorber heterostructures include Pt/MAPbCl3/Ti/Au47 and Au/MAPbI3 PDs45, which display lower R ~ 0.0469 and 0.10 A/W, respectively, while the Pt/MAPbCl3/Ti/Au46 and Au/MAPbI347 showed 103 X lower values of D compared to the Ag-perovskite PD demonstrated here.
Figure 4b displays the EQE obtained for both PDs as a function of T at F ~ 5.24 μW/cm2 (0.00524 mW/cm2). The EQE is defined as the number of electron–hole pairs generated for an incident photon impinging onto the PD, and takes the following form:
where h ~ 6.6 × 10−34 J s is Planck’s constant, and all the other variables are as denoted previously with λ ~ 630 nm for the laser source used. The EQE seems to increase with increasing T for both PDs, reaching ~78% and 103% at ~300 K for the Gr-perovskite and Ag-perovskite, respectively. High EQE values have previously been reported48,49,50 for WSe2, graphene/Si, and GeS-based PDs. The situation of EQE exceeding 100% arises as charge traps localize the photogenerated carriers, increasing their lifetime and results in their recirculation multiple times before recombination. With this gain mechanism, a higher responsivity and EQE often result50. The inset in Fig. 4b shows the EQE as a function of F, where the EQE decreases with increasing F. At F ~ 5.24 μW/cm2 (~0.00524 mW/cm2), the EQE ~ 103%, whereas at F ~ 10.75 mW/cm2, the EQE decreased dramatically to ~0.05% for the Ag-perovskite PD. Figure 4c displays the ON/OFF ratio for the Gr-perovskite and Ag-perovskite PDs for T ranging from ~4 to 350 K, which establishes an important figure-of-merit that is defined as the “ON” state referring to the collected current under illumination, and the “OFF” state referring to the current in the dark. As seen from Fig. 4c, the “ON/OFF” ratio increased with increasing T for both PDs, although at T ~ 4–170 K, the ON/OFF ratio decreased due to the orthorhombic-to-tetragonal phase transition explained in reference to the data in Fig. 3c. At ~300 K, the ON/OFF ratios were found to be ~2 × 103 and 3.4 × 103 for the Gr-perovskite and Ag-perovskite PDs, respectively, which supports our previous results on the lower Schottky barrier height calculated for the Ag contacts. Table 1 summarizes the ON/OFF ratios of our inkjet-printed perovskite with Gr and Ag contacts. The high ON/OFF ratios of ~3.4 × 103 obtained for the Ag-perovskite PDs are at least ~30 X higher compared to prior PD reports based on other perovskites, such as CH3NH3PbI3 6,47 and CsPbBr351, where the ON/OFF ratios reported were ~102. In yet other similar studies, where polycrystalline α-FAPbI352 were used to fabricate PDs, the ON/OFF ratios obtained were somewhat higher ~8.6 × 104.
We also conducted additional optoelectronic measurements on our PD devices using a tunable fiber-coupled laser source from NKT Photonics (part #: A371-200-000 and A371-500-000), where λ was varied from 400 to 2300 nm. The filters were switched between the measurements due to the restriction in ranges (400–1000 nm, Filter- M000010357; 1000–2300 nm, Filter- M000010266). Figure 4d exhibits the Ip versus λ plot for the Gr-perovskite PD at T ~ 200, 300, and 350 K, while the inset shows the corresponding Ip versus λ for the Ag-perovskite PD, where the measurements were made in vacuum at a bias of 40 V. In both cases, the maximum Ip was found at λ ~ 630 nm, which is consistent with the bandgap Eg ~ 1.96 eV for our 2D perovskite material. The Eg value obtained closely matches the data from prior reports on 2D (BA)2(MA)3Pb4I13, where Eg ~ 1.91 eV was reported21, which suggests that the photons with energy < 1.96 eV will not cause optical excitation and thus there is little absorption within the PD devices. Although our synthesized 2D perovskite showed absorption arising over a relatively broad range from λ ~ 400 to 880 nm, the Ip was least for λ > 850 nm, given the maximal λ range measured was 2300 nm. Apart from the photon energy of 1.96 eV, this Ip reduction may also be due to defects and trap states within the layers, which annihilate the generated electron–hole pairs due to non-radiative decay mechanisms.
Figure 5a, b displays the temporal response of Ip to ON/OFF optical radiation pulses at T ~ 100, 200, 300, and 350 K with F ~ 10.75 mW/cm2 for the Gr-perovskite and Ag-perovskite PDs, respectively, where the “ON” pulses are shaded in the first two cycles, as examples. The ON/OFF cycling measurements were conducted using a semiconductor parameter analyzer B1500A and Thorlabs DC2200 pulse modulator for the broadband light source, where the pulse width was fixed at 500 ms. The rise and decay of Ip is governed by trap states and recombination dynamics within the perovskite, and this temporal response thus serves as a gauge, to first order, to shed insights on the degree to which trap states influence photo-induced carrier dynamics. A good photosensitive material, such as a perovskite not only shows a high Ip during the “ON” state, but it also yields a fast response time to the incoming radiation, as our measurements reveal. If the carrier dynamics are influenced by defects that serve as trapping centers, the response time is typically much slower53. In Fig. 5a, b, a fast increase and fast decay of Ip were observed with good repeatability, followed by the saturation of Ip, where the Ag-perovskite PD demonstrated higher Ip compared to the Gr-perovskite PD biased at 40 V over the entire temperature range tested. Figure 5c, d shows a more in-depth analysis of the rise and decay time measurements obtained from our devices. The rise time τrise and fall time τfall are defined as the time it takes for the PD to reach 90% and drop to 10% of the maximum steady-state Ip, respectively54. At ~300 K, τrise ~ 31 ms and τfall ~ 27 ms were determined for the Gr-perovskite PD, while τrise ~ 17 ms and τfall ~ 45 ms were measured for the Ag-perovskite PD. Our data reveal that the Ag-perovskite PD is at least 8 X faster compared to some previous reports where evaporated Au served as the metal contact to CH3NH3PbI3 PD devices47. Table 1 summarizes the τrise and τfall of our inkjet-printed 2D perovskite PD devices contacted with solution-processed Gr and Ag, along with a comparison of other figures of merits for PD to prior studies. While the fast photocurrent rise is attributed to the initial equilibration of photocarrier generation and recombination rates, the fast decay is due to the recombination of free carriers55. For both PDs, the τrise and τfall seem to decrease nonlinearly with increasing T, although the τfall for the Ag-perovskite PD at ~ 300 K seems to increase compared to the τrise, which suggests that recombination of the photocarriers occurs over a longer duration at room T for the Ag-perovskite. Generally, the values of τrise and τfall were lowest for T ~ 100 up to 150 K for both PDs, which is intriguing and may likely be associated with the orthorhombic-to-tetragonal crystal phase transition occurring in 2D perovskites within this temperature regime, as discussed previously39. The transients appear to be faster within this temperature range due possibly to the structural changes occurring within the 2D perovskite absorber layer, where carrier effective masses are likely to change from the crystalline phase transformation, which will influence switching speeds.
Temporal response of Ip to periodic broadband light pulses, represented by shaded regions as examples for the first two switching cycles, where Ip is plotted for T ~ 100, 200, 300, and 350 K at F ~ 10.75 mW/cm2 for a Gr-perovskite and b Ag-perovskite PDs. The τrise and τfall as a function of T, where the τrise ~ 31 ms and τfall ~ 27 ms were measured for c Gr-perovskite PD, while for d Ag-perovskite PD, the τrise ~ 17 ms and τfall ~ 45 ms at 300 K. At T ~ 4 K, the τrise and τfall values were found to be ~59 and 28 ms, respectively, for Ag-perovskite PD.
Strain-dependent photoresponse of Ag-perovskite PD
Strain engineering has been broadly applied to semiconducting materials, such as Si with the addition of Ge, to achieve high switching speed transistors with both compressive and tensile strain. As the Ag-perovskite PD showed superior performance compared to the Gr-perovskite PDs, we then performed mechanical durability tests on the Ag-perovskite PD. The mechanical bending tests were carried out using 3D printed structures constructed at five different radii of curvatures: 0.072, 0.087, 0.112, 0.157, and 0.262 cm−1. The experiment was performed under a bias voltage of ~20 V, and the Ip response was measured as a function of strain with varying light intensity. Figure 6a displays the five repetitive cycles of Ip measured as a function of F on a flat surface. In the first cycle, F was increased from ~58 μW/cm2 up to the maximum of 32 mW/cm2 with a time delay of 5 s in between each incremental F to stabilize the response. The F was then lowered from ~32 mW/cm2 back down to ~58 μW/cm2, prior to initiating the second measurement cycle, all on a flat surface. As seen in Fig. 6a, there is no significant change in the Ip at low F ~ 58 μW/cm2 and 20 V, while at higher F, the Ip increased, likely due to electrical annealing of the contacts and the film, which requires further investigation in the future to better understand the underlying phenomenon. The increase in Ip was tabulated to be ~57%, 26%, 21%, 16%, and 12% for F ~ 1.2, 8.2, 18.9, 26.8, and 32 mW/cm2, respectively, which indicates a gradual reduction in the net percent increase as F increases.
a Five repetitive cycles of the Ip versus F, when the Ag-perovskite PD was on a flat surface. The Ip did not change significantly for all the five cycles tested over the entire range of F tested, which confirms the reproducibility of our inkjet-printed PD devices. b Schematic diagram of the strained Ag-perovskite PDs, while under illumination which was inkjet printed on the flexible PI substrate. c The change in Ip as a function of F for various strain/curvature levels: ~0.072, 0.087, 0.112, 0.157, and 0.262 cm−1. d The dependency of Ip as a function of curvature for various F, where the Ip decreased as the curvature increased.
Figure 6b displays the schematic diagram of the strained flexible Ag-perovskite PD while under illumination. Figure 6c shows the Ip versus F as a function of strain for all the five curvatures tested, where the increase in Ip is consistent with increasing F over all the curvatures. Similarly, the Ip dependency with curvature at various F is illustrated in Fig. 6d, and it is apparent the Ip decreases with increasing strain levels over the range of F used. The strain causes mechanical deformation and produces piezoelectric charges in the perovskite at the heterojunction interface. The electric field at the interface and the increased MS junction effective area provides a smaller driving force to separate the photogenerated electron–hole pairs, which reduces Ip. Also, Zhang et al.56 have discussed that the external strain also possibly changes the Pb–I bond lengths, the Pb–I–Pb bond angles, and the orientations of the CH3NH3+ molecules, and these strain-induced structural variations in the crystalline order result in reduced photocarrier generation. Their studies56 also shed insights on the photovoltaic properties of CH3NH3PbI3 under external strain, where the absorption efficiency of incoming photons was lower.
In summary, we have synthesized (CH3(CH2)3NH3)2(CH3NH3)n−1PbnI3n+1 (n = 4) family of 2D perovskites and characterized their properties using XRD (including at low-grazing angles) and SEM. Contact engineering of 2D layered perovskites is presented with Gr and Ag metals, where inkjet printing was used to fabricate heterostructure flexible PD devices on PI substrates. The ΦB for our Gr-perovskite and Ag-perovskite PDs was extracted to be ~920 and 712 meV, respectively, in the T regime from ~100 to 150 K. The measured R and D for the Gr-perovskite and Ag-perovskite PDs confirmed the higher R ~ 0.53 A/W and D ~ 3.24 × 1013 Jones for the Ag-contacted 2D perovskite. Similarly, the EQE was found to be higher for Ag-perovskite when compared to Gr-perovskite PD. The ON/OFF ratio and response times, τrise and τfall for the Ag-perovskite PD were at least 30 X and 8 X higher, respectively, compared to prior reports. The λ-dependent Ip measurement revealed that the maximum Ip occurred at λ ~ 630 nm for both types of devices, which is consistent with the energy bandgap of the 2D perovskite of our n = 4 formulation. Lastly, strain-dependent bending tests showed the modulation of Ip as a function of strain. The study presented here validates the importance of contacts to influence charge carrier dynamics, and our exceptional figures of merits particularly with inkjet-printed Ag contacts to 2D perovskites suggests that our solution-processed 2D perovskites are well positioned to have a significant impact on flexible optoelectronics and flexible PV research in the future.
Methods
Synthesis of the 2D perovskite crystal
We synthesized the (CH3(CH2)3NH3)2(CH3NH3)3Pb4I13 perovskites, which is a family of layered compounds with tunable semiconducting properties. The PbO (part #: 402982), HI (part #: 210021), H3PO2 (part #: 214906), CH3NH3Cl (part #: 8060200250), and n-CH3(CH2)3NH2 (part #: 471305) were purchased from Sigma-Aldrich. The PbO powder (2232 mg) was dissolved in a mixture of 57% w/w aqueous HI solution (10.0 mL) and 50% aqueous H3PO2 (1.7 mL) by heating at 130 °C and subsequent boiling under constant magnetic stirring of 350 rpm for about 25 min, that led to the formation of a bright yellow solution. Subsequent addition of solid CH3NH3I (507 mg) to the hot yellow solution initially caused the precipitation of a black powder that rapidly redissolved under stirring to afford a clear bright yellow solution. Additionally, the n-CH3(CH2)3NH3I (248 μL) and hydriodic acid (5 mL) were mixed separately in a glass vial and the mixture was then added dropwise to the solution under vigorous stirring for 10 min, which did not result in any visible changes to the solution. After 10 min, we stopped stirring and heating, which were previously at 350 rpm and 130 °C, respectively. The solution was left to cool to room temperature during which time deep black, rectangular-shaped platelets started to crystallize. The precipitation was deemed to be complete after ~2 h. The crystals were isolated by suction filtration and thoroughly dried under reduced pressure21.
2D perovskite ink formulation
Perovskite inks were formed using a magnetically stirred solvent engineering process. The 30 mg/mL of (CH3(CH2)3NH3)2(CH3NH3)3Pb4I13 powder was dissolved in 10 mL of DMF and magnetically stirred overnight at 500 rpm at room T, as shown in Fig. 1a—left. Then the solution was kept at room T for 30 min to stabilize the solution for inkjet printing. The solubility of the perovskite precursor in DMF is excellent, as DFM is less volatile and hygroscopic in nature compared to other typical solvents used in inkjet printing, such as N-methylpyrrolidon. Using DFM as the solvent for perovskite inks has previously been reported57, which guided us to adopt this for our ink formulations. The top 3 mL of the perovskite ink was then transferred to the cartridge of the Dimatix Materials Printer (DMP-2850 Series) for our subsequent device fabrication efforts using inkjet printing.
Gr and Ag ink formulations
Both Gr (SKU # 496596) and Ag (SKU # 327085) powders were purchased from Sigma-Aldrich, which had a purity of ≥99.99% for trace metals, while the particle size was ~45 and 2–3.5 μm as received, for the two materials, respectively. Additionally, the liquid exfoliated Gr ink was characterized using Raman spectroscopy where three distinct Raman peaks were observed at 1361 cm−1 (D-band), at 1580 cm−1 (G-band), and at 2713 cm−1 (2D-band). The D-band indicates the defective structure of exfoliated graphite sheets, while the G- and 2D-bands indicate the order and purity of the characteristic graphite/graphene sheets, respectively58. Raman Spectroscopy has previously been used to tabulate the ID/IG and I2D/IG ratios, where the latter is correlated to thickness. For example, Nguyen et al.58 notes that when the ratio I2D/IG ~ 2–3, it is reflective of monolayer graphene, when 2 > I2D/IG > 1, bilayer graphene results, and finally for multilayer graphene, the I2D/IG < 1. Our liquid exfoliated graphene showed ratios for ID/IG ~ 0.04 and I2D/IG ~ 0.28, where the latter clearly indicates that our liquid exfoliated graphene is multilayer58. The conducting inks for the electrodes were produced through ultrasonic bath sonication of Gr or Ag powder in 2-propanol (IPA) as shown in Fig. 1a—right. An initial concentration of ethyl cellulose of ~0.8 wt% and 50 mg/ml of Gr or Ag powder was then added, respectively, in 10 ml of IPA and placed in a Branson Bath Sonicator (CPX2800) for 24 h. The top 8 ml of the supernatant was removed and placed in a new vial, which was later transferred to the cartridge of the inkjet printer. The formulation of the Gr or Ag with IPA is challenging compared to the other inks, such as MoS2 ink with Cyclohexanone/Terpineol solvent59, because the IPA-based inks frequently clog the nozzles; the IPA solvent dries out fast and makes the Gr/Ag platelets to compromise the performance of the nozzle head, so frequent nozzle cleaning is necessary, as reflected in Fig. 1b. For nozzle cleaning, the cartridge head was placed in a small glass beaker filled with IPA, which was then sonicated for 2 min to remove the nozzle clogs.
Inkjet-printed heterostructure PD fabrication
A 2 × 1.5 mm perovskite layer was first printed with 30 ink passes on a flexible PI substrate. Printing the perovskite ink is challenging compared to other 2D printed materials such as MoS2 or graphene inks59,60. Solubility is one issue even after the printed layer becomes solid, since the subsequent layer can dissolve the initial layer, as the addition of the newly printed ink makes it soluble again. That is why a stable base layer is required so that the other printed layers can stay confined within the printed area. To make a stable base layer, four nozzles were used to print five passes and allowed to stabilize for 15 min to alleviate the surface tension between the printed ink and the flexible PI substrate. Then, the rest of the 25 passes were printed. The printing parameters, such as drop spacing, were kept at 30 μm, platen T ~ 40 °C, the jetting voltage ~21 V, and these parameters have been optimized after many iterations. The printed perovskite was annealed at 30 °C for 30 min on a hot plate, where the T was ramped to 100 °C (T ramp rate ~30 °C/min) and, subsequently, the film was annealed for 30 min. Thermal annealing is a crucial step to accelerate the reaction between the organic and inorganic species in the perovskite compound. Dualeh et al.61 established that densely interconnected films are obtained by annealing the perovskite at 80 °C for 3 h, or 100 °C for 45 min, respectively. When the T is lower than 80 °C, the perovskite phase formation appeared to be hindered. Furthermore, prolonging the annealing time at low-T does not provide any advantage for film quality. On the other hand, the perovskite films annealed at T more than 100 °C will produce secondary phases of PbI2, likely originating from the decomposition of MAPbI361. Using excessively high or low processing T will thus cause undesired film quality, as a result of slow reaction rates or additional side/decomposition reactions.
After annealing the perovskite layer, the PI substrate was placed back onto the platen at the same (x,y) coordinates for printing the Gr/Ag contacts, where ~25 ink passes were used, and the films were annealed at 100 °C for 30 min. The separation between the metal electrodes was ~800 μm and the width of each electrode was ~600 μm, as the contact layers were printed on top of the perovskite layer.
Data availability
The data that support the findings of this study are available upon the request from the corresponding author.
References
Zhou, H. et al. Interface engineering of highly efficient perovskite solar cells. Science 345, 542–546 (2014).
Green, M. A., Ho-Baillie, A. & Snaith, H. J. The emergence of perovskite solar cells. Nat. Photon. 8, 506 (2014).
Boix, P. P., Agarwala, S., Koh, T. M., Mathews, N. & Mhaisalkar, S. G. Perovskite solar cells: beyond methylammonium lead iodide. J. Phys. Chem. Lett. 6, 898–907 (2015).
Guo, Y., Liu, C., Tanaka, H. & Nakamura, E. Air-stable and solution-processable perovskite photodetectors for solar-blind UV and visible light. J. Phys. Chem. Lett. 6, 535–539 (2015).
Zhang, Y. et al. Synthesis, properties, and optical applications of low-dimensional perovskites. Chem. Commun. 52, 13637–13655 (2016).
Liu, J. et al. Two-dimensional CH3NH3PbI3 perovskite: synthesis and optoelectronic application. ACS Nano 10, 3536–3542 (2016).
Qi, X. et al. Photonics and optoelectronics of 2D metal‐halide perovskites. Small 14, 1800682 (2018).
Stranks, S. D. et al. Electron-hole diffusion lengths exceeding 1 micrometer in an organometal trihalide perovskite absorber. Science. 342, 341–344 (2013).
Kojima, A., Teshima, K., Miyasaka, T. & Shirai, Y. Novel photoelectrochemical cell with mesoscopic electrodes sensitized by lead-halide compounds (2). In: Meeting Abstracts, Vol. 397 (The Electrochemical Society, 2006).
Green, M., Dunlop, E., Hohl-Ebinger, J., Yoshita, M., Kopidakis, N. & Hao, X. Solar cell efficiency tables (version 57). Prog. Photovolt. Res. Appl. 29, 3–15 (2021).
Kim, Y. et al. Multicolored organic/inorganic hybrid perovskite light‐emitting diodes. Adv. Mater. 27, 1248–1254 (2015).
Dou, L. et al. Solution-processed hybrid perovskite photodetectors with high detectivity. Nat. Commun. 5, 1–6 (2014).
Lu, H. et al. A self‐powered and stable all‐perovskite photodetector–solar cell nanosystem. Adv. Funct. Mater. 26, 1296–1302 (2016).
Xie, C. & Yan, F. Flexible photodetectors based on novel functional materials. Small 13, 1701822 (2017).
Konstantatos, G. Current status and technological prospect of photodetectors based on two-dimensional materials. Nat. Commun. 9, 1–3 (2018).
Kim, J. et al. Near-ultraviolet-sensitive graphene/porous silicon photodetectors. ACS Appl. Mater. Interfaces 6, 20880–20886 (2014).
Haugan, H. J. et al. Study of residual background carriers in midinfrared In As∕Ga Sb superlattices for uncooled detector operation. Appl Phys. Lett. 92, 71102 (2008).
Jin, Y., Wang, J., Sun, B., Blakesley, J. C. & Greenham, N. C. Solution-processed ultraviolet photodetectors based on colloidal ZnO nanoparticles. Nano Lett. 8, 1649–1653 (2008).
Ruddlesden, S. N. & Popper, P. New compounds of the K2NiF4 type. Acta Crystallogr. 10, 538–539 (1957).
Birowosuto, M. D. et al. X-ray scintillation in lead halide perovskite crystals. Sci. Rep. 6, 37254 (2016).
Stoumpos, C. C. et al. Ruddlesden–Popper hybrid lead iodide perovskite 2D homologous semiconductors. Chem. Mater. 28, 2852–2867 (2016).
Min, M., Hossain, R. F., Adhikari, N. & Kaul, A. B. Inkjet-printed organohalide 2D layered perovskites for high-speed photodetectors on flexible polyimide substrates. ACS Appl. Mater. Interfaces 12, 10809–10819 (2020).
Yuan, Z., Shu, Y., Xin, Y. & Ma, B. Highly luminescent nanoscale quasi-2D layered lead bromide perovskites with tunable emissions. Chem. Commun. 52, 3887–3890 (2016).
Aharon, S. & Etgar, L. Two dimensional organometal halide perovskite nanorods with tunable optical properties. Nano Lett. 16, 3230–3235 (2016).
Sze, S. M. & Ng, K. K. Physics of Semiconductor Devices (John Wiley & Sons, 2006).
Fan, Z. -Q. et al. In-plane Schottky-barrier field-effect transistors based on 1T/2H heterojunctions of transition-metal dichalcogenides. Phys. Rev. B 96, 165402 (2017).
Bandyopadhyay, A. S., Adhikari, N. & Kaul, A. B. Quantum Multibody Interactions in Halide-assisted vapor-synthesized monolayer WSe2 and its integration in a high responsivity photodetector with low-interface trap density. Chem. Mater. 31, 9861–9874 (2019).
Michel, M. et al. A thermally-invariant, additively manufactured, high-power graphene resistor for flexible electronics. 2D Mater. 4, 25076 (2017).
Jayanand, K. et al. Sc 3 N@ C 80 and La@ C 82 doped graphene for a new class of optoelectronic devices. J. Mater. Chem. C 8, 3970–3981 (2020).
Hossain, R. F., Deaguero, I. G., Boland, T. & Kaul, A. B. Solution dispersed 2D graphene & MoS2 for an inkjet printed biocompatible photodetector. In: 2016 Lester Eastman Conference (LEC), Vol. 2016, 19–22 (IEEE, 2016).
Lin, C. -H. et al. Metal contact and carrier transport in single crystalline CH3NH3PbBr3 perovskite. Nano Energy 53, 817–827 (2018).
Guo, Y., Saidi, W. A. & Wang, Q. 2D halide perovskite-based van der Waals heterostructures: contact evaluation and performance modulation. 2D Mater. 4, 35009 (2017).
Kim, N. -K. et al. Investigation of thermally induced degradation in CH 3 NH 3 PbI 3 perovskite solar cells using in-situ synchrotron radiation analysis. Sci. Rep. 7, 1–9 (2017).
Zhang, Y. et al. Efficient inverted planar formamidinium lead iodide perovskite solar cells via a post improved perovskite layer. RSC Adv. 6, 79952–79957 (2016).
Gangadharan, D. T. & Ma, D. Searching for stability at lower dimensions: current trends and future prospects of layered perovskite solar cells. Energy Environ. Sci. 12, 2860–2889 (2019).
Eaton, S. W. et al. Lasing in robust cesium lead halide perovskite nanowires. Proc. Natl Acad. Sci. 113, 1993–1998 (2016).
Liu, X. -D. et al. Solution-phase growth of organolead halide perovskite nanowires and nanoplates assisted by long-chain alkylammonium and solvent polarity. Mater. Lett. 206, 75–79 (2017).
Wang, Q. et al. Large fill-factor bilayer iodine perovskite solar cells fabricated by a low-temperature solution-process. Energy Environ. Sci. 7, 2359–2365 (2014).
Weller, M. T., Weber, O. J., Henry, P. F., Di Pumpo, A. M. & Hansen, T. C. Complete structure and cation orientation in the perovskite photovoltaic methylammonium lead iodide between 100 and 352 K. Chem. Commun. 51, 4180–4183 (2015).
Anwar, A., Nabet, B., Culp, J. & Castro, F. Effects of electron confinement on thermionic emission current in a modulation doped heterostructure. J. Appl Phys. 85, 2663–2666 (1999).
Chen, Y. -F. et al. Evidence of band bending induced by hole trapping at MAPbI 3 perovskite/metal interface. J. Mater. Chem. A 4, 17529–17536 (2016).
Hu, X. et al. High‐performance flexible broadband photodetector based on organolead halide perovskite. Adv. Funct. Mater. 24, 7373–7380 (2014).
Wang, W., Ma, Y. & Qi, L. High‐performance photodetectors based on organometal halide perovskite nanonets. Adv. Funct. Mater. 27, 1603653 (2017).
Li, P., Shivananju, B. N., Zhang, Y., Li, S. & Bao, Q. High performance photodetector based on 2D CH3NH3PbI3 perovskite nanosheets. J. Phys. D Appl Phys. 50, 94002 (2017).
Deng, H. et al. Flexible and semitransparent organolead triiodide perovskite network photodetector arrays with high stability. Nano Lett. 15, 7963–7969 (2015).
Maculan, G. et al. CH3NH3PbCl3 single crystals: inverse temperature crystallization and visible-blind UV-photodetector. J. Phys. Chem. Lett. 6, 3781–3786 (2015).
Zhang, X. et al. High-switching-ratio photodetectors based on perovskite CH3NH3PbI3 nanowires. Nanomaterials 8, 318 (2018).
Yao, J. D., Zheng, Z. Q., Shao, J. M. & Yang, G. W. Stable, highly-responsive and broadband photodetection based on large-area multilayered WS 2 films grown by pulsed-laser deposition. Nanoscale 7, 14974–14981 (2015).
Riazimehr, S. et al. High responsivity and quantum efficiency of graphene/silicon photodiodes achieved by interdigitating Schottky and gated regions. ACS Photonics 6, 107–115 (2018).
Ulaganathan, R. K. et al. High photosensitivity and broad spectral response of multi-layered germanium sulfide transistors. Nanoscale 8, 2284–2292 (2016).
Lv, L. et al. Generalized colloidal synthesis of high-quality, two-dimensional cesium lead halide perovskite nanosheets and their applications in photodetectors. Nanoscale 8, 13589–13596 (2016).
Zhang, M. et al. High-performance photodiode-type photodetectors based on polycrystalline formamidinium lead iodide perovskite thin films. Sci. Rep. 8, 1–9 (2018).
Law, J. B. K. & Thong, J. T. L. Simple fabrication of a ZnO nanowire photodetector with a fast photoresponse time. Appl Phys. Lett. 88, 133114 (2006).
Wang, Y. et al. High sensitivity and fast response solution processed polymer photodetectors with polyethylenimine ethoxylated (PEIE) modified ITO electrode. Opt. Express 25, 7719–7729 (2017).
Cunningham, G. et al. Photoconductivity of solution-processed MoS 2 films. J. Mater. Chem. C 1, 6899–6904 (2013).
Zhang, L. et al. Strain induced electronic structure variation in methyl-ammonium lead iodide perovskite. Sci. Rep. 8, 1–9 (2018).
Gu, Z., Huang, Z., Li, C., Li, M. & Song, Y. A general printing approach for scalable growth of perovskite single-crystal films. Sci. Adv. 4, eaat2390 (2018).
Nguyen, V. T. et al. Synthesis of multi-layer graphene films on copper tape by atmospheric pressure chemical vapor deposition method. Adv. Nat. Sci. Nanosci. Nanotechnol. 4, 35012 (2013).
Hossain, R. F., Deaguero, I. G., Boland, T. & Kaul, A. B. Biocompatible, large-format, inkjet printed heterostructure MoS 2-graphene photodetectors on conformable substrates. npj 2D Mater. Appl. 1, 1–10 (2017).
Fadil, D., Hossain, R. F., Saenz, G. A. & Kaul, A. B. On the chemically-assisted excitonic enhancement in environmentally-friendly solution dispersions of two-dimensional MoS2 and WS2. J. Mater. Chem. C 5, 5323–5333 (2017).
Dualeh, A. et al. Impedance spectroscopic analysis of lead iodide perovskite-sensitized solid-state solar cells. ACS Nano. 8, 362–373 (2014).
Acknowledgements
We thank the Office of Naval Research (Grant Number ONR N00014-20-1-2597) that enabled us to pursue this work. A.B.K. is also grateful to the support from the PACCAR Technology Institute at UNT and the Endowed Professorship support.
Author information
Authors and Affiliations
Contributions
A.B.K. conceived the overall project. R.F.H. conducted the experiments related to ink formulation, inkjet printing, material characterization, and device measurements. M.M. developed techniques to synthesize the 2D perovskites. L.-C.M. and S.R.S. contributed to discussions related to figure edits. A.B.K and R.F.H. analyzed the data, conducted significant paper edits, and came up with the conclusions. All reviewed the paper writing and approved of its content.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Hossain, R.F., Min, M., Ma, LC. et al. Carrier photodynamics in 2D perovskites with solution-processed silver and graphene contacts for bendable optoelectronics. npj 2D Mater Appl 5, 34 (2021). https://doi.org/10.1038/s41699-021-00214-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41699-021-00214-3
This article is cited by
-
Ionic liquid passivated black phosphorus for stabilized compliant electronics
Nano Research (2023)
-
Exploration of sub-bandgap states in 2D halide perovskite single-crystal photodetector
npj 2D Materials and Applications (2022)
-
Ruddlesden–Popper 2D perovskites of type (C6H9C2H4NH3)2(CH3NH3)n−1PbnI3n+1 (n = 1–4) for optoelectronic applications
Scientific Reports (2022)
-
Vibrational spectroscopy on solution-dispersed MoS2 for inkjet-printed photodetectors
Emergent Materials (2022)