Abstract
Layered semiconductors such as transition metal dichalcogenides (TMDs) offer endless possibilities for designing modern photonic and optoelectronic components. However, their optical engineering is still a challenging task owing to multiple obstacles, including the absence of a rapid, contactless, and the reliable method to obtain their dielectric function as well as to evaluate in situ the changes in optical constants and exciton binding energies. Here, we present an advanced approach based on ellipsometry measurements for retrieval of dielectric functions and the excitonic properties of both monolayer and bulk TMDs. Using this method, we conduct a detailed study of monolayer MoS2 and its bulk crystal in the broad spectral range (290–3300 nm). In the near- and mid-infrared ranges, both configurations appear to have no optical absorption and possess an extremely high dielectric permittivity making them favorable for lossless subwavelength photonics. In addition, the proposed approach opens a possibility to observe a previously unreported peak in the dielectric function of monolayer MoS2 induced by the use of perylene-3,4,9,10-tetracarboxylic acid tetrapotassium salt (PTAS) seeding promoters for MoS2 synthesis and thus enables its applications in chemical and biological sensing. Therefore, this technique as a whole offers a state-of-the-art metrological tool for next-generation TMD-based devices.
Similar content being viewed by others
Introduction
Two-dimensional (2D) materials possess unique electrical and optical properties1,2, which make them suitable for a variety of practical applications in photonics and optoelectronics1. In this regard, one of the most promising is a family of transition metal dichalcogenides (TMDs)3. These materials have already been successfully implemented in solar cells4,5, ultrasensitive photodetectors6,7, sensors8,9, optical modulators10,11, light emitters12,13, and lasers14,15, demonstrating even better performance than that of the devices based on graphene16. Their low dimensionality confines electrons movement perpendicular to the layer and provides weak dielectric screening for the electric field outside the material, giving rise to strong Coulomb interaction. Therefore, upon light illumination, TMDs support tightly bound electron–hole pairs, named excitons17, with the enormous binding energy of about 500 meV. Interestingly, not only monolayer but also bulk configurations of TMDs have an excitonic response, and, as a result, the high refractive index in the near- and mid-infrared spectral intervals following from large excitonic absorption and the Kramers–Kronig relations18. More importantly, excitons play the dominant role in optical absorption, photoluminescence, and spin–valley dynamics in TMDs even at room temperatures allowing the room-temperature excitonic devices19,20. With such a broad range of optoelectronic applications, it is vitally important to precisely know optical constants of TMDs, i.e., real and imaginary parts of the dielectric permittivity, ε1 and ε2. Nevertheless, the accurate determination of the optical constants of these materials is nontrivial owing to their complicated excitonic structure.
Nowadays, atomically thin TMDs are characterized by a variety of optical techniques such as photoluminescence21,22, absorbance23,24, and micro-reflectance spectroscopy25,26. Nevertheless, the most convenient way for precise determination of optical constant is spectroscopic ellipsometry (SE) because it allows extracting the dielectric function in a broad wavelength range directly from the raw data27. SE has already been successfully applied to characterize TMDs19,27,28,29. Although the results obtained show a similar trend of a dielectric function (ε), the absolute values of its real (ε1) and imaginary (ε2) parts differ by up to 50% between different measurements. These differences are caused by the sensitivity of the physical properties of TMDs to their dielectric surroundings30, optically active defects29, and the synthesis method31. As a consequence, it is not clear which data should be used for the TMD-based device design; i.e., one has to measure optical constants for each sample32 in order to avoid mistakes. Hence, a reliable and reproducible technique for the TMDs dielectric function determination is in high demand.
In this work, we thus accurately investigated monolayer MoS2 (synthesized via different methods) and found that the estimated values for optical constants are highly reproducible for the samples obtained under the same fabrication conditions. Apart from monolayer form, we also received optical constants for bulk MoS2, which is now being actively investigated both theoretically33,34, and experimentally18,35. Furthermore, optical constants of monolayer and bulk MoS2 in near- to the mid-infrared region were determined and showed almost no absorption (ε2 ≈ 0) and high dielectric permittivity (ε1 > 12 for monolayer and >16 for bulk), making this material an ideal platform for lossless subwavelength photonics in the infrared wavelength range. Besides, we present experimental evidence of the theoretically predicted transformation of the dark exciton into bright36, which we explain by the presence of organic molecules on the monolayer.
Results
Sample characterization
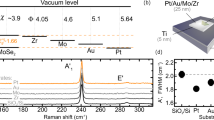
Monolayers of MoS2 were prepared through chemical vapor deposition fabrication technology (Methods), leading to uniform, high-crystalline samples as confirmed by an exemplified optical and scanning electron microscopy (SEM) images shown in Fig. 1c, d. Indeed, monolayer uniformly covers the oxidized silicon with an average crystallite size of 8.4 μm, confirming the high quality of the samples. Next, we validated that synthesized MoS2 is atomically thin using atomic force microscopy (AFM) and resonant Raman spectroscopy. The measured topography in Fig. 1b yields 0.7 ± 0.2 nm for film thickness, which is consistent with the previous results for monolayer21,32. Also, the Raman spectrum in Fig. 1e reveals intense photoluminescence, which is a distinctive property of monolayer MoS2 thanks to its direct bandgap, in contrast to the indirect bandgap of its multilayer and bulk counterparts24. Besides, the characteristic Raman spectrum in Fig. 1f exhibits all the features inherent to molybdenum disulfide37, with thickness-dependent vibrational modes \(E_{2{\mathrm{g}}}^1\) = 384 cm−1 and \(A_{1g}\) = 404 cm−1 corresponding to a monolayer, and thereby certifies MoS2 is a just one-layer thick.
a The scheme of the ellipsometry measurements. b AFM topography mapping and a cross-sectional profile of the edge of monolayer MoS2 on SiO2/Si substrate. The scan area was 4.5 × 2.1 μm.2 c Optical image of the MoS2 on top of SiO2/Si substrate. MoS2 covers more than 97% of the surface. d SEM image of the MoS2 revealing a high crystallinity of the samples with the crystallite size 8.4 ± 2.1 μm. e Photoluminescence of the monolayer MoS2 due to the recombination of the A-excitons. High photoluminescence response due to monolayer MoS2 being a direct gap semiconductor, unlike its bulk counterpart. f Resonant Raman spectrum of the MoS2 film at excitation wavelength λ = 632.8 nm. The Raman spectral features are labeled according to Chakraborty and et al.37. The positions of two first-order Raman modes, namely the \(E_{2{\mathrm{g}}}^1\) = 384 cm−1 and the \(A_{1g}\) = 404 cm−1, which are sensitive to the number of layers, correspond to a monolayer37.
Dielectric response analysis
To explore the dielectric response of the samples, we performed SE measurements (Fig. 1a) at multiple incident angles (Methods). In order to precisely retrieve the dielectric permittivity of MoS2 from SE spectra and thus enable predictive capabilities for future optical engineering, it is imperative to introduce an accurate dielectric function model. The best route is to utilize the excitonic nature of the dielectric function, which is described by the TL oscillator model (Methods) since it captures the essential exciton features38. It allows us to develop an algorithm described in the experimental section for MoS2 dielectric response determination with the results displayed in Fig. 2. Apart from the dielectric function, we can analyze the peaks presented in the optical constants because our approach relies on the physical origin of the TMDs absorption, to be exact, on the material’s exciton resonances. As expected, all monolayer samples show similar behavior and values by that proving the reproducibility of the proposed method. Surprisingly, samples grown via PTAS-assisted technique have an additional peak at around 3.5 eV. Multiple experiments were conducted for different samples, and the additional peak appeared only for samples where PTAS molecules were used, as shown in Supplementary Fig. 3. Furthermore, we observed another peak at about 2.2 eV in all samples (with and without PTAS), which, to our knowledge, has not been reported in the literature on optical constants before. We assume that this peak is related to the excited states of A- and B-excitons. The latter have been theoretically predicted39,40 for the range 2.1–2.4 eV and experimentally observed in differential reflectance spectra for MoS2 encapsulated between hexagonal boron nitride41. From Fig. 2b, we infer that the efficiency of this peak depends on the substrate. In particular, for MoS2 samples on SiO2/Si substrate, it is comparable with A- and B-excitons, while for those on quartz, it is barely visible in Fig. 2 (see Supplementary Fig. 1 for more details). Presumably, it is related to the interference effect caused by silicon oxide with the central wavelength λ0 ≈ 570 nm (E = hc/λ0 ≈ 2.2 eV) defined by the Bragg–Snell law42. More importantly, the change of the substrate does not lead to the emergence of the peak at 3.5 eV for the samples synthesized without PTAS promoters; thus, it is independent of the substrate. Moreover, recent theoretical studies36,43 predicted that the environment could transform dark states (i.e., ones that are not excited by light), into bright excitons, which can be excited with light, as could be in our case. These dark states usually are not accessible by light due to the required spin-flip and/or momentum transfer corresponding to spin- and momentum-forbidden electronic transitions44. Nevertheless, Feierabend et al.36 theoretically demonstrated that the presence of organic molecules could change a momentum-forbidden dark exciton into a bright one, while our observation shows exactly the same trend: an additional peak at 3.5 eV appears only for monolayers MoS2 with PTAS-molecules on top (see Supplementary Fig. 2).
a The real part ε1 and b the imaginary part ε2 of the dielectric permittivity. The inset in Fig. 2b shows a comparison with previously published works19,27,29 for the A- and B-excitons. c Refractive index n and d extinction coefficient k. Due to the presence of the PTAS molecules, an additional peak at 3.5 eV appears in the dispersion. For the tabular data, see Supplementary Tables 2–6.
In addition, our algorithm relies on the excitonic nature of absorption, permitting the track of individual exciton contribution into the dielectric function, as illustrated in Fig. 3a (see also the Methods section for more details). In the proposed approach, we exploit one TL oscillator for describing the individual excitonic transition. Therefore, each TL oscillator describes the physical properties of the corresponding exciton. More specifically, model parameters E0 (oscillator central energy) and C (oscillator broadening) giving a critical point and broadening, respectively. The best-fitting parameters are collected in Table 1 with the found critical points for the most studied A-, B-, and C-excitons in Fig. 3b, showing an excellent agreement with previously reported experimental24,27,45 and theoretical46,47 studies. It is also worth noting that excited states of A- and B-excitons have small binding energies, and, as a result, their energy should be approximately equal to the Coulomb-renormalized bandgap energy. In our case, the central energy (E0 = 2.3 eV) of the oscillator linked to the excited states of A- and B-excitons matches with the theoretically predicted value 2.3 eV by Berghauser and Malic40. Moreover, using 2.3 eV as bandgap energy, we determine the binding energies for A- and B-excitons: \(E_A^{\rm{binding}} \approx E_B^{\rm{binding}} = 2.3 - E_0^A = 450\) meV, which agree well with the results of analytic calculations for MoS2 on SiO2 substrate (\(E_A^{\rm{binding}} \approx E_B^{\rm{binding}} = 460\) meV)40. Regarding the peak at 4 eV, it has not been investigated theoretically so far; even so, it was observed in multiple experiments26,27,29, but whether its nature is excitonic remains unknown. At the same time, the TL oscillator perfectly describes it (Fig. 3a) and, thus, our results suggest its relation to a high energy exciton.
a The imaginary part of the dielectric function and contributions from individual Tauc–Lorentz oscillators (excitons) in it. b Comparison of the position of critical points for A-, B-, and C- excitons obtained from the oscillator’s peaks (solid lines) and the previously published experimental24,27,45 and theoretical46,47 works.
Further, to demonstrate the predictive capabilities of our method for the far-field measurements, we recorded the transmission spectrum and compared it with the transfer matrix calculations48 employing the optical constants obtained from SE analysis in Fig. 4a. The measured and calculated transmittance spectra plotted in Fig. 4b match perfectly within a spectrophotometer accuracy (of only 1%). For a complete picture, we also determined optical constants for bulk MoS2 shown in Fig. 2a by exploiting the point-by-point inversion49 (Methods) and calculated its critical points (see Supplementary Table 1) presented in Supplementary Fig. 3. Similarly to a monolayer, it has almost no absorption (from 1240 nm and up to 3300 nm) as well as strong dielectric response (ε ≈18) comparable with traditionally used in nanophotonics semiconductors50, including Si (ε ≈13), Ge (ε ≈18), and GaSb (ε ≈15), at the important telecommunication wavelength interval 1525–1565 nm. In summary, the proposed method has a solid physical background—the excitonic nature of the optical response in MoS219 and, therefore, could be potentially applied for any TMDs due to their similarity in the formation of excitons upon light illumination2.
Discussion
In this work, we have presented a broadband (290–3300 nm) SE of monolayer MoS2 grown on SiO2 by atmospheric pressure chemical vapor deposition and bulk MoS2. In ellipsometry data analysis, we took into account the dominating influence of excitons on the optical response of monolayer materials and resulted in Kramers–Kronig-consistent dielectric functions. It allows us to provide an insight into the exciton physics of monolayer MoS2. In particular, we have observed a previously unreported bright exciton appearing only in monolayer MoS2 samples fabricated by the PTAS-assisted growth process. We speculate that this bright exciton is a result of the dark-to-bright exciton transformation induced by the leftover PTAS molecules. Our results prove that the optical properties of monolayer MoS2 are strongly affected by the environment and the fabrication technology. On the other hand, for bulk MoS2, we note a very high dielectric constant exceeding that of traditionally used Si, GaSb, and Ge in near-infrared, which, combined with zero optical absorption, makes this material very promising for applications in integrated nanophotonics. From a broader perspective, our technique opens up great opportunities to tailor an optical response from van der Waals heterostructures and applications of 2D materials in bio- and chemical sensing.
Methods
Materials
Full area coverage monolayer samples purchased from the 2D Semiconductors Inc. and SixCarbon Technology. Samples from the 2D Semiconductors Inc. were synthesized by atmospheric pressure chemical vapor deposition (APCVD)51 on silicon wafers covered by a 285-nm-thick layer of SiO2. During the synthesis, perylene-3,4,9,10-tetracarboxylic acid tetrapotassium salt (PTAS) was used to promote the nucleation and growth of MoS2. At the same time, samples from the SixCarbon Technology were also synthesized with APCVD technology on sapphire (Al2O3) but without PTAS52, and then transferred by water-assisted technique53 on SiO2/Si substrate or quartz (SiO2). Bulk 2H-phase MoS2 crystals with low defect density, ultra-flat surfaces, and high crystallinity were also purchased from the 2D Semiconductors Inc.
Samples characterization
The SE measurements were performed on a variable-angle spectroscopic ellipsometer (VASE, J.A. Woollam Co.), as shown in Fig. 1a, over a wide wavelength range from 290 to 3300 nm (0.37–4.28 eV) in steps of 1 nm. The SE data were taken at multiple angles of incidence from 60° to 75° in steps of 5°. The thickness of each sample was independently determined by step height AFM measurements (NT-MDT Ntegra Aura). The quality of MoS2 monolayer was assessed with a Horiba LabRAM HR Evolution confocal Raman microscope with He–Ne laser excitation (λ = 632.8 nm). The morphology characterization was performed by SEM (JEOL JSM-7001F), while the surface quality of the sample was evaluated by an optical microscope (Olympus BX51M). Cary 5000 UV–vis–NIR Spectrophotometer (Agilent Technologies) was used for recording transmittance spectra in the range of 290–2500 nm.
Ellipsometry analysis
The ellipsometry data for monolayer MoS2 samples were analyzed as follows:
(1) In this step, the number of layers is set. For our samples, we had three layers—Si, SiO2, and MoS2 (as it is shown in Fig. 1a). The upper one was the MoS2 with the unknown optical constants and thickness of 0.7 nm obtained from AFM measurements shown in Fig. 1b. The interlayer had optical constants of silicon dioxide and a thickness of 285 nm. The substrate was a semi-infinite layer with the optical constants of silicon. Note that some authors fit the thickness of the monolayer as well as optical constants29. However, such an approach leads to overestimation or underestimation of the optical constants due to the high correlation between the thickness and optical constants for atomically thin samples54, which allows one to reliably determine only the product of complex refractive index and the thickness from ellipsometry spectra alone.
(2) Optical constants of the MoS2 monolayer are fitted point-by-point54 to ellipsometry spectra using the Levenberg–Marquardt algorithm.
(3) Based on ε2 obtained in the previous step, the number of peaks N is determined. Afterward, we fit the ε2 curve with N Tauc–Lorentz (TL) oscillators38
where E is the photon energy, A is the strength of the oscillator, C is the broadening term, Eg is the optical band gap, and E0 is the peak central energy. The real part ε1 of the dielectric function is derived from the expression of ε2 using the Kramers–Kronig integration. Then, ε1 from the integration is adjusted to the obtained ε1 in step 2 via changing the constant \(\varepsilon _1^\infty\) in order to take into account electronic transitions at higher energies. The advantages of TL oscillators in the case of TMDs are described in detail in our recent work38.
(4) Finally, the parameters of N TL oscillators and \(\varepsilon _1^\infty\) are fit to the ellipsometry spectra using the Levenberg–Marquardt algorithm. The parameters from the previous step are taken as the initial guess.
Bulk MoS2 was thick enough (~1 mm) for implementation of usual spectroscopic analysis for one interface problem by the formula54
where φ is the angle of incidence, ρ is defined via ellipsometry equation
where ψ and Δ are the measured quantities in ellipsometry, showing the change of the light polarization after reflection from the sample. All ellipsometry analysis was carried out in a software package WVASE3255. The quality of the ellipsometry model is defined via mean squared error (MSE), which is given by
where P is the total number of data points taken, m is the number of fitting parameters, ρexp,j and ρcal,j are experimental and calculated values of the data point54. A lower value of MSE represents a better match between the model and the experiment. For all our samples, MSE was in the range from 1 to 8, which, in the case of the complicated excitonic structure of the dielectric function of 2D materials, is a very good result. Since MoS2 is an anisotropic material, what we obtained is the in-plane component of dielectric tensor because, according to the Snell law, due to a high refractive index of MoS2 ~4, the refracted lightwave propagates almost normally to its surface. As a result, the electric field mostly interacts with the in-plane component, which justifies our isotropic treatment of the spectra.
Data availability
The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.
References
Mueller, T. & Malic, E. Exciton physics and device application of two-dimensional transition metal dichalcogenide semiconductors. npj 2D Mater. Appl. 2, 1–12 (2018).
Wang, G. et al. Colloquium: excitons in atomically thin transition metal dichalcogenides. Rev. Mod. Phys. 90, 021001 (2018).
Manzeli, S., Ovchinnikov, D., Pasquier, D., Yazyev, O. V. & Kis, A. 2D transition metal dichalcogenides. Nat. Rev. Mater. 2, 17033 (2017).
Sangwan, V. K. & Hersam, M. C. Electronic transport in two-dimensional materials. Annu. Rev. Phys. Chem. 69, 299–325 (2018).
Furchi, M. M. et al. Device physics of van der Waals heterojunction solar cells. npj 2D Mater. Appl. 2, 1–7 (2018).
Yu, S. H. et al. Dye-sensitized MoS2 photodetector with enhanced spectral photoresponse. ACS Nano 8, 8285–8291 (2014).
Lopez-Sanchez, O., Lembke, D., Kayci, M., Radenovic, A. & Kis, A. Ultrasensitive photodetectors based on monolayer MoS2. Nat. Nanotechnol. 8, 497–501 (2013).
Cho, B. et al. Chemical sensing of 2D graphene/MoS2 heterostructure device. ACS Appl. Mater. Interfaces 7, 16775–16780 (2015).
Zeng, S. et al. Graphene–MoS2 hybrid nanostructures enhanced surface plasmon resonance biosensors. Sens. Actuators B Chem. 207, 801–810 (2015).
Newaz, A. K. M. et al. Electrical control of optical properties of monolayer MoS2. Solid State Commun. 155, 49–52 (2013).
Kravets, V. G. et al. Measurements of electrically tunable refractive index of MoS2 monolayer and its usage in optical modulators. npj 2D Mater. Appl. 3, 1–10 (2019).
Zhang, Y. J., Oka, T., Suzuki, R., Ye, J. T. & Iwasa, Y. Electrically switchable chiral light-emitting transistor. Science 344, 725–728 (2014).
Ross, J. S. et al. Electrically tunable excitonic light-emitting diodes based on monolayer WSe2 p-n junctions. Nat. Nanotechnol. 9, 268–272 (2014).
Wang, K. et al. Ultrafast saturable absorption of two-dimensional MoS2 nanosheets. ACS Nano 7, 9260–9267 (2013).
Chen, B. et al. Q-switched fiber laser based on transition metal dichalcogenides MoS2, MoSe2, WS2, and WSe2. Opt. Express 23, 26723 (2015).
Mak, K. F. & Shan, J. Photonics and optoelectronics of 2D semiconductor transition metal dichalcogenides. Nat. Photonics 10, 216–226 (2016).
Mupparapu, R., Bucher, T. & Staude, I. Integration of two-dimensional transition metal dichalcogenides with Mie-resonant dielectric nanostructures. Adv. Phys. X 5, 1734083 (2020).
Munkhbat, B. et al. Self-hybridized exciton-polaritons in multilayers of transition metal dichalcogenides for efficient light absorption. ACS Photonics 6, 139–147 (2019).
Yu, Y. et al. Exciton-dominated dielectric function of atomically thin MoS2 films. Sci. Rep. 5, 16996 (2015).
Unuchek, D. et al. Room-temperature electrical control of exciton flux in a van der Waals heterostructure. Nature 560, 340–344 (2018).
Amani, M. et al. Near-unity photoluminescence quantum yield in MoS2. Science 350, 1065–1068 (2015).
Zeng, H. et al. Optical signature of symmetry variations and spin-valley coupling in atomically thin tungsten dichalcogenides. Sci. Rep. 3, 4908–4916 (2013).
Chernikov, A. et al. Exciton binding energy and nonhydrogenic Rydberg series in monolayer WS2. Phys. Rev. Lett. 113, 076802 (2014).
Mak, K. F., Lee, C., Hone, J., Shan, J. & Heinz, T. F. Atomically thin MoS2: a new direct-gap semiconductor. Phys. Rev. Lett. 105, 2–5 (2010).
Hsu, C. et al. Thickness‐dependent refractive index of 1L, 2L, and 3L MoS2, MoSe2, WS2, and WSe2. Adv. Opt. Mater. 7, 1900239 (2019).
Niu, Y. et al. Thickness-dependent differential reflectance spectra of monolayer and few-layer MoS2, MoSe2, WS2 and WSe2. Nanomaterials 8, 725 (2018).
Li, W. et al. Broadband optical properties of large-area monolayer CVD molybdenum disulfide. Phys. Rev. B 90, 195434 (2014).
Liu, H.-L. et al. Optical properties of monolayer transition metal dichalcogenides probed by spectroscopic ellipsometry. Appl. Phys. Lett. 105, 201905 (2014).
Diware, M. S. et al. Characterization of wafer-scale MoS2 and WSe2 2D films by spectroscopic ellipsometry. Curr. Appl. Phys. 17, 1329–1334 (2017).
Kylänpää, I. & Komsa, H.-P. Binding energies of exciton complexes in transition metal dichalcogenide monolayers and effect of dielectric environment. Phys. Rev. B 92, 205418 (2015).
Cai, Z., Liu, B., Zou, X. & Cheng, H. M. Chemical vapor deposition growth and applications of two-dimensional materials and their heterostructures. Chem. Rev. 118, 6091–6133 (2018).
Yakubovsky, D. I. et al. Ultrathin and ultrasmooth gold films on monolayer MoS2. Adv. Mater. Interfaces 6, 2–7 (2019).
Molina-Sánchez, A., Sangalli, D., Hummer, K., Marini, A. & Wirtz, L. Effect of spin-orbit interaction on the optical spectra of single-layer, double-layer, and bulk MoS2. Phys. Rev. B 88, 045412 (2013).
Zhao, W. et al. Origin of indirect optical transitions in few-layer MoS2, WS2, and WSe2. Nano Lett. 13, 5627–5634 (2013).
Verre, R. et al. Transition metal dichalcogenide nanodisks as high-index dielectric Mie nanoresonators. Nat. Nanotechnol. 14, 679–684 (2019).
Feierabend, M., Berghäuser, G., Knorr, A. & Malic, E. Proposal for dark exciton based chemical sensors. Nat. Commun. 8, 14776 (2017).
Chakraborty, B., Matte, H. S. S. R., Sood, A. K. & Rao, C. N. R. Layer-dependent resonant Raman scattering of a few layer MoS2. J. Raman Spectrosc. 44, 92–96 (2013).
Ermolaev, G. A., Yakubovsky, D. I., Stebunov, Y. V., Arsenin, A. V. & Volkov, V. S. Spectral ellipsometry of monolayer transition metal dichalcogenides: Analysis of excitonic peaks in dispersion. J. Vac. Sci. Technol. B 38, 014002 (2020).
Wu, F., Qu, F. & MacDonald, A. H. Exciton band structure of monolayer MoS2. Phys. Rev. B 91, 075310 (2015).
Berghäuser, G. & Malic, E. Analytical approach to excitonic properties of MoS2. Phys. Rev. B 89, 125309 (2014).
Robert, C. et al. Optical spectroscopy of excited exciton states in MoS2 monolayers in van der Waals heterostructures. Phys. Rev. Mater. 2, 1–6 (2018).
Kushnir, S. E. & Napolskii, K. S. Thickness-dependent iridescence of one-dimensional photonic crystals based on anodic alumina. Mater. Des. 144, 140–150 (2018).
Feierabend, M., Brem, S. & Malic, E. Optical fingerprint of bright and dark localized excitonic states in atomically thin 2D materials. Phys. Chem. Chem. Phys. 21, 26077–26083 (2019).
Malic, E. et al. Dark excitons in transition metal dichalcogenides. Phys. Rev. Mater. 2, 1–7 (2018).
Shen, C.-C., Hsu, Y.-T., Li, L.-J. & Liu, H.-L. Charge dynamics and electronic structures of monolayer MoS2 films grown by chemical vapor deposition. Appl. Phys. Express 6, 125801 (2013).
Ramasubramaniam, A. Large excitonic effects in monolayers of molybdenum and tungsten dichalcogenides. Phys. Rev. B 86, 115409 (2012).
Qiu, D. Y., Da Jornada, F. H. & Louie, S. G. Optical spectrum of MoS2: many-body effects and diversity of exciton states. Phys. Rev. Lett. 111, 1–5 (2013).
Passler, N. C. & Paarmann, A. Generalized 4 × 4 matrix formalism for light propagation in anisotropic stratified media: study of surface phonon polaritons in polar dielectric heterostructures. J. Opt. Soc. Am. B 34, 2128 (2017).
Cho, Y. J. et al. Spectroscopic ellipsometry characterization of high-k dielectric HfO2 thin films and the high-temperature annealing effects on their optical properties. Appl. Phys. Lett. 80, 1249–1251 (2002).
Baranov, D. G. et al. All-dielectric nanophotonics: the quest for better materials and fabrication techniques. Optica 4, 814 (2017).
Lee, Y. H. et al. Synthesis of large-area MoS2 atomic layers with chemical vapor deposition. Adv. Mater. 24, 2320–2325 (2012).
Huang, C. C. et al. Scalable high-mobility MoS2 thin films fabricated by an atmospheric pressure chemical vapor deposition process at ambient temperature. Nanoscale 6, 12792–12797 (2014).
Gurarslan, A. et al. Surface-energy-assisted perfect transfer of centimeter-scale monolayer and few-layer MoS2 films onto arbitrary substrates. ACS Nano 8, 11522–11528 (2014).
Tompkins, H. G. & Irene, E. A. Handbook of Ellipsometry. (Springer, Berlin, Heidelberg, 2005).
Woollam, J. A. Co. Guide to Using WVASE Spectroscopic Ellipsometry Data Acquisition and Analysis Software. 1–696 (WVASE Man., 2012).
Acknowledgements
This research was funded by the Russian Science Foundation, grant No. 18-79-10208. The authors thank Dr. Vasyl Kravets, Prof. Alexander Grigorenko for fruitful discussions. The authors thank the MIPT’s Shared Research Facilities Center for the use of their equipment.
Author information
Authors and Affiliations
Contributions
Y.V.S., A.V.A., and V.S.V. suggested and directed the project with help from T.S. and A.Y.N. G.A.E. and Y.V.S. designed and fabricated the samples. G.A.E., D.I.Y., S.M.N., D.E.T., and Y.V.S. performed the measurements and analyzed the data. A.Y.N., T.S., A.A.V., and D.G.B. provided theoretical support. G.A.E., Y.V.S., A.A.V., D.G.B., T.S., A.Y.N., A.V.A., and V.S.V. contributed to the interpretation of the experimental results. G.A.E., A.A.V., and V.S.V. wrote the paper. All authors contributed to discussions and commented on the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ermolaev, G.A., Stebunov, Y.V., Vyshnevyy, A.A. et al. Broadband optical properties of monolayer and bulk MoS2. npj 2D Mater Appl 4, 21 (2020). https://doi.org/10.1038/s41699-020-0155-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41699-020-0155-x
This article is cited by
-
Refractiveindex.info database of optical constants
Scientific Data (2024)
-
The future of two-dimensional semiconductors beyond Moore’s law
Nature Nanotechnology (2024)
-
Highly responsive broadband Si-based MoS2 phototransistor on high-k dielectric
Science China Information Sciences (2024)
-
Performance Enhancement of Gold Coated D-shaped PCF Sensor Using Monolayer MoS2
Plasmonics (2024)
-
New insights into APCVD grown monolayer MoS2 using time-domain terahertz spectroscopy
Scientific Reports (2023)