Abstract
Surface passivation is crucial for many high-performance solid-state devices, especially solar cells. It has been proposed that 2D hexagonal boron nitride (hBN) films can provide near-ideal passivation due to their wide bandgap, lack of dangling bonds, high dielectric constant, and easy transferability to a range of substrates without disturbing their bulk properties. However, so far, the passivation of hBN has been studied for small areas, mainly because of its small sizes. Here, we report the passivation characteristics of wafer-scale, few monolayers thick, hBN grown by metalorganic chemical vapor deposition. Using a recently reported ITO/i-InP/p+-InP solar cell structure, we show a significant improvement in solar cell performance utilizing a few monolayers of hBN as the passivation layer. Interface defect density (at the hBN/i-InP) calculated using C–V measurement was 2 × 1012 eV−1cm−2 and was found comparable to several previously reported passivation layers. Thus, hBN may, in the future, be a possible candidate to achieve high-quality passivation. hBN-based passivation layers can mainly be useful in cases where the growth of lattice-matched passivation layers is complicated, as in the case of thin-film vapor–liquid–solid and close-spaced vapor transport-based III–V semiconductor growth techniques.
Similar content being viewed by others
Introduction
At the semiconductor surface, abrupt termination of the lattice can lead to defect states (called surface defect states) within the semiconductor bandgap. These surface defect states can significantly impair the working of semiconductor devices, such as solar cells. Passivation is a method for reducing recombination through these surface defect states and is one of the most fundamental requirements for achieving high-efficiency solar cells. In conventional III–V solar cells, epitaxially grown, lattice-matched III–V materials allowed very high-quality passivation1. However, most of these lattice-matched wide bandgap III–Vs are only available for GaAs. Although high-efficiency InP solar cells have been realized using lattice-matched InGaAs and InAlAs passivation layers, when used at the front, both of these materials have a sizeable parasitic absorption due to low bandgaps2,3,4,5. The lack of a wide bandgap passivation layer for InP has significantly impeded its development compared to that of GaAs solar cells1.
Other than epitaxial passivation layers, a substantial amount of work has also been done to find suitable non-epitaxial passivation layers (mainly high k-dielectric), including but not limited to Al2O3, Gd2O3, LaF3, ZnO, ZnS, GaS, SiO2, MgO, Ta2O3, POx, Si3Nx, etc.1,6,7,8,9,10. Many of these dielectric materials have been shown to function as suitable passivation layers; however, in most cases, controlled and reproducible formation of high quality and defect-free passivation layer remains a challenging task11. Also, most of the work is reported for III–V transistors with very few reports on high-efficiency III–V solar cells, using dielectric passivation.
On the other hand, pristine 2D materials, in particular, hexagonal boron nitride (hBN) possess many desirable attributes, which makes them an ideal passivation layer. For instance, hBN and other 2D materials lack dangling bond and can be transferred to a range of substrates without disturbing its bulk properties11,12. Also, hBN has a wide bandgap, high chemical and thermal stability, and high dielectric constant (~2.4), which makes it ideal for surface passivation13. So far, the most pristine form of hBN is obtained through mechanical exfoliation from bulk crystals; however, the lateral size of exfoliated flakes is limited to only a few tens of microns, which severely limits the scalability and large area application of hBN. Therefore, new methods such as chemical vapor deposition (CVD), metalorganic chemical vapor deposition (MOCVD), and physical vapor deposition (e.g., DC magnetron sputtering) are being investigated to achieve large area hBN11,14.
hBN has recently been used as a passivation layer in silicon, GaAs, chalcogenide, organic, and 2D transition metal chalcogenides-based solar cells13,15,16,17,18,19. However, in most of these cases, hBN used were very small in size, which is not practical for real solar cells application. In this study, we extend the application of hBN films for the passivation of InP-based solar cells. Centimeter-size MOCVD-grown hBN films were transferred onto InP to study their passivation effect. We show that MOCVD-grown hBN can successfully passivate i-InP/p+-InP solar cells to reduce the dark current, as well as the reverse leakage current by orders of magnitude, leading to a better performance of the device. The cells passivated with hBN has a Voc of >800 mV, in comparison to 720 mV for unpassivated i-InP/p+-InP device. We also investigate the effect of hBN film thicknesses and demonstrate that while a thinner hBN is required to achieve a sufficiently high Jsc, a thicker hBN film leads to better passivation and higher Voc. External quantum efficiency (EQE) measurement of hBN passivated solar cells clearly show a significantly improved (~20%) response in the blue region of the solar spectrum, thereby confirming the passivation of the solar cells in the presence of hBN monolayers. The passivation due to hBN is further corroborated by double diode fitting and analysis of the dark IV curves. To gain further insight into the passivation effects of hBN, ultraviolet photoelectron spectroscopy (UPS) and C–V measurements were performed. Based on the analysis of our results, we postulate that the effectiveness of hBN as a passivation layer is a combined effect of direct quantum mechanical tunneling and interface charge transfer. We also discuss the electron selectivity of hBN.
Results and discussion
hBN characterization
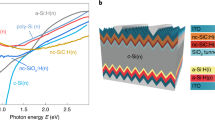
Before and after transferring hBN on InP for device fabrication, we performed some basic characterizations of our hBN samples, as shown in Fig. 1. Figure 1a shows an optical micrograph of 7 ML hBN transferred onto SiO2/Si substrate. The hBN covered region can be easily identified due to the difference in its refractive index with air. The thickness of the hBN film was measured using atomic force microscope (AFM). Figure 1b, c respectively shows the thickness of 5 and 7 ML hBN films measured along the step edge, using AFM linescans. Raman spectra of 5 and 7 ML hBN films are shown in Fig. 1d. The peak at 1368 cm−1 corresponds to the E2g vibrational mode of the sp2 bonded boron nitride20, and its intensity increase with film thickness. Furthermore, prior to device fabrication, the successful transfer of hBN onto the InP substrate was also confirmed using x-ray photoelectron spectroscopy (XPS). Figure 1e, f shows the spectrum corresponding of B-1s and N-1s core levels at 190.6 and 398.2 eV, respectively, which confirmed the presence hBN on InP.
a Optical micrograph of hBN monolayer transferred onto a SiO2/Si substrate for AFM and Raman characterization. AFM results of b 5 ML and c 7 ML hBN. The scanned height variation of the film is shown below the AFM image. d Thickness-dependent Raman intensity of the hBN layer. XPS spectra of e B-1s and f N-1s of the hBN layer transferred onto InP.
Solar cell IV and EQE characterization
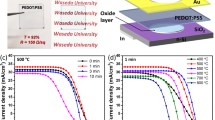
Figure 2 shows a 3D schematic and the cross-sectional transmission electron microscopy (TEM) images of the solar cell. To assess the performance of hBN as a passivation layer, IV (light and dark) and quantum efficiency measurements were performed on InP solar cells with and without hBN. For both 5 and 7 ML hBN passivated samples, we fabricated three devices, and the results were highly reproducible. Figure 3a shows IV characteristics of the hBN-InP solar cell @ 1 sun. It is quite evident from the figure that the introduction of hBN significantly improves both the Voc and Jsc of the solar cell, while also improving its fill factor. The maximum efficiency of 17.2% was obtained for 5 ML hBN with a Voc of 0.78 V, Jsc of 29.4 mA cm−2 and a FF of 75.2%. The efficiency of InP solar cell with 7 ML hBN was measured to be 15.7% with a Voc, Jsc, and FF of 0.8 V, 27.1 mA cm−2, and 72.1%, respectively. This clearly shows that a thicker hBN gives a slightly higher Voc, but significantly lower Jsc suggesting that the hBN must not be too thick to achieve optimum performance of the device. In comparison to both 5 and 7 ML passivated InP solar cells, the efficiency of unpassivated ITO/i-InP/p-InP remains significantly lower at 11.5% with a Voc of 0.72 V, Jsc of 27.4 mA cm−2, and a FF of 58.6%. Here, we would like to mention that for the MOCVD-grown hBN films, it has been shown that for the continuous coverage over the entire 2 in. sapphire substrate, a minimum growth time of 1 h was necessary20. This growth duration resulted in hBN films with a thickness of 5 ML. Hence in the present study, hBN films thinner than 5 ML could not be obtained. Nonetheless, in the future, it will be exciting to see if monolayers <5 ML can also provide sufficiently high passivation to achieve high efficiency. As expected, the lower Voc and Jsc for unpassivated ITO/i-InP/p-InP solar cells are mainly due to interface recombination and are consistent with previously reported results1,5.
a A schematic showing different layers of the solar cell. b A cross-sectional transmission electron microscope (TEM) image of the solar cell showing the different layers (scale bar: 200 nm). c A magnified TEM image showing 2.55-nm thick hBN sandwiched between ITO and i-InP (scale bar: 20 nm). Inset shows the layered structure of hBN.
The EQE of a solar cell is a function of wavelength and is a direct measure of its Jsc. It can be written as a ratio of the number of photogenerated electrons collected to the number of photons of a given wavelength or energy incident onto the device:
where, Iph is the measured current in short-circuit condition when illuminated with light of frequency, \(\upsilon\) and optical power, Popt, e is the electronic charge, h is the Planck’s constant, and \({\Phi} _{\mathrm{p}}\) is the photon flux. The EQE calculated is related to Jsc of a solar cell using Eq. (2).
where Jsc is the short-circuit current calculated for EQE measured between \(\lambda\)1 and \(\lambda\)2. Using Eq. (2), the Jsc calculated for the unpassivated device is 26.7 mA cm−2, whereas the Jsc calculated for 5 ML and 7 ML passivated samples are 28.9 and 27.1 mA cm−2, respectively. As expected, the calculated Jsc is very close to the Jsc measured using light generated IV curve shown in Fig. 3a.
Moreover, because the different wavelength of light is absorbed in different regions of the solar cell, wavelength-dependent EQE can provide information about optoelectronic losses in the different regions of the device. In particular, the smaller wavelength light is absorbed in the topmost part of the absorber layer, and the quantum efficiency in this regime reflects the losses due to surface recombination. Figure 3b shows measured EQE as a function of wavelength. It can be seen that there is a significant improvement in the EQE of the solar cell after 5 ML hBN passivation in the lower wavelength region, i.e., between 350 and 600 nm. An improvement of ~20% of EQE at the lower wavelength region for 5 ML hBN passivated samples in comparison to the unpassivated samples, indicate a significant reduction in front surface recombination. Moreover, similar to 5 ML passivated samples, 7 ML passivated samples also show better EQE in the lower wavelength regime compared to unpassivated samples, and a slightly higher EQE near 350 nm in comparison to 5 ML hBN passivated samples, suggesting slightly better passivation than 5 ML passivated samples. However, its overall quantum efficiency is lower than that of 5 ML hBN due to reduced tunneling (as discussed later), with increased hBN thickness leading to a lower charge carrier collection, and Jsc according to Eqs.(1) and (2).
Dark IV characteristics of a solar cell provide several useful information about device behavior in terms of recombination current, ideality factor, reverse leakage current, and series and shunt resistances. The dark experimental IV of a solar cell can be fitted almost accurately using Eq. (3) below to derive parameters such as J01, J02, n1, n2, Rs, and Rsh (ref. 10).
In Eq. (3), the parameters, J01 and J02, respectively, denote dark current due to diffusion and recombination in the depletion region, whereas, n1 and n2, denote the ideality factor of diodes, and Rs and Rsh denote the series and shunt resistances, respectively. Table 1 compares fitting parameters of three different samples, and it is quite apparent that for all the samples, J01 is almost similar, which signifies that the recombination in bulk is identical in all the samples. However, J02 is nearly an order of magnitude lower for hBN passivated samples compared to the unpassivated sample. This is primarily due to the passivation effect of hBN layer, which modifies the carrier transport across i-InP/ITO interface (as discussed later), and reduces the recombination in the depletion regions. Also, all the solar cells have very high series and low shunt resistance that is also reflected in the lower fill factor of the devices. Assuming a double diode model, the fill factor loss due to series (\({\mathrm{{\Delta} }}{\mathrm{FF}}_{R_{\mathrm{s}}}\)) and shunt resistances (\({\mathrm{{\Delta} }}{\mathrm{FF}}_{R_{\mathrm{sh}}}\)) can be given by Eq. (4) (ref. 21).
In the above equation, FF0 denotes the fill factor of the resistance-free cell and \({\mathrm{{\Delta} }}{\mathrm{FF}}_{R_{\mathrm{s}}}\) and \({\mathrm{{\Delta} }}{\mathrm{FF}}_{R_{\mathrm{sh}}}\), respectively, denote the fill factor loss due to series and shunt resistances. Moreover, in addition to resistances, recombination in the depletion region can also lead to lower fill factor. To calculate loss due to depletion region recombination, we firstly need to calculate an upper limit of fill factor for the cell, which can be given using an analytical equation proposed by Green22.
where
Combining Eqs. (7) and (4), the fill factor loss due to recombination in the depletion region is simply the difference between FFJ01 and FF0. Moreover, using Eq. 7, the upper limit of the fill factor (FFJ01) for both passivated and unpasssivated samples come out to be >85%. For 5 ML hBN passivated samples, the fill factor loss due to series and shunt resistance comes out to be 4.1% and 0.1%, respectively, whereas the J02 recombination loss is ~6.3%. For 7 ML hBN passivated samples, with an increased thickness of hBN, series resistance increases slightly, leading a slightly higher series resistance loss. However, as expected, fill factor loss due to shunt resistance and J02 recombination is almost similar to 5 ML passivated samples. Most importantly, for unpasssivated samples, the most prominent fill factor loss mechanism is the recombination loss due to J02 current, which is consistent with the results discussed earlier.
UPS and band alignment
To better understand the effect of hBN on the hBN/i-InP interface, we performed UPS measurements on ITO, i-InP, and hBN/i-InP. The UPS spectra for samples with and without hBN are plotted in Fig. 4a, with binding energy (B.E.) on the x-axis and intensity on the y-axis. Before every measurement, the instrument was calibrated against a standard silver sample and the valence band maxima (VBM) was calculated by extrapolating the valence band contribution to the B.E. axis. The work function of the samples was calculated using the following equation:
where \(h\upsilon\) = 21.2 eV for He-I line, \(E_{{\mathrm{cut - off}}}\) is calculated by extrapolating the secondary electron onset to the x-axis, and \(E_{{\mathrm{Fermi}}}\) is the corrected Fermi level. Because we calibrated the Fermi level before every measurement (using an Ag sample), for work function calculation, we assume \(E_{{\mathrm{Fermi}}}\) = 0. Using Eq. (8), the work function of ITO and i-InP were calculated to be 4.8 and 5.1 eV, respectively. Surprisingly, there was no significant change in the work function of i-InP before and after hBN transfer, as shown in Fig. 4a. However, there was a shift in VBM of i-InP after hBN transfer. Figure 4b shows the magnified valence band region of the i-InP, with and without hBN. The VBM of i-InP moves by almost 0.27 eV toward the Fermi level in the presence of hBN. Based on UPS results, we draw a band diagram shown in Fig. 4c. It is quite evident in the band diagram that there is an accumulation of electrons at the hBN/i-InP interface, which has an important consequence toward reducing the interface recombination and increasing the selectivity of electrons, as discussed later in the passivation mechanisms section.
Passivation mechanism
To further corroborate the observed passivation at the hBN/i-InP interface, high-frequency (100 kHz) capacitance–voltage (C–V) measurements were performed on Au/ITO/hBN/i-InP/n-InP test structures, where ITO and Au were deposited through a shadow mask to form circular gate contacts. Interface state density (Dit) was extracted via the method of Terman (see Fig. 5)23, and similar energy-dependent interface state density was observed both 5 and 7 ML hBN passivated samples, with a Dit of 2–3 × 1012 eV−1 cm−2 at midgap. This compares favorably with reports for other passivating 3D thin films on InP, as compared in Table 2. However, unlike 3D passivation layers, the passivation in the case of 2D hBN is not due to the passivation of dangling bonds. Based on previous reports, we postulate that 2D hBN passivates the surface defects through the transfer of charges from surface defects states to hBN, which renders them electronically inactive and reduces electronically active interface defect density24.
The energy-dependent interface state density extracted for the hBN films of different thickness from high-frequency (100 kHz) C–V measurements. Note that the apparent dip/minima between 0 and 0.4 eV is an expected artifact of the extraction method and should be ignored. Dit at the intrinsic Fermi level Ei is ~2 × 1012 eV−1 cm−2 in both cases, and slightly higher at midgap (~37 meV <Ei for InP at room temperature).
Although C–V measurement provides evidence of hBN passivation, it does not provide the reasoning for thickness-dependent hBN passivation, as evidenced in IV and EQE measurements. To further explain thickness-dependent hBN passivation and electron selectivity, we discuss the mechanism of charge carrier tunneling across hBN monolayers. Almost all quantum mechanical tunneling equation is an extension of standard Fowler–Nordheim (FN) tunneling equation, which in its simplest form is given by:
where, A, B, and Fox are given as follows:
In the above equation, Vox is the voltage across the dielectric, \(\phi _{\mathrm{b}}\) is the effective barrier height, and \(m_{{\mathrm{ox}}}^ \ast\) is the effective electron mass in the dielectric layer (hBN). FN tunneling equation mainly predicts that the tunneling current in the presence of a sufficiently high electric field, depends exponentially on the barrier height to the power 3/2. However, the FN equation is only applicable to the triangular tunnel barrier, which mainly occurs when Vox > \(\phi _{\mathrm{b}}\). In the current case, we are mainly interested in the low voltage regime, i.e., Vox < \(\phi _{\mathrm{b}}\), where most current flow across hBN through direct tunneling. Most recently, Lee and Hu proposed a modified FN model to calculate the direct tunneling current (Ji) (Eq. 10)25.
The most significant difference between Eqs. (9) and (10) is that they introduce a correction factor \(C\left( {V,V_{{\mathrm{ox}}},t_{{\mathrm{ox}}},\phi _{i,{\mathrm{ox}}}} \right)\) given by:
where, \(i\left( = {\mathrm{ECB}}\, {\mathrm{or}}\, {\mathrm{HVB}} \right)\) are the indexes to define tunneling of an electron from the conduction band (i = ECB) or tunneling of holes from the valence band (i = HVB), N is the density of carriers in the inversion or accumulation layer, and \(\alpha _{i,{\mathrm{ox}}}\) is a fitting parameter. The exponential term associated with the correction factor accounts for secondary effects and only affects the curvature of tunneling characteristics. But, one of the benefits of using Lee and Hu’s equation is that it directly correlates the tunneling current with the accumulation and inversion of carriers, and the conduction and valence band offsets of i-InP/hBN (please see Fig. 6). Overall, Eqs. (9) and (10) respectively show that the tunneling current at any given voltage is inversely proportional to the thickness of the dielectric layer and band offsets, and is directly proportional to the charge carrier density at the dielectric/semiconductor interface (hBN/i-InP). Therefore, in the present scenario, a thinner hBN layer provides higher Jsc compared to thicker hBN films. At the same time, with increased thickness of the hBN layer, the tunneling current of holes (minority carrier) will also be reduced along with electrons, which will reduce the front contact recombination and lower the dark current, leading to a higher Voc for thicker hBN compared to a thinner film.
A band diagram depicting the direct quantum mechanical tunneling from i-InP to ITO. Primarily two tunneling components can be calculated using Eq. (10): electron tunneling current from the conduction band (JECB), and hole tunneling from the valence band (JHVB). ϕECB is the barrier height for electron tunneling from the i-InP conduction band with ITO, and ϕHVB is the barrier height for holes tunneling from the i-InP valence band to ITO. Because ϕECB < ϕHVB, and there is an accumulation of electrons at the interface, JECB ≫ JHVB.
In addition to the passivation layer, hBN may also be acting as a selective contact. Previously, tunnel barriers have also been used as selective contacts26,27,28. For solar cells using dielectric as selective contact, Peibst et al. showed that under first-order approximation, the contact resistance ρc (determined by majority carrier flow), and the dark current J0 (determined by minority carrier flow) are proportional to the transmission of electrons and holes25. Assuming a rectangular dielectric barrier (as shown in Fig. 6) and ignoring the image charge effects, we can write the ratio for electrons and holes tunnel probabilities as follows26:
In the above equation, Te and Th are electrons and holes tunneling probabilities, respectively, tox is the thickness of the dielectric layer, \(m_{{\mathrm{ox,e}}}^ \ast\) and \(m_{{\mathrm{ox,h}}}^ \ast\) are the effective mass of electrons and holes in the dielectric, respectively. The mass of electrons and holes in 2D hBN is similar at ~0.54 m0 (ref. 29). Therefore, for a given thickness of hBN, selectivity toward electrons or holes is solely decided by the barrier height. Therefore, when there is an accumulation of electrons at the semiconductor/hBN interface (as in the current case), the barrier height for electron tunneling reduces, and hBN acts as an electron selective. In contrast, when there is an accumulation of holes at the interface, it will become selective to holes. This is why hBN has previously been reported to act as both electron and hole selective contacts depending on whether there is of electron or hole accumulation at the hBN/semiconductor interface30.
Methods
hBN growth and characterization
The hBN films were grown on commercially available 2 in. sapphire substrate using MOCVD, as described in ref. 14. The thickness of the films was controlled by varying the growth time. Although several different thicknesses of hBN were investigated for passivation, to keep our discussion concise, here we only discuss the results from two different hBN films with a thickness of ~1.65 and ~2.15 nm corresponding to five and seven monolayers of hBN (also referred to as 5 ML and 7 ML), respectively.
For the passivation of the InP surface, cm-size hBN films were transferred from sapphire to InP using the methods described in ref. 20. First, the sapphire substrate (with hBN) was broken into cm-size pieces. Thereafter, PMMA was spin-coated onto the hBN/sapphire substrate and baked on a hot plate to remove excess solvent. The hBN layer was then floated in a 2% HF acid bath. The acid wetted the hBN–sapphire interface and etched the sapphire substrate laterally. After a short time, the hBN layer separated from the sapphire and floated on the surface of the HF bath. Subsequently, the floating hBN–PMMA stack was fished out of the solution and washed several times in deionized (DI) water to remove any residual HF. The hBN–PMMA was then carefully refloated on the surface of a DI water bath and then transferred onto the InP substrate. The samples were allowed to dry under ambient for a few hours. Finally, PMMA was removed in acetone. Using the same process, the hBN–PMMA stack was also transferred on to a planar SiO2/Si substrate for further characterization. After removing the PMMA layer, the transferred hBN films were characterized using AFM and Raman spectroscopy. Finally, cross-sectional TEM lamella was prepared by focused ion beam milling using FEI’s Helios 600 NanoLab, and high-resolution TEM was performed with a JEOL 2100 F instrument.
Device fabrication and characterization
A 3D schematic and the cross-sectional TEM images of the solar cell are shown in Fig. 1. It consists of back ohmic contact of low resistance, a p+-InP base, an i-InP absorber layer, a hBN layer, an ITO layer, and a metal contact over ITO. The device fabrication started with the epilayer growth of 2 microns thick i-InP on a p+-InP wafer. Next, a Zn/Au (20 nm/100 nm) metal contact layer was evaporated on the back of the p+-InP substrate, followed by annealing at 400 °C in forming gas (5% H2:95% N2) for 40 min to create a low resistance back contact. Next, MOCVD-grown hBN was transferred onto the InP substrate, as described above. The hBN adhered to the InP through van der Waals bonding and remains unaffected during further processing of the samples. Thereafter, ITO was sputter-deposited on top of the hBN using conditions reported in ref. 5 Finally, a 500-nm thick silver is evaporated through a shadow mask to form the top contact. For comparison, an InP solar cell without hBN layer was also fabricated in parallel under identical processing conditions.
The device characterization started with the confirmation of the successful transfer of hBN on InP using XPS. To understand the band bending at the interface of ITO/hBN/i-InP, UPS measurements were performed on i-InP, hBN/i-InP, and ITO. The IV characteristics of the devices were obtained using an Oriel solar simulator and IV test station, under the 1-sun @ air mass 1.5 G (at 25 °C) and in the dark. Before every measurement, the solar simulator was calibrated to 1-sun @ air mass 1.5 G (at 25 °C), using a standard test sample provided by the manufacturer. The dark IV curve was fitted using the double diode equation to study the effect of hBN passivation. The algorithm used for fitting was based on the work of Suckow et al.21,22. The EQE of the sample was measured at room temperature using a quantum efficiency setup from Oriel. Similar to the solar simulator, the EQE setup was calibrated using a commercially available test sample obtained from the manufacturer.
Data availability
The data used in this study are available upon request from the corresponding author V.R.
References
Raj, V., Tan, H. H. & Jagadish, C. Non-epitaxial carrier selective contacts for III-V solar cells: a review. Appl. Mater. Today 18, 100503 (2019).
Raj, K. Jain. InP solar cell with window layer. USA patent, US5322573 (1994).
Connolly, J. P. & Mencaraglia, D. in Materials Challenges: Inorganic Photovoltaic Solar Energy, 209–246 (The Royal Society of Chemistry, Cambridge, 2015).
Mar, J. M. State-of-the-art of III-V solar cell fabrication technologies, device designs and applications. in Advanced Photovoltaic Cell Design, Ch. 1, 1−8 (EN548, 2004).
Raj, V. et al. Indium phosphide based solar cell using ultra-thin ZnO as an electron selective layer. J. Phys. D Appl. Phys. 51, 395301 (2018).
Robertson, J., Guo, Y. & Lin, L. Defect state passivation at III-V oxide interfaces for complementary metal–oxide–semiconductor devices. J. Appl. Phys. 117, 112806 (2015).
Lin, L. & Robertson, J. Defect states at III-V semiconductor oxide interfaces. Appl. Phys. Lett. 98, 082903 (2011).
Zhou, L. et al. Brief review of surface passivation on III-V semiconductor. Crystals 8, 226 (2018).
Raj, V., Fu, L., Tan, H. H. & Jagadish, C. Design principles for fabrication of InP-based radial junction nanowire solar cells using an electron selective contact. IEEE J. Photovolt. 9, 980–991 (2019).
Raj, V., Vora, K., Fu, L., Tan, H. H. & Jagadish, C. High-efficiency solar cells from extremely low minority carrier lifetime substrates using radial junction nanowire architecture. ACS Nano 13, 12015–12023 (2019).
Hui, F. et al. On the use of two dimensional hexagonal boron nitride as dielectric. Microelectron. Eng. 163, 119–133 (2016).
Cinzia C. F. W. 2D Materials for Nanoelectronics (CRC Press, Boca Raton, 2016).
Shanmugam, M., Jacobs-Gedrim, R., Durcan, C. & Yu, B. 2D layered insulator hexagonal boron nitride enabled surface passivation in dye sensitized solar cells. Nanoscale 5, 11275–11282 (2013).
Chugh, D. et al. Flow modulation epitaxy of hexagonal boron nitride. 2D Mater. 5, 045018 (2018).
Cho, A.-J. & Kwon, J.-Y. Hexagonal boron nitride for surface passivation of two-dimensional van der Waals heterojunction solar cells. ACS Appl. Mater. Interfaces 11, 39765–39771 (2019).
Kalita, G., Kobayashi, M., Shaarin, M. D., Mahyavanshi, R. D. & Tanemura, M. Schottky barrier diode characteristics of graphene-GaN heterojunction with hexagonal boron nitride interfacial layer. Phys. Status Solidi A 215, 1800089 (2018).
Li, X. et al. Graphene/h-BN/GaAs sandwich diode as solar cell and photodetector. Opt. Express 24, 134–145 (2016).
Li, Q., Zhou, Q., Shi, L., Chen, Q. & Wang, J. Recent advances in oxidation and degradation mechanisms of ultrathin 2D materials under ambient conditions and their passivation strategies. J. Mater. Chem. A 7, 4291–4312 (2019).
Shanmugam, M., Jain, N., Jacobs-Gedrim, R., Xu, Y. & Yu, B. Layered insulator hexagonal boron nitride for surface passivation in quantum dot solar cell. Appl. Phys. Lett. 103, 243904 (2013).
Chugh, D., Jagadish, C. & Tan, H. Large-area hexagonal boron nitride for surface enhanced raman spectroscopy. Adv. Mater. Technol. 4, 1900220 (2019).
Khanna, A. et al. A fill factor loss analysis method for silicon wafer solar cells. IEEE J. Photovolt. 3, 1170–1177 (2013).
Green, M. A. Accuracy of analytical expressions for solar cell fill factors. Sol. Cells 7, 337–340 (1982).
Terman, L. M. An investigation of surface states at a silicon/silicon oxide interface employing metal-oxide-silicon diodes. Solid State Electron. 5, 285–299 (1962).
Park, J. H. et al. Defect passivation of transition metal dichalcogenides via a charge transfer van der Waals interface. Sci. Adv. 3, e1701661 (2017).
Wen-Chin, L. & Chenming, H. Modeling gate and substrate currents due to conduction- and valence-band electron and hole tunneling [CMOS technology]. In 2000 Symposium on VLSI Technology. Digest of Technical Papers (Cat. No.00CH37104) 198–199 (IEEE, Honolulu, HI, 2000).
Peibst, R. et al. Working principle of carrier selective poly-Si/c-Si junctions: is tunnelling the whole story? Sol. Energy Mater. Sol. 158, 60–67 (2016).
Rienäcker, M. et al. Junction resistivity of carrier-selective polysilicon on oxide junctions and its impact on solar cell performance. IEEE J. Photovolt. 7, 11–18 (2017).
Wietler, T. F. et al. Pinhole density and contact resistivity of carrier selective junctions with polycrystalline silicon on oxide. Appl. Phys. Lett. 110, 253902 (2017).
Cao, X. K., Clubine, B., Edgar, J. H., Lin, J. Y. & Jiang, H. X. Two-dimensional excitons in three-dimensional hexagonal boron nitride. Appl. Phys. Lett. 103, 191106 (2013).
Chu, D., Lee, Y. H. & Kim, E. K. Selective control of electron and hole tunneling in 2D assembly. Sci. Adv. 3, e1602726 (2017).
Acknowledgements
This work is supported by the Australian Research Council through the Discovery-Project grants. Access to the epitaxial growth and fabrication facilities is made possible through the support of the Australian National Fabrication Facility, ACT Node.
Author information
Authors and Affiliations
Contributions
L.E.B. and M.M.S. performed CV measurement and analysis. L.L. and F.K. performed FIB and TEM, respectively. D.H.M., H.H.T., and C.J. supervised the project. V.R. wrote the manuscript with contribution from all the authors. All authors have given approval to the final version of the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Raj, V., Chugh, D., Black, L.E. et al. Passivation of InP solar cells using large area hexagonal-BN layers. npj 2D Mater Appl 5, 12 (2021). https://doi.org/10.1038/s41699-020-00192-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41699-020-00192-y