Abstract
In atomically thin transition metal dichalcogenide semiconductors, there is a crossover from indirect to direct band gap as the thickness drops to one monolayer, which comes with a fast increase of the photoluminescence signal. Here, we show that for different alloy compositions of WS2(1−x)Se2x this trend may be significantly affected by the alloy content and we demonstrate that the sample with the highest Se ratio presents a strongly reduced effect. The highest micro-PL intensity is found for bilayer WS2(1−x)Se2x (x = 0.8) with a decrease of its maximum value by only a factor of 2 when passing from mono-layer to bi-layer. To better understand this factor and explore the layer-dependent band structure evolution of WS2(1−x)Se2x, we performed a nano-angle-resolved photoemission spectroscopy study coupled with first-principles calculations. We find that the high micro-PL value for bilayer WS2(1−x)Se2x (x = 0.8) is due to the overlay of direct and indirect optical transitions. This peculiar high PL intensity in WS2(1−x)Se2x opens the way for spectrally tunable light-emitting devices.
Similar content being viewed by others
Introduction
Continuous improvements in the synthesis of two-dimensional materials have enabled the use of these materials in photonics, opto-electronics as well as the emergence of advanced nano-technologies1,2. Particularly, transition metal dichalcogenides (TMDs), which possess a high carrier mobility2 and several interesting spin properties3,4,5 constitute promising candidates for the study of emergent physical phenomena and functionalities in electronics5, photonics, and superconductivity6. The successful manipulation of these properties makes it possible to exploit the full potential of the TMDs, such as the synthesis of semiconductor alloys with tunable band gaps obtained through the change of chemical compositions7,8,9,10 and their integration into catalytic11,12, opto-electronic, and energy-related devices13. More interestingly, stacked structures of TMDs can improve device performances leading to original device concepts14. As examples, multilayer and van der Waals (vdW) heterostructures were notably integrated in vertical tunneling FETs and LEDs15. The physical characteristics of those 2D materials (bandgap, carrier mobility, doping, etc.)16 can be tailored by controlling the number of layers (i.e., the thickness)17,18, the stoichiometric composition, the strain19,20,21,22, the dielectric or electric field environments23. There is a very active competitive field, mainly driven by exfoliation, to achieve bilayer or multilayer of 2D material, especially for superconductivity but also for optics. Synthesis techniques such as chemical vapor deposition (CVD) give access to large-scale well-controlled bilayer structures with on-demand properties, like a controlled angle between the two lattices. For many reasons, 2D materials, where the optical response remains high in a bilayer or multilayer configurations, are highly sought after.
Furthermore, numerous studies on particular TMDs (MoS2, MoSe2, WSe2, WS2) have revealed that they present a tunable band gap that transits from the indirect to direct band gap when these materials are reduced to a single layer thin film accompanied by a significant improvement in the photoluminescence PL intensity (an increase by one or two order of magnitude)24. However, this property which was considered as a common point of all the semiconducting TMDs does not seem to be applicable for certain materials such as MoTe225. Indeed, recent works have shown that the indirect-to-direct band gap crossover occurs in the MoTe2 trilayer thus showing that the single and bi-layer being direct bandgap semiconductors. In particular, it was demonstrated that MoTe2 bilayer still maintains a high PL intensity, which is only 2–3 times weaker than that of the single layer.
In this paper, few-layers of different alloy compositions of WS2(1−x)Se2x (WSSe) have been studied in order to uncover the indirect to direct gap crossover as a function of the number of layers. To this purpose, the optical band gap evolution of few-layer alloys was studied using μ-PL measurements and compared to few thin-layers of WS2 and WSe2. We establish that the measured photoluminescence in WS2(1−x)Se2x follows the same trend as that observed in WSe2 and WS2 for the alloy compositions where x = 0.3, 0.5, and 0.8. However, the μ-PL associated to the bilayer thickness for the alloys with higher Se content (x = 0.8) still exhibits a high intensity compared to the monolayer (ML), similarly to thin-layer semiconducting MoTe2. To better understand this phenomenon and its origin, the electronic properties have been studied using nano-angle-resolved photoemission spectroscopy (nano-ARPES) and density functional theory (DFT) calculations. Our results directly demonstrate the presence of a direct band gap for ML alloys and of an indirect band gap for the increasing number of layers. Therefore, the WS2(1−x)Se2x alloy ML is a direct-gap semiconductor, while the WS2(1−x)Se2x bilayer presents an overlay of direct and indirect optical transitions. This robustness of PL intensity will ease material integration because it is more tolerant to thickness fluctuation.
Results and discussion
Band gap tunability
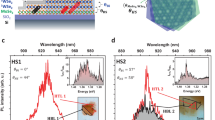
Using CVD (see the “Methods” section), we synthesized few-layer WS2(1−x)Se2x samples with different chemical compositions (where x = 0.3, 0.5, and 0.8) on SiO2/Si substrates26. The resulting samples are typically made of single-crystal domains with well-defined hexagonal or triangular shapes27. Because WS2 and WSe2 share same crystal structure, the random WS2(1−x)Se2x alloy can be simply represented as in Fig. 1a where the chalcogen atom site can be either occupied by S or Se (within their relative abundance), without any other distortion or super-periodicity. In Fig. 1b, we show an optical image of a representative flake, identified from its darker optical contrast with respect to the underlying substrate, exhibiting an equilateral triangle shape.
a Schematic view of the atomic structure of WSSe. For clarity, only two superposed atomic sheets are displayed, in which the atoms in the top layer have been drawn slightly smaller than the ones in the bottom layer. b Typical optical image of the as-grown WS2(1−x)Se2x flakes on the SiO2/Si substrate. c Normalized PL spectra from monolayer WS2, WSe2 and different alloy compositions of monolayer WSSe. d The evolution of the relative PL intensity of mono-, bi- and tri-layers of WS2, WSe2 and WSSe. All measurements were recorded at room temperature with a 532 nm laser excitation.
To study the band gap tunability associated to the modification of the S/Se stoichiometric ratio in the WSSe layer28, we performed μ-PL measurements, using a confocal microscope setup29. We recorded PL spectra for each alloy on mono-, bi- and tri-layer (1, 2, and 3 ML) thick flakes, which we compared to the ones of pure WS2 and WSe2 samples. As shown in Fig. 1c and Supplementary Fig. 1, the PL spectral peaks of the single-layer WS2(1−x)Se2x crystals with a Se composition at 0.8, 0.5, and 0.3 are located at 1.70, 1.77, and 1.81 eV, respectively28. Their intermediate position between the single-layer WSe2 and WS2 peaks (located at 1.63 and 1.95 eV, respectively) confirms that the band gap can be continuously adjusted by alloying two TMDs. The absence of any signal at the location of the pure compounds (1.63 or 1.95 eV) and the conservation of the PL line width along the compositional range, are strong indications for a complete intermixing of the two different chalcogen atoms in the alloy (i.e., random alloy), excluding the presence of separate WS2 or WSe2 domains29,30. Upon increasing the number of layers, the PL peak shifts to lower energies and decreases in intensity for all S/Se ratios (see Supplementary Fig. 2). In contrast to the findings for Mo(1−x)WxS231, we do not see any bowing of the band gap as a function of x for WS2(1−x)Se2x. Our results are in agreement with a previous PL study on the WS2(1−x)Se2x alloy28. Note that these are very different materials, Mo(1−x)WxS2 is obtained by varying the metal (W,Mo) composition, while the present WS2(1−x)Se2x alloys only differ by the chalcogen fraction (S, Se). This has strong implications in the respective composition of the highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbitals (LUMO) orbitals. In the case of the metal alloying (W, Mo), the contribution of metal elements to the HOMO is identical for MoS2 and WS2 (dxy and dx2−y2 orbitals), while the LUMO changes from dz2 orbital in MoS2 to dxy, dx2−y2, and dz2 orbitals in WS2. In the case of chalcogen alloying (Se, S), the orbital contributions to both the HOMO and LUMO of WS2 and WSe2 are identical. The HOMO is composed of the dxy and dx2−y2 orbitals of W, while the LUMO contains the dxy and dx2−y2 orbitals of W and the px, py orbitals of S and Se. These matching contributions explain the simple linear dependence of the bandgap as a function of the chalcogen composition in WS2(1−x)Se2x as measured by PL measurements and confirmed by DFT simulations (see Supplementary Fig. 3).
Atypical behavior of WS2(1−x)Se2x (x = 0.8)
To compare PL signals originating from different layer thicknesses at given chemical composition, we normalize all the data to the maximum PL intensity of the 1 ML sample (see Fig. 1d). The WS2(1−x)Se2x (x = 0.3) exhibits a similar behavior as WSe2 and WS2: by increasing the layer thickness from mono- to bilayer, the maximum PL intensity decreases by one order of magnitude26. For higher Se contents x = 0.5 (x = 0.8, respectively), the 2 ML maximum PL intensity is reduced by a factor of 5 (2, respectively) with respect to the 1 ML sample. Note that a similar low factor of 2 has been previously observed in MoTe2 by I. Lezama et al. 25, in which the authors concluded that bilayer MoTe2 is a direct band gap semiconductor. Another important peculiarity of WS2(1−x)Se2x (x = 0.8) is the PL broadening increase going from 1 ML (69 meV FWHM) to 2 ML (92 meV FWHM) (see Supplementary Fig. 2). This indicates the presence of additional radiative contributions to PL spectrum, other than the direct band transition.
Similar attenuated drop of the maximum PL intensity by only a factor of 2 when passing from mono- to bi-layer of WS2(1−x)Se2x (x = 0.8), can be traced on two distinct flakes presenting 2H and 3R stackings32. In Fig. 2a, e, we present the optical images, obtained from a triangular and another hexagonal flake. The change in contrast represents different thicknesses of the flake. Their corresponding PL intensity and peak position maps are reported in Fig. 2b, c for the triangular flake and in Fig. 2f, g for the hexagonal one, respectively. The changing in the intensity contrast in the PL intensity maps confirms that the number of layers varies across each flake: a higher intensity scale actually indicates a decrease in the number of layers and vice versa29. This is also proved by taking punctual PL spectra in each region of each flake (see Fig. 2d, h). By comparing the spectra of Fig. 2d, h to the ones of Supplementary Fig. 2e, obtained from another sample with the same S/Se stoichiometric ratio, we find a high degree of reproducibility of our results. Thus, the observed peculiar behavior of the sample with the Se content at 80% does not depend on the shape of the flake or on its stacking order16. Note that the PL intensity and peak position maps show a high contrast and composition uniformity for each thickness, which indicates that the optical properties are homogeneous in each region and that the samples are of high crystalline purity. The micro-Raman data also confirm that, in the limits of the experimental resolution of our setup (around 0.5 µm), the pure WS2/WSe2 phases are absent (see Supplementary Fig. 4).
a, e Optical images obtained from two distinct triangular and hexagonal flakes, showing that the 1, 2 and 3 ML regions present different optical contrasts. b, f PL intensity maps and c, g peak position maps acquired on the triangular and hexagonal flakes of a, e with a 532 nm laser excitation. d, h Typical PL spectra obtained from different positions on the flakes of a, e indicated by 1–4 in (a), corresponding to 1, 2, 3 and 4 ML, respectively.
Evidence for an indirect-to-direct band gap crossover
Further insight into the electronic properties of WS2(1−x)Se2x (x = 0.8) can be obtained by performing nano-XPS/nano-ARPES measurements at low temperature (Tsample = 70 K)33,34. The precise electronic characterization of the distinct regions on the flakes becomes possible by adding spatial resolution to ARPES experiments33. The CVD-grown flakes were transferred onto epitaxial graphene on SiC before conducting the nano-XPS/ARPES measurements to avoid charging effects35,36,37,38 (see the “Methods” section). By integrating the photoemission intensity within a selected energy window around the Se 3d peak, while scanning the sample along two in-plane directions, we can first get morphological information on the sample (see Fig. 3a). Red-, orange- and yellow-colored regions correspond to the 1, 2 and 3 ML thicknesses, respectively, and the blue-colored regions are those of the substrate. Each of these regions display a very uniform intensity, attributed to the homogeneity of the electronic properties. Note that in the limits of our spatial resolution, we do not detect any small domains of WS2 or WSe2, related to the presence of structural defects and grain boundaries. The left (right) panel of Fig. 3b shows three μ-XPS spectra of the Se 3d (W 4f, respectively) core level acquired on three distinct points of each region. The experimental data points are represented as black, red and blue circles, the Voigt envelop of fitted components is shown as a green solid line, and the fitting components are plotted as orange and blue curves30. All the Se 3d spectra consist of a single pair of spin–orbit doublet, corresponding to Se 3d5/2 and Se 3d3/2 and attributed to the bonding with W (spin–orbit splitting of 0.83 eV, 3d3/2:3d5/2 ratio of 0.6, and FWHM of 0.5 eV). The W 4f spectra (Fig. 3c), on the other hand, can be well fitted by two pair of spin–orbit doublets, corresponding to W 4f5/2 and W 4f7/2 and relative to the bonding with the two chalcogen atoms S and Se (spin–orbit splitting of 2.15 eV, 4f5/2:4f7/2 ratio of 0.7, and FWHM of 0.4 eV)39. The ratio between the area of the S-related component is about 20% of the total one (the sum of the components related to S and Se), which reflects the chemical composition of the alloy. No additional components are present in the nano-XPS spectrum confirming the homogeneity of the sample and excluding the presence of possible covalent bonds between the WSSe and the graphene substrate, as expected in a sharp van der Waals WSSe/graphene interface. Moreover, the Se 3d and W 4f energy positions vary according to the region. This shift can be related to the band alignment at the interface between graphene and WSSe40,41, in agreement with the nano-ARPES results discussed in the coming paragraph. These photoemission spectra are used to estimate the Se contents of the WSSe alloys. The total amount of Se atoms is calculated from the Se 3d and W 4f peak area ratio in the surface-sensitive configuration, weighted by their relative cross sections.
a Spatially resolved photoemission map (of 300 × 300 μm2 area) of the Se 3d core level obtained from the WS2(1−x)Se2x (x = 0.8) sample by using a photon energy of 100 eV. b, c Left (Right) panel corresponds to the μ-XPS spectra of the Se 3d (W 4f) core level acquired on three distinct points represented as crosses in panel (a).
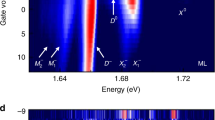
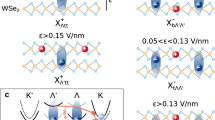
In order to unambiguously evaluate the direct or indirect bandgap character of the 1 ML, 2 ML and 3 ML of WS2(1−x)Se2x (x = 0.8), we investigated the electronic band structure of this alloy crystal experimentally by means of ARPES and theoretically with DFT calculations42,43. Figure 4a–c present the photoemission intensity maps acquired at 100 eV on mono, bi- and tri-layers of WS2(1−x)Se2x (x = 0.8), respectively along the Γ−K direction44. Their second derivatives on which the theory (blue dashed lines) is overplotted are instead reported in Fig. 4d–f. The top of the valence band at the K point is mostly formed by planar dxy and dx2−y2 orbitals of tungsten, while at the Γ point the band is mostly composed by W dz orbitals and S, Se pz orbitals based on DFT calculations30. Because of their out-of-plane character, the bands with the lowest energy at Γ are the most sensitive to the number of layers composing the system and, as shown in Fig. 4, the single down-dispersing parabola of the 1 ML splits into two (three) parabolas for 2 ML (3 ML)45. This detailed evolution of the valence band structure for different WS2(1−x)Se2x (x = 0.8) thicknesses is highly useful in terms of offering a direct way to determine the WS2(1−x)Se2x ML number (Table 1).
For 1 ML, the valence band maximum (VBM) is located at the K point at 1.16 eV binding energy (BE), while for 2 and 3 ML it is positioned at the Γ point at 1.16 and 1.27 eV BE, respectively. Consequently, by increasing the number of ML, the WS2(1−x)Se2x (x = 0.8) quasiparticle band gap decreases, inducing also a shift in the VBM position. Going from Γ to K, the character of the valence band at the top changes from out-plane to in-plane. Thus, the split due to the number of layers is removed in favor of only a spin–orbit coupling split at the K point of the in-plane W d orbitals. The values of the spin–orbit coupling (SOC) are of 500, 420, and 380 meV for mono-, bi- and tri-layer WSSe, respectively, which represent high values compared to other 2D materials45. Besides, the energy difference between the K and Γ points (EK−EΓ) is about 500, −60, and −480 meV for mono-, bi- and tri-layer WSSe, respectively. A similar trend was already observed for few layer WSe2 by Y. Zhang et al.46 In their case, the energy difference between the K and Γ points at the VBM (EK−EΓ) was about 560, −80, and −11 meV for mono-, bi- and tri-layer WSe2, respectively. For bi-layer WS2(1−x)Se2x (x = 0.8), the fact that the top of the VB at K point is slightly lower than the one at Γ suggests that 2 ML of WS2(1−x)Se2x (x = 0.8) may show a significant contribution from both direct and indirect emissions in the final PL spectrum47. In Fig. 4d–f, the second derivatives of the experimental data were compared with the band structure calculations in the DFT framework for freestanding 2H-WS2(1−x)Se2x (x = 0.8) layers. The DFT calculated bands are shifted to account for the Fermi level position. The main features are well reproduced by the calculated band structures along the ΓK high-symmetry direction for all thicknesses. Both the measured and DFT calculated band structures agree for the 2H ordering of WS2(1−x)Se2x (x = 0.8). As expected, 1 ML WSSe is a direct-gap semiconductor (at the K point). On the other hand, 3 ML WSSe behaves differently, showing a VBM located at Γ and a conduction band minimum (CBM) located at K. Consistently with the ARPES image of bilayer WSSe (Fig. 4b), the local maximum of the VB at K is very close to the one at Γ. Similarly, the local minimum of the CB at the Λ point (the middle-point between K and Γ) is very close to the CBM at K. This is a consequence of the increased hopping between the pz orbitals of the chalcogen atoms in multi-layer TMDs, which tends to increase the top of the VB at Γ and decrease the minimum of the CB at Λ. From this result we can deduce that bilayer WS2(1−x)Se2x (x = 0.8) is a semiconductor where direct and indirect optical transitions can both contribute to the PL spectra. The additional contribution of these two transitions explains the relatively large PL intensity of 2 ML with respect to 1 ML WS2(1−x)Se2x (x = 0.8).
In summary, we have successfully studied the electronic properties of different thicknesses of WS2(1−x)Se2x alloys with tunable content on sulfur and selenium. We demonstrated that the PL intensity increases when the number of layer decreases. Remarkably, we found that for the high Se content, WS2(1−x)Se2x (x = 0.8) exhibits an atypical behavior when the number of layers is reduced. For this particular composition, we observe a high PL signal for both ML and bilayer with a drop of the maximum intensity by only a factor 2 when switching from mono- to bilayers. This is interpreted as the signature of the presence of competing contributions of direct and indirect optical transitions, which was confirmed experimentally by ARPES and theoretically by means of DFT calculations. Consequently, by changing the alloy content and the thickness, one can achieve spectrally tunable and robust electroluminescent devices.
Methods
Growth of WS2(1−x)Se2x/SiO2/Si(001)
WS2(1−x)Se2x samples were grown by CVD in a 1″ quartz tube furnace. A quartz boat contained WS2 and WSe2 powder was loaded at the center of the furnace. SiO2/Si substrate was placed at the downstream of the furnace. Before heating, an Ar gas flow was introduced into the system for 10 min in order to exhaust the air and maintain the flow at 70 standard-state cubic centimeter per minute (sccm). The furnace was then rapidly heated to 1100 °C in 30 min. After keeping the growth at this temperature for 5 min, the furnace was then cooled down to room temperature naturally.
µ-PL measurements
The µ-PL measurements were conducted at room temperature, using a commercial confocal Horiba micro-Raman microscope with a ×100 objective and a 532 nm laser excitation. The laser beam was focused onto a small spot having a diameter of ~1 μm on the sample and its incident power was about 5 μW. All measurements are acquired with a 532 nm laser excitation at room temperature.
Band structure of few layers WS2(1−x)Se2x
The ARPES measurements were conducted at the ANTARES beamline of Synchrotron SOLEIL (Saint-Aubin, France). We used linearly horizontal polarized photons of 100 eV and a hemispherical electron analyzer with vertically confining entrance slit to allow band mapping. The total angle and energy resolutions were 0.25° and 10 meV. All nano-XPS/ARPES experiments were done at low temperature (70 K).
Theoretical calculations
We performed plane-wave density functional theory (DFT) simulations by means of the QUANTUM ESPRESSO code48. To include the spin–orbit interaction, we realized noncollinear calculations with the adoption of fully relativistic norm-conserving pseudopotentials. In order to attain a better estimation of the band gap, we adopted the HSE hybrid functional49 to approximate the exchange-correlation term. The self-consistent solution was obtained by using a 15 × 15 × 1 Monkhorst–Pack k-points grid centered around the Γ point and a cutoff energy of 50 Ry. In layered materials, the van der Waals forces were accounted by means of the semiempirical Grimme DFT-D3 correction50. A vacuum space of 24 Å in the z direction was assumed in the unit cell to suppress the interaction between two adjacent sheets in the periodic arrangement. The cell parameters and atomic coordinates were fully relaxed by using a convergence threshold for forces and energy of 10−3 and 10−4 (a.u.), respectively. The WSSe was simulated within the virtual crystal approximation (VCA), where at each chalcogen position we located a virtual atom whose pseudopotential is given by a linear interpolation of the pseudopotentials for S and Se. Such a mean-field approximation is expected to provide the correct trends of the band-structure evolution of samples with sufficiently large surfaces.
Data availability
The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.
References
Geim, A. K. & Grigorieva, I. V. Van der Waals heterostructures. Nature 499, 419–425 (2013).
Radisavljevic, B., Radenovic, A., Brivio, J., Giacometti, V. & Kis, A. Single-layer MoS2 transistors. Nat. Nanotechnol. 6, 147–150 (2011).
Xiao, D., Liu, G.-B., Feng, W., Xu, X. & Yao, W. Coupled spin and valley physics in monolayers of MoS2 and other group-VI dichalcogenides. Phys. Rev. Lett. 108, 196802 (2012).
Mak, K. F., He, K., Shan, J. & Heinz, T. F. Control of valley polarization in monolayer MoS2 by optical helicity. Nat. Nanotechnol. 7, 494–498 (2012).
Zeng, H., Dai, J., Yao, W., Xiao, D. & Cui, X. Valley polarization in MoS2 monolayers by optical pumping. Nat. Nanotechnol. 7, 490–493 (2012).
Cao, Y. et al. Unconventional superconductivity in magic-angle graphene superlattices. Nature 556, 43–50 (2018).
Li, F., Wei, W., Zhao, P., Huang, B. & Dai, Y. Electronic and optical properties of pristine and vertical and lateral heterostructures of Janus MoSSe and WSSe. J. Chem. Lett. 8, 5959–5965 (2017).
Zheng, B. et al. Band alignment engineering in two-dimensional lateral heterostructures. J. Am. Chem. Soc. 140, 11193–11197 (2018).
Li, H. et al. Lateral growth of composition graded atomic layer MoS2(1-x)Se2x nanosheets. J. Am. Chem. Soc. 137, 5284–5287 (2015).
Li, H. et al. Growth of alloy MoS2xSe2x(1-x) nanosheets with fully tunable chemical compositions and optical properties. J. Am. Chem. Soc. 136, 3756–3759 (2014).
Lagarde, D. et al. Carrier and polarization dynamics in monolayer MoS2. Phys. Rev. Lett. 112, 047401 (2014).
Magnozzi, M. et al. Optical dielectric function of two-dimensional WS2 on epitaxial graphene. 2D Mater. 7, 2 (2020).
Noumbé, U. N. et al. Ionic glass-gated 2D material-based phototransistor: MoSe2 over LaF3 as case study. Adv. Funct. Mater. 29, 1902723 (2019).
Britnell, L. et al. Strong light–matter interactions in heterostructures of atomically. Thin Films. 340, 1311–1314 (2013).
Zhou, X. et al. Tunneling diode based on WSe2/SnS2 heterostructure incorporating high detectivity and responsivity. Adv. Mater. 30, 1703286 (2018).
Wang, G. et al. Spin-orbit engineering in transition metal dichalcogenide alloy monolayers. Nat. Commun. 6, 10110 (2015).
Yun, W. S., Han, S. W., Hong, S. C., Kim, I. G. & Lee, J. D. Thickness and strain effects on electronic structures of transition metal dichalcogenides: 2H-MX2 semiconductors (M = Mo, W; X = S, Se, Te). Phys. Rev. B 85, 033305 (2012).
Jin, W. et al. Direct measurement of the thickness-dependent electronic band structure of MoS2 using angle-resolved photoemission spectroscopy. Phys. Rev. Lett. 111, 106801 (2013).
Ben Aziza, Z. et al. Bandgap inhomogeneity of MoS2 monolayer on epitaxial graphene bilayer in van der Waals p-n junction. Carbon 110, 396–403 (2016).
Chaste, J. et al. Intrinsic properties of suspended MoS2 on SiO2/Si pillar arrays for nanomechanics and optics. ACS Nano 12, 3235–3242 (2018).
Blundo, E. et al. Evidence of the direct-to-indirect band gap transition in strained two-dimensional WS2, MoS2, and WSe2. Phys. Rev. Res. 2, 012024(R) (2020).
Pető, J. et al. Moderate strain induced indirect bandgap and conduction electrons in MoS2 single layers. npj 2D Mater. Appl. 3, 39 (2019).
Waldecker, L. et al. Rigid band shifts in two-dimensional semiconductors through external dielectric screening. Phys. Rev. Lett. 123, 206403 (2019).
Mak, K. F., Lee, C., Hone, J., Shan, J. & Heinz, T. F. Atomically thin MoS2: a new direct-gap semiconductor. Phys. Rev. Lett. 105, 136805 (2010).
Lezama, I. G. et al. Indirect-to-direct band gap crossover in few-layer MoTe2. Nano Lett. 15, 2336–2342 (2015).
Conley, H. J. et al. Bandgap engineering of strained monolayer and bilayer MoS2. Nano Lett. 13, 3626–3630 (2013).
Yang, T. et al. van der Waals epitaxial growth and optoelectronics of large-scale WSe2/SnS2 vertical bilayer p–n junctions. Nat. Commun. 8, 1906 (2017).
Duan, X. et al. Synthesis of WS2xSe2-2x alloy nanosheets with composition-tunable electronic properties. Nano Lett. 16, 264–269 (2016).
Zribi, J. et al. Strong interlayer hybridization in the aligned SnS2/WSe2 hetero-bilayer structure. npj 2D Mater. Appl. 3, 27 (2019).
Henck, H. et al. Electronic band structure of two-dimensional WS2/graphene van der Waals heterostructures. Phys. Rev. B 97, 155421 (2018).
Chen, Y. et al. Tunable band-gap photoluminescence from atomically thin transition-metal dichalcogenide alloys. ACS Nano 7, 4610–4616 (2013).
Paradisanos, I. et al. Controlling interlayer excitons in MoS2 layers grown by chemical vapor deposition. Nat. Commun. 11, 2391 (2020).
Pierucci, D. et al. Band alignment and minigaps in monolayer MoS2–Graphene van der Waals heterostructures. Nano Lett. 16, 4054–4061 (2016).
Henck, H. et al. Flat electronic bands in long sequences of rhombohedral-stacked graphene. Phys. Rev. B 97, 245421 (2018).
Henck, H. et al. Direct observation of the band structure in bulk hexagonal boron nitride. Phys. Rev. B 95, 085410 (2017).
Ben Aziza, Z. et al. Van der Waals epitaxy of GaSe/Graphene heterostructure: electronic and interfacial properties. ACS Nano 10, 9679–9686 (2016).
Forti, S. et al. Electronic properties of single-layer tungsten disulfide on epitaxial graphene on silicon carbide. Nanoscale 9, 16412–16419 (2017).
Nakamura, H. et al. Spin splitting and strain in epitaxial monolayer WSe2 on graphene. Phys. Rev. B 101, 165103 (2020).
Pierucci, D. et al. Tunable doping in hydrogenated single layered molybdenum disulfide. ACS Nano 11, 1755–1761 (2017).
Dau, M. T. et al. Beyond van der Waals interaction: the case of MoSe2 epitaxially grown on few-layer graphene. ACS Nano 12, 2319–2331 (2018).
Henck, H. et al. Interface dipole and band bending in the hybrid p–n heterojunction MoS2/GaN(0001). Phys. Rev. B 96, 115312 (2017).
Zhang, Y. et al. Direct observation of the transition from indirect to direct bandgap in atomically thin epitaxial MoSe2. Nat. Nanotechnol. 9, 111–115 (2014).
Ulstrup, S. et al. Nanoscale mapping of quasiparticle band alignment. Nat. Commun. 10, 3283 (2019).
Pierucci, D. et al. Large area molybdenum disulphide-epitaxial graphene vertical Van der Waals heterostructures. Sci. Rep. 6, 26656 (2016).
Wilson, N. R. et al. Determination of band offsets, hybridization, and exciton binding in 2D semiconductor heterostructures. Sci. Adv. 3, e1601832 (2017).
Zhang, Y. et al. Electronic structure, surface doping, and optical response in epitaxial WSe2 thin films. Nano Lett. 16, 2485–2491 (2016).
Steinhoff, A. et al. Efficient excitonic photoluminescence in direct and indirect band gap monolayer MoS2. Nano Lett. 15, 6841–6847 (2015).
Giannozzi, P. et al. QUANTUM ESPRESSO: a modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 21, 39 (2009).
Heyd, J., Scuseria, G. E. & Ernzerhof, M. Hybrid functionals based on a screened Coulomb potential. J. Chem. Phys. 118, 8207 (2003).
Grimme, S., Antony, J., Ehrlich, S. & Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 132, 154104 (2010).
Acknowledgements
We acknowledge the financial support by RhomboG (ANR-17-CE24-0030), MagicValley (ANR-18-CE24-0007), and Graskop (ANR-19-CE09-0026) grants. This work is supported by a public grant overseen by the French National Research Agency (ANR) as part of the “Investissements d’Avenir” program (Labex NanoSaclay, ANR-10-LABX-0035). Support from the Materials Engineering and Processing program of the National Science Foundation, Award Number CMMI 1538127 is greatly appreciated. Support from the National Natural Science Foundation of China (51525202 and U19A2090).
Author information
Authors and Affiliations
Contributions
B.Z. and A.P. fabricated the samples. C.E., L.K., D.P., A.O., J.A., and P.D. carried out the nano-XPS/nano-ARPES experiments. J.C., A.O., and T.B. characterized the samples by means of µ-Raman/PL spectroscopy and analyzed the Raman/PL data. M.P. carried the DFT calculation. C.E., J.C., L.K., J.A., D.P., F.B., F.O., A.O., and E.L. analyzed the data. C.E., M.P., and A.O. wrote the manuscript. All the authors discussed the results and commented on the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ernandes, C., Khalil, L., Almabrouk, H. et al. Indirect to direct band gap crossover in two-dimensional WS2(1−x)Se2x alloys. npj 2D Mater Appl 5, 7 (2021). https://doi.org/10.1038/s41699-020-00187-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41699-020-00187-9