Abstract
Monolayer transition metal dichalcogenides (TMD) have numerous potential applications in ultrathin electronics and photonics. The exposure of TMD-based devices to light generates photo-carriers resulting in an enhanced conductivity, which can be effectively used, e.g., in photodetectors. If the photo-enhanced conductivity persists after removal of the irradiation, the effect is known as persistent photoconductivity (PPC). Here we show that ultraviolet light (λ = 365 nm) exposure induces an extremely long-living giant PPC (GPPC) in monolayer MoS2 (ML-MoS2) field-effect transistors (FET) with a time constant of ~30 days. Furthermore, this effect leads to a large enhancement of the conductivity up to a factor of 107. In contrast to previous studies in which the origin of the PPC was attributed to extrinsic reasons such as trapped charges in the substrate or adsorbates, we show that the GPPC arises mainly from the intrinsic properties of ML-MoS2 such as lattice defects that induce a large number of localized states in the forbidden gap. This finding is supported by a detailed experimental and theoretical study of the electric transport in TMD based FETs as well as by characterization of ML-MoS2 with scanning tunneling spectroscopy, high-resolution transmission electron microscopy, and photoluminescence measurements. The obtained results provide a basis for the defect-based engineering of the electronic and optical properties of TMDs for device applications.
Similar content being viewed by others
Introduction
Persistent photoconductivity (PPC) has long been studied in amorphous as well as highly compensated wide-bandgap bulk semiconductors and was attributed to the presence of large spatial fluctuations of the potential energy of charge carriers (electrons and holes)1,2,3. In the case of transition metal dichalcogenides (TMD), the PPC effect with the respective time constant, τ, of 102–104 s was reported for monolayer MoS2 (ML-MoS2) after their irradiation with visible light at room temperature (RT)4,5,6,7. An even higher τ ∼ 106 s was observed for a few layers of MoS2 after UV irradiation (λ = 254 nm)8. In these studies, the PPC effect was related to the charge traps caused by inhomogeneities either in the substrate4,5,6,9 or in the adsorbates5,8 on the TMD surface. Here we show that the long-living photo-generated charge carriers may also originate from intrinsic, material-specific lattice defects resulting in a prolonged recombination time of photo-generated carriers.
We demonstrate the extremely long-living giant PPC (GPPC) in field-effect transistors (FETs) fabricated from single crystalline ML-MoS2 grown by chemical vapor deposition10,11 (CVD) after their exposure to UV light (λ = 365 nm), Fig. 1. At RT the photo-generated charge carriers lead to an increase of the conductivity by a factor of up to ~107, which depends on both the applied gate voltage (Vg) and the irradiation intensity (Fig. 1b). The high conductivity state persists for a long time with a time constant of ~30 days (3 × 106 s) at Vg = 0 V (Fig. 1c). We explain these experimental findings with a model considering the presence of large spatial fluctuations of the potential energy of carriers (electrons and holes) in the ML-MoS2. These fluctuations lead to a spatial separation of photo-generated carriers, as electrons (holes) concentrate in the minima (maxima) of random potential energy landscape (see schematic in Fig. 1d) resulting in a giant increase of their recombination time12,13,14. Transport of these photo-generated carriers displays two regimes: (i) the thermal activation regime at RT and the variable-range hopping regime at low temperatures (LT). Carrying out a quantitative analysis of the transfer characteristics in both regimes, we extract such parameters of the random potential energy landscape as the characteristic amplitude and the correlation radius as well as the variation of the concentration of photo-generated carriers with time (inset in Fig. 1c) and UV irradiation intensity (Fig. 2e, f). Large fluctuations of the potential energy result in a substantial concentration of strongly localized states in the forbidden energy gap. By performing scanning tunneling spectroscopy (STS) we experimentally confirm the presence of such localized states in ML-MoS2. Atomically resolved transmission electron microscopy (TEM) enables us to correlate these findings with the density of the point defects in the samples.
a Schematic diagram of the MoS2-FET device and experimental setup. b Experimental observation of GPPC in a MoS2-FET device. The black curve represents the transfer characteristics of the MoS2 device before UV irradiation, the red curve represents the transfer characteristics immediately after UV irradiation (λ = 365 nm) for 5 min with an intensity of ~30 mW cm−2. The colored curves represent the time-dependent transfer curves after UV irradiation. The measurements continued up to 30 days (the complete data set is provided in Supplementary Fig. 4). The inset shows an optical microscopy image of the MoS2-FET device (scale bar: 10 µm). c The decay of the drain current with time at Vg = 0 V. The experimental data were fitted (red curve) using a two-stage exponential decay function to extract the GPPC time constants. Calculated decay of the photoelectron concentration with time is shown in the inset. d Schematic representation of large spatial fluctuations of the potential energy of carriers in a MoS2 monolayer. The incident photons excite electrons from the valence band to the conduction band resulting in their spatial separation ∆x. µe,D and µe,I are quasi-Fermi energy levels corresponding to equilibrium electrons and photo-generated electrons, respectively.
Transfer characteristics of a MoS2 FET at the pristine condition and after UV irradiation with various intensities. The irradiation time for each intensity was 5 min, and all transfer curves were recorded in dark immediately after irradiation. Experimental transfer curves at RT (a) and at 6 K (b). Theoretically calculated transfer curves RT (c) and at 6 K (d). Calculated photoelectron density as a function of the irradiation intensity at RT (e) and at 6 K (f). The dashed lines in e and f are presented as a guide for the eye. The GPPC as a function of time for this device is presented in Supplementary Fig. 5.
Results and Discussion
Transport measurements of MoS2-FETs and observation of GPPC
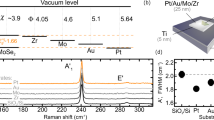
In Fig. 1a, a schematic representation of the experimental setup for the transport measurements is shown. As-grown ML-MoS2 were characterized by optical microscopy, Raman spectroscopy, and atomic force microscopy (Supplementary Figs. 1 and 2). Afterward, the FETs were fabricated using e-beam lithography. An optical microscopy image of a typical device is shown in the inset of Fig. 1b. We measured the transfer characteristics of these devices, i.e., the drain-source current, Ids, vs. Vg before and after UV irradiation (λ = 365 nm, intensity ~30 mW cm−2 for 5 min). All measurements were performed in a high vacuum (~10−6 mbar) and under dark conditions; these data are shown in Fig. 1b. Note that we studied a possible effect of the UV irradiation-induced damage of the ML-MoS2 by conducting Raman spectroscopy before and after the irradiation and did not find any noticeable changes in the spectra (see Supplementary Fig. 3).
From the transfer characteristics of the pristine device (black line in Fig. 1b) we estimate a field-effect mobility of 1.5 cm2 V−1 s−1, which is a typical value for CVD grown ML-MoS211,15. Directly after UV irradiation, we observe a very strong enhancement in the Ids (see red line in Fig. 1b) of up to \(\frac{{I_{\rm{irr}}}}{{I_{\rm{non - irr}}}} \approx\) 107 at Vg = − 40 V, which is close to the device threshold voltage. We found that the GPPC persists even for days at RT, albeit decaying in its strength over time (transfer characteristics recorded between 1 and 30 days are shown in Fig. 1b; Supplementary Fig. 4 shows the full data set). During these measurements, the devices were always kept in a high vacuum and under dark conditions. The obtained decay of Ids over time is shown in Fig. 1c at Vg = 0 V. These data can be described using a two-stage exponential decay function. In the initial stage, the Ids decays with a time constant of τ1 ≈ 1 day, whereas in the following stage, the GPPC relaxation slows down yielding a time constant of τ2 ≈ 34 days. Similar values were obtained for more than ten devices made of ML-MoS2 synthesized in different CVD experiments (see, e.g., Supplementary Fig. 5). Note that after a few months, the transfer characteristics of the devices completely recover to their pristine state before irradiation (Supplementary Fig. 6a). We also found that vacuum annealing (~10−2 mbar) at 170 °C results in a significantly faster decrease of the persistent photocurrent (Supplementary Fig. 6b), which agrees well with the thermally enhanced recombination of the photo-generated carriers. After the complete decay of persistent photocurrent, a subsequent UV irradiation restores the initially observed GPPC effect (Supplementary Fig. 6b).
To investigate the GPPC in detail, we measured the transfer characteristics of the MoS2-FETs at RT and LT (6 K) after UV irradiation of varying intensities between 2 and 30 mW cm−2 for 5 min as shown in Fig. 2a, b, respectively. In both cases, we observed an enhancement of the Ids with increasing UV intensity. At LT, the absolute values of Ids were lower than at RT for all Vg, which we attribute to the variable range hopping type of transport caused by the strong localization of the charge carriers16,17,18.
Model of the photo-induced charge transport
To rationalize the experimental observations of the GPPC in MoS2-FETs, we apply the following model. We assume that the crystal lattice defects and lattice strain lead to large spatial fluctuations of the potential energy of carriers in the ML-MoS2, predominantly because of the deep-lying traps in the proximity of the conduction band (CB)/valence band (VB) edges as schematically depicted in Fig. 1d. We describe these fluctuations effectively by a coordinate dependent potential with zero mean value, \(U\left( {\boldsymbol{r}} \right) = U_0f({\boldsymbol{r}}/r_{\rm{corr}})\), where U0 is the typical amplitude of the random potential and in our case, T is the temperature, kB is the Boltzmann constant, and rcorr is the correlation radius12.
By using such a model, we carry out a quantitative analysis of the transfer characteristics in two regimes. At RT, the conductivity of the ML-MoS2 is defined by thermally induced activation of localized electrons surpassing the percolation level (the mobility edge), EP. The EP is the characteristic energy above which electrons are delocalized, i.e., propagate along a conduction channel experiencing only weak scattering12,13. In this regime, the concentration of delocalized electrons depends strongly on the temperature as well as Vg and thus allows one to tune the conductivity (see dotted line in Fig. 2a). The conductivity in the thermal activation regime is obtained as
where µe is the quasi-Fermi energy level considering both equilibrium electrons (µe,D), i.e., the electrons which are present in the absence of irradiation, and nonequilibrium, photo-generated electrons (µe,l) (see Fig. 1d), and σ0 is a coefficient which depends only weakly on both Vg and the intensity of the UV radiation. In strongly disordered materials with many localized states, µe is determined by the concentration of electrons according to12,19
where neq is the concentration of equilibrium electrons given by \(n^{\rm{eq}}\left( {V_g} \right) = \varepsilon _r\varepsilon _0V_g/ed\), where εr = 3.9 and d = 300 nm are the relative dielectrics constant and the thickness of the SiO2 gate insulator, respectively, ε0 is the vacuum permittivity, e is the electron charge, nnon-eq is the concentration of non-equilibrium electrons, J is the intensity of UV irradiation, n0 is the maximum possible concentration of electrons in the CB and g(E) is the density of states. The density of localized states in the bandgap is approximated by13,20
where E is the energy of localized states and \(E_{\rm{CB}}^0\) is the bottom of the CB in the absence of spatial fluctuations. Note that for disordered two-dimensional (2D) materials the percolation level is given as \(E_p = E_{\rm{CB}}^0\)13. The calculated transfer characteristics for the pristine, i.e., non-irradiated sample (see dotted line in Fig. 2b), are in good agreement with the experimental data (dotted line in Fig. 2a) giving the values of \(U_0 \cong 0.18\,{\rm{eV}}\) and \(n_0 \cong 2.7 \times 10^{18}\,{\rm{m}}^{- 2}\). Since the recombination time of photoexcited carriers is expressed as \(\tau = \tau _0\exp \left[ {\frac{{E_a}}{{k_BT}}} \right]\), where the activation energy \(E_a \approx 2U_0\), in the limit of \(U_0 \gg k_BT\) one can expect the GPPC effect.
At LT, a transition to Mott’s variable-range hopping regime is observed, and for 2D disordered semiconductor materials, the conductivity is expressed by13
with \(T_0 = \frac{{13.8}}{{k_Bg(\mu _e)r_{\rm{corr}}^2}}\). Using (4) to fit the experimental transfer characteristics for the pristine sample (the dotted lines in Fig. 2b, d), we extract the correlation radius of the random potential U(r), rcorr = 5 nm. Now, by fitting our experimental transfer data at different UV irradiation doses, \(I_{ds}^{\rm{RT}}\left( {V_g} \right) = V_{ds}\sigma _{ph}^{\rm{RT}}(V_g)\) and \(I_{ds}^{LT}\left( {V_g} \right) = V_{ds}\sigma _{ph}^{LT}(V_g)\), to the theoretical model (see Fig. 2c, d) we calculate the variation of the concentration photo-generated electrons, nnon-eq (J, t), with time at RT (inset Fig. 1c) and with UV intensity at RT and LT (see Fig. 2e, f). In agreement with our experiment, the decay of the long-living photo-generated electrons with time shows a bi-exponential decay process (see Fig. 1c). We attribute the two different exponents to the variation of the spatial separation between photo-generated electrons and holes, i.e., a part of photo-generated electrons and holes are localized in close proximity and thus recombine faster, whereas another part is separated at longer distances further away from each other and therefore recombine slower14. Furthermore, the previously reported photogating4,6,7 effect may also contribute to faster exponent. Summarizing this part, we conclude that our experimental transport data and the theoretical analysis suggest large spatial fluctuations of the band structures in MoS2-FETs, with the minima of the CB and maxima of the VB serving as trap sites for the photo-generated carriers.
As we show next, our spectroscopy and microscopy study enables us to identify atomic vacancies21,22,23 and strain24 in the MoS2 monolayers as the main reasons for the spatial variation of the band structure responsible for the observed GPPC effect. On the other hand, such extrinsic sources as adsorbates on the FET channel6 or trapped charged at the ML-MoS2/substrate interface and photogating4,6,7 play a secondary role here (see Supplementary Note 1 and Supplementary Figs. 7–10 for details of this study).
Visualizing spatial fluctuations in band structure by STS
To visualize the presence of spatial inhomogeneities in the band structure of ML-MoS2, we performed STS at LT (1.1 K). To this end, CVD grew ML-MoS2 was transferred onto a Pt(111) single crystal passivated by a monolayer of hexagonal boron nitride (h-BN) (see Methods section, Supplementary Fig. 11 for details), and the derivative of the tunneling current, dI/dV, was measured, which is considered to be proportional to the local density of states25. Indeed, by STS we observe a spatial dependency of the dI/dV curves from which two extremes are plotted in Fig. 3a. While both curves essentially show the bandgap in ML-MoS2, the green curve additionally reveals features within the bandgap, which we identify as deep-lying trap states. By evaluating the respective onset of the VB and CB regions we find that bandgap variations are mainly caused by the trap states nearby the CB. As can be seen from Fig. 3b, these trap states spatially form patches with dimensions of about 5–10 nm and show the energy variation of 0.25 eV. Both values are in very good agreement with the respective parameters U0 and rcorr obtained from the theoretical analysis of the transport data. The variation of the band structure in the VB region is less pronounced, as can be seen from Fig. 3c. Note that the topography of the ML-MoS2 obtained by scanning tunneling microscopy (STM) reveals some corrugations (Supplementary Fig. 12). However, these corrugations do not correlate with the spatial distribution of the trap states26 (compare Fig. 3b, c and Supplementary Fig. 13). Therewith we conclude that the apparent monolayer roughness obtained by STM is caused by its interaction with the substrate playing a minor role in the observed fluctuations on the CB and VB. We expect the intrinsic structure to be responsible for that.
a STS data obtained at two different positions on MoS2/hBN/Pt(111) showing the onset values determined from the trapped states below the CB and above the VB. STS maps (50 nm × 50 nm) visualizing the spatial distribution of the band structure inhomogeneity are shown in (b) and (c), respectively (scale bar: 10 nm). The positions where the blue and green curves shown in a were obtained are marked with crosses. The corresponding topography map is provided in Supplementary Fig. 13.
Effect of defects and strain on band structure fluctuations
In order to study the origin of the observed band structure fluctuations in the ML-MoS2, we performed structural study using aberration-corrected high-resolution TEM (HRTEM)27. A representative unprocessed image of the ML-MoS2 is shown in Fig. 4a, which clearly demonstrates the presence of the sulfur vacancies28,29. In Fig. 4b, the same image is shown after Fourier filtering of the ML-MoS2 lattice frequency. This procedure facilitates direct counting of the vacancies, as they can be recognized as black dots. In this way, we obtain a total concentration of the vacancies in ML-MoS2 of 0.79(6) vac per nm2. Note that for this evaluation only clean areas of the sample were analyzed and an effect of the electron beam induced damage on the ML-MoS2 upon imaging was eliminated (see Supplementary Note 2 and Supplementary Fig. 14 for details). As the differentiation between single (S1) and double (S2) sulfur vacancies is not possible by counting the black dots in Fig. 4b (S2 vacancies are emphasized in the inserts of Fig. 4a, b with red circles), the contrast of each vacancy was additionally analyzed in the unprocessed HRTEM images (see Supplementary Note 2 and Supplementary Fig. 15 for details). As a result, the concentration of the S2 vacancies was found to be 0.067(2) vac per nm2, which corresponds to ∼8.5% of the total concentration. Summarizing these results, we ascribe the point detects in ML-MoS2 (S1 and S2 vacancies), their concentration, and spatial distribution to the observed fluctuation of the band structure presented in the previous section.
60 kV chromatic (Cc) and spherical (Cs) aberration-corrected HRTEM images of CVD grown ML-MoS2 (a, b) and ML-WS2 (c, d). a shows the raw image of the ML-MoS2. The area within the white square is magnified in the lower left. A few red circles mark vacancies, which are difficult to see even in the magnified image. Thus, Fourier-filtering was applied to remove the frequencies of the MoS2 lattice, which is shown in (b). In b, the same area as in (a) is magnified. Due to the Fourier-filtering, the vacancies are better visible (black dots, surrounded by red circles). The same procedure was also applied for WS2 (c) raw image and (d) Fourier-filtered image). Due to the filtering, contaminations become also more visible outside the framed area, thus only clean areas were evaluated with certainty for the defect concentration. The scale bars in (a–d) is 5 nm. The scale bars in the inset of (a) and (b) is 1 nm.
As ML-MoS2 grown by the CVD method is known to build up biaxial strain during the cooling step due to mismatch of the thermal expansion coefficients with the underlying SiO2 substrate24, this lattice strain can also cause the band structure fluctuations30, which contribute to the observed photoconductivity in the MoS2-FETs. From the frequencies of Raman peaks of in-plane and out-of-plane phonon modes experimentally measured on as-grown MoS2 flakes, we estimate that our CVD grown MoS2 flakes contain a biaxial strain of 0.34 ± 0.08% (see Supplementary Note 3) relative to the MoS2 flakes exfoliated from the bulk crystal assumed to have zero strain24. Most probably the lattice strain results in smaller fluctuations of the band structure and therewith contribute along with the photogate effect to the faster relaxation exponent of the photoconductivity (τ1 ≈ 1 day, Fig. 1c), whereas the atomic vacancies cause the deep-lying states21,22,31 resulting in the slower relaxation time (τ2 ≈ 34 days, Fig. 1c).
Comparison with monolayer WS2-FETs
To further support the defect induced origin of the observed GPPC in MoS2-FETs, we carried out a comparative study of WS2-FETs made of CVD grown monolayers. Evaluation of the HRTEM data presented in Fig. 4c, d shows that in this case, the total intrinsic concentration of sulfur vacancies in ML-WS2 is 0.49(9) vac per nm2, which is a factor of 1.6 lower than in ML-MoS2. In addition, the concentration of S2 vacancies is about 0.022(5) vac per nm2, which means that the relative concentration of S2 vacancies in ML-WS2 in comparison to ML-MoS2 is a factor of 3 lower. In agreement with this evaluation, we found that in WS2-FETs the PPC is significantly weaker in comparison to MoS2-FETs (see Supplementary Fig. 16). At similar conditions, the PCC reveals a time constant (τ) of only ~6 h. In contrast to MoS2-FETs, our control experiments with WS2-FETs show that rather the external factors, i.e., the adsorbates, the monolayer/substrate interaction and photogating4,6,7 than the internal structural defects contribute to the observed PPC of in the latter devices (Supplementary Fig. 17, Supplementary Note 1 for details).
Modification of the optical emission by UV irradiation
Finally, in addition to the modification of the transport properties by UV irradiation, we also expect that the optical properties of the ML-MoS2 are modified. After the irradiation, a significant amount of VB electrons is excited and localized in the trap states below the CB, which has to result in a significantly quenching of the photoluminescence (PL). We performed PL emission mapping of as grown ML-MoS2 crystals on SiO2/Si substrate before and after UV irradiation, see Fig. 5a, b, respectively. As can be seen, after the irradiation with UV irradiation the PL emission is significantly diminished, which is in agreement with our expectation. We further tested this effect by preparing suspended ML-MoS2 on TEM grids and observed similar behavior (see Supplementary Fig. 18 and Supplementary Note 5 for details). Thus, the GPPC induced by UV irradiation also allows one to effectively modify the related physical properties of ML-MoS2.
In summary, we presented an experimental observation of the GPPC in the CVD grown ML-MoS2 after their irradiation with UV light. The respective time constant of the slow GPPC component is about 30 days at RT. Our theoretical study suggests that the GPPC results from the large spatial fluctuations of the random potential energy of the charge carriers (photo-electrons and photo-holes) in the ML-MoS2, leading to their significant spatial separation and therefore prolonged recombination time. This description is supported by the spectroscopy and microscopy study of the ML-MoS2 on the atomic scale, which allows us to identify the atomic vacancies in the monolayer as a major factor for the observed GPPC effect. Besides the transport properties, we also demonstrate that the related optical properties such as PL emission are significantly diminished in the ML-MoS2 after UV irradiation. Our results shed light to the fact that atomic defects play a crucial role in the optoelectronic properties of ML-TMDs, and it is highly essential to understand defect-related properties to further develop the field of TMD based electronics and optoelectronics. Furthermore, efficient routes towards defect engineering of ML-TMDs may enhance their applicability. We anticipate that the GPPC effect can be effectively exploited further for applications in electronic, optoelectronic, and biotechnological devices (see, e.g., refs. 32,33,34,35,36).
Methods
Growth of monolayer MoS2 (ML-MoS2) and monolayer WS2 (ML-WS2)
ML-MoS2 and ML-WS2 crystals were grown by the CVD process10,11. Silicon substrates with a thermally grown SiO2 layer of 300 nm were used as substrates (Siltronix, roughness 0.3 nm RMS). The growth was carried out in a two-zone tube furnace with a tube diameter of 55 mm. The substrates were cleaned initially by ultrasonication in acetone for 5 min followed by washing in isopropanol and blown dry with argon. A quartz crucible containing sulfur powder (99.98%, Sigma Aldrich) was placed in the center of the first zone of the tube furnace. The substrates were placed next to a wafer containing ∼1 μg MoO3 powder (99.97%, Sigma Aldrich) for MoS2 growth or 5 mg WO3 (99.99%, Alfa Aesar) mixed with 250 µg NaCl for WS2 growth and loaded to the center of the second zone of the furnace. Subsequently, the quartz tube was evacuated to 5 × 10−2 mbar pressure and refilled with argon. The growth was carried out at atmospheric pressure under an argon flow of 100 cm3/min. The second zone containing the metal oxide precursor and the substrates were heated to the growth temperature of 770 °C (for MoS2) or 860 °C (for WS2) at a rate of 40 °C/min and held at that temperature for 15 min. The sulfur temperature was adjusted to reach 200 °C when the second zone reaches 750 °C (for MoS2) or 800 °C (for WS2). A flow of H2 gas at a rate of 10 cm3/min was introduced to the chamber during the growth time. After the growth, the furnace was turned off and allowed to cool down under an argon flow of 100 cm3/min until 350 °C was reached. Then the tube furnace was opened to rapidly cool down to RT. These procedures result in the growth of ML-MoS2 and ML-WS2 crystals of mainly triangular shape with a typical size of about 50–100 μm.
Preparation of the hBN monolayer on Pt(111)
The Pt(111) single crystal (purchased from MaTecK GmbH) was cleaned by means of several Ar+ sputtering (1 kV, 4 μA, 5 × 10−5 mbar, 30 min) and annealing (800 °C for 30 min) cycles. The absence of contaminations was controlled by X-ray photoelectron spectroscopy (XPS). For XPS an x-ray source (SPECS XR50) with Al Kα excitation (1486.7 eV) in combination with a hemispheric electron analyzer (SPECS EA-200) was used.
For the growth of the 2D h-BN layer, we followed the steps described by Orlando et al.37. They showed that the adsorption of borazine on Ir(111) at RT followed by an annealing step at 800 °C reduces the number of different adsorption configurations and results in an h-BN layer exhibiting a low defect density. We thus exposed the substrate to borazine (B3N3H6, Katchem spol. s.r.o.) vapor with a pressure of 5 × 10−8 mbar for 10 min with the substrate being held at RT. Immediately after that, we increased the substrate temperature to 800 °C for 10 min followed by an annealing step at 800 °C for another 10 min without borazine exposure in order to guarantee the complete dehydrogenation of the precursor molecules on the substrate. This growth progress is known to be monolayer-terminated37,38.
The quality of the h-BN layer was verified with XPS. Supplementary Fig 11b shows the corresponding B 1s and N 1s spectra. We used a polar angle of 70° to increase the surface sensitivity of the measurement. Both spectra show only one component, which was modeled by an asymmetric Mahan line shape39. The asymmetry of the peak can be explained by the slight corrugation of the h-BN layer as well as by scattering of the photoelectrons at electronic states near the fermi edge39. The number of contaminations like oxygen and carbon was less than 1%. Point defects in the h-BN layer should cause a second component in the B 1s and N 1s spectra at lower binding energy which is not visible in the observed XP spectra40. In conclusion, our results show a high-quality h-BN layer which is a suitable substrate for STS investigations of a MoS2 film.
Basic characterization of the grown monolayers
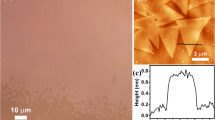
After the CVD growth the TMDs were characterized by optical microscopy (OM), atomic force microscopy (AFM), and Raman spectroscopy (see Supplementary Figs. 1 and 2). The OM images were taken with a Zeiss Axio Imager Z1.m microscope equipped with a 5 megapixel CCD camera (AxioCam ICc5) in bright-field operation.
The AFM measurements were performed with a Ntegra (NT-MDT) system in contact mode at ambient conditions using n-doped silicon cantilevers (CSG01, NT-MDT) with a typical tip radius of 6 nm and a typical force constant of 0.03 N m−1.
The Raman spectra were acquired using a Bruker Senterra spectrometer operated in backscattering mode. Measurements at 532 nm were obtained with a frequency-doubled Nd:YAG Laser, a 50× objective, and a thermoelectrically cooled CCD detector. The spectral resolution of the system is 2–3 cm−1. For all spectra, the Si peak at 520.7 cm−1 was used for peak shift calibration of the instrument. The Raman spectrum shown in supplementary Fig. 1b reveals the characteristic peaks of ML-MoS2 at 384 and 404 cm−1, which are originated from the in-plane (E12g band) vibrations of the Mo-S bonds and out-of-plane (A1g band) vibrations of S atoms in the MoS2 lattice41, respectively. The difference between the peak positions is 20 cm−1 confirming that the crystal is a monolayer41.
Preparation of ML-MoS2 and ML-WS2 FET devices
After the growth, the ML-MoS2 and ML-WS2 crystals were transferred onto the device substrates (Siltronix, heavily p-doped silicon substrates with thermally grown SiO2 layer of 300 nm)11. To transfer, a PMMA layer of 200 nm (950 kDa, All-Resist, AR-P 679.04) was spin-coated onto the SiO2 substrate with CVD grown crystals and hardened for 10 min at 90 °C. Then the substrate was kept floating on top of a bath of KOH solution to etch away the SiO2 layer and to release the monolayer crystals supported by PMMA, followed by washing several times with ultrapure water (18.2 MΩcm, Membrapure) to remove any residual KOH. Then the PMMA supported crystals were placed on the marked SiO2/Si chips and baked at 90 °C for 10 min, followed by immersion in acetone for 2 h to remove the PMMA support. For defining the source and drain electrodes we employed e-beam lithography (EBL). A PMMA resist layer was spin-coated on top of the samples, patterned by EBL (Vistec EBPG 5000plus), and subsequently developed. Then the Au/Ti (30 nm/5 nm) electrodes were deposited by e-beam evaporation process followed by the dissolution of the PMMA resist in acetone for 2 h. The heavily p-doped silicon base functioned as the gate electrode and 300 nm thermal oxide functioned as the gate dielectric.
Electrical transport measurements
The electrical characterization was carried out with two Keithley 2634B source measure units (SMU). One SMU was used to change the voltage of the gate (Vg) with respect to the source/drain in the range between −60 and 60 V for the back-gated devices in a vacuum (~10−6 mbar). The other SMU was used to apply the source-drain voltage (Vds) and measure the source-drain current (Ids). A Lakeshore cryogenic vacuum needle probe station TTPX was used to measure the devices in vacuum at a residual pressure of about 10−6 mbar. The mobility is extracted from the linear region of the transfer curve using the equation \(\mu = \left( {\frac{{dI_{ds}}}{{dV_{bg}}}} \right)\left( {\frac{L}{{WC_{ox}V_{ds}}}} \right)\), where L is the channel length, W is the channel width, Cox is the capacitance of the 300 nm gate oxide and Vds is the source-drain voltage11. For UV irradiation a light-emitting diode (LED) with a wavelength of 365 nm (Thorlabs, M365L2), with a typical power output of 360 mW, was used. Also, LEDs with wavelengths 455 nm (Thorlabs, M455L3) and 617 nm (Thorlabs, M617L4), respectively, were used to irradiate the devices. The LEDs were controlled using a Thorlabs four-channel LED driver (DC4100).
Scanning tunneling microscopy and spectroscopy (STM/STS)
CVD grown ML-MoS2 crystals were transferred onto an hBN layer grown on a single crystalline Pt(111) substrate. The hBN monolayer thereby serves as an atomically flat, electrically insulating overlayer. The quality of hBN was confirmed by means of STM (JT-STM/AFM from SPECS Surface Nano Analysis GmbH operated at 1.1 K with tungsten tips) (Supplementary Fig. 11) before transferring the MoS2 crystals. Prior to the STM/STS experiments, the sample was thoroughly degassed in an ultrahigh vacuum at about 120 °C for 2 h. For STS we directly measured the derivative of the tunneling current dI/dV using the lock-in technique. We recorded STS spectra in a grid with dimensions of 50 nm × 50 nm and 1 nm spacing in each direction (2500 spectra in total). No hysteresis was observed between forward (1.5 V → −2.75 V) and backward (reverse) bias sweeps, which proves that we do not permanently influence the band structure by the measurement process itself. In order to visualize the spatial distribution of trap states, we plotted their onsets as color maps as shown in Fig. 3b, c.
High-resolution TEM (HRTEM)
The HRTEM images were acquired with the Cc/Cs-corrected sub-angstrom low-voltage electron microscope27. A voltage of 60 kV was used with typical dose rates of about 105 e− nm−2 s−1. The values for the chromatic aberration Cc and the spherical aberration Cs were between −10 µm to −20 µm. All Cc/Cs-corrected HRTEM images were acquired with bright atom contrast and recorded on a 4 k × 4 k camera with exposure times of 1 s.
PL measurements
PL from ML-MoS2 crystals was characterized with a MicroTime 200 laser-scanning confocal fluorescence microscope from PicoQuant GmbH. A pulsed laser of wavelength 532 nm and repetition rate of 80 Hz was used to excite the ML-MoS2 crystals and measure their PL emission with a single-photon avalanche diode detector. A microscope objective of 40× magnification and a numerical aperture 0.65 was used to focus the laser onto the crystals, forming a spot of diameter ~1 µm. The PL emission was collected using the same objective. PL maps were acquired by raster scanning of the microscope objective and collecting the PL emission in the spectral range of 650–720 nm using a bandpass filter, essentially to collect the A-exciton and trion emissions. Care was taken in all the measurements to block the excitation light reaching the detector using a dichroic mirror and a notch filter for the excitation wavelength of 532 nm, in addition to bandpass and long-pass filters.
Data availability
Data presented in this study are available on request from the authors.
References
Choi, S.-H., Park, G.-L., Lee, C. & Jang, J. Persistent photoconductivity in hydrogenated amorphous silicon. Solid State Commun. 59, 177–181 (1986).
Lin, J. Y., Dissanayake, A. & Jiang, H. X. Electric-field-enhanced persistent photoconductivity in a Zn0.02Cd0.98Te semiconductor alloy. Phys. Rev. B 46, 3810–3816 (1992).
Arslan, E., Bütün, S., Lisesivdin, S. B., Kasap, M., Ozcelik, S. & Ozbay, E. The persistent photoconductivity effect in AlGaN/GaN heterostructures grown on sapphire and SiC substrates. J. Appl. Phys. 103, 103701 (2008).
Lopez-Sanchez, O., Lembke, D., Kayci, M., Radenovic, A. & Kis, A. Ultrasensitive photodetectors based on monolayer MoS2. Nat. Nanotechnol. 8, 497–501 (2013).
Zhang, W., Huang, J.-K., Chen, C.-H., Chang, Y.-H., Cheng, Y.-J. & Li, L.-J. High-gain phototransistors based on a CVD MoS2 monolayer. Adv. Mater. 25, 3456–3461 (2013).
Wu, Y.-C. et al. Extrinsic origin of persistent photoconductivity in monolayer MoS2 field effect transistors. Sci. Rep. 5, 11472 (2015).
Di Bartolomeo, A. et al. Electrical transport and persistent photoconductivity in monolayer MoS2 phototransistors. Nanotechnology 28, 214002 (2017).
Cho, K. et al. Gate-bias stress-dependent photoconductive characteristics of multi-layer MoS2 field-effect transistors. Nanotechnology 25, 155201 (2014).
Roy, K. et al. Graphene–MoS2 hybrid structures for multifunctional photoresponsive memory devices. Nat. Nanotech. 8, 826–830 (2013).
van der Zande, A. M. et al. Grains and grain boundaries in highly crystalline monolayer molybdenum disulphide. Nat. Mater. 12, 554–561 (2013).
George, A. et al. Controlled growth of transition metal dichalcogenide monolayers using Knudsen-type effusion cells for the precursors. J. Phys. Mater. 2, 016001 (2019).
Shik, A. Y. Photoconductivity of randomly inhomogeneous semiconductors. Zh. Eksp. Teor. Fiz. 68, 1859–1867 (1975).
Shklovskii, B.I., Efros, A.L. Electronic properties of doped semiconductor. in Springer Series in Solid-State Sciences (Berlin, 1984).
Queisser, H. J. & Theodorou, D. E. Decay kinetics of persistent photoconductivity in semiconductors. Phys. Rev. B 33, 4027–4033 (1986).
Najmaei, S. et al. Tailoring the physical properties of molybdenum disulfide monolayers by control of interfacial chemistry. Nano Lett. 14, 1354–1361 (2014).
Ghatak, S., Pal, A. N. & Ghosh, A. Nature of electronic states in atomically thin MoS2 field-effect transistors. ACS Nano 5, 7707–7712 (2011).
Radisavljevic, B. & Kis, A. Mobility engineering and a metal–insulator transition in monolayer MoS2. Nat. Mater. 12, 815–820 (2013).
Lo, S.-T., Klochan, O., Liu, C.-H., Wang, W.-H., Hamilton, A. R. & Liang, C.-T. Transport in disordered monolayer MoS2 nanoflakes-evidence for inhomogeneous charge transport. Nanotechnology 25, 375201 (2014).
Razeghi, M. Equilibrium charge carrier statistics in semiconductors. in Fundamentals of Solid State Engineering. 252–274 (Springer, Berlin, 2019).
Koropecki, R. R., Schmidt, J. A. & Arce, R. Density of states in the gap of amorphous semiconductors determined from modulated photocurrent measurements in the recombination regime. J. Appl. Phys. 91, 8965 (2002).
Santosh, K. C., Longo, R. C., Addou, R., Wallace, R. M. & Cho, K. Impact of intrinsic atomic defects on the electronic structure of MoS2 monolayers. Nanotechnology 25, 375703 (2014).
Zhou, W. et al. Intrinsic structural defects in monolayer molybdenum disulfide. Nano Lett. 13, 2615–2622 (2013).
Hong, J. et al. Exploring atomic defects in molybdenum disulphide monolayers. Nat. Commun. 6, 6293 (2015).
Chae, W. H., Cain, J. D., Hanson, E. D., Murthy, A. A. & Dravid, V. P. Substrate-induced strain and charge doping in CVD-grown monolayer MoS2. Appl. Phys. Lett. 111, 143106 (2017).
Mårtensson, P. & Feenstra, R. M. Geometric and electronic structure of antimony on the GaAs(110) surface studied by scanning tunnelling microscopy. Phys. Rev. B 39, 7744–7753 (1989).
Shin, B. G. et al. Indirect bandgap puddles in monolayer MoS2 by substrate-induced local strain. Adv. Mater. 28, 9378–9384 (2016).
Linck, M. et al. Chromatic aberration correction for atomic resolution TEM imaging from 20 to 80 kV. Phys. Rev. Lett. 117, 076101 (2016).
Lin, Z. et al. Defect engineering of two-dimensional transition metal dichalcogenides. 2D Mater. 3, 022002 (2016).
Algara-Siller, G., Kurasch, S., Sedighi, M., Lehtinen, O. & Kaiser, U. The pristine atomic structure of MoS2 monolayer protected from electron radiation damage by graphene. Appl. Phys. Lett. 103, 203107 (2013).
Johari, P. & Shenoy, V. B. Tuning the electronic properties of semiconducting transition metal dichalcogenides by applying mechanical strains. ACS Nano 6, 5449–5456 (2012).
Tongay, S. et al. Defects activated photoluminescence in two-dimensional semiconductors: interplay between bound, charged and free excitons. Sci. Rep. 3, 2657 (2013).
Poole, V. M., Jokela, S. J. & McCluskey, M. D. Using persistent photoconductivity to write a low-resistance path in SrTiO3. Sci. Rep. 7, 6659 (2017).
Snyder, P. J., Kirste, R., Collazo, R. & Ivanisevic, A. Persistent photoconductivity, nanoscale topography, and chemical functionalization can collectively influence the behavior of PC12 cells on wide bandgap semiconductor surfaces. Small 13, 1700481 (2017).
Giubileo, F. et al. Effect of electron irradiation on the transport and field emission properties of few-layer MoS2 field-effect transistors. J. Phys. Chem. C 123, 1454–1461 (2019).
Tu, L. et al. Ultrasensitive negative capacitance phototransistors. Nat. Commun. 11, 101 (2020).
Furchi, M. M., Polyushkin, D. K., Pospischil, A. & Mueller, T. Mechanisms of photoconductivity in atomically thin MoS2. Nano Lett. 14, 6165–6170 (2014).
Orlando, F. et al. Epitaxial growth of a single-domain hexagonal boron nitride monolayer. ACS Nano 8, 12063–12070 (2014).
Mahan, G. D. Collective excitations in x-ray spectra of metals. Phys. Rev. B 11, 4814 (1975).
Preobrajenski, A. B. et al. Influence of chemical interaction at the lattice-mismatched h-BN\Rh(111) and hBN\Pt(111) interfaces on the overlayer morphology.Phys. Rev. B 75, 245412 (2007).
Bachmann, P., Düll, F., Späth, F., Bauer, U., Steinrück, H.-P. & Papp, C. HR-XPS study of the formation of h-BN on Ni(111) from the two precursors, ammonia borane and borazine. J. Chem. Phys. 149, 164709 (2018).
Lee, C., Yan, H., Brus, L. E., Heinz, T. F., Hone, J. & Ryu, S. Anomalous lattice vibrations of single- and few-layer MoS2. ACS Nano 4, 2695–2700 (2010).
Acknowledgements
We acknowledge financial support of the Thüringer MWWDG via the “ProExzellenz 2014–2019” program under the grants “ACPExplore2016” and “ACPExplore2018” as well as the Deutsche Forschungsgemeinschaft (DFG) through a research infrastructure grant INST 275/257-1 FUGG and CRC 1375 NOA (Project B2). This project has also received funding from the joint European Union’s Horizon 2020 and DFG research and innovation program FLAG-ERA under grant TU149/9-1. T.L. and U.K. acknowledge funding from the DFG and the Ministry of Science, Research and the Arts (M.W.K.) of the federal state of Baden-Württemberg (Germany) in the frame of the SALVE project (www.salve-project.de) as well as the European Union in the frame of the Graphene Flagship. M.V.F. acknowledges the financial support of the Ministry of Education and Science of the Russian Federation in the framework of Increase Competitiveness Program of NUST”MISiS” K2-2020-001. We thank Stephanie Höppener and Ulrich S. Schubert for enabling our Raman spectroscopy and microscopy studies at the Jena Center for Soft Matter (JCSM).
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Contributions
A.G., M.V.F., and A.T. conceived the research and designed the experiments. A.G performed the FET measurements analyzed all the data. M.V.F. developed and performed the theoretical analysis. M.G., M.S., and T.F. synthesized the hBN monolayer, performed the STS measurements, and analyzed these data with respect to the observed transport behavior. T.L. performed the HRTEM measurement and analysis supervised by U.K. R.M., and I.S. performed the PL imaging and analysis. U.H. performed device fabrication. D.K. contributed to the transport measurements and interpretation of the results. C.N. performed the AFM and Raman spectroscopy measurements and analysis. A.G., N.M., and L.M.R.A. synthesized the MoS2 and WS2 monolayer crystals. A.G., M.V.F., and A.T. wrote the paper with inputs from all authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
George, A., Fistul, M.V., Gruenewald, M. et al. Giant persistent photoconductivity in monolayer MoS2 field-effect transistors. npj 2D Mater Appl 5, 15 (2021). https://doi.org/10.1038/s41699-020-00182-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41699-020-00182-0
This article is cited by
-
Extreme mechanical tunability in suspended MoS2 resonator controlled by Joule heating
npj 2D Materials and Applications (2023)
-
Multilayer SnS2/few-layer MoS2 heterojunctions with in-situ floating photogate toward high-performance photodetectors and optical imaging application
Science China Materials (2023)
-
Research progress of optoelectronic devices based on two-dimensional MoS2 materials
Rare Metals (2023)
-
Van der Waals interfaces in multilayer junctions for ultraviolet photodetection
npj 2D Materials and Applications (2022)