Abstract
Monolayer iron germanium telluride Fe3GeTe2, one of the typical two-dimensional ferromagnetic materials, hitherto, has only been studied by exfoliated micron-sized samples. We achieve high-quality wafer-scale growth of thin Fe3GeTe2 films by molecular beam epitaxy, greatly expanding the types of characterization tools employable and providing the possibility for its integration in devices like consumer electronics. Thickness-dependent transport measurements are used to characterize and probe for magnetic order. Ferromagnetic states exist in 1–10 layer thick Fe3GeTe2, with Curie temperatures ranging from ~75 K in one layer samples to above 175 K in ten layer samples. A single ferromagnetic phase with significant magnetic anisotropy is revealed for all layer numbers. We submit the capability of synthesizing, wafer-scale Fe3GeTe2 as an essential step towards its fulfillment in any applications involving magnetism, such as spintronics.
Similar content being viewed by others
Introduction
The integration of magnetic materials into electronic and photonic devices has been taking place for decades1,2,3. One well-known example is the discovery of giant magnetoresistance and its applications4. Much research has focused on engineering new magnetic structures, especially in two-dimensions (2D). Prospects of which are plentiful in device application, not only in replacing magnets in current applications, but also in new structures, such as, in magnetic tunnel junctions and magnetic random access memories (MRAM)5,6.
The discovery of graphene7 inspired a new generation of materials known as van der Waals (vdW) materials with intrinsic 2D nature8. Samples were often accessible by exfoliating bulk crystals. After processed as a device, the electronic properties of these 2D materials could be controlled via strain, doping, gating, as well as “stacking”9 to reveal exotic states leading to an era of “vdW materials by design”10. Fundamental physical properties have been realized that were proposed long-ago11,12, in 2D vdW materials, including the 2D superconductivity found in thin films of NbSe213, FeSe14, WTe215, and Bi2Sr2CaCu2O816 and so on. New opportunities in applications and a new generation of devices have become available due to the properties found in reduced dimensions.
Exfoliated 2D flakes of CrI317, Fe3GeTe218, Cr2Ge2Te619, and others20 have shown clear long-range magnetic order that are promising for applications involving properties such as above-room-temperature Curie temperature (TC) and antiferromagnetic interlayer exchange. Yet, scalability and poor stability continue to hinder the progression toward the realization of the industrial-scale production of such devices20. To date, the synthesis of many 2D magnetic materials still is all limited to micron-sized flakes21, eliminating any production scale applications. Here we focus on the wafer-scale synthesis of the vdW layered ferromagnetic material Fe3GeTe2 (FGT), which has a TC above room temperature18 and is one of the few 2D magnetic materials that show evidence of topological states22,23.
Single-crystal FGT was synthesized in 200624, revealing a relatively high TC ~ 220 K in bulk, in comparison to the absence of magnetism in the isostructural Ni3GeTe2. This material has an out-of-plane magnetization vector with respect to the vdW planes25, showing a large anisotropy defined as the energy dependence on each magnetization vector direction. Calculations indicate its easy axis is stabilized by a large magnetocrystalline anisotropy caused by spin-orbit coupling26. Angle-resolved photoemission spectroscopy (ARPES) measurements imply the FGT bulk belongs to a class of topological nodal line semimetals27. Another ARPES experiments suggest the ferromagnetic state is accompanied by a heavy-fermion state, which has only been seen in 4 f and beyond electron systems28.
Exfoliated FGT monolayers and multilayers18,29 preserve the characteristic ferromagnetic order of bulk. TC reaches 310 K upon ionic liquid gating in trilayer samples18, one of the highest ferromagnetic transition recorded in the 2D nature. Unlike CrI3, no interlayer exchange coupling has been observed in FGT films. It has been shown that FGT hosts a large Berry curvature, which is responsible for the anomalous Hall effect27. Thin-film measurements substantiate claims of topological properties in the observation of Néel-type skyrmions in FGT/WTe2 heterostructures and large anomalous Nernst effect23,30.
To date, FGT film remains the only metallic, rare-earth free, and layered ferromagnet with out-of-plane magnetization in 2D. Because of the metallic characteristics, its fundamental magnetic properties can be studied via transport measurements, together with optical measurements such as the magneto-optic Kerr effect. Metallicity also enables easy control of charge as well as spin degrees of freedom by electrical currents, useful in device applications. For example, FGT films have been made into ultrathin devices, realizing current control of the perpendicular magnetization via spin-orbit torque, with efficiencies comparable to that of 3d ferromagnetic heterostructures—the current leader of the field31. This makes FGT all the more desirable for MRAM32. Closely related application prospects are found in magnetic tunnel junction heterostructures of FGT/graphite/FGT, which display promising characteristics of 160% tunneling magnetoresistance at low temperature33.
We employ molecular beam epitaxial (MBE) technique to synthesize atomically smooth and single crystalline FGT films, with thickness ranging from one quintuple layer (QL, ~0.8 nm) to ten QLs on 5 × 5 mm substrates. Among reported monolayer samples, ours display the highest Tc probed by anomalous Hall measurements, together with an order of magnitude larger coercivity18,34. Large switching ratios have been found in all samples at low temperatures as well as significant magnetocrystalline anisotropy energy. Our wafer-scale samples yield the opportunity for measurements and applications, which can be extremely difficult on the micron-sized flakes yielded by exfoliation techniques, such as ARPES and x-ray spectroscopies. One can begin integrating FGT films into commercial devices following the established techniques of Si.
Results
Structural analysis of Fe3GeTe2 films
The FGT unit cell is described by a hexagonal symmetry (space group P63/mmc) composed by two weakly coupled quintuple layer (QL) substructures, with bulk lattice parameters a = b = 3.99 Å and c = 16.33 Å24, as shown in Fig. 1a. The middle three layers of each QL form a heterometallic slab of Fe2+Ge4- surrounded by Fe3+ atoms. Encapsulating the slabs are tellurium layers. Theoretical calculations of monolayer magnetic moments yield Fe3+ and Fe2+ atoms contribute 1.723 and 1.005 μB, respectively, where μB is the Bohr magneton26.
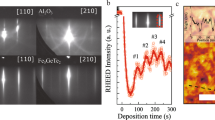
a Lattice structure of Fe3GeTe2 (FGT), where a single unit cell (two quintuple layers (QL)) is outlined. The arrows indicate the local magnetic moments on the Fe atoms. b Top: in situ reflection high-energy electron diffraction (RHEED) images of a 2 × 2 reconstructed Ge (111) substrates along the [10\(\bar 1\)] and [11\(\bar 2\)] direction. Bottom: 4-QL Fe3GeTe2 with electron beam along [10\(\bar 1\)0] direction and [11\(\bar 2\)0] direction. c RHEED intensity oscillations during the growth of Fe3GeTe2, indicating atomic smoothness and its epitaxial growth mode. Single QL growth times are extracted from the period of oscillation to be ~80 s. d X-ray diffraction pattern of 18-QL FGT film grown on Ge (111), indicating the films are grown in the (001) direction.
We have optimized high-quality growth of epitaxial FGT(0001) ultrathin films with thicknesses ranging from 1 QL to 10 QL on atomically smooth Ge(111) substrates (See Methods). Reflection high-energy electron diffraction (RHEED) images of the Ge substrate and the 4-QL FGT are shown in Fig. 1b. For a hexagonal lattice, to which FGT and Ge(111) belong, there exist two distinct crystallographic directions separated by 30 degrees, the [11\(\bar 2\)] and [10\(\bar 1\)] directions. It is essential to note the diffraction patterns of the two crystallographic directions of the substrate and film are aligned, which confirms an epitaxial growth (Fig. 1b). Observations of intense, point-like diffraction spots indicate an atomically smooth surface of both Ge and FGT. In-plane lattice parameters are measured in situ throughout the growth process using RHEED line intensity profiles of the associated diffraction patterns. The lattice constant of the FGT film 3.99 Å agrees with the known in-plane lattice constant for bulk Ge(111), as well as the bulk FGT measurements24. A layer-by-layer growth mode is established via observation of RHEED intensity oscillations (Fig. 1c). The oscillation period allows the precise control of the number of layers deposited (Fig. 1c). Thus we confirm single-crystalline, atomically flat, and epitaxial growth of wafer-scale thin FGT films.
The Lattice structure of FGT films were further characterized by ex situ x-ray diffraction (XRD). A single phase of FGT (001) films is confirmed by the (002) family of diffraction peaks in Fig. 1d. The diffraction pattern suggests a out-of-plane lattice constant c = 16.355 Å, in good agreement with bulk measurements of 16.33 Å24. Fe vacancies in the Fe2+ site have been shown to decrease in-plane lattice constants and increase c35, which are not observed in our films.
Transport results showing the conductivity and ferromagnetism in Fe3GeTe2 films
Electronic and magnetic properties of FGT films were characterized by transport measurements. We measure the entire wafer (Fig. 2a) with no lithography involved. Longitudinal and transverse resistances Rxx and Rxy (Fig. 2b–d) were measured on both capped and uncapped samples ranging from 1 QL to 10-QL films. Samples are capped unless otherwise stated in the following text (see Methods regarding the capping layer). We note uncapped monolayer and bilayer films did not permit transport measurements due to insulating behavior, likely due to the oxidization of the FGT surface36. Differences in transport behavior are negligible between capped and uncapped samples when the thickness ≥ 5 QL (Fig. 2d).
a A photo of an FGT sample measured with van der Pauw geometry. b Longitudinal resistivity Rxx vs. temperature T taken of various QL numbers and capped substrate. c Fit of the Rxx with the Mott variable range hopping model, indicating the existence of localized states. d RAH vs. applied field of select QL numbers at 5 K showing the anomalous Hall and hysteresis loops. The applied magnetic field H is perpendicular to the sample surface and parallel to the c axis of FGT. All samples are capped except the two samples marked as non-capped (NC). Insets in b, d are the respective measurement geometry.
Rxx measurements show resistance values consistent with exfoliated samples18 and indicate a weak insulating behavior at low temperatures (Fig. 2b). Below 200 K, Rxx fit the variable range hopping model in 2D (Fig. 2c), where \(R_{{\mathrm{xx}}} \propto {\mathrm{e}}^{T^{ - 1/3}}\). This is in agreement with previous transport studies37, which could be attributed to the emergence of localized electrons with decreasing temperature. These localized states likely originate from the Fe 3 d orbitals, which are also responsible for the itinerant electrons. The transition temperature agrees well with previous reports of a heavy-fermion state (“localized”) in bulk28 and correlated electrons.
In control samples of Te capped Ge substrates (as shown by the purple line in Fig. 2b), we observe a stronger insulating behavior and a much higher resistance than FGT films at low temperatures. Above 200 K, the conduction through Ge substrates is responsible for the higher temperature transition in Rxx.
To characterize intrinsic magnetic order, transverse resistance (Rxy) measurements that host the anomalous Hall (AH) effect were carried out at 5 K, as shown in Fig. 2d. Here the RAH is extracted from Rxy = RNH + RAH, where RN is the normal Hall coefficient, and H is the applied field. At 5 K, all samples display clear hysteresis indicating ferromagnetic order. 5-QL capped and uncapped samples are shown in Fig. 2d, revealing an almost identical remanent (RR) and saturation resistance (RS). This implies that, in uncapped samples above 5 QL, the top 1–2 FGT oxide layers do not significantly affect transport properties of the underneath pristine FGT layers, suggesting the electronic channels are not confined to the surface. This result is significant considering previous reports of antiferromagnetic coupling between oxidized and pristine FGT, where one would expect uncapped samples to display a two-part hysteresis. We do not observe such a superposition in hysteresis shape.
Temperature dependence of the anomalous Hall behavior
Temperature-dependent RAH measurements were also carried out on all samples from 5 K to 225 K to study the temperature evolution of the AH effect, as presented in Fig. 3. The observed textbook-like square shape of the hysteresis is a good indication of strong perpendicular magnetic anisotropy (PMA). It is important to note that PMA and hysteresis width are proportional38. It is also indicative of a single domain38, where all Ising like spins coherently flip at the coercive field (Hc) along the easy axis.
Analysis of the anomalous Hall results
We extract the coercive field and the remanent and saturation resistance of samples at various temperatures (Fig. 4). The coercive field (Hc) is defined as the value of the applied magnetic field at which the loop’s curve crosses through RAH = 0. The remanent and saturation resistance RR and RS are defined as the value of RAH at zero applied field and upon saturation, respectively. It is well established that RR and RS are directly proportional to the magnetic remanence MR (the magnetic signal at zero applied field) and magnetic saturation MS (the magnetic signal when all magnetic moments are maximally aligned)38. To investigate the layer and temperature-dependent evolution of the magnetic phases, we compare RR, RS, and Hc as a function of layer number at a fixed temperature. With increasing layer number, all samples decrease in the remanent MR and saturation magnetization MS (Fig. 4a, b) at a fixed temperature below the respective TC. This progression is consistent with previous reports18.
a Remanent resistance (RR) and b Saturation resistance (RS) plotted against QL number at various temperatures. Both exhibit a monotonic decrease with increasing layer numbers. c RR/RS ratios remain ~1 at different temperatures, suggesting FGTs viability in applications. d Coercive field (Hc) of various QL layer numbers. e Arrott plot analysis of a 5-QL sample, indicating a TC of 176 K extracted by the x-intercept of the fitted line. f Magnetic phase diagram of FGT as a function of QL number. Tc on the RAH method line is chosen at the lowest temperature at which RR vanishes in AH measurements. Arrott plot points are found using methods as in e.
The ratio of RR and RS is plotted in Fig. 4c. The ratio remains nearly 1 for all QL numbers up to 100 K, where the ratios for 5- and 10-QL samples exceed 0.9 at room temperature. A ratio near unity is an attractive quality for storage and spintronic applications39, such as MRAM. We also note that the energy loss decreases as the layer number is increased, as indicated by the area enclosed by the hysteresis loop after a complete magnetic field sweep.
The field needed to reverse the direction of magnetization, known as the coercive field Hc, provides valuable information for assessing the stability of magnetic structures and is often used as an indication of the hardness of the magnetic domains (Fig. 4d). Hc in monolayer samples is greater than 1 T and roughly 0.5, 0.8, and 0.6 T for 2, 5, and 10 QL, respectively. Bilayer samples do not fit into a monotonic decrease of Hc with respect to layer number. One possible explanation is related to hole doping by Fe vacancies, which has been shown to decrease the perpendicular anisotropy40. A more thorough layer dependent study is required to reveal the underlying cause. The spin flip transition shown by the gradual progression of RAH around the coercive field could be due to a lack of magnetic anisotropy or the existence of multiple magnetic domains.
We use two methods to extract TC. The remanent resistance RR serves as a direct probe of spontaneous magnetic order MR and allows us to extract TC of samples by tracking the temperature at which RR vanishes (Fig. 4f). TC monotonically increases with layer number. For 1, 2, 5, and 10-QL transitions take place at roughly 75, 125, 150, and 175 K, respectively. A secondary method to extract TC is by Arrott plot analysis39 (Fig. 4e). Arrott plot employ the equation \(R_{{\mathrm{AH}}}^2 = \mu _0H/R_{{\mathrm{AH}}}\), from which the high field portion is linearly flitted (inset of Fig. 4e). The intercept of \(R_{{\mathrm{AH}}}^2\) is then found for multiple temperatures and again linearly fitted as a function of temperature. The resulting temperature intercept is then used as TC. This method yields an exact temperature for TC as compared to the range generated from RAH measurements. Using this method, we have extracted TC to be 126 K in monolayer samples, 145 K in bilayer samples 176 K, and 178 K in 5 and 10-QL samples, respectively. The two methods show different TC in <10-QL samples but are in agreement with RAH measurements of 10-QL samples. Upon comparison with the exfoliated layer dependant phase diagram of Deng et al., we see a significant increase in TC for monolayer and bilayer samples (roughly 100 K increase), but good agreement for 5- and 10-QL samples.
Discussion
We note that for all layer numbers, a strong anisotropy is maintained as indicated by the shape of the hysteresis, implying that there is limited hole doping, which has been shown to decrease the MAE and lead to small coercive fields40. This is corroborated by bulk sample measurements, which also show strong perpendicular anisotropy29. Ultrathin UHV-grown monolayer samples seem to be of significantly higher TC and more robust ferromagnetism compared to exfoliated samples, as indicated by Hc, RR/RS ratio, and the field at which samples saturate indicated by a flat AH signal. This is most obvious upon comparison to monolayer hysteresis reported by ref. 18, for example, the coercivity of our epitaxial samples is nearly an order of magnitude larger than exfoliated samples. For monolayer, magnetic saturation was not achieved past 10 T while saturation was reached at only 2 T in exfoliated samples, yet bilayer coercivity samples agree. At low temperatures, the magnetic remanence to magnetic saturation ratio is also much larger in epitaxial samples for layer number less than 5. TC of monolayer and bilayer samples is higher than any previously reported using anomalous Hall measurements. Considering the decrease in coercivity caused by oxidation, indicated by differences in 5-QL capped and uncapped samples, previous monolayer data could be explained by a partially oxidized sample.
The lack of apparent interlayer coupling should be discussed with respect to recent reports of systems such as CrI3, and CrBr3. It is well known that interlayer coupling is extremely sensitive to interlayer distances, which allow for orbital overlap. The considerable distance between adjacent QL containing Fe of roughly 8 Å does not lend itself to strong interlayer interaction, compared to systems such as CrBr3 where the interlayer distance is smaller. A recent study using immense pressures revealed that the antiferromagnet-ferromagnet switching is not a result of the interlayer coupling, but due to stacking order differences in CrBr341. Looking forward, a recent publication shows the coupling of ferromagnetism and topological states introduces controllable currents in helical edge states in CrI3 and WTe2 heterostructures42, suggesting an interesting future in the heterostucture design of 2D magnetic materials.
In conclusion, we have synthesized high-quality ultrathin epitaxial FGT (001) films ranging from monolayer to ten layers. The ability to grow at the wafer-scale with precise control of layer number makes production-scale device fabrication a possibility. Epitaxial thin films also allow for the growth of heterostructures and interface engineering relative to stacked samples. One particularly important aspect of the growth of thin FGT is that it opens the possibility of interfacial coupling of ferromagnetism with various materials such as superconductors and topological materials.
METHODS
MBE growth
Ge (111) substrates were chosen in our experiment, which provides a hexagonal surface with in-plane lattice constants of a = b = 4.013 Å, resulting in a tensile strain of 0.55% with respect to FGT. We chose Ge (111) substrate to grow monolayer films by MBE for its nonmagnetic, lattice-matched structure, and commercial availability. Single crystalline Ge (111) substrates were prepared ex situ by a Piranha and HF etching process. Ge (111) substrates were initially etched in a 1:3 solution of hydrogen peroxide (H2O2) to sulfuric acid (H2SO4) for ~90 s to remove organic materials from the surface. Substrates were subsequently rinsed and submerged into room temperature deionized (DI) water for an inconsequential amount of time. Substrates were then submerged in a 1:5 DI water hydrofluoric acid solution for 30 s removing the native oxide layer on the Ge (111) surface. Substrates were again rinsed with DI water and loaded into a Veeco GENxplor MBE system with a base pressure of 1 × 10−10 Torr. Substrates were annealed at 480 °C for ~7 min upon which a 2 × 2 surface reconstruction was achieved. The reconstruction was not attempted, but rather invariably emerged during the annealing process. The reconstruction served as a criterion for removing oxide or impurities from the surface but the direct influence on FGT film is not clear. Ge was then deposited to improve the substrate surface. Ge buffer layers were grown at a rate of roughly 80 s per layer as determined by a quartz crystal microbalance (QCM). As a result, RHEED diffraction patterns were significantly improved as indicated by the intensity increase and focusing of diffraction points as shown in Supplementary Fig. 1.
Fe3GeTe2 films were synthesized using a Veeco GENxplor system. Standard effusion cells are mounted at the bottom of the chamber facing the same point at the center of the chamber where the substrate is facing downwards. Source materials of Fe (99.98%), Ge (99.999%), and Te (99.9999%) were evaporated from the effusion cells at 1320 °C, 1100 °C, and 325 °C, respectively. Elements were co-deposited on the substrate at 330 °C to grow FGT. The ratio of Fe:Ge:Te was set at 3:1: 5.6 measured by QCM prior to growth. The deposition rate was 80 s per QL. RHEED oscillations confirmed layer-by-layer growth (Fig. 1c and Supplementary Fig. 2). After growth of FGT, 10 nm of Te was deposited at room temperature as a capping layer. Without capping layer, loss of RHEED pattern of FGT confirmed amorphous surface oxidation after exposure to the air for a few minutes.
X-ray diffraction
X-ray diffraction was performed in a Rigaku Smartlab system at room temperature. A parallel beam (PB) configuration was implemented with a copper anode where both Kα1 and Kα2 emission channels were used. The voltage and current were set to 40 kV and 44 mA, respectively.
Electrical transport
Transport measurements were carried out in a Quantum Design physical properties measurement system (PPMS), where van der Pauw geometry was used to measure Rxx and anomalous Hall response. Contacts were made via indium cold welding and attached via a gold wire. An example of the longitudinal geometry is shown in Fig. 2.
Hall resistance was measured as a function of the magnetic field at fixed temperatures. Theoretically, this should result in a transverse resistance of the form Rxy = RNH + RAH, where RN is the normal Hall coefficient, and H is the applied field. Magnetization is then related to the second term, where RAH is the anomalous Hall resistance, and it’s proportional to M, the magnetization of the sample.
Arrott plot analysis was done by linearly fitting the saturated portion of RAH2 vs. (B/RAH). From the linear fit, it is possible to extract a B = 0 intercept. This analysis was performed for various temperatures around TC. These intercepts were then plotted as a function of temperature and again linearly fitted. The intercept = 0 value was then used to indicate TC18.
Data availability
All data in this published article (and its Supplementary Information files) are available from the authors.
References
Ortega, N., Kumar, A., Scott, J. F. & Katiyar, R. S. Multifunctional magnetoelectric materials for device applications. J. Phys. Condens. Matter 27, 504002 (2015).
Joshi, V. K. Spintronics: a contemporary review of emerging electronics devices. Eng. Sci. Technol. Int. J. 19, 1503–1513 (2016).
Bigot, J. Y., Vomir, M. & Beaurepaire, E. Coherent ultrafast magnetism induced by femtosecond laser pulses. Nat. Phys. 5, 515–520 (2009).
Dieny, B. Magnetism Giant magnetoresistance in spin-valve multilayers. J. Magn. Magn. Mater. 136, 335–359 (1994).
Song, C., Cui, B., Li, F., Zhou, X. & Pan, F. Recent progress in voltage control of magnetism: materials, mechanisms, and performance. Prog. Mater. Sci. 87, 33–82 (2017).
Bhatti, S. et al. Spintronics based random access memory: a review. Mater. Today 20, 530–548 (2017).
Novoselov, K. S. et al. Electric field effect in atomically thin carbon films. Science 306, 666–669 (2004).
Li, X. et al. Large-area synthesis of high-quality and uniform graphene films on copper foils. Science 324, 1312–1314 (2009).
Cao, Y. et al. Unconventional superconductivity in magic-angle graphene superlattices. Nature 556, 43–50 (2018).
Das, S., Robinson, J. A., Dubey, M., Terrones, H. & Terrones, M. Beyond Graphene: progress in novel two-dimensional materials and van der Waals solids. Annu. Rev. Mater. Res. 45, 1–27 (2015).
Kosterlitz, J. M. & Thouless, D. J. Ordering, metastability and phase transitions in two-dimensional systems. J. Phys. C. Solid State Phys. 6, 1181–1203 (1973).
Mermin, N. D. & Wagner, H. Absence of ferromagnetism or antiferromagnetism in one- or two-dimensional isotropic Heisenberg models. Phys. Rev. Lett. 17, 1133–1136 (1966).
Xi, X. et al. Ising pairing in superconducting NbSe2 atomic layers. Nat. Phys. 12, 139–143 (2016).
Huang, D. & Hoffman, J. E. Monolayer FeSe on SrTiO3. Annu. Rev. Condens. Matter Phys. 8, 311–336 (2017).
Sajadi, E. et al. Gate-induced superconductivity in a monolayer topological insulator. Science 362, 922–925 (2018).
Yu, Y. et al. High-temperature superconductivity in monolayer Bi2Sr2CaCu2O8+δ. Nature 575, 156–163 (2019).
Huang, B. et al. Layer-dependent ferromagnetism in a van der Waals crystal down to the monolayer limit. Nature 546, 270–273 (2017).
Deng, Y. et al. Gate-tunable room-temperature ferromagnetism in two-dimensional Fe3GeTe2. Nature 563, 94–99 (2018).
Gong, C. et al. Discovery of intrinsic ferromagnetism in two-dimensional van der Waals crystals. Nature 546, 265–269 (2017).
Zhang, W., Wong, P. K. J., Zhu, R. & Wee, A. T. S. Van der Waals magnets: wonder building blocks for two‐dimensional spintronics? InfoMat 1, 479–495 (2019).
Gong, C. & Zhang, X. Two-dimensional magnetic crystals and emergent heterostructure devices. Science 363, eaav4450 (2019).
Ding, B. et al. Observation of magnetic skyrmion bubbles in a van der Waals ferromagnet Fe3GeTe2. Nano Lett. 20, 868–873 (2020).
Wu, Y. et al. Néel-type skyrmion in WTe2/Fe3GeTe2 van der Waals heterostructure. Nat. Commun. 11, 3860 (2020).
Deiseroth, H. J., Aleksandrov, K., Reiner, C., Kienle, L. & Kremer, R. K. Fe3GeTe2 and Ni3GeTe2-Two new layered transition-metal compounds: Crystal structures, HRTEM investigations, and magnetic and electrical properties. Eur. J. Inorg. Chem. 2006, 1561–1567 (2006).
León-Brito, N., Bauer, E. D., Ronning, F., Thompson, J. D. & Movshovich, R. Magnetic microstructure and magnetic properties of uniaxial itinerant ferromagnet Fe3GeTe2. J. Appl. Phys. 120, 2–7 (2016).
Zhuang, H. L., Kent, P. R. C. & Hennig, R. G. Strong anisotropy and magnetostriction in the two-dimensional Stoner ferromagnet Fe3GeTe2. Phys. Rev. B 93, 1–7 (2016).
Kim, K. et al. Large anomalous Hall current induced by topological nodal lines in a ferromagnetic van der Waals semimetal. Nat. Mater. 17, 794–799 (2018).
Zhang, Y. et al. Emergence of kondo lattice behavior in a van der waals itinerant ferromagnet, Fe3GeTe2. Sci. Adv. 4, 1–9 (2018).
Tan, C. et al. Hard magnetic properties in nanoflake van der Waals Fe3GeTe2. Nat. Commun. 9, 1–7 (2018).
Xu, J., Phelan, W. A. & Chien, C. L. Large anomalous Nernst effect in a van der Waals ferromagnet Fe3GeTe2. Nano Lett. 19, 8250–8254 (2019).
Alghamdi, M. et al. Highly efficient spin-orbit torque and switching of layered ferromagnet Fe3GeTe2. Nano Lett. 19, 4400–4405 (2019).
Ralph, D. C. & Stiles, M. D. Erratum to ‘spin transfer torques’. J. Magn. Magn. Mater. 320, 1190–1216 (2008).
Albarakati, S. et al. Antisymmetric magnetoresistance in van der Waals Fe3GeTe2/graphite/Fe3GeTe2 trilayer heterostructures. Sci. Adv. 5, eaaw0409 (2019).
Fei, Z. et al. Two-dimensional itinerant ferromagnetism in atomically thin Fe3GeTe2. Nat. Mater. 17, 778–782 (2018).
Verchenko, V. Y., Tsirlin, A. A., Sobolev, A. V., Presniakov, I. A. & Shevelkov, A. V. Ferromagnetic order, strong magnetocrystalline anisotropy, and magnetocaloric effect in the layered telluride Fe3-δGeTe2. Inorg. Chem. 54, 8598–8607 (2015).
Kim, D. et al. Antiferromagnetic coupling of van der Waals ferromagnetic Fe3GeTe2. Nanotechnology 30, 245701 (2019).
L Liu, S. et al. Wafer-scale two-dimensional ferromagnetic Fe3GeTe2 thin films grown by molecular beam epitaxy. npj 2D Mater. Appl. 1, 1–6 (2017).
Nagaosa, N., Sinova, J., Onoda, S., MacDonald, A. H. & Ong, N. P. Anomalous Hall effect. Rev. Mod. Phys. 82, 1539–1592 (2010).
Li, A. P., Shen, J., Thompson, J. R. & Weitering, H. H. Ferromagnetic percolation in MnxGe1-x dilute magnetic semiconductor. Appl. Phys. Lett. 86, 1–3 (2005).
Park, S. Y. et al. Controlling the magnetic anisotropy of the van der Waals ferromagnet Fe3GeTe2 through hole doping. Nano Lett. 20, 95–100 (2019).
Chen, W. et al. Direct observation of van der Waals stacking–dependent interlayer magnetism. Science 366, 983–987 (2019).
Zhao, W. et al. Magnetic proximity and nonreciprocal current switching in a monolayer WTe2 helical edge. Nat. Mater. 19, 503–507 (2020).
Acknowledgements
This research was supported by Max Planck-UBC-UTokyo Centre for Quantum Materials, by Canada First Research Excellence Fund, Quantum Materials and Future Technologies Program, by Natural Sciences and Engineering Research Council of Canada (NSERC), and by Canada Foundation for Innovation (CFI).
Author information
Authors and Affiliations
Contributions
R.R. and K.Z. designed the project. R.R. grew the films, carried out diffraction measurements, and wrote the manuscript. R.R. and C.L. performed transport measurements and analyzed the data. All authors discussed the results and commented on the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Roemer, R., Liu, C. & Zou, K. Robust ferromagnetism in wafer-scale monolayer and multilayer Fe3GeTe2. npj 2D Mater Appl 4, 33 (2020). https://doi.org/10.1038/s41699-020-00167-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41699-020-00167-z
This article is cited by
-
Three-stage ultrafast demagnetization dynamics in a monolayer ferromagnet
Nature Communications (2024)
-
Hard ferromagnetism in van der Waals Fe3GaTe2 nanoflake down to monolayer
npj 2D Materials and Applications (2024)
-
Hole induced half-metallic 2H VSe2 thin film with high Curie temperature and optical transparency
Journal of the Korean Physical Society (2024)
-
Electron transport and scattering mechanisms in ferromagnetic monolayer Fe3GeTe2
npj 2D Materials and Applications (2023)
-
Unraveling effects of electron correlation in two-dimensional FenGeTe2 (n = 3, 4, 5) by dynamical mean field theory
npj Computational Materials (2023)