Abstract
MoS2 single layers are valued for their sizeable direct bandgap at the heart of the envisaged electronic and optoelectronic applications. Here we experimentally demonstrate that moderate strain values (~2%) can already trigger an indirect bandgap transition and induce a finite charge carrier density in 2D MoS2 layers. A conclusive proof of the direct-to-indirect bandgap transition is provided by directly comparing the electronic and optical bandgaps of strained MoS2 single layers obtained from tunneling spectroscopy and photoluminescence measurements of MoS2 nanobubbles. Upon 2% biaxial tensile strain, the electronic gap becomes significantly smaller (1.45 ± 0.15 eV) than the optical direct gap (1.73 ± 0.1 eV), clearly evidencing a strain-induced direct to indirect bandgap transition. Moreover, the Fermi level can shift inside the conduction band already in moderately strained (~2%) MoS2 single layers conferring them a metallic character.
Similar content being viewed by others
Introduction
Tuning the band structure of two-dimensional (2D) materials by applying mechanical strain can provide an efficient way to fit the properties of the material to the specific requirements of various applications. This could have a particularly high impact on electronic and opto-electronic applications. Numerous experimental1,2,3,4 and theoretical5,6,7,8 studies have been conducted so far to reveal the effect of strain on the band structure of MoS2 single layers. Theoretical studies predict a steady decrease of the bandgap upon increasing strain for both uniaxial and biaxial strain. Moreover, it is expected that increasing the strain leads to a direct-to-indirect bandgap transition, predicted to occur between 1% and 5% strain, depending on the theoretical model.5,6,7,8 Further increasing the strain up to 8–10% is predicted to give rise to a semiconductor-to-metal transition by closing the bandgap.9 Photoluminescence (PL) measurements indeed revealed a closely linear decrease of the bandgap as a function of the applied strain, which confirms the possibility of bandgap engineering.1,2 However, in PL measurements the most intense peak originates from the direct bandgap10 (the smallest energy difference between the valence and conduction bands measured at the same position in the Brillouin zone) reduced by the exciton binding energy. Indirect transitions require the assistance of phonons that strongly reduce the intensity of the corresponding PL peaks. By contrast, transport measurements and electronic applications rely on the electronic (fundamental) bandgap, which is the energy difference between the global conduction band minimum and valence band maximum. Consequently, the electronic gap can only be smaller than the energy of the main PL peak (originating from the direct bandgap and reduced by the exciton binding energy) in indirect bandgap semiconductors. It is well known that, in contrast to their bulk crystal, MoS2 single layers are direct bandgap semiconductors, evidenced by a highly increased luminescence quantum yield.11 As discussed above, upon mechanical strain even single layers are predicted to become indirect bandgap semiconductors, which in principle should be reflected in the PL intensity. Indeed, PL measurements reveal that not only the optical gap is decreased by tensile strain but the PL intensity also substantially changes upon straining.1,2 However, the PL intensity can be influenced by several factors, such as strain and doping dependent on many particle effects12 or exciton funneling.13,14 As a consequence, both decreasing1,2 and increasing13,14 PL intensities have been observed upon increasing strain. Therefore, based on PL intensity alone it is difficult to unambiguously determine the direct/indirect nature of the bandgap. A clear proof of the widely predicted bandgap transition can be provided by the direct experimental comparison of the electronic and optical gaps of the same strained MoS2 sample. A comparison of PL and tunneling spectroscopy data have been reported by Li et al.13. However, the systems measured with the two techniques were significantly different (MoS2/SiO2/Si—PL, MoS2/Au/SiO2/Si—tunneling spectroscopy). Owing to the strong renormalization effect of gold on the tunneling spectra (electronic gap) of MoS2 single layers,15 it is difficult to separate the effect of strain from that of the Au substrate.
Here we employ tunneling spectroscopy and PL investigations to directly measure the electronic and optical bandgap of MoS2 nanobubbles emerging at the 2D MoS2/Au(111) interface. Since in the bubble areas the MoS2 single layers are decoupled from the Au substrate by the several nanometer high contamination volume trapped inside the bubbles, the renormalization effect of the gold substrate is absent in our case.16 Raman spectroscopy reveals that such bubbles are characterized by a few percentage of biaxial tensile strain. The direct comparison of the electronic and optical bandgap of the same sample enables us to provide conclusive evidence on the strain-induced direct-to-indirect bandgap transition in MoS2 single layers. Furthermore, our results evidence that, in the strained MoS2 single layers, the Fermi level can shift into the conduction band providing a finite conductivity already at moderate (few percentage) strain levels.
Results
Nanobubble formation
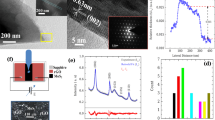
We used a gold-assisted mechanical exfoliation technique developed by us17 to exfoliate MoS2 single layers onto Au(111) substrate. The topographic scanning tunneling microscopic (STM) investigations of such samples revealed the formation of circular protrusions (Fig. 1) that can be identified as MoS2 nanobubbles. Larger area atomic force microscopic (AFM) investigations also revealed the presence of MoS2 bubbles with diameters >100 nm (Fig. S1). The origin of such bubbles is the relatively strong Van der Waals interaction that squeezes the contaminants trapped at the MoS2/Au(111) interface into bubbles in order to maximize direct contact area between the two materials at the expense of the local elastic deformation (strain) energy of the 2D MoS2 lattice in the bubble areas. Khestanova et al.18 demonstrated that such bubbles are characterized by a universal shape (aspect ratio) and pressure (strain), determined only by the strength of the van der Waals interaction with the substrate and the elastic properties of the 2D crystal. The characteristic aspect ratio (hmax/R) of bubbles in our sample was found to be 0.2. A higher aspect ratio indicates a stronger adhesion to the substrate. The 0.2 value measured by us for the MoS2/Au(111) system is higher than the 0.17 measured by Khestanova et al. for MoS2 on MoS2 substrate, which is in agreement with the fact that we exploit the stronger adhesion of the MoS2 to Au(111) in order to exfoliate single layers from the bulk crystal.17 The universal behavior of nanobubbles is highly appealing as all bubbles are expected to display similar properties substantially facilitating the interpretation of their measurements. We also note that deviations from the 0.2 aspect ratio were found for the smallest bubbles. However, these deviations are only apparent and can be attributed to the tip convolution effects.19
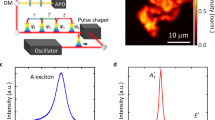
Nanobubble formation at the MoS2/Au(111) interface. a Topographic STM image of MoS2 single layer exfoliated onto Au(111) substrate displaying nanometer height bright protrusions identified as MoS2 nanobubbles trapping the contamination at the MoS2/Au(111) interface. Scale bar length is 20 nm. b 3D STM image of an individual MoS2 nanobubble of 1 nm height and 10 nm diameter
Raman spectroscopy
In order to experimentally determine the amount of mechanical strain induced in the MoS2 lattice in the bubble areas, we performed confocal Raman spectroscopic measurements. One of the main peaks, the E’ peak located around 380 cm−1 in strain-free MoS2 single layers, is expected to shift considerably due to mechanical strain,3,20 while it is practically unaffected by doping.21 By contrast, the A1 peak (~400 cm−1) is affected by both strain and doping.21,22 Our confocal Raman mapping of the samples provided Raman spectra with a spatial resolution of about 500 nm. Even though most bubbles are much smaller than the laser spot and the Raman signal can stem from an ensemble of bubbles with various diameters, we can extract the corresponding average strain information. This is made possible by the universal shape of the bubbles,18 meaning that the average strain within a bubble is proportional to (hmax/R)2, which is constant. A Raman intensity map can be seen in the left inset of Fig. 2. The bright areas on the map correspond to larger bubbles based on the correlation of Raman maps with topographic AFM images. Figure 2 shows the Raman spectrum averaged over bubbles (bright regions), as well as the average spectrum corresponding to the flat (dark) regions. While for the flat areas the two main Raman peaks are located around 380 and 400 cm−1, as often reported in the literature, in the bubble areas the E’ peak is apparently split, and the main peak is downshifted, by >10 cm−1. This significant downshift of the E’ peak can be attributed to a substantial amount of tensile strain.20,22 The reason for the apparently double E’ peak is that the Raman spot size is larger than the characteristic bubble diameter. This way both strained (bubble) and unstrained (flat) MoS2 areas are sampled. Another important observation is that the substantially downshifted E’ peak does not vary significantly on various bubbles, providing a well-defined peak in the spectra averaged over all bubbles. This indicates that the pressure (strain) inside the bubbles is approximately constant, in excellent agreement with the findings of Khestanova et al.18 The significantly increased Raman intensity on the bubbles can mainly be attributed to the decoupling of the MoS2 sheet from the Au(111) substrate in the bubble area, since the proximity of the substrate is known to strongly quench optical signals.14,23 To further support our interpretation, we have performed simulations of the Raman spectrum of MoS2 single layers subjected to biaxial tensile strain using the frequency-dependent Placzek approximation:
where αρ,σ(ωL) is the polarizability tensor calculated at the laser energy ωL, Qv and ωv are the phonon normal modes and frequencies, ωs is the frequency of the scattered light, n(ωv) is the Bose–Einstein distribution at room temperature, and Γ(x) is a normalized Lorentzian function with full width at half maximum of 10 cm−1. The right inset of Fig. 2 shows the calculated Raman spectrum for strained and relaxed MoS2 monolayers, together with the average Raman spectrum measured on bubbles. The best agreement with the experimental data was found when considering 2% of biaxial tensile strain in our calculations. This strain value obtained from Raman spectroscopy corresponds very well to the average strain one can expect from purely geometrical considerations,18 as well as with previous Raman measurements quantifying the strain emerging in MoS2 bubbles.1 It is apparent that the agreement between experiments and simulations is almost perfect for the E’ peak, while it displays a small discrepancy (~2 cm−1) for the A1 peak. The reason for this is the sensitivity of the A1 peak to doping, which is not considered in our calculation. From the larger redshift of the A1 peak as expected from strain alone, we can estimate an electron (n) doping of order of 1012 cm−2 in MoS2 bubbles.
Quantifying the strain in MoS2 bubbles. Raman spectra averaged over bubbles (red) and flat regions (black). Left inset shows a Raman intensity map of the MoS2/Au(111) interface, where bright regions can be associated with the presence of larger MoS2 bubbles. Right inset shows the comparison with theoretically calculated Raman spectrum displaying the best agreement for 2% biaxial tensile strain
PL and tunneling spectroscopy
To determine the optical gap of strained MoS2, we have performed PL measurements on the bubbles and flat areas of the MoS2/Au(111) sample. PL measurements on bubbles have been performed in the bright areas of the Raman map that previously have been identified as the areas with 2% strain. The results are shown in Fig. 3a evidencing a 150 meV redshift of the PL peak in the strained (bubble) areas as compared to the flat MoS2/Au(111) regions. Note that both PL spectra display a small secondary peak at the main peak position of the other spectrum. This is due to the larger size of the measurement spot as compared to the bubbles, as well as the fact that no completely bubble-free areas can be found. The main PL peak corresponding to the direct transition reveals a 1.73 ± 0.1 eV large optical direct bandgap in strained bubbles, in good agreement with optical gap values reported in the literature on large bubbles with similar 2% strain.1,14 We found similar PL intensities in strained bubbles and unstrained flat areas. The reason for this is the competition of several factors that influence the PL intensity, such as the direct/indirect nature of the bandgap1 and the exciton funneling effect in bubbles,14 as well as the quenching of the PL signal by the substrate.14
Optical and electronic gap of strained MoS2 bubbles. a Photoluminescence spectra on strained MoS2 bubbles (red) and flat MoS2/Au(111) areas (blue) evidencing an optical direct gap of 1.73 eV in strained MoS2, corresponding to a 150 meV redshift of the PL peak as compared to unstrained areas. b Tunneling spectra acquired on three different MoS2 nanobubbles revealing electronic gap values of 1.45 ± 0.15 eV. Inset shows that the Fermi level of strained bubbles can shift inside the conduction band, conferring a conductive character to MoS2 layers strained >2%
To obtain the electronic bandgap of strained MoS2 bubbles, we have performed tunneling spectroscopic measurements. We have acquired tunneling spectra over MoS2 bubbles of various diameters. The measurements always took place at the top of the nanobubbles. Representative tunneling spectra are shown in Fig. 3b. A bandgap value of about 1.45 ± 0.15 eV was found for all 23 different bubbles measured, with no dependence on the geometry (diameter) of the bubbles.
Discussion
The most important finding is that the 1.45 ± 0.15 eV electronic gap value measured by tunneling spectroscopy is well below the optical direct gap (1.73 ± 0.1 eV) obtained from our PL measurements on the same sample. The fact that the electronic gap is smaller than the optical direct gap clearly evidences that the direct-to-indirect bandgap transition has already occurred for 2% of biaxial tensile strain in MoS2 single layers.
Another important observation from the tunneling spectra is the position of the Fermi level in strained MoS2 bubbles. MoS2 single layers are known to be intrinsically n-doped, with their Fermi level shifted toward the conduction band.15,16 However, on the MoS2 nanobubbles with 2% of strain, the Fermi level is located right at the edge of the conduction band. This is in contrast to unstrained MoS2 single layers, for which the Fermi level lies typically a few hundreds of meV below the conduction band (Fig. S2).15,16 This implies that by further increasing the strain the conduction band minimum shifts below the Fermi level, providing a metallic character to the MoS2 bubbles already at moderate strain values. The inset of Fig. 3b shows an example where we observed a non-zero density of states at the Fermi level on several bubbles. The displayed spectra are the average of several individual spectra to smooth out the fluctuations. The non-zero density of states at the Fermi level is expected to have significant effects on the electrical transport characteristics of strained MoS2 single layers. The emergence of a metallic character in mildly strained MoS2 as observed here is in contrast with the theoretical predictions, where only a large amount of strain (~10%) was shown to induce a semiconductor–metal transition.9,24 The reason for this discrepancy is that in calculations the Fermi level lies close to the valence band, while in the experiments, the Fermi level is much closer to the conduction band, due to the inherent n doping. This way, even without closing the bandgap, free charge carriers become available upon moderate strain in MoS2 single layers, which is expected to substantially increase their electrical conductivity. The ability of easily accessible strain values to induce a conductive state in MoS2 single layers (in combination with their intrinsic n-doping) can be exploited in various applications, such as electro-catalysis, where an increased sheet conductivity is highly desired.25 We also mention that owing to the Fermi level being very close to the conduction band edge we do not expect any significant tip-induced band bending to occur on bubbles, which is known to enlarge the bandgap measured by STM.26
We would like to emphasize that, although the measurements have been performed on the curved surfaces of MoS2 nanobubbles, the curvature radius was >20 nm even for the smallest investigated bubbles. Therefore, the curvature is not expected to influence the electronic band structure, in accordance with calculations predicting that >4 nm curvature radius the curvature effects on the electronic band structure are negligible.27 The negligible effect of curvature in our case is also experimentally verified by tunneling spectra acquired on bubbles with various curvature radii revealing the same, universal bandgap value of 1.45 ± 0.15 eV. This finding clearly evidences that the observed effect is entirely due to the in-plane biaxial strain in our case.
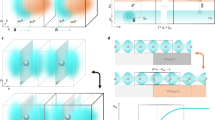
To understand the mechanism of strain-induced changes in the band structure, we have performed density functional theory (DFT) calculations at the Perdew–Burke–Ernzerhof (PBE) level. We used the DFT optimized lattice constant 3.18 Å as a reference (corresponding to 0% strain). Figure 4a shows the band structure of 2D MoS2 with 0% strain, characterized by a direct bandgap at the K point of the Brillouin zone. It is worth noting that the Fermi level in the DFT calculations of the freestanding MoS2 is close to valance band in contrast to the measurements, where the MoS2 layer is generally n-doped. By increasing the strain, the valence and conduction bands near the K point downshift in energy while the valence band position near the Γ point remains almost unaffected relative to the Fermi energy. This behavior stems from the strain-induced modification of orbital overlaps.28 The modification trends of the bands under strain is independent of the different DFT calculation methods5 highlighting the robustness of the phenomenon. In Fig. 4b at 2% of tensile strain, we can clearly see that the bandgap is reduced by about 0.46 eV and becomes an indirect gap between the K and Γ points of the Brillouin zone, in agreement with our experiments. We note that DFT calculation employing various exchange–correlation (XC) functionals and more accurate description of many-body electron–electron interaction predict various bandgap values,29,30 but the trend that the fundamental gap is more sensitive to the strain and a direct-to-indirect bandgap transition occurs at relatively low strain values is robustly predicted,5,6,7,8,31 in excellent agreement with our experimental findings.
While our findings experimentally demonstrate a particularly efficient strain-tunability of the electronic bandgap of MoS2 single layers, they also evidence strong limitations of the strain-engineering approach. The transition to an indirect bandgap restricts the opto-electronic applications, while the conductive nature emerging >2% of strain puts a strong limitation on electronic device applications, as such small strain values can accidentally occur during sample fabrication and processing.
Methods
Sample preparation
MoS2 single layers have been prepared by mechanical exfoliation of synthetic bulk MoS2 crystals of high structural quality (2D semiconductors). We have employed a gold-assisted mechanical exfoliation technique developed by us and discussed in detail in ref. 17, providing single-layer transition metal dichalcogenide flakes with hundreds of microns of lateral dimensions on atomically flat Au (111) surfaces. The single-layer nature of the investigated MoS2 crystals has also been confirmed by Raman spectroscopy and AFM measurements.
Characterization
STM and spectroscopic measurements have been performed on RHK PanScan Freedom STM under ultra-high vacuum conditions at room temperature. Large area flakes could be easily identified through optical microscope access enabling the guided landing of the STM tip on MoS2 single-layer areas. STM imaging were acquired with typical parameter ranges of |Ubias| = 100–500 mV and Itunnel = 100–500 pA. PL and Raman measurements have been conducted on a confocal Raman microscope (Witec 300RSA) with an excitation wavelength of λ = 532 nm and W = 1 mW.
Computational details
DFT calculations including spin-polarized coupling were carried out using the projector augmented wave method32,33 as implemented in the Vienna ab initio simulation package.34,35 The generalized gradient approximation of PBE was adopted for the XC functional.36 The band structure calculations were performed with plane wave cutoff of 500 eV and the Brillouin zone was sampled with (8 × 8 × 1) Monkhorst–Pack mesh of K points.37 To avoid artificial interactions between periodic replicas of nanosheet planes, a vacuum interval of 12 Å was introduced in the z-direction. The structural and vibrational properties of the monolayer were calculated with plane wave cutoff of 700 eV and a 30 × 30 × 1 Γ centered Monkhorst–Pack grid. Geometry optimization were performed until all atomic forces fell below 0.003 eV/Å. Vibrational frequencies were carried out within the frozen phonon approximation with finite displacement of 0.015 Å. Dynamic polarizability was calculated within the linear response theory,38 with similar parameters used during the frequency calculation and geometrical optimization. Numeric derivatives of the polarizability tensor were calculated using symmetric derivatives by manually shifting the atoms according to normal modes in both the positive and negative directions. The normal modes were normalized to 0.015 Å during the Raman calculations.
Data availability
The authors confirm that the data supporting the findings of this study are available within the article. Related additional data are available on reasonable request from the authors.
References
Lloyd, D. et al. Band gap engineering with ultralarge biaxial strains in suspended monolayer MoS2. Nano Lett. 16, 5836–5841 (2016).
Conley, H. J. et al. Bandgap engineering of strained monolayer and bilayer MoS2. Nano Lett. 13, 3626–3630 (2013).
Castellanos-Gomez, A. et al. Local strain engineering in atomically thin MoS2. Nano Lett. 13, 5361–5366 (2013).
He, K. et al. Experimental demonstration of continuous electronic structure tuning via strain in atomically thin MoS2. Nano Lett. 13, 2931–2936 (2013).
Shi, H. et al. Quasiparticle band structures and optical properties of strained monolayer MoS2 and WS2. Phys. Rev. B 87, 155304 (2013).
Wang, L., Kutana, A. & Yakobson, B. I. Many body and spin orbit effects on direct indirect band gap transition of strained monolayer MoS2 and WS2. Ann. Phys. 526, L7 (2014).
Li, T. Ideal strength and phonon instability in single-layer MoS2. Phys. Rev. B 85, 235407 (2012).
Zhang, Q. et al. Giant valley drifts in uniaxially strained monolayer MoS2. Phys. Rev. B 88, 245447 (2013).
Scalise, E. et al. Strain-induced semiconductor to metal transition in the two-dimensional honeycomb structure of MoS2. Nano Res. 5, 43–48 (2012).
Splendiani, A. et al. Emerging photoluminescence in monolayer MoS2. Nano Lett. 10, 1271 (2010).
Mak, K. F. et al. Atomically thin MoS2: a new direct-gap semiconductor phys. Rev. Lett. 105, 136805 (2010).
Steinhoff, A. et al. Efficient excitonic photoluminescence in direct and indirect band. gap monolayer MoS2. Nano Lett. 15, 6841–6847 (2015).
Li, H. et al. Optoelectronic crystal of artificial atoms in strain-textured molybdenum disulphide. Nat. Commun. 6, 7381 (2015).
Tyurnina, A. V. et al. Strained bubbles in van der Waals heterostructures as local emitters of photoluminescence with adjustable wavelength. ACS Photonics 6, 516–524 (2019).
Bruix, A. et al. Single-layer MoS2 on Au(111): band gap renormalization and substrate interaction. Phys. Rev. B 93, 165422 (2016).
Hong, M. et al. Decoupling the Interaction between wet-transferred MoS2 and graphite substrate by an interfacial water layer. Adv. Mater. Interfaces 5, 1800641 (2018).
Magda, G. Z. et al. Exfoliation of large-area transition metal chalcogenide single layers. Sci. Rep. 5, 14714 (2015).
Khestanova, E. et al. Universal shape and pressure inside bubbles appearing in van der Waals heterostructures. Nat. Commun. 7, 12587 (2016).
Márk, G., Biró, L. P. & Gyulai, J. Simulation of STM images of three-dimensional surfaces and comparison with experimental data: carbon nanotubes. Phys. Rev. B. 58, 12645–12648 (1998).
Rice, C. et al. Raman-scattering measurements and first-principles calculations of strain-induced phonon shifts in monolayer MoS2. Phys. Rev. B 87, 081307(R) (2013).
Chakraborty, B. et al. Symmetry-dependent phonon renormalization in monolayer MoS2 transistor. Phys. Rev. B 85, 161403(R) (2012).
Kukucska, G. & Koltai, J. Theoretical investigation of strain and doping on the Raman spectra of monolyaer MoS2. Phys. Stat. Sol. B 254, 1700184 (2017).
Bhanu, U. et al. Photoluminescence quenching gold - MoS2 hybrid nanoflakes. Sci. Rep. 4, 5575 (2014).
Yun, W. S. et al. Thickness and strain effects on electronic structures of transition metal dichalcogenides: 2H-MX2 semiconductors (M=Mo, W; X=S, Se, Te). Phys. Rev. B 85, 033305 (2012).
Voiry, D. et al. Conducting MoS2 nanosheets as catalysts for hydrogen evolution reaction. Nano Lett. 13, 6222 (2013).
Dombrowski, R., Steinebach, C., Wittneven, C., Morgenstern, M. & Wiesendanger, R. Tip-induced band bending by scanning tunneling spectroscopy of the states of the tip-induced quantum dot on InAs(110). Phys. Rev. B. 59, 8043–8048 (1999).
Ghorbani, M. et al. Electromechanics in MoS2 and WS2: nanotubes vs. monolayers. Sci. Rep. 3, 2691 (2013).
Chang, C. H. et al. Orbital analysis of electronic structure and phonon dispersion in MoS2, MoSe2, WS2, and WSe2 monolayers under strain. Phys. Rev. B 88, 195420 (2013).
Ding, Y. et al. First principles study of structural, vibrational and electronic properties of graphene-like MX2 (M=Mo, Nb, W, Ta; X=S, Se, Te) monolayers. Phys. B 406, 2254–2260 (2011).
Kuc, A. et al. Influence of quantum confinement on the electronic structure of the transition metal sulfide TS2. Phys. Rev. B 83, 245213 (2011).
Roldán, R. et al. Electronic properties of single-layer and multilayer transition metal dichalcogenides MX2 (M = Mo, W and X = S, Se) Ann. Phys. (Berlin) 526, 347–357 (2014).
Blöchl, P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953 (1994).
Kresse, G. & Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758 (1999).
Kresse, G. & Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 47, 558 (1993).
Kresse, G. & Furthmuller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169 (1996).
Perdew, J. P. et al. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865 (1996).
Monkhorst, H. J. & Pack, J. D. Special points for Brillouin-zone integrations. Phys. Rev. B 13, 5188 (1976).
Gajdos, M. et al. Linear optical properties in the projector-augmented wave methodology. Phys. Rev. B 73, 045112 (2006).
Acknowledgements
The work has been performed in the framework of the Korea Hungary Joint Laboratory for Nanosciences and the NanoFab2D ERC Starting grant. L.T. and P.N.-I. acknowledges the “Lendület” Program. Support from the Hungarian National Research, Development and Innovation Office (NKFIH, Grant Nos. KH-130413 and K-115608) is acknowledged. G.K. and J.K. acknowledge NIIF for awarding access to a resource based in Hungary at Debrecen. J.K. acknowledges the Bolyai and Bolyai+ program of the HAS.
Author information
Authors and Affiliations
Contributions
L.T., P.N.-I., and C.H. conceived and designed the experiments. J.P. prepared the samples and performed the STM measurements. G.D. conducted the photoluminescence and Raman spectroscopic investigations. G.K. and J.K. performed the Raman spectra calculations. P.V. carried out the DFT band structure calculations. A.A.K. measured the reference tunneling spectra on graphite substrate. L.T., P.N.-I., and C.H. supervised the project. J.P. and L.T. wrote the paper. All authors discussed the results and commented on the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Pető, J., Dobrik, G., Kukucska, G. et al. Moderate strain induced indirect bandgap and conduction electrons in MoS2 single layers. npj 2D Mater Appl 3, 39 (2019). https://doi.org/10.1038/s41699-019-0123-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41699-019-0123-5
This article is cited by
-
Tunable strain and bandgap in subcritical-sized MoS2 nanobubbles
npj 2D Materials and Applications (2023)
-
Revealing the topological phase diagram of ZrTe5 using the complex strain fields of microbubbles
npj Computational Materials (2022)
-
Reversible strain-induced magnetic phase transition in a van der Waals magnet
Nature Nanotechnology (2022)
-
Indirect to direct band gap crossover in two-dimensional WS2(1−x)Se2x alloys
npj 2D Materials and Applications (2021)
-
Electron–phonon coupling in superconducting 1T-PdTe2
npj 2D Materials and Applications (2021)