Introduction

With the discovery of graphene, electronics at the atomically thin limit has become a realistic possibility within the foreseeable future.1 However, graphene lacks a semiconducting energy gap inhibiting many standard applications. Transition metal dichalcogenides (TMDC) have become an attractive alternative.2,3 Monolayers can be exfoliated from the bulk materials or synthesized by other means and do show sizable gaps. Single-, few- and multilayer MoS2 have been integrated into device demonstrators with promising performance parameters.4,5,6 Moreover, MoS2 exhibits an amazing variety of possible applications, which are all actively investigated, including optoelectronics,7,8 bio-sensors,9 hydrogen production,10,11 and water disinfection,12 apart from the more conventional use as a lubricant.

The optical properties show an intriguing dependence on thickness. The gap increases from \({E}_{{\rm{g}}}=1.3\) eV in the bulk to \({E}_{{\rm{g}}}=1.9\) eV for the monolayer for MoS2 and changes character from indirect to direct when the monolayer is reached, accompanied by an orders of magnitude increase of the photoluminescence yield.7,13 The direct gap is located at the \(K\) point of the Brillouin zone, the indirect gap of thicker layers between the \(\Gamma\) and \(\Lambda\) points (see Fig. 1). The optical response is dominated by excitons, which acquire anomalously large binding energies in the 2D-TMDCs due to reduced screening and strong many-body interactions.14 Also the absolute light absorbance of monolayers is much larger than conventionally expected because of the strong electron–photon interaction triggered by nested band regions giving rise to large joint density of states.8,15,16 The latter are situated in the vicinity of \(\Gamma\), where parallel segments of valence and conduction band exist (see Fig. 1a). Attempts have been made to implement MoS2 and other monolayer dichalcogenides into optoelectronic devices and photovoltaic applications.17,18,19

Fig. 1
figure 1

Band structure. a Three dimensional visualization of the highest valence and lowest conduction band of monolayer MoS2 obtained by DFT. The color scale represents the energy. b Two dimensional map of the conduction band energy locus on the same color scale

Full size image

Optical transitions, i.e., the excitation of a valence band electron to the conduction band by the absorption of a photon, are bound to a momentum transfer \({\bf{q}}=0\), because the photon itself carries negligible momentum in the visible range. For 2D-TMDCs such an excitation leads to the formation of a direct, or bright exciton, since the latter may recombine and emit a photon. Nevertheless, detailed understanding of many optical processes requires knowledge of all possible transitions in the pertinent energy range, including \({\bf{q}}\ \ne \ 0\). Such transitions give rise to the formation of indirect or dark excitons. The importance of excited states with \({\bf{q}}\ \ne \ 0\) is increasingly recognized and its relevance for various observable quantities has been shown, such as the quantitative description of the photoluminescence yield.20,21 However, this branch of the current research on TMDCs faces the challenge that \({\bf{q}}\)-dependent electronic transitions are difficult to assess by experiment. This is all the more true for monolayer materials. The techniques in principle capable of providing \({\bf{q}}\)-resolution are inelastic light scattering, when the photon energy is sufficiently large, and electron energy loss spectroscopy (EELS). However, the latter requires specialized spectrometers as well. While some EELS studies have been reported22,23,24,25 the actual available experimental information on the \({\bf{q}}\)-dependent exciton landscape is still limited and often derived indirectly from optical experiments.

The relevant physical quantity describing all the electronic transitions is the dielectric function \(\epsilon ({\bf{q}},\omega )\). It is directly related to observable quantities like the optical absorption or the EELS intensity. The dielectric function itself depends on the underlying one-particle bandstructure and, in addition, on many-body interactions.

Here, we study the momentum dependence of \(\epsilon ({\bf{q}},\omega )\) with an emphasis on the energy regions of the A/B-excitons, which refers to the spin–orbit split pair of excitons arising from transitions around the \(K\)-point on the one side, and the C-exciton, originating from band nested regions near \(\Gamma\), on the other side. We start by measuring the electronic structure of the occupied states by angle-resolved photoemission spectroscopy (ARPES) and compare them to density functional theory (DFT) derived bandstructure calculations. The latter are used to calculate a model dielectric function within a single-particle approximation. Then, the model is compared to experimental EELS data. We find agreement of key aspects between model and experiment and focus afterwards on the momentum dependence of the C-exciton. The C-exciton features its own energy landscape with distinct local maxima in \(({\bf{q}},\omega )\) space. The possible relevance of these nested dark excitons is discussed.

Results

ARPES

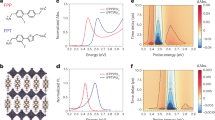
Figure 2 shows the photoemission results of the valence band in the angle-resolved mode along \(\Gamma K\) for a monolayer, bilayer and a thick, bulk-like flake on Au (see the Supplemental Material for details about the sample characterization and measuring configuration). In order to enhance the visibility of weak ARPES features a deconvolution procedure has been applied, which is based on Fourier transformation and inverse Fourier transformation and assuming a Gaussian energy broadening. There are prominent hole-bands centered at \(\Gamma\) and \(K\) in all cases. Significant changes of the bandstructure as a function of layer number can be seen. Whereas the \(\Gamma\) point band consists only of a single component for the monolayer, it is split into two for the bilayer, as expected from bandstructure calculations and from general considerations of the quantum confinement. The shape of the \(K\) point bands, on the other hand, does not change qualitatively. At the \(K\) point the band is split due to spin–orbit coupling for the monolayer, which is not discernible in Fig. 2 but demonstrated in SFig. 2 in the Supplemental Material. The absence of confinement related splittings indicates the weak \(c\)-axis hybridization at \(K\) in contrast to \(\Gamma\). Although the photoemission intensity directly at the \(\Gamma\) point is suppressed for layernumbers \(N\ >\ 1\) due to matrix element effects26,27 it is clear that the overall valence band maximum is situated at the \(\Gamma\) point for \(N\ >\ 1\), while the maximum of the \(K\) point band is lower. As can be seen in SFig. 2 this order reverses for \(N=1\) for the valence band position as well as for the onset consistent with the change of the gap character and in agreement with previous photoemission studies.26 The position of the uppermost valence band at \(E\approx 2.1\) eV for the monolayer means that the Fermi level is situated close to the conduction band edge, since the single particle gap is in the order of 2.5 eV.28,29 This indicates the typical n-type doping of MoS2. The latter is found even though the Au substrate features a large work function, which tends to induce hole doping.30 It has been suggested that the Fermi level is pinned close to the conduction band edge due to defects.31

Fig. 2
figure 2

Angle resolved photoemission spectroscopy. \(\Gamma K\) energy distribution maps after deconvolution as a function of thickness. Black lines: DFT results

Full size image

The valence band maximum shifts upwards with increasing thickness. We attribute this effect to the decreasing gap value: while the optical gap is \({E}_{{\rm{gap}}}^{{\rm{ML}}}=1.9\) eV for the monolayer it decreases to \({E}_{{\rm{gap}}}^{{\rm{bulk}}}=1.3\) eV for the bulk.7,13 The results are very similar if Pt coated substrate is used instead of Au (not shown). We compare the experimental results in Fig. 2 to DFT based bandstructure calculations for freestanding MoS2. The energy of the calculated bands has been shifted to match experiment. The agreement is satisfactory. It indicates a weak flake–substrate interaction, probably due to an intermediate buffer layer consisting of PDMS residuals and air adsorbates. This is consistent with the absence of a substrate dependence of the photoemission and Raman results (see Supplemental Material for the latter). In particular, hybridization related changes of the bandstructure around \(\Gamma\) have been observed for epitaxial MoS2 monolayers on clean Au (111) but are absent here.32 Moreover, the optical properties may change under such conditions, as shown by the exciton quenching in gold–MoS2 hybrid nanoflakes.33

EELS

The correspondence of the ARPES data with the bandstructure calculation in Fig. 2 shows that DFT is an appropriate starting point for the description of the electronic structure of MoS2. However, since photoemission is sensitive to the occupied states only, the agreement with the unoccupied states remains elusive. Moreover, photoemission is a one-particle probe whereas the optical properties are dictated by electronic transition from the occupied to the unoccupied states, i.e., by two-particle excitations. In order to facilitate a connection to the optical properties we consider now EELS, where transitions from the occupied to the unoccupied states are caused by a primary high-energy electron beam. EELS is conducted here as a momentum resolved probe, which allows the investigation of non-vertical transitions with momentum transfer \({\bf{q}}\ \ne \ 0\). The vast majority of relevant studies, on the other hand, relies on optical spectroscopy, that is, \({\bf{q}}\approx 0\).

EELS intensity is proportional to the loss function, a quantity closely related to the generalized dielectric function via \({\rm{Im}}(-1/\epsilon ({\bf{q}},\omega ))\). We start from a simplified model for the susceptibility

$${\chi }_{0}({\boldsymbol{q}},\omega )=\sum _{v,c,{\boldsymbol{k}}}\frac{1}{\omega -({E}_{{\boldsymbol{k}}+{\boldsymbol{q}}}^{c}-{E}_{{\boldsymbol{k}}}^{v})+{\rm{i}}\delta }$$
(1)

where \({E}_{{\boldsymbol{k}}}^{c(v)}\) correspond to the conduction (valence) bands derivded from DFT, \(\delta\) is treated as a phenomenological broadening parameter and the sum runs over all VB and CB states. From this we obtain the effective dielectric function according to

$$\frac{1}{\tilde{\epsilon }({\boldsymbol{q}},\omega )}=1+\frac{1}{{q}^{2}}{\chi }_{0}({\boldsymbol{q}},\omega )$$
(2)

from which the loss function can be calculated.34,35 The \(1/{q}^{2}\) term in Eq. (2) reflects the Fourier transform of the Coulomb potential for bulk materials. The model ignores many-body interactions, in particular excitonic effects, and the matrix element mediating the transition from VB to CB. Although these assumptions appear to be crucial for TMDC, especially when the monolayer is approached where the exciton binding energies are known to be large, we will show below that the agreement with experiment works surprisingly well in many aspects, reflecting the importance of the underlying bandstructure.

Figure 3 presents EELS data in comparison to theoretical spectra obtained implementing Eqs. (1), (2). See the methods section for details. Figure 3a presents \({\bf{q}}\)-dependent EELS measurements of bulk MoS2 with \({\bf{q}}\) parallel to \(\Gamma K\) ranging from \({\bf{q}}=0.1\) Å (close to the optical limit) to \({\bf{q}}=1.33\) Å (equal to the distance of \(\Gamma\) and \(K\)).36 The experimental spectra exhibit increasing intensity above the gap energy \(E\approx 1.5-2\) eV, becoming stronger at higher energies. Especially in these high energy regions the agreement with theory is excellent. From the point of view of the optical properties the energy region around \(E=2.5\) eV is particularly important, because there the C-exciton is observed in the absorption spectra. The C-exciton originates from a band nesting region near \(\Gamma\) giving rise to a multitude of excitonic states.37,38,39 The effects of band nesting and the interband transitions at higher energies are captured by Eq. (1), but not the many-body interactions, which are expected to increase when the thickness is reduced towards the monolayer due to reduced screening. In order to test the reliability of the single particle description for thin layers we compare thickness dependent EELS data in the C-exciton region reproduced from Ref. 24 with our model. Figure 3b shows a spectra measured near a thinner part of the sample (red, 5 layer) compared to a thicker part (blue, 10 layer). A two-peak structure is observed with thickness dependent relative intensity, separation and energy position, which has been explained by a mirror resonance in Ref. 24 The intensity of the high energy component increases for the thicker layer and the energy separation increases. The model spectra on the right-hand side of Fig. 3b nicely reproduce these effects. There, the thickness dependence is represented by the comparison of a monolayer (red) and the bulk (blue) for simplicity. Also, a high-energy cutoff has been applied to Eq. (1), which suppresses higher lying transitions for clarity. Figure 3 illustrates that the single particle model describes the higher energy region including the C-exciton of the EEL spectra reasonably well. Clear deviations occur closer to the gap. In particular, two sharp peaks are observed for \({\bf{q}}=0.1\) Å at \(E\approx 2\) eV which we assign to the prominent A and B-excitons, corresponding to direct transitions at the \(K\)-points of the Brillouin zone. They are absent in the theoretical spectrum as expected from the noninteracting particle approximation. Previously, we evaluated the A and B-exciton masses from their dispersion in the \({\bf{q}}\)-dependent EELS data for MoS2 and WSe235,40 and studied dark excitonic transitions with finite momentum.36

Fig. 3
figure 3

Electron energy loss spectroscopy. a Electron energy loss spectra of bulk MoS2 with momentum transfer \({\bf{q}}\) parallel to \(\Gamma K\).36 Black curves are experimental data, red curves correspond to the single particle model developed by Eqs. (1), (2). The theoretical curves have been shifted to higher energy by \(\Delta E=0.1\) eV for better comparison. b Electron energy loss spectra in the optical limit in the energy region of the C-exciton. Left panel: Data reproduced from Ref. 24 for a 5 layer (red) and 10 layer (blue) sample. Right panel: Model calculation for monolayer (red) and bulk (blue) for \({\boldsymbol{q}}=0\)

Full size image

Although the absorption coefficients of indirect transitions are much lower than of direct transitions, they are crucial for many optical properties. For instance, it has been shown that the emission efficiency of bright transitions depends sensitively on the energy separation from nearby dark excitons.20,21,41,42 This is because excitons are subject to fast thermalization in the TMDCs,43 hence the population of bright excitonic states is rapidly depleted by energetically lower lying dark states, which suppresses the photoluminescence yield by orders of magnitude.7

Model description

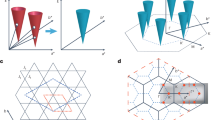
In Fig. 4, we investigate the \({\bf{q}}\)-dependent exciton landscape in more detail. Figure 4a presents a gray scale representation of the low-energy region of the EELS bulk measurements along \(\Gamma M\) and \(\Gamma K\) normalized at \(E=5\) eV. The A- and B-excitons are seen close to \({\bf{q}}=0\) dispersing to higher energy for increasing \({\bf{q}}\). The dispersion follows approximately a parabola, which appears to be rather isotropic along \(\Gamma M\) and \(\Gamma K\).40 In addition, other parabola-shaped structures centered at finite \({\bf{q}}\), that is, dark excitons, are identified, that superimpose each other, e.g., at the \(K\) point. \({\bf{q}}=\overline{\Gamma K}\) corresponds to transitions where an electron is excited from the \(\Gamma\) point to a \(K\) valley, or from a \(K\) point to a neighboring \(K^{\prime}\) valley. The experimental data are again compared to the single particle model in Fig. 4b. Here, we concentrate on the low energy region and include only the two lowest valence/conduction bands into the sum in Eq. (1). In order to facilitate better comparison to the EELS data, the \(q\) dependent term in Eq. (2) has been skipped, which renders the loss function equivalent to \(-{\rm{Im}}{\chi }_{0}({\bf{q}},\omega )\). Note that \({\chi }_{0}({\bf{q}},\omega )\) is proportional to the dielectric function itself within the random phase approximation. Figure 4 and what follows is, therefore, not restricted to the specific case of EELS, but describes the optical properties in general. Although the excitons itself are not captured by this model, there is an apparent similarity with the experimental results. In particular, the dispersion parabola of the central A/B-excitons can be clearly recognized as well as the parabolas at the \(K\) point and in between \(\Gamma M\) and even some of the overlapping features at higher energies. The main difference is the missing red dashed parabola centered at \(\Lambda\), which matches the transition from \(\Gamma\) to the overall conduction band minimum at \(\Lambda\) and forms the lowest lying dark exciton for bulk MoS2. Its absence in the experimental spectra is probably due to weak transition probabilities. However, we consider the general agreement between Fig. 4a vs b significant. The conclusion from this agreement is that the exciton dispersion follows largely joint band edge dispersions and the excitons acquire large intensity enhancements due to many-body interactions.

Fig. 4
figure 4

Exciton landscape. a \({\bf{q}}\) dependent EELS data of bulk MoS2 in grayscale representation. b,d Low energy region of the \({\bf{q}}\)- dependent model susceptibility representing the dielectric function along \(\Gamma K\) and \(\Gamma M\) for bulk b, bilayer c and monolayer d

Full size image

Figure 4c, d present the model calculations for mono- and bilayer. The exciton landscape of the bilayer shows similarities with the bulk. The direct transition at \({\bf{q}}=0\) shifts closer to the lowest states and the indirect excitons centered at \(\Lambda\) (\({\bf{q}}=\overline{\Gamma \Lambda }\)) and \(K\) (\({\bf{q}}=\overline{\Gamma K}\)) are almost degenerate. Qualitative differences occur for the monolayer. Here, the overall minimum is located at \({\bf{q}}=0\), i.e., the materials becomes a direct band gap semiconductor. In addition to the dark excitons at \(K\) and \(\Lambda\) another transition is found at \(M\) with \({\bf{q}}\) connecting \(K\) points and \(\Lambda\) valleys.

Figure 5a presents the low-energy onset of the susceptibility (i.e., \(-{\rm{Im}}{\chi }_{0}({\bf{q}},\omega )\)) calculated as in Fig. 4 for mono-, bilayer and bulk as two-dimensional gray scale images as \({q}_{x}-{q}_{y}\) maps. In each case there are four distinct local minima: at \(\Gamma\) (\({\bf{q}}=0\)) which corresponds to the direct, optically bright transition, and the indirect, dark transitions at \(K\), \(M\) and \(\Lambda\). The exciton centered at \(K\) arises from transitions between \(K\) and \(K^{\prime}\) and \(\Gamma\) and \(K/K^{\prime}\). The \(M\) point exciton is due to transitions from \(K\) to \(\Lambda\), and the \(\Lambda\) excitons are due to the transition from \(\Gamma\) to the \(\Lambda\) point, which is halfway between \(\Gamma\) and \(K\) (see Fig. 1). It is not only the order of the energy locations of the excitons that changes with thickness but also their intensity (see Fig. 5b). Here we show \(-{\rm{Im}}{\chi }_{0}({\bf{q}},\omega )\) at fixed energies corresponding to the direct gap values (\(E\approx 1.7\) eV), i.e., on resonance, as a function of \({\bf{q}}\). For the monolayer the overall exciton minima at \(\Gamma\) and the indirect transition at \(K\) are energetically very close to each other, which gives sharp maxima in intensity for each of these points. For the bilayer, the dark \(\Lambda\) and \(K\) excitons are situated at lower energies than the bright direct transition at \(\Gamma\). Hence, the cut at the direct gap results in large intensity contours centered at \(\Lambda\) and \(K\).

Fig. 5
figure 5

Low energy maps. a Maps of the low energy onset of the dielectric function. Local minima correspond to band edge excitons. b Constant energy cuts of \(-{\rm{Im}}{\chi }_{0}({\bf{q}},\omega )\) at the energy of the direct transitions

Full size image

The susceptibility governs many material properties. The susceptibility defined in Eq. (1) can be considered as a \({\bf{q}}\) dependent joint density of states. Therefore, it is a measure of the available electronic phase space for scattering events of any kind. In particular, inelastic light scattering, i.e., Raman spectroscopy, depends on the susceptibility via the Raman tensor, which is a derivative of it. Inelastic light scattering is closely related to EELS, which can be considered as inelastic electron scattering. In first order, Raman scattering is restricted to \({\bf{q}}=0\) since the photon itself has negligible momentum. However, higher order Raman scattering may involve the full Brillouin zone when the momentum is provided by phonons. An example is defect assisted Raman scattering, where the electronic transition is accompanied by the emission of a phonon of momentum \({\bf{q}}\). Momentum conservation is ensured by defect scattering providing a phonon with momentum \(-{\bf{q}}\). From the sharp intensity maximum at the \(K\) point in Fig. 5b for the monolayer one would conjecture a dominating propensity for scattering events involving \(K\) point phonons under resonance conditions. This is consistent with the mode assignment in Ref. 44 where the most intense defect induced Raman peak is associated with an acoustic zone edge phonon at \(K\). Similar arguments apply for the double resonant Raman scattering, where two phonons of opposite momenta are created during the light scattering process. The relative intensity of two-phonon modes related to \(K\) and \(M\) as a function of thickness is reflected by the intensity evolution of the susceptibility maps in Fig. 5b on a qualitative level. Quantitative treatment of the resonant Raman process requires the consideration of the intermediate states and the phonon density of states.44 Nevertheless, higher order Raman scattering is an example of a \({\bf{q}}\)-dependent process entering optical properties and an established tool for the investigation of the interplay of phonons, photons and excitons at finite momentum.45,46,47,48 It is also at the origin of excitonic upconversion, where the outgoing photon has larger energy than the incoming one due to an anti-Stokes process in the intermediate state, thereby cooling the sample. This has been demonstrated for WSe2.49 Scattering process involving zone boundary phonons are also believed to be responsible for the notorious valley depolarization, which represents a serious obstacle for valleytronics.50,51,52

After we have confirmed that our approach based on DFT derived bandstructure and the model dielectric function defined in Eq. (2) adequately describes key elements of the photoemission and the EELS data in the energy region of the A and B-excitons we focus now on the momentum dependence of the C-exciton. The single particle description is expected to work even better here because the C-exciton is due to nesting around the \(\Gamma\) point, which becomes enhanced by many-body effects, however, the key ingredient (nesting) is a property of the underlying bandstructure and as such well captured by Eq. (1). Figure 6 presents the \({\bf{q}}\)-dependent susceptibility as a function of energy and thickness. Figure 6a–c is equivalent to Fig. 4b–d, but plotted on a larger energy range and set to a common susceptibility scale. Several important properties can be identified by visual inspection: (i) the main intensity is concentrated around \({\bf{q}}=0\) for each layer number. The intensity at \({\bf{q}}=0\), i.e., propensity to vertical nesting, increases towards the monolayer. (ii) The C-exciton is well localized in \(({\bf{q}},\omega )\)-space. Its dispersion has a parabola-like shape. The bandwidth decreases for decreasing thickness. Hence, the effective mass increases. We performed a fit to a parabola (see SFig. 3 of the Supplemental Material) and summarize the effective masses of the C-exciton thus obtained in Table 1. They appear to be rather isotropic with a slight enhancement in \(\Gamma M\) direction. A value of \({m}_{{\rm{eff}}}^{{\rm{bulk}}}=0.25{m}_{0}\) has been reported in Ref. 53 based on modeling of the thickness dependent energy shift of the C-exciton, which is in approximate agreement with Table 1 lending further confidence to the method. The increase of the effective mass with decreasing thickness is qualitatively consistent with the simultaneous increase of the exciton binding energy towards the monolayer, since in the hydrogen model \({E}_{B}\propto {m}_{{\rm{eff}}}\). On the same level of sophistication, one may argue that the size of the C-exciton exceeds the size of the A/B-excitons: \({m}_{{\rm{eff}}}\) of the A/B-excitons \(({m}_{{\rm{eff}}}^{A}=1.12{m}_{0})\) is larger than of the C-exciton40 and the size can be approximated by the Bohr radius \({a}_{B}\). In the hydrogen model holds: \({a}_{B}\propto 1/{m}_{{\rm{eff}}}\). Therefore \({a}_{B}^{C}\ >\ {a}_{B}^{A/B}\), which is in agreement with previous conclusions.48,54 Note, however, the non-hydrogen like character of the 2D-TMDC excitons and the strong influence of screening. iii) The energy location of the C-exciton increases as the monolayer is approached in agreement with optical data and reflecting the increasing optical gap.55,56

Fig. 6
figure 6

C-exciton. a–c Energy distribution of the model dielectric function along high symmetry directions in the region of the C-exciton. Green rectangle in a highlights a local intensity maximum in \(({\bf{q}}, \omega)\)-space. d, e Energy distribution curves from (a–c) at certain high symmetry points for monolayer and bulk. g–i Constant energy maps at the position of the C-exciton

Full size image
Table 1 C-exciton effective masses in units of \({m}_{0}\)
Full size table

Apart from the central C-exciton other well defined \(({\bf{q}},\omega )\) regions with enhanced intensity can be recognized, e.g., the region near the \(K\) point highlighted by a green dashed rectangle in Fig. 6a. Figure 6d–f show intensity curves at the \(\Gamma\) point, at \(\Gamma K/2\) and at \(K\) of the monolayer and the bulk (bilayer has been skipped for clarity). At \(\Gamma\) a pronounced sharpening of \({\chi }_{0}(\omega )\) is observed and an increase of the maximum intensity of the monolayer with respect to the bulk. At \(\Gamma K/2\) no such enhancement is seen. Rather, the monolayer shifts slightly to higher energies but the shape remains the same. At \(K\), on the other hand, the situation is similar to the \(\Gamma\) point, albeit with weaker intensity enhancement. This effect can be monitored for the full momentum space by considering \({q}_{x}-{q}_{y}\) maps. Figure 6g–i plot constant energy surfaces of \(-{\rm{Im}}{\chi }_{0}({\bf{q}},\omega)\) at the energy of the C-exciton of the corresponding thickness. These susceptibility maps show some similarities to the equivalent maps of the low-energy region (Fig. 5b): The maximum intensity is always located at the center. However, for the mono-, and bilayer additional weaker maxima are found around \(K\) and \(M\). These local maxima at finite \({\bf{q}}\) represent preferential scattering channels at the given energy. In analogy to the low-energy region we refer to them as nested dark excitons. Their thickness-dependent intensity enhancement best seen in Fig. 6d–f is purely a property of the bandstructure. Many-body interactions probably enhance their spectral weight and renormalize their energy similar to the C-exciton itself.37,38,53,57

Discussion

In the following we discuss the possible physical relevance of nested dark excitons.

Phonon scattering

Our arguments surrounding Fig. 6 rely on the \({\bf{q}}\)-dependent electronic susceptibility. Incidentally, the acoustic phonon density of states peaks at the same \({\bf{k}}\) locations as the susceptibility, namely near \(K\) and \(M\). This corroborative behavior may enhance the scattering efficiency towards these dark states and act beyond simple phonon broadening.

Higher order optical processes

Higher order optical processes involving phonon scattering could inherit a dependence on the \(({\bf{q}},\omega )\) distribution and intensity of nested dark excitons. An example is resonant Raman scattering where such processes are well known for the lower energy transitions at the A/B-exciton thresholds as discussed above.44 The susceptibility is a decisive quantity for inelastic scattering events.

Light harvesting

Some TMDCs show large optical absorption in the visible range.15 Even the absorption of monolayers is anomalously large and exceeds traditional solar cell materials by far.8 The origin of this effect is the large joint density of states underlying the C-exciton. A beneficial aspect of the electronic structure in terms of light harvesting applications is the opposite momentum gradient of excited electron and holes, respectively in that energy region, which is a direct consequence of the nesting. The opposite momentum gradient drives electrons and holes away from each other in \({\bf{k}}\)-space by intraband scattering, suppressing unwanted optical recombination. However, the latter is also efficiently excluded by large \({\bf{q}}\) transfer to the electron or hole. Hence, the charge carrier recombination and relaxation could be influenced by the presence of effective scattering channels due to nested dark excitons.

Contrary to the situation for the low-energy band-edge region, where only certain \({\bf{q}}\) connect a small number of indirect excitons, the available indirect states for scattering of the C-exciton form a continuum. However, the C-exciton itself is part of this continuum and still has great impact on the optical properties of TMDCs. Hence, we believe that the occurrence of similar objects at finite \({\bf{q}}\) might have observable consequences as well, especially if they are further enhanced by many-body interactions. The latter should be the subject of future theoretical effort.

Finally, we would like to comment on the relationship of the bandstructure effects underlying the model used throughout this paper Eqs. (1), (2) and many-body interactions. The agreement between many aspects of the experimental data and the model description (Figs 3, 4; Table 1) emphasizes the general importance of the bandstructure for the exciton dispersion and spectral shape. However, their exact energy is renormalized by many-body interactions (i.e., exciton binding energy) and their intensity is enhanced (see Fig. 3). In particular, the intensity of the C-exciton depends on the degree of nesting within our model, but is expected to be amplified by many-body interactions.

In summary, the combination of one-particle and two-particle spectroscopic experiments and modeling of the dielectric function on a single-particle/RPA level gives a simplified yet powerful insight in the optical properties of TMDC. In particular, the energy region where strong nesting occurs, relevant for the C-exciton, is described well and spans a more complex exciton landscape than previously anticipated. Its local maxima in \(({\bf{q}}\ \ne \ 0,\omega )\) space can be considered as dark excitons and might be relevant for higher order optical processes. Therefore, the investigation of nested dark excitons could lead to a more complete understanding of optical properties of TMDCs and calls for a \({\bf{q}}\)-dependent treatment of many-body interactions.

Methods

Samples

Natural single crystals of 2H–MoS2 have been purchased from Manchester Nanomaterials. Few-layer MoS2 flakes down to monolayers are isolated by mechanical exfoliation of the bulk crystal. In order to do so, the crystal is placed between two poly-dimethyl siloxane (PDMS) sheets. The thickness of the produced flakes is checked with an optical microscope in transmission mode with a magnification up to ×500. The MoS2 flakes are transferred to a silicon substrate with an oxide thickness of 90 nm. The substrate is coated with a thin gold layer to avoid charging effects during photoemission measurement. The optical contrast is sufficient to distinguish single layer differences. AFM measurements were carried out, using a Bruker Dimension Icon microscope in tapping mode.

Spectroscopy

Photoemission spectroscopy measurements were accomplished with a NanoESCA system (Omicron) equipped with a helium lamp with an energy of 21.21 eV (He I) and an energy resolution \(\le\) 0.2 eV at room temperature. A deconvolution scheme has been implemented in order to enhance the visibility of weak features. In particular, the data are deconvolved along the energy axis in order to minimize the broadening effects of finite energy resolution. In a first step, the Fourier transform is calculated from the intensity I(E). Generally, the effect of finite energy resolution amounts to the convolution of the unperturbed signal by a Gaussian function of certain width. To remove this effect the Fourier transform of I(E) is divided by a transformed Gaussian and the result is converted back by an inverse Fourier transformation. The electron energy-loss measurements were done in a 172 keV transmission spectrometer equipped with a helium flow cryostat (see Ref. 34 for a description of the spectrometer). The energy and momentum resolution of the instrument were set to \(\Delta E=82\) meV and \(\Delta q=0.04\) Å\({}^{-1}\), respectively, and the sample temperature to 20 K. The Raman scattering were collected on a Horiba confocal Raman spectrometer with a 458 nm laser line and a ×50 objective at room temperature. The laser spot size is about 2 \(\mu\)m.

Model implementation

\(\delta\) is always set to 0.05 eV. The number of bands considered in the sum of Eq. (1) depends on the purpose: In Fig. 3a, where the high energy features are compared to experiment, all the valence and conduction bands in an energy window of 5 eV are considered. In Fig. 3b four conduction/valence bands are included to reproduce the high energy features in comparison to the TEM-EELS data. In Figs 4–6, where the excitons are investigated, only the two lowest valence and conduction bands are taken into account. In general, the susceptibility converges to a spectral shape such as shown in Fig. 3a where the complete band structure has been used. However, the excitons are mostly determined by the lowest bands and it improves clarity and reduces numerical effort when the higher lying bands are skipped in this case.

Density functional theory

The band structure calculations were performed using the full-potential local-orbitals method (FPLO)58 and the Perdew-Wang 92 exchange-correlation-functional.59 For 1- and 2-layer MoS2, we constructed super-cells with about 20 nm of vacuum between layers and sampled the Brillouin zone with a (24 \(\times\) 24 \(\times\) 1) point mesh. For bulk MoS2, a (12 \(\times\) 12 \(\times\) 12) point mesh was used. To find the optimized lattice parameters, the total energy of bulk MoS2 was minimized resulting in \(a=3.152\ \mathring{\rm{A}}\) and \(c=12.48\ \mathring{\rm{A}}\) in good agreement with the experimental values (\(a=3.16\ \mathring{\rm{A}}\) and \(c=12.294\ \mathring{\rm{A}}\)60). The lattice constants determined by this way were used for the 1- and 2-layer calculations as well. All calculations were performed in fully relativistic mode to account for the sizable spin–orbit splitting. The calculations have been performed for freestanding flakes, i.e., no interaction with the substrate is taken into account. The latter approximation of weak substrate–flake interaction is justified a posteriori.

Data availibility

Data available on request from the authors.