Abstract
The ReX2 system (X = S, Se) exhibits unique properties that differ from other transition metal dichalcogenides. Remarkably, its reduced crystal symmetry results in a complex electronic band structure that confers this material in-plane anisotropic properties. In addition, multilayered ReX2 presents a strong 2D character even in its bulk form. To fully understand the interlayer interaction in this system, it is necessary to obtain an accurate picture of the electronic band structure. Here, we present an experimental and theoretical study of the electronic band structure of ReS2 and ReSe2 at high-hydrostatic pressures. The experiments are performed by photoreflectance spectroscopy and are analyzed in terms of ab initio calculations within the density functional theory. Experimental pressure coefficients for the two most dominant excitonic transitions are obtained and compared with those predicted by the calculations. We assign the transitions to the Z k-point of the Brillouin zone and other k-points located away from high-symmetry points. The origin of the pressure coefficients of the measured direct transitions is discussed in terms of orbital analysis of the electronic structure and van der Waals interlayer interaction. The anisotropic optical properties are studied at high pressure by means of polarization-resolved photoreflectance measurements.
Similar content being viewed by others
Introduction
The ReX2 crystals (X = S, Se) are semiconductors from the family of two-dimensional layered transition metal dichalcogenides (TMDCs) that exhibit special properties. Rhenium-based TMDCs have received increasing interest during the last few years owing to their large in-plane anisotropic properties. These properties result from their particular band structure and reduced crystal symmetry, as well as a strong 2D character that has been attributed to weak van der Waals interlayer bonding even in their bulk form.1,2 Besides the large fundamental interest, ReX2 has also shown to be a highly interesting technological material for many potential applications, including photodetectors,3,4,5,6,7,8 solar cells,9 photonics,10 flexible electronics,11 and field-effect transistors.12,13,14,15,16 Remarkably, the small interlayer coupling of ReX2 opens an exciting field of new possibilities, as it may allow to design bulk devices that retain 2D functionalities only present in single-layered materials.17 To fully exploit the applications of ReX2 for developing novel optoelectronic devices, it is crucial to further characterize its fundamental properties.
Optical modulation spectroscopy is a very powerful method to study the optical properties of semiconductors. Owing to its differential-like character, interband-related features are highly enhanced and background signal is suppressed, thus allowing to accurately measure direct optical transitions.18 So far, different modulation spectroscopies have shown to be very useful for studying the optical transitions of ReX2: piezoreflectance,19 electrolyte electroreflectance,20 thermoreflectance,21 and polarization-dependent measurements22,23,24 revealed two and three excitonic transitions for ReS2 and ReSe2, respectively. These works provided evidence that these excitons, which exhibit a strongly polarized dipole character, were confined within single layers.
However, the extent to which ReX2 behaves as stacked decoupled layers has recently been a topic of intense debate.2,22,23,25,26,27 On the one hand, direct photoreflectance (PR) measurements on the electronic dispersion found that ReX2 indeed exhibits a significant degree of electronic coupling.22 This result is also supported by angle-resolved photoemission experiments (ARPES), which showed that there exists a significant electronic dispersion along the van der Waals gap.25,26 Also, recent calculations show that the fundamental bandgap shrinks by 32.7% in ReX2 from monolayer to bulk, and the interlayer binding energy is similar to other TMDCs such as MoS2.28
On the other hand, optical, vibrational, and structural measurements indicate that ReX2 exhibits a strong 2D character. For instance, photoluminescence experiments revealed that the emission energy of ReS2 is almost independent to the number of layers (∆E ≈ −50 meV from one monolayer to bulk) in contrast with other G6-TMDCs (e.g., ∆E ≈ −600 meV for MoS2).2 For the case of ReSe2, it was shown that it retains a direct bandgap regardless of its crystal thickness, with excitons strongly confined within single layers for bulk crystals, indicating a weak interlayer interaction.23 Moreover, the Raman spectrum of monolayer ReS2 is almost identical to that of bulk, which evidences an ultraweak interlayer coupling.27 Also, low-frequency Raman measurements showed that interlayer force constant in ReX2 is significantly smaller than other G6-TMDCs (by a factor of ≈40%).29 One of the most direct ways to probe interlayer interaction is to modulate the interlayer distance from high-pressure (HP) measurements. In this regard, HP X-ray diffraction measurements show that the bulk modulus of ReX2 (23–31 GPa)30,31 is significantly lower than group 6 TMDCs (57–72 GPa).32,33,34,35 HP Raman measurements on ReS2 showed a twofold decreased pressure coefficient of the out-of-plane A1g phonon mode with respect to other TMDCs,2 reinforcing the decoupled behavior in bulk ReS2.2 Also, the large pressure metallization of ReS2 (70 GPa) in comparison with MoS2 (19 GPa) has been attributed to the larger interlayer coupling in MoS2.36 In spite of the fundamental properties of this crystal system being relatively well-known at ambient pressure, HP optical measurements are highly desirable to evaluate the degree of electronic interlayer coupling in ReX2.
HP optical measurements are widely employed to obtain detailed structural and band structure information of semiconductors.37 Moreover, HP optical measurements provide a highly useful benchmark to test first-principles calculations (such as those based on density functional theory) on challenging systems such as TMDCs. For the case of ReX2, which exhibits weak interlayer forces at ambient pressure, HP optical measurements would shed new light into the role of orbital composition and van der Waals bonding on the excitonic energies and their pressure dependence. To date, the amount of HP optical studies on ReX2 is scarce. The pressure dependence of the bandgap has only been experimentally investigated for ReS2 by means of photoluminescence and absorption.2,36 These works found that the bandgap of ReS2 does not increase with pressure and an almost-direct-to-indirect bandgap transition takes place around 27 kbar. At higher pressures, calculations suggest that ReS2 exhibits a metallization and superconducting state.38
Despite the previous investigations, there are still many questions that remain to be addressed with regard to the HP optical properties of ReX2. First, an experimental assignment of the different excitonic transitions around the bandgap is desirable. So far, piezoreflectance measurements on the ReSe2−xSx alloy suggested that the nature of the direct band edges is similar for each compositional end member,39 but electronic dispersion calculations together with ARPES measurements suggested that the first direct electronic transitions take place either at the Z high-symmetry point of the Brillouin zone (BZ) or away from the zone center, far from any particular high-symmetry direction.25,26,28,40,41 Second, while the orbital composition of the states of ReS2 has been described for different numbers of layers,28 the interplay of orbital composition on the pressure dependence on the electronic band structure has not yet been investigated. Finally, the anisotropic properties of ReX2 at high pressure remain to be explored.
To address these questions, we conduct PR measurements at high-hydrostatic pressure on thin ReS2 and ReSe2 exfoliated flakes. Polarization-dependent measurements performed at different pressures are used to energetically resolve the different excitonic transitions that exhibit very similar energies. Our results show that the two main direct transitions for ReS2 and ReSe2 exhibit a negative-pressure coefficient, in contrast to other TMDCs, such as MoS2, MoSe2, WS2, or WSe2.42 Such findings provide valuable information to assess the degree of electronic interlayer coupling and the role of orbital composition on the energies of the band edge states. We discuss the experimental results in light of ab initio band structure calculations. These calculations are performed using different functionals and considering different hydrostatic pressures. We find good agreement between the experimental and calculated pressure coefficients for the two main transitions. The experimentally observed transitions are assigned by inspecting the calculated electronic dispersion curves along a large grid of k-points in the whole 3D-BZ. Finally, we discuss the negative sign of the measured pressure coefficients in terms of orbital contributions to the states of the valence and conduction band of each transition and van der Waals interaction.
Results
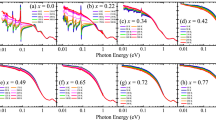
We conducted PR measurements in order to determine the pressure dependence of the first two direct optical transitions in ReX2. To ensure the reproducibility of the experimental results, samples obtained from different sources and grown in different conditions are used for the experiments. The PR spectra obtained for ReS2 and ReSe2 at different pressure values are shown in Fig. 1. Two main features can be observed for all samples, which correspond to the direct excitonic transitions A and B. These excitonic transitions have been previously reported at ambient pressure from modulated spectroscopies for ReS219,21 and ReSe2.43
Photoreflectance spectra obtained at different pressures for ReS2 (sample I and II) and ReSe2 (sample III and IV). Straight lines around the fitted transition energies are shown as a guide to the eye for transitions A and B. Both features decrease in energy with increasing pressure for all studied samples. Fittings are shown as dotted gray curves
The strongest transition (i.e., B for ReS2 and A for ReSe2) is clearly visible at all pressures. The weakest transition merges at high (low) pressure for ReS2 (ReSe2) as a consequence of different pressure coefficients between the A and B transitions. It is worth noting that weaker, energetically close transitions have been previously reported from low-temperature and polarization measurements for ReS220 and ReSe2.23,24 We are able to resolve these transitions from polarization-dependent measurements at different pressures (shown in the Supplementary Information, S.I.). Our polarization measurements allow us to conclude that the relative amplitude and angular dependence for each transition are preserved at the studied pressure range (i.e., up to 20 kbar). Hence, the sample orientation and structural stability are maintained throughout the studied pressure range.
The energy of each transition was obtained from the PR spectra by fitting the Aspnes formula,44 given by
where n, C, and θ are the number of transitions, amplitude, and phase of the resonance, Ej and Γ are the energy and broadening parameter of the transition, respectively. For excitonic transitions we take m = 2. Two transitions are enough to successfully reproduce all the spectra shown in Fig. 1 (dotted curves). Note that the differences in line shape between different samples of the same compound are accounted for by different phase values of the resonance, defined by different built-in electric fields and differences in chopper settings. However, the fitted energy values of the transitions are not affected by these differences. For the fitting procedure, we left all parameters unfixed for the spectrum obtained at ambient pressure, while only the amplitude and the energy of the transition were left as free parameters for spectra at higher pressures, since these are expected to change with pressure. The pressure dependence of the energy of each transition is plotted in Fig. 2 for both samples.
The energy of the fitted transitions in the photoreflectance experiments is plotted as a function of pressure for ReS2 (up) and ReSe2 (bottom). The fitted energies of transitions A and B are shown in red and blue colors, respectively. Linear fits have been performed for both transitions and fitted values are included in the figure
As can be seen in Fig. 2, the energy of the transition A (red symbols) decreases with increasing pressure at a different rate than the energy of the transition B (blue symbols). Note that the fitted energies of the transition B between different samples of the same material are scattered to a certain degree. This can be attributed to two factors: i) sample misorientations and ii) uncertainties in the fitting procedure that naturally arise for weak PR features energetically close (≈60 meV) to a strong PR transition with a relatively strong broadening parameter (typically ≈20 meV). Despite uncertainties in the fitted energies of transition B, the pressure coefficient of different samples of the same material was consistent. For ReS2, the fitted pressure coefficient of the B transition, −4.2 meV/kbar, is much larger than that of the A transition, −2.3 meV/kbar. The latter value is in agreement with previous HP photoluminescence (PL) measurements, which yielded a pressure coefficient of −2.0 meV/kbar.36 In contrast, for ReSe2, the pressure coefficient of the A transition, −3.5 meV/kbar, is more pronounced than that of the B transition, −1.3 meV/kbar. The latter result is qualitatively in agreement with the reported absorption measurements, which show a redshift of the absorption edge with increasing pressure.2 The fact that the pressure coefficient of the A transitions is much larger for ReSe2 and smaller for ReS2 (with respect to the B transition), evidences that the origin of the transitions is different for each material, as discussed in the next section.
First-principles calculations were carried out in order to assign the experimentally observed transitions and to provide further insight into the electronic and optical properties of ReX2. The electronic band structure and the optical matrix element were calculated for a k-path intersecting the first BZ in a three-dimensional manner. Figure 3 shows the electronic dispersion curves for 0 kbar (black curves) and 20 kbar (red curves), as obtained from density functional theory (DFT) calculations within the meta-generalized gradient approximation (GGA) strongly constrained and appropriately normed (SCAN) functional.45 The normalized values of the optical matrix element as well as the bandgap value along the k-path are also shown. The first and second direct transitions for ReS2 (ReSe2) are at Z (J1) and K1 (Z) points, respectively. Note that the matrix element maxima correspond with the bandgap minima, which indicate that these transitions are optically active. The calculated quasi-direct gaps for ReS2 and ReSe2 are 1.2 and 1.15 eV, respectively. These values are smaller than the measured optical gaps, around 1.5 and 1.31 eV, respectively. The discrepancies between calculations and experiments are accounted for by the systematic bandgap underestimation of the meta-GGA functional (SCAN) used. This functional neither accounts for independent particle effects nor for excitonic effects.46 To better reproduce the experimental values, we performed calculations at a higher level of theory using the hybrid functional HSE06.47 At this level of theory, our calculations are able to predict the bandgap energies more accurately, around 1.42 and 1.43 eV (including the excitonic binding energy) for ReS2 and ReSe2, respectively. More detail on the HSE06 calculations can be found in the S.I.
Electronic dispersion curves for ReS2 (left) and ReSe2 (right) as calculated using the SCAN functional at zero pressure (black curves) and 20 kbar (red curves). The corresponding matrix elements have been calculated for each k-point, the stronger transitions are located around Z and K1 for ReS2 and around Z and J1 points for ReSe2. In the lower panels, the direct bandgap energy is plotted along the studied wave vectors
Owing to the complex band structure of ReX2, which exhibits very close direct and indirect bandgaps in energy and position in the k-space,25,28 some computational considerations should be taken into account. For instance, a number of theoretical works predict the valence band maximum (VBM) of bulk ReS2 to be either at Γ2,36,48 or at Z.49 This may result from choosing only a few high-symmetry paths for the calculation of the band structure, or choosing functionals that fail to capture the details of the complex electronic structure of ReX2. Hence, in order to accurately describe the band structure of complex materials like ReX2, it is important to consider the whole 3D-BZ, and to devote careful attention to the choice of the functional. Recent contributions show that the choice of the functional influences the number and location of VBM and conduction band minimum (CBM) in ReX2.25,41,49 The results of the meta-GGA SCAN functional employed here seem to reproduce the experimental results well and with low-computational cost.
The location of the fundamental direct gap of ReS2, predicted by our calculations to be at Z, is in agreement with recent direct measurements of the band dispersion using ARPES25,40,41 and a recent theoretical study employing quasiparticle approximations.28 For the case of ReSe2, our high-density k-mesh calculations predict an indirect fundamental bandgap of 1.10 eV, with both the VBM and the CBM located away from high-symmetry points (named J2 and J3, respectively, coordinates shown in Table S1 of the S.I.). This is in agreement with recent studies, which also found an indirect bandgap with the VBM close to the J2 point.26,49 Several other studies that take only high-symmetry k-paths into account for evaluating the band structure predict either direct or indirect bandgaps for ReSe2 near the Z or Γ point.23,28,38,50,51 It has also been suggested that the indirect and the direct bandgap are close in energy, and the discussion about the nature of the fundamental bandgap for ReSe2 is still ongoing.49,50,51,52 At higher pressure, an overall narrowing of the bandgap takes place along the whole BZ with increasing pressure, as previously evidenced in theoretical studies.38,53 This trend can be seen in the lowest panel of Fig. 3 and results in an enhancement of the indirect nature of the fundamental gap for both ReS2 and ReSe2 at HP.
To assign the A and B transitions, we compare the experimental and calculated pressure dependence of the first two direct transitions. This is shown in Fig. 4, where the pressure dependence of the variation of energy is plotted for both, calculated bandgaps (crosses) and measured excitonic transitions (full symbols). The figure plots the variation of energy rather than absolute values. This allows to directly compare theoretical calculations with experimental results, neglecting energetic differences arising from the DFT bandgap underestimation and excitonic binding energy. As can be seen in the figure, our calculations predict distinct pressure coefficients for each transition, which is also observed experimentally. The calculated pressure coefficients of ReS2 (−1 and −3.4 meV/kbar−1) and ReSe2 (−4.2 and −0.7 meV/kbar−1) slightly differ from the measured values. We attribute the differences to the effect of structural distortion at high pressure on the position of the maximum of the matrix elements in the reciprocal space. Taking this into account, the differences between calculated and experimental pressure coefficients agree within the experimental and calculated errors (which are lower than ±0.3 and ±1.2 meV/kbar, respectively). Most importantly, the qualitative trend is reproduced in our calculations, namely a negative-pressure coefficient of distinct magnitude for both transitions. After comparing the pressure coefficients (see Fig. 4), transitions A (red symbols) and B (blue symbols) are unambiguously assigned to the Z (J1) and K1 (Z) k-point for ReS2 (ReSe2), respectively. The calculated pressure coefficients within the SCAN functional can be reproduced by HSE06 calculations (differences in the pressure coefficients are below ±0.5 meV/kbar, as shown in Tables S3 and S4 in the S.I.), which further supports the provided assignation.
Increment of exciton energy versus pressure plotted for the transitions A (red color) and B (blue color) from measurements on ReS2 (top) and ReSe2 (bottom), as well as the calculated values of the transport bandgap using the SCAN functional (crosses). The straight lines are linear fits to the experimental values. Pressure coefficients of each transition are included
The current assignation of the transition A at the J1 k-point for ReSe2 is in contrast with previous assumptions that all the excitonic transitions took place around the Z point of the BZ.23 This result should be taken into account for future work on the compositional dependence of the bandgap of the ReSe2−xSx alloy, since J1 is away from either Z or K1 (coordinates are shown in Table S1 of the S.I.). Previous absorption54 and piezoreflectance39 measurements along the entire composition range found evidence that the nature of the bandgaps is similar for the ReSe2−xSx compositional end members. However, while we found that both direct excitonic transitions are similar in energy (the transition energy in J1 is only ≈40 meV below that at Z), they belong to different k-points between different compositional end members. Hence, it is expected that the compositional dependence of the lowest direct transition (i.e., transition A) exhibits a crossover from the J1 for ReSe2 to Z for ReS2.
Discussion
Owing to its different crystallographic structure, the optoelectronic properties of ReX2 are drastically different from those of group 6 TMDCs. Remarkably, the pressure coefficient of the first direct optical transition is negative, in contrast to other TMDCs. Figure 5 shows the pressure coefficient of the first direct optical transition for MX2 TMDCs (M = Mo, W, and Re and X = S and Se), as measured by HP PR spectroscopy elsewhere,42 together with the present experimental results for ReX2. While MoX2 and WX2 exhibit positive-pressure coefficients, this is not the case for ReX2, which exhibits negative-pressure coefficients. As a general trend, a closing of the bandgap with increasing pressure (i.e., negative-pressure coefficient) is expected for all TMDCs, since all TMDCs metallize at HP (metallization takes place around 350 kbar for ReX2). Still, while their indirect bandgaps decrease with pressure, all group 6 TMDCs exhibit a positive-pressure coefficient of the direct gaps.53,55 Such striking difference is accounted for by the particular crystallographic structure of ReX2, and the particular electronic configuration of Re: with respect to group 6 transition metals, rhenium compounds possess one more valence electron, and the valence and conduction band states are importantly characterized by the Re-d orbitals. To investigate the physical origin of the negative direct pressure coefficient, and its connection with the reduced van der Waals interaction in ReX2, we performed an orbital analysis of the states associated with the A and B transitions.
Histogram showing the pressure coefficient of the first direct optical transitions of MoX2 and WX2 published elsewhere42 and ReX2 (X = S and Se), as obtained from high-pressure photoreflectance measurements
The orbital composition of the states of the A and B direct transitions is shown in Table 1 for ReS2 and ReSe2. The CBM and VBM of ReS2 are dominated by Re-\({\it{d}}_{{\it{z}}^2}\) orbitals, in agreement with recent calculations,25 while for ReSe2, the orbital contributions are more diverse. In the table, Re-\({\it{d}}_{{\it{z}}^2}\) and X-pz orbital contributions, which importantly contribute to the band edge states25 and show out-of-plane character,40,52 are highlighted since these are expected to be highly sensitive to the interlayer interaction. The z-axis denotes the out-of-plane direction, so that z orbitals are located at least partially within the van der Waals gap. With increasing pressure, states with large contributions from Re-\({\it{d}}_{{\it{z}}^2}\) and X-pz orbitals destabilize, and therefore rise in energy with increasing pressure. Such destabilization has been attributed to Coulomb repulsion of antibonding p orbitals between interlayer chalcogen atoms for MoS2.56,57,58 Similarly, \({\it{d}}_{{\it{z}}^2}\) orbitals are fairly delocalized and directed perpendicular to the layers. The role of orbital contribution to the bandgap dependence on interlayer distance is well studied for other TMDCs, and is the state-of-the-art explanation for the direct-to-indirect bandgap crossover of MoS2 at its transition from monolayer to bulk.56,59 Quantitatively, increasing pressure has a similar effect on the electronic structure as increasing the number of layers, i.e., pressure results in a stronger interaction of electrons along the van der Waals gap and a reduction of interlayer distance. In fact, the pressure and strain dependence of the bandgap of MoX2 has been explained in terms of orbital contributions to the bandgap states.60,61 Hence, larger contributions of the Re-\({\it{d}}_{{\it{z}}^2}\) and X-pz orbitals in the VBM with respect to the CBM would result in a narrowing of the bandgap with increasing pressure, which is the case for ReX2 as discussed in detail below.
The orbital interplay on the bandgap reduction of ReX2 with increasing pressure/strain has been previously hinted11,36, but never evaluated from orbital analysis. For the case of ReS2, the highest contribution to the analyzed states arises from Re-\({\it{d}}_{{\it{z}}^2}\). In Table 1, it can be seen that larger contributions of the pz orbital take place in the VBM with respect to the CBM. Hence, at higher pressures, the VBM experiences a stronger destabilization than the CBM, resulting in a narrowing of the bandgap, as observed experimentally. Furthermore, the transition at K1 (i.e., transition B) exhibits a significantly higher contribution from the S-pz states, which accounts for its more negative pressure coefficient with respect to the transition at Z (i.e., transition A), as observed experimentally (see Fig. 4). Similarly, for the case of ReSe2, the contributions from the Se-pz and Re-\({\it{d}}_{{\it{z}}^2}\) orbitals to the VBM are large, which implies a large redshift of the transition at J1 (i.e., transition A) with increasing pressure, in agreement with the experimentally observed large negative pressure coefficients for the transition A (see Fig. 4). In contrast, the transition at Z (i.e., transition B) shows only moderate contributions of Se-pz in the VBM. To account for the negative pressure coefficient of transition B, we suggest that the Re-dyz orbitals might play a significant role. In conclusion, the bandgap narrowing with increasing pressure on the transitions A and B of ReX2 is mainly accounted for by an increased contribution of X-pz orbitals in the VBM.
So far, it has been shown that the negative-pressure coefficients observed for the direct transitions in ReX2 can be qualitatively explained from orbital theory. However, the value of the pressure coefficient could be influenced by the reduced van der Waals interactions present in ReX2 with respect to other TMDCs. To elucidate whether ReX2 exhibits a decreased van der Waals interaction with respect to MoS2, we compare the effect of orbital interplay on the pressure coefficient between both compounds. For MoS2, a negative pressure coefficient of the indirect bandgap has been predicted to be in the range −3.79 to −7.9 meV/kbar.42 Such a low-pressure coefficient is a consequence of a strong blueshift of the VBM at Γ, where the orbital contributions from \({\it{d}}_{{\it{z}}^2}\) and pz orbitals are strong, i.e., 60% Mo-\({\it{d}}_{{\it{z}}^2}\) + 30% S-pz.56 However, the contribution of the \({\it{d}}_{{\it{z}}^2}\) and pz to the CBM (at K) is in the same order of magnitude, i.e., 86% Mo-\({\it{d}}_{{\it{z}}^2}\) + 9% S-pxy + 5% S-pz. Since the direct pressure coefficients of ReS2 and ReSe2 (i.e., −4.2 meV/kbar and −3.5 meV/kbar) are similar to the indirect pressure coefficient in MoS2, we conclude that the decreased van der Waals interactions in ReX2 (as evidenced by HP XRD30,31 and low-frequency Raman measurements29) do not play a significant role in its pressure coefficient.
To summarize, we performed HP PR measurements on ReS2 and ReSe2 samples obtained from different sources and grown on different conditions. Our results reveal that two main excitonic transitions decrease in energy with increasing pressure for each material. For the case of ReS2, the obtained pressure coefficients for the A and B transitions are −2.3 and −4.2 meV/kbar, respectively, and for ReSe2, −3.5 and −1.3 meV/kbar, respectively. Polarization-resolved measurements allowed to measure a third transition for ReS2, as well as determining the crystal orientation and assessing the structural stability up to 20 kbar in ReX2.
The electronic band structure of ReS2 and ReSe2 was calculated from ab initio calculations within the density functional theory, using the meta-GGA SCAN functional. We probed the whole BZ in order to explore all the possible direct transitions around the bandgap. The calculations were performed at different pressure values, which allowed the comparison of the experimental and theoretical results and assignment of each transition. For ReS2, the transitions A and B were assigned to Z and K1 k-points of the BZ, whereas for ReSe2, the A and B transitions were assigned to the J1 and Z points, respectively (with both K1 and J1 located away from the high-symmetry k-points). The negative pressure coefficients measured in ReX2 were explained in terms of orbital analysis. This allowed us to conclude that the destabilization of the pz orbital with increasing pressure is mostly responsible for the measured pressure coefficients. This work evidences that ReX2 does not exhibit a strong electronic decoupling and hence the optoelectronic properties of few-layered ReX2 could be drastically different from the bulk form.
Methods
Experimental details
Two samples of different origins were used for each set of ReS2 and ReSe2 materials. One sample for each material was commercially obtained from HQgraphene, which consisted of thin flakes mechanically exfoliated from synthetic bulk crystals (99.995% purity). These are here labeled as samples I and III for ReS2 and ReSe2, respectively. The ReS2 (sample II) and ReSe2 (sample IV) samples were synthesized by the chemical vapor transport growth technique using Re (99.9999% purity), S, or Se (99.9999% purity) pieces. These precursors were mixed at atomic stoichiometric ratios and sealed into 0.5-in. diameter and 9-in.-long quartz tubes at 10−6 Torr. Extra ReI3 was added as a transport agent to initiate the crystal growth and successfully transport Re, S, and Se atomic species. Closely following Re–S–Se binary-phase diagrams, we have synthesized crystals with temperature variation (drop) of 50 °C over 5 weeks to complete the growth. Samples were cooled down to room temperature and ampoules were opened in a chemical glove box. The use of two samples grown under different conditions for each material allows to further validate the reproducibility of the here-presented experimental results.
To perform the HP hydrostatic measurements, the samples were mounted inside a UNIPRESS piston cylinder cell. The chosen pressure hydrostatic medium was Daphne 7474, which remained hydrostatic and transparent during the whole measurement, up to pressures of 18 kbar. The pressure was determined by measuring the resistivity of an InSb probe, which provides a 0.1-kbar sensitivity. A sapphire window in the press allowed optical access to perform PR measurements. For the PR measurements, a single grating of 0.55-m focal length and a Si pin diode were used to disperse and detect the light reflected from the samples. A chopped (270 Hz) 405-nm laser line was pumped into the sample, together with a probe tungsten lamp (power of 150 W). Phase-sensitivity detection of the PR signal was processed with a lock-in amplifier. Further details on the experimental setup can be found elsewhere.62 All measurements were performed at ambient temperature and pressures up to ≈18 kbar. At this pressure range, no phase transition was observed and only the Td crystal structure was investigated.
Computational details
Ab initio calculations on the the DFT level were carried out using the Vienna Ab initio Simulation Package (VASP),63,64 with the projector-augmented wave65 potentials as implemented by Kresse and Joubert.66 The SCAN45 semilocal exchange-correlation functional was employed. SCAN belongs to the meta-general-gradient-approximation (meta-GGA) functionals and has shown to produce more accurate results than conventional GGA functionals at a very comparable computational cost.45,46,67 In particular, SCAN is recommended for electronic structure prediction of materials with heterogeneous bond types67 (e.g., covalent and van der Waals) as well as layered materials.46 It is therefore well suited for the band structure prediction of ReX2. In addition, a revised Vydrov–van Voorhis (rVV10) long-range van der Waals interaction68,69,70 was used.
Structure information of ReS2 and ReSe2 was taken from Murray et al.71 and Alcock and Kjekshus,72 respectively. Structure relaxation was undertaken with a Monkhorst–Pack73 k-mesh of 5 × 5 × 5 with the above-mentioned basis set and functionals. Seven electrons were considered for the valence of Re (5d5 6s2). The cutoff energy for the plane-wave expansion was set to 323.4 and 282.8 eV for ReS2 and ReSe2, respectively, which is 25% above the recommended values in the pseudopotential files. Relevant properties (pressure coefficient, bandgaps, and band character) were carefully checked for convergence with the kinetic energy cutoff as it can be seen in Figures S12–S17 of the S.I. Structures were relaxed until the total energy change and the band structure energy change dropped below 10−7 eV, and the residual atomic forces were less than 0.02 eV/Å in their absolute value. Crystallographic information files with atomic structures at 0 and 20 kbar, as used in the calculations, can be accessed through the Cambridge crystallographic data center (CCDC deposition numbers 1862132–1862135).
For calculations of the band structure and optical properties, spin–orbit interaction was taken into account. The cutoff energy was set to normal accuracy, which is 258.7 eV for ReS2 and 226.2 eV for ReSe2. High-density gamma-centered k-mesh calculations (34 × 34 × 34) were performed to investigate possible VBM and CBM located off the symmetry points.
Data availability
All data derived from the experiments and calculations of this study are available from the corresponding author upon reasonable request.
References
Jariwala, B. et al. Synthesis and characterization of ReS2 and ReSe2 layered chalcogenide single crystals. Chem. Mater. 28, 3352–3359 (2016).
Tongay, S. et al. Monolayer behaviour in bulk ReS2 due to electronic and vibrational decoupling. Nat. Commun. 5, 3252 (2014).
Zhang, E. et al. ReS2-based field-effect transistors and photodetectors. Adv. Funct. Mater. 25, 4076–4082 (2015).
Qin, J.-K. et al. Photoresponse enhancement in monolayer ReS2 phototransistor decorated with CdSe–CdS–ZnS quantum dots. ACS Appl. Mater. Interfaces 9, 39456–39463 (2017).
Yang, S. et al. High-performance few-layer Mo-doped ReSe2 nanosheet photodetectors. Sci. Rep. 4, 5442 (2014).
Liu, E. et al. High responsivity phototransistors based on few‐layer ReS2 for weak signal detection. Adv. Funct. Mater. 26, 1938–1944 (2016).
Zhang, E. et al. Tunable ambipolar polarization-sensitive photodetectors based on high-anisotropy ReSe2 nanosheets. ACS Nano 10, 8067–8077 (2016).
Najmzadeh, M., Ko, C., Wu, K., Tongay, S. & Wu, J. Multilayer ReS2 lateral p–n homojunction for photoemission and photodetection. Appl. Phys. Express 9, 055201 (2016).
Cho, A.-J., Namgung, S. D., Kim, H. & Kwon, J.-Y. Electric and photovoltaic characteristics of a multi-layer ReS2/ReSe2 heterostructure. APL Mater. 5, 076101 (2017).
Wu, K. et al. Domain architectures and grain boundaries in chemical vapor deposited highly anisotropic ReS2 monolayer films. Nano Lett. 16, 5888–5894 (2016).
Yang, S. et al. Tuning the optical, magnetic, and electrical properties of ReSe2 by nanoscale strain engineering. Nano Lett. 15, 1660–1666 (2015).
Liu, E. et al. Integrated digital inverters based on two-dimensional anisotropic ReS2 field-effect transistors. Nat. Commun. 6, 6991 (2015).
Corbet, C. M., Sonde, S. S., Tutuc, E. & Banerjee, S. K. Improved contact resistance in ReSe2 thin film field-effect transistors. Appl. Phys. Lett. 108, 162104 (2016).
Corbet, C. M. et al. Field effect transistors with current saturation and voltage gain in ultrathin ReS2. ACS Nano 9, 363–370 (2015).
Mohammed, O. B. et al. ReS2-based interlayer tunnel field effect transistor. J. Appl. Phys. 122, 245701 (2017).
Yang, S. et al. Layer-dependent electrical and optoelectronic responses of ReSe2 nanosheet transistors. Nanoscale 6, 7226–7231 (2014).
Hafeez, M., Gan, L., Bhatti, A. S. & Zhai, T. Rhenium dichalcogenides (ReX2, X = S or Se): an emerging class of TMDs family. Mater. Chem. Front. 1, 1917–1932 (2017).
Kudrawiec, R. & Misiewicz, J. Optical modulation spectroscopy. Semicond. Res. 95, 95–124 (2012).
Ho, C. H., Liao, P. C., Huang, Y. S. & Tiong, K. K. Temperature dependence of energies and broadening parameters of the band-edge excitons of ReS2 and ReSe2. Phys. Rev. B 55, 15608–15613 (1997).
Ho, C. H., Huang, Y. S., Chen, J. L., Dann, T. E. & Tiong, K. K. Electronic structure of ReS2 and ReSe2 from first-principles calculations, photoelectron spectroscopy, and electrolyte electroreflectance. Phys. Rev. B 60, 15766–15771 (1999).
Ho, C. H., Lee, H. W. & Wu, C. C. Polarization sensitive behaviour of the band-edge transitions in ReS2 and ReSe2 layered semiconductors. J. Phys. 16, 5937 (2004).
Aslan, O. B., Chenet, D. A., van der Zande, A. M., Hone, J. C. & Heinz, T. F. Linearly polarized excitons in single- and few-layer ReS2 crystals. ACS Photonics 3, 96–101 (2016).
Arora, A. et al. Highly anisotropic in-plane excitons in atomically thin and bulklike 1T′-ReSe2. Nano Lett. 17, 3202–3207 (2017).
Jian, Y.-C., Lin, D.-Y., Wu, J.-S. & Huang, Y.-S. Optical and electrical properties of Au- and Ag-doped ReSe2. Jpn. J. Appl. Phys. 52, 04CH06 (2013).
Biswas, D. et al. Narrow-band anisotropic electronic structure of ReS2. Phys. Rev. B 96, 085205 (2017).
Hart, L. S. et al. Electronic bandstructure and van der Waals coupling of ReSe 2 revealed by high-resolution angle-resolved photoemission spectroscopy. Sci. Rep. 7, 5145 (2017).
Feng, Y. et al. Raman vibrational spectra of bulk to monolayer Re2 with lower symmetry. Phys. Rev. B 92, 054110 (2015).
Echeverry, J. P. & Gerber, I. C. Theoretical investigations of the anisotropic optical properties of distorted 1T ReS2 and ReSe2 monolayers, bilayers, and in the bulk limit. Phys. Rev. B 97, 075123 (2018).
Lorchat, E., Froehlicher, G. & Berciaud, S. Splitting of interlayer shear modes and photon energy dependent anisotropic raman response in N-Layer ReSe2 and ReS2. ACS Nano 10, 2752–2760 (2016).
Hou, D. et al. High pressure X-ray diffraction study of ReS2. J. Phys. Chem. Solids 71, 1571–1575 (2010).
Kao, Y.-C. et al. Anomalous structural phase transition properties in ReSe2 and Au-doped ReSe2. J. Chem. Phys. 137, 024509 (2012).
Wang, X. et al. Pressure-induced iso-structural phase transition and metallization in WSe2. Sci. Rep. 7, 46694 (2017).
Nayak, A. P. et al. Pressure-induced semiconducting to metallic transition in multilayered molybdenum disulphide. Nat. Commun. 5, 3731 (2014).
Zhao, Z. et al. Pressure induced metallization with absence of structural transition in layered molybdenum diselenide. Nat. Commun. 6, 7312 (2015).
Bandaru, N. et al. Structural stability of WS2 under high pressure. Int. J. Mod. Phys. B 28, 1450168 (2014).
Yan, Y. et al. Associated lattice and electronic structural evolutions in compressed multilayer ReS2. J. Phys. Chem. Lett. 8, 3648–3655 (2017).
Suski, T. & Paul, W. High pressure in semiconductor physics I and II. Semiconductors and Semimetals. Vols. 54 and 55, (Academic Press, 1998).
Zhou, D. et al. Pressure-induced metallization and superconducting phase in ReS 2. npj Quant. Mater. 2, 19 (2017).
Ho, C. H., Huang, Y. S., Liao, P. C. & Tiong, K. K. Piezoreflectance study of band-edge excitons of ReS2−xSex single crystals. Phys. Rev. B 58, 12575–12578 (1998).
Webb, J. L. et al. Electronic band structure of ReS2 by high-resolution angle-resolved photoemission spectroscopy. Phys. Rev. B 96, 115205 (2017).
Eickholt, P. et al. Location of the valence band maximum in the band structure of anisotropic 1T ReSe2. Phys. Rev. B 97, 165130 (2018).
Dybała, F. et al. Pressure coefficients for direct optical transitions in MoS2, MoSe2, WS2, and WSe2 crystals and semiconductor to metal transitions. Sci. Rep. 6, 26663 (2016).
Hu, S. Y. et al. Growth and characterization of tungsten and molybdenum-doped ReSe2 single crystals. J. Alloy. Compd. 383, 63–68 (2004).
Aspnes, D. E. Third-derivative modulation spectroscopy with low-field electroreflectance. Surf. Sci. 37, 418–442 (1973).
Sun, J., Ruzsinszky, A. & Perdew, J. P. Strongly constrained and appropriately normed semilocal density functional. Phys. Rev. Lett. 115, 036402 (2015).
Buda, I. G. et al. Characterization of thin film materials using SCAN meta-GGA, an accurate nonempirical density functional. Sci. Rep. 7, 44766 (2017).
Krukau, A. V., Vydrov, O. A., Izmaylov, A. F. & Scuseria, G. E. Influence of the exchange screening parameter on the performance of screened hybrid functionals. J. Chem. Phys. 125, 224106 (2006).
Gehlmann, M. et al. Direct observation of the band gap transition in atomically thin ReS2. Nano Lett. 17, 5187–5192 (2017).
Gunasekera, S. M., Wolverson, D., Hart, L. S. & Mucha-Kruczynski, M. Electronic band structure of rhenium dichalcogenides. J. Elec Mater. 47, 4314–4320 (2018).
Wolverson, D., Crampin, S., Kazemi, A. S., Ilie, A. & Bending, S. J. Raman spectra of monolayer, few-layer, and bulk ReSe2: an anisotropic layered semiconductor. ACS Nano 8, 11154–11164 (2014).
Zhao, H. et al. Interlayer interactions in anisotropic atomically thin rhenium diselenide. Nano Res. 8, 3651–3661 (2015).
Hart, L. S. et al. Electronic bandstructure and van der Waals coupling of ReSe2 revealed by high-resolution angle-resolved photoemission spectroscopy. Sci. Rep. 7, 5145 (2017).
Zhuang, Y. et al. Deviatoric stresses promoted metallization in rhenium disulfide. J. Phys. D 51, 165101 (2018).
Ho, C. H., Huang, Y. S., Liao, P. C. & Tiong, K. K. Crystal structure and band-edge transitions of ReS2-xSex layered compounds. J. Phys. Chem. Solids 60, 1797–1804 (1999).
Naumov, P. G. et al. Pressure-induced metallization in layered ReSe 2. J. Phys. 30, 035401 (2018).
Samadi, M. et al. Group 6 transition metal dichalcogenide nanomaterials: synthesis, applications and future perspectives. Nanoscale Horiz. 3, 90–204 (2018).
Li, T. & Galli, G. Electronic properties of MoS2 nanoparticles. J. Phys. Chem. C 111, 16192–16196 (2007).
Sorkin, V., Pan, H., Shi, H., Quek, S. Y. & Zhang, Y. W. Nanoscale transition metal dichalcogenides: structures, properties, and applications. Crit. Rev. Solid State Mater. Sci. 39, 319–367 (2014).
Jin, W. et al. Direct measurement of the thickness-dependent electronic band structure of MoS2 using angle-resolved photoemission spectroscopy. Phys. Rev. Lett. 111, 106801 (2013).
Johari, P. & Shenoy, V. B. Tuning the electronic properties of semiconducting transition metal dichalcogenides by applying mechanical strains. ACS Nano 6, 5449–5456 (2012).
Fan, X., Chang, C.-H., Zheng, W. T., Kuo, J.-L. & Singh, D. J. The electronic properties of single-layer and multilayer MoS2 under high pressure. J. Phys. Chem. C 119, 10189–10196 (2015).
Kudrawiec, R. & Misiewicz, J. Photoreflectance spectroscopy of semiconductor structures at hydrostatic pressure: a comparison of GaInAs/GaAs and GaInNAs/GaAs single quantum wells. Appl. Surf. Sci. 253, 80–84 (2006).
Kresse, G. & Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186 (1996).
Kresse, G. & Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 6, 15–50 (1996).
Blöchl, P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953–17979 (1994).
Kresse, G. & Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758–1775 (1999).
Sun, J. et al. Accurate first-principles structures and energies of diversely bonded systems from an efficient density functional. Nat. Chem. 8, 831–836 (2016).
Vydrov, O. A. & Van Voorhis, T. Nonlocal van der Waals density functional: the simpler the better. J. Chem. Phys. 133, 244103 (2010).
Sabatini, R., Gorni, T. & de Gironcoli, S. Nonlocal van der Waals density functional made simple and efficient. Phys. Rev. B 87, 041108 (2013).
Peng, H., Yang, Z.-H., Perdew, J. P. & Sun, J. Versatile van der Waals density functional based on a meta-generalized gradient approximation. Phys. Rev. X 6, 041005 (2016).
Murray, H. H., Kelty, S. P., Chianelli, R. R. & Day, C. S. Structure of rhenium disulfide. Inorg. Chem. 33, 4418–4420 (1994).
Alcock, N. W. et al. The crystal structure of ReSe2. Acta Chem. Scand. 19, 79–94 (1965).
Monkhorst, H. J. & Pack, J. D. Special points for Brillouin-zone integrations. Phys. Rev. B 13, 5188–5192 (1976).
Acknowledgements
This work was supported by the National Science Centre (NCN) Poland OPUS 11 no. 2016/21/B/ST3/00482. R.O. acknowledges the support by POLONEZ 3 no. 2016/23/P/ST3/04278. This project is carried out under POLONEZ program, which has received funding from the European Union’s Horizon 2020 research and innovation program under the Marie Sklodowska-Curie grant agreement No. 665778. F.D. acknowledges the support from NCN under Fuga 3 grant no. 2014/12/S/ST3/00313. We thank Xavier Rocquefelte for discussions regarding the structure of transition metal dichalcogenides. M.L. and O.R. would like to acknowledge the funding provided by the Natural Sciences and Engineering Research Council of Canada under the Discovery Grant Program RGPIN-2015-04518. The computations were performed using Compute Canada (Calcul Quebec and Compute Ontario) resources, including the infrastructure funded by the Canada Foundation for Innovation. Finally, S.T. acknowledges funding provided by National Science Foundation DMR-1552220 and DMR-1838443.
Author information
Authors and Affiliations
Contributions
R.O. wrote the paper, took part in PR measurements, and analyzed PR data, M.L. carried out first-principles calculations and contributed to the drafting of the discussion, F.D. and J.K. performed the high-pressure PR experiments, Y.Q. and S.T. grew the samples, O.R. planned and supervised the calculations, and R.K. planned the research and coordinated it. All authors discussed the results and commented on the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Oliva, R., Laurien, M., Dybala, F. et al. Pressure dependence of direct optical transitions in ReS2 and ReSe2. npj 2D Mater Appl 3, 20 (2019). https://doi.org/10.1038/s41699-019-0102-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41699-019-0102-x
This article is cited by
-
Direct visualization of out-of-equilibrium structural transformations in atomically thin chalcogenides
npj 2D Materials and Applications (2020)