Abstract
In recent years, two-dimensional materials have risen as an attractive platform for integrated optoelectronics, due to their atomic scale thickness, favorable electrical, mechanical, and optical properties. In particular, graphene has been exploited as an ultrafast light modulator and photodetector, operating at telecommunication wavelengths. However, materials with larger bandgaps are required for light detection in the visible range of the spectrum, with wide applications in space communication, industrial quality controls, light sensing, etc. Even though TMDC-based light emitting and detecting devices in the visible spectrum have already been realized, efficient light absorption and photocurrent generation on integrated devices has not been achieved yet. Here, we demonstrate the integration of an ultrasensitive MoS2 photodetector with a silicon nitride photonic circuit. In contrast to the limited vertical light absorption, we observe near-unity lateral absorption, which results in even higher responsivity. By fabricating an alternative device where the MoS2 semiconducting channel is combined with a hexagonal boron nitride (h-BN) substrate, we significantly improve the speed of the photodetector. Low power operation is further achieved in a third device with graphene local gates. These results pave the way for future TMDC-based integrated optoelectronic devices.
Similar content being viewed by others
Introduction
One of the main challenges for today’s information networks is to reduce power consumption while increasing speed of data transfer. In conventional networks, electrical signal is processed, transferred, and read by metallic interconnects, where dense packing and speed of data processing are limited by Joule heating1 and parasitic capacitance, respectively. Silicon photonics, on the contrary, holds promise for increasing speed and power efficiency of these networks.2,3 However, challenges in the design of integrated light emitting devices and photodetectors have prevented the realization of practical circuits.4,5
Miniaturization of integrated devices for light modulation on silicon photonic platforms has brought attention to atomically thin two-dimensional (2D) materials,6 which can be easily fabricated on photonic structures, due to their outstanding mechanical and structural properties.7,8
Graphene has been extensively studied for data processing9 and light detection.10 However, this material suffers from high off currents9, as well as limited light absorption and responsivity due to the absence of a band gap.11 The remarkable electrical12 and optoelectronic13,14 properties of 2D transition-metal dichalcogenides (TMDCs), including the presence of a direct band gap in the visible light range,15,16 make them ideal candidates for this purpose. Besides realization of basic logic electrical devices,12 2D semiconductors were demonstrated to be a promising material for light emission17 and detection,18 with potential for the realization of optical to electrical interconnects.19,20 Such interconnects would be expected to operate over meter-scale distances or less, relaxing the wavelength requirements from those set by the optical fiber transmission windows. Large-scale growth by chemical vapor deposition has also been demonstrated,21 which together with simplicity of device fabrication makes MoS2 a good candidate for the fabrication of future optoelectronic devices. While MoS2-based high responsivity photodetectors have already been reported,18 their implementation in photonic circuits is still lacking. Here, we bridge this gap by demonstrating integration of MoS2 photodetectors with Si3N4 photonic circuits, with three different device architectures to achieve either high photoresponse, fast operation speed, or low operation voltages.
Results and Discussion
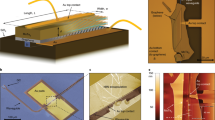
Figure 1a shows a cross section of the fabricated device, where MoS2 is directly exfoliated on top of Si3N4, in order to couple the flake with the evanescent field of the mode traveling inside the high-index contrast waveguide (WG). The waveguide is designed so that only the first fundamental quasi-transverse electric (TE) and quasi-transverse magnetic (TM) modes propagate at a wavelength of 647 nm, while higher order modes are radiative. Calculated electric field profile for the fundamental TE mode based on Finite-Difference Time-Domain (FDTD) simulations is plotted in Fig. 1b. The evanescent field extends through a large area over the waveguide, which allows optical excitation of the attached monolayer. Figure 1c presents the operation of the fabricated photodetector. Incident laser light at 647 nm is focused on the diffraction grating coupler (GC), which redirects light for propagation through the waveguide. Light is linearly polarized perpendicularly to the propagation direction, which leads to excitation of the TE mode in the waveguide, which is known for a stronger absorption by the MoS2 film than the TM mode.22 Part of the light is then absorbed and converted into an electrical signal in the biased MoS2 flake. An optical image of the fabricated device is shown in Fig. 1d (See the Methods section and Supplementary Section 1 for more details on device fabrication). Inset corresponds to a photoluminescence (PL) image of monolayer MoS2 transferred onto the waveguide. Enhanced PL emission in the region above the waveguide indicates efficient coupling of the flake with the photonic circuit (Supplementary Fig. S3).
MoS2-based photodetector integrated in a photonic circuit. a Cross-sectional schematics of the photodetector, with monolayer MoS2 directly exfoliated on top of the waveguide. b Calculated TE field magnitude |E| for the Si3N4 waveguide. Evanescent field overlaps with the transferred MoS2 flake. c Schematics of light coupling by focusing a 647 nm CW laser on the diffraction grating. Light propagates through the Si3N4 waveguide (WG) and generates electron-hole (e-h) pairs in MoS2, which leads to photocurrent generation in the biased MoS2 monolayer. d Optical image of the fabricated MoS2 photodetector integrated in the photonic structure. MoS2 channel is highlighted in violet. The diffraction grating coupler (GC) used for light coupling, waveguide (WG) source and drain are also indicated. Scale bar is 20 µm. Insets show a photoluminescence image of monolayer MoS2 after transfer and scanning electron microscopy (SEM) image of the WG with GC. Scale bar is 10 µm for both insets
Limited absorption of normally incident light in 2D materials due to their atomic-scale thickness23 can be overcome by lateral excitation via the waveguide. In order to demonstrate this experimentally, we measure the lateral absorption of MoS2 as a function of the flake length. (See Methods). Figure 2a shows how lateral absorption overcomes the vertical one (taken from ref. 16) and approaches unity. From an exponential fit of transmission (T = e−L/α), the absorption coefficient is found to be α = 7.7 ± 1.1 μm. It is clear that lateral absorption can be fine-tuned by modifying the length of the flake, which could be defined by an extra etching step after transfer.
Effect of monolayer MoS2 and metal contacts on light propagation in the waveguide. a Comparison between MoS2 lateral (experimental data points) and vertical absorption (taken from ref. 16) as a function of the flake length. Error bars represent the standard deviation of the measurements. b Calculated relative transmission for TE (red) and TM (blue) modes after deposition of 65 µm long metal contacts at a distance d from the waveguide. Inset shows the calculated losses per micrometer in log scale
For the optoelectronic characterization of the waveguide-integrated photodetector, the amount of light incident on the device needs to be quantified. While optical losses due to scattering in the waveguide surface and coupling to the surrounding Si3N4 layer can be neglected (Supplementary Fig. S4), interaction of light with the evaporated metal contacts can alter its propagation. In order to maximize the photocurrent in the fabricated photodetector, contacts should be as close as possible to the waveguide so as to reduce the device resistance. However, this can modify light propagation if the evanescent field couples to the metallic contacts, leading to optical losses in the waveguide. To find the minimum distance between source and drain for which TE and TM mode profiles are not altered, we perform FDTD simulations for different positions of contacts with respect to the waveguide. Relative transmission for both TE and TM modes after deposition of 10 nm Ti, 60 nm Au is shown in Fig. 2b. The inset presents propagation losses on a logarithmic scale. Long contacts (L = 65 µm) are chosen in order to maximize the channel length after the transfer of large MoS2 monolayers onto the waveguide. For edge-to-edge distances larger than 600 nm, the influence of metal contacts on light propagation is negligible. Therefore, we design contacts with 700 nm separation to exclude the effect of light coupling to the metal.
Optoelectronic measurements are performed in vacuum (10−6 mbar) at room temperature, under continuous-wave (cw) laser illumination at a wavelength λ = 647 nm, unless stated otherwise. The three main mechanisms for photocurrent generation in MoS2 are photogating, photoconductive, and photothermoelectric effects.24,25 In our case, photogating is dominant, leading to a slow photocurrent ~80 times higher than the fast photocurrent associated with the photoconductive effect25 (see Supplementary Section 4). Photothermoelectric current can be neglected, since no appreciable current is measured at zero bias under light illumination (Supplementary Fig. S7).
Figure 3a shows the schematics of the device band alignment in three different conditions: dark (1), vertical illumination (2), and lateral illumination via the waveguide (3), leading to the corresponding Ids−Vg curves in Fig. 3b. In the dark, current follows the characteristic behavior of an MoS2 transistor,12 with a threshold voltage Vth = −11 V and an on/off ratio above 105, limited by the noise level of the measurement setup. When focusing the laser light onto the flake, electron-hole (e-h) pairs are generated across the channel. The device stays in the on-state for the entire range of back-gate voltages, with trapped holes shifting the Fermi level, effectively gating the flake. Since the lifetime of trapped holes is much larger than that of the electrons, many carriers can flow for each generated e-h pair, resulting in a large photogain. The ratio of photocurrents under vertical illumination and in dark reaches values as high as Iflake/Idark > 6·103 at Vg = −12 V and is again limited by the noise level. When the flake is excited through the waveguide by focusing the laser on the grating coupler, creation of e-h pairs occurs only in the overlapping region between the waveguide and the flake, creating a potential profile for electrons which allows turning off the photocurrent. The off-state for lateral illumination is found at a new threshold voltage Vg = −37.5 V.
Optoelectronic properties of the device at room temperature. a Schematics of band alignment for device under applied bias in different conditions: dark (1), vertical (2) and lateral illumination (3). b Drain-source current (Ids) dependence on the applied back gate voltage (Vg) for the three regimes represented in a obtained at bias voltage Vds = 1 V and laser power Plaser = 25 nW. c Modulation of the photoresponse with back-gate voltage for lateral and vertical illumination at Vds = 1 V and Plaser = 25 nW. Responsivity is normalized by its value at zero gate voltage. d Measured photoresponsivity R as a function of incident power Pin at Vg = 0 V and Vds = 1 V. e Responsivity dependence on the excitation wavelength, normalized by its value at 647 nm (wavelength used for measurements shown in b, c, and photoluminescence spectra from MoS2 on Si3N4
From the Ids−Vg curves, we can further derive the external responsivity of the photodetector, defined as the ratio between the generated photocurrent Iph = Ilight − Idark and optical power Pin incident to the flake. Figure 3c shows the dependence of the photoresponse on the gate voltage for a fixed laser power of 25 nW. Due to the characteristic band alignment, in the case of lateral coupling the gate modulation of photoresponsivity is three orders of magnitude larger compared to vertical illumination, with responsivity dropping to zero for back-gate voltages below the threshold voltage. Dependence of responsivity on incident optical power at Vg = 0 V is shown in Fig. 3d. The responsivity for the waveguide is calculated by taking into account that the grating coupler efficiency is 3.4% at 647 nm wavelength (see Supplementary Section 6), so that Pin ~ 0.034 × Plaser. For low incident power we obtain an extremely high photoresponse above 1000 A/W, which is the result of higher lateral absorption compared to vertical illumination. Flake responsivity depends strongly on the excitation wavelength, as shown in Fig. 3e, and can be further enhanced by increasing the energy of incident photons. Photoresponse for wavelengths below the optical bandgap vanishes, as photons cannot be absorbed by the 2D material. It should be noted that photoresponse depends directly on the conductivity of the channel, and therefore slightly varies with time since MoS2 is known to experience Fermi level shifts on substrates such as SiO2 and S3N4 upon thermal, light or current annealing.26
The realization of chip-integrated devices with TMDCs requires precise alignment of light sources, such as optical fibers or lasers, on the material. However, relaxed alignment conditions can be achieved with the usage of grating couplers. Figure 4 presents photocurrent maps for vertical illumination on MoS2 and the grating coupler when a DC bias is applied to MoS2. For the latter, the map represents the spatial distribution of the coupling efficiency since it shows the photocurrent generated in the MoS2 when the light from the laser is focused onto the diffraction grating, then coupled to the waveguide and finally absorbed in the MoS2 layer (Supplementary Section 5). For the diffraction grating, significant photoresponse (>1/2 Imax) can be obtained over a larger area compared to the flake. In addition, response is homogeneous around the grating lines, which indicates that alignment could be greatly facilitated by simply increasing the diffraction grating area. The flake photocurrent map reveals an active channel length L ~14 μm, which corresponds to a lateral absorption of 84%, according to measurements presented in Fig. 2a. This leads to an external quantum efficiency for photons traveling in the waveguide ηext = 0.84. Photogain can then be calculated as \(G = R \times h\upsilon /q\eta _{{\mathrm{ext}}} > \ 2300\), for low incident powers, where hυ is incident photon energy and q is the elementary charge.
Normalized photocurrent maps for the case of direct vertical excitation on the flake (a) and excitation through the grating coupler (b) at Vds = 2 V, Vg = 0 V and laser power of 1 µW and 110 µW, respectively. Laser light is modulated using the chopper with a frequency of 30 Hz. The value of alternating current (AC) at the modulation frequency of light is obtained by a lock-in amplifier. Scale bar is 5 µm. Dashed lines denote the contacts in a and the outline of the grating coupler in b
The main limitation of MoS2-based photodetectors is the low speed of operation, which in our case is restricted by the photocurrent rise and decay times \(\tau _{{\mathrm{rise}}} \ > \ 13\,{\mathrm{s}}\) and \(\tau _{{\mathrm{decay}}} \ > \ 11\,{\mathrm{s}}\), respectively (Supplementary Fig. S6a). These slow response times are associated with the photogating mechanism which manifests itself as a change in the threshold voltage due to charge transfer to adjacent molecules, in particular when transferred onto SiO225 or Si3N4, as in our case. On the contrary, fast response is related to photoconductive and photoelectric effects.25 In order to avoid photogating and realize a device with a fast response, an alternative device is fabricated, where a multilayer h-BN flake with a thickness of ∼11 nm is first transferred on top of the waveguide, which serves as the van der Waals (vdW) substrate for MoS2 (Supplementary Fig. S8). We expect similar response time for vertical and lateral illumination via the waveguide, since the response time is associated with the mechanism responsible for photocurrent generation. This mechanism is the same regardless of whether we excite locally (waveguide coupling) or over the entire active area (vertical illumination), since the MoS2 flake is supported by a flat and homogeneous h-BN layer. When illuminating with a continuous wave laser, a constant photocurrent is generated. After adding a chopper rotating at 20 Hz at the output of the laser, the response of the device is still fast enough to reach maximum (constant illumination) and minimum (dark) values of photocurrent, which demonstrates that all the response is faster than 20 Hz. To determine more precisely the speed of the response, photocurrent is measured as a function of the chopper rotation frequency. Figure 5a shows the ratio between DC photocurrent (IDC) obtained for constant illumination, and oscillating photocurrent (IAC) at the frequency of the chopper, measured by the lock-in amplifier. The oscillating (fast) photocurrent is constant for frequencies of up to 1 kHz, the limit of the measurement setup. The response time of the monolayer MoS2/h-BN photodetector is therefore shorter than 1 ms, overcoming the performance of previously reported MoS2 photodetectors.27 Similar results are obtained when exciting via the waveguide, with lower photocurrents due to weaker coupling after the addition of thick h-BN, leading to a fast responsivity of 1.5 μA/W at Pin = 7 mW (Fig. 5a, inset).
Fast response and low-power operation of MoS2-based photodetectors. a Fast operation of the MoS2/h-BN photodetector: Lock-in amplifier measurements of AC photocurrent dependence on chopper frequency at Pin = 7 mW, Vg = 0 V and Vds = 1 V, under vertical illumination. Inset shows schematic structure of the photodetector and operation under dark (OFF) and chopped illumination at 1 kHz (ON) on the grating coupler with Pin = 7 mW, Vg = 0 V and Vds = 1 V. b Low voltage operation of the MoS2/h-BN/Gr photodetector. Main graph shows Ids−Vg curves under dark and illumination at Pin = 11 mW and Vds = 250 mV, showing low threshold voltage Vth = −250 mV without illumination. Inset graph shows Ids−Vds curves with and without illumination for Pin = 11 mW, Vg = −500 mV. Inset schematic depicts the structure of the photodetector
For low-power applications of integrated optoelectronic devices, operation voltages need to be decreased. In order to have more efficient electrostatic control over the charge carrier density in the MoS2 flake, we fabricate a third device where multilayer graphene is used as a back gate, with an 11 nm thick h-BN dielectric layer. Resulting Ids−Vg curves for the device in the dark and under vertical illumination are shown in Fig. 5b. The off state is reached at a back gate voltage as low as Vg = −250 mV, due to the higher capacitance (C = 2800 μF/m2) of the thin h-BN dielectric compared to the 1 µm thick SiO2 (C = 34.5 μF/m2). High values of photocurrent on the order of µA can be measured for the complete range of back gate voltages. Figure 5b inset presents measured Ids−Vds curves in the off state, with gate voltage below the threshold. Photocurrent to dark current ratio over 105 is achieved at Vds = 300 mV and incident power of 11 mW.
In summary, we demonstrate the integration of MoS2 photodetectors on photonic structures, and present device architectures for practical optoelectronic circuits. The first figure of merit is the large responsivity of the photodetector for lateral illumination at wavelengths close to the optical bandgap. Light emission from MoS2 at these wavelengths has already been demonstrated17 and therefore a platform for light emission and detection with monolayer MoS2 could be potentially realized. In addition, photocurrent can also be suppressed for gate voltages below a given threshold, leading to three different regimes in photoresponse. Homogeneous and large coupling area in the diffraction gratings facilitates alignment for future optical interconnects. Furthermore, by realizing more complex structures we demonstrate potential of this device as a platform for the development of MoS2-based integrated photodetectors aiming at various applications. In a second device, photoresponse times below 1 ms can be achieved by adding an h-BN layer between MoS2 and Si3N4. The use of a graphene back gate with thin h-BN as the dielectric in a third device reduces the voltage range needed to operate the phototransistor. Altogether, results from this work rise the prospects of MoS2 as a promising material for future integrated optoelectronic circuits.
Methods
Device fabrication
Degenerately doped silicon wafers with 250 nm/1 µm Si3N4/SiO2 layers grown by low pressure chemical vapor deposition (LPCVD) were used for device fabrication. The thickness of SiO2 is high enough to decouple waveguide modes from the optically dense substrate. Photonic structures were patterned using electron beam lithography after spin coating of ZEP, followed by dry etching with CHF3/SF6. The polymer was then removed using O2 plasma and the resulting structure was submerged in KOH to smooth the waveguide sidewalls. Dimensions of photonic circuits were optimized for wavelengths at the MoS2 excitonic resonance, so that it can also be used for transmission of light emitted by MoS2-based devices. We further confirmed resulted dimensions of fabricated structures by scanning electron microscopy (SEM), focused ion beam (FIB) and atomic force microscopy (AFM), as shown in Supplementary Fig. S1. Calculated electric field profile for fundamental TE and TM mode based on FDTD simulations is plotted in Supplementary Fig. S2. Ultrathin layers of MoS2 were obtained by mechanical exfoliation with low residue tape. Monolayers are then deposited on visco-elastic films with a polyethylene coversheet (Gel-Pak) and peeled-off slowly. The contrast of monolayer flakes under the optical microscope has been calibrated and confirmed by atomic force microscopy (AFM) and photoluminescence (PL) measurements. Finally, polymer films were placed on a glass slide for dry transfer on top of the photonic structure. Post-transfer thermal annealing was done at 250 °C under high vacuum (10−7 mbar) for 6 h. The resulting structure was spin coated with PMMA A2/MMA EL6 and patterned by electron beam lithography, followed by electron beam evaporation of 10 nm Ti and 60 nm Au. Standard lift-off process with acetone was used for polymer removal. Figure S3 shows optical images of the device after different fabrication steps. Photoluminescence after annealing of the transferred MoS2 monolayer decreases significantly, with the suppression of exciton states due to charge transfer from the substrate, as shown in Supplementary Fig. S3c.
Setup for optoelectronic measurements
The bias voltages were supplied by a Keithley 2400 measurement unit which was also used for current measurements. Unless otherwise specified, all optoelectronic measurements were performed in vacuum (10−6 mbar) at room temperature, with a continuous wave laser illumination at 647 nm. The setup for optoelectronic measurements is presented in Fig. S5. Laser light is directed towards the sample by the beam splitter BS1, and the focus position is set by a piezoelectric stage mounted to the ×50 objective with a numerical aperture NA = 0.65. Light reflected or re-emitted from the sample is split by BS2 and collected by the CCD camera (Andor Ixon) and the spectrometer (Andor Newton).
Determination of waveguide losses and MoS2 absorption
For measurement of waveguide losses and MoS2 absorption, laser light with a wavelength of 647 nm is focused on the input grating, and light emission from the output grating is quantified with the number of counts measured in the CCD camera. By comparing counts measured for a reference structure, waveguide losses and MoS2 absorption can be extracted. In order to remove the reflected light, a cross-polarization scheme was used. Laser light is first polarized along the grating coupler lines, and the waveguide makes a turn so that emitted light in the output grating is polarized perpendicularly to incident light (see right inset in Fig. S5). Since the polarization of reflected light is the same as for incident light, we can remove laser reflection without affecting light emission form the output grating.
Data availability
The data that support the findings of this study are available from the corresponding author on reasonable request.
References
Gurrum, S. P., Suman, S. K., Joshi, Y. K. & Fedorov, A. G. Thermal issues in next-generation integrated circuits. IEEE Trans. Device Mater. Reliab. 4, 709–714 (2004).
Rickman, A. The commercialization of silicon photonics. Nat. Photonics 8, 579–582 (2014).
Moss, D. J., Morandotti, R., Gaeta, A. L. & Lipson, M. New CMOS-compatible platforms based on silicon nitride and Hydex for nonlinear optics. Nat. Photonics 7, 597–607 (2013).
Miller, D. A. B. Device requirements for optical interconnects to silicon chips. Proc. IEEE 97, 1166–1185 (2009).
Miller, D. A. B. Rationale and challenges for optical interconnects to electronic chips. Proc. IEEE 88, 728–749 (2000).
Sun, Z., Martinez, A. & Wang, F. Optical modulators with 2D layered materials. Nat. Photonics 10, 227–238 (2016).
Bertolazzi, S., Brivio, J. & Kis, A. Stretching and breaking of ultrathin MoS2. ACS Nano 5, 9703–9709 (2011).
Akinwande, D. et al. A review on mechanics and mechanical properties of 2D materials—graphene and beyond. Extrem. Mech. Lett. 13, 42–77 (2017).
Schwierz, F. Graphene transistors. Nat. Nanotechnol. 5, 487–496 (2010).
Gan, X. et al. Chip-integrated ultrafast graphene photodetector with high responsivity. Nat. Photonics 7, 883–887 (2013).
Bonaccorso, F., Sun, Z., Hasan, T. & Ferrari, A. C. Graphene photonics and optoelectronics. Nat. Photonics 4, 611–622 (2010).
Radisavljevic, B., Radenovic, A., Brivio, J., Giacometti, V. & Kis, A. Single-layer MoS2 transistors. Nat. Nanotechnol. 6, 147–150 (2011).
Wang, Q. H., Kalantar-Zadeh, K., Kis, A., Coleman, J. N. & Strano, M. S. Electronics and optoelectronics of two-dimensional transition metal dichalcogenides. Nat. Nanotechnol. 7, 699–712 (2012).
Mak, K. F. & Shan, J. Photonics and optoelectronics of 2D semiconductor transition metal dichalcogenides. Nat. Photonics 10, 216–226 (2016).
Splendiani, A. et al. Emerging photoluminescence in monolayer MoS2. Nano Lett. 10, 1271–1275 (2010).
Mak, K. F., Lee, C., Hone, J., Shan, J. & Heinz, T. F. Atomically thin MoS2: a new direct-gap semiconductor. Phys. Rev. Lett. 105, 136805 (2010).
Lopez-Sanchez, O. et al. Light generation and harvesting in a van der Waals heterostructure. ACS Nano 8, 3042–3048 (2014).
Lopez-Sanchez, O., Lembke, D., Kayci, M., Radenovic, A. & Kis, A. Ultrasensitive photodetectors based on monolayer MoS2. Nat. Nanotechnol. 8, 497–501 (2013).
Bie, Y.-Q. et al. A MoTe2-based light-emitting diode and photodetector for silicon photonic integrated circuits. Nat. Nanotechnol. 12, 1124–1129 (2017).
Unuchek, D. et al. Room-temperature electrical control of exciton flux in a van der Waals heterostructure. Nature 560, 340 (2018).
Zhao, W. et al. Large area growth of monolayer MoS 2 film on quartz and its use as a saturable absorber in laser mode-locking. Semicond. Sci. Technol. 32, 025013 (2017).
Tan, Y. et al. Polarization-dependent optical absorption of MoS2 for refractive index sensing. Sci. Rep. 4, 7523 (2014).
Castellanos-Gomez, A., Quereda, J., Meulen, H. P., van der, Agraït, N. & Rubio-Bollinger, G. Spatially resolved optical absorption spectroscopy of single- and few-layer MoS 2 by hyperspectral imaging. Nanotechnology 27, 115705 (2016).
Buscema, M. et al. Large and tunable photothermoelectric effect in single-layer MoS2. Nano Lett. 13, 358–363 (2013).
Furchi, M. M., Polyushkin, D. K., Pospischil, A. & Mueller, T. Mechanisms of photoconductivity in atomically thin MoS2. Nano Lett. 14, 6165–6170 (2014).
Schmidt, H. et al. Transport properties of monolayer MoS2 grown by chemical vapor deposition. Nano Lett. 14, 1909–1913 (2014).
Wang, X. et al. Ultrasensitive and broadband MoS2 photodetector driven by ferroelectrics. Adv. Mater. 27, 6575–6581 (2015).
Acknowledgements
We are grateful to Oriol Lopez Sanchez, Ahmet Avsar, Dmitry Ovchinnikov, Kolyo Marinov, and Alberto Ciarrocchi for useful discussions. We acknowledge the help of Z. Benes (CMI) with e-beam lithography. J.G., D.U., and A.K. would like to acknowledge support by the European Research Council (ERC, Grant 682332) and Swiss National Science Foundation (Grant 153298). A.K. acknowledges funding from the European Union’s Horizon H2020 Future and Emerging Technologies under grant agreements No 696656 and 785219 (Graphene Flagship Core 1 and Core 2). K.W. and T.T. acknowledge support from the Elemental Strategy Initiative conducted by the MEXT, Japan, A3 Foresight by JSPS and the CREST (JPMJCR15F3), JST.
Author information
Authors and Affiliations
Contributions
D.U. and J.G. contributed equally. D.U. and J.G. fabricated devices, performed optical and electrical measurements, numerical simulations and analyzed the data. K.W. and T.T. grew the h-BN crystals. A.K. initiated and supervised the project. J.G., D.U., and A.K. wrote the manuscript with input from all authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Gonzalez Marin, J.F., Unuchek, D., Watanabe, K. et al. MoS2 photodetectors integrated with photonic circuits. npj 2D Mater Appl 3, 14 (2019). https://doi.org/10.1038/s41699-019-0096-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41699-019-0096-4
This article is cited by
-
The Roadmap of 2D Materials and Devices Toward Chips
Nano-Micro Letters (2024)
-
Controlled addition of Fe3O4 for enhancing photocarrier generation in MoS2 visible light photodetector
Journal of Materials Science: Materials in Electronics (2024)
-
MoSe2/WS2 heterojunction photodiode integrated with a silicon nitride waveguide for near infrared light detection with high responsivity
Light: Science & Applications (2023)
-
Research progress of optoelectronic devices based on two-dimensional MoS2 materials
Rare Metals (2023)
-
Excitonic devices with van der Waals heterostructures: valleytronics meets twistronics
Nature Reviews Materials (2022)