Abstract
Realization of unconventional physical properties in two-dimensional (2D) transition-metal dichalcogenides (TMDs) is currently one of the key challenges in condensed-matter systems. However, the electronic properties of 2D TMDs remain largely unexplored compared to those of their bulk counterparts. Here, we report the fabrication of a high-quality monolayer NbSe2 film with a trigonal prismatic structure by molecular beam epitaxy, and the study of its electronic properties by scanning tunneling microscopy, angle-resolved photoemission spectroscopy, and electrical transport measurements, together with first-principles band-structure calculations. In addition to a charge density wave (CDW) with 3 × 3 periodicity and superconductivity below 1.5 K, we observed sizable (~0.1 eV) band splitting along the Γ-K cut in the Brillouin zone due to inversion symmetry breaking in the monolayer crystal. This splitting is highly anisotropic in k space, leading to a spin-split van-Hove singularity in the band structure. The present results suggest the importance of spin–orbit coupling and symmetry breaking for unconventional superconductivity and CDW properties in monolayer TMDs.
Similar content being viewed by others
Introduction
Layered transition-metal dichalcogenides (TMDs) MX2 (M = transition metal, X = chalcogen) have been extensively studied since they exhibit a variety of physical properties, such as superconductivity and charge density waves (CDWs).1 Recently, monolayer MX2 has attracted particular attention because it provides a useful platform to realize exotic physical properties such as field-induced superconductivity, and advanced electronic devices such as optical/thermoelectric devices, by coupling the spin-degree and valley-degree of freedom.2,3,4,5,6,7,8,9,10
It is known that bulk 2H-NbSe2 exhibits a unique ground state, where an incommensurate CDW and superconductivity coexist below 7 K.11 On the other hand, monolayer NbSe2 films obtained by exfoliating the bulk crystal or via a molecular beam epitaxy (MBE) method exhibit lower superconducting transition temperatures of Tc = 3 K and 0.65–1.9 K, respectively.7,12,13 It is also reported that the CDW transition temperature increases as the number of layers is reduced.7 These characteristic variations in the physical properties as a function of thickness may be understood in terms of crystal symmetry breaking. As shown in Fig. 1a, the monolayer NbSe2 with a trigonal prismatic structure (note that its bulk counterpart with an AB stacking sequence is known as the 2H phase) has no inversion center.10,14 Because of the inversion symmetry breaking and the strong spin–orbit coupling (SOC) of the Nb 4d orbital, the spin degeneracy should be lifted.14 This band splitting and the resultant peculiar spin texture may induce unconventional superconductivity with an enhanced in-plane upper critical field Hc2//.10,15,16,17 However, the existence of such band splitting in monolayer NbSe2 has not been experimentally verified because previous spectroscopic studies have been performed with samples having multiple domains.12 Therefore, the relationship between the band splitting and the CDW has not been conclusively investigated. Thus, a precise spectroscopic investigation of the high-quality monolayer NbSe2 with a single domain is required.
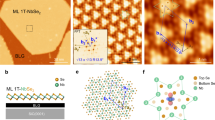
Characterizations of the monolayer NbSe2 on bilayer graphene. a Crystal structure of the monolayer NbSe2 with a trigonal prismatic structure. b, c RHEED patterns of bilayer (BL) graphene and monolayer NbSe2, respectively, obtained along the [11\(\bar 2\)0] direction of the SiC(0001) substrate. d Constant-current STM image of a surface area of 100 nm × 50 nm (sample bias voltage Vs = 0.5 V).19 Scale bar: 20 nm. e High-resolution STM image measured in the region enclosed by the red rectangle in d (Vs = 10 mV). Scale bar: 1 nm. f FFT of STM image in e. g Sheet resistance (Rsheet) of monolayer NbSe2 as a function of temperature for various B⊥ (0-1.6 T with 0.2 T step). Inset shows the temperature dependence of μ0Hc2⊥, which is independently estimated from the temperature dependence of Rsheet (red points) and the B⊥dependence of Rsheet at fixed temperatures (squares). μ0Hc2⊥ was estimated from the magnetic field where Rsheet is a half of the normal-state value. The solid line shows the result of numerical fitting with GL theory
In this paper, we report the MBE growth of highly oriented monolayer NbSe2, and its characterization by scanning tunneling microscopy (STM), angle-resolved photoemission spectroscopy (ARPES), and electrical transport measurements, together with first-principles band structure calculations. We found that the monolayer NbSe2 film exhibits a 3 × 3 CDW and superconductivity below 1.5 K, hosted by a spin-polarized Fermi surface (FS). In addition, we observed sizable (~0.1 eV) band splitting along the Γ-K cut in the Brillouin zone (BZ) due to inversion symmetry breaking in the monolayer crystal. This splitting is highly anisotropic in k space, creating a spin-split van-Hove singularity. We discuss implications for superconductivity and CDW of the inversion symmetry breaking and the strong SOC.
Results and discussion
We employed the van der Waals epitaxy technique18 to fabricate monolayer NbSe2 using bilayer graphene grown on silicon carbide as a substrate.12,19 Figure 1b shows the reflection high-energy electron diffraction (RHEED) pattern of pristine bilayer graphene grown on 6H-SiC(0001), featuring the 1 × 1 streak pattern originating from both bilayer graphene and SiC. After co-evaporation of Nb and Se atoms onto the substrate, which is maintained at 500 °C in ultrahigh vacuum (UHV), the intensity from SiC and graphene is reduced, and a new 1 × 1 streak pattern appears (Fig. 1c), as is the case for other monolayer TMD films on the bilayer graphene.19,20,21 While the MBE-grown monolayer NbSe2 film was reported to contain domains rotated by 30° with respect to each other,12 we found no indication of such a domain mixture in the RHEED pattern, demonstrating that our film was highly oriented. This is corroborated by our ARPES data, which is shown later. Such selective fabrication of a highly oriented film has become possible by carefully tuning the substrate temperature during the epitaxy (500 °C in the present study, while 330 °C was reported in a previous study.12) As shown in Fig. 1d, the STM image reveals the formation of monolayer NbSe2 with atomically flat terraces on the graphene substrate.12 The high-resolution STM image displays the 3 × 3 intensity modulation as well as the 1 × 1 pattern, as shown in Fig. 1e. Such periodicity is clearly visualized in the fast Fourier transform (FFT) of the STM image, shown in Fig. 1f. This indicates that the film is in the CDW phase at low temperature (T = 6 K), as in bulk 2H-NbSe2.12,22,23,24
We characterized the electrical transport properties of our film with the in situ four-point-probe (4PP) method. Figure 1g shows the sheet resistance Rsheet as a function of temperature under various out-of-plane magnetic field strengths B⊥. Rsheet at B⊥ = 0 T shows a sharp reduction at around 1.5 K (Tconset = 1.5 K), and reaches zero at 1.4 K. Upon increasing B⊥, the Tc value is monotonically reduced, and the superconductivity finally disappears at B⊥ = 1.6 T. From the magnitude of B⊥ at which the resistivity takes half of the normal-state resistivity, we have estimated the out-of-plane upper critical field μ0Hc2⊥, and plotted its temperature dependence in the inset to Fig. 1g [note that μ0Hc2⊥ is also estimated from the B⊥-dependence of Rsheet at fixed temperatures (open diamonds), besides the data in Fig. 1g (red circles)]. One can clearly see a linear dependence of μ0Hc2⊥ on temperature. The obtained Tc (1.5 K) and μ0Hc2⊥ at T = 0 K (~1.7 T) are slightly lower than those of the monolayer NbSe2 obtained by exfoliation (3 K and ~4 T, respectively),10 suggesting that Tc is influenced by the substrate. By numerically fitting the data using Ginzburg–Landau (GL) theory,25 we estimated the in-plane GL coherence length at 0 K as ξ(0) = 14.0 ± 0.1 nm, which is five times larger than that of the bulk NbSe2 (2.7 nm).26 Furthermore, the Tc of our epitaxial monolayer film (1.5 K) is about 1/5 of the Tc of bulk NbSe2 (7.2 K). This can be essentially understood in terms of the known inverse proportional relationship between Tc and coherence length. The enhancement of coherence length in the NbSe2 film resembles the case of Ca-intercalated graphene/graphite, where the coherence length of the ultrathin film [ξ(0) = 49 nm for C6CaC627] is much larger than that of the bulk crystal [ξ(0) = 29 nm for C6Ca,28] essentially due to the difference in their Tc values.
After establishing the transport properties, the next important issue is to elucidate the electronic structure inherent to monolayer NbSe2. Figure 2a shows the ARPES-intensity plot of the monolayer NbSe2 in the valence-band region measured along the Γ-M and Γ-K cuts in the BZ. We found several dispersive bands reflecting the high single crystallinity of film. The hole-like bands that have the top of dispersion around the binding energy (EB) of 1 eV originate from the Se 4p orbitals, and the bands which disperse within 0.5 eV with respect to the Fermi level (EF) are attributed to the Nb 4d states.12,29,30,31 These features are qualitatively reproduced by our first-principles band calculations, incorporating the SOC for free-standing monolayer NbSe2, as illustrated in Fig. 2b. We remark here that hybridization between NbSe2 and graphene bands is expected to be very weak, because the C 2p σ band topped at 4 eV below EF at Γ and the π band near EF at K in the graphene BZ are outside the energy/momentum range of Fig. 2a. The interaction between NbSe2 and graphene is likely to be more sensitive to the physical parameters governed by low-energy excitations such as Tc, but less sensitive to high-energy characteristics like overall valence-band dispersion.
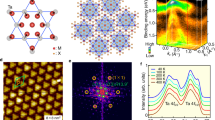
Valence-band structure of monolayer NbSe2. a Valence-band ARPES intensity of monolayer NbSe2 measured along the Γ-M and Γ-K cuts at T = 40 K with the He-Iα line (hv = 21.218 eV). b Band structure obtained from first-principles band-structure calculations for free-standing monolayer NbSe2. c Second-derivative of ARPES intensity in the area enclosed by the red rectangle in a. d Same as c but for bulk 2H-NbSe2. Dashed curves in c and d are a guide for the eyes to trace the band dispersion. e (upper panel) Arrangement of Se and Nb atoms and its relationship to (lower panel) hexagonal BZ
Figure 2c highlights the band dispersion around the top of the Se 4p bands (area enclosed by red rectangle in Fig. 2a), obtained by taking the second derivative of the ARPES intensity. One can clearly see that the band located at EB = 0.95 eV at the Γ point splits into two branches at the midway between Γ and K (k y ≈ 0.2–0.8 Å−1). However, this band shows no splitting along the Γ-M cut. This behavior is well reproduced by the band-structure calculation in Fig. 2b (see area enclosed by blue rectangle) and is interpreted as a consequence of the SOC and inversion symmetry breaking. To be more specific, the anisotropic band splitting may be intuitively understood by taking into account the D3h symmetry of the monolayer crystal9,10 in which the atomic arrangement is symmetric with respect to the yz plane (M-Γ-M plane), but not with respect to the xz plane (K′-Γ-K plane) as shown in Fig. 2e.
To further corroborate anisotropic band splitting due to inversion symmetry breaking in monolayer NbSe2, we have also performed the ARPES measurement for inversion-symmetric bulk 2H-NbSe2. As shown in Fig. 2d, one can immediately recognize apparent differences in the band dispersion from its monolayer counterpart. The Se 4p band in the bulk crystal (Fig. 2d) splits along the ΓM cut on moving away from Γ (white dashed lines), unlike monolayer (Fig. 2c). This suggests that the origin of band splitting is different between monolayer and bulk. The splitting is caused by the 2H-type stacking of NbSe2 layers in the bulk crystal (unit cell contains two Nb atoms), producing isotropic band splitting.31,32,33 However, the band splitting in monolayer cannot be explained within the same framework, since the unit cell contains only one Nb atom and thereby we expect one half-filled band under spin degeneracy.
To address whether the band splitting influences the FS responsible for the anomalous physical properties, we have performed ARPES measurements in the vicinity of EF. As shown in Fig. 3a, b, the FS mapping reveals large hole pockets centered at the Γ and K points. According to the band calculation results in Fig. 2b, these pockets originate from a single Nb 4d band which crosses EF twice along the Γ-K cut (when neglecting SOC). The hexagonal shape of the Γ-centered pocket is an indication of the highly oriented nature of our film, since the existence of multiple domains results in the rounded shape of pockets.12 Figure 3c shows the energy distribution curves (EDCs) measured along the cut in between two hole pockets (cut A in Fig. 3a). The EDCs were obtained by plotting the data at specific k y points indicated on the right-hand side, which were selected from the original ARPES intensity recorded in k x –k y space. One can clearly recognize two peaks located at EB = 170 and 50 meV on the Γ-K line (highlighted by the blue EDC), both of which display hole-like dispersion along this cut. We have estimated the energy position of the peaks from numerical fitting using two Lorentzians with constant background multiplied by the Fermi–Dirac distribution function. As shown in the representative fit result for the EDC at k y = 0 (blue line in Fig. 3c) in Fig. 3d, one finds a good agreement between the fit result (red) and the experimental data (black) over the entire energy range. This supports the existence of two bands. The two-peaked structure is also visualized in the second derivative of the ARPES intensity in Fig. 3e, and is attributed to the spin-split Nb 4d bands due to the aforementioned inversion symmetry breaking, supported by a qualitative agreement of the band dispersion between the experiment (circles) and the calculation (solid lines). It is noted here that the band splitting is not clearly resolved in the Fermi-surface mapping in Fig. 3a due to strong lifetime broadening and shallow band dispersion. Nevertheless, we were able to extract triangular shapes of the K-centered pockets (open circles in Fig. 3a) from the momentum distribution curves at EF, which are consistent with the calculation result shown in Fig. 3b. As shown in Fig. 3f, this band splitting is also seen in the ARPES data along the cut perpendicular to cut A (cut B in Fig. 3a; the Γ-K cut) as a pair of electron-like bands. It is thus strongly suggested from the EDCs, numerical fits, and second-derivative plots, all together, that the Nb 4d bands are spin split, and each branch forms a van-Hove singularity with the saddle point at the top (bottom) of the hole-like (electron-like) band in cut A (B). The magnitude of the band splitting at the saddle point is 120 meV, comparable to that for the Se 4p bands (~100 meV) in Fig. 2c. All these results suggest a spin-polarized nature of the FS in monolayer NbSe2.34 It is noted that band splitting has been observed or predicted in some semiconducting TMDs with a trigonal prismatic structure,34,35,36,37,38,39 and it commonly originates from inversion symmetry breaking and SOC. The present study reveals that band splitting also exists in a TMD showing a CDW.
Fermi surface and electronic structure near EF in monolayer NbSe2. a ARPES intensity at EF plotted as a function of 2D wave vector (k x and k y ) for monolayer NbSe2. Intensity at EF was obtained by integrating the intensity within ± 20 meV with respect to EF. Open circles indicate the location of the Fermi vectors (kF) for the K-centered pocket estimated by tracing the peak position of the momentum distribution curves at EF. The size of the circles reflects experimental uncertainty. b Fermi surface obtained from the band calculation for monolayer NbSe2. Red and blue lines indicate the up and down out-of-plane spin components, respectively. The area enclosed by the green rectangle corresponds to the k region where the Fermi-surface mapping in a was obtained. Arrows and yellow areas indicate QCDW and hot spots, respectively. Gray lines denote the 1 × 1 BZ. c EDCs measured along cut A in a. The EDC delineated in blue is that for the Γ-K line (ky = 0), which corresponds to the saddle point of the van-Hove singularity in the band structure. Blue and green dots correspond to the energy position of peaks estimated from numerical fits with two Lorentzians. The error bars reflect the standard deviation in the peak position of the Lorentzians and the energy resolution. d EDC at the saddle point (black line) extracted from c. The red line is the result of a numerical fit with two Lorentzians (green and blue lines) and a constant background multiplied by the Fermi-Dirac distribution function. e, f Second derivative of ARPES intensity along cut A and B, respectively. Open circles and solid lines are band dispersions obtained from the peak position of the EDCs and the band calculations, respectively. The error bars reflect the standard deviation in the peak position of the Lorentzians, together with the energy and momentum resolutions
We now discuss the implications of the observed band splitting for superconductivity. It is expected that the intrinsic effective magnetic field HSO is parallel to k × ε (ε is the crystal field, i.e., the net dipole moment) in a non-centrosymmetric superconductor with strong SOC.15,16 In monolayer NbSe2, HSO has only an out-of-plane component since ε has only an in-plane component due to the mirror symmetry with respect to the Nb plane in monolayer NbSe2, in contrast to the cases of Rashba metals40 and Dirac-cone surface states in 3D topological insulators, which generally show an in-plane spin texture.41 In fact, we have confirmed by our band calculation that the spin polarization has only the out-of-plane component irrespective of the k location in the BZ, and the outer (inner) pocket at K has a down (up) spin component.14 Such spin texture would be responsible for the observed robustness of superconductivity against the in-plane magnetic field in monolayer NbSe2.10 To validate this point, we have estimated the expected Hc2// value from the magnitude of the observed band splitting. If HSO is much larger than the Pauli paramagnetic limit (HP), Hc2// is defined as ~√HSOHP.10,16 HSO in monolayer NbSe2 with D3h symmetry10,15 is expressed as
where H0 characterizes the magnitude of the spin–orbit field and a is the in-plane lattice constant (3.45 Å). From the magnitude of the observed band splitting (120 meV) at the saddle point ((k x , k y ) = (0.7, 0 Å−1)), we obtain μ0Hc2// ~64 T [note that this value was estimated from the kF (Fermi vector) points of the K-centered pockets], well above μ0HP (~2.8 T). A large μ0Hc2// value has been also reported in exfoliated monolayer NbSe2 with Tc = 3 K (μ0Hc2// ≳ 31.5 T)10 and ionic-gated MoS2 with Tc = 6.5-7.6 K (μ0Hc2// = 32–52 T).8,9 While the Tc values are different and one cannot directly compare the μ0Hc2// values among these inversion symmetry-broken TMDs, the commonality of the large μ0Hc2// values would point to a possible connection between the band splitting and μ0Hc2// (note that μ0Hc2// in our film needs to be confirmed by the electrical transport measurement under parallel magnetic field, though this is not currently feasible due to a limitation of measurement geometry in our 4PP system).
Finally, we discuss the relationship between the spin-split FS and the CDW in monolayer NbSe2. To the best of our knowledge, the present study is a rare case of CDW realization that involves a spin-polarized FS. As for the origin of the CDW, we can rule out the simple FS nesting scenario at the Γ-centered hexagonal pocket since the k vector connecting the parallel segments of this pocket is much larger than the 3 × 3 CDW vector (QCDW) as in bulk 2H-NbSe2 and highlighted in Fig. 3b.42 The van Hove singularity scenario43,44 is also ruled out since the saddle point is far (~50 meV) from EF. Recently, it has been suggested that k-dependent electron–phonon coupling is the major mechanism of the CDW in bulk 2H-NbSe2.23,24,31,32,45 In this scenario, there exists a specific k region called a “hot spot” spanned by the CDW vector where electrons are strongly coupled to phonons. In monolayer NbSe2, the FS is spin split and the situation may be different from that of the bulk crystal. In particular, electron scattering connecting the CDW vector should not involve the spin flip process and therefore the FS segments with the same spin texture need to be connected with each other by the CDW vector. At first sight, this appears to be less favorable for the stabilization of the CDW in monolayer NbSe2. However, taking into account the experimental fact that phonon softening was observed in the finite Q region (QCDW ± α) in the bulk crystal45 and assuming that similar softening also occurs in the monolayer, it is expected that the hot-spot region is wide enough in k space to connect the Fermi-surface segments with the same spin texture even when the FS is spin polarized, as schematically illustrated by the yellow area in Fig. 3b. To further examine this conjecture, observation of phonon dispersion in monolayer NbSe2 is highly desired.
In conclusion, we report the MBE growth of monolayer NbSe2 with a trigonal prismatic crystal structure on bilayer graphene. Besides the superconductivity (Tc = 1.5 K) and the 3 × 3 CDW transition, we found direct evidence for sizable band splitting due to inversion symmetry breaking in the monolayer crystal and a resultant characteristic spin–split van-Hove singularity in the band dispersion. We conclude that the observed band splitting is closely related to the robustness of the superconductivity against the in-plane magnetic field as well as the formation of a CDW with strong periodic charge modulation. The present study opens an avenue for understanding of the interplay between symmetry breaking and unconventional physical properties in atomic layer materials.
Methods
Monolayer NbSe2 film was grown on bilayer graphene by the MBE method.12,18,19,20,21 Bilayer graphene was prepared by annealing an n-type Si-rich 6H-SiC(0001) single-crystal wafer by resistive heating at 1100 °C for 20 min in an UHV chamber at pressures lower than 1.0 × 10−9 Torr. Monolayer NbSe2 film was grown by evaporating Nb on a bilayer graphene substrate in Se atmosphere at ~5.0 × 10−9 Torr. The substrate was maintained at 500 °C during the epitaxy.19 The as-grown film was annealed at 400 °C for 30 min, and then transferred to the ARPES-measurement chamber without breaking the vacuum. The film thickness was monitored by a quartz-oscillator thickness meter and STM. ARPES measurements were carried out using a MBS-A1 electron-energy analyzer with a high-flux helium discharge lamp and a toroidal grating monochromator at Tohoku University. The energy and angular resolutions were set at 16 meV and 0.2°, respectively. The Fermi level (EF) of samples was referenced to that of a gold film deposited onto the sample substrate. We performed the electrical transport and STM measurements in separate vacuum chambers. To avoid contamination of the surface of sample during the transfer, we covered the NbSe2 film with amorphous Se immediately after the epitaxy, transferring it to the separate UHV chambers for the measurements, and then de-capping it by annealing the film under UHV. The electrical transport measurements were carried out with a Unisoku USM-1300S, of which STM head has a 4PP of 100-μm diameter copper wire with a probe spacing of 200 μm. The sheet resistance Rsheet was obtained by the 4PP dc current–voltage measurement by using the dual configuration method.46 The custom-made STM system for obtaining the atomic image was operated at T = 6 K under UHV better than 2 × 10−10 Torr. First-principles band-structure calculations for free-standing monolayer NbSe2 was carried out by using the Quantum Espresso code47 with generalized gradient approximation.48 Spin–orbit interactions were included in the calculations. Ultrasoft pseudopotentials49 were used, and the wavefunctions and charge densities were expanded using a 50 Ry and 400 Ry cutoff, respectively. The k-point mesh was set to be 14 × 14 × 1. The crystal structure was relaxed using the supercell geometry with a vacuum region of more than 10 Å.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
References
Chhowalla, M. et al. The chemistry of two-dimensional layered transition metal dichalcogenide nanosheets. Nat. Chem. 5, 263–275 (2013).
Cao, T. et al. Valley-selective circular dichroism of monolayer molybdenum disulphide. Nat. Commun. 3, 887 (2012).
Mak, K. F., He, K., Shan, J. & Heinz, T. F. Control of valley polarization in monolayer MoS2 by optical helicity. Nat. Nanotech. 7, 494–498 (2012).
Zeng, H., Dai, J., Yao, W., Xiao, D. & Cui, X. Valley polarization in MoS2 monolayers by optical pumping. Nat. Nanotech. 7, 490–493 (2012).
Mak, K. F., McGill, K. L., Park, J. & McEuen, P. L. The valley Hall effect in MoS2 transistors. Science 344, 1489–1492 (2014).
Tahir, M. & Schwingenschlögl, U. Tunable thermoelectricity in monolayers of MoS2 and other group-VI dichalcogenides. New J. Phys. 16, 115003 (2014).
Xi, X. et al. Strongly enhanced charge-density-wave order in monolayer NbSe2. Nat. Nanotech. 10, 765–769 (2015).
Lu, J. M. et al. Evidence for two-dimensional Ising superconductivity in gated MoS2. Science 350, 1353–1357 (2015).
Saito, Y. et al. Superconductivity protected by spin–valley locking in ion-gated MoS2. Nat. Phys. 12, 144–149 (2015).
Xi, X. et al. Ising pairing in superconducting NbSe2 atomic layers. Nat. Phys. 12, 139–143 (2016).
Wilson, J. A., Di Salvo, F. J. & Mahajan, S. Charge-density waves and superlattices in the metallic layered transition metal dichalcogenides. Adv. Phys. 24, 117–201 (1975).
Ugeda, M. M. et al. Characterization of collective ground states in single-layer NbSe2. Nat. Phys. 12, 92–97 (2016).
Onishi, S. et al. Selenium capped monolayer NbSe2 for two-dimensional superconductivity studies. Phys. Status Solidi B 253, 2396–2399 (2016).
He, W.-Y., Zhou, B. T., He, J. J., Zhang, T. & Law, K. T. Nodal topological superconductivity in monolayer NbSe2. Preprint at https://arxiv.orh/abs/1604.02867 (2016).
Bauer, E. & Sigrist, M. Non-centrosymmetric Superconductors: Introduction and Overview. (Springer, Berlin, 2012).
Sigrist, M. Introduction to unconventional superconductivity in non-centrosymmetric metals. AIP Conf. Proc. 1162, 55–96 (2009).
Gor’kov, L. P. & Rashba, E. I. Superconducting 2D system with lifted spin degeneracy: mixed singlet-triplet state. Phys. Rev. Lett. 87, 037004 (2001).
Koma, A., Sunouchi, K. & Miyajima, T. Fabrication and characterization of heterostructures with subnanometer thickness. Microelectron. Eng. 2, 129–136 (1984).
Nakata, Y. et al. Monolayer 1T-NbSe2 as a Mott insulator. NPG Asia Mater. 8, e321 (2016).
Sugawara, K., Sato, T., Tanaka, Y., Souma, S. & Takahashi, T. Spin- and valley-coupled electronic states in monolayer WSe2 on bilayer graphene. Appl. Phys. Lett. 107, 071601 (2015).
Sugawara, K. et al. Unconventional charge-density-wave transition in monolayer 1T-TiSe2. ACS Nano 10, 1341–1345 (2016).
Giambattista, B., Johnson, A., Coleman, R. V., Drake, B. & Hansma, P. K. Charge-density waves observed at 4.2 K by scanning-tunneling microscopy. Phys. Rev. B 37, 2741–2744 (1988).
Soumyanarayanan, A. et al. Quantum phase transition from triangular to stripe charge order in NbSe2. Proc. Natl. Acad. Sci. USA 110, 1623–1627 (2013).
Arguello, C. J. et al. Visualizing the charge density wave transition in 2H-NbSe2 in real space. Phys. Rev. B 89, 235115 (2014).
Tinkham, M. Introduction to Superconductivity. (Courier Corporation, New York, 2012).
de Trey, P., Gygax, S. & Jan, J. P. J. Anisotropy of the Ginzburg-Landau parameter κ in NbSe2. Low. Temp. Phys. 11, 421–434 (1973).
Weller, T. E., Ellerby, M., Saxena, S. S., Smith, R. P. & Skipper, N. T. Superconductivity in the intercalated graphite compounds C6Yb and C6Ca. Nat. Phys. 1, 39–41 (2005).
Ichinokura, S., Sugawara, K., Takayama, A., Takahashi, T. & Hasegawa, S. Superconducting calcium-intercalated bilayer graphene. ACS Nano 10, 2761–2765 (2016).
Corcoran, R. et al. Quantum oscillations in the mixed state of the type II superconductor 2H-NbSe2. J. Phys. Condens. Matter 6, 4479–4492 (1994).
Yokoya, T. et al. Fermi surface sheet-dependent superconductivity in 2H-NbSe2. Science 294, 2518–2520 (2001).
Rahn, D. J. et al. Gaps and kinks in the electronic structure of the superconductor 2H-NbSe2 from angle-resolved photoemission at 1 K. Phys. Rev. B 85, 224532 (2012).
Valla, T. et al. Quasiparticle spectra, charge-density waves, superconductivity, and electron-phonon coupling in 2H-NbSe2. Phys. Rev. Lett. 92, 086401 (2004).
Borisenko, S. V. et al. Two energy gaps and fermi-surface “Arcs” in NbSe2. Phys. Rev. Lett. 102, 166402 (2009).
Zhu, Z. Y., Cheng, Y. C. & Schwingenschlögl, U. Giant spin-orbit-induced spin splitting in two-dimensional transition-metal dichalcogenide semiconductors. Phys. Rev. B 84, 153402 (2011).
Cheiwchanchamnangij, T. & Lambrecht, W. R. L. Quasiparticle band structure calculation of monolayer, bilayer, and bulk MoS2. Phys. Rev. B 85, 205302 (2012).
Kośmider, K., González, J. W. & Fernández-Rossier, J. Large spin splitting in the conduction band of transition metal dichalcogenide monolayers. Phys. Rev. B 88, 245436 (2013).
Sun, L. et al. Spin-orbit splitting in single-layer MoS2 revealed by triply resonant Raman scattering. Phys. Rev. Lett. 111, 126801 (2013).
Zhang, Y. et al. Direct observation of the transition from indirect to direct bandgap in atomically thin epitaxial MoSe2. Nat. Nanotech. 9, 111–115 (2014).
Bawden, L. et al. Spin–valley locking in the normal state of a transition-metal dichalcogenide superconductor. Nat. Commun. 7, 11711 (2016).
Takayama, A., Sato, T., Souma, S., Oguchi, T. & Takahashi, T. Tunable spin polarization in bismuth ultrathin film on Si(111). Nano Lett. 12, 1776–1779 (2012).
Souma, S. et al. Spin polarization of gapped dirac surface states near the topological phase transition in TlBi(S1−xSex)2. Phys. Rev. Lett. 109, 186804 (2012).
Joohannes, M. D. & Mazin, I. I. Fermi surface nesting and the origin of charge density waves in metals. Phys. Rev. B 77, 165135 (2008).
Rice, T. M. & Scott, G. K. New mechanism for a charge-density-wave instability. Phys. Rev. Lett. 35, 120 (1975).
Kiss, T. et al. Charge-order-maximized momentum-dependent superconductivity. Nat. Phys. 3, 720–725 (2007).
Weber, F. et al. Extended phonon collapse and the origin of the charge-density wave in 2H-NbSe2. Phys. Rev. Lett. 107, 107403 (2011).
Yamada, M. et al. Surface electrical conductivity measurement system with micro-four-point probes at sub-Kelvin temperature under high magnetic field in ultrahigh vacuum. e-J. Surf. Sci. Nanotechnol. 10, 400–405 (2012).
Giannozzi, P. et al. Quantum espresso: a modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 21, 395502 (2009).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865 (1996).
Vanderbilt, D. Soft self-consistent pseudopotentials in a generalized eigenvalue formalism. Phys. Rev. B 41, 7892 (1990).
Acknowledgements
We thank N. Shimamura, Y. Umemoto, and S. Souma for their assistance in the ARPES measurements. This work was supported by JSPS KAKENHI Grants (JP25107003, JP15H05853, JP16H00924, JP25110010, JP25287079, and JP15H02105), Grant for Basic Science Research Projects from the Sumitomo Foundation, Science Research Projects from Iketani Science and Technology Foundation, the Program for Key Interdisciplinary Research, and World Premier International Research Center, Advanced Institute for Materials Research. Y.N. acknowledges support from GP-Spin at Tohoku University.
Author information
Authors and Affiliations
Contributions
Y.N. and K.S. carried out the fabrication of the thin films, their characterization and ARPES measurements. S.I. and S.H. performed the transport measurements. Y.O and T.H. performed the STM experiments. T.K. performed the band calculations. K.U. carried out the fabrication of the bulk crystals. Y.N., K.S., T.T., and T.S. finalized the manuscript with input from all the authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Nakata, Y., Sugawara, K., Ichinokura, S. et al. Anisotropic band splitting in monolayer NbSe2: implications for superconductivity and charge density wave. npj 2D Mater Appl 2, 12 (2018). https://doi.org/10.1038/s41699-018-0057-3
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41699-018-0057-3
This article is cited by
-
High anisotropy in electrical and thermal conductivity through the design of aerogel-like superlattice (NaOH)0.5NbSe2
Nature Communications (2023)
-
Tailored Ising superconductivity in intercalated bulk NbSe2
Nature Physics (2022)
-
Robust charge-density wave strengthened by electron correlations in monolayer 1T-TaSe2 and 1T-NbSe2
Nature Communications (2021)
-
Visualizing electronic structures of quantum materials by angle-resolved photoemission spectroscopy
Nature Reviews Materials (2018)