Abstract
The out-of-plane electric polarization at the surface of SrTiO3 (STO), an archetypal perovskite oxide, may stabilize new electronic states and/or host novel device functionality. This is particularly significant in proximity to atomically thin membranes, such as graphene, although a quantitative understanding of the polarization across graphene–STO interface remains experimentally elusive. Here, we report direct observation and measurement of a large intrinsic out-of-plane polarization at the interface of single-layer graphene and TiO2-terminated STO (100) crystal. Using a unique temperature dependence of anti-hysteretic gate-transfer characteristics in dual-gated graphene-on-STO field-effect transistors, we estimate the polarization to be as large as ≈12 μC cm−2, which is also supported by the density functional theory calculations and low-frequency noise measurements. The anti-hysteretic transfer characteristics is quantitatively shown to arise from an interplay of band bending at the STO surface and electrostatic potential due to interface polarization, which may be a generic feature in hybrid electronic devices from two-dimensional materials and perovskite oxides.
Similar content being viewed by others
Introduction
The rich and diverse phenomenology of perovskite oxides,1,2,3,4 which includes electronic and structural phase transitions, colossal magnetoresistance to ferroelectricity and superconductivity, holds great promise for new concepts in device technology and material engineering. The crystal structure of SrTiO3 (STO), a crucial member of the perovskite oxide family that forms the building block of complex oxide heterostructures,5,6 is centrosymmetric and hence a paraelectric in the bulk. STO approaches an incipient ferroelectric state at low temperatures, but quantum fluctuations prohibit a long-range ferroelectric order to develop.7 The quest for stabilizing ferroelectricity in STO has a long history, and it is now known that chemical doping,8,9 nanostructuring,10 manipulation of oxygen stoichiometry11,12 or application of inhomogeneous deformation (flexoelectricity)13 can cause spontaneous electric polarization in the bulk. However, the surface of a STO (100) crystal, in both TiO2 and SrO terminations, can intrinsically host out-of-plane dipole moments due to inversion symmetry breaking at surface, where the Ti or the Sr ions are vertically displaced away from the corresponding oxygen planes. Although surface reconstruction in STO has been established with multiple spectroscopic14,15,16 and surface topography16,17 probes, a direct evaluation of the resulting electric polarization has been difficult. Experiments with piezoresponse force microscopy17,18 and flexoelectric response13 yield surface polarization of ~0.5–10 μC cm−2, which is strongly influenced by local oxygen stoichiometry,19,20 grain boundaries20,21 or surface strain.20 Apart from the natural relevance to in-built ferroelectricity, the importance of surface electrostatics in STO is paramount because it can directly impact charge transfer superconductivity,6 oxide heterostructures5,22,23 and two-dimensional (2D) electronics as active substrates.24,25,26
Hybrid field-effect transistors (FETs) from atomic membranes of layered solids such as graphene and molybdenum disulfide (MoS2) on STO substrate aim to combine the high crystallinity and atomically clean interface to spectacular bulk dielectric properties of STO (dielectric constant >104 at low temperatures). It is however unclear if the out-of-plane polarization at the STO surface is stable in the presence of graphene, for example, against possible atomic reorganization and screening. Recent observations of (anti-)hysteretic gate-transfer characteristics at slow sweep rates in graphene FETs fabricated on STO(100) substrate25,26 are attributed to “ferroelectric-like” electric polarization at the STO surface, which indeed bear close resemblance to transfer characteristics of graphene FET on ferroelectric substrates.27,28,29,30,31 While this has been described as the effect of gate voltage-dependent dynamic trapping and detrapping of charge at the channel–substrate interface, identifying the microscopic origin of such interface states, and its connection to electric polarization at the surface, remains an outstanding experimental challenge.
Here we have probed the interface of graphene and STO by constructing dual-gated graphene-on-STO FETs, which allow direct calibration of the graphene–STO interface against the interface between graphene and hexagonal boron nitride (hBN), a conventional trap-free32 well-characterized dielectric for graphene devices. While the transfer characteristics using hBN top gate shows no hysteresis, that using STO back gate becomes strongly anti-hysteretic at low temperature (≲200 K), which is quantitatively associated with in-built electric polarization at the graphene–STO interface. From detailed temperature dependence of the anti-hysteresis, and independently from noise measurements, we estimate out-of-plane polarization magnitude P ~ 12 μC cm−2, which also agrees with that obtained from density functional theory (DFT) calculations within a factor of two. We have also developed a phenomenological model for anti-hysteretic transfer characteristics using band reconstruction and electrostatic potential at the STO surface, which may be applicable to graphene FETs on other polarized substrates as well.
Results and discussion
Device fabrication and electrical measurement
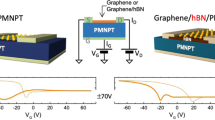
The transport and 1/f noise measurements were carried out in a dual-gated single-layer graphene (SLG) field-effect transistor with hBN as the top gate and STO as the back gate dielectric. The schematic of a typical dual-gated SLG transistor with the electrical layout is shown in Fig. 1a. The TiO2 surface termination of the 0.5 mm thick STO (100) substrate (from CrysTec GmbH) was achieved through chemical processes and annealing (Fig. S1 in Supplementary Information). The SLG and hBN flakes were exfoliated on SiO2/Si++ substrates, and subsequently transferred onto the TiO2−terminated surface of STO through van der Waals epitaxy33,34 (see Methods for more details). The layer number of graphene was verified by Raman spectroscopy as shown in Fig. 1d. The absence of D peak at 1350 cm−1 in the Raman spectrum confirms a defect-free graphene channel. The metal contacts were patterned by e-beam lithography followed by thermal deposition of 5/50 nm of chromium/gold. The optical microscope image of the SLG/hBN heterostructure before transferring onto STO, and the dual-gated transistor after depositing contact pads, are shown in Fig. 1b, c, respectively. All measurements of resistance and noise were carried out using low-frequency AC technique34,35,36,37,38,39,40 in four probe geometry under high vacuum condition (~10−5 torr). The carrier mobility of the graphene channel, similar for both electrons and holes, was found to be ~2000 cm2 Vs−1 at 140 K which increases to ~7300 cm2 Vs−1 at 10 K, in agreement with recent experimental report24 (Fig. S2 in the Supplementary Information). The resistivity of the graphene channel increases with increasing temperature upto ~60 K beyond which it either saturates or decreases marginally (Fig. S3 in the Supplementary Information).
Structure and electrical characterization of graphene–STO hybrid. a Schematic of a dual-gated single-layer graphene (SLG) transistor on STO substrate with STO and hBN as back and top gate dielectrics, respectively, together with the circuit diagram for electrical transport measurement. Optical microscope images of SLG-hBN stack b on the transfer tape before transferring on STO and c after fabricating dual-gated transistor on STO. Scale bars in both (b, c) are 25 μm. d Raman spectroscopy of graphene layer used to make the dual-gated transistor showing single-layer characteristics. e Transfer characteristics with respect to top gate voltage (VTG) at 85 K. The solid and dashed lines depict the resistance of SLG channel with forward and reverse sweeps of top gate voltage respectively. f Transfer characteristics of device D1 with respect to VTG at 100 K showing the shift of charge neutrality points (CNP) at different fixed VBG from 126 V to 158 V. g The locus of the charge neutrality points (\(V_{{\mathrm{TG}}}^{{\mathrm{CNP}}}\)) with varying VBG at different temperatures from 5 K to 200 K. h The dielectric constant of STO (\(\varepsilon _{\mathrm{r}}^{{\mathrm{STO}}}\)) with varying temperatures estimated from three different devices D1, D2 and D3. For device D4, \(\varepsilon _{\mathrm{r}}^{{\mathrm{STO}}}\) was measured from Hall measurement at low temperatures
Measurement of dielectric constant of STO
The resistance of the dual-gated SLG transistor with varying top gate voltage (VTG) shows conventional bell curve with a charge neutrality point (CNP) or Dirac point at \(V_{\mathrm{TG}} \approx - 1.6\) V (Fig. 1e). The hysteresis in the top gate sweep is nearly negligible, as expected from trap-free interface of SLG and hBN.32,41 The dual-gated geometry allows a direct measurement of the dielectric constant of STO (\(\varepsilon _{\mathrm{r}}^{{\mathrm{STO}}}\)) from the locus of the CNP in the (VTG, VBG) space, which balances the STO back gate capacitance with the known capacitance of hBN top gate. In Fig. 1f, the resistance (at T = 100 K) of the dual-gated SLG transistor is shown while sweeping VTG at different fixed back gate voltages (VBG). The CNP (\(V_{{\mathrm{TG}}}^{{\mathrm{CNP}}}\)) shifts expectedly to the left with increasing VBG.42,43 Plotting \(V_{{\mathrm{TG}}}^{{\mathrm{CNP}}}\) vs. VBG (Fig. 1g) gives a straight line which can be fitted with the equation,
where CB and CT are the capacitances of the back gate with STO as dielectric and the top gate with hBN as dielectric, respectively, n0 is the intrinsic carrier density in graphene and e is the electronic charge. Since CT (=2.7 × 10−3 F m−2) is known from the thickness of hBN (≈13 nm, measured from atomic force microscopy), we obtain the dielectric constant \(\varepsilon _{\mathrm{r}}^{{\mathrm{STO}}} = C_{\mathrm{B}}d_{{\mathrm{STO}}}{\mathrm{/}}\varepsilon _0\) (dSTO being the thickness of STO and ε0 the vacuum permittivity) (also see Fig. S4 in the Supplementary Information). The magnitude of \(\varepsilon _{\mathrm{r}}^{{\mathrm{STO}}}\), measured at different temperatures, as shown in Fig. 1h, are in agreement with previous reports7,44,45,46,47 and matches well with the value of \(\varepsilon _{\mathrm{r}}^{{\mathrm{STO}}}\) estimated from Hall measurement at low temperatures. This agreement confirms that both graphene–hBN and graphene–STO interfaces in our device are atomically clean, and free of undesired adsorbates and chemical species.
Anti-hysteretic transfer characteristics
Unlike the top gate, sweeping of the back gate voltage VBG in forward and reverse directions led to strong anti-hysteresis in the transfer characteristics. The extent of anti-hysteresis depends on both temperature and sweep range of VBG. As shown in Fig. 2a, the anti-hysteresis decreases with increasing temperature and vanishes at the temperature range of 150–180 K whereas, it decreases with decreasing sweep range (Fig. 2b). See Fig. S5 in the Supplementary Information for results from different devices. Hysteretic transfer characteristics in graphene FET48 on SiO2 and other substrates49,50,51 are commonly attributed to slow charge transfer in the presence of impurity states and absorbed water molecules. Although our experiment was performed under high vacuum condition, and the collapse of the anti-hysteretic transfer characteristics is observed at significantly low temperature (~180 K), the possibility of physi/chemisorption of OH− and H+ on individual atomic site52 cannot be ruled out. However, the independence of the anti-hysteretic behaviour to the ramp rate in VBG (Fig. S6 in the Supplementary Information) suggests a fundamentally different physical mechanism in our case.
Temperature and gate voltage range-dependent transfer characteristics. a Anti-hysteresis in transfer characteristics with respect to back gate voltage (VBG) at different temperatures showing the decrease in anti-hysteresis with increasing temperature. b Anti-hysteresis in transfer characteristics with respect to VBG at 70 K showing the decrease in anti-hysteresis with decreasing sweep range of VBG. The arrows indicate the direction of VBG sweep in (a, b). c The CNP of forward and reverse sweep directions as a function of overall sweep range of VBG (ΔVBG) at different temperatures for devices D2 and D1 (inset). d The difference in CNP of forward and reverse sweep directions of VBG as a function of temperature at different sweep ranges for devices D2 and D1 (inset)
The similarity of the transfer characteristics to that observed in the earlier studies of graphene transistors on STO substrate25,26 and also in the single/multilayer graphene on ferroelectric substrates27,28,29,30,31 strongly suggests that electric polarization at the surface gives rise to quantum confined states that trap, store and release charge from graphene periodically as VBG is swept back and forth. The temperature and sweep range dependence provide crucial insight into the energy and confinement scale of these states. Figure 2c shows the CNPs (VCNP) for varying sweep range ΔVBG of the back gate. The symmetric positions of the CNPs about VBG = 0 for the forward and reverse sweep directions eliminate oxygen vacancy-mediated anti-hysteretic transfer characteristics.53 In all devices, the (anti-)hysteresis becomes undetectable for ΔVBG ≲ 20 V, i.e., maximum |VBG| = 10 V, which is insensitive to temperature (for T ≲ 200 K). This indicates the energy of the localized trapping state (measured from the Dirac point), \(E_{\mathrm{t}} \sim E_{\mathrm{F}} = \hbar \upsilon_{\mathrm{F}}\sqrt {\pi C_{\mathrm{B}}\left( {V_{{\mathrm{BG}}} - V_{{\mathrm{CNP}}}} \right){\mathrm{/}}e} \sim 0.15\) eV, where υF is the Fermi velocity. The inset of Fig. 2c confirms similar behaviour in a different device (D1).
The temperature dependence of the hysteresis (Fig. 2a) provides an estimate of the energy barrier to charge exchange between the substrate (STO) and graphene. To quantify this, we have plotted the difference in CNP (ΔVCNP) for the forward and the reverse sweep directions in Fig. 2d as a function of temperature. For large sweep range ΔVBG ≳ 100 V, the anti-hysteresis in both D1 (inset) and D2 vanishes at \(\approx 150 - 200\) K, suggesting a confinement energy scale \(\Phi _{\mathrm{P}} \simeq 0.02\) eV. At lower ΔVBG, the hysteretic behaviour vanishes at lower T, possibly due to lower magnitude of effective polarization due to remnant domains.
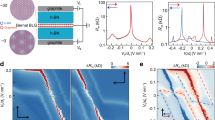
The temperature-dependent anti-hysteretic behaviour can arise from two possible mechanisms. First, the structural transition to the tetragonal phase at low temperatures is known to form domains in the near-surface region, causing rumpling of the surface. This may potentially cause trap states of possibly both structural (domain) and electrostatic (dipole moments) origin. Although the tetragonal domains have been observed to persist up to ~105 K, the temperature dependence of resistance in our case seems to indicate the structural transition to be limited below ~60 K (Fig. S3 in supplementary information). The structural origin is further unlikely because the temperature scale of disappearance of the anti-hysteresis is found to be strongly sweep range dependent, being ~30 K and >200 K (extrapolated) for sweep ranges of ±10 and ±40 V, respectively, in the same device (D2, Fig. 2d). Second, an alternative origin of the hysteretic behaviour can be traced to electrostatically confined trap states arising due to formation of surface dipoles. Our DFT calculations at the graphene–STO interface indicate a possible origin of such surface dipole moments which can be attributed to the movement of Ti and Sr atoms at the surface of STO (Fig. 3a–d). The DFT calculation was performed to estimate the surface polarization, following the formalism adopted by Vanderbilt et al.54 considering slab geometries of paraelectric/ferroelectric bulk compounds.
Calculation of surface band renormalization and out-of-plane dipole moment at the graphene-STO interface. Schematic representation of atomic displacements in [001] (z-direction)-oriented TiO2 terminated STO substrate under different conditions: a non-optimized, b optimized and c optimized with single-layer graphene (SLG) on top, as obtained in DFT calculations in the absence of any external electric field. The displacements of Ti atoms in the topmost TiO2 layer and Sr atoms in the next SrO layer are shown explicitly. The surface polarizations of STO with and without graphene are denoted as \(\bar P_{{\mathrm{STO}} + {\mathrm{SLG}}}\) and \(\bar P_{{\mathrm{STO}}}\), respectively. d Average vertical displacements (Δz) of Ti and Sr atoms at the surface of bare STO and STO with SLG calculated from DFT. e Density of states (DOS) of STO derived from DFT calculation showing the energy band gap of the surface (\(\Delta E_{{\mathrm{gap}}}^{\mathrm{s}}\)) and bulk (\(\Delta E_{{\mathrm{gap}}}\)). f Energy band diagram of STO, SLG and their interface showing the trapped states with potential energy barrier, \(\Phi _{\mathrm{P}}\) appeared due to the presence of surface dipoles. The energy band diagram of the same at g VBG > 0 and h VBG < 0
Two key aspects of the DFT calculations can be summarized as below (see Fig. S8 and associated discussions in the Supplementary Information for more details). First, the vertical displacement (Δz, shown in Fig. 3d) of Ti atoms in TiO2 layer and Sr atoms in SrO layer result in a formation of out-of-plane dipole moment on the surface of STO. The surface dipole moment of bare STO (\(\bar P_{{\mathrm{STO}}} = - 13.89\,\) μC cm−2, in agreement with ref. 54) is significantly enhanced to \(\bar P_{{\mathrm{STO}} + {\mathrm{SLG}}} = - 34.90\,\) μC cm−2 in the presence of graphene. This result is obtained by assuming an epitaxial registration between graphene and STO (model-1). Calculations were also carried out considering model-2, where the lattice parameters of graphene were kept intact. See Supplementary Information section for details. The polarization (\(\bar P_{{\mathrm{STO}} + {\mathrm{SLG}}}\)) calculated for model-1 and model-2 turned out to be −34.9 and −24 μC cm−2, respectively. Thus, the polarization computed from model-2 geometry gives better agreement to experimental value and that obtained from simple phenomenological model. Such enhancement is presumably caused by the rumpling of the surface TiO2 layer in the presence of graphene, as observed in DFT optimized structure. Second, the band gap at the STO surface \(\Delta E_{{\mathrm{gap}}}^{\mathrm{s}} \sim 0.21\) eV is considerably smaller than the band gap of bulk STO \(\Delta E_{{\mathrm{gap}}} \sim 1.84\) eV (Fig. 3e). Notwithstanding the intrinsic underestimation of band gap in DFT due to over-screening problem,55 this indicates a gradual bending of the bulk bands to surface,56 as shown in the schematic of Fig. 3f.
The competing effects of band bending and electrostatic energy due to polarization at the surface can be combined to develop a phenomenological model for the observed anti-hysteretic behavior (Fig. 3f–h). A quantum well may be formed by the decrease in the band gap and the increase in the electrostatic potential \(\approx\)ΔzP2Acell/2ε0εr at the surface due to the dipolar field, where Acell is the area of the TiO2 unit cell. Equating the latter to the confinement scale ΦP ≈ 0.02 eV, and assuming air gap between Ti and O atoms (εr = 1) at the surface, we get P ≈ 13 μC cm−2, which is similar to that obtained from DFT for bare STO, but smaller than expected from graphene–STO hybrid. DFT is well known to overestimate the polarization value even as much as by an order of magnitude, as observed in bulk materials.57 Thus, we consider the agreement between DFT and the value obtained experimentally to be reasonable. The expected trap layer energy \(E_{\mathrm{t}} \approx \Delta E_{{\mathrm{gap}}}^{\mathrm{s}}{\mathrm{/}}2\), where \(\Delta E_{{\mathrm{gap}}}^{\mathrm{s}} \approx 0.21\) eV (Fig. 3e) is the surface band gap, is also close to that (~0.15 eV) estimated experimentally, although the underestimation of the band gap in DFT limits the accuracy of such a comparison.
Figure 3g, h describes the anti-hysteresis process schematically. As the sweep range of VBG (ΔVBG) increases beyond Et, more charge carriers (electrons or holes) get trapped at the interface quantum well which increase the screening of VBG leading to an increase in anti-hysteresis (Fig. 2c). At higher temperature ≳200 K, the anti-hysteresis decreases as thermal energy of the trapped charge carriers becomes too large to remain confined by ΦP.
Unconventional low-frequency 1/f noise
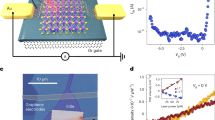
In addition to the transport measurement, the low-frequency 1/f noise in the channel resistance is also sensitive to the interface dipoles. We assume trapping–detrapping noise to be the dominant mechanism for resistnce fluctuation, which is the case for graphene FETs on conventional substrates.37 In the presence of out-of-plane polarization P at STO surface, the interfacial potential barrier that determines the trapping–detrapping rate of charge across the interface, and hence the 1/f noise, is modified by the local effective electric field (\({\vec{\mathbf E}}_{{\mathbf{eff}}}\)) (Fig. 4a, b). The typical time dependence of resistance fluctuations of the graphene channel is shown in Fig. 4d for two representative VBG, with a 1/f-like power spectral density (SR/R2) (Fig. 4e). The details of the noise measurement technique58,59 are discussed in the Methods section and Supplementary Information. Figure 4c, f correlates the variation in noise magnitude with VBG (Fig. 4f) with the anti-hysteretic behavior in the channel resistance R (Fig. 4c). We find that \(\left\langle {\left( {\Delta R} \right)^2} \right\rangle {/R}^2\) (obtained by integrating SR/R2 over the experimental frequency range) displays a strong (anti-)hysteretic two-state behaviour as a function of VBG. The top gate dependence of noise in the same graphene channel is non-hysteretic and exhibits conventional ‘V’-shaped behavior37,60 (Fig. S7 in the Supplementary Information section), confirming that the anti-hysteretic behaviour is due to surface electrical polarization on STO. Remarkably, the VBG dependence of \(\left\langle {\left( {\Delta R} \right)^2} \right\rangle {/R}^2\) collapses on a single trace as function of density n, irrespective of the sweep directions or temperature (Fig. 4g). Since \(n = |{\vec{\mathbf E}}_{{\mathbf{eff}}}|\varepsilon _0/e\), the monotonic change in noise across the Dirac point (\({\vec{\mathbf E}}_{{\mathbf{eff}}} = 0\)) indicates an unconventional microscopic origin that depends on the direction of \({\vec{\mathbf E}}_{{\mathbf{eff}}}\), rather than just its magnitude.
Low-frequency 1/f noise. Schematics of the potential energy barrier of STO surface, a Vb1 at electron-doped region with positive effective electric field (\({\vec{\mathbf E}}_{{\mathbf{eff}}}\)) and b Vb2 at hole-doped region with negative \({\vec{\mathbf E}}_{{\mathbf{eff}}}\) showing Vb2 > Vb1, where \({\vec{\mathbf p}}\) represents the interface dipole moment. c The anti-hysteresis in the transfer characteristics of device D1 at 30 K. d The time series of resistance fluctuations at VBG = 90 V and −30 V, showing higher noise for VBG = 90 V. e Power spectral density (SR/R2) of the resistance fluctuations showing 1/f noise characteristics. f Normalized 1/f noise (\(\left\langle {\Delta R^2} \right\rangle {\mathrm{/}}R^2\)) of SLG on STO with forward sweep (FS) and reverse sweep (RS) of VBG at 30 K, showing a very large magnitude on the right side of the charge neutrality point (CNP) and almost two order of magnitude lower value on the left side of CNP for both FS and RS directions of VBG. g Normalized 1/f noise (\(\left\langle {\Delta R^2} \right\rangle {\mathrm{/}}R^2\)) vs. carrier density (n) of the SLG channel at different temperatures from 7 K to 150 K showing a bistable feature in the electron-doped (red background) and hole-doped (blue background) regions for both FS and RS directions of VBG. h The exponential fitting (blue line) of the noise magnitude near CNP which provides the magnitude of interfacial polarization
When the STO surface is spontaneously polarized, the interface potential barrier \(V_{\mathrm{b}} \approx E_{\mathrm{t}} - {\vec{\mathbf p}}.{\vec{\mathbf E}}_{{\mathbf{eff}}}\) naturally leads to correlated number-mobility fluctuation noise in the graphene channel37,38 that is sensitive to the direction of \({\vec{\mathbf E}}_{{\mathbf{eff}}}\) with respect to the dipole moment \({\vec{\mathbf p}}\) at the surface. Here, \(E_{\mathrm{t}}\left( { \approx \Delta E_{{\mathrm{gap}}}^{\mathrm{s}}{\mathrm{/}}2 \sim 0.1\,{\mathrm{eV}}} \right)\) is the zero-field surface barrier for electron exchange. When the characteristic trapping time scale \(\tau ( = \tau _0exp[2\alpha d])\) is distributed as ~1/τ,61 where \(\alpha = \sqrt {\frac{{2m_{\mathrm{e}}^ \ast V_{\mathrm{b}}}}{{\hbar ^2}}}\), and \(d\) are the tunnelling wave vector and the distance between the channel and surface states of STO substrate, respectively, one obtains
As shown in Fig. 4h, from the exponential fitting of the experimental \(1{\mathrm{/}}f\) noise magnitude with Eq. 2, we obtain \({\vec{\mathbf p}} \approx 3 \times 10^{ - 30}\) C m by assuming \(d \approx 3 \pm 0.5\) nm for the experimental bandwidth. Here, \(m_{\mathrm{e}}^ \ast\) is the effective mass of the electron in STO.62 Estimation of surface polarization through slab calculation14 yields \(P \approx 10\,\) μC cm−2, which is in good agreement to that obtained from the T dependence of anti-hysteresis (Fig. 2a).
In conclusion, we have shown that the dipole field at the surface of STO, created due to the off-centric movement of atoms at the TiO2-terminated surface, strongly impacts both transfer characteristics and low-frequency noise in the graphene-STO hybrid FETs. The key observation of temperature and back gate voltage sweep range-dependent anti-hysteretic transfer characteristics in both resistance and noise suggest formation of trap states at the STO surface due to band renormalization and electrostatic confinement. We quantitatively estimate surface polarization \(P \sim 12\,\) μC cm−2, which is in good agreement with DFT calculated polarization at graphene/STO interface. Our experiment will be useful in characterizing and exploiting interfaces of graphene and polarizable materials.
Methods
TiO2 surface termination of STO
The STO substrates were held with a teflon holder and ultrasonicated in ethanol, deionized (DI) water, buffered hydrofluoric acid and then again in DI water for 30 min in each of them. After cleaning, the STO substrates were placed in a tube furnace and annealed for 2.5 h in an oxygen flow of 300 cc min−1 at 960 °C. Then, the substrates were cooled down to room temperature naturally which generates TiO2 terminated surface63,64 on STO.
Device fabrication and measurements
Graphene and hBN layers were first exfoliated on SiO2 substrate by conventional micromechanical exfoliation. We used a drop of EL9 (baked at 80 °C for 2 h) placed on a transparent plastic sheet to lift suitable layers of graphene and hBN with appropriate orientation and sequence from SiO2 substrate at ~60 °C. For this, we have used a custom-made transfer set-up consisting of an optical microscope-based high-precision mechanical micromanipulator. Subsequently, the stack of 2D heterostructure attached to the EL9 was transferred on to STO surface at T > 100 °C, and the EL9 was dissolved away with acetone to obtain the required heterostructure. Since the EL9 does not come into contact with the graphene/STO or graphene/hBN interfaces at any stage of the fabrication process, the method leads to highly clean van der Waals interfaces.
Transport and noise measurements were performed using a lock-in amplifier while biasing the device in the ohmic regime. The \(1{\mathrm{/}}f\) noise in the graphene channel on STO was measured by calculating the Fourier transform of the auto-correlation function of resistance fluctuations, \(\Delta R(t)\)(=\(R(t) - \langle R\rangle\)), where \(\langle R\rangle\) is the resistance averaged over the experimental time period. We simultaneously measured the time series data for both in-phase and out-of-phase component of the channel resistance, which give total noise and background noise respectively. By subtracting the background noise from the total noise, we get the sample noise. See the Supplementary Information section for details.
DFT calculations
DFT calculations were performed within the framework of plane-wave basis set as implemented in VASP65,66 with projector augmented-wave potential.67,68 For details please see Supplementary Information section.
Data availability
The data regarding experimental and theoretical matter that support the findings of this study are available from A.S. (email: aninditas@iisc.ac.in) and T.S.D. (email: tanusri@boson.bose.res.in), respectively, upon reasonable request.
References
Zubko, P., Gariglio, S., Gabay, M., Ghosez, P. & Triscone, J. M. Interface physics in complex oxide heterostructures. Annu. Rev. Condens. Matter Phys. 2, 141–165 (2011).
Catalan, G. Progress in perovskite nickelate research. Phase Transit. 81, 729–749 (2008).
Cohen, R. E. Origin of ferroelectricity in perovskite oxides. Nature 358, 136–138 (1992).
Bednorz, J. G. & Müller, K. A. Perovskite-type oxides-the new approach to high-Tc superconductivity. Rev. Mod. Phys. 60, 585 (1988).
Ohtomo, A. & Hwang, H. Y. A high-mobility electron gas at the LaAlO3/SrTiO3 heterointerface. Nature 427, 423–426 (2004).
Reyren, N. et al. Superconducting interfaces between insulating oxides. Science 317, 1196–1199 (2007).
Müller, K. A. & Burkard, H. SrTiO3: An intrinsic quantum paraelectric below 4 k. Phys. Rev. B 19, 3593–3602 (1979).
Durán, A., Martínez, E., Díaz, J. A. & Siqueiros, J. M. Ferroelectricity at room temperature in pr-doped SrTiO3. J. Appl. Phys. 97, 104109 (2005).
Kumar, A. S. et al. Magnetic and ferroelectric properties of Fe doped SrTiO3−δ films. J. Phys. Conf. Ser. 200, 092010 (2010).
Lee, D. et al. Emergence of room-temperature ferroelectricity at reduced dimensions. Science 349, 1314–1317 (2015).
Kim, Y. S. et al. Localized electronic states induced by defects and possible origin of ferroelectricity in strontium titanate thin films. Appl. Phys. Lett. 94, 202906 (2009).
Jang, H. W. et al. Ferroelectricity in strain-free SrTiO3 thin films. Phys. Rev. Lett. 104, 197601 (2010).
Zubko, P., Catalan, G., Buckley, A., Welche, P. R. L. & Scott, J. F. Strain-gradient-induced polarization in SrTiO3 single crystals. Phys. Rev. Lett. 99, 167601 (2007).
Bickel, N., Schmidt, G., Heinz, K. & Müller, K. Ferroelectric relaxation of the SrTiO3 (100) surface. Phys. Rev. Lett. 62, 2009 (1989).
Herger, R. et al. Surface of strontium titanate. Phys. Rev. Lett. 98, 076102 (2007).
Dagdeviren, O. E. et al. Surface phase, morphology, and charge distribution transitions on vacuum and ambient annealed SrTiO3 (100). Phys. Rev. B 93, 195303 (2016).
Kholkin, A., Bdikin, I., Ostapchuk, T. & Petzelt, J. Room temperature surface piezoelectricity in SrTiO3 ceramics via piezoresponse force microscopy. Appl. Phys. Lett. 93, 222905 (2008).
Khanbabaee, B. et al. Large piezoelectricity in electric-field modified single crystals of SrTiO3. Appl. Phys. Lett. 109, 222901 (2016).
Petzelt, J. et al. Dielectric, infrared, and raman response of undoped SrTiO3 ceramics: evidence of polar grain boundaries. Phys. Rev. B 64, 184111 (2001).
Kim, M. et al. Nonstoichiometry and the electrical activity of grain boundaries in SrTiO3. Phys. Rev. Lett. 86, 4056 (2001).
Rupprecht, G. & Bell, R. O. Microwave losses in strontium titanate above the phase transition. Phys. Rev. 125, 1915 (1962).
Bousquet, E. et al. Improper ferroelectricity in perovskite oxide artificial superlattices. Nature 452, 732–736 (2008).
Li, Y. L. et al. Interfacial coherency and ferroelectricity of BaTiO3/SrTiO3 superlattice films. Appl. Phys. Lett. 91, 252904 (2007).
Couto, N. J. G., Sacépé, B. & Morpurgo, A. F. Transport through graphene on SrTiO3. Phys. Rev. Lett. 107, 225501 (2011).
Saha, S. et al. Unconventional transport through graphene on SrTiO3: a plausible effect of SrTiO3 phase-transitions. Sci. Rep. 4, 6173 (2014).
Sachs, R., Lin, Z. & Shi, J. Ferroelectric-like SrTiO3 surface dipoles probed by graphene. Sci. Rep. 4, 3657 (2014).
Song, E. B. et al. Robust bi-stable memory operation in single-layer graphene ferroelectric memory. Appl. Phys. Lett. 99, 042109 (2011).
Hong, X. et al. Unusual resistance hysteresis in n-layer graphene field effect transistors fabricated on ferroelectric Pb(Zr0.2Ti0.8)O3. Appl. Phys. Lett. 97, 033114 (2010).
Yusuf, M. H., Nielsen, B., Dawber, M. & Du, X. Extrinsic and intrinsic charge trapping at the graphene/ferroelectric interface. Nano Lett. 14, 5437–5444 (2014).
Hong, X. Emerging ferroelectric transistors with nanoscale channel materials: the possibilities, the limitations. J. Phys. Condens. Matter 28, 103003 (2016).
Kurchak, A. I. & Strikha, M. V. Antihysteresis of the electrical resistivity of graphene on a ferroelectric Pb(ZrxTi1−x)O3 substrate. J. Exp. Theor. Phys. 116, 112–117 (2013).
Dean, C. R. et al. Boron nitride substrates for high-quality graphene electronics. Nat. Nanotechnol. 5, 722–726 (2010).
Roy, K. et al. Graphene-MoS2 hybrid structures for multifunctional photoresponsive memory devices. Nat. Nanotechnol. 8, 826–830 (2013).
Karnatak, P. et al. Current crowding mediated large contact noise in graphene field-effect transistors. Nat. Commun. 7, 13703 (2016).
Pal, A. N. & Ghosh, A. Resistance noise in electrically biased bilayer graphene. Phys. Rev. Lett. 102, 126805 (2009).
Paul, T., Ghatak, S. & Ghosh, A. Percolative switching in transition metal dichalcogenide field-effect transistors at room temperature. Nanotechnology 27, 125706 (2016).
Pal, A. N. et al. Microscopic mechanism of 1/f noise in graphene: Role of energy band dispersion. ACS Nano 5, 2075–2081 (2011).
Pal, A. N., Bol, A. A. & Ghosh, A. Large low-frequency resistance noise in chemical vapor deposited graphene. Appl. Phys. Lett. 97, 133504 (2010).
Kochat, V. et al. Origin of 1/f noise in graphene produced for large-scale applications in electronics. IET Cir. Dev. Syst. 9, 52–58 (2015).
Pal, A. N. & Ghosh, A. Ultralow noise field-effect transistor from multilayer graphene. Appl. Phys. Lett. 95, 082105 (2009).
Zomer, P. J., Dash, S. P., Tombros, N. & van Wees, B. J. A transfer technique for high mobility graphene devices on commercially available hexagonal boron nitride. Appl. Phys. Lett. 99, 232104 (2011).
Avouris, P. Graphene: electronic and photonic properties and devices. Nano Lett. 10, 4285–4294 (2010).
Amet, F., Williams, J. R., Watanabe, K., Taniguchi, T. & Goldhaber-Gordon, D. Insulating behavior at the neutrality point in single-layer graphene. Phys. Rev. Lett. 110, 216601 (2013).
Sakudo, T. & Unoki, H. Dielectric properties of SrTiO3 at low temperatures. Phys. Rev. Lett. 26, 851 (1971).
Tian, J. et al. Quantum and classical magnetoresistance in ambipolar topological insulator transistors with gate-tunable bulk and surface conduction. Sci. Rep. 4, 4859 (2014).
Takashima, H., Wang, R., Prijamboedi, B., Shoji, A. & Itoh, M. Frequency dependence of dielectric constant of strontium titanate films with single-crystal-like behavior. Ferroelectrics 335, 45–50 (2006).
Hemberger, J., Lunkenheimer, P., Viana, R., Böhmer, R. & Loidl, A. Electric-field-dependent dielectric constant and nonlinear susceptibility in SrTiO3. Phys. Rev. B 52, 13159–13162 (1995).
Wang, H., Wu, Y., Cong, C., Shang, J. & Yu, T. Hysteresis of electronic transport in graphene transistors. ACS Nano 4, 7221–7228 (2010).
Mohrmann, J., Watanabe, K., Taniguchi, T. & Danneau, R. Persistent hysteresis in graphene-mica van der waals heterostructures. Nanotechnology 26, 015202 (2014).
Tan, J. Y. et al. Electronic transport in graphene-based heterostructures. Appl. Phys. Lett. 104, 183504 (2014).
Rajapitamahuni, A., Hoffman, J., Ahn, C. H. & Hong, X. Examining graphene field effect sensors for ferroelectric thin film studies. Nano Lett. 13, 4374–4379 (2013).
Henderson, M. A. The interaction of water with solid surfaces: fundamental aspects revisited. Surf. Sci. Rep. 46, 1–308 (2002).
Kang, K. T., Kang, H., Park, J., Suh, D. & Choi, W. S. Quantum conductance probing of oxygen vacancies in SrTiO3 epitaxial thin film using graphene. Adv. Mater. 29, 1700071 (2017).
Meyer, B. & Vanderbilt, D. Ab initio study of BaTiO3 and PbTiO3 surfaces in external electric fields. Phys. Rev. B 63, 205426 (2001).
Perdew, J. P. & Levy, M. Physical content of the exact Kohn-Sham orbital energies: band gaps and derivative discontinuities. Phys. Rev. Lett. 51, 1884 (1983).
Shen, J., Lee, H., Valentí, R. & Jeschke, H. O. Ab initio study of the two-dimensional metallic state at the surface of SrTiO3: importance of oxygen vacancies. Phys. Rev. B 86, 195119 (2012).
Picozzi, S., Yamauchi, K., Sanyal, B., Sergienko, I. A. & Dagotto, E. Dual nature of improper ferroelectricity in a magnetoelectric multiferroic. Phys. Rev. Lett. 99, 227201 (2007).
Sahoo, A., Ha, S. D., Ramanathan, S. & Ghosh, A. Conductivity noise study of the insulator-metal transition and phase coexistence in epitaxial samarium nickelate thin films. Phys. Rev. B 90, 085116 (2014).
Chandni, U. & Ghosh, A. Simple kinetic sensor to structural transitions. Phys. Rev. B 81, 134105 (2010).
Zhang, Y., Mendez, E. E. & Du, X. Mobility-dependent low-frequency noise in graphene field-effect transistors. ACS Nano 5, 8124–8130 (2011).
Jayaraman, R. & Sodini, C. G. A 1/f noise technique to extract the oxide trap density near the conduction band edge of silicon. IEEE Trans. Electron Devices 36, 1773–1782 (1989).
Wunderlich, W., Ohta, H. & Koumoto, K. Enhanced effective mass in doped SrTiO3 and related perovskites. Phys. B Condens. Matter 404, 2202–2212 (2009).
Koster, G., Kropman, B. L., Rijnders, G. J. H. M., Blank, D. H. A. & Rogalla, H. Quasi-ideal strontium titanate crystal surfaces through formation of strontium hydroxide. Appl. Phys. Lett. 73, 2920–2922 (1998).
Kawasaki, M. et al. Atomic control of the SrTiO3 crystal surface. Science 266, 1540–1542 (1994).
Kresse, G. & Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 47, 558 (1993).
Kresse, G. & Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169 (1996).
Blöchl, P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953 (1994).
Kresse, G. & Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758 (1999).
Acknowledgements
The authors thank the Department of Science and Technology (DST) and The Netherlands Organisation for Scientific Research (NWO) for a funded project. A.S., T.P. and A.G. thank the Centre for Nano Science and Engineering (CeNSE), Indian Institute of Science for providing National Nanofabrication (NNfC) and Micro and Nano Characterization Facility (MNCF).
Author information
Authors and Affiliations
Contributions
A.S., D.N., T.P., R.R., A.R., M.M., T.B., T.S.-D. and A.G. designed the experiments. R.R. prepared the TiO2 terminated STO substrate. A.S. and T.P. fabricated the devices and performed the measurements. D.N. and T.S.-D. performed the DFT calculations. A.S., D.N., T.S.-D. and A.G. analysed the data and discussed the results.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Sahoo, A., Nafday, D., Paul, T. et al. Out-of-plane interface dipoles and anti-hysteresis in graphene-strontium titanate hybrid transistor. npj 2D Mater Appl 2, 9 (2018). https://doi.org/10.1038/s41699-018-0055-5
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41699-018-0055-5