Abstract
Heterostructures based on atomically thin semiconductors are considered a promising emerging technology for the realization of ultrathin and ultralight photovoltaic solar cells on flexible substrates. Much progress has been made in recent years on a technological level, but a clear picture of the physical processes that govern the photovoltaic response remains elusive. Here, we present a device model that is able to fully reproduce the current–voltage characteristics of type-II van der Waals heterojunctions under optical illumination, including some peculiar behaviors such as exceedingly high ideality factors or bias-dependent photocurrents. While we find the spatial charge transfer across the junction to be very efficient, we also find a considerable accumulation of photogenerated carriers in the active device region due to poor electrical transport properties, giving rise to significant carrier recombination losses. Our results are important to optimize future device architectures and increase power conversion efficiencies of atomically thin solar cells.
Similar content being viewed by others
Introduction
Two-dimensional (2D) semiconductors1,2,3,4,5 provide a unique opportunity for the realization of ultrathin and ultralight photovoltaic solar cells,6 owing to their strong optical absorption in the solar spectrum region,3,7 high internal radiative efficiencies,8 and favorable band gaps for both single-junction and tandem cells.9 Theoretical estimates of power conversion efficiencies (PCEs) have predicted efficiency values exceeding 25%,9 indicating that 2D semiconductors may become competitive with conventional photovoltaic technologies. The suitability of 2D materials for photovoltaic applications was first demonstrated in lateral p-n junctions,10,11,12 defined by split-gate electrodes, and in lateral Schottky junctions.13 However, those device architectures do not allow for easy scalability of the photoactive area, for which a vertical junction would be desirable. Vertical van der Waals heterostructures14 can be obtained by manual stacking15,16 or growth17,18,19 of different 2D materials in a layered configuration. It has been shown that MoS2 and WSe2, when placed on top of each other, form a type-II heterojunction,20,21,22,23,24 with the lowest-energy conduction band states spatially located in the MoS2 layer and the highest-energy valence band states in WSe2. Relaxation of photogenerated carriers, driven by the conduction and valence band offsets, then results in a charge transfer across the 2D junction and a sizeable photovoltaic effect.20,21,22 Similar results have been obtained using other material combinations that exhibit type-II band alignment, including MoS2/WS2,25 MoS2/black phosphorus,26,27 MoTe2/MoS2,28,29 GaTe/MoS2,30 MoSe2/WSe2,31,32 MoS2/carbon nanotubes,33 MoS2/pentacene,34 MoS2/silicon,35,36 and many more. In addition, homojunction architectures have been explored, in which chemical doping is applied to form a vertical p–n junction in the same 2D material. Examples include plasma-induced p-doping of the upper layers in an n-type MoS2 multi-layer crystal37 and mechanical stacking of few-layer flakes of n-type MoS2:Fe on top of p-type MoS2:Nb.38 In an optimized ~15 nm thick MoS2/WSe2 heterostructure, an experimental absorbance of >90%, an external quantum efficiency (EQE; the ratio between collected charge carriers and incident photons) exceeding 50%, and a (single-wavelength) PCE of 3.4% have been achieved.39
The PCE, defined as the fraction of incident optical power Popt that is converted into electricity with output power Pel, is the most important parameter describing a photovoltaic device. It is given by the product of open-circuit voltage VOC, short-circuit current ISC, and fill factor FF:
Today, fill factors in 2D heterostructure photovoltaic structures are typically in the range 0.3–0.5, only half as large as in conventional silicon solar cells. Closely connected to low fill factors are excessively high (≫2) ideality factors and low short-circuit currents, pointing towards substantial carrier recombination losses. Open-circuit voltages are typically less than 0.6 V, implying a band gap-VOC offset larger than 0.8 V.9 For all these reasons, PCEs in 2D photovoltaic devices have as yet remained below 5%, much lower then the Shockley–Queisser limit for their band gaps.
Besides technological challenges, the lack of a clear picture of the device physics in 2D heterostructure solar cells hampers further progress. Optimization of device architectures, however, will require an in-depth understanding of exciton dissociation, carrier transport processes, and recombination losses. Here, we address these questions by presenting a systematic experimental study of a MoS2/WSe2 van der Waals heterostructure and, based on the results, a model that reproduces the current–voltage characteristics under optical illumination. While we find the exciton dissociation to be very efficient, we also find a considerable pile-up of photocarriers in the device due to poor electrical transport properties, giving rise to carrier recombination and consequently low FF, ISC, and VOC-values. We finally provide guidelines to optimize future device layouts and increase PCEs.
Results
Van der Waals heterostructure solar cell
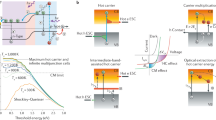
Figure 1a shows a schematic illustration of the MoS2/WSe2 heterostructure investigated in this work. Both layers exhibit monolayer thickness, as verified by Raman spectroscopy.40,41 An optical micrograph of the device can be found in Supplementary Fig. S1a and details about the fabrication process in the Methods section. The corresponding band diagram under short-circuit conditions is schematically depicted in Fig. 1b. As demonstrated later, the charge transfer from one layer into the other occurs with high efficiency. For the subsequent carrier transport to the contacts, driven by the lateral built-in field, it is hence justified to consider electron concentrations in MoS2 (with quasi-Fermi level EF,e) and hole concentrations in WSe2 (with quasi-Fermi level EF,h) only, as schematically depicted in Fig. 1d. For this reason, we refer to the MoS2 sheet as electron transport layer (ETL) and the WSe2 as hole transport layer (HTL). From the data reported in ref.42, we estimate an effective band gap of Eg,eff = EETL − EHTL = ECB,M − EVB,W≈1.3 eV.
Van der Waals heterostructure solar cell. a Schematic illustration of the device structure. b Band diagram in lateral direction under short-circuit conditions. CB conduction band, VB valence band. c Temperature dependent device current, recorded by scanning the back-gate voltage VG. The arrows indicate the p–n regime, in which the device shows a photovoltaic response. Inset: Current-voltage characteristic at room-temperature, recorded at VG = −75 V. Dashed line: dark current; solid line: under optical illumination. d Charge transport model, with effective band gap Eg,eff = ECB,M − EVB,W. The electron concentration in MoS2 is described by the quasi-Fermi level EF,e and hole concentration in WSe2 by EF,h. The quasi-Fermi level splitting, expressed as voltage, is qVint. EF,e and EF,h are assumed to exhibit the same constant tilt throughout the entire device. ETL electron transport layer, HTL hole transport layer. Electron and hole conductivities in the ETL and HTL are denoted as σe and σh, respectively. Note, that in an ideal solar cell with infinite carrier mobility, Vint is zero under short-circuit conditions (illustrated by the black dotted line)
As reported previously,20 the electrical characteristics can be controlled by electrostatic doping via a back-gate voltage VG, applied to the silicon substrate (Fig. 1c). For a large positive VG we find resistive n–n behavior, whereas for an appropriate choice of VG an atomically thin p–n junction is formed and the device current I as a function of external bias voltage V displays diode-like rectification behavior (inset in Fig. 1c, dashed line). All further measurements reported in this article were performed in the p–n regime, indicated by the arrows in Fig. 1c. Under optical illumination (solid line), the curve then passes through the fourth quadrant, meaning that electrical power can be extracted. The EQE is ~1% under low-intensity (~1 kWm-2) illumination at 532 nm wavelength and decreases for higher intensities. Compared to traditional solar cells, the device exhibits some unusual behaviors. For example, the photocurrent (PC), defined as Iph = −(Iillum − Idark), changes sign and becomes negative at V ≳ VOC. Iph also does not become fully saturated under reverse bias, which is an indication for insufficient carrier extraction. These characteristics have been consistently observed not only in all devices that we investigated, but also in many other van der Waals heterostructures reported in literature.
Transport model
The current–voltage I(V) characteristic of a photovoltaic solar cell is usually described by the Shockley diode equation43
where I0 is the dark generation current, q the elementary charge, kB Boltzmann’s constant, and T the temperature. IG denotes the photogenerated current and nid is the ideality factor whose value depends on the type of recombination mechanism: nid = 1 for direct bimolecular (Langevin) recombination and nid = 2 for trap-mediated (Shockley–Read–Hall) recombination. Under open-circuit conditions (V = VOC) the current becomes zero and the well-known relation ∂VOC/∂In(Popt) = nidkBT/q is derived, from which the ideality factor can be determined. Figure 2a shows I(V) characteristics of our device at different optical excitation powers (symbols) from which we can readily extract the open-circuit voltages VOC. Together with the incident optical power Popt, we then determine an ideality factor of nid = 1.6 (see Supplementary Fig. S2), which indicates an involvement of both recombination mechanisms.20,21 However, if we plot Eq. (1) with nid = 1.6 in Fig. 2a (dash-dotted line; Popt = 16 nW) we find very poor agreement with the experimental data. The Shockley equation strongly overestimates short-circuit current, fill factor, and forward current. This is in contrast to lateral 2D semiconductor p–n junctions defined by split-gate electrodes, that can be well described by the Shockley model.10,11
Current–voltage characteristics. a Illumination power dependent I(V) curves at room temperature. Symbols: experimental data; solid lines: fit of Eq. (2); dash-dotted line: fit of Shockley equation to the data recorded with Popt = 16 nW. b Same data as in a, but plotted versus compensation voltage VOC − V on a double-logarithmic scale c Temperature dependent I(V) characteristics
To obtain better modeling of solar cells a series (contact) resistance is often taken into account. However, as shown in Supplementary Fig. S3, an extended Shockley model does not either fit our data. Particularly, the strong illumination dependence of the forward current and the interception of the I(V) curves cannot be explained. Another mechanism that can affect the electrical characteristics of solar cells is the build-up of space charge regions at the contacts or in the bulk, as a result of strongly unbalanced electron and hole transport.44 In order to explore this mechanism, we plot in Fig. 2b the current versus compensation voltage VOC − V on a double-logarithmic scale (symbols). The current shows the usual linear dependence at low compensation voltages, due to the competition between drift and diffusion of photogenerated carriers, and then a smooth transition to the saturation regime for larger voltages. The characteristic fingerprint of space charge-limited transport44—a region with square-root dependence I∝(VOC − V)1/2—is absent. Hence, we conclude that the carrier transport in our device is balanced. A third mechanism that can affect the I(V) characteristics of diodes are interface inhomogeneities. A prominent example are barrier height variations in Schottky diodes,45 that can result in nid > 2. We rule out this possibility for the following reasons. First, the forward current in atomically thin p–n junctions is of different origin than in conventional diodes; it is governed by tunneling-mediated interlayer recombination, rather than carrier injection over a potential barrier.20,21 Second, sample inhomogeneities cannot explain the illumination dependent device behavior.
In the following we will instead argue that the photovoltaic response is transport-limited. It is thus inappropriate to employ Shockley’s model, as it does not account for the impact of charge transport (it assumes infinitely large conductivities for electrons and holes). In order to obtain better modelling of the I(V) characteristics we follow the approach by Würfel et al. initially developed for organic solar cells.46 In brief, carrier accumulation due to poor transport properties leads to a quasi-Fermi level splitting qVint = EF,e − EF,h in the electron and hole transport layers that differs from the externally applied voltage: Vint = V − ξI/σ where σ is the electrical conductivity under optical illumination and ξ is a geometry factor with unit m−1. It is only for open-circuit conditions that Vint = V, and the Shockley equation (2) can be employed. For all other biases, where I ≠ 0, it has been suggested46 to use Vint in (2) instead of V. A closed form approximation of the I(V) curves can then be derived,47 that has been shown to reproduce the results of full drift-diffusion simulations for a wide range of parameters:
with a dimensionless figure of merit α, that is a direct measure of non-ideal device behavior as a result of insufficient carrier extraction. It is given by
where σi denotes the intrinsic electrical conductivity in the dark (see Supplementary Note S1 and ref. 47). If we fit Eq. (3) to the experimental data (solid lines in Figs. 2a, b) we find excellent agreement for all illumination intensities. The photogenerated current IG scales linearly with Popt, as expected (see Supplementary Fig. S4). The ideality parameter α varies over a wide range and reaches values as high as ~78. Insufficient carrier extraction, described by large α values, leads to high carrier densities and consequently to a large quasi-Fermi level splitting Vint, even under short-circuit conditions. As the interlayer recombination is governed by Vint, this results in recombination losses and ISC < IG. Under forward bias, the accumulated charge enhances the conductivity, resulting in the experimentally observed crossing of dark and illuminated I(V) curves. As shown in Supplementary Note S2, expression (4) can be further simplified to yield
where μ denotes the effective carrier mobility in the electron and hole transport layers, krec is the interlayer recombination coefficient, and all other physical constants and geometry factors have been lumped into the prefactor K. The expression predicts a square-root dependence of α on the optical power, which is indeed observed experimentally (Fig. 3a).
Device non-ideality due to transport-limitations. a Parameter α extracted from the I(V) curves versus incident optical power (symbols). Dashed line: fit of Eq. (5). b Arrhenius plot of (normalized) conductivity σi, as extracted from dark-current measurements (red symbols) and photovoltaic measurements (blue symbols). Dashed line: thermally activated transport model. c Circular symbols: FF versus α for all measurements presented in this article. Yellow symbols: application of our model to the data in Refs. 21,37,39. Yellow area: plot of the empirical equation from Ref. 47 for open-circuit voltages between 0.4 and 0.65 V
The question that remains to be addressed is why the carrier extraction in our device is inefficient, given the rather high mobility of 2D semiconductors (typically 10–100 cm2/Vs). In high-mobility materials, such as crystalline silicon, α approaches zero and the impact of charge transport is negligible. In organic materials, on the other hand, μ is extremely low and transport-limitations are expected. From the dark I(V)s in Fig. 1c it is apparent that varying the sample temperature provides us with an opportunity to tune σi (∝Idark) in the p-n regime over almost three orders of magnitude. In Fig. 3b (blue symbols) we depict its temperature variation, and we find that it can be described by a thermally activated transport model,48 σi(T) ∝ exp(−Ea/kBT), with an activation energy Ea≈80 meV (dashed line). Next, we record the temperature dependent photovoltaic properties (Fig. 2c). From that we determine α(T) and then, with Eq. (4), the temperature dependence of σi. If we plot the results as red symbols in Fig. 3b, we find a striking similarity with the dark current measurements. The limitation of the present device architecture becomes clear now. For efficient carrier injection/extraction the heterojunction has to be operated in the p–n regime, in which both layers are strongly depleted (sub-threshold regime). Transport of photogenerated carriers then occurs via thermal activation from the impurity band tails (intrinsic or induced by disorder),49,50,51 which results in low effective carrier mobility and, hence, recombination losses.
As the parameter α determines the shape of the I(V) curves, it is a good figure of merit to assess the quality of solar cells. Neher et al. suggested an empirical expression that relates α to the fill factor.47 In Fig. 3c we plot this expression for the range of open-circuit voltages that is relevant in this work. In the same plot we summarize our experimental results as circular symbols, where the fill factor was determined, as usual, from the maximum power point: FF = max(Pel)/(VOCISC). We conclude that higher conductivities and lower illumination intensities result in better device performance.
Interlayer charge transfer
So far, we have assumed an ultrafast interlayer charge transfer (exciton dissociation), and subsequent charge transport in the ETL and HTL on a longer time scale. We now substantiate this claim by presenting PC autocorrelation measurements, a powerful technique to study the carrier dynamics in 2D materials52,53 and heterostructures.54 It exploits the non-linearity of the photoresponse to infer the underlying dynamics of the system. Using this technique, the device is optically excited with a pair of femtosecond laser pulses (0.2 ps pulse duration), and the integrated PC is recorded as a function of the temporal delay between the pulses. Experimental details are presented in the Methods section and Supplementary Figs. S6 and S7.
Figure 4a shows the absorbance of our device, as determined by a Kramers–Kronig analysis55 of the reflectance spectrum. We identify absorption peaks at 1.65, 1.89, and 2.03 eV, that can be associated with the excitonic ground-state transition of WSe2 and the A and B-excitons in MoS2, respectively. We set the excitation energy of our pulsed laser to 1.65 eV (laser spectrum in Fig. 4a) to resonantly excite excitons in the WSe2 layer only. The resulting PC thus originates from the electron transfer from WSe2 into MoS2. Figure 4b depicts the power dependence, where above ~0.5 μW average incident power a clear saturation behavior is observed. The non-linearity might either stem from phase–space filling, that leads to absorption saturation, or from many-body interactions, such as exciton-exciton annihilation or Auger recombination. Figure 4c shows autocorrelation traces taken for different pulse energies (symbols). Below saturation (bottom curve), a symmetric trace is obtained with (undersampled) optical interference fringes around zero time delay. The linear photoresponse corresponds to the interferometric first-order autocorrelation of the incident light and does not provide any insight in dynamical device behavior. However, when the pulse energy is increased to exceed the saturation threshold, the autocorrelation data become increasingly asymmetric. The characteristic time constant of the nonlinear background signal can be associated with the exciton dissociation time (see Supplementary Note S3). This time is shorter than the pulse duration and we conclude that the dissociation occurs within less than 0.2 ps, similar to what has been obtained in all-optical pump/probe experiments.56 The charge transfer on a time scale shorter than characteristic transport times, confirms the validity of the transport model in Fig. 1d. It also suggests an efficient charge separation from bound excitons after absorption, despite the large exciton binding energy in 2D materials.
Time-resolved photocurrent measurement. a Absorbance spectrum of the heterostructure (symbols) and femtosecond laser spectrum (black line). b Power dependence of the PC (symbols: measurement, solid line: theoretical model). Above ~0.5 μW a clear deviation from an unsaturated behavior (dashed line) is observed. c PC autocorrelation traces for different pulse energies (symbols: measurement, lines: theoretical model). The curves are offset for clarity
Discussion
2D semiconductors contain a significant amount of electronic band tail states.49,50,51 As shown in the previous section, these defects trap charge and adversely affect the electronic transport and, consequently, the PCE. We conclude that the performance of van der Waals heterojunction solar cells is transport-limited and we suggest that Eq. (3) should be used to describe the photovoltaic response, instead of the commonly used Shockley equation. An investigation of the role of defects in the limitation of the open-circuit voltage is beyond the scope of this article, but we note that it is well understood that defects not only reduce FF and ISC, but also VOC.57
To further test out model, we analyzed some exemplary cases from literature. The symbols in Fig. 5a show data points extracted from ref. 21, along with a fit of Eq. (3) as solid line. This work employed a device structure similar to the one presented in this article, but with more favorable (unintentional) doping of the MoS2 and WSe2 layers. This resulted in a comparably high FF despite the high illumination intensity used in the experiment (diamond-shaped symbol in Fig. 3c). We believe that transport-limitations also occur in device architectures that employ optically transparent (graphene or indium-tin-oxide) electrodes for vertical carrier extraction. There, the charge transport occurs on much shorter length scales, but also with extremely low out-of-plane mobilities (~10−2 cm2/Vs).54 In Fig. 5b and c we present two examples taken from refs. 37,39, respectively. The data can again be well fitted by Eq. (3) and the results are summarized as yellow symbols in Fig. 3c. Interestingly, lateral p–n junctions, based on split-gate electrodes, typically show better photovoltaic properties (VOC > 0.85 V,10 FF > 0.7,58 ideality factor < 211) than van der Waals structures. This is explained by the higher electrical conductivities in these devices, because of independent doping of the p and n-type regions.
Based on our results, we finally provide guidelines that might allow to avoid charge pile-up in future device architectures and harness the true potential of 2D materials in photovoltaic applications. We suggest (i) to increase the device conductivity, e.g., by elimination of charge traps or by (chemical) doping, and (ii) to make the active region as thin/short as possible to facilitate more efficient charge extraction before recombination.
Methods
Device fabrication
The van der Waals heterojunction device was fabricated by stacking of mechanically exfoliated MoS2 and WSe2 flakes on a SiO2/silicon substrate, as described in our previous work.20 2D semiconductor monolayer thicknesses were verified beforehand by Raman spectroscopy and photoluminescence (see Supplementary Figs. S1b and S5). Palladium/gold contact electrodes were defined using electron-beam lithography and metal evaporation. Palladium was chosen as trade-off between forming an n-type contact to MoS2 and a p-type contact to WSe2. After fabrication, the samples were annealed in vacuum (~5 × 10−6 mbar) for several hours at a temperature of T = 380 K and mounted on a chip holder.
Optical measurements
The photovoltaic response was measured using a 532 nm wavelength laser, that was focused to a ~1 μm full-width-at-half-maximum (FWHM) spot on the device. The sample was mounted on a motorized XYZ-stage for precise alignment with the laser spot. A camera allowed us to view the illumination position on the device. The optical excitation power was adjusted using a variable optical attenuator and the electrical characteristics were acquired using a Keithley source-meter. Room-temperature measurements were performed under ambient conditions and low-temperature measurements in a flow-cryostat.
Time-resolved measurements
In time-resolved photocurrent measurements, a sequence of two ultrashort laser pulses (τ p = 0.2 ps FWHM pulse duration, f R = 76 MHz repetition rate) was generated using a wavelength-tunable Ti:Sapphire laser and a Michelson interferometer. The time delay between the two pulses was adjustable via a computer-controlled mechanical translation stage in one of the interferometer arms. The laser pulses were then focused with a microscope objective to a ~0.7 μm diameter (FWHM) spot on the sample. Time-resolved experiments were performed at T = 300 K and under ambient conditions.
Data availability
The data used in this study are available upon request from the corresponding author.
References
Novoselov, K. S. et al. Two-dimensional atomic crystals. Proc. Nat. Acad. Sci. USA 102, 10451–10453 (2005).
Podzorov, V., Gershenson, M. E., Kloc, C., Zeis, R. & Bucher, E. High-mobility field-effect transistors based on transition metal dichalcogenides. Appl. Phys. Lett. 84, 3301–3303 (2004).
Mak, K. F., Lee, C., Hone, J., Shan, J. & Heinz, T. F. Atomically thin MoS2: a new direct-gap semiconductor. Phys. Rev. Lett. 105, 136805 (2010).
Splendiani, A. et al. Emerging photoluminescence in monolayer MoS2. Nano Lett. 10, 1271–1275 (2010).
Radisavljevic, B., Radenovic, A., Brivio, J., Giacometti, I. V. & Kis, A. Single-layer MoS2 transistors. Nat. Nanotechnol. 6, 147–150 (2011).
Bernardi, M., Palummo, M. & Grossman, J. C. Extraordinary sunlight absorption and one nanometer thick photovoltaics using two-dimensional monolayer materials. Nano Lett. 13, 3664–3670 (2013).
Gourmelon, E. et al. MS2 (M = W, Mo) photosensitive thin films for solar cells. Sol. Energy Mater. Sol. Cells 46, 115–121 (1997).
Amani, M. et al. Near-unity photoluminescence quantum yield in MoS2. Science 350, 1065–1068 (2015).
Jariwala, D., Davoyan, A. R., Wong, J. & Atwater, H. A. Van der Waals materials for atomically-thin photovoltaics: promise and outlook. ACS Photonics 4, 2962–2970 (2017).
Pospischil, A., Furchi, M. M. & Mueller, T. Solar-energy conversion and light emission in an atomic monolayer p-n diode. Nat. Nanotechnol. 9, 257–261 (2014).
Baugher, B. W. H., Churchill, H. O. H., Yang, Y. & Jarillo-Herrero, P. Optoelectronic devices based on electrically tunable p-n diodes in a monolayer dichalcogenide. Nat. Nanotechnol. 9, 262–267 (2014).
Ross, J. S. et al. Electrically tunable excitonic light-emitting diodes based on monolayer WSe2 p-n junctions. Nat. Nanotechnol. 9, 268–272 (2014).
Fontana, M. et al. Electron-hole transport and photovoltaic effect in gated MoS2 Schottky junctions. Sci. Rep. 3, 1634 (2012).
Geim, A. K. & Grigorieva, I. V. Van der Waals heterostructures. Nature 499, 419–425 (2013).
Castellanos-Gomez, A. et al. Deterministic transfer of two-dimensional materials by all-dry viscoelastic stamping. 2D Mater. 1, 011002 (2014).
Withers, F. et al. Light-emitting diodes by band-structure engineering in van der Waals heterostructures. Nat. Mater. 14, 301–306 (2015).
Gong, Y. et al. Vertical and in-plane heterostructures from WS2/MoS2 monolayers. Nat. Mater. 13, 1135–1142 (2014).
Choudhary, N. et al. Centimeter scale patterned growth of vertically stacked few layer only 2D MoS2/WS2 van der Waals heterostructure. Sci. Rep. 6, 25456 (2016).
Koma, A. Van der Waals epitaxy—a new epitaxial growth method for a highly lattice-mismatched system. Thin Solid Films 216, 72–76 (1992).
Furchi, M. M., Pospischil, A., Libisch, F., Burgdörfer, J. & Mueller, T. Photovoltaic effect in an electrically tunable van der Waals heterojunction. Nano Lett. 14, 4785–4791 (2014).
Lee, C.-H. et al. Atomically thin p-n junctions with van der Waals heterointerfaces. Nat. Nanotechnol. 9, 676–681 (2014).
Cheng, R. et al. Electroluminescence and photocurrent generation from atomically sharp WSe2/MoS2 heterojunction p–n diodes. Nano Lett. 14, 5590–5597 (2014).
Rivera, P. et al. Observation of long-lived interlayer excitons in monolayer MoSe2-WSe2 heterostructures. Nat. Commun. 6, 6242 (2015).
Fang, H. et al. Strong interlayer coupling in van der Waals heterostructures built from single-layer chalcogenides. Proc. Nat. Acad. Sci. USA 111, 6198–6202 (2014).
Huo, N. et al. Novel and enhanced optoelectronic performances of multilayer MoS2-WS2 heterostructure transistors. Adv. Funct. Mater. 24, 7025–7031 (2014).
Deng, Y. et al. Black phosphorus-monolayer MoS2 van der Waals heterojunction p–n diode. ACS Nano 8, 8292–8299 (2014).
Hong, T. et al. Anisotropic photocurrent response at black phosphorus-MoS2 p-n heterojunctions. Nanoscale 7, 18537–18541 (2015).
Pezeshki, A., Shokouh, S. H. H., Nazari, T., Oh, K. & Im, S. Electric and photovoltaic behavior of a few-layer α-MoTe2/MoS2 dichalcogenide heterojunction. Adv. Mater. 28, 3216–3222 (2016).
Zhang, K. et al. Interlayer transition and infrared photodetection in atomically thin type-II MoTe 2 /MoS2 van der Waals heterostructures. ACS Nano 10, 3852–3858 (2016).
Wang, F. et al. Tunable GaTe-MoS2 van der Waals p-n junctions with novel optoelectronic performance. Nano Lett. 15, 7558–7566 (2015).
Flöry, N. et al. WSe2/MoSe2 heterostructure photovoltaic device. Appl. Phys. Lett. 107, 123106 (2015).
Ross, J. S. et al. Interlayer exciton optoelectronics in a 2D heterostructure p-n junction. Nano Lett. 17, 638–643 (2017).
Jariwala, D. et al. Gate-tunable carbon nanotube-MoS2 heterojunction pn diode. Proc. Nat. Acad. Sci. USA 110, 18076–18080 (2013).
Jariwala, D. et al. Hybrid, Gate-Tunable, van der Waals p-n heterojunctions from pentacene and MoS2. Nano Lett. 16, 497–503 (2015).
Tsai, M.-L. et al. Monolayer MoS2 heterojunction solar cells. ACS Nano 8, 8317–8322 (2014).
Lopez-Sanchez, O. et al. Light generation and harvesting in a van der Waals heterostructure. ACS Nano 8, 3042–3048 (2014).
Wi, S. et al. Enhancement of photovoltaic response in multilayer MoS2 induced by plasma doping. ACS Nano 8, 5270–5281 (2014).
Svatek, S. A. et al. Gate tunable photovoltaic effect in MoS2 vertical p-n homostructures. J. Mater. Chem. C. 5, 854–861 (2017).
Wong, J. et al. High photovoltaic quantum efficiency in ultrathin van der Waals heterostructures. ACS Nano 11, 7230–7240 (2017).
Li, H. et al. From bulk to monolayer MoS2: evolution of Raman scattering. Adv. Funct. Mater. 22, 1385–1390 (2012).
Tonndorf, P. et al. Photoluminescence emission and Raman response of monolayer MoS2, MoSe2, and WSe2. Opt. Express 21, 4908–4916 (2013).
Chiu, M. H. et al. Determination of band alignment in the single-layer MoS2/WSe2 heterojunction. Nat. Commun. 6, 7666 (2015).
Shockley, W. The Theory of p-n Junctions in Semiconductors and p-n Junction Transistors. Bell Syst. Tech. J. 28, 435–489 (1949).
Mihailetchi, V. D., Wildeman, J. & Blom, P. W. M. Space-charge limited photocurrent. Phys. Rev. Lett. 94, 126602 (2005).
Chand, S. & Kumar, J. Effects of barrier height distribution on the behavior of a Schottky diode. J. Appl. Phys. 82, 5005–5010 (1997).
Würfel, U., Neher, D., Spies, A. & Albrecht, S. Impact of charge transport on current-voltage characteristics and power-conversion efficiency of organic solar cells. Nat. Commun. 6, 6951 (2015).
Neher, D., Kniepert, J., Elimelech, A. & Koster, L. J. A. A new figure of merit for organic solar cells with transport-limited photocurrents. Sci. Rep. 6, 24861 (2016).
Radisavljevic, B. & Kis, A. Mobility engineering and a metal-insulator transition in monolayer MoS2. Nat. Mater. 12, 815–820 (2013).
Furchi, M. M., Polyushkin, D. K., Pospischil, A. & Mueller, T. Mechanisms of photoconductivity in atomically thin MoS2. Nano Lett. 14, 6165–6170 (2014).
Zhu, W. et al. Electronic transport and device prospects of monolayer molybdenum disulphide grown by chemical vapour deposition. Nat. Commun. 5, 3087 (2014).
Ghatak, S. & Ghosh, A. Observation of trap-assisted space charge limited conductivity in short channel MoS2 transistor. Appl. Phys. Lett. 103, 122103 (2013).
Urich, A., Unterrainer, K. & Mueller, T. Intrinsic response time of graphene photodetectors. Nano Lett. 11, 2804–2808 (2011).
Wang, H., Zhang, C., Chan, W., Tiwari, S. & Rana, F. Ultrafast response of monolayer molybdenum disulfide photodetectors. Nat. Commun. 6, 8831 (2015).
Massicotte, M. et al. Picosecond photoresponse in van der Waals heterostructures. Nat. Nanotechnol. 11, 42–46 (2016).
Mak, K. F. et al. Tightly bound trions in monolayer MoS2. Nat. Mater. 12, 207–211 (2013).
Hong, H. et al. Ultrafast charge transfer in atomically thin MoS2/WS2 heterostructures. Nat. Nanotechnol. 9, 682–686 (2014).
Garcia-Belmonte, G. & Bisquert, J. Open-circuit voltage limit caused by recombination through tail states in bulk heterojunction polymer-fullerene solar cells. Appl. Phys. Lett. 96, 113301 (2010).
Memaran, S. et al. Pronounced photovoltaic response from multilayered transition-metal dichalcogenides PN-junctions. Nano Lett. 15, 7532–7538 (2015).
Acknowledgements
We thank Karl Unterrainer for providing access to a Ti:Sapphire laser and acknowledge financial support by the Austrian Science Fund FWF (START Y 539-N16) and the European Union (grant agreement No. 696656 Graphene Flagship).
Author information
Authors and Affiliations
Contributions
T.M. conceived the experiment. M.M.F. and L.D. fabricated the samples. F.H. and M.M.F. carried out the electrical and optical measurements. D.K.P. and S.S. assisted with the measurements and the sample fabrication. T.M., M.M.F., and F.H. analyzed the data. T.M. prepared the manuscript. All authors discussed the results and commented on the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Furchi, M.M., Höller, F., Dobusch, L. et al. Device physics of van der Waals heterojunction solar cells. npj 2D Mater Appl 2, 3 (2018). https://doi.org/10.1038/s41699-018-0049-3
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41699-018-0049-3
This article is cited by
-
Tailoring electronic and optical properties of hBN/InTe and hBN/GaTe heterostructures through biaxial strain engineering
Scientific Reports (2024)
-
Strain-induced modulation of electronic and optical properties in hBN/InSe heterostructure
Optical and Quantum Electronics (2024)
-
Intriguing type-II g-GeC/AlN bilayer heterostructure for photocatalytic water decomposition and hydrogen production
Scientific Reports (2023)
-
Recent progress in 2D van der Waals heterostructures: fabrication, properties, and applications
Science China Information Sciences (2022)
-
Investigation of optical and electrical properties of graphene oxide/silicon nanowires heterojunction
Journal of Materials Science: Materials in Electronics (2022)