Abstract
In monolayer semiconductor transition metal dichalcogenides, the exciton–phonon interaction strongly affects the photocarrier dynamics. Here, we report on an unusual oscillatory enhancement of the neutral exciton photoluminescence with the excitation laser frequency in monolayer MoSe2. The frequency of oscillation matches that of the M-point longitudinal acoustic phonon, LA(M), suggesting the significance of zone-edge acoustic phonons and hence the deformation potential in exciton-phonon coupling in MoSe2. Moreover, oscillatory behavior is observed in the steady-state emission linewidth and in time-resolved PLE data, which reveals variation with excitation energy in the exciton lifetime. These results clearly expose the key role played by phonons in the exciton formation and relaxation dynamics of two-dimensional van der Waals semiconductors.
Similar content being viewed by others
Introduction
The electron–phonon interaction in solid state systems plays a major role in carrier dynamics,1 particularly in the relaxation of photoexcited carriers in semiconductor nanostructures, such as quantum wells,2 quantum wires,3 and quantum dots.4 Monolayer semiconducting transition metal dichalcogenides (TMDs) have attracted much interest lately due to intriguing two-dimensional (2D) exciton physics, especially relating to their valley degrees of freedom.5, 6 In addition, reduced Coulomb screening in the 2D limit leads to nonhydrogenic exciton series7,8,9 and strong many-body exciton physics.10, 11 Recently, signatures of a strong exciton–phonon interaction have been observed,12, 13 such as the preservation of valley coherence in double-resonant Raman scattering,14 trion to exciton luminescence upconversion in monolayer WSe2 assisted by \(A_1^\prime\) phonons,15 and exciton enhanced anti-Stokes shifts in few layer MoTe2.16 Despite a few theoretical proposals on the role of optical phonons in exciton dynamics,17,18,19 and several experimental studies on phonon-limited exciton relaxation,20,21,22 the details behind how and which phonons impact metrics such as the formation and relaxation of excitons remains largely unexplored. This knowledge is important for interpreting a wide range of 2D exciton phenomena and for exploring the potential of exciton-based 2D optoelectronics.
In this work, we investigate the role of exciton–phonon interaction in exciton dynamics using the model system of monolayer MoSe2 (Fig. 1a). Performing photoluminescence excitation (PLE) spectroscopy, we observe that the neutral exciton PL intensity, as well as its linewidth, oscillates as a function of excitation energy with a period matching that of the longitudinal acoustic phonon at the M point, LA(M). Nested within the oscillations are fine structures, with linewidths one order of magnitude smaller than that of ordinary PL, originating from resonant Raman scattering. Analysis of the emission lineshape of the neutral exciton reveals that the oscillatory behavior also presents in the homogeneous linewidth. Moreover, time-resolved PLE shows that exciton dynamics varies with respect to excitation energy, where shorter emission lifetime is measured for off-phonon-resonance excitation. This might due to the elevated lattice temperature arising from long-wavelength (small k-vector) acoustic phonons, which enhances radiative exciton recombination. Our results show that acoustic LA(M) phonons play an important role in electron-phonon coupling and hot-carrier cooling in monolayer MoSe2, and also suggest the involvement of intermediate indirect excitonic states (with Q-valley electrons) in the formation of K-valley excitons.
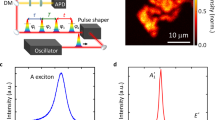
Oscillatory enhancements of neutral exciton PL intensity in monolayer MoSe2. a Optical micrograph of an MoSe2 monolayer on 285-nm-thick SiO2 on silicon. Scale bar: 10 μm. b PLE intensity map of the monolayer shown in a, indicating neutral exciton (X0) and trion (X−) emission centered at 1.650 and 1.624 eV, respectively. Arrows indicate regions of PL enhancement. Color bar: counts per second. c PL spectra at two distinct excitation energies showing the variation of X0 (but not X−) PL with excitation energy
Results and discussions
In our steady-state measurement, we detect PL at 5 K while scanning the excitation energy of a continuous wave (CW) laser, i.e., PLE spectroscopy (see Method Section for experimental details). The PLE intensity plot of Fig. 1b shows excitonic emission energies as a function of laser excitation. Two luminescence peaks are identified23: the neutral A exciton (X0), centered at 1.650 eV, and the negative trion (X−), centered at 1.624 eV. Evidently, the intensity of X0 emission oscillates as a function of excitation laser frequency, while the behavior of X− is monotonic. Figure 1c shows PL spectra taken at the excitation energies 1.699 eV (red) and 1.686 eV (green), which exemplify the contrasting excitation energy dependencies of X0 and X− PL. Within our laser scan range, which has a high-energy limit of 1.77 eV (700 nm), five equally spaced regions of luminescence enhancement, indicated by the white arrows, can be seen in X0, with an average energy separation of 18.5 meV. Such oscillations of X0 emission intensity in PLE, first reported in CdS24 for longitudinal optical phonons, is the hallmark of resonant excitation of phonon modes.
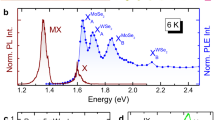
A closer look at Fig. 1b shows that each PLE resonance region contains several narrow peaks. Figure 2a offers an expanded view of the spectral regime highlighted by the white square in Fig. 1b. Three narrow lines shift in parallel with the excitation laser detuning, implying a Raman scattering origin of these lines. Their sub-meV linewidths are consistent with “conventional” Raman spectra measured on a different monolayer MoSe2 sample (Supplementary Discussion), as well as with those reported in the literature.25,26,27 The combined spectral features of PL emission and Raman scattering give rise to the overall emission spectrum, as shown in the example of Fig. 2b. As with earlier studies in monolayer WSe2,14 on top of the spectrally broad features (conventional X0 PL) sits a narrow peak arising from resonant Raman scattering. The intensity of broad X0 PL changes gradually with excitation energy, resulting in a rising PLE background on both ends of the scan range, as apparent in Fig. 2c. This observation has been reported28 and is most probably due to increased absorption near excitonic resonances, e.g., 1 s excitonic state (1.650 eV) on the low energy side and 2 s (1.830 eV) on the high energy side.
Phonon peaks in monolayer MoSe2 PLE spectra. a Magnified view of the region enclosed by the white square in Fig. 1b, showing narrow resonance peaks with corresponding phonon modes indicated. b PL spectrum for 1.678 eV excitation, showing a narrow resonance associated with the \(A_1^\prime\) phonon superimposed on the broader X0 emission. c Vertical line cut of the PLE map at the X0 resonance, plotted in terms of excess energy, defined as the excitation energy subtracted by the X0 resonance. Selected phonon enhanced peaks are labeled with excesses energy in parenthesis (in meV, with 1 meV uncertainty), along with possible assignments
Now we turn to the assignment of the observed phonon modes. The dominant feature in the X0 PLE is the average oscillation period of 18.5 meV. From recent studies of Raman scattering on monolayer MoSe2,25, 27 this period matches that of the M-point longitudinal acoustic phonon, LA(M). Figure 3a shows the locations of M points in the Brillouin zone. According to ab initio calculations reported on monolayer MoS2 and WS2,29, 30 the electron–phonon interaction strength is largest for LA phonons in the vicinity of the M points. Since monolayer MoSe2 is structurally similar to MoS2 and WS2, we expect mode specific characteristics of electron-phonon coupling to qualitatively resemble those of these compounds.30 Therefore, we assign the oscillation in PLE as overtones (harmonic series) of the LA(M). This assignment is corroborated by plotting the PL intensity at the neutral exciton resonance as a function of excess energy (Fig. 2c), defined as the photon energy difference between the excitation laser and the X0 resonance (1.650 eV). Compared to the phonon assignment in ref. 27 we identify the 38-meV peak as the resonant Raman scattering of the 2LA(M) mode. The other higher overtones from 3LA(M) to 6LA(M) are also identified and indicated in Fig. 2c with their respective excess energies. Likewise, we assign the 30 and 35-meV peaks to \(A_1^\prime \left( {{\Gamma }} \right)\) and \({E^\prime }\left( {{\Gamma }} \right)\), respectively. Additional higher-order phonon mode assignments can be found in the Supplementary Discussion. Similar PLE features with identical phonon modes are also observed in a second sample (Supplementary Discussion). Results in Figs. 1 and 2 suggest that the LA(M) mode plays a dominant role in hot exciton relaxation in monolayer MoSe2, giving rise to periodical modulation of PL intensity of the A exciton as a function of excitation photon energy. The importance of LA(M) phonons in exciton dynamics is perhaps ubiquitous in TMDs based on recent studies in few-layer MoS2 31 and WS2.32
Scattering between K-valley electrons and LA(M) phonons. a Wavevectors of M-point phonons in a hexagonal Brillouin zone. b Phonon-mediated transitions of an electron between K and \(\bar Q\) valleys within the Brillouin zone. Here, three M-phonons are involved, with zero net change of electron k-vector. Blue- and red-shaded regions correspond to \(\bar Q\) and Q valleys, respectively. c Lowest conduction band and top valence band of monolayer MoSe2, with the \(\bar Q\) valley indicated. Upon the LA(M) phonon-mediated intervalley scattering of an electron between \(\bar Q\) and K valleys, the optically dark indirect exciton X0(M) can be interconverted with the optically bright exciton X0. Red and blue curves correspond to different spins
As required by momentum conservation during the Raman process, the total phonon wavevector of each phonon enhanced PLE peak indicated in Fig. 2c must be zero. This requirement is easily fulfilled by \(A_1^\prime \left( {{\Gamma }} \right)\) and \(E^\prime \left( {\Gamma } \right)\) modes, but not the fundamental LA(M) mode. However, for the LA(M) overtones, the requirement can be satisfied through the following scenarios. In the case of 2LA(M), a combination of M and \(\bar M\) wavevectors conserves momentum. In 3LA(M), this requirement is met following the scheme shown in Fig. 3b, where an equilateral triangle is formed by three M-vectors, also resulting in a zero vector sum. In monolayer MoSe2, in addition to the K and \(\bar K\) valleys (band edges), the conduction band also has Q and \(\bar Q\) valleys located close to halfway between \({{\Gamma }}\) and K/\(\bar K\) points. The momentum carried by an LA(M) phonon, therefore, matches the momentum separation between the \(K/\bar K\) and \(\bar Q\)/Q valleys (Fig. 3a, b). Thus, following the involvement of M-point phonons, conservation of momentum stipulates that the electron be scattered between K- and \(\bar Q\)-valleys; see Fig. 3c. In other words, phonon-assisted scattering occurs between the optically bright exciton X0 with both the electron and hole in K valley, and the optically dark indirect exciton X0(M) with an electron in \(\bar Q\) and a hole in K valley (Fig. 3c). Here, X0(M) can be a virtual intermediate state such that its energy is not required to match that of X0 + LA(M). Besides, despite the estimated 0.2-eV (ref. 33 ) electron band energy difference between K and Q valleys, the larger effective mass of the Q-valley34 might result in a larger exciton binding energy of X0(M) than that of X0. This binding energy difference can partially cancel the electron band energy difference between Q and K valleys, leading to a smaller energy separation between X0(M) and X0, which enhances the role of X0(M) as an intermediate state. A seemingly related intervalley exciton-phonon scattering is proposed to explain the strong 2LA(M) peak in excitation-dependent Raman spectroscopy of WS2,32 although the excitation therein is well above band edge and involves higher lying conduction bands.
We note that while oscillations due to phonon resonance feature prominently in the X0 transition, the X− emission intensity is relatively constant, except for excitation below 1.68 eV, close to the X0 resonance of 1.65 eV. The lack of oscillatory enhancement in X− is possibly due to its distinct radiative properties compared to X0, together with the availability of multiple formation pathways35 (e.g., via the exciton–electron interaction following exciton relaxation36). For X0, only those inside the light cone (\(k \le {\omega _{{X^0}}}/c\)) can radiate. In contrast, X− with a much larger range of momentum can radiate due to the electron recoil effect.23 As a result, X0 PL intensity depends strongly on its momentum distribution, as determined by the resonance condition of the excitation energy, while such dependency is weak for X−. Moreover, the X− formation process is largely independent of the excitation energy, because even for excitation away from the phonon resonances, optically dark excitons can still be generated at large momentum (outside the light cone), which can interact with electrons to form trions. The lack of sensitivity to the excitation energy in both trion formation and relaxation processes diminishes any oscillatory features in the X− emission. A more detailed discussion can be found in the Supplementary Discussion.
Aside from spectral information, the PLE map also offers insights into the exciton dynamics. From the fit to the spectrum taken at each excitation energy, we found that both X− and X0 lineshapes are well-described by Voigt profiles, from which one can infer the homogeneous linewidths of the excitonic transitions, as well as the widths of the Gaussian-broadened spectral distributions of their resonances (Supplementary Discussion). The latter is associated with the inhomogeneous broadening of the excitonic transitions. Oscillatory behavior is found in the homogeneous linewidth, γ 0, of X0, which is smaller for excitation resonant with phonon harmonics (Fig. 4a). Its inhomogeneous (Gaussian) width remains relatively constant, consistent with the expectation that inhomogeneous broadening should depend only weakly on excitation energy. γ 0 is associated with the coherence lifetime of the exciton, and is given by γ 0 = γ/2 + Γ, where γ is the inverse of exciton population lifetime and Γ the pure dephasing rate. Since Γ is proportional to the rate of dephasing processes such as exciton-phonon scattering,22 it is reasonable to assume that the oscillations in γ 0 is largely due to the creation of long-wavelength phonons during the relaxation of excited (hot) excitons. Our analysis on time-resolved PLE data (more details discussed below and in the Supplementary Discussion) seems to support this interpretation.
LA(M) phonon-induced modulation of exciton dynamics in monolayer MoSe2. a Oscillations in the best-fit homogeneous linewidth, γ 0, of the X0 resonance with the excess energy as defined in Fig. 2c. Error bars represent 99% confidence intervals of the fits. Inset: Width of inhomogeneous (Gaussian) broadening, σ. b An example of raw streak camera data for excitation centered at 1.732 eV. The trion (X−) and neutral exciton (X0) resonances are marked by dashed lines P–P' and Q−Q', respectively. Color bar: signal intensity in log-scale, arbitrary unit. c, d Time-traces of the X− and X0 resonances, respectively, after a 2D Gaussian filter and deconvolution (Supplementary Discussion), in log-scale. The 10–90% rise-times are indicated, along with the best-fit exponential decay lifetimes, τ. Circles and red solid lines represent data points and linear fits to the exponential decay, respectively. e Lifetimes, τ, of X− (crosses) and X0 (circles) extracted from a series of streak camera measurements with varying excitation energy. In the x-axis, similar to how the excess energy is defined, a constant X0 energy (1.650 eV) is subtracted from the excitation center frequency. Error bars represent standard deviations, while the dashed line serves as guide to the eye. Shaded regions indicate phonon resonances as obtained from Fig. 1b
To explore the phonon-assisted dynamics directly, we measure time-resolved emission of X0 and X− with a streak camera. Figure 4b presents an example of the measured spectra with the pulsed excitation centered at 1.732 eV. The time evolution of the emission is characterized by a rapid onset within a few picoseconds, followed by an exponential decay. This is shown by extracting time traces along P−P' and Q−Q' from Fig. 4b for X− and X0 and plotted in Fig. 4c, d, respectively. Here, a 2D Gaussian filter is applied to the raw data, followed by deconvolution with Tikhonov regularization (see Supplementary Discussion), resulting in smooth temporal profiles from which the 10–90% rise time and lifetime (τ) can be estimated. By stepping the center frequency of the pulses, excitation energy dependent rise times and lifetimes are obtained and the latter is plotted in Fig. 4e, where shaded regions indicate energies of phonon-enhanced PL seen in the PLE map in Fig. 1b.
Although fluctuation with the excitation energy is apparent in the rise times of X0 and X− emission (Supplementary Discussion), due to the measurement noise and the resolution of the streak camera, we are unable to observe an unambiguous systematic variation with the excitation energy. A further study with improved experimental method and cleaner data is needed to determine whether the rise times oscillate in accordance to the phonon modes seen in Fig. 1b. Nonetheless, in Fig. 4e showing the emission lifetimes, despite the noise caused by excitation pulse leak-through at energies below 1.73 eV, the remaining data shows clear oscillations of the X0 emission lifetime, i. e., the exciton relaxation dynamics is affected by resonant excitation of the LA(M) phonon mode. To understand this effect, we propose a framework using rate equations to model phonon-assisted interconversions between excitons inside and outside the light cone (Supplementary Discussion). In brief, a thermalized population of excitons both inside and outside the light cone is formed shortly after excitation. The bright (inside the light cone) excitons quickly recombine,37, 38 leaving behind the dark excitons, which are then scattered into the light cone by phonons (Fig. 5a) and recombine at a later time, producing the observed exponential decay. When the excitation is off-resonant, excitonic relaxation results in the emission of many long-wavelength phonons (Fig. 5b), forming a phonon bath that increases the scattering rate. On the other hand, on-resonance excitation (Fig. 5c) produces only a small number of LA(M) phonons which are ineffective in the aforementioned scattering process due to momentum mismatch. This picture is consistent with the oscillations of γ 0 shown in Fig. 4a, i.e., the creation of long-wavelength phonon bath during off-resonance excitation increases exciton-phonon scattering and manifests as a broadening of the X0 homogeneous linewidth.
Exciton-phonon scattering processes with off/on phonon resonance excitation. a Schematic showing inward and outward scattering of the excitons across the light cone due to long-wavelength phonons. b Energy level scheme showing optical excitation (blue arrow) away from a phonon resonance, intervalley relaxations accompanied by the emission of LA(M) phonons (purple wavy arrows) and the eventual fluorescence-producing radiative decay of X0 (red arrow). The laser generates X0 with finite kinetic energies following the emission of LA(M) phonons. X0 then relaxes to the minimum energy by emitting long wavelength phonons (green curved arrows). c On-phonon-resonance excitation where only a small number of LA(M) phonons are emitted in the ensuing relaxation
To summarize, we observed excitation energy-dependent oscillatory behavior of X0 luminescence and dynamics, which largely stems from resonant excitation of LA(M) phonon modes in monolayer MoSe2. Remarkably, it is the phonon at the Brillouin zone edge (M-point) that dominates the multiple-phonon scattering during hot exciton relaxation. This suggests the involvement of an intermediate X0(M) state and may present an opportunity to investigate the dynamics of intervalley excitonic transitions in 2D semiconductors. The prevailing involvement of acoustic phonons, rather than of optical phonons, is in agreement with density functional theory calculations.29, 30 This implies that the deformation potential coupling dominates over Fröhlich coupling in our samples, although the converse is normally expected, as reported in CdS.24 Further studies are needed to fully elucidate the process of carrier-phonon interactions in semiconducting TMDs, especially with regard to material- and phonon-mode-specific details. Nonetheless, our results can potentially be exploited to understand exciton related physics and design optoelectronics applications based on 2D semiconductors.
Methods
Bulk MoSe2 crystals are synthesized using chemical vapor transport technique with iodine as transport agent. To obtain monolayer MoSe2 samples, thin MoSe2 flakes are mechanically exfoliated from bulk crystals onto 285-nm-thick SiO2 thermally grown on Si wafers. Monolayers are first identified visually by their optical contrast under a microscope and then confirmed by measuring their thickness (~ 0.7 nm) using atomic force microscopy. Throughout the experiments, the samples are maintained at a temperature of 5 K in a cold finger cryostat.
All optical studies are made in reflection geometry, where the incident beam and fluorescence traverse the same microscope objective mounted on a micrometer stage assembly. The use of a high-power microscope objective with cover-slip correction results in a focal spot size of less than 1 μm in diameter. For PLE measurements, a Ti-Sapphire tunable CW laser (Solstis from M-Squared Lasers, LTD) is used to produce the excitation beam. The incident power is held at 20 μW, below the PL saturation threshold of about 100 μW. The excitation frequency is scanned at a rate of 5 s per step and with a step size of 1 meV (~ 0.42 nm at 721 nm). Rejection of the reflected excitation laser is accomplished first by an analyzer and then by spectral filtering. The spectral filter consists of a pair of achromatic doublets forming a 1:1 telescope, and a pair of gratings positioned at the outward conjugate focal planes. At the central focal plane, the spectral distribution of the fluorescence is mapped into spatial separation, and a graphite rod mounted on a translational stage is used to block the frequency component belonging to the excitation laser. Finally, fluorescence spectra are measured with a liquid-nitrogen-cooled charge-coupled device (CCD) camera attached to the output port of a spectrometer (Princeton Acton SP2500). The final spectral resolution is 0.027 nm (~ 0.06 meV at 755 nm), limited by the pixel size of the CCD camera. Each spectrum is taken with an accumulation time of 5 s.
In time-resolved PLE measurements, the excitation beam is produced by a wavelength-tunable, mode-locked Ti-Sapphire laser with a pulse repetition rate of 80 MHz, and a pulse duration of 150 fs. The bandwidth of the output pulses, of about 17 meV, is unsuitable for resolving the oscillatory behavior, which is expected to have a period of about 18.5 meV. The pulse bandwidth is therefore reduced to about 5 meV with the aid of the spectral filter described above, only with the graphite rod now replaced by a slit. This introduces a chirp to the pulses, which is then compensated by passing the beam through a single mode fiber with a predetermined length. The fiber serves a secondary purpose of producing a clean Gaussian beam profile to help achieving the best beam spot on the sample. The central wavelength of the pulses is tuned with 1-nm steps (~ 2.4 meV at 721 nm), and the average power is held constant at 50 μW. This corresponds roughly to a photogenerated exciton density on the order of 1011–1012 cm−2. A streak camera (Hamamatsu C10910-05) with a nominal resolution of 1 ps is used to register the time-resolved fluorescence spectra. The streak camera is operated at a moderate gain, optimized for the best signal-to-noise ratio, with a 100-s integration time for each spectrum.
Procedures for PL lineshape fitting, data post-processing and analysis, and further discussions can be found in the Supplementary Discussion accompanying the paper.
Data availability
Data that supports the findings of this study is available from the corresponding authors upon reasonable request.
References
Ueta, M., Kanzaki, H., Kobayashi, K., Toyozawa, Y. & Hanamura, E. Excitonic Processes in Solids. (Springer-Verlag Berlin Heidelberg, 1986). https://doi.org/10.1007/978-3-642-82602-3.
Seilmeier, A., Hübner, H., Abstreiter, G., Weimann, G. & Schlapp, W. Intersubband relaxation in GaAs-AlxGa1-xAs quantum well structures observed directly by an infrared bleaching technique. Phys. Rev. Lett. 59, 1345–1348 (1987).
Bellessa, J. et al. Quantum-size effects on radiative lifetimes and relaxation of excitons in semiconductor nanostructures. Phys. Rev. B 58, 9933–9940 (1998).
Bockelmann, U. Exciton relaxation and radiative recombination in semiconductor quantum dots. Phys. Rev. B 48, 17637–17640 (1993).
Yu, H., Cui, X., Xu, X. & Yao, W. Valley excitons in two-dimensional semiconductors. Natl Sci. Rev. 2, 57–70 (2015).
Xu, X., Yao, W., Xiao, D. & Heinz, T. F. Spin and pseudospins in layered transition metal dichalcogenides. Nat. Phys. 10, 343–350 (2014).
He, K. et al. Tightly bound excitons in monolayer WSe2. Phys. Rev. Lett. 113, 26803 (2014).
Chernikov, A. et al. Exciton binding energy and nonhydrogenic Rydberg series in monolayer WS2. Phys. Rev. Lett. 113, 76802 (2014).
Ye, Z. et al. Probing excitonic dark states in single-layer tungsten disulphide. Nature 513, 214–218 (2014).
Mak, K. F. et al. Tightly bound trions in monolayer MoS2. Nat. Mater. 12, 207–211 (2012).
Ugeda, M. M. et al. Giant bandgap renormalization and excitonic effects in a monolayer transition metal dichalcogenide semiconductor. Nat. Mater. 13, 1091–1095 (2014).
Qiu, D. Y., da Jornada, F. H. & Louie, S. G. Optical spectrum of MoS2: many-body effects and diversity of exciton states. Phys. Rev. Lett. 111, 216805 (2013).
Carvalho, B. R., Malard, L. M., Alves, J. M., Fantini, C. & Pimenta, M. A. Symmetry-dependent exciton-phonon coupling in 2D and bulk MoS2 observed by resonance Raman scattering. Phys. Rev. Lett. 114, 136403 (2015).
Wang, G. et al. Double resonant Raman scattering and valley coherence generation in monolayer WSe2. Phys. Rev. Lett. 115, 117401 (2015).
Jones, A. M. et al. Excitonic luminescence upconversion in a two-dimensional semiconductor. Nat. Phys. 12, 323–327 (2016).
Goldstein, T. et al. Raman scattering and anomalous stokes–anti-stokes ratio in MoTe2 atomic layers. Sci. Rep. 6, 28024 (2016).
Dery, H. & Song, Y. Polarization analysis of excitons in monolayer and bilayer transition-metal dichalcogenides. Phys. Rev. B 92, 125431 (2015).
Danovich, M., Aleiner, I., Drummond, N. D. & Fal’ko, V. Fast relaxation of photo-excited carriers in 2D transition metal dichalcogenides. IEEE J. Sel. Top. Quantum Electron. 23, 6000105 (2017).
Kaasbjerg, K., Bhargavi, K. S. & Kubakaddi, S. S. Hot-electron cooling by acoustic and optical phonons in monolayers of MoS2 and other transition-metal dichalcogenides. Phys. Rev. B 90, 165436 (2014).
Salehzadeh, O., Tran, N. H., Liu, X., Shih, I. & Mi, Z. Exciton kinetics, quantum efficiency, and efficiency droop of monolayer MoS2 light-emitting devices. Nano Lett. 14, 4125–30 (2014).
Dey, P. et al. Optical coherence in atomic-monolayer transition-metal dichalcogenides limited by electron-phonon interactions. Phys. Rev. Lett. 116, 127402 (2016).
Moody, G. et al. Intrinsic homogeneous linewidth and broadening mechanisms of excitons in monolayer transition metal dichalcogenides. Nat. Commun. 6, 8315 (2015).
Ross, J. S. et al. Electrical control of neutral and charged excitons in a monolayer semiconductor. Nat. Commun. 4, 1474 (2013).
Conradi, J. & Haering, R. R. Oscillatory exciton emission in CdS. Phys. Rev. Lett. 20, 1344–1346 (1968).
Zhang, M. et al. Two-dimensional molybdenum tungsten diselenide alloys: photoluminescence, Raman scattering, and electrical transport. ACS Nano 8, 7130–7137 (2014).
Zhang, X. et al. Phonon and Raman scattering of two-dimensional transition metal dichalcogenides from monolayer, multilayer to bulk material. Chem. Soc. Rev. 44, 2757–2785 (2015).
Soubelet, P., Bruchhausen, A. E., Fainstein, A., Nogajewski, K. & Faugeras, C. Resonance effects in the Raman scattering of monolayer and few-layer MoSe2. Phys. Rev. B 93, 155407 (2016).
Wang, G. et al. Exciton states in monolayer MoSe2: impact on interband transitions. 2D Mater 2, 45005 (2015).
Li, X. et al. Intrinsic electrical transport properties of monolayer silicene and MoS2 from first principles. Phys. Rev. B 87, 115418 (2013).
Jin, Z., Li, X., Mullen, J. T. & Kim, K. W. Intrinsic transport properties of electrons and holes in monolayer transition-metal dichalcogenides. Phys. Rev. B 90, 45422 (2014).
Nie, Z. et al. Ultrafast electron and hole relaxation pathways in few-layer MoS2. J. Phys. Chem. C 119, 20698–20708 (2015).
Berkdemir, A. et al. Identification of individual and few layers of WS2 using Raman spectroscopy. Sci. Rep. 3, 1755 (2013).
Zhang, C. et al. Probing critical point energies of transition metal dichalcogenides: surprising indirect gap of single layer WSe2. Nano Lett. 15, 6494–6500 (2015).
Kormányos, A. et al. k·p theory for two-dimensional transition metal dichalcogenide semiconductors. 2D Mater 2, 22001 (2015).
Gao, F. et al. Valley trion dynamics in monolayer MoSe2. Phys. Rev. B 94, 245413 (2016).
Singh, A. et al. Trion formation dynamics in monolayer transition metal dichalcogenides. Phys. Rev. B 93, 41401 (2016).
Poellmann, C. et al. Resonant internal quantum transitions and femtosecond radiative decay of excitons in monolayer WSe2. Nat. Mater. 14, 889–893 (2015).
Robert, C. et al. Exciton radiative lifetime in transition metal dichalcogenide monolayers. Phys. Rev. B 93, 205423 (2016).
Acknowledgements
This work is mainly supported by the Department of Energy, Basic Energy Sciences, Materials Sciences and Engineering Division (DE-SC0008145 and SC0012509). H.Y. and W.Y. are supported by the Croucher Foundation (Croucher Innovation Award), HKU ORA, and the RGC and UGC of Hong Kong (HKU17305914P, AoE/P-04/08). M.K. and D.G.M. are supported by US DoE, BES, Materials Sciences and Engineering Division. R.M. is supported by the MRSEC Program of the NSF under Grant No. DMR-1120923. X.X. acknowledges a Cottrell Scholar Award, support from the State of Washington funded Clean Energy Institute, and Boeing Distinguished Professorship.
Author information
Authors and Affiliations
Contributions
X.X. and W.Y. conceived and supervised the experiments. C.M.C. fabricated the sample and performed the measurements assisted by A.M.J. and J.R.S. C.M.C., X.X., H.Y., W.Y., R.M. analyzed the data. M.K. and D.G.M. provided and characterized the bulk MoSe2. C.M.C., X.X., W.Y., H.Y., R.M. wrote the paper. All authors discussed the results.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Chow, C.M., Yu, H., Jones, A.M. et al. Phonon-assisted oscillatory exciton dynamics in monolayer MoSe2 . npj 2D Mater Appl 1, 33 (2017). https://doi.org/10.1038/s41699-017-0035-1
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41699-017-0035-1
This article is cited by
-
Theory of coherent phonons coupled to excitons
npj 2D Materials and Applications (2024)
-
Raman scattering excitation in monolayers of semiconducting transition metal dichalcogenides
npj 2D Materials and Applications (2024)
-
Probing the optical near-field interaction of Mie nanoresonators with atomically thin semiconductors
Communications Physics (2023)
-
K-point longitudinal acoustic phonons are responsible for ultrafast intervalley scattering in monolayer MoSe2
Nature Communications (2022)
-
Temperature induced modulation of resonant Raman scattering in bilayer 2H-MoS2
Scientific Reports (2022)