Abstract
Light properties in the mid-infrared can be controlled at a deep subwavelength scale using hyperbolic phonons-polaritons of hexagonal boron nitride. While propagating as waveguided modes hyperbolic phonons-polaritons can concentrate the electric field in a chosen nano-volume. Such a behavior is at the heart of many applications including subdiffraction imaging and sensing. Here we employ HPPs in heterostructures of hexagonal boron nitride and graphene as new nano-optoelectronic platform by uniting the benefits of efficient hot-carrier photoconversion in graphene and the hyperbolic nature of hexagonal boron nitride. We demonstrate electrical detection of hyperbolic phonons-polaritons by guiding them towards a graphene pn-junction. We shine a laser beam onto a gap in metal gates underneath the heterostructure, where the light is converted into hyperbolic phonons-polaritons. The hyperbolic phonons-polaritons then propagate as confined rays heating up the graphene leading to a strong photocurrent. This concept is exploited to boost the external responsivity of mid-infrared photodetectors, overcoming the limitation of graphene pn-junction detectors due to their small active area and weak absorption. Moreover this type of detector exhibits tunable frequency selectivity due to the hyperbolic phonons-polaritons, which combined with its high responsivity paves the way for efficient high-resolution mid-infrared imaging.
Similar content being viewed by others
Introduction
Hexagonal boron nitride has found multiple uses in van der Waals heterostructures1,2,3,4,5,6,7,8, such as a perfect substrate for graphene,9, 10 a highly uniform tunnel barrier,11, 12 and an environmentally robust protector. In particular, h-BN substrates enable one to achieve high carrier mobility and homogeneity in graphene.9, 10 In addition, h-BN is a natural hyperbolic material as in the two so called reststrahlen bands (760–825 cm−1 and 1360–1610 cm−1) the in plane (\({\epsilon _{{\rm{x,y}}}}\)) and the out of plane (\({\epsilon _{\rm{z}}}\)) permittivity are of opposite sign.1, 3, 4 As a consequence, h-BN supports propagating hyperbolic phonon-polaritons (HPPs) which are electromagnetic modes1, 3 originating in the coupling of photons to optical phonons. Because of their unique physical properties such as long lifetime, tunability,2 slow propagation velocity,8 and strong field confinement the HPPs have a great potential for applications in nanophotonics. The capability to concentrate light into small volumes can also have far-reaching implications for opto-electronic technologies, such as mid-infrared photodetection,13,14,15,16,17,18,19 on-chip spectroscopy and sensing. These concepts, however, remain underexplored.
Here we present a hyperbolic opto-electronic device that takes taking advantage of that fact that h-BN is at the same time an ideal substrate for graphene as well as an excellent waveguide for HPPs. We show how HPPs can be exploited to concentrate the electric field of incident mid-infrared beam towards a graphene pn-junction, where it is converted to a photovoltage. The impact of the HPPs leads to a strongly increased responsivity of the graphene pn-junction in the mid-infrared up to 1 V/W, with zero bias applied.
In previous studies graphene pn-junctions have shown very high internal efficiencies20,21,22,23,24,25 due to the strong photo-thermoelectric effect in graphene. However, the active area of this type of devices is extremely small, leading to poor light collection. For detecting mid-infrared light this issue is even more acute. By exciting hyperbolic phonon polaritons we strongly enhance the effective absorption. We compare our experimental results with FDTD simulations and an analytical model, providing insight into the underlying physical processes and the frequency tunability of our novel mid-infrared detectors.
Results
The investigated devices consist of heterostructures of monolayer graphene encapsulated in h-BN, obtained by the polymer-free van der Waals assembly technique,10 and placed on top of two metal gates separated by a narrow gap (Fig. 1a). The graphene layer has a mobility of ~30,000 cm2 Vs−1. It is electrically connected to the source and drain electrodes by edge contacts10 (Methods section). An optical micrograph of a typical device is shown in Fig. 1b. The individually tunable carrier density on both sides of the split gate is used to tune the photosensitivity of our device.20,21,22, 24
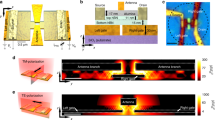
Device schematic and working principle. a Schematic of the encapsulated graphene pn-junction. The h-BN/graphene/h-BN is placed on two gold split gates and contacted electrically by the edges. b Optical image of one device: the top (bottom) BN is blue (yellow). The black rectangle indicates the measurement region in d. The distance between the two gates in this device is 100 nm. c Side view of the propagating hyperbolic phonon-polaritons simulated by FDTD for the device in b. The thickness of the bottom h-BN is 50 nm and the top h-BN is 55 nm. HPPs are launched at the edges of the split gates and propagate as directional rays. While they cross the graphene plane they are partially absorbed leading to a temperature increase in the graphene. d Spatial map of the device responsivity for a polarization of the laser perpendicular to the gap of the split gate. The photoresponse arises at the junction, indicated by the dashed dotted line. The graphene edge is indicated by the solid black line. The gate voltages used here are (V g1 = 1.2 V and V g2 =−0.21 V). The electric field polarization and propagation direction (E, k) are represented in c and d
The operation of our device is as follows. HPPs are launched at the sharp gold edges of the split gate when the laser beam illuminates the sample under normal incidence with the polarization perpendicular to the gap between the gate electrodes.3, 8, 26 While the HPPs propagate as highly directional rays in both bottom and top h-BN slabs of the stack, they are absorbed when they pass through graphene (Fig. 1c) creating hot carriers. The hot carriers diffuse over a length scale of the electron cooling length (about 0.5–1 μm) and generate a temperature increase peaking at the graphene junction defined by the position of the gap in the metal gates. This inhomogeneous temperature distribution induces a photovoltage due to the Seebeck effect. Thus, all HPPs absorbed within approximately one cooling length from the junction contribute to the photovoltage. Similar HPPs lauching presumably also occurs at the source and drain gold contacts. However, they do not contribute to the photovoltage because the electrodes are situated much further than the electron cooling length from the junction.
The measured spatially resolved photoresponse of the device is shown in Fig. 1d. The photoresponse arises mainly at the junction (shown as a dashed line). In such a graphene junction the photovoltage V ph is generated by the photo-thermoelectric effect:20,21,22, 24, 27
where, ΔS = S 1 − S 2 is the difference between the Seebeck coefficients of graphene on the left and right side of the junction and ΔT is the difference in electronic temperature at the junction and at the source/drain contacts. The photo-thermoelectric effect dominates over other possible mechanisms of photovoltage generation due to the high Seebeck coefficient of graphene (S ~ 100 μV K−1), which is in-situ tunable by gating.21, 28 By controlling the gate voltage on the two sides of the junction individually and recording the photocurrent we measure a 6-fold pattern, a clear sign that the photocurrent in our device is governed by the photo-thermoelectric effect20,21,22, 24, 27 (Supplementary Information). The highest responsivity measured when changing the gate voltages is obtained for V g1 = 1.2 V and V g2 = −0.21 V. This corresponds to a pn-configuration with a fairly low doping level of about 0.06 eV (Supplementary Information).
The spectral responsivity (Fig. 2a) is obtained by recording the photovoltage while tuning the wavelength of the quantum cascade laser source from 1000 to 1610 cm−1. A strong photocurrent enhancement for the polarization perpendicular to the gap, peaking at 1515 cm−1, is observed. The peak around 1100 cm−1 is related with the SiO2 surface phonon of the underlying substrate.27
Absorption and photocurrent spectra. a Responsivity spectrum for light polarization perpendicular (parallel) to the junction in blue (red). The gate voltages used here are (Vg1 = 1.2 V and Vg2 = −0.21 V). The main peak which lies in the upper reststrahlen band of h-BN (gray shaded region) is the result of the hyperbolic phonon-polariton assisted photoresponse. Solid lines are absorption spectra simulated by FDTD. b FDTD simulation of the spatial absorption profile in the vicinity of the junction as a function of the laser frequency. The spatial integral at each frequency is proportional to the simulated absorption cross section spectrum in a. c Near-field photocurrent measurement with subtracted background photocurrent of a similar device with 42 nm of bottom h-BN thickness, 13 nm on top and a gap width of 50 nm. The top edge of the panel is the edge of the graphene and the gap position is indicated. The left gate is set to −2 V and the right gate to 0.1 V. d Side views of the propagating HPPs at 1400 cm−1 (below the maximum), 1515 cm−1 (at the maximum) and at 1560 cm−1 (above the maximum) respectively
In order to understand the observed behavior we use finite difference time domain (FDTD) simulations to model the scattering process of far-field light into HPPs and the subsequent HPP waveguiding and absorption of the HPPs in the graphene (solid lines in Fig. 2a). A good match with the experimentally observed spectral response is obtained (points in Fig. 2a). The simulated absorption spectrum shows a peak inside the reststrahlen band of h-BN. The spatial distribution of the electric field inside the h-BN layers is shown in Fig. 2d. It is dominated by four rays which are launched at the edges of the split gate and undergo multiple reflections from the top and bottom surfaces. The rays maintain a fixed angle with the c axis. This angle is related to the anisotropy of the permittivity via the analytical formula \({\rm{tan}}\,\theta (\omega ) = i\sqrt {{\epsilon _{{\rm{x,y}}}}(\omega )} {\rm{/}}\sqrt {{\epsilon _{\rm{z}}}(\omega )}\).1, 3 It predicts that |θ| changes from π/2 to 0 as ω varies across the reststrahlen band. The unusual ray pattern of HPP emission in turn affects the spatial absorption pattern in graphene, which is shown in the simulated spectral-spatial pattern of Fig. 2b. This pattern is dominated by the four families of “hot spots” that correspond to the four HPP rays seen in Fig. 2d. The separation of hot spots within each family is 2d|tan θ|, where d = d t + d b is the total thickness of the h-BN layers (Fig. 1c).
To investigate further the origin of the observed spectral peaks in the photocurrent we carried out scanning near-field photocurrent mapping of our devices.29, 30 In this technique a metallized atomic force microscopy tip is illuminated with an infrared laser and a near-field is generated at the apex of the tip. This enables us to measure the photocurrent with a spatial resolution greatly exceeding the diffraction limit of light. The representative results are shown in Fig. 2c. The device region measured includes the gap of the split gate and one graphene edge localized at the top of the frame. The obtained photocurrent map reveals two series of sinusoidal spatial oscillations (fringes) rather than sharply peaked hot spots seen in Fig. 2b. These smooth oscillations can be explained if we recall that in an h-BN slab of small enough thickness d the HPPs are quantized into discrete eigenmodes with in-plane momenta kl = tan θ(πl + ϕ)/d where l = 0, 1, 2, … is the mode index and ϕ ~ 1 is a phase shift that depends on the boundary conditions (Fig. 3b and e.g., ref. 31). The collimated rays seen in Fig. 2d can be understood as coherent superpositions of many such modes emitted by the split gate. On the other hand, in the photocurrent microscopy the role of the HPP emitter is played by an AFM tip, which apparently couples predominantly to the l = 0 mode.32 The horizontal fringes in Fig. 2c are due to interference of l = 0 polariton waves launched by the tip, which is backreflected at the graphene edge leading to a fringe spacing corresponding to half the wavelength λ p = 2π/k 0 of this mode.32 The vertical fringes are due to interference of the l = 0 partial wave launched at the split gate8 with the tip launched waves. In this case the fringe spacing is λ p. We do not observe HPPs launched by the tip and reflected by the gap as there are no vertical fringes with half the wavelength visible. This interpretation enables us to extract λ p from the fringe spacing in the photocurrent maps. For example, at 1428 cm−1 is λ p = 460 ± 5 nm, which agrees with the calculated wavelength of 455 nm. The observed fringes parallel to the gap on the left of Fig. 2c confirm that phonons are indeed launched by the split gate and are converted into photocurrent.
Analytic calculation of absorption spectra. a Momentum distribution provided by a metallic split gate with 100 nm gap width. The associated electric field profile is shown in the inset. b HPP frequency dispersion curves showing discrete eigenmodes l = 0, 1, 2, … calculated for the full system of a metal gate, 50 nm h-BN, graphene and 55 nm h-BN on top. c Real space absorption profile obtained from the analytic calculations. d The resulting absorption spectrum calculated in k-space of the total power absorbed inside the graphene
In order to better understand which parameters determine the absorption spectrum we also modeled the system analytically.31 In this model we approximate the electric fields at the bottom surface of the h-BN by the electric field inside the gap −a < x < a cut along the y axis in a perfectly conducting plane z = 0 in vacuum:
Here V 0 is the voltage across the gap, which is proportional to the field of the incident beam (see inset Fig. 3a).
The Fourier transform of E x is given by (Fig. 3a)
where J 0(z) is the Bessel function of the first kind.
We then compute the field inside the h-BN-graphene layered structure using the transfer matrix method (Fig. 3b) by assuming that Eq. (3) represents the field incident on the structure from the bottom. The assumption is not strictly self-consistent because it does not account for the backreaction of h-BN on the split gate, in the form of the HPP rays reflected back to z = 0 plane. A more accurate but also more complicated model that obeys the self-consistency condition is presented in Supplementary. Unfortunately, that latter model can no longer can be solved in a closed form. This is why here we use the simplified analytical model to illustrate the main features of the studied phenomena. We calculate the Fourier transform of the in-plane electric field at the graphene surface as a function of momentum k. The power absorbed in the graphene is then expressed as (Fig. 3d):
where σ(ω) is the sheet conductivity of graphene at the laser frequency ω. Here, for simplicity, we neglect the spatial variation of σ near the pn-junction as the hot spots responsible for the absorption are typically found some distance away from the junction (Fig. 3c).
From this model description it becomes clear that the characteristic momentum k ~ 1/a provided by the junction plays a crucial role for the frequency of maximum absorption. By calculating the inverse Fourier transform of \({\tilde E_x}(k)\) we are able to also calculate the spatial profile of the electric field E x (x) and thus the spatial absorption profile (Fig. 3c). The validity of our analytic model can be seen by the close resemblance between the analytically calculated and FDTD simulated frequency dependent absorption profile (compare Figs. 2b and 3c).
From this model, the origin of the peak in the spectral photoresponse is the competition between the following two processes: the dielectric losses in the h-BN and the (finite) momentum provided by the junction. First, the losses in the h-BN contribute mainly to the low frequency side due to the imaginary part of the permittivity which peaks at the TO phonon frequency (1360 cm−1). The impact of this effect on the device responsivity is enhanced by the obtuse angle with which the HPPs are launched, as the intensity of the HPPs reaching the graphene becomes smaller with traveled distance. Second, the momentum provided by the junction is responsible for the responsivity decay on the high frequency side. Interestingly both of these effects depend on the h-BN thickness and on the gap size. It is important to note that the impact of the h-BN thickness is twofold since it is also changing the HPPs dispersion.1 Thus by choosing the geometrical parameters of the device, the device thickness and gap width, it is possible to tune the frequency as well as amplitude of the photocurrent maximum within the reststrahlen band of h-BN.
In order to show this tunability, and to validate the physical model, we fabricated different device geometries. Experimental responsivity spectra of the different devices are plotted in Fig. 4a. All the spectra were measured using the gate voltage configuration exhibiting the highest responsivity for the respective device. They exhibit different peak frequencies and responsivities and the trend is well captured by the analytically calculated absorption spectra presented in Fig. 4c. The peak frequencies are plotted in Fig. 4b as a function of the relevant geometrical parameters of the system. These are the stack thickness d = d t + d b, where d t and d b are the bottom and top h-BN thicknesses (Fig. 1c), and the split gate gap width 2a. The tunability of the investigated devices spans over 60 cm−1 and the peak frequencies obtained using both the FDTD simulations and the analytic model match the experimental ones. In Fig. 4d we plot the responsivities of the measured devices normalized to the highest one as a function of the peak frequencies. We find that the responsivity follows a bell shaped curve (Fig. 4d) suggesting that the optimal geometry would lead to a peak frequency where there is a trade off between low losses and high launching efficiency. Using the analytic model we obtain a theoretical dependence of the frequency and of the absorbed power as a function of the stack thickness and the gap size (Supplementary Information).
Comparison between experiments, simulation and analytic model. a Responsivity spectra of the investigated devices. b Comparison of the peak frequency of the devices obtained experimentally, by FDTD simulation, by the Galerkin method (Supplementary Information) and using the analytic model. Where d t and d b are the top and bottom thicknesses of the h-BN respectively and a is the gap width. The parameters α and β are extracted from the analytic model (Supplementary Information). c Absorption spectra calculated analytically. d Normalized peak values as a function of the detuning (see text) of its frequency. The gray dashed dotted line is a guide to the eye
In this simple analytic model the frequency dependence of the gap voltage V 0 (Eq. (2)) is neglected. Thus, the coupling between the far-field light and the split gate is not taken fully into account.33 This leads to some discrepancy between simple theory and experiment. However, the mentioned above more sophisticated model based on the Galerkin method (Supplementary Information) is in much better agreement with the experimental results and FDTD simulations (Fig. 4b).
Discussion
Finally, we will address the photodetection device performance. We remark that the device operates at zero bias, leading to an extremely low noise level (~4 nV/\(\sqrt {{\rm{Hz}}}\)) from which we estimate a noise equivalent power (NEP) of 26 pW/\(\sqrt {{\rm{Hz}}}\) (Methods section). From our simulations we found that the active area is about 2.5 μm2, i.e., only 2.5% of the device area. Thus, the device can be easily scaled to smaller dimensions, with the potential to enhance the performance by another factor of 40 because the total device resistance would be decreased and thus the Johnson-Nyquist noise would decrease as well leading to a lower NEP. Current state-of-the art detectors based on other technologies are described in refs 34, 35. At room temperature typically silicon bolometers are used. Our detectors can be further optimized to have similar detectivity as silicon bolometers, but offer several distinct advantages: it allows a smaller pixel size, higher operation speed and simpler fabrication as no suspension of the device is necessary.
Our novel nano-optoelectronic infrared detectors operate at room temperature, are highly efficient, and can be used for a wide range of on-chip sensing applications.
Methods
Sample fabrication
All the stack elements (top and bottom h-BN and graphene) are mechanically cleaved and exfoliated onto freshly cleaned Si/SiO2 substrates. First the selected top h-BN is detached from the substrate using a PPC (poly-propylene carbonate) film and is then used to lift by Van der Waals forces the graphene and the bottom h-BN consecutively. The as-completed stack is released onto the split gate. The split gate electrodes are prepared by lithography, titanium (5 nm)/gold (30 nm) evaporation and focus ion beam irradiation to create the gap. The source and drain electrodes mask is designed in a AZ-5214 photoresist film by laser lithography and is exposed to a plasma of CHF3/O2 gases to partially etch the stack. The graphene is finally contacted by the edges by evaporating titanium (2 nm)/gold (30 nm) and lift off in acetone. The recipe used for making those contacts is detailed in ref. 10.
Measurements
The device is illuminated by a linearly polarized quantum cascade laser with a frequency tunable from 1000 to 1610 cm−1. The device position is scanned using a motorized xyz-stage. The laser is modulated at 128 Hz using a chopper and the current at the junction is measured using a current pre-amplifier and lock-in amplifier. The polarization of the light is controlled using a ZnSe wire grid polarizer. The light is focused using ZnSe lenses with a numerical aperture of ~0.5. The power for each frequency is measured using a thermal power meter and the photocurrent spectra are normalized by this power to calculate the responsivity.
Noise equivalent power estimation
We calculate a noise equivalent power (NEP) given by NEP = S noise/R internal = 26pW/\(\sqrt {{\rm{Hz}}}\) where S noise is the voltage noise and R internal is the internal responsivity. Because graphene pn-junction photodetectors operate at zero bias the electrical noise is of thermal Johnson-Nyquist type given by \({S_{{\rm{noise}}}} = \sqrt {4{k_{\rm{B}}}TR} = 4{\kern 1pt} {\rm{nV/}}\sqrt {{\rm{Hz}}}\). Where k B is the Boltzmann constant, T = 300 K and R = 1 kΩ is the resistance for which the calculated NEP is minimum corresponding to a carrier concentration of n = 0.2 × 1012 cm−2. The internal responsivity is given by R internal = R external/η = 150 V/W where R external = 1 V/W is the experimental responsivity and η = A abs/A spot = 0.5% the percentage of absorbed light. A spot = 491 μm2 is the laser spot area and A abs = σW = 2.5 μm2 is the active area where σ = 250 nm is the absorption cross section obtained by FDTD simulations and W = 10 μm is the width of the device.
Simulations
The full wave simulations were performed using Lumerical FDTD. The frequency dependent permittivity of the h-BN was taken from ref. 1. The optical conductivity of the graphene was calculated using the local random phase approximation at T = 300 K with a scattering time of 500 fs. For each device the appropriate Fermi energy was simulated (Supplementary Information), however this did not influence the results significantly. In the simulations the Fermi energy of the graphene is spatially constant (see the comment after Eq. (4)) but frequency dependent. A plane wave source was used and the absorption cross section was calculated by normalizing to the incident power. For simplicity the calculated absorption does not take into account the cooling length of the graphene nor the carrier density profile.
Data availability
The data that support the plots within this paper and other findings of this study are available from the corresponding author upon reasonable request.
References
Caldwell, J. D. et al. Sub-diffractional volume-confined polaritons in the natural hyperbolic material hexagonal boron nitride. Nat. Commun. 5, 5221 (2014).
Dai, S. et al. Tunable phonon polaritons in atomically thin van der Waals crystals of boron nitride. Science 343, 1125–1129 (2014).
Dai, S. et al. Graphene on hexagonal boron nitride as a tunable hyperbolic metamaterial. Nat. Nanotech 10, 682–686 (2015).
Li, P. et al. Hyperbolic phonon-polaritons in boron nitride for near-field optical imaging and focusing. Nat. Commun. 6, 7507 (2015).
Giles, A. J. et al. Imaging of Anomalous Internal Reflections of Hyperbolic Phonon-Polaritons in Hexagonal Boron Nitride. Nano Lett. 16, 3858–3865 (2016).
Basov, D. N., Fogler, M. M. & Garcia de Abajo, F. J. Polaritons in van der Waals materials. Science 354, aag1992–aag1992 (2016).
Low, T. et al. Polaritons in layered two-dimensional materials. Nat. Mater 16, 182–194 (2016).
Yoxall, E. et al. Direct observation of ultraslow hyperbolic polariton propagation with negative phase velocity. Nat. Photon 9, 674–678 (2015).
Dean, C. R. et al. Boron nitride substrates for high-quality graphene electronics. Nat. Nanotechnol. 5, 722–726 (2010).
Wang, L. et al. One-dimensional electrical contact to a two-dimensional material. Science 342, 614–617 (2013).
Britnell, L. et al. Field-effect tunneling transistor based on vertical graphene heterostructures. Science 335, 947–950 (2012).
Withers, F. et al. WSe2 light-emitting tunneling transistors with enhanced brightness at room temperature. Nano Lett. 15, 8223–8228 (2015).
Liang, X. et al. Toward clean and crackless transfer of graphene. ACS Nano 5, 9144–9153 (2011).
Yan, J. et al. Dual-gated bilayer graphene hot-electron bolometer. Nat. Nanotech 7, 472–478 (2012).
Freitag, M. et al. Photocurrent in graphene harnessed by tunable intrinsic plasmons. Nat. Commun 4, 1951 (2013).
Yao, Y. et al. High responsivity mid infrared graphene detectors with antenna enhanced photocarrier generation and collection. Nano. Lett. 14, 3749–3754 (2014).
Freitag, M. et al. Substrate-sensitive mid-infrared photoresponse in graphene. ACS Nano 8, 8350–8356 (2014).
Sassi, U. et al. Graphene-based, mid-infrared, room-temperature pyroelectric bolometers with ultrahigh temperature coefficient of resistance. arXiv arXiv:1608.00569 (2016).
Gopalan, K. K. et al. Mid-infrared pyroresistive graphene detector on LiNbO 3. Adv. Optical Mater. doi:10.1002/adom.201600723 (2017).
Xu, X., Gabor, N. M., Alden, J. S., van der Zande, A. M. & McEuen, P. L. Photo-Thermoelectric Effect at a Graphene Interface Junction. Nano Lett. 10, 562–566 (2010).
Gabor, N. M. et al. Hot carrier-assisted intrinsic photoresponse in graphene. Science 334, 648–652 (2011).
Lemme, M. C. et al. Gate-activated photoresponse in a graphene p-n junction. Nano Lett. 11, 4134–4137 (2011).
Herring, P. K. et al. Photoresponse of an electrically tunable ambipolar graphene infrared thermocouple. Nano Lett. 14, 901–907 (2014).
Hsu, A. L. et al. Graphene-based thermopile for thermal imaging applications. Nano Lett. 15, 7211–7216 (2015).
Koppens, F. H. L. et al. Photodetectors based on graphene, other two-dimensional materials and hybrid systems. Nat. Nanotechnol. 9, 780–793 (2014).
Huber, A. J., Deutsch, B., Novotny, L. & Hillenbrand, R. Focusing of surface phonon polaritons. Appl. Phys. Lett. 92, 203104 (2008).
Badioli, M. et al. Phonon-mediated mid-infrared photoresponse of graphene. Nano. Lett. 14, 6374–6381 (2014).
Zuev, Y., Chang, W. & Kim, P. Thermoelectric and magnetothermoelectric transport measurements of graphene. Phys. Rev. Lett. 102, 96807 (2009).
Woessner, A. et al. Near-field photocurrent nanoscopy on bare and encapsulated graphene. Nat. Commun. 7, 10783 (2016).
Lundeberg, M. B. et al. Thermoelectric detection and imaging of propagating graphene plasmons. Nat. Mater. 16, 204–207 (2017).
Wu, J.-S., Basov, D. N. & Fogler, M. M. Topological insulators are tunable waveguides for hyperbolic polaritons. Phys. Rev. B 92, 205430 (2015).
Dai, S. et al. Subdiffractional focusing and guiding of polaritonic rays in a natural hyperbolic material. Nat. Commun. 6, 6963 (2015).
Alù, A. & Engheta, N. Tuning the scattering response of optical nanoantennas with nanocircuit loads. Nat. Photon 2, 307–310 (2008).
Rogalski, A. Recent progress in infrared detector technologies. Infra. Phys. Technol. 54, 136–154 (2011).
Hamamatsu. Characteristics and use of infrared detectors. Tech. Rep. (2011).
Acknowledgements
It is a great pleasure to thank Klaas-Jan Tielrooij for many fruitful discussions. This work used open source software (www.matplotlib.org, www.python.org, www.povray.org). F.H.L.K. acknowledges financial support from the Spanish Ministry of Economy and Competitiveness, through the “Severo Ochoa” Programme for Centres of Excellence in R&D (SEV-2015-0522), support by Fundacio Cellex Barcelona, the Mineco grants Ramón y Cajal (RYC-2012-12281) and Plan Nacional (FIS2013-47161-P and FIS2014-59639-JIN), and support from the Government of Catalonia trough the SGR grant (2014-SGR-1535). Furthermore, the research leading to these results has received funding from the European Union Seventh Framework Programme under grant agreement no.696656 Graphene Flagship, and the ERC starting grant (307806, CarbonLight). Y.G. and J.H. acknowledge support from the US Office of Naval Research N00014-13-1-0662. P.A.-G. acknowledges funding from the Spanish Ministry of Economy and Competitiveness through the national projects FIS2014-60195-JIN.
Author information
Authors and Affiliations
Contributions
A.W. and F.H.L.K. conceived the experiment. A.W. and R.P. performed the far-field experiments, analyzed the data and wrote the manuscript. A.W. performed the FDTD simulations. A.W. and P.A.-G. performed the near-field experiments. D.D. and Y.G. fabricated the devices. M.B.L. and S.N. assisted with measurements, interpretation and discussion of the results. J.-S.W. and M.M.F. developed the analytic model. K.W. and T.T. synthesized the h-BN. J.H., R.H. and F.H.L.K. supervised the work and discussed the results. All authors contributed to the scientific discussion and manuscript revisions.
Corresponding author
Ethics declarations
Competing interests
R.H. is co-founder of Neaspec GmbH, a company producing scattering-type scanning near-field optical microscope systems such as the ones used in this study. All other authors declare no competing financial interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Woessner, A., Parret, R., Davydovskaya, D. et al. Electrical detection of hyperbolic phonon-polaritons in heterostructures of graphene and boron nitride. npj 2D Mater Appl 1, 25 (2017). https://doi.org/10.1038/s41699-017-0031-5
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41699-017-0031-5
This article is cited by
-
Signatures of hot carriers and hot phonons in the re-entrant metallic and semiconducting states of Moiré-gapped graphene
Nature Communications (2023)
-
Photocurrent as a multiphysics diagnostic of quantum materials
Nature Reviews Physics (2023)
-
Interface nano-optics with van der Waals polaritons
Nature (2021)
-
Hyperbolic enhancement of photocurrent patterns in minimally twisted bilayer graphene
Nature Communications (2021)
-
Nano-imaging photoresponse in a moiré unit cell of minimally twisted bilayer graphene
Nature Communications (2021)