Abstract
The El Niño Southern Oscillation (ENSO) in the tropical Pacific Ocean is an important driver of winter precipitation variability over western North America as a whole, but ENSO exhibits a weak and inconsistent relationship with precipitation in several critically important headwaters including the upper Colorado River Basin. We present interactions between North Atlantic sea surface temperatures (SSTs) and ENSO that influence western U.S. precipitation, accounting for substantial variability in areas where ENSO alone yields limited guidance. Specifically, we performed a statistical analysis on hemispheric SSTs and western U.S. winter precipitation in a century of observations and a 10,000-year perpetual current-climate simulation. In both frameworks, the leading coupled pattern is ENSO, and the second pattern links an Atlantic Quadpole Mode (AQM) of SST variability to precipitation anomalies over most of the western U.S., including the transition zone where ENSO provides little predictability. The AQM SST anomalies are expansive in latitude, but its primary mechanism appears to involve a strengthening/shifting of the intertropical convergence zone (ITCZ) over northern South America and the tropical Atlantic. The ENSO pattern accounts for a larger fraction of the total covariance between SSTs and precipitation (65% versus 12% for the AQM pattern), but the percent anomalies of precipitation associated with ENSO and the AQM are comparable in magnitude, meaning 20% or larger over much of the western U.S. The interaction between ENSO and AQM influences precipitation across the western U.S., with cold AQM generally reducing precipitation irrespective of ENSO whereas warm AQM increases the amount of precipitation and the area of influence of ENSO; knowledge of these interactions can increase predictability of western U.S. precipitation.
Similar content being viewed by others
Introduction
Water resources in western North America rely on the seasonal cycle of snow accumulation over winter and melt each spring1,2,3,4,5,6,7,8. There is mounting evidence that climate change is altering the timing of snow accumulation, rate of snow melt, and the fraction of precipitation falling as rain or snow9, all of which will require changes in the management of western water resources. The impacts of climate change however, are superimposed on high interannual, decadal, and multi-decadal variability in precipitation, the drivers of which are poorly understood for much of the West. The largest source of variability in annual streamflow and water supply in these mountain catchments is the amount of precipitation that falls in any given winter10,11. For example, the coefficient of variability (ratio of standard deviation to mean) is 0.86 for winter snowfall in the western U.S., which accounts for 85% of annual precipitation12. This historic variability in precipitation has challenged water resource management for decades13,14; understanding the drivers of this variability is a critical knowledge gap underlying more efficient management of water resources. Recent work has documented a coherent, quasi-decadal periodicity in precipitation-driven groundwater recharge in both Utah and Colorado15,16, emphasizing the importance of multi-year integrated precipitation as a driver of streamflow anomalies.
The effects of tropical Pacific Ocean sea surface temperatures (SSTs) on the hydroclimate of the western U.S. have been studied for decades17,18,19,20,21,22,23, and these investigations focus mainly on variability of the El Niño Southern Oscillation (ENSO). ENSO results in a north-south precipitation dipole where the northwestern U.S. tends to be drier than average and the southwestern U.S. tends to be wetter than average during El Niño years while during La Niña years these precipitation anomalies are reversed20,23. During the warm phase (El Niño), the enhanced sensible and latent heating in the central tropical Pacific excites a poleward and eastward propagating Rossby wave. An intensification and eastward shift is seen in the Aleutian low, a semi-permanent feature of the North Pacific winter climate, and results in above average precipitation, snowpack, and streamflow in the southwestern U.S.20,24.
Observations and modeling studies indicate that North Atlantic SST variability is dominated by a multidecadal mode, which features like-signed anomalies across the basin, referred to as the Atlantic Multidecadal Oscillation (AMO) or Atlantic Multidecadal Variability (AMV)25,26. AMV has been associated with hemispheric-scale precipitation anomalies27 and a mode of circum-hemispheric atmosphere-ocean-sea ice interactions28. One possible mechanism for far-reaching effects of the Atlantic is modulation of ENSO by the AMO25,29,30,31,32,33,34,35,36,37. Decadal to multidecadal Atlantic variability contributes to the occurrence of persistent dry and wet periods across the western U.S., and correlation analyses indicate relations between persistent droughts (pluvials) and North Atlantic warming (cooling) and tropical and eastern Pacific cooling (warming)25,30,31. North Atlantic SSTs have also been associated with variability of North American hydroclimatic variables such as spring snowpack, annual streamflow, and multiyear baseflow25,30,31,32,33,34,35,38,39,40,41,42,43,44,45,46,47,48,49,50. Analysis of these relationships in conjunction with atmospheric circulation indicates that western U.S. snowpack and Atlantic SSTs are correlated with changes in the jet stream and equatorial westerlies51.
Skillful prediction of western U.S. hydroclimate is increasingly important in the context of projected climate change and contemporary drought52. Given the well-established role of ENSO in western U.S. precipitation and the potential of Atlantic SSTs to also influence regional hydroclimate, the objective of this study is to evaluate potential interactions between the two that may influence water resource availability. Specifically, we combine observations with a 10,000-year perpetual present-day global climate model simulation to investigate how the Atlantic impacts western U.S. hydroclimate, including its potential role in modulating ENSO.
Results
Coupled modes
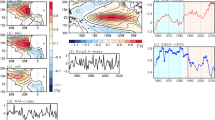
The first mode of coupled variability between winter precipitation and SSTs (M1) is the familiar ENSO pattern linking above-average tropical east-central Pacific SSTs (Fig. 1a) to a dry-north/wet-south precipitation dipole over the western U.S. (Fig. 1c). This leading pattern was derived from lagged Maximum Covariance Analysis (MCA; Methods) between December-March precipitation with SST leading it by one month (November–February) to capture the delayed response of the atmosphere53. The squared covariance fraction (SCF) of this mode is 0.65, meaning it accounts for 65% of the squared covariation between the variables. The associated 300-hPa geopotential height (Z300) pattern shows the canonical poleward and eastward propagating Rossby wave, producing a strong trough in the northeast Pacific (Fig. 1b) responsible for the positive precipitation anomalies in the southwestern U.S. (Fig. 1c). This mode’s indices of SST (S1) and precipitation (P1) reflect strong interannual variability with Pearson correlation r(S1, P1) = 0.54, p < 0.01 (Fig. 1d).
The first mode of coupled variability (M1) between SSTs and western-U.S. precipitation, where SSTs lead December-March precipitation by one month. a The M1 SST pattern (homogeneous correlation of SA SST with S1). b S1 correlation with Z300 (shading) and with outgoing longwave radiation (contoured south of 30∘N at 0.2 interval with negative values dashed and zero contour suppressed). c The M1 precipitation pattern (homogeneous correlation of precipitation with P1). d The M1 indices S1 and P1 with their correlation statistics. Stippling on maps indicates shaded correlations significant at the 95% confidence level, and magenta boxes in (a) and (c) indicate the MCA analysis domain.
The second coupled mode (M2; SCF = 0.12) accounts for SST variability most strongly in the Atlantic (Fig. 2a), and we refer to this as the Atlantic Quadpole Mode (AQM) because it has four SST anomalies which alternate in sign—two in the North Atlantic and two flanking the equator in the tropics. Positive values of the AQM SST index S2 correspond to the Warm AQM and negative values correspond to the cold AQM (Fig. 2d). The M2 pattern has a weak El Niño-like signature in the tropical Pacific, but M2 and M1 are statistically orthogonal, meaning the singular vectors that define them have zero dot product by definition.
Same as Fig. 1 but for the second mode of coupled variability (M2) referred to as the Atlantic Quadpole Mode (AQM). a The M1 SST pattern. b S2 correlation with Z300 (shading) and with outgoing longwave radiation (contoured south of 30°N at 0.2 interval with negative values dashed and zero contour suppressed). c The M2 precipitation pattern (homogeneous correlation of precipitation with P2). d The M2 indices S2 and P2, and the AMO index.
M2 captures precipitation variability across much of the West Coast and intermountain U.S., including the transition zone between the wet and dry anomalies associated with ENSO (Fig. 2c). These transition areas encompass regionally important water resource areas including the headwaters of the Colorado River Basin, The Great Basin, and the central Sierra Nevada mountain range. The M2 Z300 pattern features a trough-ridge dipole over the Gulf of Alaska into Canada, shifted east relative to the M1 dipole, with weaker correlations in the tropical Pacific (Supplementary Fig. 1). Correlation between the M2 indices S2 and P2 is r = 0.54 (p < 0.01), matching that of the M1 mode. These first two modes together account for 77% of the squared covariation between SST and precipitation. The SCF of M3 was 0.07 and this mode is not considered further here.
Precipitation patterns
The M1 coupled mode generates the familiar wet-north/ dry-south pattern of La Niña years and wet-south/ dry-north pattern of El Niño years (Fig. 1c and Supplementary Fig. 2a, b). These ENSO precipitation anomalies provide little predictability in the transition zone between the anomalously wet and dry regions over western North America. The AQM patterns are a complement to ENSO, providing significant precipitation anomalies in the ENSO transition zone, with the Warm AQM corresponding to anomalously wet conditions and the Cold AQM corresponding to anomalously dry conditions (Fig. 2c and Supplementary Figs. 2c, d).
Considering various combinations of ENSO and the AQM reveals some important interactions between the two modes in which the AQM alters the alignment or strength of the seasonal precipitation impacts of ENSO (Fig. 3). During El Niño, Warm AQM shifts the zero precipitation anomaly transition zone north and expands the region of above average precipitation (Fig. 3c vs. Fig. 3b). The associated atmospheric circulation change is a strengthening and eastward shift of the Aleutian Low (Fig. 1b; Supplementary Fig. 3c). Cold AQM shifts the transition zone south and expands the region of below average precipitation (Fig. 3a vs. Fig. 3b) in conjunction with a weakening of the Aleutian Low’s response to ENSO (Supplementary Fig. 3a). Previously ambiguous precipitation anomalies in the transition zone extending west to east from northern California through northern Colorado, become drier (wetter) during the cold (warm) AQM.
Percent anomalies of December–March precipitation corresponding to combinations of the MCA SST indices S1 and S2. The rows correspond to a–c the S1 upper third (El Niño), d–f middle third (neutral ENSO), and g–i lower third (La Niña). The columns correspond to the S2 lower third (Cold AQM), middle third (neutral AQM), and upper third (Warm AQM). Stippling in each panel indicates statistical significance at the 95% confidence level.
During La Niña, the warm phase of the AQM extends the transition zone farther south (Fig. 3i vs. Fig. 3h), increasing the extent and magnitude of the above average precipitation anomaly. The cold phase of the AQM extends the transition zone farther north (Fig. 3g vs. Fig. 3h), increasing the extent and magnitude of the below average precipitation anomaly. During La Niña and Neutral AQM, the classic La Niña Gulf of Alaska ridge is evident (Supplementary Fig. 3h), and Cold AQM strengthens this ridge (Supplementary Fig. 3g). Warm AQM tends to shift the Gulf of Alaska ridge west (Supplementary Fig. 3i), consistent with the expanded region of above-average precipitation anomalies (Fig. 3i).
The barcharts in Fig. 4 summarize how the AQM alters precipitation in basins where ENSO provides limited predictability—Northern California, Great Basin, and Upper Colorado. Precipitation anomalies tend to be weak in these three basins during neutral AQM, exhibit larger positive values during warm AQM, and shift toward negative values during cold AQM.
For three watersheds, percent anomalies of December–March precipitation corresponding to combinations of ENSO and AQM. The map shows the three watershed boundaries75, where the southern edge of northern California (37.5∘N) is near the latitude south of which El Niño precipitation anomalies become significant (Supplementary Fig. 2b).
Multi-millennial climate simulation
To complement the observational results and provide a much larger sample size for the coupled variability analysis, we analyzed a multimillennial (10,000-year) present-day climate control simulation performed with a fully coupled configuration of the Geophysical Fluid Dynamics Laboratory (GFDL) Climate Model, Version 2.154,55. MCA on the simulation produced an ENSO-like leading mode of variability (GFDL M1, Supplementary Fig. 4) similar in spatial pattern to that found in observations; spatial correlation between the observed and simulated M1 singular vectors was 0.88 for SST and 0.75 for precipitation. The associated time series of SST (S1) and precipitation (P1) exhibited correlation comparable to observations (r = 0.61, p < 0.01; Supplementary Fig. 4d). However, GFDL M1 had a substantially larger SCF (0.95) compared to the observed M1 (0.65), indicating a more dominant role for ENSO-like variability in the GFDL simulation. This contrast in SCF is consistent with prior findings on the strength of ENSO relative to observations in this model56.
The second coupled mode (GFDL M2) captured the Gulf of Alaska trough with wetter than average conditions extending eastward into the Intermountain U.S. (Supplementary Fig. 5b, c). The SST pattern in GFDL M2 (Supplementary Fig. 5a) featured a quadpole structure over the Atlantic similar to but less well defined than in observations. GFDL M2 captured the SST anomaly north of the equator in the Atlantic, but the cross-equatorial dipole is not as clearly present, and a stronger dipole appeared in the western tropical Pacific. The spatial correlation between the observed and simulated M2 singular vectors was 0.59 for SST and 0.78 for precipitation. The associated time series S2 and P2 exhibited correlation somewhat smaller than observations (r = 0.41, p < 0.01; Supplementary Fig. 5d).
The SCF for GFDL M2 is 0.04, meaning this second mode accounts for essentially all of the covariation orthogonal to the ENSO mode (i.e., 0.95 + 0.04 = 0.99). In observations, the SCF for the first two MCA modes totals a more modest 0.65 + 0.12 = 0.77. Although the SCF magnitudes and partitioning contrasted between observations and the GFDL simulation, the control of these modes on western U.S. precipitation was more comparable. To illustrate, we consider the correlations between precipitation and the indices P1 and P2 (shading in Figs. 1c and 2c for observations and Supplementary Figs. 4c and 5c for the model); for M1, spatially averaging the absolute correlation over the magenta boxes yielded \({|{\bar{r}}| }=0.36\) in observations and \({|{\bar{r}}| }=0.31\) in the model; for M2 this yielded \({| {\bar{r}}| }=0.27\) in observations and \({|{\bar{r}}| }=0.14\) in the model. The correlation between the MCA indices was also more comparable: r(S1, P1) is 0.54 in observations versus 0.61 in the model; r(S2, P2) was 0.54 in observations versus 0.41 in the model (Figs. 1d and 2d and Supplementary Figs. 4d and 5d).
Composite precipitation anomalies for GFDL M1 and M2 considered separately align well with observed patterns (compare Supplementary Figs. 6 and 2). Composite precipitation anomalies for different combinations of GFDL M1 and M2 (Fig. 5) are consistent with corresponding observed patterns (Fig. 3) but smoother because of the larger sample size. The canonical ENSO north/south precipitation dipole is present in the neutral phase of the AQM (Fig. 5b and h). As in observations, the AQM shifts the El Niño dipole north to produce wetter conditions during Warm AQM and south to produce drier conditions during Cold AQM (upper row, Fig. 5). The AQM shifts the La Niña dipole north to produce drier conditions during Cold AQM and south to produce wetter conditions during Warm AQM (lower row, Fig. 5).
Same as Fig. 3, but for the multi-millennial climate simulation. Percent anomalies of December-March precipitation corresponding to combinations of the MCA SST indices S1 and S2. The rows correspond to a–c the S1 upper third (El Niñño), d–f middle third (neutral ENSO), and g–i lower third (La Niña). The columns correspond to the S2 lower third (Cold AQM), middle third (neutral AQM), and upper third (warm AQM).
Discussion
As a dominant mode of climate variability, ENSO is ingrained in our understanding and prediction of western-U.S. hydroclimate. The AQM mode we identify here is an effective complement to ENSO because it accounts for precipitation anomalies where predictability from ENSO is weak, and this desirable property of the AQM arises in part from the orthogonality provided by MCA. In observations and the multi-millennial climate simulation, the AQM is linked to significant precipitation anomalies during neutral ENSO and also north-south shifts in the ENSO precipitation dipole during El Niño and La Niña. The appearance of a pattern resembling the observed AQM in our multi-millennial current climate simuation suggests that the physics of this mode do not require transient anthropogenic forcing. However, tree-ring reconstructions caution that this region’s prominent contemporary cycles in precipitation may not have been stable features over the past six centuries57, suggesting that the patterns we study here are characteristic of anthropogenically modified climate.
The extratropical portion of the AQM SST pattern resembles the first mode of North Atlantic variability obtained via empirical orthogonal function analysis, which has been described as featuring a “quadpole pattern” in prior work58. The extratropical SST signature of the AQM also features a “horseshoe” pattern (red shading, Fig. 2a) characteristic of the AMO or AMV more generally. However, the AQM index S2 is not significantly correlated with the AMO index (r < 0.01, p > 0.90), reflecting differences in timescale and phase apparent in Fig. 2d. It is interesting that the AQM appears in our multi-millennial climate simulation without transient anthropogenic forcing; in contrast, AMO-like multidecadal oscillations are largely absent in unforced climate model simulations, suggesting that AMV is a combination of natural multidecadal variability and anthropogenic forcing59,60.
Considering the extratropical portion of the AQM, the dominant air-sea interaction over the North Atlantic is forcing of the ocean by the atmosphere61. The preceding draws attention to the tropical portion of the AQM SST pattern. This appears consistent with prior research concluding that tropical North Atlantic (TNA) SST variability modulates North American precipitation based on an atmospheric model’s response to observed versus climatological TNA SSTs62. The AQM pattern features a dipole flanking the mean Intertropical Convergence Zone (ITCZ) resembling what is known as the Atlantic Meridional Mode (AMM)63, and the correlation between S2 and the AMM index is modest but statistically significant (r = 0.37, p < 0.01). Mechanistically, the AMM SST pattern is paired with surface cross winds that traverse the equator and shift the ITCZ64, and the correlation of tropical outgoing longwave radiation (OLR) with S2 (green contours, Fig. 2b) features a dipole between West Africa and the Caribbean indicative of a northwest shift in the ITCZ during Warm AQM paired with increased convection over the central tropical Pacific.
We have a one-month lag incorporated into the statistical analyses presented here so that SST leads the precipitation patterns, allowing for a response time of the atmosphere to the ocean53. In a sensitivity test, we found that similar results were obtained with SST leading precipitation by zero months, two months and three months (Supplementary Fig. 7). Southern tropical Atlantic warming may also be important at longer lead times, contributing to predictability of water supply shortages in the Colorado River at multi-year timescales65. Although the Atlantic mechanism explored here is physically plausible, causality is challenging to infer from observations and fully coupled GCM experiments alone, motivating additional boundary forcing experiments to investigate causal mechanisms in the AQM teleconnection.
Methods
Observations
For SSTs, we utilized the Hadley Centre Sea Ice and SST data set (HadISST)66 Version 3 for 1869-2019 on a 1∘ grid. Precipitation data for the western U.S. were obtained from Global Precipitation Climatology Center (GPCC)67,68 for 1891–2019. These GPCC data are gauge-based values interpolated onto a 0.5∘ grid. From the Twentieth Century Reanalysis69 (20CR) Version 3, we used ensemble mean 300-hPa geopotential heights (Z300) and outgoing longwave radiation (OLR) for 1891–2015. The resultant period for the MCA of SST and precipitation was 1891–2019. Correlations displayed based on 20CR were for the overlapping period 1891–2015. All fields were averaged over the months December–March (or November–February for SST), the least-squares linear trend was then removed, and results were labeled with the year in which March occurred. SSTs were averaged over November–February to lead the December–March precipitation data by one month.
The AMO Index was obtained from the Climate Analysis Section of NCAR and was defined as the area average of detrended low-pass filtered North Atlantic HadISST anomalies70. Monthly AMO index values were averaged over November–February for consistency with the averaging period we used for the Hadley SST data in the MCA. The AMM index63 was obtained from NOAA PSL and averaged over November-February (overlap with our analysis period is winters 1948-2015).
Multi-millennial climate simulation
To complement the observational results and provide a much larger sample size for the coupled variability analysis, we analyzed a multi-millennial (10,000-year) present-day climate control simulation54,55 performed with a fully coupled configuration of the GFDL Climate Model, Version 2.171. Greenhouse gases, ozone concentrations, and other external forcings were held constant at 1990 levels to remove the confounding effects of transient climate change. The simulation was performed on a 2∘ latitude by 2.5∘ longitude horizontal grid. After discarding a spin-up period, there were 7990 years used focusing on monthly mean SSTs, Z300, and precipitation.
Statistical methods
We identified modes of coupled variability using maximum covariance analysis (MCA), also known as singular value decomposition (SVD)72. In this application, the left field was hemispheric SST from 10∘S-70∘N (magenta box in Fig. 1a), and the right field was western-U.S. precipitation (domain 30∘S-50∘N and 125∘W-100∘W, magenta box in Fig. 1c). To prevent spatial heterogeneity in precipitation variance from heavily influencing the results, the time series of SST and precipitation were standardized to have zero mean and unit standard deviation at each grid point, meaning the elements of the spatial cross-covariance matrix (C) were correlations73.
In the nth MCA mode (Mn), Sn was the time series index of SST variability and was the projection of SST onto the nth left singular vector of C. Pn was the time series index of precipitation variability in Mn, and was the projection of precipitation onto the nth right singular vector of C. Homogeneous correlation maps were used to show the SST and precipitation spatial patterns associated with Mn, meaning the correlation of SST at each grid point with Sn and the correlation of precipitation at each grid point with Pn. The squared covariance fraction (SCF) indicates the portion of the total covariation between SST and precipitation captured by a MCA mode. The MCA modes were arranged so that M1 had the largest SCF, and subsequent modes had progressively smaller SCFs. In this study, the first two MCA modes were presented.
Correlations, anomalies, and trends were tested for significance at the 95% confidence level using t-tests assuming one degree of freedom per year. All calculations were performed in MATLAB74 and maps were produced using its Mapping Toolbox.
Data availability
Data analyzed here that are publicly available were obtained from the following sources: HadISST Version 3 from https://www.metoffice.gov.uk/hadobs/hadisst/, GPCC from https://psl.noaa.gov/data/gridded/data.gpcc.html, 20CR Version 3 from https://psl.noaa.gov/data/20thC_Rean/, and AMO index from NOAA PSL at https://psl.noaa.gov/data/timeseries/AMO/. Due to its large size, the multi-millennial, perpetual-climate GFDL simulation is archived at NERSC and can be made available upon request.
References
Meybeck, M., Green, P. & Vörösmarty, C. A new typology for mountains and other relief classes: an application to global continental water resources and population distribution. Mt. Res. Dev. 21, 34–45 (2001).
Barnett, T. P., Adam, J. C. & Lettenmaier, D. P. Potential impacts of a warming climate on water availability in snow-dominated regions. Nature 438, 303–309 (2005).
Viviroli, D., Dürr, H. H., Messerli, B., Meybeck, M. & Weingartner, R. Mountains of the world, water towers for humanity: typology, mapping, and global significance. Water Resour. Res. https://doi.org/10.1029/2006WR005653 (2007).
Mankin, J. S., Viviroli, D., Singh, D., Hoekstra, A. Y. & Diffenbaugh, N. S. The potential for snow to supply human water demand in the present and future. Environ. Res. Lett. 10, 114016 (2015).
Li, D., Wrzesien, M. L., Durand, M., Adam, J. & Lettenmaier, D. P. How much runoff originates as snow in the western United States, and how will that change in the future? Geophys. Res. Lett. 44, 6163–6172 (2017).
Sturm, M., Goldstein, M. A. & Parr, C. Water and life from snow: a trillion dollar science question. Water Resour. Res. 53, 3534–3544 (2017).
Immerzeel, W. W. et al. Importance and vulnerability of the world’s water towers. Nature 577, 364–369 (2020).
Qin, Y. et al. Agricultural risks from changing snowmelt. Nat. Clim. Change 10, 459–465 (2020).
Gordon, B. L. et al. Why does snowmelt-driven streamflow response to warming vary? A data-driven review and predictive framework. Environ. Res. Lett. 17, 053004 (2022).
Cayan, D. R. Interannual climate variability and snowpack in the Western United States. J. Clim. 9, 928–948 (1996).
Bohr, G. S. & Aguado, E. Use of April 1 SWE measurements as estimates of peak seasonal snowpack and total cold-season precipitation. Water Resour. Res. 37, 51–60 (2001).
Harpold, A. et al. Changes in snowpack accumulation and ablation in the intermountain west. Water Resour. Res. https://doi.org/10.1029/2012WR011949 (2012).
Milly, P. C. D. et al. Stationarity is dead: Whither water management? Science 319, 573–574 (2008).
Sterle, K., Hatchett, B. J., Singletary, L. & Pohll, G. Hydroclimate variability in snow-fed river systems: local water managers’ perspectives on adapting to the new normal. Bull. Am. Meteorol. Soc. 100, 1031–1048 (2019).
Brooks, P. D. et al. Groundwater-mediated memory of past climate controls water yield in snowmelt-dominated catchments. Water Resou. Res. 57, e2021WR030605 (2021).
Wolf, M. A., Jamison, L. R., Solomon, D. K., Strong, C. & Brooks, P. D. Multi-year controls on groundwater storage in seasonally snow-covered headwater catchments. Water Resour. Res. 59, e2022WR033394 (2023).
Namias, J. & Cayan, D. El Nino: implications for forecasting. Oceanus 27, 41–47 (1984).
Ropelewski, C. F. & Halpert, M. S. Precipitation patterns associated with the high index phase of the Southern Oscillation. J. Clim. 2, 268–284 (1989).
McCabe, G. J. & Dettinger, M. D. Decadal variations in the strength of ENSO teleconnections with precipitation in the western United States. Int. J. Climatol. 19, 1399–1410 (1999).
Redmond, K. T. & Koch, R. W. Surface climate and streamflow variability in the Western United States and their relationship to large-scale circulation indices. Water Resour. Res. 27, 2381–2399 (1991).
Cole, J. E. & Cook, E. R. The changing relationship between ENSO variability and moisture balance in the continental United States. Geophys. Res. Lett. 25, 4529–4532 (1998).
Dettinger, M. D., Cayan, D. R., Diaz, H. F. & Meko, D. M. North-south precipitation patterns in western North America on interannual-to-decadal timescales. J. Clim. 11, 3095–3111 (1998).
Cayan, D. R., Redmond, K. T. & Riddle, L. G. ENSO and hydrologic extremes in the western United States. J. Clim. 12, 2881–2893 (1999).
Clark, M. P., Serreze, M. C. & McCabe, G. J. Historical effects of El Nino and La Nina events on the seasonal evolution of the montane snowpack in the Columbia and Colorado River Basins. Water Resour. Res. 37, 741–757 (2001).
Enfield, D. B., Mestas-Nuñez, A. M. & Trimble, P. J. The Atlantic Multidecadal Oscillation and its relation to rainfall and river flows in the continental U.S. Geophys. Res. Lett. 28, 2077–2080 (2001).
Zhang, R. et al. A review of the role of the Atlantic Meridional overturning circulation in Atlantic multidecadal variability and associated climate impacts. Rev. Geophys. 57, 316–375 (2019).
Ting, M., Kushnir, Y., Seager, R. & Li, C. Robust features of Atlantic multi-decadal variability and its climate impacts. Geophys. Res. Lett. https://doi.org/10.1029/2011GL048712 (2011).
Dima, M. & Lohmann, G. A hemispheric mechanism for the Atlantic multidecadal oscillation. J. Clim. 20, 2706–2719 (2007).
Nicholson, S. E., Leposo, D. & Grist, J. The relationship between El Niño and drought over Botswana. J. Clim. 14, 323–335 (2001).
Schubert, S. D., Suarez, M. J., Pegion, P. J., Koster, R. D. & Bacmeister, J. T. On the cause of the 1930s dust bowl. Science 303, 1855–1859 (2004).
McCabe, G. J., Palecki, M. A. & Betancourt, J. L. Pacific and Atlantic Ocean influences on multidecadal drought frequency in the United States. Proc. Natl Acad. Sci. USA 101, 4136–4141 (2004).
Seager, R., Kushnir, Y., Herweijer, C., Naik, N. & Velez, J. Modeling of tropical forcing of persistent droughts and pluvials over western North America: 1856-2000. J. Clim. 18, 4065–4088 (2005).
Sutton, R. T. & Hodson, D. L. R. Atlantic Ocean forcing of North American and European summer climate. Science 309, 115–118 (2005).
Cook, E. R., Seager, R., Cane, M. A. & Stahle, D. W. North American drought: Reconstructions, causes, and consequences. Earth-Sci. Rev. 81, 93–134 (2007).
Goodrich, G. B. Multidecadal climate variability and drought in the United States. Geogr. Compass 1, 713–738 (2007).
Mo, K. C., Schemm, J.-K. E. & Yoo, S.-H. Influence of ENSO and the Atlantic Multidecadal Oscillation on Drought over the United States. J. Clim. 22, 5962–5982 (2009).
Levine, A. F. Z., McPhaden, M. J. & Frierson, D. M. W. The impact of the AMO on multidecadal ENSO variability. Geophys. Res. Lett. 44, 3877–3886 (2017).
Rogers, J. C. & Coleman, J. S. M. Interactions between the Atlantic Multidecadal Oscillation, El Niño/La Niña, and the PNA in winter Mississippi Valley stream flow. Geophys. Res. Lett. https://doi.org/10.1029/2003GL017216 (2003).
Hidalgo, H. G. Climate precursors of multidecadal drought variability in the western United States. Water Resour. Res. https://doi.org/10.1029/2004WR003350 (2004).
Hunter, T., Tootle, G. & Piechota, T. Oceanic-atmospheric variability and western U.S. snowfall. Geophys. Res. Lett. https://doi.org/10.1029/2006GL026600 (2006).
Hu, Q. & Feng, S. Variation of the North American summer monsoon regimes and the Atlantic Multidecadal Oscillation. J. Clim. 21, 2371–2383 (2008).
Shabbar, A. & Skinner, W. Summer drought patterns in Canada and the relationship to global sea surface temperatures. J. Clim. 17, 2866–2880 (2004).
Tootle, G. & Piechota, T. Relationships between Pacific and Atlantic Ocean sea surface temperatures and US streamflow variability. Water Resour. Res. https://doi.org/10.1029/2005WR004184 (2006).
Sutton, R. T. & Hodson, D. L. R. Climate response to basin-scale warming and cooling of the North Atlantic Ocean. J. Clim. 20, 891–907 (2007).
Curtis, S. The Atlantic Multidecadal Oscillation and extreme daily precipitation over the US and Mexico during the hurricane season. Clim. Dyn. 30, 343–351 (2008).
Feng, S., Oglesby, R. J., Rowe, C. M., Loope, D. B. & Hu, Q. Atlantic and Pacific SST influences on Medieval drought in North America simulated by the Community Atmospheric Model. J. Geophys. Res. Atmos. https://doi.org/10.1029/2007JD009347 (2008).
Nigam, S., Guan, B. & Ruiz-Barradas, A. Key role of the Atlantic Multidecadal Oscillation in 20th century drought and wet periods over the great plains. Gephys. Res. Lett. https://doi.org/10.1029/2011GL048650 (2011).
Nowak, K., Hoerling, M., Rajagopalan, B. & Zagona, E. Colorado River Basin hydroclimatic variability. J. Clim. 25, 4389–4403 (2012).
Chylek, P., Dubey, M., Lesins, G., Li, J. & Hengartner, N. Imprint of the Atlantic Multi-decadal Oscillation and Pacific Decadal Oscillation on southwestern climate: Past, present, and future. Clim. Dyn. 43, 119–129 (2014).
Mccabe, G., Betancourt, J. & Hidalgo, H. Associations of decadal to multidecadal sea-surface temperature variability with Upper Colorado River flow. J. Am. Water Resour. Assoc. 43, 183–192 (2007).
Pathak, P. et al. Climatic variability of the Pacific and Atlantic Oceans and western US snowpack. Int. J. Climatol. 38, 1257–1269 (2018).
Williams, A. P., Cook, B. I. & Smerdon, J. E. Rapid intensification of the emerging southwestern North American megadrought in 2020-2021. Nat. Clim. Change 12, 232–234 (2022).
Kumar, A. & Hoerling, M. P. The nature and causes for the delayed atmospheric response to El Niño. J. Clim. 16, 1391–1403 (2003).
Staten, P. W. & Reichler, T. On the ratio between shifts in the eddy-driven jet and the Hadley cell edge. Clim. Dyn. 42, 1229–1242 (2014).
Horan, M. F. & Reichler, T. Modeling seasonal sudden stratospheric warming climatology based on polar vortex statistics. J. Clim. 30, 10101–10116 (2017).
Wittenberg, A. T., Rosati, A., Lau, N.-C. & Ploshay, J. J. GFDL’s CM2 Global Coupled Climate Models. Part III: Tropical Pacific Climate and ENSO. J. Clim. 19, 698–722 (2006).
Williams, A. P. et al. Tree rings and observations suggest no stable cycles in Sierra Nevada cool-season precipitation. Water Resour. Res. 57, e2020WR028599 (2021).
Loder, J. W. & Wang, Z. Trends and variability of sea surface temperature in the Northwest Atlantic from three historical gridded datasets. Atmosphere-Ocean 53, 510–528 (2015).
Ting, M., Kushnir, Y. & Li, C. North Atlantic Multidecadal SST Oscillation: External forcing versus internal variability. J. Mar. Syst. 133, 27–38 (2014).
Mann, M. E., Steinman, B. A. & Miller, S. K. Absence of internal multidecadal and interdecadal oscillations in climate model simulations. Nat. Commun. 11, 49 (2020).
Frankignoul, C., Friederichs, P. & Kestenare, E. Influence of Atlantic SST anomalies on the atmospheric circulation in the Atlantic-European sector. Ann. Geophys. 46, 71–85 (2003).
Kushnir, Y., Seager, R., Ting, M., Naik, N. & Nakamura, J. Mechanisms of Tropical Atlantic SST Influence on North American Precipitation Variability. J. Clim. 23, 5610–5628 (2010).
Chiang, J. C. H. & Vimont, D. J. Analogous Pacific and Atlantic meridional modes of tropical atmosphere-ocean variability. J. Clim. 17, 4143–4158 (2004).
Veiga, S. F., Giarolla, E., Nobre, P. & Nobre, C. A. Analyzing the influence of the North Atlantic Ocean variability on the Atlantic Meridional Mode on decadal time scales. Atmosphere https://doi.org/10.3390/atmos11010003 (2020).
Chikamoto, Y., Wang, S.-Y., Yost, M., Yocom, L. & Gillies, R. R. Colorado River water supply is predictable on multi-year timescales owing to long-term ocean memory. Commun. Earth Environ. https://doi.org/10.1038/s43247-020-00027-0 (2020).
Rayner, N. A. et al. Global analyses of sea surface temperature, sea ice, and night marine air temperature since the late nineteenth century. J. Geophys. Res. Atmos. https://doi.org/10.1029/2002JD002670 (2003).
Becker, A. et al. A description of the global land-surface precipitation data products of the global precipitation climatology centre with sample applications including centennial (trend) analysis from 1901-present. Earth Syst. Sci. Data 5, 71–99 (2013).
Schneider, U. et al. GPCC full data reanalysis version 6.0 at 0.5∘: monthly land-surface precipitation from rain-gauges built on GTS-based and historic data, https://doi.org/10.5676/DWD_GPCC/FD_M_V7_050 (2011).
Slivinski, L. C. et al. Towards a more reliable historical reanalysis: Improvements for version 3 of the Twentieth Century Reanalysis system. Q. J. R. Meteorol. Soc. 145, 2876–2908 (2019).
Trenberth, K. E. & Shea, D. J. Atlantic hurricanes and natural variability in 2005. Geophys. Res. Lett. https://doi.org/10.1029/2006GL026894 (2006).
Delworth, T. L. et al. GFDL’s CM2 Global Coupled Climate Models. Part I: Formulation and Simulation Characteristics. J. Clim. 19, 643–674 (2006).
Bretherton, C. S., Smith, C. & Wallace, J. M. An intercomparison of methods for finding coupled patterns in climate data. J. Clim. 5, 541–560 (1992).
Wallace, J. M., Smith, C. & Bretherton, C. S. Singular value decomposition of wintertime sea surface temperature and 500-mb height anomalies. J. Clim. 5, 561–576 (1992).
The MathWorks Inc. Matlab version: 9.13.0 (r2022b) (2022).
U.S. Geological Survey / USDA Natural Resources Conservation Service / U.S. Environmental Protection Agency. Watershed Boundary Dataset (WBD). https://data.nal.usda.gov/dataset/watershed-boundary-dataset-wbd.Accessed2022-12-13. Accessed: 2022-12-01.
Acknowledgements
This work was supported and funded by the Salt Lake City Department of Public Utilities. Additional support was provided by the Western Water Assessment (a NOAA-funded Regional Integrated Sciences and Assessment (RISA) Grant NA21OAR4310309). We also acknowledge the University of Utah Center of High Performance Computing (CHPC) for computational resources and computer support services.
Author information
Authors and Affiliations
Contributions
C.S. conceived the study, numerical analyses were performed by L.S., C.S., and H.B., and all authors contributed to writing.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Stone, L., Strong, C., Bai, H. et al. Atlantic-Pacific influence on western U.S. hydroclimate and water resources. npj Clim Atmos Sci 6, 139 (2023). https://doi.org/10.1038/s41612-023-00471-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41612-023-00471-7