Abstract
Benchmarking climate model simulations against observations of the climate is core to the process of building realistic climate models and developing accurate future projections. However, in many cases, models do not match historical observations, particularly on regional scales. If there is a mismatch between modeled and observed climate features, should we necessarily conclude that our models are deficient? Using several illustrative examples, we emphasize that internal variability can easily lead to marked differences between the basic features of the model and observed climate, even when decades of model and observed data are available. This can appear as an apparent failure of models to capture regional trends or changes in global teleconnections, or simulation of extreme events. Despite a large body of literature on the impact of internal variability on climate, this acknowledgment has not yet penetrated many model evaluation activities, particularly for regional climate. We emphasize that using a single or small ensemble of simulations to conclude that a climate model is in error can lead to premature conclusions on model fidelity. A large ensemble of multidecadal simulations is therefore needed to properly sample internal climate variability in order to robustly identify model deficiencies and convincingly demonstrate progress between generations of climate models.
Similar content being viewed by others
Introduction
Climate models are remarkably successful in reproducing many earth-system phenomena such as atmospheric jet streams, oceanic currents, monsoons, the El Niño Southern Oscillation (ENSO), the North Atlantic Oscillation (NAO), and the response of global climate to external forcing1,2,3. From their basis in the Navier-Stokes equations of fluid dynamics, even extreme events like heatwaves and cold snaps, floods and droughts, cyclones, and storms all appear spontaneously in climate model simulations. In some cases, models also warn us of more intense extreme events than we have yet experienced but which could plausibly occur at any time in the current climate4,5,6,7. Scientists also use climate models to understand the physical mechanisms behind past changes in climate8, to understand and predict extreme events9, to project future climate change, and to inform governments and policymakers about the impacts of climate change10.
To gain confidence in model projections, the fidelity of models is assessed by comparing model simulations of the historical climate with observations. This trial of models using observations is core to identifying current model deficiencies and prioritizing areas for further development11. The scientific literature presents many examples where a mismatch between model and observed climate features has been reported, such as trends in regional rainfall amount and temperature12,13,14, multidecadal changes in atmospheric circulation15 and climatology16, the frequency or magnitude of extreme events17,18, global teleconnections19, interaction between different modes of climate variability20 or external forcing effects21,22. There can be many reasons why models disagree with observations. However, even in the case of perfect models, perfect boundary conditions, and perfect observations, a lack of agreement between the modeled and observed climate can still arise simply due to chaotic internal variability13,23,24,25,26,27,28,29.
Due to the inevitable presence of internal variability, each realization of climate, in both observations and models, represents only one possible realization out of many30,31. When evaluating models against observations, this issue (known as sampling variability) is supposed to be handled through statistical tests, but the power of those tests relies heavily on the assumed chance process generating internal variability. This leads to a misinterpretation of significance tests, which is widespread in climate science, leading to overly lax criteria32. This problem is only exacerbated if the statistical tests do not take proper account of multidecadal internal variability, which is very difficult to quantify from single or small ensembles of models, or from observations.
Many of the studies claiming a mismatch between models and observations, including some cited in the IPCC WG1 report10, continue to use only a single or a small ensemble of simulations from a given model. These studies generally show that the differences are statistically significant, typically for time periods that are considered sufficiently long. Here, we provide three illustrative examples to demonstrate how internal variability cannot be easily ruled out as a cause of commonly reported discrepancies even when decades of observations and model data are available.
Methods
We use an ensemble of initialized climate simulations from the Climate Historical Forecasts Project (CHFP) database. The ensemble member rainfall from each model was spatially averaged over the selected domains (i.e. 20-28°N, 76-87°E for north-central India and all-India land region) and bias-adjusted using the difference between the ensemble mean and observations for each model’s hindcast period. Model fidelity was then tested using the UNprecedented Simulated Extremes in Ensembles (UNSEEN) method4,27 and rainfall multimodel ensemble (MME) was created using a selected set of models that passed the UNSEEN tests and are statistically indistinguishable from the observations (GloSea5, CFS, and the MPI models for north-central India for 1950-2013, and GloSea5, ECMWF-S4, CFS, MIROC5, and MPI-LR for all-India for 1901–2013) (see Table 1 of Ref. 4 for details of models, Ref. 33 for details on the CHFP). We have also previously tested the fidelity of the CHFP models in representing JJA rainfall over India and found a reasonably realistic simulation of JJA rainfall in most of these models, i.e. the spatial distributions were comparable to the observations, models show statistically significant skill in simulating the interannual variability of JJA rainfall, and the ENSO-rainfall teleconnections were similar to the observations4,34. The ensemble mean trend was removed from each ensemble member time series for each model to remove any influence of climate change before creating MME. A total of 10,000 time series of length 51 years were resampled from MME by randomly selecting ensemble members in sets of three consecutive years to preserve the interannual autocorrelation in rainfall. Linear trends were calculated as the slope of the line of best fit for each time series to obtain 10,000 values of trends. Each trend value was then multiplied by the length of the time series (i.e. 51 years) to obtain the change in JJA total rainfall over a 51-year period, shown on the x-axis (Fig. 1a, b). We also tested the sensitivity of the extreme values shown in Fig. 1 to the model variance by removing one of the models with the highest variance while resampling. We find no substantial influence of the differences in the models’ variance on the extreme values presented in Fig. 1.
Change in June-July-August (JJA) total rainfall over a 51-year period from internal variability in a multimodel ensemble (MME) of climate predictions for (a) north-central India (20-28°N, 76-87°E) and (b) all-India (land-only) rainfall. The darker color indicates wetter trends. The dotted lines show the most extreme 51-year trends in the IMD observational record during 1950–2013 (the period for which drying trends were observed over north-central India) and 1901–2013 for all-India. The MME here is from the Climate Historical Forecasts Project (CHFP). See Methods for more details.
The rainfall MME created for Fig. 1b was used to randomly resample 10,000 time series of lengths 20 and 50 years for all-India rainfall and corresponding sea-surface temperatures (SSTs) for the Nino3.4 region (5°S to 5°N, 170°W to 120°W). The correlation coefficient between all-India rainfall and corresponding Nino3.4 SSTs was calculated for each of the 10,000 time series for both 20 (Fig. 4a) and 50 years (Figure not shown). Similar to rainfall, the SSTs were detrended before resampling to remove the influence of forced climate change on SSTs. For Fig. 4b, we randomly selected 30 correlation values from the 10,000 correlation values for the length of 50 years. We then calculated the average of the selected 30 correlation values to obtain the mean correlation and this was repeated 10,000 times to obtain the distribution in Fig. 4b.
Do models reproduce observed trends?
Over the latter half of the 20th century, historical observations show a significant reduction in the summer monsoon rainfall over parts of India14,35,36,37. However, most historical climate model simulations from different CMIP generations have shown a consistent increase in rainfall during this period and beyond into the 21st century under increasing greenhouse gas forcing14,38,39.
Several hypotheses have been proposed to explain the apparent mismatch in observed and model-simulated trends in monsoon rainfall over north-central India, including large observational uncertainty40, the recent warming of the Indian Ocean41, radiative forcing due to aerosols42 or changes in land-use and land-cover43. In most cases, these factors are found to have systematic effects on the modeled monsoon rainfall. However, it is also possible that internal variability on multidecadal timescales contributes to this mismatch.
We find that the most extreme drying and wetting trends in the Indian Meteorological Department (IMD) observational record for both regional (Fig. 1a) as well as all-India rainfall (Fig. 1b) lie within the range of plausible trends from chaotic internal variability in the current climate. (Note that only the models that pass fidelity tests for observed Indian monsoon rainfall have been used for this analysis.) Even more extreme values than have been observed in the IMD record so far are possible, solely due to internal variability, in the absence of any systematic forced effects. For example, there is around a 1-in-160-year chance of a wetting trend of magnitude larger than the wettest trend, and a 1-in-18-year chance of a drying trend of magnitude larger than the driest trend in the observational record. Therefore, for this case, internal variability cannot easily be rejected as the cause of the models’ apparent failure to capture the observed drying trend (also see Ref. 44,45).
Unprecedented climate extremes are often a manifestation of both internal variability and external forcing. However, in many cases, the internal variability is so large that it can easily negate or greatly overwhelm any forced response in climate trends, even on multidecadal time scales27,46). For example, in this case, internal variability can be large enough to overwhelm the wetting trend due to greenhouse gas forcing and give temporary drying trends in monsoon rainfall.
Another example where the role of internal variability was ignored is the recent paper by Scafetta47, which claimed that no model with a climate sensitivity >3 °C was consistent with observed trends since 1979. However, this claim is based on comparing each model’s ensemble mean change with an observational estimate (from ERA5) without taking either observational uncertainty or model internal variability into account. When these elements are included and appropriate statistical tests were employed (following Ref. 48), it was demonstrated that the majority of the models with sufficiently large ensembles, even some of those with high climate sensitivity of 5 °C, are consistent with the observations49.
There also exists a selection bias when comparing the most extreme trends in the observational record with model-simulated trends50. Inspection of observational time series, with no a priori reason to select the particular period of most extreme trends, followed by comparison with model-simulated trends for the same time period introduces a selection bias and the impression that models fail to produce observed trends. In many cases, those extreme trends in regional climate can appear at any time in the model simulation and not necessarily during the observed period, irrespective of any forced changes which are often smaller than the internal variability for short- or medium-term periods. It is therefore very difficult to argue that models cannot reproduce observed extremes by pre-selecting extreme periods in the observations and then testing models for the same historical period. Significance testing of these extreme trends is difficult in such cases and simple tests based on a single or limited ensembles of simulations to reject the null hypothesis of internal variability in favor of a model error are often invalid51.
Whilst the Indian rainfall trend presented here is only one example, many other cases of models apparently failing to reproduce observed trends for other regions and variables also exist15,16,52,53,54. Therefore, it is necessary to re-examine such cases and carefully rule out internal variability as a cause of apparent mismatch between observed and modeled trends to robustly identify the true model errors.
How should we test models for extreme events?
In addition to the selection bias in time, there also exists a selection bias in space. If we preselect a particular extreme event from the observational record, which, by definition, is a rare event, and look for similar events in climate model simulations, then the chances of finding rare events of the same magnitude, duration, and spatial scale, at the same location will necessarily be low. However, in this case, it is premature to then conclude that models cannot simulate the observed extreme event. For instance, if we then use a large ensemble of climate simulations and search for a similar intense event with no a priori specification of exactly where it should happen, it is often possible to find a similar extreme event in the simulations, leading to very different conclusions about model fidelity46,55.
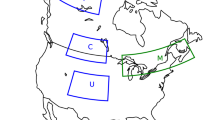
To illustrate this, we use the example of the German floods of 2021. The observed event in July 2021 was associated with daily mean rainfall reaching as high as 150 mm over parts of Germany (Fig. 2c). Searching ensembles of climate simulations from multiple models for European rainfall extremes of similar magnitude to that observed, reveals several instances with rainfall intensity in climate models reaching, and in some cases even exceeding the rainfall rate seen in the observational record (Fig. 3a–d). We can also examine the mean sea level pressure (MSLP) to determine if the simulated extreme corresponds to a realistic circulation pattern. In all cases, the extreme rainfall events in the models are co-located with extreme low-pressure regions (Fig. 3e–h), indicating low-level convergence and enhanced probability of intense rainfall, similar to the observed event which had low MSLP in the vicinity.
To illustrate the point further, we also examined a large ensemble from a single model, the CESM156, as this isolates the impact of internal variability. While we find similar mid-latitude extremes occurring randomly anywhere over the selected domain in some simulations of the large ensemble, other simulations from the same model did not simulate any such events. This shows that a-priori constraining the regional scale and location in the model to that of the pre-selected local record event invalidates commonly used statistical significance tests and hence can lead to the erroneous conclusion that models cannot reproduce the observed extreme. One potential way to handle this issue is to employ a spatially aggregated probability perspective, for example as demonstrated by Ref. 46, and aggregate rainfall distributions over a spatial domain (e.g. for Köppen Geiger climate zones or regions with similar topographic features or climate variability). However, any such aggregation raises other questions, as the distribution is no longer independent and identically distributed.
Are teleconnections changing?
Large-scale internal variability from phenomena such as ENSO, NAO, or the Indian Ocean Dipole (IOD), are known to influence regional climate across the globe through teleconnections. These teleconnections lead to systematic changes in regional climate far from the center of action of the variability itself57,58,59,60 and often contribute to the predictability of regional weather and climate events. For example, the ENSO-rainfall teleconnection is crucial for tropical rainfall prediction at seasonal lead times34,61.
Recent literature questions the stationarity of these and other teleconnections and in many cases argues that causal mechanisms, such as externally forced climate change, are driving systematic change in either the pattern or the strength of the teleconnection from one epoch to another, and that these changes are not represented in climate models. For instance, changes in the ENSO-rainfall teleconnection have been reported for several tropical regions including India62, East Asia63, North America64, and Africa65,66, as well as many other large-scale teleconnections, such as the recently discovered connection between the Quasi-Biennial Oscillation and Madden Julian Oscillation20,67 and the ENSO-Asian teleconnection68.
Several studies already highlight internal variability as a cause of the apparent mismatch between model and observed teleconnections69,70,71,72,73,74 but many others continue to suggest that mismatch implies model error. Therefore, we re-examine one well-known example: ENSO and Indian summer monsoon rainfall teleconnection.
Figure 4 (a) shows that the distribution of ENSO teleconnections in rainfall resamples covers an enormous range of correlations on 20-year timescales (r = −0.90 to 0.47). A similar result holds for 50-year timescales (r = −0.80 to 0.22). Note that this range occurs due to sampling variability rather than any true systematic non-stationarity, and includes the historical periods such as 1980–2010 when non-stationarity in the ENSO-Indian rainfall teleconnection has been reported in observations62. Whilst methodologies to calculate the ENSO-monsoon relationship vary in the literature, even the extreme examples of apparent non-stationarity in observed teleconnections sit well within the spread of plausible ENSO-monsoon teleconnections due to the internal variability of the climate system. The model resamples even show the possibility of a positive correlation on 20-year timescales; opposite in sign to the observed teleconnection.
Probability distribution of Pearson’s correlation coefficient between detrended Nino3.4 sea-surface temperatures (SSTs) and all-India rainfall from the Climate Historical Forecasts Project (CHFP) multimodel ensemble. Panel (a) is for resampled rainfall and SST time series of length 20 years and shows the range of correlations corresponding to individual ensemble member time series. Panel (b) is for 50-year time series and correlation values were randomly resampled in sets of 30 and therefore represent the range of mean correlations for 30 ensemble members (see Methods). The dotted lines show some extreme examples of correlation values from the literature for corresponding timescales. Examples shown in panel (b) are from Ref. 72 for the ensemble size of 30 and for the SSP5-8.5 scenario.
In addition, there is also a growing body of literature suggesting that the ENSO-Indian rainfall teleconnection could change in the future under climate change75,76. However, Fig. 4 (b) shows that the mean ENSO-rainfall correlation for the CMIP6 multimodel ensembles (of size ~30) for both historical and future periods72 sits within the range of internal variability (r = −0.31 to −0.51). Therefore, great care is needed before we can conclude with confidence that there is any robust change in the ENSO-monsoon relationship in the future.
Finally, given the broad range of possibilities in Fig. 4a, b, and the fact that simulated future changes are well within this range, it is unlikely that observational data will yield significant examples of changes in teleconnections that are extreme enough to rule out internal variability and detect any true non-stationarity on any reasonable timescale into the future.
A call for more rigorous model assessment
We find that studies claiming a mismatch between model and observed climate phenomena are often too quick to ignore the null hypothesis that such apparent discrepancies between models and observations can arise due to chaotic internal variability. We have presented examples where this applies to changes on multidecadal timescales, such as global and regional trends, recent extreme events, and apparent changes in observed teleconnections. Assessing models against the rare and most extreme observed cases automatically introduces a selection bias into the process of model evaluation, which is particularly compounded for extreme events on small spatial scales. Limited observational records can easily show apparent non-stationary or spurious teleconnections due to internal variability and sampling error. Using a single simulation or small ensembles of simulations can easily lead to premature conclusions about model fidelity. Therefore, a large ensemble of multidecadal simulations is needed to properly sample initial condition uncertainty and convincingly demonstrate model failure to capture observed phenomena, as well as to assess the progress or deterioration in performance between older and newer generations of models. Initialized large ensembles are already being used for seasonal predictions33,77, and more recently for multidecadal predictions78 and projections53,79. Using these ensembles to isolate internal variability from true model errors provides a powerful second application.
Future outlook and summary
While a large ensemble is desirable to account for fluctuations due to internal variability, we acknowledge that these are computationally expensive and may not be always available. Therefore, we also highlight other potential model evaluation methodologies that could be used. For instance, in contrast to picking a single period in observations and testing a single model simulation against that, we suggest using a longer time period, and sampling all possible periods of a fixed length within that interval. For example, sampling 20-year trends over 50 years for both observations and models and comparing the distribution of trends4,51. Comparing multimodel mean trends directly with the observations is also not a fair comparison49 and for these cases, statistical tests, similar to the UNSEEN method6, could be employed to test model fidelity.
Grid point comparisons for extremes, such as calculating spatial distributions of extremes (e.g., 1-day maximum rainfall) and comparing those with the model spatial distribution, are likely to show apparent disagreement. A similar problem has been recognized as ‘double-penalty’ in high-resolution weather prediction where verification scores are penalized twice, i.e. for simulating a feature in the wrong place and not simulating a feature at the right place80. Simple approaches, such as pooling daily maximum rainfall values over a time period and spatial domain for both observations and models, and then comparing the distributions, or extending more sophisticated methodologies (such as Hi-RA81) used in high-resolution weather prediction, could be considered for evaluating climate models for extremes.
There are also new emerging methodologies, such as resampling of observational records to create pseudo-observational large ensembles5, quantification of the degree of discrepancy between models and observations using Bayes factors32, spatial aggregation of regional extremes46, ensemble boosting methods where a climate model is reinitialized to generate large samples of extreme events at relatively low cost82, physical or process-based evaluation of models using storyline methods32, and intelligent use of machine learning methods to differentiate variability from model errors83, all of which could be employed for better control of internal variability and sampling error.
Finally, we emphasize that models will always contain errors. The proper sampling of internal variability is a necessary but not sufficient condition for assessing model fidelity; it is also crucial to assess if the model simulates the phenomena of interest and is fit for purpose. Certainly, not all disagreements between models and observations can be attributed to internal variability. However, this only underscores the need for large ensembles of multidecadal simulations to bolster our efforts toward the development of more realistic climate models.
References
Broecker, W. S. Climatic Change: Are We on the Brink of a Pronounced Global Warming? Science 189, 460–463 (1975).
Hansen, J. et al. Climate Impact of Increasing Atmospheric Carbon Dioxide. Science 213, 957–966 (1981).
Hausfather, Z., Drake, H. F., Abbott, T. & Schmidt, G. A. Evaluating the Performance of Past Climate Model Projections. Geophys. Res. Lett. 47, e2019GL085378 (2020).
Jain, S., Scaife, A. A., Dunstone, N., Smith, D. & Mishra, S. K. Current chance of unprecedented monsoon rainfall over India using dynamical ensemble simulations. Environ. Res. Lett. 15, 094095 (2020).
McKinnon, K. A. & Deser, C. The inherent uncertainty of precipitation variability, trends, and extremes due to internal variability, with implications for Western US water resources. J. Clim. 1–46 (2021). https://doi.org/10.1175/JCLI-D-21-0251.1.
Thompson, V. et al. High risk of unprecedented UK rainfall in the current climate. Nat. Commun. 8, 107 (2017).
Kent, C. et al. Estimating unprecedented extremes in UK summer daily rainfall. Environ. Res. Lett. 17, 014041 (2022).
Mitchell, J. F. B., Johns, T. C., Gregory, J. M. & Tett, S. F. B. Climate response to increasing levels of greenhouse gases and sulphate aerosols. Nature 376, 501–504 (1995).
Hardiman, S. C. et al. Predictability of European winter 2019/20: Indian Ocean dipole impacts on the NAO. Atmos. Sci. Lett. 21, e1005 (2020).
IPCC, 2021: Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change [Masson-Delmotte, V., et al. (eds.)]. Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA, 2391 pp. https://doi.org/10.1017/9781009157896.
Flato, G., et al. (2013). Evaluation of Climate Models. In: Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change [Stocker, T. F., D. Qin, G.-K. Plattner, M. Tignor, S. K. Allen, J. Boschung, A. Nauels, Y. Xia, V. Bex and P. M. Midgley (eds.)]. Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA.
Mishra, S. K., Sahany, S., Salunke, P., Kang, I.-S. & Jain, S. Fidelity of CMIP5 multi-model mean in assessing Indian monsoon simulations. Npj Clim. Atmos. Sci. 1, 1–8 (2018).
Mitchell, D. M., Thorne, P. W., Stott, P. A. & Gray, L. J. Revisiting the controversial issue of tropical tropospheric temperature trends. Geophys. Res. Lett. 40, 2801–2806 (2013).
Saha, A., Ghosh, S., Sahana, A. S. & Rao, E. P. Failure of CMIP5 climate models in simulating post-1950 decreasing trend of Indian monsoon. Geophys. Res. Lett. 41, 7323–7330 (2014).
Gillett, N. P., Zwiers, F. W., Weaver, A. J. & Stott, P. A. Detection of human influence on sea-level pressure. Nature 422, 292–294 (2003).
Seidel, D. J., Fu, Q., Randel, W. J. & Reichler, T. J. Widening of the tropical belt in a changing climate. Nat. Geosci. 1, 21–24 (2008).
Tyrrell, N. L., Koskentausta, J. M. & Karpechko, A. Y. Sudden stratospheric warmings during El Niño and La Niña: sensitivity to atmospheric model biases. Weather Clim. Dyn. 3, 45–58 (2022).
Slingo, J. et al. Ambitious partnership needed for reliable climate prediction. Nat. Clim. Change 12, 499–503 (2022).
Butler, A. H. & Polvani, L. M. El Niño, La Niña, and stratospheric sudden warmings: A reevaluation in light of the observational record. Geophys. Res. Lett. 38, L13807 (2011).
Martin, Z., Orbe, C., Wang, S. & Sobel, A. The MJO–QBO Relationship in a GCM with Stratospheric Nudging. J. Clim. 34, 4603–4624 (2021).
Schmidt, G. A., Shindell, D. T. & Tsigaridis, K. Reconciling warming trends. Nat. Geosci. 7, 158–160 (2014).
LeGrande, A. N., Tsigaridis, K. & Bauer, S. E. Role of atmospheric chemistry in the climate impacts of stratospheric volcanic injections. Nat. Geosci. 9, 652–655 (2016).
Tebaldi, C. & Knutti, R. The use of the multi-model ensemble in probabilistic climate projections. Philos. Trans. R. Soc. Math. Phys. Eng. Sci. 365, 2053–2075 (2007).
Deser, C., Knutti, R., Solomon, S. & Phillips, A. S. Communication of the role of natural variability in future North American climate. Nat. Clim. Change 2, 775–779 (2012).
Deser, C., Terray, L. & Phillips, A. S. Forced and Internal Components of Winter Air Temperature Trends over North America during the past 50 Years: Mechanisms and Implications*. J. Clim. 29, 2237–2258 (2016).
Deser, C., Simpson, I. R., Phillips, A. S. & McKinnon, K. A. How Well Do We Know ENSO’s Climate Impacts over North America, and How Do We Evaluate Models Accordingly? J. Clim. 31, 4991–5014 (2018).
Jain, S. & Scaife, A. A. How extreme could the near term evolution of the Indian Summer Monsoon rainfall be? Environ. Res. Lett. 17, 034009 (2022).
Fasullo, J. T., Phillips, A. S. & Deser, C. Evaluation of Leading Modes of Climate Variability in the CMIP Archives. J. Clim. 33, 5527–5545 (2020).
McKinnon, K. A. & Simpson, I. R. How Unexpected Was the 2021 Pacific Northwest Heatwave? Geophys. Res. Lett. 49, e2022GL100380 (2022).
Lorenz, E. N. The predictability of a flow which possesses many scales of motion. Tellus 21, 289–307 (1969).
Lorenz, E. N. Deterministic Nonperiodic Flow. J. Atmos. Sci. 20, 130–141 (1963).
Shepherd, T. G. Bringing physical reasoning into statistical practice in climate-change science. Clim. Change 169, 2 (2021).
Tompkins, A. M. et al. The Climate-System Historical Forecast Project: Providing Open Access to Seasonal Forecast Ensembles from Centers around the Globe. Bull. Am. Meteorol. Soc. 98, 2293–2301 (2017).
Jain, S., Scaife, A. A. & Mitra, A. K. Skill of Indian summer monsoon rainfall prediction in multiple seasonal prediction systems. Clim. Dyn. 52, 5291–5301 (2019).
Kumar, V., Jain, S. K. & Singh, Y. Analysis of long-term rainfall trends in India. Hydrol. Sci. J. 55, 484–496 (2010).
Ramesh, K. V. & Goswami, P. Assessing reliability of regional climate projections: the case of Indian monsoon. Sci. Rep. 4, 4071 (2014).
Jin, Q. & Wang, C. A revival of Indian summer monsoon rainfall since 2002. Nat. Clim. Change 7, 587–594 (2017).
Katzenberger, A., Schewe, J., Pongratz, J. & Levermann, A. Robust increase of Indian monsoon rainfall and its variability under future warming in CMIP6 models. Earth Syst. Dyn. 12, 367–386 (2021).
Shashikanth, K., Salvi, K., Ghosh, S. & Rajendran, K. Do CMIP5 simulations of Indian summer monsoon rainfall differ from those of CMIP3? Atmos. Sci. Lett. 15, 79–85 (2014).
Singh, D., Ghosh, S., Roxy, M. K. & McDermid, S. Indian summer monsoon: Extreme events, historical changes, and role of anthropogenic forcings. WIREs Clim. Change 10, e571 (2019).
Roxy, M. K. et al. Drying of Indian subcontinent by rapid Indian Ocean warming and a weakening land-sea thermal gradient. Nat. Commun. 6, 7423 (2015).
Monerie, P.-A., Wilcox, L. J. & Turner, A. G. Effects of Anthropogenic Aerosol and Greenhouse Gas Emissions on Northern Hemisphere Monsoon Precipitation: Mechanisms and Uncertainty. J. Clim. 35, 2305–2326 (2022).
Paul, S. et al. Weakening of Indian Summer Monsoon Rainfall due to Changes in Land Use Land Cover. Sci. Rep. 6, 32177 (2016).
Huang, X. et al. The recent decline and recovery of Indian summer monsoon rainfall: relative roles of external forcing and internal variability. J. Clim. 33, 5035–5060 (2020).
Sinha, A. et al. Trends and oscillations in the Indian summer monsoon rainfall over the last two millennia. Nat. Commun. 6, 6309 (2015).
Fischer, E. M., Beyerle, U. & Knutti, R. Robust spatially aggregated projections of climate extremes. Nat. Clim. Change 3, 1033–1038 (2013).
Scafetta, N. Advanced Testing of Low, Medium, and High ECS CMIP6 GCM Simulations Versus ERA5-T2m. Geophys. Res. Lett. 49, e2022GL097716 (2022).
Santer, B. D. et al. Consistency of modelled and observed temperature trends in the tropical troposphere. Int. J. Climatol. 28, 1703–1722 (2008).
Pubs.GISS: Schmidt et al. 2023, accepted: Comment on “Advanced testing of low, medium, and high ECS CMIP6… https://pubs.giss.nasa.gov/abs/sc05800h.html.
Rahmstorf, S., Foster, G. & Cahill, N. Global temperature evolution: recent trends and some pitfalls. Environ. Res. Lett. 12, 054001 (2017).
Eade, R., Stephenson, D. B., Scaife, A. A. & Smith, D. M. Quantifying the rarity of extreme multi-decadal trends: how unusual was the late twentieth century trend in the North Atlantic Oscillation? Clim. Dyn. 58, 1555–1568 (2022).
Swart, N. C., Fyfe, J. C., Hawkins, E., Kay, J. E. & Jahn, A. Influence of internal variability on Arctic sea-ice trends. Nat. Clim. Change 5, 86–89 (2015).
Deser, C. et al. Insights from Earth system model initial-condition large ensembles and future prospects. Nat. Clim. Change 10, 277–286 (2020).
Deser, C. & Phillips, A. S. A range of outcomes: the combined effects of internal variability and anthropogenic forcing on regional climate trends over Europe. Nonlinear Process. Geophys. 30, 63–84 (2023).
Fischer, E. M., Sippel, S. & Knutti, R. Increasing probability of record-shattering climate extremes. Nat. Clim. Change 11, 689–695 (2021).
Kay, J. E. et al. The Community Earth System Model (CESM) Large Ensemble Project: A Community Resource for Studying Climate Change in the Presence of Internal Climate Variability. Bull. Am. Meteorol. Soc. 96, 1333–1349 (2015).
Branstator, G. Circumglobal Teleconnections, the Jet Stream Waveguide, and the North Atlantic Oscillation. J. Clim. 15, 1893–1910 (2002).
Hurrell, J. W., Kushnir, Y., Ottersen, G. & Visbeck, M. An overview of the North Atlantic Oscillation. in Geophysical Monograph Series (eds. Hurrell, J. W., Kushnir, Y., Ottersen, G. & Visbeck, M.) vol. 134 1–35 (American Geophysical Union), (2003).
Trenberth, K. E. ENSO in the Global Climate System. in Geophysical Monograph Series (eds. McPhaden, M. J., Santoso, A. & Cai, W.) 21–37 (Wiley), (2020). https://doi.org/10.1002/9781119548164.ch2.
Yamagata, T. et al. Coupled ocean-atmosphere variability in the tropical Indian Ocean. Wash. DC Am. Geophys. Union Geophys. Monogr. Ser. 147, 189–211 (2004).
Scaife, A. A. et al. Tropical rainfall predictions from multiple seasonal forecast systems. Int. J. Climatol. 39, 974–988 (2019).
Kumar, K. K., Rajagopalan, B. & Cane, M. A. On the weakening relationship between the indian monsoon and ENSO. Science 284, 2156–2159 (1999).
Wu, R. & Wang, B. A Contrast of the East Asian Summer Monsoon–ENSO Relationship between 1962–77 and 1978–93. J. Clim. 15, 3266–3279 (2002).
Coats, S., Smerdon, J. E., Cook, B. I. & Seager, R. Stationarity of the tropical pacific teleconnection to North America in CMIP5/PMIP3 model simulations. Geophys. Res. Lett. 40, 4927–4932 (2013).
Losada, T. et al. Tropical SST and Sahel rainfall: A non-stationary relationship. Geophys. Res. Lett. 39, L12705 (2012).
Bahaga, T. K., Fink, A. H. & Knippertz, P. Revisiting interannual to decadal teleconnections influencing seasonal rainfall in the Greater Horn of Africa during the 20th century. Int. J. Climatol. 39, 2765–2785 (2019).
Lee, J. C. K. & Klingaman, N. P. The effect of the quasi-biennial oscillation on the Madden–Julian oscillation in the Met Office Unified Model Global Ocean Mixed Layer configuration. Atmos. Sci. Lett. 19, e816 (2018).
He, S., Wang, H. & Liu, J. Changes in the relationship between ENSO and Asia–Pacific midlatitude winter atmospheric circulation. J. Clim. 26, 3377–3393 (2013).
Kitoh, A. Variability of Indian monsoon-ENSO relationship in a 1000-year MRI-CGCM2.2 simulation. Nat. Hazards J. Int. Soc. Prev. Mitig. Nat. Hazards 42, 261–272 (2007).
Bódai, T., Drótos, G., Herein, M., Lunkeit, F. & Lucarini, V. The Forced Response of the El Niño–Southern Oscillation–Indian Monsoon Teleconnection in Ensembles of Earth System Models. J. Clim. 33, 2163–2182 (2020).
Deser, C., Simpson, I. R., McKinnon, K. A. & Phillips, A. S. The Northern Hemisphere Extratropical Atmospheric Circulation Response to ENSO: How Well Do We Know It and How Do We Evaluate Models Accordingly? J. Clim. 30, 5059–5082 (2017).
Lee, J.-Y. & Bódai, T. Chapter 20 - Future changes of the ENSO–Indian summer monsoon teleconnection. in Indian Summer Monsoon Variability (eds. Chowdary, J., Parekh, A. & Gnanaseelan, C.) 393–412 (Elsevier), (2021). https://doi.org/10.1016/B978-0-12-822402-1.00007-7.
Yun, K.-S. & Timmermann, A. Decadal Monsoon-ENSO Relationships Reexamined. Geophys. Res. Lett. 45, 2014–2021 (2018).
Gershunov, A., Schneider, N. & Barnett, T. Low-Frequency Modulation of the ENSO–Indian Monsoon Rainfall Relationship: Signal or Noise? J. Clim. 14, 2486–2492 (2001).
Climate Phenomena and their Relevance for Future Regional Climate Change — IPCC. https://www.ipcc.ch/report/ar5/wg1/climate-phenomena-and-their-relevance-for-future-regional-climate-change/.
Roy, I., Tedeschi, R. G. & Collins, M. ENSO teleconnections to the Indian summer monsoon under changing climate. Int. J. Climatol. 39, 3031–3042 (2019).
Buontempo, C., Hewitt, C. D., Doblas-Reyes, F. J. & Dessai, S. Climate service development, delivery and use in Europe at monthly to inter-annual timescales. Clim. Risk Manag. 6, 1–5 (2014).
Boer, G. J. et al. The Decadal Climate Prediction Project (DCPP) contribution to CMIP6. Geosci. Model Dev. 9, 3751–3777 (2016).
Maher, N., Lehner, F. & Marotzke, J. Quantifying the role of internal variability in the temperature we expect to observe in the coming decades. Environ. Res. Lett. 15, 054014 (2020).
Hagelin, S. et al. The Met Office convective-scale ensemble, MOGREPS-UK. Q. J. R. Meteorol. Soc. 143, 2846–2861 (2017).
Mittermaier, M. P. A Strategy for Verifying Near-Convection-Resolving Model Forecasts at Observing Sites. Weather Forecast 29, 185–204 (2014).
Gessner, C., Fischer, E. M., Beyerle, U. & Knutti, R. Very Rare Heat Extremes: Quantifying and Understanding Using Ensemble Reinitialization. J. Clim. 34, 6619–6634 (2021).
Barnes, E. A., Hurrell, J. W., Ebert-Uphoff, I., Anderson, C. & Anderson, D. Viewing Forced Climate Patterns Through an AI Lens. Geophys. Res. Lett. 46, 13389–13398 (2019).
Acknowledgements
The data that support the findings of this study are openly available at the following URLs: https://cds.climate.copernicus.eu/cdsapp#!/dataset/projections-cmip6, https://www.wcrp-climate.org/wgsip-chfp/chfp-data-archive and https://www.cesm.ucar.edu/projects/community-projects/LENS/data-sets.html. The IMD rainfall data can be obtained from the following link: https://www.imdpune.gov.in/Clim_Pred_LRF_New/Grided_Data_Download.html. The authors thank two anonymous reviewers for their suggestions on this paper. AAS and ND were supported by the Met Office Hadley Centre Climate Programme (HCCP) funded by BEIS and Defra. SJ thanks June Yi Lee and Tamas Bodai for their inputs on ENSO and Indian rainfall teleconnection. The authors thank the two reviewers for their comments and the editor for handling this manuscript.
Author information
Authors and Affiliations
Contributions
S.J. and A.A.S. jointly wrote the first draft. S.J. performed the data analysis. All co-authors contributed to the discussion and writing/editing of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Jain, S., Scaife, A.A., Shepherd, T.G. et al. Importance of internal variability for climate model assessment. npj Clim Atmos Sci 6, 68 (2023). https://doi.org/10.1038/s41612-023-00389-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41612-023-00389-0