Abstract
The North Pacific Oscillation (NPO), a representative midlatitude atmospheric variability, plays an important role in the development of the El Niño-Southern Oscillation (ENSO). To explain this extratropical–tropical linkage, previous studies have focused on the atmospheric boundary layer processes coupled with the mixed-layer ocean. Different from the existing hypothesis, in this study, we propose a new mechanism to link the NPO to ENSO via upper-tropospheric teleconnections. Analyses of the wave activity flux show that wave energy associated with the NPO directly propagates from midlatitude to the tropics, modulating the tropical circulation. During the NPO event, this equatorward energy flux becomes pronounced after the NPO peak phase and persists for more than two weeks. As a result, when a positive NPO grows (here, north anticyclonic–south cyclonic circulation), upper-level easterly wind anomalies are situated along the equatorial Pacific. Accordingly, anomalous lower-level westerly winds simultaneously occur in the equatorial Pacific, contributing to the development of El Niño events. To demonstrate the wave energy propagation via the upper-level troposphere, a stationary wave model experiment was performed with an NPO-like barotropic vorticity forcing. The results show equatorward wave propagation consistent with the observation.
Similar content being viewed by others
Introduction
The North Pacific Oscillation (NPO) is an important internal atmospheric variability of the climate system over the North Pacific during boreal winter (for convenience, in this study, seasons follow those of the northern hemisphere) that drives the North Pacific Gyre Oscillation as the oceanic expression1. Analogous to the North Atlantic Oscillation2,3, the NPO is characterized by a north–south dipole of sea level pressure (SLP) anomalies, which is conventionally represented by the second empirical orthogonal function (EOF) mode of SLP over the North Pacific4,5,6, and it usually bears a quasi-barotropic structure7,8 over the extra-tropics. Recent studies identified that the NPO has both upstream and downstream impacts on winter climate extremes over East Asia9 and North America10,11, highlighting its cruciality for adjacent regional climates. When the northern lobe of the NPO is anticyclonic (referred to as the positive NPO phase in this study), North America experiences colder than normal conditions, as the northerly wind prevails across the central to eastern parts of the continent.
Meanwhile, it has been suggested that the circulation of the NPO southern lobe has a profound effect on tropical variability. Numerous studies have shown that the NPO during winter can trigger El Niño-Southern Oscillation (ENSO) events in the subsequent winter5,12,13,14. A previous study15 first proposed a dynamical mechanism, the so-called seasonal footprinting mechanism (SFM), focusing on the lower-level zonal wind anomalies related to the NPO. During the positive NPO phase, the westerly wind anomalies in the subtropics, accompanied by the cyclonic southern lobe of the NPO, weakened the climatological trade winds to warm the local sea surface temperature (SST) by reducing upward latent heat flux16,17. This leaves a “footprint” of SST anomalies over the subtropical eastern North Pacific during spring in conjunction with the Pacific Meridional Mode as its crucial conduits18,19,20. Thereafter, the positive SST anomalies persist into the following summer, intensifying equatorial westerly wind anomalies to trigger the El Niño event through the Bjerknes feedback. These SFM processes primarily manifest within the boundary layers of the tropical atmosphere and oceanic mixed layer.
In addition to the contributions by the wind-evaporation-SST (WES) feedback, the NPO influences ENSO variability via oceanic heat content charging/discharging by trade wind stress20,21,22. The low SLP anomalies over the southern lobe of the positive NPO phase accompany lower-level westerly wind anomaly in the subtropical North Pacific, which acts to accumulate oceanic heat content within the equatorial Pacific by Sverdrup transport. Such accumulated heat contents facilitate ENSO initiation.
The abovementioned studies attribute the extratropical–tropical Pacific linkages by the NPO mostly to the boundary layer processes, which suggests the gradual progress of the NPO-related SST signals beginning from the midlatitudes to reach the equatorial Pacific. However, the observational result does not always show continuous footprints of the NPO-induced signals that extend into the equator23,24 (also shown in Fig. 2b, d); namely, the NPO-related SST anomalies are observed in both subtropical and equatorial Pacific separately, not being connected to each other. Such discontinuous feature raises the possibility of another pathway linking the extratropical–tropical circulations. Therefore, we investigated energy propagation aloft in the upper troposphere and suggested a new mechanism to explain how the NPO impacts tropical climate.
Several previous studies have examined the upper-level Rossby wave energy propagation associated with the NPO25,26,27,28. Nonetheless, they mainly considered the northward and eastward propagation of wave energy, focusing on the downstream impacts of the NPO on the North American climate. In this study, by examining both seasonal and subseasonal evolutions of the NPO events, we show that the upper-level wave activity flux (WAF) induced by the NPO can significantly transport energy from the midlatitude to tropics, modulating the equatorial winds in both the upper and lower troposphere.
The rest of this article is organized as follows. The main finding of the NPO impact on tropical variability and its associated mechanism are presented in “Results” part. A brief conclusion and discussion are given in Conclusions and discussion part. The Methods and data, as well as the statistics are introduced lastly. This is our Part I study; our Part II study will further substantiate the WAF impact on the tropics in models of the Coupled Model Intercomparison Project Phases 5 and 6 (CMIP5/6).
Results
The NPO impact on the tropics on a monthly timescale
In this study, it should be introduced first that the subseasonal variability of the NPO was examined using the daily NPO index, which is constructed by projecting the daily SLP anomalies onto the second EOF pattern of November-March (ND0JFM1) averaged SLP (Fig. 1a). The daily NPO timeseries are shown in Fig. 1b. Then, the anomalies of SLP, lower- and upper-level wind, and stream function (SF) are regressed upon the daily NPO index to show the NPO evolution.
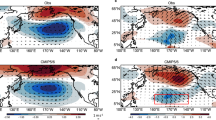
We examined the evolution of variables based on monthly mean data over the north and equatorial Pacific during positive and negative NPO winters. Figure 2 shows the composite difference of wind and geopotential anomalies at 300 and 850 hPa, as well as the SST anomalies, between the positive and negative NPO years from December to February (D0JF1) and March. We separately presented the D0JF1 anomaly patterns to show early growth features of the NPO-induced signals. In D0JF1, a strong cyclonic circulation anomaly associated with the positive NPO phase dominates over the midlatitudes, whereas the high-latitudes are overwhelmed by anticyclonic circulation anomaly (Fig. 2a). Besides these, the tropical circulation is featured by an anomalous anticyclonic circulation and positive geopotential height anomalies that accompany easterly wind anomalies at 300 hPa along the equator, although the geopotential signal is weak (Fig. 2a). In the lower level, strong cyclonic wind anomalies prevail over the North Pacific, and significant westerly wind anomalies are observed over the equatorial western Pacific, indicating a weakening of the Pacific Walker circulation (Fig. 2b). The westerly winds are crucial as they act to initiate the development of ENSO events. These equatorial westerly wind anomalies are concurrent with the upper-level easterly wind anomalies, constructing a vertically baroclinic structure. Moreover, the NPO-induced horseshoe-like SST anomalies (shading in Fig. 2b), which are reckoned to be the SFM signal, are confined to the subtropical eastern North Pacific region, being separated from the equatorial positive SST anomalies. Notably, positive precipitation anomalies are observed over the western Pacific warm pool region, which is unlikely to be involved with the SFM signal. It seems that the equatorial positive SST anomalies are rather tightly connected with the lower-level westerly and upper-level easterly winds anomalies.
Composite difference of D0JF1-averaged a 300 hPa winds (vector; unit: m s−1) and geopotential (shading; unit: 10 gpm), and b 850 hPa winds (vector; unit: m s−1), precipitation (represented by dots) and SST (shading; unit: °C) anomalies between 10 positive and 10 negative NPO events. c, d are the same as (a) and (b), except that they are for March. The areas with shades represent anomalies significant above 90% confidence level, and the areas with black arrows represent the zonal wind above 90% confidence level based on the Student’s t-test. The red (blue) dots in (b) and (d) represent the positive (negative) precipitation anomalies significant at 90% confidence level, whereas the size represents the magnitude.
In March, the extratropical NPO signals become weaker, but the upper-level geopotential height and wind anomalies are further intensified in the subtropics (Fig. 2c). In particular, the anticyclonic anomalies overwhelm the entire subtropical Pacific so that the equatorial easterly anomalies are dominant. In the lower level, the equatorial westerly anomalies are extended and intensified, showing a clear vertically baroclinic structure at the equator, with the enhanced equatorial SST anomalies (Fig. 2d). The horseshoe-like SST anomalies in the subtropics also become stronger in March, having the positive SST anomalies extended from the eastern North Pacific to the equator, which is a key feature of the SFM process (Fig. 2d). However, the wind and SST anomalies are not well-connected between subtropical and equatorial signals. In addition, the westerly anomalies over the equatorial Pacific at the lower level appear to precede the SFM-related SST anomalies; later on, the positive SST anomalies extend from the eastern North Pacific to the tropics, which suggests that the equatorial wind anomalies are not only contributed by the boundary layer processes but also possibly promoted by the upper-level NPO-related processes.
Figure 3 shows the WAF during the NPO events. To show the NPO-related WAF, we separately calculated the WAF for the positive and negative NPO composites and took the average, as the wave energy of the two different polarities of the NPO is headed in the same direction. In D0JF1, the WAF exhibits northward and eastward propagation in the extratropics, which agrees with previous studies that suggested the NPO-induced WAF could affect North America4,11,29. Notably, there is also clear southward wave propagation in the subtropics, which can reach deep tropics over the central Pacific (Fig. 3a). To the best of our knowledge, this southward propagation has never been reported regarding tropical modulation of the NPO.
The composite differences of SF (shading; unit: 106 m2 s−1) between the positive and negative NPO years and calculated WAF (vector; unit: m2 s−2) based on SF anomalies for a D0JF1 and b March. Only the magnitude of the WAF larger than 0.1 is displayed. The area with red dots means that the SF anomalies are significant above 90% confidence level based on Student’s t-test.
The southward wave propagation can induce subtropical anticyclonic (cyclonic) flow at the upper level during the positive (negative) NPO events, which can explain the significant equatorial wind anomalies at the upper level during the NPO events (Fig. 2a). In March, the southward WAF becomes more prevalent over the central Pacific region, which induces stronger equatorial easterly anomalies in the upper troposphere. It is conceived that the lower-level westerly anomalies are concomitant with the upper-level easterly anomalies in the tropics due to the baroclinity accompanied by the tropical convection. From previous studies, the lower-level westerly anomalies in spring are crucial for the following ENSO development by triggering the equatorial westerly wind30,31,32,33,34 (Fig. 2b, d).
Mechanism of the NPO impact on the tropics on a daily timescale
In the previous subsection, we revealed a clear southward propagation of the NPO-related extratropical circulation into the subtropics. As for the positive NPO phase, the southward WAF is linked to the upper-level subtropical anticyclonic circulation, which is suggested to be responsible for the lower-level westerly anomalies along the equator. However, the monthly or seasonal mean data are results of various complex interactions; hence, it is difficult to draw a strong conclusion on causality. For example, the equatorial westerly and SST anomalies in Fig. 2c might be results of their mutual interaction; therefore, it is difficult to determine which one precedes the other from the seasonal mean data. To resolve this issue and support the role of the WAF further, we check the daily evolution of NPO-related atmospheric circulations.
First, using the daily NPO index, we calculated the lead–lag regression of the upper- and lower-level circulation and associated WAF. Figure 4 shows the wind and SF anomalies at 300 hPa, computed from November to March. We presented SF anomalies instead of geopotential, as they better display subtropical features. On the −10 day (i.e., 10 days before the peak NPO phase), significant cyclonic circulation anomalies appeared in the upper troposphere around 30°N over the North Pacific, whereas the wind anomalies were tenuous over lower latitudes (Fig. 4a). On the −5 day, the NPO developed; both the SF and wind anomalies intensified. Concurrently, a weak anomalous anticyclonic circulation grew over the lower latitudes accompanying easterly wind anomalies over the equatorial region, consistent with the positive SF (Fig. 4b). On 0 day, namely, when the NPO reached the mature phase, a strong tripole pattern was observed across the North Pacific (Fig. 4c). At this time, significant easterly wind anomalies occupied over the equatorial western Pacific and southwesterly wind anomalies over the eastern Pacific region. From +5 to +15 days, the NPO slowly decayed (Fig. 4d–f).
a Regressed 300 hPa wind (unit: m s−1) and SF (unit: 106 m2 s−1) anomalies with 10 days leading the NPO index; b the same as (a) but for a 5-day lead; c simultaneously regressed wind and SF anomalies onto the daily NPO index; d–f regressed 300 hPa winds and SF anomalies with 5- to 15-day lags, respectively. The area with black arrows shows the zonal winds above 90% confidence level based on Student’s t-test.
Interestingly, the developing and decaying stages are not symmetric, especially over the tropics; during the NPO decaying stage, the circulation anomalies over the extratropics gradually weakened and moved westward. Nonetheless, the easterly wind anomalies over the equatorial region continued intensifying and even extended further northeastward (Fig. 4d, e). In addition, the tropical anticyclonic branch sustains longer than two weeks and helps the equatorial easterly wind anomalies to be maintained.
These upper-tropospheric circulation anomalies changed the lower-level circulation. Figure 5 shows the lead–lag regression of 850-hPa wind and SLP anomalies onto the daily NPO index. Over the midlatitudes, it shows a barotropic vertical structure characterized by the cyclonic southern circulation anomalies in both the upper and low troposphere (Figs. 4a, 5a). On the −10 day, the 850-hPa westerly wind anomalies were observed only within the region over the extratropics (Fig. 5a). Over time, these westerly wind anomalies intensified over the central Pacific and extended equatorward (Fig. 5b). On 0 day, when the upper-level easterly wind anomalies became strong (Fig. 4c), promoting the westerly wind anomalies in the lower level intensified in the southern lobe of the NPO and extended to the equator. The strong upper-level circulation anomalies also induced easterly wind anomalies over the equatorial eastern Pacific (Fig. 5c). During the decaying period (+5 to +15 days), the southern SLP anomaly of the NPO weakened, but the equatorial westerly wind anomalies sustained until the +15 day over the central Pacific (160°E-120°W).
(a) Regressed 850-hPa wind (unit: m s−1) and SLP (unit: hPa) anomalies with 10-day leading the NPO index; (b) the same as (a) but for 5-day lead; (c) simultaneously regressed wind and SLP pattern; (d–f) regressed 850-hPa winds and SLP anomalies with 5- to 15-day lag, respectively. The area with black arrows shows the zonal winds above 90% confidence level based on Student’s t-test.
A natural question arises: why can equatorial wind persist after the NPO decays. To answer this, we further speculated the WAF at 300 hPa to provide the pathway of the NPO impact on the tropics. Figure 6 shows the WAF evolution calculated from the lead–lag regression of the SF anomalies. From −10 to −5 day, the wave energy only propagated northward (Fig. 6a, b). Accordingly, cyclonic and anticyclonic wind anomalies were intensified over the mid- and high-latitudes (Fig. 4a, b), as well as the lower-level wind anomalies in Fig. 5a, b. However, the equatorial wind anomalies were not yet significantly strong due to the lack of southward propagation of the WAF (Fig. 6a). On 0 day, the WAF shows both northward and southward propagation. That is, the southward WAF was established after the extratropical circulation was sufficiently developed and meridionally expanded. The southward WAF (Fig. 6c) could induce significant anticyclonic anomalies (Fig. 4c) in the upper troposphere over the tropics, leading to strong easterly wind anomalies over the equator. The tropical anticyclonic circulation developed with a delay compared with the extratropical circulation, eventually leading to the lower-level westerly anomalies over the tropical western Pacific (Fig. 5c).
a 300 hPa WAF (unit: m2 s−2) and SF (unit: 106 m2 s−1) anomalies with 10-day leading the NPO index; b the same as (a) but for −5-day lead; c simultaneous regressed stream function anomalies and calculated WAF; d–f 300 hPa WAF and SF anomalies from +5 to +15 day, respectively. The area with black arrows shows the WAF magnitudes larger than 0.1 m2 s−2.
After the peak phase of the NPO, the upper-level northward WAF largely weakened from +5 to +15 day. However, the WAF still shows strong southeastward propagation to the central-eastern Pacific (Fig. 6d, e). As a result, the upper-level anticyclonic circulation over the tropical region further intensified and exhibited northeast–southwest tilt, distinct from the developing stage of the NPO. On account of the continuous impact of the WAF (Fig. 6e, f), the 300 hPa easterly wind anomalies over the equatorial western Pacific sustained until the +15 day (Fig. 4e, f), and significant westerly anomalies occurred at the lower level (Fig. 5e, f).
The temporal evolution of the WAF can be seen more clearly in Fig. 7, which shows the cross-section of SF anomalies and the meridional WAF averaged over 150°E–120°W. The meridional WAF first showed a strong northward propagation 10 days earlier than the NPO peak. By contrast, the NPO-induced southward WAF propagation lags the northward energy propagation. It started to propagate southward and affected the tropics when approaching the peak NPO phase. Then, it reached the peak intensity around +5 days and sustained for about two weeks. This process should be crucial for inducing the upper- and lower-level wind anomalies over the equatorial regions. The persistence of the southward wave energy propagation in subseasonal scale resulted in the asymmetric evolution of wind anomalies that persisted after the peak NPO phase at both upper and lower levels (Figs. 4 and 5), which implied that the wind anomalies accumulated in subseasonal scales could also contribute to the seasonal mean circulation changes (Figs. 2 and 3). We found that the seasonal averaged upper-level easterly wind anomalies in Fig. 2 agreed with the accumulated impacts of the WAF on the subseasonal scale (Fig. 7).
Although the WAF analysis showed apparent southward energy propagation from the midlatitude to the tropics during the NPO events, we further unraveled contributing processes to the southward pathway by decomposing each term in the WAF equation. Focusing on the meridional component from Eq. (4) (see “Methods”), we separated the meridional terms into two: one related to the climatological zonal wind (Fy1) and the other carried by the climatological meridional wind (Fy2). These terms can be rewritten with the anomalous wind as follows:
The top panels of Fig. 8 show the meridional WAF at −5, 0, and +5 day, and the middle and bottom panels show its subcomponents related to Fy1 and Fy2, respectively. On −5 day, the total value of the meridional WAF mainly showed northward propagation (Fig. 8a) since the NPO was initialized over the middle and high latitudes. The southward component was feeble at this time, although it was weakly generated by Fy2, the term associated with mean meridional wind (Fig. 8c). On 0 day, it shows both strong northward and southward propagation, mostly due to Fy2 (Fig. 8f). Five days later, the contribution by Fy2 slightly attenuated (Fig. 8i), but the total southward energy propagation escalated over wider regions (Fig. 8g). Unlike the early period, this escalation was mainly contributed by Fy1, the term associated with mean zonal wind (Fig. 8h).
These temporal changes of the relative contributions by Fy1 and Fy2 can be better understood from the spatial structure of climatological winds shown in Fig. 9. Basically, the northward and southward transports of the WAF arose from the climatological meridional flow that comprised meridional energy flux. Over the Pacific region, the climatological meridional wind was southerly over the low latitudes, which yielded a favorable condition for transporting energy southward (notably, in Fy2, both eddy kinetic energy component \(u\prime ^2\) and anomalous meridional shear component \(\psi ^\prime \frac{{\partial u^\prime }}{{a\partial \phi }}\) are positive).
Contrariwise, energy propagation by Fy1 depends on the horizontal structure of the eddy. Since the background U is positive at the upper level, the energy propagation is determined by \(- u^\prime v^\prime\) and \(- \psi \prime \frac{{\partial v\prime }}{{\partial \phi }}\), which corresponds to the horizontal structure of the eddy. Under a westerly background flow condition (U > 0), the wave energy does not propagate southward when an eddy has an isotropic structure (i.e., \(u^\prime v^\prime \sim 0\) and \(\psi \prime \frac{{\partial v\prime }}{{\partial \phi }}\sim 0\)). However, when it is deformed to have a northeast–southwest tilt (i.e., \(u^\prime v^\prime > 0\) and \(\psi \prime \frac{{\partial v\prime }}{{\partial \phi }} > 0\)), its energy is headed southward—in Fig. 6, the horizontal shape of the cyclonic southern lobe of the NPO is in nearly isotropic structure on the −10 day, but gradually turns to have its eastern (western) edge shifted northward (southward). Strong shear in the southern flank of the North Pacific jet (Fig. 9a) can act to deform the southern lobe of the NPO and its subtropical branch to realize a northeast–southwest tilt. This horizontal deformation by the jet is pronounced after the peak NPO phase; thus, southward energy propagation by Fy1 becomes prominent for this period. Eventually, the enhanced southward energy flux intensifies the equatorial easterly winds in the upper troposphere, followed by westerly anomalies in the lower level.
To address the importance of meridional shear, we checked the Rossby wave ray paths35 forced by the southern lobe of the NPO as shown in Fig. 10. The Rossby wave energy is easily trapped in zonally symmetric flow based on previous studies36,37. However, when considering the meridional shear in real situation (Fig. 9a), we found that the Rossby wave energy can propagate to both northward and equatorward in wavenumber (WN) 1 (Fig. 10a). The WN1 energy can affect deep tropical region over the whole Pacific basin, which is delivered by both zonal jet and meridional winds (Fig. 9). However, the Rossby energy mainly shows southward propagation in WN3, and it displays a downstream effect over the eastern Pacific in WN5. So, the southward propagation of Rossby wave energy is reflected from WN1 and WN3, which is crucially contributed by the meridional shear of zonal wind and the strong basic state of southerly wind.
a The Rossby wave ray paths in WN1, b same as (a) but for WN3, and c same as (a) but for WN5. The mean state is derived from 300 hPa climatological winds in NDJFM from 1979 to 2020 as shown in Fig. 8. The forcing is over 180°–140°W, 20°–40°N, which basically represents the southern lobe of NPO-induced forcing.
To further verify the gradual changes in the tropics induced by the midlatitude NPO, a nonlinear stationary wave model experiment was performed. To confirm the influence of midlatitude forcing, two anomalous forcings with different signs were superimposed over the winter mean background flow at (35°N, 170°W) and (60°N, 170°W). These vorticity forcings with zonal 10° length and meridional 10° width were similar to typical NPO-induced vorticity anomalies, although their spatial structures were further simplified. From the stationary SF response given in Fig. 11, the NPO-like vorticity induced a significant positive SF anomaly over the tropical Pacific region by the southward energy propagation, which quite resembles those in Figs. 3 and 6. This reaffirmed that the NPO could directly modulate deep tropical circulations through energy propagation, even without the aid of boundary layer processes.
Discussion
Various observational and modeling results have shown a pronounced tendency of the NPO that proceeds ENSO events, which suggests that the extratropical internal atmospheric variability can affect tropical circulation. So far, the linkage between the NPO and ENSO was explained by the SFM that mediates the NPO impact on tropical circulations through the SST footprints12,17,38. In this study, we proposed a new mechanism to explain how the NPO-related extratropical circulation modulates the tropical Pacific circulation and equatorial air–sea interaction. Different from the SFM that manifests through the WES feedback in relaying the NPO impact, we found a direct modulation through the southward Rossby wave energy propagation. Daily evolutions of the NPO corroborated that the southward WAF could induce wind anomalies in the upper troposphere over the tropical Pacific, which lead to lower-level wind anomalies. We further delineated the conditions that facilitate the southward WAF, arising from the climatological southerly wind and zonal wind shear that deformed the NPO structure to have a northeast–southwest tilt. A simple wave model experiment consistently showed that the atmospheric wave propagation could convey the extratropical signal into the tropics without the aid of the WES feedback. However, our findings do not mean that only the NPO-induced WAF can induce ENSO. Although we highlighted the NPO-induced WAF impact on tropical circulation, many processes were presumed to cooperate to affect tropical variability. In addition to the SFM and WAF, previous literatures also documented the impacts of Arctic Oscillation39,40,41,42, Aleutian Low43,44 and tropical North Atlantic SST anomalies45,46,47 on following winter ENSO. Regarding the relative contributions of these processes, more studies are required.
As we have substantiated, the extratropical circulation can lead to equatorial Pacific wind anomalies in the upper troposphere through wave energy propagation. However, it may not be sufficient to draw a concrete conclusion on how the upper-level easterly anomalies induce the lower-level westerly anomalies, although we simply attributed it to a tropical baroclinic structure. The baroclinic vertical structure in the tropics is often formed by mid-tropospheric diabatic heating. The initial upper-level anticyclonic circulation directly induces upper-level easterly anomalies, and ensuing anomalous convection and lower-level westerly anomalies lead to the baroclinic structure. A previous study48 theoretically showed that easterly vertical shear can induce baroclinic structure response stronger in the lower troposphere than that in the upper troposphere through convection-low level convergence feedback. In addition, the upper-level easterly anomalies provide a background easterly vertical shear, which yields a favorable condition for an enhanced short-term atmospheric and convective activity48,49,50,51. For example, in the idealized AGCM experiment51, the equatorial high-frequency variabilities, such as the westerly wind burst, were enhanced when the easterly vertical shear was imposed on the background flow. It is obvious that stronger convective activity contributes to forming baroclinic structures in the equatorial region. In addition, general features of short-term convective and wind responses that are highly positive-skewed in the tropics underpin that strong convective activity itself can induce low-level westerlies. Nonetheless, a more detailed understanding of how the upper-level easterly anomalies led to the lower-level wind and further verification using numerical experiments are required.
Our conclusion on the role of the NPO-induced WAF is mostly based on the modulations in the equatorial wind variability during boreal winter, which is implicitly linked to ENSO development. However, we did not address in detail how the NPO-related process affects ENSO variability, given that several studies have already shown a close relationship between the NPO and ENSO in observations. It is not quite easy to quantify the influence of the NPO-induced WAF on the ENSO. The ENSO development is largely controlled by oceanic conditions over the tropical Pacific, such as recharge/discharge conditions52. In addition, the WAF is affected by the teleconnection induced by the equatorial diabatic heating associated with the ENSO. This complexity prevents quantifying the effect of the WAF process in the observational data. To complement this issue, the WAF impact on tropical variability needs to be further supported by modeling results. To this end, in Part II, we will show that there are diverse WAF magnitudes across the models of CMIP5/6 and that equatorward WAF by the NPO is crucial for tropical circulation anomalies during winter–spring, which is essential for triggering the ENSO events in the following winter.
Methods
Observational analysis and definitions
In this study, to explore the NPO variability on subseasonal to seasonal time scales, both daily and monthly climate variables were analyzed from 1979 to 2020, focusing on winter. Zonal and meridional winds, temperature, geopotential height, surface pressure, and SLP data were obtained from the National Centers for Environmental Prediction/National Centers for Atmospheric Research reanalysis I (NCEP/NCAR I) with a horizontal resolution of 2.5° latitude and 2.5° longitude53. The monthly Extended Reconstructed SST version 5 (ERSSTv5) data with a 2° × 2° horizontal resolution were downloaded from the National Oceanic and Atmospheric Administration54 (NOAA). The monthly and daily anomalies of atmospheric variables were calculated by removing the monthly or daily climatology for the past 42 years from the raw data.
We used the EOF analysis to obtain an intrinsic NPO spatial pattern based on the NDJFM averaged SLP anomalies over 20°N–70°N; 110°E–120°W11. Figure 1a shows the second EOF mode that was considered as the NPO pattern. For convenience, when the pattern has negative SLP anomalies to the south and positive to the north, it is defined as the positive NPO phase. Previous studies have suggested that the ENSO can influence the NPO55,56,57,58. To minimize the possible simultaneous ENSO impact on NPO, we linearly removed the ENSO signal59,60, which is represented by the Niño3.4 index, from both NPO and circulation fields, before conducting further analyses. To examine the NPO connection to tropics on the seasonal mean time scale, we selected 10 positive NPO years (1981, 1984, 1986, 1995, 1996, 1997, 2011, 2014, 2015, and 2017) and 10 negative NPO years (1985, 1987, 1988, 1990, 1998, 1999, 2000, 2001, 2012, and 2016) based on a threshold of 0.7 standard deviation of the principal component timeseries of the second EOF. Moreover, we also tested to remove the simultaneous La Niña cases from the 10 positive NPO years and El Niño events from the negative NPO years. The results are similar.
A statistical significance of lead–lag regression and correlation coefficients between the daily NPO index and daily anomalous atmospheric circulation is estimated based on the Student’s t-test with an effective number of degrees of freedom. In this study, the effective number of degrees of freedom is calculated using the approximation following the previous studies:61,62,63
where N is the sample size of the NPO index, and rx(j) and ry(j) are the autocorrelations of the NPO and circulation fields at time lag j, respectively.
Based on the daily regressed SF and winter climatological winds, we could trace horizontal wave energy propagation associated with the NPO by adopting the WAF64, which can capture a snapshot of the wave propagation both in zonal and meridional directions. Though the WAF analysis can include non-negligible errors when QG approximation is not valid, this limitation is inferred not to be crucial for our case dealing with the NPO, a basin-scale quasi-stationary phenomenon. Given that the formulation approximates beta-plane, it offers advantages in our study for analyzing extratropical-tropical linkage. The WAF in spherical coordinates can be written as follows:
where U = (U, V) are, respectively, the climatological zonal and meridional winds;\(\psi \prime\) is the monthly or daily SF anomaly associated with the NPO; a,ϕ, and λ are the Earth’s radius, latitude, and longitude, respectively; p is the air pressure at 1000 hPa. Instead of using a quasigeostrophic approximation to derive the SF based on geopotential height, we derive the SF anomaly based on the zonal and meridional winds by solving the Poisson equation from\(u\prime = \frac{1}{a}\frac{{\partial \psi \prime }}{{\partial \phi }}\) and \(v^\prime = - \frac{1}{{a\cos \phi }}\frac{{\partial \psi \prime }}{{\partial \lambda }}\). However, we checked if the spatial pattern of the SF anomalies is similar to the geopotential height anomalies at 300 hPa. The WAF equation delineates that the wave energy propagation is determined by the climatological wind, wind anomalies, and their zonal and meridional gradients. In this study, we quantify how each component modulates the NPO energy propagation toward the tropical Pacific.
The Rossby wave ray35, which represents the Rossby wave energy propagation, is occupied in this study to reveal the Rossby wave energy propagation and cross-validate the WAF impact. Different from previous equations that assume the Rossby wave propagation in a zonally symmetric flow36, the derived equations allow the Rossby wave to propagate in a horizontally nonuniform flow.
Model experiments
A nonlinear stationary wave model65,66 was used to validate our findings. In the model, the climatological means (NDJFM-average) of surface pressure, three-dimensional temperature, as well as the zonal and meridional winds were used as background conditions, wherein the NPO-like vorticity anomalies are embedded as a forcing. First, we interpolated data from the Cartesian coordinate to \(\sigma\)-coordinate. Then, the prognostic equations were analyzed for the vorticity perturbation, and the anomalous geopotential height and vertical velocity were calculated from the hydrostatic balance and mass continuity equation. The basic equations are as follows:
where ζ, D, T, lnPs, ϕ, and \(\dot \sigma\) represent the vorticity, divergence, temperature, surface pressure, geopotential height, and sigma coordinate vertical velocity, respectively; V represents the zonal and meridional wind vector; the tiles represent the vertical average; ε is the Rayleigh friction and Newtonian cooling coefficients; ν is the biharmonic diffusion coefficient. All variables in the above equations can be categorized into the basic-state variables and deviations from the basic state, and we checked the anomalous SF in the model. A detailed description of this model can be found in a previous study65.
Statistical significance
In this study, we adopted the two-tailed Student’s t-test with a significance level of 0.1 in all analyses. The degree of freedom of the Student’s t-test in Figs. 2 and 3 is 18 based on the monthly data. For the daily datasets, the degree of freedom of the Student’s t-test used for regression analysis is adjusted based on Eq. (1) introduced in “Methods”.
Data availability
The monthly and daily NCEP/NCAR reanalysis data can be downloaded from https://psl.noaa.gov/data/gridded/data.ncep.reanalysis.html. The ERSSTv5 dataset is retrieved from NOAA https://psl.noaa.gov/data/gridded/data.noaa.ersst.v5.html. The Rossby wave ray paths and stationary wave model data can be downloaded from figshare (https://doi.org/10.6084/m9.figshare.21802923.v1).
Code availability
The source codes for the analysis of this study can be requested from the first and corresponding authors.
References
Di Lorenzo, E. et al. North Pacific Gyre Oscillation links ocean climate and ecosystem change. Geophys. Res. Lett. 35, L08607 (2008).
Hurrell, J. W. Decadal trends in the North Atlantic Oscillation: regional temperatures and precipitation. Science 269, 676–679 (1995).
Hurrell, J. W., Kushnir, Y., Ottersen, G. & Visbeck, M. Geophysical Monograph Series (eds Hurrell, J. W., Kushnir, Y., Ottersen, G. & Visbeck, M.) Vol. 134, 1–35 (American Geophysical Union, 2003).
Wang, L., Chen, W. & Huang, R. Changes in the variability of North Pacific Oscillation around 1975/1976 and its relationship with East Asian winter climate. J. Geophys. Res. 112, D11110 (2007).
Yu, J.-Y. & Kim, S. T. Relationships between extratropical sea level pressure variations and the Central Pacific and Eastern Pacific types of ENSO. J. Clim. 24, 708–720 (2011).
Tseng, Y., Ding, R., Zhao, S., Kuo, Y. & Liang, Y. Could the North Pacific oscillation Be modified by the initiation of the East Asian winter monsoon? J. Clim. 33, 2389–2406 (2020).
Walker, M. & Bliss, E. World weather V. Meml. R. Meterol. Soc. 4, 53–84 (1932).
Rogers, J. C. The North Pacific oscillation. J. Climatol. 1, 39–57 (1981).
Pak, G., Park, Y.-H., Vivier, F., Kwon, Y.-O. & Chang, K.-I. Regime-dependent nonstationary relationship between the East Asian winter monsoon and North Pacific oscillation. J. Clim. 27, 8185–8204 (2014).
Yeh, S.-W., Yi, D.-W., Sung, M.-K. & Kim, Y. H. An eastward shift of the North Pacific oscillation after the mid-1990s and its relationship with ENSO. Geophys. Res. Lett. 45, 6654–6660 (2018).
Sung, M.-K. et al. Tropical influence on the North Pacific Oscillation drives winter extremes in North America. Nat. Clim. Change 9, 413–418 (2019).
Alexander, M. A., Vimont, D. J., Chang, P. & Scott, J. D. The impact of extratropical atmospheric variability on ENSO: testing the seasonal footprinting mechanism using coupled model experiments. J. Clim. 23, 2885–2901 (2010).
Park, J.-Y., Yeh, S.-W., Kug, J.-S. & Yoon, J. Favorable connections between seasonal footprinting mechanism and El Niño. Clim. Dyn. 40, 1169–1181 (2013).
Chen, S. & Yu, B. Projection of winter NPO-following winter ENSO connection in a warming climate: uncertainty due to internal climate variability. Clim. Change 162, 723–740 (2020).
Vimont, D. J., Battisti, D. S. & Hirst, A. C. Footprinting: a seasonal connection between the tropics and mid-latitudes. Geophys. Res. Lett. 28, 3923–3926 (2001).
Vimont, D. J., Wallace, J. M. & Battisti, D. S. The seasonal footprinting mechanism in the Pacific: implications for ENSO. J. Clim. 16, 2653–2667 (2003).
Vimont, D. J., Battisti, D. S. & Hirst, A. C. The seasonal footprinting mechanism in the CSIRO general circulation models. J. Clim. 16, 2653–2667 (2003).
Chiang, J. C. H. & Vimont, D. J. Analogous Pacific and Atlantic meridional modes of tropical atmosphere–ocean variability. J. Clim. 17, 4143–4158 (2004).
Chang, P. et al. Pacific meridional mode and El Niño-Southern Oscillation: Pacific meridional mode and ENSO. Geophys. Res. Lett. 34, L16608 (2007).
Amaya, D. J. The Pacific meridional mode and ENSO: a review. Curr. Clim. Change Rep. 5, 296–307 (2019).
Anderson, B. T. On the joint role of subtropical atmospheric variability and equatorial subsurface heat content anomalies in initiating the onset of ENSO events. J. Clim. 20, 1593–1599 (2007).
Anderson, B. T., Perez, R. C. & Karspeck, A. Triggering of El Niño onset through trade wind-induced charging of the equatorial Pacific: trade wind Charging of the EQ. Pacific. Geophys. Res. Lett. 40, 1212–1216 (2013).
Zhao, J., Kug, J., Park, J. & An, S. Diversity of North Pacific meridional mode and its distinct impacts on El Niño‐Southern oscillation. Geophys. Res. Lett. 47, e2020GL088993 (2020).
Wang, S.-Y., L’Heureux, M. & Chia, H.-H. ENSO prediction one year in advance using western North Pacific sea surface temperatures: predicting ENSO by NW Pacific SST. Geophys. Res. Lett. 39, n/a–n/a (2012).
Schulte, J. A. & Lee, S. Strengthening North Pacific influences on United States temperature variability. Sci. Rep. 7, 124 (2017).
Ding, Q. et al. Tropical forcing of the recent rapid Arctic warming in northeastern Canada and Greenland. Nature 509, 209–212 (2014).
Chen, S. & Song, L. Impact of the winter North Pacific oscillation on the surface air temperature over Eurasia and North America: sensitivity to the index definition. Adv. Atmos. Sci. 35, 702–712 (2018).
Linkin, M. E. & Nigam, S. The North Pacific oscillation–West Pacific teleconnection pattern: mature-phase structure and winter impacts. J. Clim. 21, 1979–1997 (2008).
Sung, M.-K., Kim, B.-M., Baek, E.-H., Lim, Y.-K. & Kim, S.-J. Arctic-North pacific coupled impacts on the late autumn cold in North America. Environ. Res. Lett. 11, 084016 (2016).
Harrison, D. & Vecchi, G. A. Westerly wind events in the tropical Pacific, 1986–95. J. Clim. 10, 3131–3156 (1997).
Lian, T., Chen, D., Tang, Y. & Wu, Q. Effects of westerly wind bursts on El Niño: a new perspective: effects of westerly wind bursts on ENSO. Geophys. Res. Lett. 41, 3522–3527 (2014).
Hu, S., Fedorov, A. V., Lengaigne, M. & Guilyardi, E. The impact of westerly wind bursts on the diversity and predictability of El Niño events: an ocean energetics perspective: Hu et al.: WWB and ENSO diversity: energetics view. Geophys. Res. Lett. 41, 4654–4663 (2014).
Kug, J.-S. Preconditions for El Niño and La Niña onsets and their relation to the Indian Ocean. Geophys. Res. Lett. 32, L05706 (2005).
Kug, J.-S., Sooraj, K.-P., Li, T. & Jin, F.-F. Precursors of the El Niño/La Niña onset and their interrelationship. J. Geophys. Res. 115, D05106 (2010).
Li, Y., Li, J., Jin, F. F. & Zhao, S. Interhemispheric propagation of stationary Rossby waves in a horizontally nonuniform background flow. J. Atmos. Sci. 72, 3233–3256 (2015).
Hoskins, B. J. & Karoly, D. J. The steady linear response of a spherical atmosphere to thermal and orographic forcing. J. Atmos. Sci. 38, 1179–1196 (1981).
Rossby, C.-G. On the propagation of frequencies and energy in certain types of oceanic and atmospheric waves. J. Meteorol. 2, 187–204 (1945).
Park, J.-H. et al. Role of the climatological intertropical convergence zone in the seasonal footprinting mechanism of the El Niño-Southern Oscillation. J. Clim. 34, 5243–5256 (2021).
Chen, S., Chen, W., Yu, B. & Graf, H.-F. Modulation of the seasonal footprinting mechanism by the boreal spring Arctic Oscillation: Modulation of the SFM by AO. Geophys. Res. Lett. 40, 6384–6389 (2013).
Chen, S., Chen, W. & Yu, B. Modulation of the relationship between spring AO and the subsequent winter ENSO by the preceding November AO. Sci. Rep. 8, 6943 (2018).
Chen, S., Yu, B. & Chen, W. An analysis on the physical process of the influence of AO on ENSO. Clim. Dyn. 42, 973–989 (2014).
Chen, S., Song, L. & Chen, W. Interdecadal modulation of AMO on the winter North Pacific oscillation-following winter ENSO relationship. Adv. Atmos. Sci. 36, 1393–1403 (2019).
Chen, S., Chen, W., Wu, R., Yu, B. & Graf, H.-F. Potential impact of preceding Aleutian low variation on El Niño–Southern oscillation during the following winter. J. Clim. 33, 3061–3077 (2020).
Park, J.-H. et al. Role of climatological North Pacific high in the North tropical Atlantic-ENSO connection. J. Clim. 35, 3215–3226 (2022).
Ham, Y.-G., Kug, J.-S., Park, J.-Y. & Jin, F.-F. Sea surface temperature in the North tropical Atlantic as a trigger for El Niño/Southern Oscillation events. Nat. Geosci. 6, 112–116 (2013).
Ham, Y.-G., Kug, J.-S. & Park, J.-Y. Two distinct roles of Atlantic SSTs in ENSO variability: North tropical Atlantic SST and Atlantic Niño: role of Atlantic SSTS on ENSO. Geophys. Res. Lett. 40, 4012–4017 (2013).
Ham, Y.-G. & Kug, J.-S. Role of North tropical Atlantic SST on the ENSO simulated using CMIP3 and CMIP5 models. Clim. Dyn. 45, 3103–3117 (2015).
Wang, B. & Xie, X. Low-frequency equatorial waves in vertically sheared zonal flow. Part I: Stable waves. J. Atmos. Sci. 53, 449–467 (1996).
Wang, B. & Xie, X. Low-frequency equatorial waves in vertically sheared zonal flow. Part II: Unstable waves. J. Atmos. Sci. 53, 3589–3605 (1996).
Li, T. Origin of the summertime synoptic-scale wave train in the Western North Pacific. J. Atmos. Sci. 63, 1093–1102 (2006).
Sooraj, K. P. et al. Effects of the low-frequency zonal wind variation on the high frequency atmospheric variability over the tropics. Clim. Dyn. 33, 495–507 (2009).
Jin, F.-F. An equatorial ocean recharge paradigm for ENSO. Part I: conceptual model. J. Atmos. Sci. 54, 811–829 (1997).
Kalnay, E. et al. The NCEP/NCAR 40-year reanalysis project. Bull. Am. Meteorol. Soc. 77, 437–471 (1996).
Huang, B. et al. Extended reconstructed sea surface temperature, Version 5 (ERSSTv5): upgrades, validations, and intercomparisons. J. Clim. 30, 8179–8205 (2017).
Di Lorenzo, E. et al. Central Pacific El Niño and decadal climate change in the North Pacific Ocean. Nat. Geosci. 3, 762–765 (2010).
Furtado, J. C., Di Lorenzo, E., Anderson, B. T. & Schneider, N. Linkages between the North Pacific Oscillation and central tropical Pacific SSTs at low frequencies. Clim. Dyn. 39, 2833–2846 (2012).
Zhang, Y. et al. Atmospheric forcing of the Pacific meridional mode: tropical Pacific‐driven versus internal variability. Geophys. Res. Lett. 49, e2022GL098148 (2022).
Stuecker, M. F. Revisiting the Pacific meridional mode. Sci. Rep. 8, 3216 (2018).
Ashok, K., Guan, Z. & Yamagata, T. A Look at the Relationship between the ENSO and the Indian Ocean Dipole. J. Meteorol. Soc. Jpn. 81, 41–56 (2003).
Zhao, J., Zhan, R., Wang, Y. & Tao, L. Intensified interannual relationship between tropical cyclone genesis frequency over the Northwest Pacific and the SST gradient between the Southwest Pacific and the Western Pacific warm pool since the mid-1970s. J. Clim. 29, 3811–3830 (2016).
Pyper, B. J. & Peterman, R. M. Comparison of methods to account for autocorrelation in correlation analyses of fish data. Can. J. Fish. Aquat. Sci. 55, 2127–2140 (1998).
Li, J., Sun, C. & Jin, F. NAO implicated as a predictor of Northern Hemisphere mean temperature multidecadal variability. Geophys. Res. Lett. 40, 5497–5502 (2013).
Sun, C., Li, J. & Jin, F.-F. A delayed oscillator model for the quasi-periodic multidecadal variability of the NAO. Clim. Dyn. 45, 2083–2099 (2015).
Takaya, K. & Nakaruma, H. A formulation of a phase-independent wave-activity flux of stationary and migratory quasi-geostrophic eddies on a zonally varying basic flow. J. Atmos. Sci. 58, 608–627 (2001).
Ting, M. & Yu, L. Steady response to tropical heating in wavy linear and nonliear baroclinic models. J. Atmos. Sci. 55, 3565–3582 (1998).
Lim, Y.-K. The East Atlantic/West Russia (EA/WR) teleconnection in the North Atlantic: climate impact and relation to Rossby wave propagation. Clim. Dyn. 44, 3211–3222 (2015).
Acknowledgements
We thank Prof. Jianping Li and Dr. Sen Zhao for providing us the Rossby wave ray code. This research was supported by a National Research Foundation of Korea (NRF) grant funded by the Korean government (NRF-2022R1A3B1077622, NRF-2018R1A5A1024958). MK Sung was supported by NRF- 2021R1A2C1003934. Authors JJ Luo and JW Zhao were supported by National Natural Science Foundation of China (Grant No. 42105022, 42088101, and 42030605).
Author information
Authors and Affiliations
Contributions
J.Z. compiled the data, conducted analyses, prepared the figures, and wrote the manuscript. M.-K.S. designed the research and wrote the manuscript. All authors discussed the study results and reviewed the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Zhao, J., Sung, MK., Park, JH. et al. Part I observational study on a new mechanism for North Pacific Oscillation influencing the tropics. npj Clim Atmos Sci 6, 15 (2023). https://doi.org/10.1038/s41612-023-00336-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41612-023-00336-z
This article is cited by
-
Strengthened impact of boreal winter North Pacific Oscillation on ENSO development in warming climate
npj Climate and Atmospheric Science (2024)
-
Improved simulation of the influence of the North Pacific Oscillation on El Niño-Southern Oscillation in CMIP6 than in CMIP5 models
Climate Dynamics (2024)