Abstract
The wintertime extratropical general circulation may be viewed as being primarily governed by interactions between Rossby waves and the background flow. These Rossby waves propagate vertically and meridionally away from their sources and amplify within the core of the tropopause-level jet, which acts as a waveguide. The strength of this waveguide is in part controlled by tropopause sharpness, which itself is a function of the strength of tropopause inversion layer (TIL), a layer of enhanced static stability just above the tropopause. Here, we report a strong relation between interannual-to-multidecadal variations in the strength of the mid-latitude TIL and features of the general circulation (e.g., jet latitude, strength of the Hadley cell) in a reanalysis and climate models. Similar relationships hold for the variability across climate models. Experiments with a mechanistic model show that a sharper tropopause promotes an intensified general circulation and an equatorward shifted jet.
Similar content being viewed by others
Introduction
The general circulation of the atmosphere is primarily composed of planetary-scale features such as the overturning meridional circulations in the tropics and extratropics (the so-called Hadley and Ferrel cells) and meandering jet streams that at places curl up into eddies (mid-latitude highs and lows). These features are not just interesting for an overall depiction of the atmospheric circulation but in recent years have also received increased attention due to their varied responses to climate change. For example, climate model projections show a robust poleward shift of the mid-latitude jets1,2, as well as a widening (and weakening) of the Hadley cells3,4. Moreover, models with a more equatorward jet in their control (preindustrial/historical) climate may produce a stronger poleward jet shift5. This is interesting as most models appear to exhibit an equatorward jet bias and raises the question which processes are important in regulating the average jet position6. While climate model biases may stem from a multitude of processes, primarily those that are due to numerical diffusion or parametrizations7,8,9, some may be due to misrepresentations of salient features of atmospheric structure. One such feature is the tropopause. Its sharpness10, among other things, affects the strength of the tropopause-level waveguide (for, e.g., Rossby waves) and thereby the dynamics of the mid-latitude jet stream.
Interactions between Rossby waves and the background mean flow, such as near the tropopause-level jet stream, are a crucial driver of the wintertime extratropical general circulation and its variability on a range of time scales11,12. These Rossby waves originate, for example, from flow over large-scale topography13,14 and due to baroclinic instability of the eastward mean flow embedded within an equatorward temperature gradient15,16 (grey dashed lines in Fig. 1). As these Rossby waves propagate upward and meridionally (grey arrows in Fig. 1) away from their source region (red shading in Fig. 1), they flux westward momentum out of it, thereby leaving an eastward surface wind behind—the eddy-driven surface westerlies in mid-latitudes11,12 (black contours in Fig. 1). Likewise, these waves flux westward momentum into their sink/dissipation region (blue shading in Fig. 1) where they exert a westward forcing onto the mean flow. Wave dissipation is enhanced along the tropopause-level jet (peak black contour in Fig. 1), which acts as a waveguide due to its accompanying strong potential vorticity (PV) gradients, resulting in amplification and eventually wave breaking and dissipation17,18. The PV gradient, in turn, is governed by meridional and vertical structures of the wind and temperature fields. The strong PV gradient and tropopause-level waveguide (black dashed line in Fig. 1) are in part associated with the tropopause inversion layer (TIL; grey shading in Fig. 1), a layer of enhanced static stability just above the tropopause that produces enhanced tropopause sharpness10,19.
Figure shows a meridional cross-section of climatological winter mean zonal mean zonal wind (black solid and dashed contours; based on reanalysis data) with maximum wind corresponding to subtropical jet and black star denoting the location of maximum wind at 850 hPa (location of eddy-driven jet); climatological winter mean tropopause height (thick black dashed line; based on reanalysis data) where tropopause waveguide is located; typical wave source at the surface (red shading) and typical wave sink in the upper-troposphere (blue shading) with corresponding wave propagation (grey arrows); the location of the tropopause inversion later (TIL; grey shading); and typical potential temperature profile (Θ; grey dashed lines). For details about the schematic see text.
To see the connection between the TIL and PV gradient consider the definition of PV (P) in isentropic coordinates20 (see also Methods): P = ζ/σ, where ζ = ξ + f is the vertical component of absolute vorticity composed of relative vorticity ξ and planetary vorticity f (equal to the Coriolis parameter), and \(\sigma =-{(g{\partial }_{{{{\rm{p}}}}}\theta )}^{-1}\) (with θ potential temperature, g gravitational acceleration, p pressure) is the so-called thickness (or isentropic density). The meridional PV gradient is then proportional to the meridional vorticity gradient and inversely proportional to thickness gradient. Since thickness is inversely proportional to static stability (∂pθ) it follows that the meridional PV gradient is proportional to that of static stability. In other words, the enhanced static stability associated with the TIL is expected to be associated with an enhanced PV gradient near the tropopause, hence a sharper tropopause.
The TIL has been documented extensively from observations, reanalyses, and models10,21,22,23. Its underlying potential mechanisms have been illuminated, although their relative roles still remain elusive24,25,26,27,28. In weather and climate models, the tropopause sharpness may also depend on model biases: for example, the moist bias in the lowermost stratosphere due to excessive dispersion produces excessive tropopause-level radiative cooling and thereby a sharper tropopause29. This may then lead to biases in the general circulation, along the lines of results presented below.
Potential impacts of the enhanced tropopause sharpness due to the TIL include modifications of vertical wave propagation across the tropopause (gravity and Rossby waves) and troposphere-stratosphere exchange30,31,32. However, its potential impact on the general circulation as a whole has not been studied in detail. This may be in part because previous studies have considered other (tropopause-related) competing impacts on general circulation, such as the tropopause height, cooling in the lower stratosphere, and static stability in mid-to-high latitudes1. However, only a few studies7,33 have considered the impacts of the tropopause sharpness.
What mechanistic relationships may exist between the TIL and aspects of the general circulation? First, a strong TIL could be associated with a strong vertically confined cold anomaly at the mid-to-high latitude tropopause10,28,29. This corresponds to enhanced negative meridional temperature gradients near the equatorward edge of this TIL region due to the downward sloping tropopause with increasing latitude (black dashed line in Fig. 1). By thermal wind balance, this temperature anomaly structure is associated with positive vertical zonal wind shear, thus stronger zonal wind near the tropopause. Moreover, it corresponds to enhanced upper level baroclinicity and higher available potential energy; hence, the TIL signature may cause intensified baroclinic eddy life cycles.
Second, the TIL is associated with an enhanced tropopause-level PV gradient (as mentioned above), hence a stronger waveguide. The associated enhanced channelling of Rossby waves near the mid-latitude tropopause may lead to less meridional wave dispersion (leakage), stronger (“well-guided”) vertical wave propagation into the winter stratosphere, and stronger wave dissipation in mid-latitudes8,18,34. These processes may further feed back onto the zonal wind and thereby affect the general circulation35. Notably, they may cause jet shifts, which require eddy feedbacks and cannot be explained in terms of the direct response to forcings.
Since the TIL (tropopause sharpness) may impact several aspects of the general circulation, including jet position and strength, it may be important for inter-model variability, as well as for climate variations in general. Here, we explore the impact of the TIL on the general circulation in the state-of-the-art atmospheric reanalysis (ERA5)36,37, Coupled Model Intercomparison Project Phase 6 (CMIP6) climate models38, and in a mechanistic general circulation model39,40 (see also Methods).
Results
Interannual variability
To start exploring the relationship between tropopause sharpness (i.e., TIL strength) and the zonal mean circulation, we first analyze their interannual variations in the northern hemisphere (NH) winter in both a reanalysis (ERA5) and in CMIP6 climate models (Methods). Note that TIL strength—a measure of vertical temperature structure—is expected to be a function of vertical resolution and even ERA5’s resolution of ~200 m near the mid-latitude tropopause may not suffice to fully resolve the TIL structure. Furthermore, reanalyses may underestimate the TIL strength due to data assimilation22. However, our focus here is not so much on the absolute strength of the TIL, but rather on climate variations in TIL strength. We found the latter to be robust across different methodological choices.
First, we define a measure of TIL strength in terms of the maximum static stability parameter (\({N}_{\max }^{2}\)) just above the tropopause (Methods). Since we are interested primarily in the TIL strength of the atmospheric background (basic) state we obtain \({N}_{\max }^{2}\) from spatially resolved monthly mean temperature data. A TIL index is then constructed by averaging zonally, seasonally (winter: January-February-March, JFM), as well as over a specified latitudinal band (we use 40–60∘N). We tested alternative TIL-index calculations based on 6-hourly gridded temperature data, 6-hourly zonal mean temperature data or monthly mean zonal mean temperature data. The first index results in a stronger diagnosed TIL strength (i.e., less smoothing of the sharp tropopause structures before diagnosing \({N}_{\max }^{2}\)) compared to the latter two indices. However, these alternative TIL indices are highly correlated (≥0.85) with the TIL index based on spatially resolved monthly means. The latter index is used here because it represents a more appropriate measure of the TIL of the background state of the atmosphere and is less affected by reversible eddy variations. That is, we intend to measure the TIL of the average state rather than the average state of the TIL.
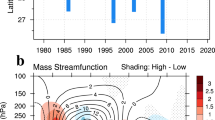
Figure 2a shows the long-term evolution of the NH winter TIL index relative to its climatological value. The climatological TIL strength (Fig. 2b, Supplementary Fig. 2) largely ranges from 5 × 10−4 s−2 to 5.55 × 10−4 s−2 with the multi-model mean of the CMIP6 models at ~5.3 × 10−4 s−2, which is slightly higher than the ERA5 value (~5 × 10−4 s−2). Interannual variability (Fig. 2a) of similar magnitude is seen in both ERA5 (black line) and the models (blue thin lines in Fig. 2a). A multidecadal trend toward weaker TIL strength is found starting in the late 1970’s in both ERA5 (−1.45 × 10−7 s−2 year−1) and the multi-model mean (−1.55 × 10−7 s−2 year−1). Note that both trends are significant at 97% level based on one-tailed t test. This multidecadal trend could be a part of “natural” climate variability (e.g., related to the Atlantic Multidecadal Variability41), and/or it could be a part of a climate change signal1. Determining the exact origin of this multidecadal trend is left for future work. Overall, these time series suggest that these interannual-to-multidecadal variations in TIL strength are a robust feature of the Earth’s atmosphere.
Figure shows JFM-mean squared buoyancy frequency (\({N}_{\max }^{2}\)) in s−2 averaged zonally and meridionally between 40 and 60∘N: (a) timeseries relative to climatology over the period 1951-2014, and (b) range of climatological values. Thick black line (black circle) represents ERA5 data, thick blue line represents CMIP6 multi-model-mean data, and thin light-blue lines (light-blue box-plot) represent individual CMIP6 models. Box plot is constructed the following way: light blue box represent the 25th (Q1) to 75th (Q3) percentile range, light blue whiskers represent the values that are between Q3 + 1.5IQR and Q1 − 1.5IQR (with IQR = Q3 − Q1), light blue circles represent the outliers (values outside the whiskers range), and dark blue line represents the mean (not median) value for consistency with panel (a).
How do these TIL variations co-vary with the general circulation? Figure 3 shows that the NH winter TIL index is strongly correlated with the zonal-mean zonal wind on interannual time scales (see shading). A stronger TIL is associated with a more equatorward eddy-driven jet (EDJ) and a strengthened subtropical jet (STJ). This zonal wind signature resembles that of the Arctic Oscillation (AO; NH annular mode) in its negative phase. Indeed, the correlation between the TIL index and the AO index (Methods) is −0.58 (ERA5) and similar correlations ranging between −0.3 and −0.75 are found for the majority of climate models (Supplementary Fig. 1). Note that there is also an indication that models with stronger TIL show stronger AO-TIL correlation (Supplementary Fig. 1). Consistent with the zonal wind correlation pattern, the Hadley cell exhibits strengthening and equatorward contraction with a stronger TIL index (not shown).
Figure shows a JFM-mean correlation (in shading) of zonal mean zonal wind (u) with squared buoyancy frequency anomaly (\({N}_{\max }^{2}\), from Fig. 2a) for the period 1951-2020 in ERA5. Black contours (contour interval is 10 m s−1, i.e., ... −10, 0, 10, ...) show climatological zonal mean zonal wind over the same period. Stippling denotes statistically significant values that pass 95% threshold (based on a two-sided t-test). Note that corresponding regression coefficients are provided in Supplementary Fig. 5.
The relationship between the TIL strength and the AO (zonal wind variability) is consistent with the hypothesis that the eddy-feedbacks associated with the TIL changes (mentioned in the Introduction) are related to changes in the jet streams (modified strength of the STJ, meridional shift of the EDJ), although the direction of causality remains unclear based on interannual variability alone.
Inter-model variability
Given the strong relationship between the TIL index and the AO on interannual timescales, we now test if differences in zonal mean zonal wind across models are related to their TIL strength. To do this, we compute NH winter climatological (1870-2014) zonal mean zonal wind in every model (see Supplementary Table 1 for the list of the models) as well as their climatological TIL strength (\({N}_{\max }^{2}\); see Fig. 2b for the variability across models; they are listed also in Supplementary Fig. 2). We then compute correlations between the zonal wind and TIL strength across different models to identify potential links between TIL strength and the general circulation across different mean climate states (as represented by inter-model variability; see also Methods). Note that results remain qualitatively similar if composites are computed instead (not shown).
Consistent with the interannual variability discussed above, Fig. 4 shows an equatorward shift of the EDJ and strengthening of the STJ with a stronger TIL. This suggests that models with a more equatorward EDJ (and similarly stronger STJ) have a sharper tropopause. This is interesting because models in general have an equatorward EDJ bias2, which suggests that a sharper (i.e., potentially more realistic) tropopause may worsen this bias or alternatively a more poleward jet may worsen the TIL bias. However, we note that the TIL strength is expected to be a strong function of model resolution (see also Methods) and this would have to be taken into account to assess a potential TIL-jet bias link in more detail. Here we simply leverage the range of control climates provided by the different models to assess pointers to mechanistic TIL-jet coupling, regardless of model biases.
Figure shows a correlation (in shading) of 1850–2014 climatological JFM-mean zonal mean zonal wind (u) with squared buoyancy frequency anomaly (\({N}_{\max }^{2}\), from Fig. 2) across different CMIP6 models. Black contours (contour interval is 10 m s−1, i.e., ... −10, 0, 10, ...) show multi-model-mean climatological JFM-mean zonal mean zonal wind over the same period. Stippling is the same as in Fig. 3. Note that the two models (MIROC6, IITM-ESM) with extremely strong tropopause sharpness were excluded (see outliers in Fig. 2b, and Supplementary Fig. 2) to avoid over-estimations. Note also that corresponding regression coefficients are provided in Supplementary Fig. 6.
Interestingly, if one considers trends in the TIL strength and in the EDJ between 1980 and 2014 a similar picture emerges: models with a stronger weakening of the TIL in this period tend to exhibit more of a poleward shift in the EDJ (Supplementary Fig. 3). A poleward shift of the EDJ has been observed in analyses of the recent-past changes42 and is also expected for the EDJ response to climate change1,2. This suggests that the climate change response may also involve coupling between the jet and the TIL.
While Figs. 3, 4 demonstrate strong relations between interannual variations in TIL strength and aspects of the zonal mean circulation as well as a relationship between the TIL strength and the inter-model variability in zonal mean general circulation, the direction of causality remains unclear. It is conceivable that internal atmospheric variability from year to year and inter-model variability in zonal mean general circulation simply manifest themselves in consistent variations between the zonal circulation and meridional temperature structure. For example, shifts in the STJ and tropopause break are expected to be coupled via thermal wind balance43, which may involve projections onto the TIL. However, such shifts may simply be associated with latitudinal displacements of the TIL structure without variations in TIL strength. Indeed, we find that latitudinal displacements of the subtropical tropopause break are hardly coupled to the TIL strength (not shown). Furthermore, thermal wind balance merely relates horizontal temperature gradients to vertical wind shear, which may or may not involve modifications to the vertical temperature structure (hence, TIL strength).
To test for a potential causal connection between TIL strength and aspects of the general circulation, specifically designed mechanistic model experiments are needed. This is what we turn to next.
Mechanistic general circulation model experiments
To assess the impact of TIL strength on the general circulation, we use an idealized dry dynamical core model in two configurations (see Methods): (i) a conventional reference run including two idealised mountains39,40 (denoted HS) with a “weak” TIL; and (ii) a TIL run (denoted HSTIL) with an imposed stronger TIL via cooling at the tropopause (grey dashed contours in Fig. 5b; see Methods below and Supplementary Methods). The region (and difference in strength) of the TIL (using zonal mean static stability N2, see Methods) is shown with grey solid contours in Fig. 5a. Because of the enforced difference in tropopause sharpness via TIL strength between the two model runs we are able to analyze causal linkages between tropopause sharpness and the atmospheric general circulation. The HSTIL run is designed to have a somewhat stronger TIL than the strongest model’s TIL (Fig. 2b;26) to account for underestimated TIL strength in models and reanalyses.
Figure shows meridional cross-sections of (a) meridional gradient in PV and (b) zonal mean zonal wind. Black contours (solid for positive values, dashed for negative values) represent their climatologies in the reference model run (HS), shading represents the difference between the TIL and reference runs (HSTIL-HS). Contour interval in (a) is: 0.3 x 10−6 PVU m−1, i.e., ..., −0.15, 0.15, 0.45, ...; contour interval in (b) is: 5 m s−1, i.e., ..., −2.5, 2.5, 7.5, ... Black dashed and dotted lines represent the tropopause height in the TIL and reference runs, respectively. Grey contours in (a) represent the difference in buoyancy frequency (N2; in 10−4 s−2) between the TIL and the reference runs (HSTIL-HS), where only contours for ± 1 and ± 2.5 × 10−4 s−2 were plotted for clarity; and in (b) grey dashed contours represent the imposed temperature anomaly (in K) in the equilibrium temperature profile. Grey diamond and star in (b) represent the latitude of the maximum 850hPa zonal mean zonal wind (i.e., the latitude of the eddy-driven jet stream) in the TIL and the reference runs, respectively.
Figure 5 confirms our expectation (see Introduction) that, compared to the reference run, the TIL run produces significantly stronger, more confined PV gradients near the tropopause (shading in Fig. 5a), which should act as a stronger waveguide for Rossby waves8,18,34. Shading in Fig. 5b further shows that the jet stream is overall stronger and displaced further equatorward in the TIL run (at 34.9 degrees; grey diamond) compared to the reference run (at 37.7 degrees (grey star); see also black contours). This response is qualitatively similar to the interannual co-variability between TIL strength and Arctic Oscillation and to zonal wind inter-model variability that is related to the TIL strength (discussed above). However, given that, here, our imposed TIL forcing is the only difference between the two mechanistic model experiments, the strengthening and equatorward shift of the jet stream in the TIL run must be due to the imposed forcing (i.e., tropopause-level cooling). Note that this occurs despite a slightly higher tropopause in the TIL run (compare dashed and dotted lines in Fig. 5), which is typically related to a poleward shift of the EDJ44.
The response of the Hadley cell to a sharper tropopause is an overall strengthening and weak contraction (at lower levels; shading in Fig. 6a), broadly consistent with interannual variations in ERA5 (typically, 1-standard deviation change in the TIL strength corresponds to ~2% change in the Hadley cell strength; not shown). Similarly, the Ferrel cell (midlatitude thermally indirect overturning circulation) also strengthens in the TIL run, which indicates that the entire atmospheric general circulation is invigorated due to the sharper tropopause.
Figure shows meridional cross-sections of (a) streamfunction, (b) eddy momentum flux, and (c) eddy heat flux. Black contours (solid for positive values, dashed for negative values) represent their climatologies in the reference model run (HS), and shading represents the difference between the TIL and reference runs (HSTIL-HS). Contour interval in (a) is 0.2 × 1011 kg s−1, i.e., ..., −0.3, −0.1, 0.1, 0.3, ...; contour interval in (b) is 10 m2 s−2, i.e., ..., −15, −5, 5, 15, ...; and contour interval in (c) is 2.5 K m s−1: +2.5, 5., 7.5, ... Black dashed lines represent the tropopause height in the TIL run (HSTIL). Grey contours represent the difference in buoyancy frequency (N2; in 10−4 s−2) between the TIL and the reference runs (HSTIL-HS) (as in Fig. 5a). Note that in (b) and (c) values were multiplied by \(\cos \phi\) (as in EP flux, Eq. 4).
The responses in jet latitude and strength, and in overturning circulation should go along with modified eddy fluxes of momentum and heat, and this is indeed the case (Fig. 6b, c). The latitude region of the strongest heat flux (strongest baroclinic eddy activity) is more pronounced, shifted equatorward, and extends further upward (Fig. 6c). Likewise, the characteristic momentum flux pattern of positive and negative fluxes equatorward and poleward of the main wave source, respectively, is more pronounced and extends further upward in the TIL run (Fig. 6b). Interestingly, the momentum flux pattern does not show a clear equatorward shift; if anything, the region of positive momentum fluxes extends a bit further poleward near the jet core (seen also in Supplementary Fig. 4a). This may be consistent with weaker meridional spreading of waves and stronger upward wave propagation (also indicated in Supplementary Fig. 4b). The more pronounced eddy fluxes in the TIL run suggest intensified baroclinic life cycles, likely induced by the enhanced upper level baroclinicity and greater available potential energy (by ~25%) due to the sharper tropopause.
The documented changes to the eddy fluxes induced by the sharper tropopause may be linked to changes in wave activity fluxes and wave sources/sinks (see also Methods). Stronger tropospheric heat fluxes translate into stronger upward wave activity fluxes (stronger upward wave propagation; arrows in Fig. 7). The overall intensified circulation is associated with a stronger wave source near the surface and stronger wave sink (dissipation) near the tropopause (shading in Fig. 7). Interestingly, horizontal wave fluxes (meridional wave propagation; arrows in Fig. 7) out of the region of strongest baroclinic eddy activity are enhanced by a smaller amount (by ~20%) compared to the vertical wave fluxes (by ~45%) in the TIL run (Supplementary Fig. 4). This is consistent with the stronger waveguide in the TIL run, which causes more latitudinal confinement of wave fluxes and relatively less horizontal wave dispersion/leakage34. Consistently, wave dissipation (blue shading in Fig. 7) in the upper-troposphere becomes more confined to the tropopause and strengthens with sharper tropopause (compare Fig. 7a and b), which generally means stronger residual circulation45. Again, this confirms the notion of stronger baroclinic life cycles, relatively weaker equatorward wave propagation, stronger general circulation, and thus a resulting stronger and equatorward shifted jet stream.
Figure shows meridional cross-sections of wave (Eliassen-Palm, EP) fluxes (grey arrows; in m2 s−2; scale is shown in top right corner of each panel), zonal mean wave (EP) flux divergence (sources and sinks; shading; in m s−1 day−1), and zonal mean zonal wind (contours); contour interval: 5 m s−1: ..., −7.5, −2.5, 2.5, 7.5, ... Panel (a) for the reference model run (HS), and panel (b) for the TIL model run (HSTIL). Thick black dashed line represents the tropopause height in (a) the reference run, (b) the TIL run. Grey contours in (b) represent the difference in buoyancy frequency (N2; in 10−4 s−2) between the TIL and the reference runs (HSTIL-HS) (as in Fig. 5a).
We furthermore find slightly shorter dynamical memory with sharper tropopause—both baroclinic (using eddy-kinetic-energy as a measure of eddy activity) and annular mode variability are faster by a few days (assessed via e-folding-time analysis46; not shown). This is different from previous work47 that showed more persistent annular modes in model configurations with a more equatorward EDJ, suggesting an additional role of the tropopause sharpness in weakening the persistence of annular modes (and atmospheric variability in general), likely due to relatively weaker meridional wave propagation.
Note that in the reanalysis we have found signals in momentum fluxes that are consistent with annular mode dynamics (not shown), i.e., less equatorward wave propagation with an equatorward EDJ shift. Interestingly, heat fluxes strengthen on the equatorward side with an equatorward jet shift, consistent with the sharper tropopause argument from mechanistic model experiments. This suggests a potential role for tropopause sharpness in interannual variability in addition to annular mode dynamics.
Discussion
The above results suggest a robust link between tropopause sharpness (affected by the strength of the TIL) and the position and strength of the subtropical and midlatitude eddy-driven jet streams, as well as other general circulation metrics during NH winter. This relationship does not only hold on interannual timescales (e.g., associated with the Arctic Oscillation) as seen from the reanalysis and climate models (Figs. 2a, 3, Supplementary Figure 1), but also on multidecadal timescales (i.e., associated with the recent trend towards a weaker TIL, Fig. 2a) and in a climatological-mean sense (e.g., Figs. 4, 5b). Note that such TIL-circulation coupling also exists in the SH, albeit with more nuanced structures due to different coupled STJ-EDJ regimes there (not shown).
Our analysis of mechanistic model experiments suggests that a sharper tropopause is related to a more equatorward eddy-driven jet, stronger subtropical jet, stronger subtropical and tropopause waveguides, stronger and potentially narrower Hadley cell, stronger (and faster) baroclinic variability and thus also intensified wave generation and (vertical) wave propagation, etc. (Figs. 5–7). The opposite is true for a smoother tropopause. While the impact of the tropopause sharpness on the tropospheric general circulation is clear in the case of the mechanistic model experiments, it remains to be seen whether other mechanistic coupling between the tropopause sharpness and general circulation features17,25,48 exists in the comprehensive climate models and/or the real atmosphere. Nevertheless, the similarity of the TIL-circulation relation across many different sources of variability suggests a robust link between the tropopause sharpness and the aspects of the general circulation. Also, to the extent that some of the documented TIL-forcings may be considered to be effectively external, our hypothesized cause-effect relation may indeed be present in the real atmosphere (e.g., related to water vapour radiative effects19,29, although the water vapour structure is certainly not independent of the circulation).
We hypothesize that a stronger TIL (sharper tropopause) is related to an enhanced tropopause-level waveguide, amplified and more concentrated eddy activity in the baroclinic zone, and thereby intensified mid-latitude circulation. Changes to the jet strength and latitude, however, require eddy-feedbacks that we envision to act in the following way. First, the enhanced waveguide effect of a sharper mid-latitude tropopause may cause stronger latitudinally confined channelling of Rossby waves and thereby relatively reduced meridional “leakage” and/or meridional propagation during their upward propagation18. This is associated with stronger wave dissipation locally near the mid-latitude tropopause (Fig. 7). At the same time, the reduced meridional wave dispersion is related to an equatorward shift of the EDJ (similar to the negative phase of the annular mode)35,49 and reduced wave dissipation into the subtropics, i.e., a strengthened STJ and Hadley cell50,51,52.
Our results also suggest that the strength of the TIL may be important for the changes in the general circulation under climate change (in addition to many other factors1), however its relative role compared to (and its relationship to) the other mechanisms needs to be explored in more detail in the future.
This study has focused on the evidence for a TIL-driven response of the general circulation, and has not explored the drivers of the TIL strength. These range from above mentioned radiative processes associated with water vapour and cloud structures near the tropopause27,29 (also important for weather and climate model biases) to dynamical processes, e.g., associated with secondary circulations in upper tropospheric anticyclones53 and stratospheric subsidence associated with variability in the polar vortex26. For example, it has been documented that sudden stratospheric warming events (SSWs) lead to enhanced TIL26. Interestingly, SSWs also lead to an equatorward jet shift54; the strengthened TIL may therefore represent a partial driver of this shift, although this would have to be confirmed with dedicated mechanistic experiments. We have started to explore the role of the TIL in coupled troposphere-stratosphere dynamics using similar mechanistic model experiments as described above. Preliminary results indicate higher likelihood of SSWs with stronger TIL (not shown) consistent with suggestions of previous studies31,55,56. On the other hand, recent work has shown that a stronger TIL tends to suppress upward wave propagation32. Thus, the detailed role of the TIL in stratosphere-troposphere coupling remains to be studied in detail.
Methods
Reanalysis and model data
We use the ERA5 reanalysis36 and its backward extension37, which are provided by the European Centre for Medium-Range Weather Forecasts. The analyses are based on monthly mean data (zonal wind and temperature) for JFM season over the time period 1951-2020. Data are analysed on a 1.5∘ horizontal grid and on 37 vertical (pressure) levels.
We also use output from the CMIP6 climate models38. The models used in this study (and their characteristics) are listed in the Supplementary Table 1. We use 1-2 model runs per modelling centre and have limited ourselves to the first ensemble member (variant label r1i1p1f1) of each model. Due to variable resolutions, models were interpolated to a common horizontal grid with resolution 1.25∘ in longitude and 0.9375∘ in latitude, and are analysed on 17 common vertical (pressure) levels. As for ERA5, we use monthly mean zonal wind and temperature for the JFM season, but over the available period 1870–2014.
Model configuration
We use a dry dynamical core version of the Geophysical Fluid Dynamics Laboratory (GFDL) model with a spectral dynamical core. The model is run in two configurations: (i) a reference run (denoted HS) with a Held-Suarez equilibrium temperature profile39 and with idealized wavenumber 2 (k = 2) topography with 2 km height40; and (ii) a TIL run (denoted HSTIL) that is based on the reference run, but with an imposed stronger TIL via cooling at the tropopause (grey dashed contours in Fig. 5b; see Supplementary Methods for details about the setup). Note that the inclusion of topography does not significantly change the results compared with a regular Held-Suarez39 setting (not shown). The model is forced through Newtonian relaxation of the temperature field to a prescribed equilibrium profile, with linear frictional and thermal damping. The model resolution is T42 (2.8∘ horizontal resolution at the Equator) with 50 varying vertical levels between 1,000 and 0 hPa and is run for 9990 days with the first 300 days taken as a spin-up period. Note that we did not find strong sensitivity to longer integration times or higher resolution. This type of model is used here as it allows us to isolate large-scale dynamical processes in the troposphere under different forcing conditions (here: with and without an imposed TIL). For model climatologies refer to Figs. 5–7.
Estimation of different variables
Eddy-covariance terms, such as heat (v*T*, with v meridional velocity and T temperature) and momentum (u*v*, with u zonal wind) fluxes, are computed by first subtracting the zonal means from each of the variables (i.e., computing zonal perturbations denoted with asterisk (*) above), followed by multiplication and zonal averaging. Note that eddy-covariance terms are computed on instantaneous data before averaging in time or space.
Potential vorticity (PV) meridional gradient in isentropic coordinates is computed as49
where
is PV in pressure coordinates, x and y represent cartesian longitude and latitude, respectively, θ is potential temperature, g is gravitational acceleration (g = 9.81 m s−2), ζ is absolute vorticity (ζ = f + ∂v/∂x − ∂u/∂y), and other terms are defined above.
Hadley and Ferrel cells are computed using streamfunction (ψ), which is defined as57
where a is Earth’s radius.
Tropopause height is defined using thermal tropopause definition58,59, i.e., where the temperature lapse rate falls below 2 K km−1, and its averages between this level and all higher levels within 2 km remain below this threshold. In Figs. 5–7 it is computed from instantaneous zonal mean temperature field and then averaged in time (similar results are obtained from gridded data).
TIL strength is measured by the static stability (Brunt Väisälä frequency, N2). N2 is computed as − (pg2∂θ/∂p)/(RTθ), where R is the gas constant of the dry air and other terms have been defined above. In the mechanistic general circulation model, N2 is computed on daily zonal mean data and then averaged over all days. In the reanalysis and CMIP6 models, we compute maximum N2 between 500 hPa and 50 hPa (denoted \({N}_{\max }^{2}\)) on the longitude-latitude grid for every month and then average these maximum values zonally, meridionally (between 40 and 60∘N), and over JFM season (Fig. 2). Note that we compute \({N}_{\max }^{2}\) on the same pressure-levels for both ERA5 and CMIP6 models for consistency. This results in a slightly weaker TIL strength in ERA5 (than when computed on all 37 ERA5 standard output levels), but the interannual variability remains unchanged. We use \({N}_{\max }^{2}\) as the TIL strength index. Climatological values of \({N}_{\max }^{2}\) in reanalysis and in CMIP6 models are shown in Fig. 2b and in Supplementary Figure 2. The reference model run (HS) has a similar maximum N2 value as ERA5/CMIP6 models ( ~ 5 × 10−4 s−2) just above the tropopause, and the TIL model run (HSTIL) has maximum N2 ~ 7 × 10−4 s−2 – their difference in the TIL region is shown in grey solid contours in Figs. 5a, 6, 7b. HSTIL’s N2 is somewhat larger than the strongest model’s TIL (Fig. 2b;26), but yields a clear response. Note that even though we show \({N}_{\max }^{2}\) values ( ~ 5 × 10−4 s−2) in Fig. 2b for ERA5 and CMIP6, this estimate remains similar across different estimations of the TIL strength as mentioned above and is also consistent with previous work26.
Wave propagation and its sources and sinks (Fig. 7) are assessed using Eliassen-Palm (EP) flux (propagation) and its divergence (sources/sinks). EP fluxes (F) are computed in quasi-geostrophic approximation as11,60
where ϕ is latitude, square brackets ([⋅]) denote zonal average, and other terms have been defined above. EP flux divergence is computed as ∇ ⋅ F where ∇ -operator is computed in spherical pressure coordinates. In Fig. 7 we scale the vertical component by a/p0 (a is Earth’s radius, p0 = 1, 000 hPa is reference pressure), horizontal EP flux component was scaled by π, both EP flux components were also scaled by \(\sqrt{{p}_{0}/p}\), and we plot \(\nabla \cdot {{{\bf{F}}}}\!/\!\cos \phi\) as this is the term that ultimately drives the changes in the zonal wind61.
Northern annular mode (Arctic Oscillation, AO) in reanalysis and in CMIP6 models is computed using principal component (empirical orthogonal function) analysis from zonally and vertically (between 1,000 and 100 hPa) averaged zonal wind between 20∘ and 80∘N62 for the JFM season. Its correlation with \({N}_{\max }^{2}\) in ERA5 and in different CMIP6 models is provided in Supplementary Figure 1 (see also Fig. 3 for correlation of the zonal mean zonal wind with \({N}_{\max }^{2}\) in ERA5).
Correlations are computed between the \({N}_{\max }^{2}\) climatology and the zonal-mean zonal wind climatology across CMIP6 models, by first removing multi-model-mean values of both quantities and then correlating the anomalous values. Note that the two models with extremely large \({N}_{\max }^{2}\) values (MIROC6, IITM-ESM; Fig. 2b, Supplementary Figure 2) were excluded to avoid overestimation. Note that composites (instead of correlations) yield qualitatively similar results and are thus not shown.
Statistical significance is always assessed based on the 95% level of the two-tailed t-test unless otherwise specified.
Data availability
CMIP6 model data are accessible through https://esgf-node.llnl.gov/search/cmip6/. ERA5 data are available through https://cds.climate.copernicus.eu/. Climatological data from the mechanistic model used in this study are archived on Zenodo (https://doi.org/10.5281/zenodo.7164684).
Code availability
The model code is available on GitHub (https://github.com/lina-boljka/gfdl-fms). The parameters are specified under Methods and in the Supplementary Information (Supplementary Methods) as well as in Held-Suarez (1994)39, Gerber and Polvani (2009)40. Tropopause height curve fit was computed using the statsmodels package in Python63. Other scripts are available upon request.
References
Shaw, T. A. Mechanisms of future predicted changes in the zonal mean mid-latitude circulation. Curr. Clim. Chang. Rep. 5, 345–357 (2019).
Harvey, B. J., Cook, P., Shaffrey, L. C. & Schiemann, R. The response of the Northern Hemisphere storm tracks and jet streams to climate change in the CMIP3, CMIP5, and CMIP6 climate models. J. Geophys. Res. Atmos. 125, e2020JD032701 (2020).
Hu, Y., Huang, H. & Zhou, C. Widening and weakening of the Hadley circulation under global warming. Sci. Bull. 63, 640–644 (2018).
Staten, P. W., Lu, J., Grise, K. M., Davis, S. M. & Birner, T. Re-examining tropical expansion. Nat. Clim. Change 8, 768–775 (2018).
Kidston, J. & Gerber, E. P. Intermodel variability of the poleward shift of the austral jet stream in the CMIP3 integrations linked to biases in 20th century climatology. Geophys. Res. Lett. 37, L09708 (2010).
Curtis, P. E., Ceppi, P. & Zappa, G. Role of the mean state for the Southern Hemispheric jet stream response to CO2 forcing in CMIP6 models. Environ. Res. Lett. 15, 064011 (2020).
Gray, S. L., Dunning, C. M., Methven, J., Masato, G. & Chagnon, J. M. Systematic model forecast error in Rossby wave structure. Geophys. Res. Lett. 41, 2979–2987 (2014).
Harvey, B., Methven, J. & Ambaum, M. H. P. An adiabatic mechanism for the reduction of jet meander amplitude by potential vorticity filamentation. J. Atmos. Sci. 75, 4091–4106 (2018).
Wehrli, K., Guillod, B. P., Hauser, M., Leclair, M. & Seneviratne, S. I. Assessing the dynamic versus thermodynamic origin of climate model biases. Geophys. Res. Lett. 45, 8471–8479 (2018).
Birner, T. Fine-scale structure of the extratropical tropopause region. J. Geophys. Res. Atmos. 111, D04104 (2006).
Edmon, H. J., Hoskins, B. J. & McIntyre, M. E. Eliassen-Palm cross sections for the troposphere. J. Atmos. Sci. 37, 2600–2616 (1980).
Held, I. M. & Hoskins, B. J. Large-scale eddies and the general circulation of the troposphere. In issues in atmospheric and oceanic modeling (B. Saltzman, ed.) 3-31 (Elsevier, 1985).
Charney, J. G. & Eliassen, A. A numerical method for predicting the perturbations of the middle latitude westerlies. Tellus 1, 38–54 (1949).
Held, I. M. Stationary and quasi-stationary eddies in the extratropical troposphere: theory. In Large-Scale Dynamical Processes in the Atmosphere (B. J. Hoskins and R. Pearce, eds.) 127–168 (Academic Press, 1983).
Charney, J. G. The dynamics of long waves in a baroclinic westerly current. J. Meteorol. 4, 136–162 (1947).
Eady, E. T. Long waves and cyclone waves. Tellus 1, 33–52 (1949).
Haynes, P., Scinocca, J. & Greenslade, M. Formation and maintenance of the extratropical tropopause by baroclinic eddies. Geophys. Res. Lett. 28, 4179–4182 (2001).
Wirth, V. Waveguidability of idealized midlatitude jets and the limitations of ray tracing theory. Weather Clim. Dynam. 1, 111–125 (2020).
Randel, W. J., Wu, F. & Forster, P. The extratropical tropopause inversion layer: global observations with GPS data, and a radiative forcing mechanism. J. Atmos. Sci. 64, 4489–4496 (2007).
Hoskins, B. J., McIntyre, M. E. & Robertson, A. W. On the use and significance of isentropic potential vorticity maps. Q. J. R. Meteorol. Soc. 111, 877–946 (1985).
Birner, T., Dörnbrack, A. & Schumann, U. How sharp is the tropopause at midlatitudes? Geophys. Res. Lett. 29, 45-1-45-4 (2002).
Birner, T., Sankey, D. & Shepherd, T. G. The tropopause inversion layer in models and analyses. Geophys. Res. Lett. 33, L14804 (2006).
Grise, K. M., Thompson, D. W. J. & Birner, T. A global survey of static stability in the stratosphere and upper troposphere. J. Clim. 23, 2275–2292 (2010).
Wirth, V. Static Stability in the Extratropical Tropopause Region. J. Atmos. Sci. 60, 1395–1409 (2003).
Son, S.-W. & Polvani, L. M. Dynamical formation of an extra-tropical tropopause inversion layer in a relatively simple general circulation model. Geophys. Res. Lett. 34 (2007).
Birner, T. Residual circulation and tropopause structure. J. Atmos. Sci. 67, 2582–2600 (2010).
Randel, W. J. & Wu, F. The polar summer tropopause inversion layer. J. Atmos. Sci. 67, 2572–2581 (2010).
Pilch Kedzierski, R., Matthes, K. & Bumke, K. Wave modulation of the extratropical tropopause inversion layer. Atmospheric Chem. Phys. 17, 4093–4114 (2017).
Bland, J., Gray, S., Methven, J. & Forbes, R. Characterising extratropical near-tropopause analysis humidity biases and their radiative effects on temperature forecasts. Q. J. R. Meteorol. Soc. 147, 3878–3898 (2021).
Gettelman, A. et al. The extratropical upper troposphere and lower stratosphere. Rev. Geophys. 49, RG3003 (2011).
Sjoberg, J. P. & Birner, T. Stratospheric wave-mean flow feedbacks and sudden stratospheric warmings in a simple model forced by upward wave activity flux. J. Atmos. Sci. 71, 4055–4071 (2014).
Weinberger, I., Garfinkel, C. I., White, I. P. & Birner, T. The efficiency of upward wave propagation near the tropopause: importance of the form of the refractive index. J. Atmos. Sci. 78, 2605–2617 (2021).
Haualand, K. F. & Spengler, T. Relative importance of tropopause structure and diabatic heating for baroclinic instability. Weather Clim. Dynam. 2, 695–712 (2021).
Harvey, B. J., Methven, J. & Ambaum, M. H. P. Rossby wave propagation on potential vorticity fronts with finite width. J. Fluid Mech. 794, 775–797 (2016).
Robinson, W. A. A baroclinic mechanism for the eddy feedback on the zonal index. J. Atmos. Sci. 57, 415–422 (2000).
Hersbach, H. et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 146, 1999–2049 (2020).
Bell, B. et al. The ERA5 global reanalysis: Preliminary extension to 1950. Q. J. R. Meteorol. Soc. 147, 4186–4227 (2021).
Eyring, V. et al. Overview of the Coupled Model Intercomparison Project Phase 6 (CMIP6) experimental design and organization. Geosci. Model Dev. 9, 1937–1958 (2016).
Held, I. M. & Suarez, M. J. A proposal for the intercomparison of the dynamical cores of atmospheric general circulation models. Bull. Am. Meteorol. Soc. 75, 1825–1830 (1994).
Gerber, E. P. & Polvani, L. M. Stratosphere-troposphere coupling in a relatively simple AGCM: the importance of stratospheric variability. J. Clim. 22, 1920–1933 (2009).
Omrani, N.-E. et al. Coupled stratosphere-troposphere-Atlantic multidecadal oscillation and its importance for near-future climate projection. npj Clim. Atmos. Sci. 5, 59 (2022).
Archer, C. L. & Caldeira, K. Historical trends in the jet streams. Geophys. Res. Lett. 35 (2008).
Davis, N. & Birner, T. On the discrepancies in tropical belt expansion between reanalyses and climate models and among tropical belt width metrics. J. Clim. 30, 1211–1231 (2017).
Lorenz, D. J. & DeWeaver, E. T. Tropopause height and zonal wind response to global warming in the IPCC scenario integrations. J. Geophys. Res. Atmos. 112, D10119 (2007).
Pfeffer, R. L. A study of eddy-induced fluctuations of the zonal-mean wind using conventional and transformed Eulerian diagnostics. J. Atmos. Sci. 49, 1036–1050 (1992).
Gerber, E. P., Voronin, S. & Polvani, L. M. Testing the annular mode autocorrelation time scale in simple atmospheric general circulation models. Mon. Weather Rev. 136, 1523–1536 (2008).
Barnes, E. A., Hartmann, D. L., Frierson, D. M. W. & Kidston, J. Effect of latitude on the persistence of eddy-driven jets. Geophys. Res. Lett. 37, L11804 (2010).
Ambaum, M. Isentropic formation of the tropopause. J. Atmos. Sci. 54, 555–568 (1997).
Thompson, D. W. J. & Birner, T. On the linkages between the tropospheric isentropic slope and eddy fluxes of heat during northern hemisphere winter. J. Atmos. Sci. 69, 1811–1823 (2012).
Zurita-Gotor, P. The role of the divergent circulation for large-scale eddy momentum transport in the tropics. part i: observations. J. Atmos. Sci. 76, 1125–1144 (2019).
Zurita-Gotor, P. The role of the divergent circulation for large-scale eddy momentum transport in the tropics. part ii: dynamical determinants of the momentum flux. J. Atmos. Sci. 76, 1145–1161 (2019).
Menzel, M. E., Waugh, D. & Grise, K. Disconnect between hadley cell and subtropical jet variability and response to increased CO2. Geophys. Res. Lett. 46, 7045–7053 (2019).
Wirth, V. A dynamical mechanism for tropopause sharpening. Meteorol. Zeitschrift 13, 477–484 (2004).
Baldwin, M. P. & Dunkerton, T. J. Stratospheric harbingers of anomalous weather regimes. Science 294, 581–584 (2001).
Sjoberg, J. P. & Birner, T. Transient tropospheric forcing of sudden stratospheric warmings. J. Atmos. Sci. 69, 3420–3432 (2012).
Birner, T. & Albers, J. R. Sudden stratospheric warmings and anomalous upward wave activity flux. Sci. Online Lett. Atmosphere 13A, 8–12 (2017).
Oort, A. H. & Yienger, J. J. Observed interannual variability in the hadley circulation and its connection to ENSO. J. Clim. 9, 2751–2767 (1996).
WMO. Meteorology—a three-dimensional science. WMO Bulletin 6, 134–138 (1957).
Adam, O. et al. The TropD software package (v1): standardized methods for calculating tropical-width diagnostics. Geosci. Model Dev. 11, 4339–4357 (2018).
Andrews, D. G. & McIntyre, M. E. Planetary waves in horizontal and vertical shear: the generalized Eliassen-Palm relation and the mean zonal acceleration. J. Atmos. Sci. 33, 2031–2048 (1976).
Vallis, G. K. Atmospheric and Oceanic Fluid Dynamics: Fundamentals and Large-Scale Circulation 2nd ed., i-946 (Cambridge University Press, 2017).
Lorenz, D. J. & Hartmann, D. L. Eddy-zonal flow feedback in the Southern Hemisphere. J. Atmos. Sci. 58, 3312–3327 (2001).
Seabold, S. & Perktold, J. statsmodels: Econometric and statistical modeling with python in 9th Python in Science Conference (2010).
Acknowledgements
This work was partly funded by the Climate Dynamics Program of the U.S. National Science Foundation, grant number AGS-1643167. TB further acknowledges current funding by the German Research Foundation (DFG, project no. 428312742, TRR 301: “The Tropopause Region in a Changing Atmosphere”). We thank three anonymous reviewers for their constructive comments that helped improve the original manuscript, as well as Luke Davis for the help with the model.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Contributions
L.B. ran the mechanistic general circulation model, analyzed all the data, and prepared the figures. T.B. initiated the study and helped with model setup and data analyses. Both authors wrote the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Boljka, L., Birner, T. Potential impact of tropopause sharpness on the structure and strength of the general circulation. npj Clim Atmos Sci 5, 98 (2022). https://doi.org/10.1038/s41612-022-00319-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41612-022-00319-6
This article is cited by
-
Stratospheric water vapor affecting atmospheric circulation
Nature Communications (2023)