Abstract
Anvil clouds produced by deep convection cover extensive areas of the tropics, and their response to external perturbations matters for the Earth’s climate sensitivity. It has been suggested that variations in the height and spatial extent of these clouds can be understood from basic physical arguments related to the conservation of mass and energy in the clear-sky areas of the tropics. Based on satellite observations, meteorological reanalyses, and climate model simulations, we show that these arguments can be used to interpret the response of anvil cloud fraction to a range of perturbations in the current climate and under climate change. This includes the response to interannual and long-term surface temperature changes, to the direct effect of carbon dioxide, and the decrease of anvil cloud fraction after explosive volcanic eruptions. Therefore, the control of tropical anvils by clear-sky radiative cooling and static stability in the upper troposphere can explain a large diversity of the responses of anvil cloud fraction to natural and anthropogenic perturbations. These findings should also be considered when assessing the impacts of geo-engineering techniques.
Similar content being viewed by others
Introduction
The response of high clouds to global warming is one of the largest sources of uncertainty for future projections1,2,3,4,5. Much of the tropical high-level cloudiness is composed of anvil clouds, which form at the top of convective systems at around 12–13 km6. Although the behavior of anvil clouds is expected to depend on a range of microphysical and physical processes1,7,8,9,10, theoretical arguments have been suggested to explain changes in their height and extent. In particular, it has been suggested that their altitude follows the upper-tropospheric peak of mass convergence in clear-sky regions1,7, which rises near-isothermally in response to surface warming.
In clear-sky regions, subsidence (ωr, in Pa s−1, positive downwards) is driven by the clear-sky radiative cooling rate (Qr, defined such that cooling is positive):
where p is the air pressure, S is the atmospheric static stability, T is the temperature, R is the gas constant and cp is the isobaric-specific heat of dry air. The strong pressure gradient of Qr in the upper-troposphere implies a maximum Dr in the horizontal convergence, itself directly dependent on the pressure gradient of subsidence:
Owing to mass continuity, a maximum Dr of horizontal mass convergence in clear-sky regions is associated with a maximum of horizontal mass divergence in convective regions, and therefore with the fraction and altitude of anvil clouds. This argument has been invoked to predict a decrease of anvil cloud fraction with temperature, in the framework of the stability-Iris mechanism11. This mechanism is based on thermodynamic arguments and supported by radiative-convective equilibrium simulations from General Circulation Models (GCMs) and cloud-resolving models10,11,12 as well as observations6,13.
When the surface warms, anvils and Dr rise nearly isothermally, and find themselves in a more stable atmosphere because of the dependency of S on atmospheric pressure. Due to enhanced S, the clear-sky pressure gradient of subsidence is reduced, reducing Dr, which by mass conservation leads to reduced anvil cloud fraction.
The behavior of anvil clouds does not only depend on the clear-sky radiative convergence, but can also be affected by local convective entrainment and microphysical processes. In particular, the anvil cloud fraction also depends on the mixing of cloud ice condensates with the upper-tropospheric air8,9,10. Here we examine to what extent changes in the anvil cloud fraction can be understood from changes in the clear-sky radiative convergence, in a variety of contexts, configurations and timescales.
The question arises as to whether similar arguments can explain the behavior of anvil cloud fraction under a range of natural and anthropogenic perturbations, associated or not with changes in surface temperature. Indeed, the stability-Iris mechanism is based on the relationship between anvil cloud fraction and the maximum Dr in clear-sky radiative convergence: surface temperature constitutes only one factor that can affect Dr. Perturbations independent of surface temperature variations also have the potential to cause changes in anvil cloud fraction, through variations in the atmospheric radiative cooling and temperature profile. This includes the purely radiative direct effect of CO214,15 and other radiative perturbations in the stratosphere and upper troposphere induced by ozone changes16 or volcanic eruptions.
Here we test this hypothesis by using a combination of satellite observations (GOCCP17), meteorological reanalyses (ERA518), and different simulations of the current and future climate from a GCM (IPSL-CM6A-LR19). First, we show that this GCM reproduces the stability-Iris effect observed on interannual timescales. Then we examine the different responses of anvil clouds to increased CO2 concentrations: the long-term response which is mediated by surface temperature changes, and the response to the direct effect of CO2 which is not mediated by surface temperature changes14,20. Finally, we explore the response of anvil cloud fraction to explosive volcanic eruptions in observations and in simulations, and show that it can be explained by the same basic physical mechanism. The implications of our findings are then discussed.
Results
Anvil cloud response to interannual variations of surface temperature
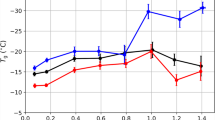
Tropical anvil cloud fraction (CFanv) has been shown to be strongly correlated with Dr in the tropics over 10 years (2006–2016) of high-resolution space-borne lidar observations6. This correlation is also found in the low-resolution observational product GOCCP6, designed to be compared to the GCM’s simulator of observations COSP (see Methods). Its value is about 0.6 over 2006–2016 using GOCCP, but goes up to about 0.8 when using another product from the same satellite instrument with a much finer vertical resolution (see Fig. 4 of Saint-Lu et al., 20206). A consistent correlation of 0.64 is found over 2006–2017 using GOCCP (Fig. 1a). It is associated with an anti-correlation between Dr and the stability at the level of Dr (SDr; see Methods), and a correlation between SDr and surface temperature (Ts), consistent with the stability-Iris effect6,11. Figure 1 shows that the IPSL model reproduces these correlations when forced by observed sea surface temperatures (SSTs), land use, radiative forcing, aerosols and ozone over the same period (see Methods). Although sensitivities of Dr to SDr and of SDr to Ts differ in the IPSL model and in ERA5 reanalyses, the simulated sensitivity of CFanv to Dr falls in the observed range. The model also reproduces the correlation between the altitude of anvils and the altitude of Dr (Supplementary Fig. 1) which is at play in the PHAT (Proportionately Higher Anvil Temperature) theory1 and in the stability-Iris mechanism.
a CFanv against Dr, b Dr against \({S{}_{D}}_{{{{\rm{r}}}}}\), c \({S{}_{D}}_{{{{\rm{r}}}}}\) against Ts, where CFanv is the anvil cloud fraction derived from GOCCP observations (orange) and from the IPSL AMIP experiment using the COSP simulator (black) (see Methods), Dr and \({S{}_{D}}_{{{{\rm{r}}}}}\) are the upper-tropospheric clear-sky maximum of horizontal mass convergence and the static stability at the level of this maximum, derived from the ERA5 reanalysis (orange) interpolated on the IPSL spatial grid, and from IPSL AMIP (black) (see Methods), and Ts is the surface temperature derived from IPSL AMIP, where SSTs are derived from observations (orange and black). Lines show linear regression with shadings showing the regression error. Bold numbers are Pearson correlation coefficients (all p-values are below 0.05). Non-bold numbers are slopes. All quantities are tropical averages (30N–30S) July-to-June annual anomalies relative to the period 2006–2017 (see Methods).
In both the meteorological reanalysis and the GCM, the relationship between CFanv and Dr is not only present when considering the 2006–2017 period, but also when considering a much longer period (1980–2017) (Fig. 2). During this 37-year period, the GCM shows that CFanv anomalies are significantly lower (99.5% confidence) during the years of negative Dr anomalies than otherwise. Figure 2 also shows that the relationship between CFanv and Dr is very robust in the IPSL model as it is found in even longer simulations, and in a wide range of configurations, including atmosphere-only and ocean-atmosphere coupled simulations, with and without anthropogenic forcing (see Methods).
From left to right: GOCCP observations (2006–2017), the IPSL AMIP COSP simulator (2006–2017), ERA5 (1980–2017), IPSL AMIP (1980-2017), AMIP-piForcing (1870–2017), historical (1850–2014) and piControl (455 years). Positive and negative Dr anomalies are taken from the last and first quartiles of the Dr anomalies, respectively. Horizontal bars give the distribution mean. Bold number are Pearson correlation coefficients between CFanv and Dr anomalies including all years (all p-values are below 0.05). Percentage numbers are confidence intervals of the Welch t-test, testing that the mean CFanv anomaly of the red distribution is strictly greater than that of the blue distribution. All anomalies are tropical averages (30N-30S) July-to-June annual anomalies relative to an 11-year running window.
Although the relationship between CFanv and Dr is robust, it no longer emerges as a linear correlation when considering periods longer than 2006–2017 in the IPSL model. It is due to the fact that over the 37-year period, the proportion of large Ts and Dr anomalies is much weaker than during the 2006–2017 period. On the other hand, relationships between Dr and SDr and between SDr and Ts exhibit linear correlations over all the periods and configurations (Supplementary Fig. 2).
Anvil cloud response to climate change
Since the IPSL model reproduces the relationship between CFanv and Dr observed in the present-day climate, we use it to investigate the response of anvil cloud fraction under climate change. As the climate warms in response to the increase of greenhouse gases in the atmosphere, CFanv and Dr are both reduced, as shown in Fig. 3a by the changes in the abrupt-4xCO2 experiment and in the future scenario SSP585. This long-term response mediated by surface temperature changes is not specific to the long-term effects of CO2 forcing (Fig. 3a): it is also found when SSTs are forced to increase by 4 K, as shown by the changes in AMIP-p4K, or when surface temperatures are affected by long-term solar perturbations, as shown by the changes in abrupt-solp4p and abrupt-solm4p (where the solar constant is increased and decreased by 4%, respectively). With increasing Ts, SDr is increased (Fig. 3c) by the upward shift of the isotherms towards lower pressures, reducing Dr (Fig. 3b) and hence CFanv (Fig. 3a) following the stability-Iris mechanism (as shown in Supplementary Fig. 3 by AMIP-p4K atmospheric profiles compared to AMIP).
a CFanv against Dr, b Dr against \({S{}_{D}}_{{{{\rm{r}}}}}\), c \({S{}_{D}}_{{{{\rm{r}}}}}\) against Ts, between nine different climates simulated by the IPSL model (see Methods). To compare SSP585 with its reference historical climate, the last 30 years of SSP585 and the first 50 years of the historical experiment are shown. Error bars show the range of July-to-June yearly means. Black lines show linear regressions. To compare with interannual relationships, the slopes of Fig. 1 for AMIP are shown here by the dashed lines with their errors as shadings. Vertical and horizontal dotted lines passing through piControl, amip and historical points are added. All quantities are tropical averages (30N-30S).
The climate response to an increase in CO2 concentration is partly due to surface warming and partly due to the direct effect of CO2. In the latter case, the large-scale control of anvils by Dr is also found, as shown in Fig. 3a by the reductions of both CFanv and Dr in a simulation where CO2 is quadrupled but SSTs remain unchanged (AMIP-4xCO2). These changes are due to the effect of increased CO2 on clear-sky radiative cooling and atmospheric temperature (Fig. 4). The weakening of the clear-sky radiative cooling (Qr, Fig. 4d) reduces the radiatively-driven subsidence (ωr, Fig. 4c and Eq. (1)), reducing the clear-sky horizontal mass convergence in the upper-troposphere (∂ωr/∂p, Fig. 4b), hence reducing Dr (Fig. 3a and Eq. (2)). At the same time, the weakening of Qr increases the upper-tropospheric temperature (T, Fig. 4f) and hence the stability (S, Fig. 4e), further reducing the clear-sky horizontal mass convergence and hence Dr. The latter increase in S contributes the most to the reduction in clear-sky subsidence and convergence (Fig. 4c and b). As a result, the upper-tropospheric cloud fraction is reduced (CF, Fig. 4a).
a cloud fraction, b clear-sky horizontal mass convergence ∂ωr/∂p, c clear-sky subsidence, d clear-sky radiative cooling (with cooling positive), e static stability and f temperature, in AMIP-4xCO2 (see Methods) compared to AMIP. Changes in convergence and subsidence are decomposed into the estimated parts due to the Qr and S changes (dashed lines; see Methods). All vertical profiles are tropical averages (30N–30S).
The clear-sky radiative convergence is only reduced above about 250 hPa (Fig. 4b) while CF is reduced in the whole upper troposphere down to 300 hPa (Fig. 4a), suggesting that the control of anvils by clear-sky convergence holds near the maximum convergence level. High stability at that level might suppress vertical mixing between cloudy and dry air, so that cloudy air would diverge horizontally, forced by clear-sky convergence. Below that level, lower stability might allow for more vertical mixing, which would affect the evaporation of cloud condensates and hence the horizontal cloud extent, while clear-sky convergence would only play a secondary role. However, owing to the vertical overlap of cloud layers, the change in cloudiness at the height of maximum anvil cloud fraction is what matters the most for radiative feedbacks.
Consistent reductions in CFanv are found in other IPSL experiments (Supplementary Fig. 4). Unlike when the surface temperature increases, in which case the reduction in Dr is caused by the increase in stability associated with the rise of the isotherms towards lower pressures, here in response to the direct effect of CO2 the altitude of Dr, and hence of anvils, does not rise (Fig. 4a and b, Supplementary Fig. 4).
When considering all the different perturbations discussed above, we find that the sensitivity of CFanv to Dr appears consistent with its sensitivity to interannual variations in Dr (Fig. 3a). In contrast, the sensitivity of Dr to SDr appears weaker than at interannual timescales and non-linear (Fig. 3b). This is because Dr and SDr depend on several quantities (Qr, T, and p) whose variation is specific to the type of perturbation applied to the climate system (Supplementary Fig. 5). On the other hand, the relationship between Dr and CFanv which is central to the stability-Iris effect, appears to be more universal across different timescales and perturbations. The same is true for the PHAT1 relationship between the altitude of anvils and the altitude of Dr, since the same sensitivity between the two is found at interannual timescales (Supplementary Fig. 6).
Anvil cloud response to volcanic eruptions
While the abrupt change in CO2 concentration is idealised, explosive volcanic eruptions are abrupt changes that are observable. These events lead to aerosol increase in the stratosphere and upper-troposphere21 that modifies the temperature and radiative cooling and thus has the potential to affect Dr and CFanv. We test this hypothesis with the ERA5 reanalysis and the IPSL model, which were both able to reproduce the observed CFanv-Dr relationship on the 2006–2017 period (Fig. 1). There was no explosive volcanic eruption during the 11 years (2006–2017) of high-resolution space-borne lidar observations. Therefore we analyze the ERA5 reanalysis, whose cloud radiative effect has been shown to be very consistent with observations22.
Vertical profiles from ERA5 show that anvil cloud fraction is reduced during the year following the large volcanic eruption of Mount Pinatubo in 1991 (Fig. 5a). The lower stratosphere and upper troposphere warm by up to 1 K (Fig. 5f) due to the absorption of solar and infrared radiation by stratospheric aerosols. As for the direct effect of CO2, this warming is associated with a reduced Qr and increased S (Fig. 5d and e), which both act to reduce ωr (Fig. 5c) and hence the clear-sky convergence in the upper-troposphere (Fig. 5b), in association with reduced CF (Fig. 5a). Near the anvils level (150–200 hPa), the reduction in Qr is small; it is thus the increase in S which contributes the most to the reduction in clear-sky subsidence and convergence (Fig. 5c and b). This reduction is maximum just above the height at which the cloud fraction maximizes, meaning that the altitude of anvils is shifted downwards. Anvils and Dr are also expected to descend in response to the decrease in surface temperatures due to volcanic aerosols blocking incoming solar radiation.
As Fig. 4 but during the year post-Pinatubo (blue) in ERA5, with all profiles except mean ones (grey line) being July-to-June annual anomalies relative to an 11-year running window (over 1980–2017). All profiles are tropical averages (30N–30S).
The IPSL AMIP experiment qualitatively exhibits the same behavior as ERA5 for the year following the Pinatubo eruption (Fig. 6). The historical experiment (1850–2014) includes five explosive volcanic eruptions, associated with the world-wide strongest and longest anomalies on stratospheric aerosols optical depth in the historical forcing23: Krakatoa (1883, very strong aerosol forcing persisting until 1885), Santa Maria (1902), Novarupta (1912), Mount Agung (1963–64) and Mount Pinatubo (1991). Figure 6 shows a composite of atmospheric anomalies associated with these five events, averaged over 11 realizations of the historical experiment24 (except for Qr, ωr and ∂ωr/∂p which are shown for only one historical realization). The results are consistent with the Pinatubo eruption from ERA5, although here the reduction in Qr is larger and strongly contributes to the reduction in clear-sky subsidence and convergence, even more so than the increase in S (Fig. 6c and b). Both the aerosol forcing and the radiative scheme differ between ERA5 and IPSL-CM6A-LR, which probably explains these differences in the radiative cooling response to volcanic eruptions. As for the direct effect of CO2, it is found in both ERA5 and IPSL AMIP that the control of anvils by clear-sky convergence holds near the maximum convergence level and above, but seems weaker below about 225 hPa, with a weaker correspondence between CF changes and convergence changes (Figs. 5a and b, 6a and b).
As Fig. 5 but during the year post-Pinatubo in IPSL AMIP (blue), and for a composite average of annual anomalies for 6 different years that are subsequent to 5 major volcanic eruptions (1883–84, 1884–85, 1902–03, 1912–13, 1963–64, 1991–92) in IPSL historical (orange). When available (a, e, and f) the historical composite profile is averaged over 11 historical members and orange shading shows the inter-members spread.
The reduction in radiative convergence and anvil cloud fraction during major volcanic eruptions is also found in the absence of anthropogenic forcing and SST variations (Supplementary Fig. 7). There is no microphysical coupling between aerosols and ice clouds in the IPSL model25, nor in the ERA5 reanalysis18, which assures that aerosols can not directly affect anvil cloud formation. The reduction in radiative convergence and anvil cloud fraction during major volcanic eruptions is thus a large-scale atmospheric response to volcanic eruptions, without any mediation by SST variations, anthropogenic forcing, or microphysical effects.
This large-scale response of anvil clouds to volcanic eruptions is also consistent with Boucher et al. (2017)26, who found in a previous version of the IPSL atmospheric model that stratospheric sulfate aerosol injections—as considered for geo-engineering—reduce the tropical high cloud cover. At odds with the interpretation of Boucher et al. (2017)26, this study suggests that the reduced cloudiness and clear-sky subsidence and convergence are primarily explained by the reduced clear-sky radiative cooling, with the stabilization playing only a secondary role. Since sulfate aerosol injections have been shown to warm the lower stratosphere in several GCMs27,28, and even to reduce the optical depth of thin ice clouds27, these results are unlikely to be specific to the IPSL model. The IPSL model has also been shown to be consistent with other GCMs in terms of predicting the climate response to the Pinatubo eruption29.
Large volcanic eruptions are known to cool the surface, which would tend to increase CFanv if Dr were primarily perturbed by surface cooling. The increase in CFanv does not occur because the Dr perturbation is dominated instead by the effect of volcanic eruptions on lower-stratospheric temperatures. This is confirmed by Fig. 7, which shows that for a given stratospheric temperature anomaly, CFanv decreases as Ts increases (consistent with the stability-Iris effect), and for a given Ts anomaly, CFanv decreases when the stratosphere gets warmer (consistent with the effect of volcanic eruptions). The volcanic eruptions of the 11 historical realizations are associated with the most strongly positive stratospheric temperature anomalies. As a result, they remain largely associated with negative CFanv anomalies regardless of the surface temperature. In these cases, Dr and CFanv anomalies are dominated by stratospheric temperatures and Ts anomalies only play a secondary role, even when they are extremely cold (most occurrences of volcanic eruptions project in the two coldest deciles of Ts). Volcanic eruptions as well as other occurrences of an extremely hot or cold stratosphere, can thus overcome the effect of Ts variations on CFanv.
The CFanv anomaly is shown for each decile of surface temperature anomaly (Ts) and lower-stratospheric temperature anomaly (T[75 hPa]), in 11 concatenated members of the IPSL historical experiment. Anomalies associated with the largest volcanic eruptions (1883–84, 1884–85, 1902–03, 1912–13, 1963–64, 1991–92) are indicated with crosses. Crosses can be of small, medium, or large size: small if they represent only one anomaly among the 66 anomalies associated with volcanic eruption (6 years times 11 members), medium if they represent between 2 and 9 anomalies, and large if they represent 10 anomalies or more. All quantities are tropical averages (30N–30S) July-to-June annual anomalies relative to an 11-year running window.
Discussion
The idea that the relationship between anvil cloud fraction CFanv and clear-sky radiative convergence Dr could induce CFanv changes in response to Ts changes has been suggested on the basis of physical arguments and idealized RCE simulations11, and then confirmed by observations in an 11-year period6. Reanalyses and climate simulations both show that this mechanism operates on much longer timescales, both in response to natural Ts variations and externally-induced changes in Ts, such as in response to CO2 or solar constant perturbations. This shows the robustness of the stability-Iris mechanism.
However, Dr is not only affected by variations in Ts. We show that the direct effect of CO2 also perturbs Dr through its impact on Qr and S and, consistently, that it is associated with changes in CFanv.
We further show that explosive volcanic eruptions also perturb Dr and hence CFanv, in a similar manner as CO2. This study thus proposes a new mechanism through which stratospheric aerosols can affect the high-level cloudiness, which is not rooted in the microphysical aerosol-cloud interactions: here, stratospheric aerosols affect anvil cloudiness remotely through their impact on Qr and S. According to this mechanism, the tropical high cloud cover is expected to shrink in response to stratospheric sulfate aerosol injections, as actually found by Boucher et al. (2017)26. It should therefore be considered when investigating the potential impacts of geo-engineering techniques.
Our study shows that the response of CFanv to a large diversity of natural and anthropogenic perturbations can be interpreted from the same basic mechanism rooted in the conservation of mass and energy. A recent assessment pointed out the large uncertainty associated with the anvil cloud fraction feedback for climate sensitivity5. It is thus encouraging that at least one robust control of CFanv by a basic physical mechanism has been identified. In the future, the robustness of our results could be assessed further by considering a larger range of models, including cloud-resolving models, both in an idealized framework (as done in Wing et al. 202030) and in more realistic configurations. Further studies will also be necessary to understand the radiative implications of CFanv changes on the Earth’s radiative budget. Ito and Masunaga (2022)13 suggest that on short timescales the stability-Iris effect is neutral regarding radiation. It remains to be investigated whether or not the same result holds on longer timescales and for volcanic eruptions.
Methods
Radiative cooling data, calculation of D r and S Dr
With the IPSL model, the clear-sky radiative cooling rate Qr is computed from the model output variables “Tendency of Air Temperature due to Clear Sky Longwave Radiative Heating” (“tntrlcs”) and “Tendency of Air Temperature due to Clear Sky Shortwave Radiative Heating” (“tntrscs”). With ERA5 reanalyses, it is computed from the “Mean temperature tendency due to short-wave radiation, clear sky” (“mttswrcs”) and the “Mean temperature tendency due to long-wave radiation, clear sky” (“mttlwrcs”). Following Eq. (2), Dr is defined (in each location and month) as the maximum value, between 600 hPa and 10 hPa, of the pressure gradient ∂ωr/∂p. At the height of this maximum, the value of S (computed from Eq. (1)) is referred to as SDr.
Tropical anvil cloud fraction
We define anvil clouds following the detection method of Saint-Lu et al.6: we consider the vertical profile of monthly cloud fraction above 8 km, at each grid cell in the tropics (30∘N–30∘S), and we select the local maximum that is the closest to its centroid. This local maximum defines the anvil cloud fraction CFanv. With the IPSL model, the raw vertical profile of monthly cloud fraction is taken from the “CALIPSO Percentage Cloud Cover” variable (“clcalipso”) when using the COSP simulator, and from the “Cloud Area Fraction” variable (“cl”) otherwise. The COSP simulator is only used when stated. With ERA5 reanalyses, the “Fraction of Cloud Cover” variable (“cc”) is used.
July-to-June annual anomalies
Monthly data are averaged from July of each calendar year to June of the next calendar year, giving July-to-June annual data, to detect interannual variations associated with El Niño-Southern Oscillation6 which peaks between November and March. The annual-mean data over an 11-year period is then subtracted to this July-to-June annual data, to give July-to-June annual anomalies.
Comparison between IPSL-CM6A-LR and observations
To best assess the realism of the anvil clouds behavior against observations, we use a simulation in which SSTs, land use, greenhouse gases, aerosols, and ozone are all consistent with observations, which is the AMIP experiment31. We also use the COSP satellite simulator32 to ensure that the definition of the cloud fraction is consistent between the model and the CALIPSO observational product GOCCP17. Note that one of the realizations of the AMIP experiment run with IPSL-CM6A-LR is extended to December 2017, covering the 11 years of space-borne lidar observations, allowing us to robustly compare model and observations.
GCM experiments
Experiments used in this paper are all part of CMIP6 (Coupled Model Intercomparison Project phase 6).
-
DECK experiments31: AMIP (atmospheric simulation with anthropogenic forcing and prescribed observed SSTs, taken over the period 1980–2017 - see above), piControl and historical (ocean-atmosphere coupling with pre-industrial 1850 forcing applied over 455 years and historical forcing applied over 1850–2014, respectively), abrupt-4xCO2 (CO2 multiplied by 4 compared to piControl at the beginning of the simulation and then held constant with time; using the last 150 years of the simulation).
-
CFMIP experiments33: AMIP-piForcing (same as AMIP but with constant pre-industrial atmospheric forcing and run over 1870–2017), abrupt-solp4p and abrupt-solm4p (solar constant increased and decreased by 4% compared to piControl, respectively; 50 year-long), AMIP-p4K (same as AMIP but SSTs are subject to a uniform warming of 4 K, over 1979–2014), AMIP-4xCO2 (same as AMIP but CO2 is quadrupled, over 1979–2014).
-
Climate change scenarios34: SSP585 (2015–2100).
Contributions of clear-sky radiative cooling and static stability changes to clear-sky subsidence and convergence changes
The change in clear-sky radiative subsidence Δωr, can be decomposed from Eq. (1) as:
where overbars denote the time-mean for the reference state from which the change or anomaly is computed.
The change in clear-sky radiative convergence Δ(∂ωr/∂p) can be approximated as ∂(Δωr)/∂p and decomposed as:
In both equations, the first and second terms on the right hand side give estimates of the contributions of Qr and S, respectively.
Data availability
GOCCP 3D cloud fraction are available at https://climserv.ipsl.polytechnique.fr/cfmip-obs/Calipso_goccp.html. ERA5 monthly means of daily means (MODA) on single levels are available on the Climate Data Store (CDS) online catalogue, at https://cds.climate.copernicus.eu/#!/search?text=ERA5, except for clear-sky mean temperature tendency due to long-wave and short-wave radiation (“mttlwrcs”, “mttswrcs”) used to compute Qr, which can be downloaded in a raw format from the CDS API client following instruction at https://confluence.ecmwf.int/display/CKB/How+to+download+ERA5#HowtodownloadERA5-4-DownloadERA5familydatathroughtheCDSAPI. CMIP6 data are available through the Earth System Grid Federation (ESGF)35, see https://pcmdi.llnl.gov/CMIP6/Guide/dataUsers.html#3-accessing-model-output. Codes for this paper are available at https://drive.google.com/drive/folders/1c6SmaeAXHnYlCwb9ivUfKLyz3w1lMDb5?usp=sharing
References
Zelinka, M. D. & Hartmann, D. L. Why is longwave cloud feedback positive? J. Geophys. Res. Atmos. 115, D16117 (2010).
Boucher, O. et al. Clouds, and aerosols. In Climate change 2013: the physical science basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, 571–657 (Cambridge University Press, 2013).
Hartmann, D. L. Tropical anvil clouds and climate sensitivity. Proc. Natl. Acad. Sci. USA. 113, 8897–8899 (2016).
Su, H. et al. Tightening of tropical ascent and high clouds key to precipitation change in a warmer climate. Nat. Commun. 8, 15771 (2017).
Sherwood, S. C. et al. An assessment of earth’s climate sensitivity using multiple lines of evidence. Rev. Geophys. 58, e2019RG000678 (2020).
Saint-Lu, M., Bony, S. & Dufresne, J.-L. Observational evidence for a stability iris effect in the tropics. Geophys. Res. Lett. 47, e2020GL089059 (2020).
Hartmann, D. L. & Larson, K. An important constraint on tropical cloud—climate feedback. Geophys. Res. Lett. 29, 1951 (2002).
Seeley, J. T., Jeevanjee, N., Langhans, W. & Romps, D. M. Formation of tropical anvil clouds by slow evaporation. Geophys. Res. Lett. 46, 492–501 (2019).
Seeley, J. T., Jeevanjee, N. & Romps, D. M. FAT or FiTT: Are anvil clouds or the tropopause temperature invariant? Geophys. Res. Lett. 46, 1842–1850 (2019).
Beydoun, H., Caldwell, P. M., Hannah, W. M. & Donahue, A. S. Dissecting anvil cloud response to sea surface warming. Geophys. Res. Lett. 48, e2021GL094049 (2021).
Bony, S. et al. Thermodynamic control of anvil cloud amount. Proc. Natl. Acad. Sci. U.S.A. 113, 8927–8932 (2016).
Cronin, T. W. & Wing, A. A. Clouds, circulation, and climate sensitivity in a radiative-convective equilibrium channel model. J. Adv. Model. Earth Syst. 9, 2883–2905 (2017).
Ito, M. & Masunaga, H. Process-level assessment of the iris effect over tropical oceans. Geophys. Res. Lett. 49, e2022GL097997 (2022).
Gregory, J. & Webb, M. Tropospheric adjustment induces a cloud component in CO2 forcing. J. Clim. 21, 58–71 (2008).
Bony, S. et al. Robust direct effect of carbon dioxide on tropical circulation and regional precipitation. Nat. Geosci. 6, 447–451 (2013).
Harrop, B. E. & Hartmann, D. L. Testing the role of radiation in determining tropical cloud-top temperature. J. Clim. 25, 5731–5747 (2012).
Chepfer, H. et al. The GCM-Oriented CALIPSO Cloud Product (CALIPSO-GOCCP). J. Geophys. Res. Atmos. 115, D00H16 (2010).
Hersbach, H. et al. The ERA5 global reanalysis. Q J R Meteorol. Soc. 146, 1999–2049 (2020).
Boucher, O. et al. Presentation and evaluation of the IPSL-CM6A-LR climate model. J. Adv. Model. Earth Syst. 12, e2019MS002010 (2020).
Sherwood, S. C. et al. Adjustments in the forcing-feedback framework for understanding climate change. Bull. Am. Meteorol. Soc. 96, 217–228 (2015).
Robock, A. Volcanic eruptions and climate. Rev. Geophys. 38, 191–219 (2000).
Wright, J. S. et al. Differences in tropical high clouds among reanalyses: origins and radiative impacts. Atmos. Chem. Phys. 20, 8989–9030 (2020).
Lurton, T. et al. Implementation of the CMIP6 forcing data in the IPSL-CM6A-LR Model. J. Adv. Model. Earth Syst. 12, e2019MS001940 (2020).
Bonnet, R. et al. Presentation and evaluation of the IPSL-CM6A-LR ensemble of extended historical simulations. J. Adv. Model. Earth Syst. 13, e2021MS002565 (2021).
Madeleine, J.-B. et al. Improved representation of clouds in the atmospheric component LMDZ6A of the IPSL-CM6A Earth System Model. J. Adv. Model. Earth Syst. 12, e2020MS002046 (2020).
Boucher, O., Kleinschmitt, C. & Myhre, G. Quasi-additivity of the radiative effects of marine cloud brightening and stratospheric sulfate aerosol injection. Geophys. Res. Lett. 44, 11,158–11,165 (2017).
Kuebbeler, M., Lohmann, U. & Feichter, J. Effects of stratospheric sulfate aerosol geo-engineering on cirrus clouds. Geophys. Res. Lett. 39, L23803 (2012).
Tilmes, S. et al. Stratospheric Ozone response to sulfate aerosol and solar dimming climate interventions based on the G6 Geoengineering Model Intercomparison Project (GeoMIP) Simulations. Atmos. Chem. Phys. 22, 4557–4579 (2022).
Zanchettin, D. et al. Effects of forcing differences and initial conditions on inter-model agreement in the VolMIP volc-pinatubo-full experiment. Geosci. Model Dev. 15, 2265–2292 (2022).
Wing, A. A. et al. Clouds and convective self-aggregation in a multimodel ensemble of radiative-convective equilibrium simulations. J. Adv. Model. Earth Syst. 12, e2020MS002138 (2020).
Eyring, V. et al. Overview of the Coupled Model Intercomparison Project Phase 6 (CMIP6) experimental design and organization. Geosci. Model Dev. 9, 1937–1958 (2016).
Bodas-Salcedo, A. et al. COSP: Satellite simulation software for model assessment. Bull. Am. Meteorol. Soc. 92, 1023–1043 (2011).
Webb, M. J. et al. The Cloud Feedback Model Intercomparison Project (CFMIP) contribution to CMIP6. Geosci. Model Dev. 10, 359–384 (2017).
O’Neill, B. C. et al. The roads ahead: Narratives for shared socioeconomic pathways describing world futures in the 21st century. Glob. Environ. Change 42, 169–180 (2017).
Balaji, V. et al. Requirements for a global data infrastructure in support of CMIP6. Geosci. Model Dev. 11, 3659–3680 (2018).
Acknowledgements
We first thank the three anonymous reviewers for their helpful and relevant comments which improved the manuscript. We thank Thibaut Lurton and Adriana Sima for running experiments with radiative temperature increment outputs, which allowed us to compute the clear-sky radiatively-driven variables essential to the study. We thank the IPSL climate modelling centre for developing the model and running the CMIP6 experiments. We thank Bernard Legras for making the ERA5 MODA data available and for useful discussions, Maxime Leuliet for his interest and help during the study, Olivier Boucher for his useful insights, and Marianne Pietschnig and Jules Kajtar for editing the text. MSL is funded by JPI climate/JPI ocean ROADMAP (ANR-19-JPOC-003) via the CNRS. SB and JLD are supported by the European Unions Horizon 2020 research and innovation program (European Research Council grant no 694768 and CONSTRAIN grant no 820829). This work was supported by CNES. The IPSL experiments were performed using the HPC resources of TGCC under the allocations 2019-A0060107732, 2020-A0080107732, and 2021-A0100107732 (gencmip6) provided by GENCI (Grand Equipement National de Calcul Intensif). To process the GOCCP, ERA5, and IPSL-CM6A-LR data, this study benefited from the IPSL mesocenter ESPRI facility which is supported by CNRS, Sorbonne Université, Labex L-IPSL, CNES, and École Polytechnique.
Author information
Authors and Affiliations
Contributions
M.S. conducted the study, analyzed the data, and wrote the paper. All authors designed the research, interpreted the results, and edited the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
41612_2022_304_MOESM1_ESM.pdf
Supplementary Information for Clear-sky control of anvils in response to increased CO2 or surface warming or volcanic eruptions
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Saint-Lu, M., Bony, S. & Dufresne, JL. Clear-sky control of anvils in response to increased CO2 or surface warming or volcanic eruptions. npj Clim Atmos Sci 5, 78 (2022). https://doi.org/10.1038/s41612-022-00304-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41612-022-00304-z
This article is cited by
-
High clouds and higher sensitivity
Nature Geoscience (2024)
-
Weak anvil cloud area feedback suggested by physical and observational constraints
Nature Geoscience (2024)
-
Greater climate sensitivity implied by anvil cloud thinning
Nature Geoscience (2024)
-
Robustness of the relationship between tropical high-cloud cover and large-scale circulations
Climate Dynamics (2024)