Introduction

Over the 1980–2012 period, the eastern tropical Pacific sea surface temperature (SST) is characterized by a cooling trend that was one of the main causes of the global surface warming slowdown observed during 1998–20121,2,3. This regional cooling contrasts with a direct radiatively forced response expected from the increase in anthropogenic greenhouse gases4 and it is associated with an intensification of the western tropical Pacific easterlies, reflecting changes in the Walker Circulation5,6,7. Such changes have been partly attributed to variations in the tropical Atlantic SST through atmospheric teleconnections8,9.

During the same 1980–2012 period, the tropical Atlantic SSTs continued warming, likely due to a combination of anthropogenic-related radiative forcing and internal climate variability10,11. In particular, the leading mode of decadal variability of the North Atlantic SST—namely the Atlantic multidecadal variability (AMV12,13; Fig. 1a, b)—shifted from a cold to a warm phase around 1995–1996, exaggerating the North Atlantic warming trend induced by anthropogenic greenhouse gases14,15. Over the longer 1920–2014 period, warm AMV conditions were also associated with cold SST anomalies in the central and eastern tropical Pacific (Fig. 1c), supporting the existence of a consistent link between the AMV and the tropical Pacific climate16,17. Yet, these observed Pacific changes cannot be unequivocally attributed to the AMV due to the presence of external forcing and internally driven variability outside of the North Atlantic, as well as because of the limited historical record with respect to the timescales considered and observational uncertainties. Coupled global climate model (CGCM) simulations offer the possibility to tackle these limitations.

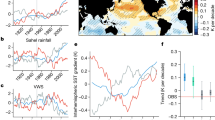
Fig. 1: Observed AMV and related anomalies.
figure 1

a Spatial structure of the AMV-SST anomalies imposed in the numerical simulations. b Time evolution of the observed AMV (dataset: ERSSTv4). c Observed 2-m air temperature difference between positive and negative AMV years (i.e., red minus blue years in (b) dataset: HadCRUT4). Due to the sparseness of the observation in the tropical Pacific before ~1920’s68, the composite in (c) is computed only from 1920 onwards, i.e., excluding data marked by the gray shading in (b). Areas, where data were not available for the whole composite period, are masked.

Full size image

Using a hierarchy of numerical models, Li et al.9 demonstrated that the tropical Pacific response to the Atlantic forcing can be decomposed into two phases: Phase-1 an initial Atlantic forcing through diabatic heating and Phase-2 an Indo-Pacific Walker Circulation feedback (cf. Fig. 3 in Li et al.9). In Phase-1, the warm tropical Atlantic SST anomalies in summer (hereafter seasons are relative to the Northern Hemisphere) intensify deep convection and lead to upper tropospheric mass divergence over the tropical Atlantic. This divergence is compensated by upper tropospheric mass convergence and descent over the Central tropical Pacific, which intensifies the surface Trade winds over western tropical Pacific8,18. In Phase-2, the so-called Indo-Pacific feedback reinforces the Trade winds, piling up warm water in the Pacific Warm Pool, where atmospheric deep convection increases. This results in an upper tropospheric mass divergence over the warm pool that enhances Central tropical Pacific descent acting as positive feedback on the anomalies generated by the Atlantic forcing in Phase 19,19. Following El Niño Southern Oscillation (ENSO) dynamics, an increase in summer easterlies in the western tropical Pacific eventually favors colder conditions than normal in the eastern and central Pacific during the following winter20.

Fig. 2: Simulated AMV impacts.
figure 2

Multi-model mean and 10-year averaged differences between AMV+ and AMV− simulations ensemble means in terms of 2-m air temperature and for the boreal (a) winter and (b) summer seasons. Stippling indicates regions where less than 80% of the models agree on the sign of the differences. Dashed black lines indicate in (a) the NIÑO3.4 region and in (b) the TROP latitudinal band and its constituent regions: TropInd, TropPac, and TropAtl (cf. indices definition in “Methods”).

Full size image

Given the global importance of the tropical Pacific variability and the predictability arising from the North Atlantic at decadal timescales21,22, this Atlantic–Pacific teleconnection is a potential source of seasonal to decadal climate predictability that needs to be further assessed in models. However, the robustness and the strength of this connection remain unknown and need to be quantified. Here, we present a multi-model assessment of this Atlantic–Pacific connection using 21 ensemble simulations from 13 CGCMs (Supplementary Tables 1 and 2) that largely comply with the CMIP6/DCPP-C protocol23. Following this protocol, the same observed AMV SST anomalies (Fig. 1a) are imposed in the North Atlantic of each CGCM to investigate the worldwide teleconnections associated with the observed AMV (see “Methods”). We note that in those idealized AMV simulations, extra heat is added to (or removed from) the climate system to maintain a stationary AMV signal in the North Atlantic for 10 years. This artificial heat prevents a realistic simulation of the relationship between AMV and the global mean surface temperature.

Results

Uncertainty in the Pacific response to AMV forcing

We start by discussing the multi-model mean (MMM; cf. “Methods”) winter response of the AMV experiments. Associated with the imposed 0.2 °C tropical North Atlantic warming, the MMM shows a 0.05 °C cooling in the tropical South Atlantic and a 0.1 °C cooling in the central equatorial Pacific (Fig. 2a). The latter extends eastward and poleward in both hemispheres, contrasting with warm anomalies in the western part of the subtropical Pacific basins. In the Indian Ocean, the MMM shows a broad warming response with maximum anomalies localized west of India. The summertime SST anomalies are similar to the winter ones but of weaker amplitude over the central equatorial Pacific (Fig. 2b). Overall, the MMM shows good agreement with observations over the whole tropical Atlantic (even south of the Equator where models are not constrained) as well as North of 10°S in other tropical regions (Fig. 1c). This similarity supports the important driving role of the AMV in the observed changes over the Pacific during the historical period8,9,17,19,24,25,26,27. In addition, the negative response of the tropical Pacific SST to the imposed North Atlantic warming in the AMV experiments implies a dynamical adjustment of the Pacific.

Fig. 3: Origins of the inter-model spread response to the observed AMV forcing.
figure 3

Inter-model relationship between several indices. Markers represent the 10-year averaged ensemble mean the difference between AMV+ and AMV− simulations from individual experiments and the three colors code for the different AMV forcing strengths: 1×AMV, 2×AMV, and 3×AMV strength in blue, orange, and magenta, respectively. a Winter NIÑO3.4 SST index versus winter tropical North Atlantic SST (averaged over 5°N–20°N/60°W–10°E). b Winter NIÑO3.4 SST index versus summer TropPac descent (sum of the net vertical mass transport at 500  hPa; a positive value indicates descent). c Summer TropPac descent versus the sum of TropInd and TropAtl ascent. d Summer TropInd ascent versus TropAtl ascent. e Summer TropInd ascent versus atmospheric vertical temperature contrast over the WarmPool region (defined as the 20°S–20°N/90°E–160°W region), and (f) summer TropPac SST versus TROP temperature at 200  hPa. R indicates the inter-model correlation (see “Methods”). The dashed line in (c) materializes a full mass compensation within the tropics; RAtl and RInd indicate the inter-model correlations between summer TropPac and TropAtl ascent and summer TropPac and TropInd ascent, respectively. The Box plots in (d) indicate the minimum/maximum values, the 20th/80th percentiles, and the median from the indices distributions.

Full size image

We now investigate the tropical Pacific response as simulated by each individual model using as a proxy the NIÑO3.4 SST index (cf. indices definition in “Methods” and Fig. 2a). In winter, all experiments simulate La Niña-like cooling in response to an AMV warming except the EC-Earth3P_1Sig experiment that shows weak NIÑO3.4 warming of +0.01 °C (Fig. 3a; see also Supplementary Fig. 8). Though models mostly agree on the sign of the tropical Pacific response, the magnitude of their response varies by an order of magnitude, from 0.01 °C to −0.23 °C, with a MMM of −0.12 °C for a similar ~0.2 °C tropical North Atlantic warming. This large inter-model spread in response to AMV forcing highlights considerable uncertainties in our ability to predict the climate at seasonal to decadal timescales28,29.

Origins of the inter-model spread

Different tropical Pacific responses among models in winter can be explained by intrinsic model differences in simulating Pacific climate dynamics such as the ones linked to ENSO30. Yet, it is known that ENSO is strongly influenced by tropical Pacific conditions in the previous summer31,32,33,34. In particular, tropical Pacific heat content anomalies and their driving surface winds are known to be predictors of ENSO several months ahead35,36. Therefore, different tropospheric responses to the Atlantic SST forcing during summer can also explain model differences in winter20,37. Here, we find that the winter NIÑO3.4 inter-model spread is mainly associated with the inter-model spread in descent anomalies over Central tropical Pacific during summer (R = −0.9; where R is the inter-model correlation, see “Methods”; Fig. 3b) and associated surface winds. This indicates that the inter-model spread in the winter Equatorial Pacific mainly arises from different tropospheric responses to the AMV forcing during summer. This inference is supported by the weaker inter-model correlation between winter NIÑO3.4 SST and winter Pacific descent responses (R = −0.64, not shown).

To further understand the inter-model spread, we explore the origins of the tropical Pacific tropospheric descent anomalies in summer. Figure 3c shows that those subsiding anomalies are nearly fully mass-compensated by ascendant anomalies in other tropical regions. The 20°S–20°N tropical band (TROP) is further decomposed into a broad Indian ocean domain (TropInd), the Central Pacific ocean (TropPac), and a broad Atlantic domain (TropAtl; cf. indices definition in “Methods” and Fig. 2b). Through an analysis of variance (see “Methods”), we find that only 19% of the inter-model variance in TropPac descent anomalies is associated with the inter-model variance in TropAtl ascent anomalies, but 69% with the TropInd ascent ones. These two sources of spread are consistent with the two-phase mechanism detailed in the Introduction to explain the tropical Pacific response to Atlantic warming. In particular, it is consistent with the amplification of the Pacific response through the adjustment feedback of the Indo-Pacific Walker Circulation9.

The key finding here is that there is no significant inter-model correlation between TropInd and TropAtl anomalies (R = 0.2, Fig. 3d). This indicates that models simulate different Indo-Pacific Walker Circulation adjustments (Phase-2 Indo-Pacific feedback) for similar Atlantic–Pacific atmospheric bridges (Phase-1 Atlantic forcing). Hence, this implies that the simulated feedback associated with the Indo-Pacific Walker Circulation adjustment is model-dependent and that the differences in this feedback are the source of most of the inter-model spread in the tropical Pacific response to the AMV forcing.

We find two possible mechanisms to explain the different Indo-Pacific Walker Circulation adjustments among models in the AMV experiments. As detailed below, either different TropInd ascent or different TropPac SST responses can be the original driver of the different circulation responses. Further targeted experiments would be required to determine which mechanism is dominating here. However, both mechanisms point to the temperature response of the upper tropical troposphere as the key process to understand the inter-model differences:

  • The inter-model spread in TropInd ascent anomalies is tightly connected to the tropospheric lapse rate over the Warm Pool (Fig. 3e). Indeed, the larger the lapse rate (less warming in the upper troposphere compared to the surface), the less stable the troposphere is, and the more convectively active the tropical troposphere becomes. The inter-model spread in TropInd ascent anomalies is therefore linked to different responses in the upper tropospheric warming over the Warm Pool among models (Supplementary Fig. 4a–c). Because in the tropics the upper-tropospheric temperature is constrained by wave dynamical adjustment to be nearly horizontally uniform38,39 (Supplementary Fig. 4d), it implies that the TropInd ascent responses and the Indo-Pacific Walker Circulation responses are controlled by the different upper tropospheric warming among models.

  • The different upper tropospheric warming can lead to different SST warming among models through a “top-down” mechanism by a decrease of the surface latent heat flux40. There is indeed an inter-model correlation of R = 0.86 between the TROP upper tropospheric temperature and the TropPac SST responses (Fig. 3f). This “top-down” warming effect eventually modulates the amplitude of the TropPac descent and of the Indo-Pacific Walker Circulation adjustment.

Therefore, for both the TropInd ascent and the TropPac SST mechanisms, the warmer the TROP upper troposphere is in response to an AMV warming, the weaker the Indo-Pacific feedback and the weaker the tropical wintertime Pacific cooling are. Then, in order to understand the inter-model spread in the wintertime Pacific response to AMV, one needs to understand the inter-model spread in TROP upper tropospheric temperature anomalies.

As the thermal stratification of the tropical troposphere is primarily controlled by deep convection, upper tropospheric temperature anomalies in the Tropics can be generally traced to regional variations in the atmospheric boundary layer. To investigate the origins of those anomalies we study the moist static energy at the surface, using as estimate the equivalent potential temperature41 (\(\theta _{\mathrm{E}}\); see “Methods”). In order to take into account the different contributions of highly active and less active convective regions in the injection of moist static energy from the surface to the upper troposphere, we weigh surface \(\theta _{\mathrm{E}}\) with local precipitation (Pr in mm d−1) following Sobel et al.42’s approach (see “Methods”):

$${\mathrm{P}}\theta _{\mathrm{E}} = a \times {\mathrm{Pr}} \times \theta _{\mathrm{E}}/ < a \times {\mathrm{Pr}} >$$
(1)

Where \(< . >\) symbols indicate the sum over TROP and \(a\) is the grid cell surface area. The inter-model correlation between the changes of upper tropospheric temperature and our weighted \(\theta _{\mathrm{E}}\) variable (\({\mathrm{P}}\theta _{\mathrm{E}}\)) summed over the tropical band is R = 0.96 (Fig. 4a), confirming the physical link between \({\mathrm{P}}\theta _{\mathrm{E}}\) and the upper tropospheric conditions in the tropics.

Fig. 4: Impacts of different injections of moist static energy into the upper troposphere.
figure 4

a Summer TROP temperature at 200 hPa versus the TROP surface equivalent temperature weighted by precipitation. b Summer TROP temperature at 200 hPa versus the \(\theta _{\mathrm{E}}\) anomalies component of the TropAtl surface equivalent potential temperature weighted by precipitation (\({\mathrm{P}}_{\mathrm{C}}\theta _{\mathrm{E}}\prime\)). c Multi-model mean weighted equivalent potential temperature anomalies (\({\mathrm{P}}\theta _{\mathrm{E}}\)) summed over TROP and its contributions from \(\theta _{\mathrm{E}}\) anomalies (\({\mathrm{P}}_{\mathrm{C}}\theta _{\mathrm{E}}\prime\)), precipitation anomalies (\({\mathrm{P}}\prime \theta _{{\mathrm{E}},{\mathrm{C}}}\)), and precipitation and \(\theta _{\mathrm{E}}\) anomalies covariance (\({\mathrm{P}}\prime \theta _{\mathrm{E}}\prime\)). d TROP \({\mathrm{P}}_{\mathrm{C}}\theta _{\mathrm{E}}\prime\) contributions from TropInd, TropPac, and TropAtl. On (c) and (d), the length of the vertical black lines indicates the inter-model standard deviation associated with the multi-model mean value, and R indicates the inter-model correlation of each component with the upper-tropospheric temperature shown in (a). e Spatial distribution of the \({\mathrm{P}}_{\mathrm{C}}\theta _{\mathrm{E}}\prime\) inter-model spread over TropAtl and its contributions from inter-model differences in f climatological precipitation, (g) \(\theta _{\mathrm{E}}\) response to AMV, and (h) their covariance. The dashed line defines the eastern border of the East Pacific region used in Fig. 6. The two MetUM-GOML simulations are excluded from the analyses (c), (d), (e)–(h).

Full size image

To further understand the origins of the inter-model spread, we decompose the \({\mathrm{P}}\theta _{\mathrm{E}}\) anomalies into a term linked to precipitation anomalies only, i.e., \({\mathrm{P}}^\prime \theta _{{\mathrm{E}},{\mathrm{C}}}\), a term linked to \(\theta _{\mathrm{E}}\) anomalies only, i.e., \({\mathrm{P}}_{\mathrm{C}}\theta _{\mathrm{E}}^\prime\), and a covariance term, i.e., \({\mathrm{P}}_{\mathrm{C}}^\prime \theta _{\mathrm{E}}^\prime\) (see “Methods”). We find that most of the inter-model spread in upper tropospheric temperature anomalies is coming from differences in the injection of surface moist static energy anomalies into the upper troposphere by the mean model vertical motions (the \({\mathrm{P}}_{\mathrm{C}}\theta _{\mathrm{E}}^\prime\) term; Fig. 4c). Furthermore, we find that the upper tropical troposphere warm anomalies are generated quasi-equally by anomalies occurring in the TropAtl and TropInd regions and, to a lesser extent, in TropPac (Fig. 4d). However, its inter-model spread is primarily driven by the TropAtl and TropPac sectors (black lines), with inter-model correlations between the upper troposphere temperature anomalies and \({\mathrm{P}}_{\mathrm{C}}\theta _{\mathrm{E}}^\prime\) summed over those regions equal to R = 0.96 and R = 0.87, respectively. Because the forcing is coming from the Atlantic in the present experiments, we assume that it is the spread in TropAtl \({\mathrm{P}}_{\mathrm{C}}\theta _{\mathrm{E}}^\prime\) that controls the spread in the tropical upper-tropospheric temperature and that the latter is amplified by the TropPac \({\mathrm{P}}_{\mathrm{C}}\theta _{\mathrm{E}}^\prime\) response.

In summary, the analysis of \({\mathrm{P}}\theta _{\mathrm{E}}\) indicates that the inter-model spread in the tropical upper tropospheric temperature anomalies can be explained by different injections of moist static energy from the TropAtl surface into the upper troposphere (Fig. 4b). This is eventually responsible for the modulation of the Indo-Pacific Walker Circulation feedback among models. Hence we identify two summertime variables centered over the TropAtl region that contribute to the inter-model spread in the tropical Pacific response: (1) the divergence of mass in the upper troposphere over TropAtl and (2) the injection of moist static energy anomalies from the TropAtl surface into the upper troposphere by the mean convective activity (\({\mathrm{P}}_{\mathrm{C}}\theta _{\mathrm{E}}\prime\)). Building a bi-linear regression model with those two variables as predictors (see “Methods”), we capture as much as 73% of the inter-model variance in the wintertime NIÑO3.4 SST response (Fig. 5a, b); TropAtl ascent and \({\mathrm{P}}_{\mathrm{C}}\theta _{\mathrm{E}}\prime\) accounting for 39% and 61% of the total regression model variance, respectively.

Fig. 5: Assessing the wintertime tropical Pacific response from two summertime Atlantic predictors.
figure 5

a Inter-model relationship between the wintertime NIÑO3.4 SST index and the outputs of a bi-linear regression model built with the summertime TropAtl ascent and \({\mathrm{P}}_{\mathrm{C}}\theta _{\mathrm{E}}\prime\) anomalies (see “Methods”). The linear regression between the statistical model and NIÑO3.4 is shown by the black line. b Whisker box plots indicating the minimum/maximum values, the 20th/80th percentiles, and the median from the inter-model distribution of several indices: the wintertime NIÑO3.4 SST index (black), the outputs of the regression model fed with summertime TropAtl ascent, and (blue) TropAtl \({\mathrm{P}}_{\mathrm{C}}\theta _{\mathrm{E}}\prime\), (red) TropAtl \({\mathrm{P}}_{{\mathrm{Obs}}}\theta _{\mathrm{E}}\prime\) (i.e., \({\mathrm{P}}_{\mathrm{C}}\theta _{\mathrm{E}}\prime\) computed using observed precipitation climatology), and (green) TropAtl \({\mathrm{P}}_{{\mathrm{Obs}}}\theta _{{\mathrm{E}},{\mathrm{cor}}}^\prime\) (i.e., \({\mathrm{P}}_{{\mathrm{Obs}}}\theta _{\mathrm{E}}\prime\) corrected for precipitation climatological biases over the East Pacific in late winter). The two latter box plots account for uncertainties coming from observation estimates (see “Methods”).

Full size image

Bias corrections and reduction of the uncertainty

Next, we investigate the origins of the model response differences over TropAtl aiming at narrowing the uncertainty of our numerical estimate of the tropical Pacific response to the observed AMV forcing. We start by decomposing further the \({\mathrm{P}}_{\mathrm{C}}\theta _{\mathrm{E}}\prime\) variable over the TropAtl region to evaluate whether its inter-model spread is coming from differences among models in climatological precipitation (\({\mathrm{P}}_{\mathrm{C}}^ \ast \left[ {\theta _{\mathrm{E}}^\prime } \right]\)), \(\theta _E\) anomalies (\(\left[ {{\mathrm{P}}_{\mathrm{C}}} \right]\theta _{\mathrm{E}}^{\prime \ast }\)), or a combination of both (\({\mathrm{COV}}\); see “Methods”). We find that all terms contribute to the inter-model spread, but that their respective importance is spatially dependent (Fig. 4e–h). Of particular interest, this analysis demonstrates that different climatological precipitation among models (Fig. 4f) is partly responsible for the inter-model spread.

Because the model climatological precipitations are biased relative to observations, it implies that the simulated \({\mathrm{P}}_{\mathrm{C}}\theta _{\mathrm{E}}\prime\) are also biased, which leads to erroneous estimates of the response to the observed AMV forcing. To minimize this error, we apply a bias correction to the \({\mathrm{P}}_{\mathrm{C}}\theta _{\mathrm{E}}\prime\) of each model by computing them using the observed climatological precipitation instead of model one: \({\mathrm{P}}_{{\mathrm{Obs}}}\theta _{\mathrm{E}}\prime\). This suppresses the spread of \({\mathrm{P}}_{\mathrm{C}}^ \ast \left[ {\theta _{\mathrm{E}}^\prime } \right]\) but it introduces a new source of spread coming from observational uncertainties (see “Methods”). This bias correction decreases overall the inter-model variance of \({\mathrm{P}}_{\mathrm{C}}\theta _{\mathrm{E}}\prime\) over TropAtl by 58%. Feeding our bi-linear NIÑO3.4 regression model with \({\mathrm{P}}_{{\mathrm{Obs}}}\theta _{\mathrm{E}}\prime\) instead of \({\mathrm{P}}_{\mathrm{C}}\theta _{\mathrm{E}}\prime\), we quantify that correcting for model mean precipitation biases helps to reduce the inter-model response variance over the tropical Pacific by 35% (Fig. 5b).

Over the eastern Pacific (i.e., the western part of the wide TropAtl sector as shown in Fig. 4g), it is mainly the different \(\theta _{\mathrm{E}}\) responses among models that drive the inter-model spread in \({\mathrm{P}}_{\mathrm{C}}\theta _{\mathrm{E}}\prime\) and, a fortiori, in \({\mathrm{P}}_{{\mathrm{Obs}}}\theta _{\mathrm{E}}\prime\) (Fig. 4g, see also Supplementary Fig. 11). \(\theta _{\mathrm{E}}\) anomalies there are largely associated with surface temperature changes but their sign and amplitude are model-dependent (Supplementary Fig. 9), leading to compensating anomalies in the MMM (Fig. 2b). In the following, we demonstrate that the spread in \({\mathrm{P}}_{{\mathrm{Obs}}}\theta _{\mathrm{E}}\prime\) over the eastern Pacific is explained by the different model climatological precipitations during February–March–April (Fig. 6g, h).

Fig. 6: Impacts of the tropical East Pacific ITCZ mean biases.
figure 6

a–f Monthly evolution of the differences between AMV+ and AMV− ensemble means zonally averaged over the East Pacific region (i.e., the western part of TropAtl) shown in (g) for the multi-model means between the five models simulating the northernmost climatological position of the ITCZ during February–March–April over East Pacific (Group 1: ECMWF-HR, IPSL-CM6, HadGEM3, ECMWF-LR, CESM1) and the southernmost (Group 2: EC-Earth3, CNRM-CM6, CNRM-CM5, EC-Earth3P, CMCC), cf. x-axis in (h). a–f show the differences in terms of SST, precipitation, and net surface fluxes, respectively (surface fluxes are defined as positive from the atmosphere to the ocean). Arrows in (e) and (f) represent the surface wind anomalies. In (a)–(g), contours indicate the climatological precipitation and stippling means that not all models in the group agree on the sign of the anomalies. Months are indicated by their first letter and a 3-month running mean is applied. g Inter-model map regression of the climatological precipitation on the \({\mathrm{P}}_{{\mathrm{Obs}}}\theta _{\mathrm{E}}^{\prime \ast }\) index (shading; units: mm d-1 per inter-model standard deviation of \({\mathrm{P}}_{{\mathrm{Obs}}}\theta _{\mathrm{E}}^{\prime \ast }\)) and multi-model mean climatological precipitation (contours; units: mm d-1). \({\mathrm{P}}_{{\mathrm{Obs}}}\theta _{\mathrm{E}}^{\prime \ast }\) was computed from five observation estimates and only their averaged regression is shown here (see “Methods”). h Inter-model relationship between summertime \({\mathrm{P}}_{{\mathrm{Obs}}}\theta _{\mathrm{E}}^{\prime \ast }\) summed over East Pacific and the late winter centroid of the climatological precipitation over East Pacific, defined as the latitude at which there is the same amount of zonally averaged precipitation North and South. The linear regression between the two indices is shown by the black line. Only the averaged values computed from the five \({\mathrm{P}}_{{\mathrm{Obs}}}\theta _{\mathrm{E}}^{\prime \ast }\) obtained from the different observation estimates are shown here. The vertical green solid lines indicate the precipitation centroids from the observation estimates and the horizontal green dashed lines reveal the \({\mathrm{P}}_{{\mathrm{Obs}}}\theta _{\mathrm{E}}^{\prime \ast }\) values associated with these observed centroids, assuming the same statistical relationship as the inter-model one. R indicates the inter-model correlation averaged over the five estimates of \({\mathrm{P}}_{{\mathrm{Obs}}}\theta _{\mathrm{E}}^{\prime \ast }\). The MetUM-GOML simulations are excluded from all the analyses of this figure.

Full size image

During summer, all models simulate westerly anomalies north of 5°N associated with a northward shift of the Inter-tropical Convergence Zone (ITCZ) over the East Pacific in response to the AMV warming (Fig. 6c–f). Yet, by dividing the models into two sub-groups based on the state of their late winter climatological precipitation, we show that this shift is more pronounced for the models simulating a more northward position of the climatological ITCZ in late winter. Those models simulate an SST cooling around 7°N on the southern flank of the ITCZ in summer (Fig. 6a, b), where the other models simulate warming, which explains the inter-model spread in \({\mathrm{P}}_{{\mathrm{Obs}}}\theta _{\mathrm{E}}\prime\). For the models with the largest ITCZ shift, we find that the westerly anomalies follow the seasonal migration of the precipitation anomalies; those are present north of the Equator since the winter when their cooling effect on the ocean is greatest (Fig. 6c, e). This suggests that preconditioning of the summertime cooling around 7°N during previous seasons occurs through feedback between ITCZ position, SST, wind, and surface flux anomalies43. Yet, all models tend to simulate a northward shift of the ITCZ in winter (Fig. 6c, d) but only some of them simulate such preconditioning. This inter-model disagreement is coming from different model climatological precipitation in late winter. For models simulating an ITCZ located north of the Equator, the northward shift of the ITCZ increases the mean south-westerlies and their associated turbulent heat fluxes around the Equator, which tends to cool locally the SST. On the other hand, for models simulating an ITCZ located South of the Equator, the northward shift of the ITCZ weakens the mean north-easterlies and their cooling effect on the equatorial SST.

Given the high correlation between the climatological precipitation in February–March–April and the summertime \({\mathrm{P}}_{{\mathrm{Obs}}}\theta _{\mathrm{E}}\prime\) response over East Pacific (R = −0.87; Fig. 6h), we use this information to further correct our estimate of the Tropical Pacific response to AMV. Associated with the observed February–March–April climatological precipitations, we estimate summertime East Pacific \(P_{{\mathrm{Obs}}}\theta _{\mathrm{E}}\prime\) values ranging from −0.09 °C and −0.13 °C (cf. green lines in Fig. 6h). Substituting these \({\mathrm{P}}_{{\mathrm{Obs}}}\theta _{\mathrm{E}}\prime\) values for each model to the contribution of the East Pacific into the TropAtl \({\mathrm{P}}_{{\mathrm{Obs}}}\theta _{\mathrm{E}}\prime\), we obtain TropAtl \({\mathrm{P}}_{{\mathrm{Obs}}}\theta _{{\mathrm{E}},{\mathrm{cor}}}^\prime\) that we consider as our best estimate of the \({\mathrm{P}}_{\mathrm{C}}\theta _{\mathrm{E}}\prime\) response to the observed AMV forcing (see “Methods”). Feeding our bi-linear regression model with \({\mathrm{P}}_{{\mathrm{Obs}}}\theta _{{\mathrm{E}},{\mathrm{cor}}}^\prime\) instead of \({\mathrm{P}}_{\mathrm{C}}\theta _{\mathrm{E}}\prime\), we quantify that correcting both summertime and late winter precipitation mean biases reduces by 65% the inter-model variance in our analytical estimate of the NIÑO3.4 response (Fig. 5b).

We also investigated the potential origin of the inter-model spread over Atlantic–Africa (i.e., the eastern part of the TropAtl region, cf. Fig. 4e–h). We found that the inter-model spread in \(\left[ {{\mathrm{P}}_{\mathrm{C}}} \right]\theta _{\mathrm{E}}^{\prime \ast }\) anomalies is associated with different signs in the SST and specific surface humidity responses around the eastern equatorial Atlantic (Supplementary Figs. 3 and 4). However, we did not identify the physical processes controlling the different model behaviors (cf. Supplementary Discussion).

Discussion

Using 21 coordinated simulations from 13 different CGCMs, we show that:

  • In response to an AMV warming, all models simulate tropical Pacific changes reminiscent of La Niña conditions. This result confirms the influence of the Atlantic on climate variability at the global scale and it supports the idea that the AMV has contributed to the 1998–2012 global warming slowdown through its impacts on the tropical Pacific. However, the strength of the connection varies by a factor of 10 between the models.

  • The tropical Pacific response to the Atlantic forcing is driven by changes in (1) the Atlantic–Pacific Walker Circulation and (2) the amount of moist static energy injected from the Atlantic surface into the upper troposphere.

  • The latter is responsible for most of the uncertainty in our current numerical model estimates of the Pacific response to the observed AMV, mainly because of different mean precipitation climatology.

Partially correcting for mean model precipitation biases, we reduce this uncertainty and we specifically quantified that the NIÑO3.4 response to an observed 0.26 °C AMV warming ranges from −0.05 °C to −0.16 °C with a median value of −0.11 °C and an inter-model standard deviation of 0.03 °C. We acknowledge that this estimate is still subject to model limitations. In particular, we reduce uncertainty by correcting a posteriori for model precipitation biases. Any possible interactions between those biases and surface equivalent potential temperature responses to AMV would still affect our estimate. Therefore, our analysis highlights the importance of reducing mean climate model biases in order to properly simulate and predict the global AMV impacts.

Although this study focuses on decadal timescales signals, the discussed mechanisms take place at monthly timescales. Our study shows then the potential for improving climate predictions from seasonal to decadal timescales through a better representation of the impacts of the Atlantic on tropical Pacific28,29,44. The discussed mechanisms very likely also act to shape the Pacific mean state and their differences among models45,46,47, which are partly responsible for the inter-model spread in climate projections48. Based on our findings, we suggest that the analysis of the injection into the upper troposphere of moist static energy from the Atlantic surface can be used as an interpretative framework to understand the inter-model uncertainties around future climate simulations.

Finally, we note that several observational and model-based studies49,50,51 suggest the existence of a two-way interaction between Atlantic and Pacific at decadal timescale: an AMV warming driving a Pacific cooling, which eventually drives an Atlantic cooling. Due to the experimental protocol used in the present article, we could only focus on the representation by models of the Atlantic impacts on the Pacific. To persist in exploring the sources of climate predictability at multi-annual timescale and their current limits due to model uncertainty, a similar multi-model study to this one should be completed but investigating the Pacific impacts on the Atlantic.

Methods

Experiments

The 21 experiments from 13 different CGCMs used in this study are listed in Supplementary Tables 1 and 2; it represents a total of 12,320 simulated years. Following the DCPP-C protocol23, two sets of ensemble simulations have been performed for each experiment, in which time-invariant SST anomalies corresponding to the warm (AMV+) and cold (AMV−) phases of the observed AMV were imposed over the North Atlantic using SST nudging. To capture the potential response and adjustment of other oceanic basins to the AMV anomalies, the simulations were integrated for 10 years with fixed external forcing conditions. Large ensemble simulations were performed in order to robustly estimate the climate impacts of the AMV (from 10 to 50 members depending on the model, cf. Supplementary Table 2). An extensive description of the experimental protocol is provided in the Technical note for AMV DCPP-C simulations: https://www.wcrp-climate.org/wgsip/documents/Tech-Note-1.pdf.

Over the North Atlantic (Equator-65°N/80°W–0°), the spatial correlation of the SST anomalies in each simulation and the observed AMV target varies between 0.66 and 0.86, with a multi-model average value of 0.79, indicating that all simulations are constrained by similar SST conditions in the North Atlantic. We note that the idealized AMV simulations underestimate by ~20% the amplitude of the observed AMV target. This is because we do not impose a very strong nudging in the experimental protocol to allow ocean-atmosphere coupling and variability at high frequency (as recommended by the CMIP6/DCPP-C protocol23), which tends to dissipate the heat anomalies imposed at the surface. Further evaluation of the experimental protocol is provided in Supplementary.

Some simulations deviate from the AMV DCPP-C protocol. CESM1 simulations used an observed AMV pattern computed from the ERSSTv3b dataset52 instead of ERSSTv453. CNRM-CM6-1-HR, EC-Earth3P-HR, EC-Earth3P-LR, ECMWF-IFS-HR, and ECMWF-IFS-LR used a constant 1950 or 1990 (instead of 1850) external forcing background (cf. Supplementary Table 2). The impact of the external forcing background on the results is tested with the CNRM-CM5 models for which AMV simulations have been performed with both 1850 and 1990 backgrounds. We did not find evidence for the impact of the protocol differences on the results discussed in this article. In addition, the MetUM-GOML-HR and MetUM-GOML-LR simulations used a 1000-m mixed-layer ocean model and 1990 external forcing background. Those models offer insights on the role played by the ocean dynamics in the documented climate responses when compared to the models with full ocean dynamics.

Finally, the imposed AMV forcing strength is not the same for all simulations. As detailed in the column “AMV strength” of Supplementary Table 2, the imposed AMV anomalies vary between 1, 2, and 3 times the observed AMV standard deviation. Assuming linearity in the AMV responses, we weight each simulation by dividing their output by the AMV forcing strength in order to compare the results from all the AMV experiments. This is done for all the figures in the article. This enables us to create a larger multi-model ensemble and to evaluate more precisely the origins of the inter-model spread. Scaled outputs from experiments performed with the same model but with different AMV strengths are often indistinguishable, which suggests that the linear assumption is a reasonable approximation for the analyses of this study. Yet, we highlight the different AMV strengths by different colors in the figures (1×AMV: blue; 2×AMV: orange; 3×AMV: magenta).

MMM and inter-model correlations (R)

The MMM is computed by averaging the ensemble mean of each simulation, regardless of the number of ensemble members (i.e, there is no weighting). The outputs of each simulation are scaled by their AMV strength forcing prior to computing the MMM (as described above). For models for which several sets of experiments have been performed (with different magnitudes of AMV anomalies and/or different external forcing backgrounds), we average all the experiments of each model together prior to computing the MMM in order to not bias the results toward an over-represented model (e.g., CNRM-CM5 or EC-Earth3P). Because of the absence of ocean dynamics in the two MetUM-GOML models, those models are not taken into account in the computation of the MMM.

Similarly to the computation of the MMM, the inter-model correlation R is computed after averaging all the ensemble means from the same model (if more than one experiment was performed) in order to give the same weight to all models. We also computed the inter-model correlation based on all the ensemble means from all the simulations (i.e., no averaging of experiments from the same model prior to the computation of the correlation) but no significant differences between the two correlations were found for the relationship investigated in this article. Because of the absence of ocean dynamics in the two MetUM-GOML models, those models are not taken into account in the computation of inter-model correlations.

Regions definition

To assess the tropical Pacific response, we use the NIÑO3.4 index defined as the SST averaged over 5°S–5°N and 170°W–120°W (Fig. 2a). Based on the summer MMM anomalies of precipitation and vertical velocity at 500hPa (Supplementary Fig. 3e, f), we decomposed the 20°S–20°N tropical band (TROP) into three main regions: a broad Indian region spanning from 30°E to 135°E, a central Pacific region spanning from 135°E to 120°W, and a broad Atlantic region spanning from 120°W to 30°E (Fig. 2b). We label those regions TropInd, TropPac, and TropAtl, respectively. In addition, an East Pacific and an Atlantic–Africa regions (embedded into TropAtl) are used in Figs. 4 and 6 that cover 120°W–80°W/20°S–20°N and 80°W–30°E/20°S–20°N, respectively.

Analysis of variance

Taking advantage of the quasi-mass compensation of the vertical motion in the TROP region (Fig. 3c), we estimate the origins of the inter-model spread in TropPac descent through an analysis of variance: \(S_{{\mathrm{TropPac}}}^2 \sim S_{{\mathrm{TropAtl}} + {\mathrm{TropInd}}}^2 = S_{{\mathrm{TropAtl}}}^2 + S_{{\mathrm{TropInd}}}^2 + {\mathrm{COV}}\), where \(S_{{\mathrm{TropPac}}}^2\), \(S_{{\mathrm{TropAtl}}}^2\) and \(S_{T{\mathrm{ropInd}}}^2\) are the inter-model variance in TropPac, TropAtl, and TropInd descent anomalies, respectively; \({\mathrm{COV}}\) is the covariance term between TropAtl and TropInd descent anomalies and \(S_{{\mathrm{TropAtl}} + {\mathrm{TropInd}}}^2\)is the inter-model variance of descent anomalies averaged over the whole Trop region excluding the TropPac region. We find that \(S_{{\mathrm{TropAtl}}}^2\), \(S_{{\mathrm{TropInd}}}^2\) and COV explains 19%, 69%, and 12% of \(S_{{\mathrm{TropAtl}} + {\mathrm{TropInd}}}^2\), respectively.

Equivalent potential temperature \(\theta _{\mathbf{E}}\)

Theoretically, the equivalent potential temperature can be defined as \(\theta _{\mathrm{E}}\sim \theta exp\left( {\frac{{L_{\mathrm{C}}q_{\mathrm{S}}}}{{C_PT}}} \right)\), where \(\theta\) is the dry potential temperature, \(L_{\mathrm{C}}\) is the latent heat of condensation, \(q_{\mathrm{S}}\) is the saturation of mixing ratio, \(C_{\mathrm{P}}\) is the specific heat of dry air, and \(T\) is the temperature. This formula explicitly shows that \(\theta _{\mathrm{E}}\) is similar to the potential temperature for dry air mass (which remains constant during adiabatic processes) but it corrects for the energy associated with the air mass moisture, assuming that all the energy released by condensation/evaporation remains in the air mass (pseudo-adiabatic process). Here we used the NCL function “pot_temp_equiv_tlcl” (https://www.ncl.ucar.edu/Document/Functions/Contributed/pot_temp_equiv_tlcl.shtml) to compute \(\theta _E\). This function is based on Eq. (39) from Bolton54, which gives more accurate results than the theoretical formula given above but that requires the computation of the temperature at the lifted condensation level. Such temperature is estimated with the NCL function “tlcl_rh_bolton” (https://www.ncl.ucar.edu/Document/Functions/Contributed/tlcl_rh_bolton.shtml), which is based on Eq. (22) from Bolton54.

Weighted equivalent potential temperature \({\mathbf{P}}\theta _{\mathbf{E}}\) as a proxy for the upper-tropospheric temperature

Over the oceans, the mean tropospheric temperature profile is often considered to be in a moist-adiabatic convective equilibrium with the mean SST55 (Supplementary Fig. 4f), as the SST controls directly the atmospheric boundary layer energy content. Yet, convective adjustment can act directly only in regions of frequent precipitation, which are mostly over warm SST regions. In regions of no convection, the surface has no direct means of influencing the free troposphere, and the SST anomalies cannot shape the tropospheric temperature profile. Hence, there is no evident physical reason for considering mean tropical SST variations as a proxy for upper tropospheric temperature anomalies. To take into account the different contributions of local SST to the upper-tropospheric temperature, Sobel et al. 42 introduced a more appropriate proxy by weighting the SST with the local precipitation before computing the tropical average. We follow this method here, but we generalize it in order to account for the effect of deep convection overland on the upper tropospheric temperature anomalies56 and we compute the precipitation weighted equivalent potential temperature \({\mathrm{P}}\theta _{\mathrm{E}}\), cf. Eq. (1).

Notation

We note \(<\, f \,>\) as the sum of the values of a given field \(f\) for all tropical grid points within 20°S–20°N. We define \(f = f_{\mathrm{C}} + f\prime\), where \(f\prime\) is the departure of \(f\) from \(f_{\mathrm{C}}\), which is the time-averaged ensemble mean of the AMV- experiments (the AMV- experiment being considered as the reference state). We also define \(= \left[ f \right] + f^ \ast\), where \(f^ \ast\) is the departure of \(f\) from its multi-model mean \(\left[ f \right]\).

Decompositions of \({\mathbf{P}}\theta _{\mathbf{E}}\)

In the article, \({\mathrm{P}}\theta _{\mathrm{E}} = \frac{{a \times {\mathrm{Pr}} \times \theta _{\mathrm{E}}}}{{ < a \times {\mathrm{Pr}} > }}\) is first decomposed into a term linked to precipitation anomalies only \({\mathrm{P}}\prime \theta _{{\mathrm{E}},{\mathrm{C}}} = \frac{{a \times {\mathrm{Pr}}\prime \times \theta _{{\mathrm{E}},{\mathrm{C}}}}}{{ < a \times {\mathrm{Pr}}\prime > }} - \frac{{a \times {\mathrm{Pr}} \times \theta _{\mathrm{E}}}}{{ < a \times {\mathrm{Pr}} > }} \times \frac{{a \times {\mathrm{Pr}} \times \theta _{\mathrm{E}} \times {\mathrm{Pr}}\prime }}{{ < a \times {\mathrm{Pr}} > }}\), a term linked to \(\theta _{\mathrm{E}}\) anomalies only \({\mathrm{P}}_{\mathrm{C}}\theta _{\mathrm{E}}\prime = \frac{{a \times {\mathrm{Pr}}_{\mathrm{C}} \times \theta _{\mathrm{E}}\prime }}{{ < a \times {\mathrm{Pr}}_{\mathrm{C}} > }}\), and a covariance term \({\mathrm{P}}\prime \theta _{\mathrm{E}}\prime = \frac{{a \times {\mathrm{Pr}}\prime \times \theta _{\mathrm{E}}\prime }}{{ < a \times {\mathrm{Pr}}\prime > }}\). In a second time \({\mathrm{P}}_{\mathrm{C}}\theta _{\mathrm{E}}\prime\) is decomposed into a term linked to the climatological precipitation differences among models \({\mathrm{P}}_{\mathrm{C}}^ \ast \left[ {\theta _{\mathrm{E}}^\prime } \right] = \frac{{a \times {\mathrm{Pr}}_{\mathrm{C}}^ \ast \times \left[ {\theta _{\mathrm{E}}\prime } \right]}}{{ < a \times {\mathrm{Pr}}_{\mathrm{C}}^ \ast > }}\), a term link to the different \(\theta _{\mathrm{E}}\) response to AMV among models \(\left[ {P_{\mathrm{C}}} \right]\theta _{\mathrm{E}}^{\prime \ast } = \frac{{a \times \left[ {{\mathrm{Pr}}_{\mathrm{C}}} \right] \times \theta _{\mathrm{E}}^{\prime \ast }}}{{ < a \times \left[ {{\mathrm{Pr}}_{\mathrm{C}}} \right] > }}\), and a covariance term \({\mathrm{COV}} = \frac{{a \times {\mathrm{Pr}}_{\mathrm{C}}^ \ast \times \theta _{\mathrm{E}}^{\prime \ast }}}{{ < a \times {\mathrm{Pr}}_{\mathrm{C}}^ \ast > }}\).

Bi-linear regression model

The coefficient of the bi-linear regression model is computed using as predicand the wintertime NIÑO3.4 SST index and as the two predictors the summertime vertical ascent summed over TropAtl and the summertime \({\mathrm{P}}_{\mathrm{C}}\theta _{\mathrm{E}}\prime\) summed over TropAtl. The two MetUM-GOML simulations are excluded from the computation of the regression model coefficients and, similarly, as for the inter-model correlation, all models share the same weight.

Bias corrections and observational uncertainties

Two bias corrections are applied to \({\mathrm{P}}_{\mathrm{C}}\theta _{\mathrm{E}}\prime\). First, we compute this variable by using observed climatological precipitation (\({\mathrm{Pr}}_{{\mathrm{Obs}}}\)) instead of model climatological precipitation: \({\mathrm{P}}_{{\mathrm{Obs}}}\theta _{\mathrm{E}}\prime = \frac{{a \times {\mathrm{Pr}}_{{\mathrm{Obs}}} \times \theta _{\mathrm{E}}\prime }}{{ < a \times {\mathrm{Pr}}_{{\mathrm{Obs}}} > }}\). Then, we decomposed the TropAtl \({\mathrm{P}}_{{\mathrm{Obs}}}\theta _{\mathrm{E}}\prime\) into its regional components coming from the Atlantic–Africa region, the East Pacific region, and their covariance term. The East Pacific component is then substituted by a value estimated from the observed climatological precipitation and the inter-model relationship between JJAS East Pacific \({\mathrm{P}}_{{\mathrm{Obs}}}\theta _{\mathrm{E}}\prime\) and February–March–April climatological precipitation centroid over East Pacific (Fig. 6h). Following this substitution, we sum again the different components of TropAtl \({\mathrm{P}}_{{\mathrm{Obs}}}\theta _{\mathrm{E}}\prime\)to obtain \({\mathrm{P}}_{{\mathrm{Obs}}}\theta _{{\mathrm{E}},{\mathrm{cor}}}^\prime\). In order to account for observational uncertainties57,58, we compute for each model five \({\mathrm{P}}_{{\mathrm{Obs}}}\theta _{\mathrm{E}}\prime\)and \({\mathrm{P}}_{{\mathrm{Obs}}}\theta _{{\mathrm{E}},{\mathrm{cor}}}^\prime\) values using different observation estimates.

Observational and reanalysis datasets

The SST from the ERSSTv453 and ERSSTv3 datasets52 were used to extract the observed AMV pattern imposed in the simulations. The HadCRUT459 data set was used to compute the observed AMV composites shown in Fig. 1c. CMAP60,61, GPCPv2.362, TRMMv7 at 0.5° of spatial resolution63,64, MSWEPv2.665, and ERA-Interim66 data sets were used for mean bias corrections of model precipitation (cf. Figs. 5 and 6). Depending on data availability, we used different periods to compute the observed estimate mean state: 1979-2017 for CMAP, GPCPv2.3, and MSWEPv2.6; 1998-2011 for TRMMv7; and 1979–2018 for ERA-Interim.