Abstract
Arctic sea-ice loss is a consequence of anthropogenic global warming and can itself be a driver of climate change in the Arctic and at lower latitudes, with sea-ice minima likely favoring extreme events over Europe and North America. Yet the role that the sea-ice plays in ongoing climate change remains uncertain, partly due to a limited understanding of whether and how the exact geographical distribution of sea-ice loss impacts climate. Here we demonstrate that the climate response to sea-ice loss can vary widely depending on the pattern of sea-ice change, and show that this is due to the presence of an atmospheric feedback mechanism that amplifies the local and remote signals when broader scale sea-ice loss occurs. Our study thus highlights the need to better constrain the spatial pattern of future sea-ice when assessing its impacts on the climate in the Arctic and beyond.
Similar content being viewed by others
Introduction
Satellite records show that Arctic sea-ice has been rapidly retreating since the mid 1990s1, and climate models predict that sea-ice cover will continue to shrink in most regions of the Arctic basin and could even disappear in summer in the coming decades2. Climate models and our theoretical understanding of the climate system further suggest that drastic changes in sea-ice cover may trigger local and remote climate responses via changes in atmospheric and oceanic circulation3,4. For instance, winter cold snaps over Southern Europe and North America, warm spells over Northern Europe, and dry spells in Central Europe could have been caused or favored by record low Arctic sea-ice cover in recent years5,6,7,8,9. Yet the importance of those changes when compared to natural variability or the direct effect of increased radiative forcings remains unclear10.
The contribution of regional sea-ice loss to changing climate conditions, both within and far away from the Arctic, is a topic of active research11,12. A number of studies have found that the climate response to sea-ice loss is dependent on both the location and amplitude of sea-ice cover anomalies12,13,14,15,16. Depending on where it occurs, sea-ice loss can have diametrically opposite effects on important features of the atmospheric circulation, such as the sea-level pressure (SLP)12,17,18. Moreover, whether the response in the Atlantic sector and over Europe is more akin to the negative or positive phase of the North Atlantic oscillation remains controversial19. What causes such disparate responses to sea-ice loss among modeling studies remains unclear, as the large variety of model configurations has made it nearly impossible to firmly establish common causes. Furthermore, a unified mechanistic understanding of the reasons behind these different climate responses to regional sea-ice loss is lacking, hampering our ability to determine whether the divergent response among studies is a consequence of modeling-related uncertainties or an intrinsic property of the response.
Here we perform and analyze a set of climate model experiments to systematically quantify and understand the atmospheric responses to regional sea-ice loss in the Arctic. Using an atmospheric general circulation model, EC-Earth320, we run a suite of atmosphere-only regional experiments with sea-ice concentration (SIC) and sea surface temperature (SST) prescribed to their present-day state everywhere, except over specific regions in the Arctic where an end-of-century distribution of SIC and SST is prescribed (see Supplementary Table 1 for the experiment list, Fig. 1a for the regional masks and Fig. 1b for the SIC pattern). Following the Polar Amplification Multimodel Intercomparison Project (PAMIP) protocol aimed at investigating the atmospheric response to regional Arctic sea-ice forcing21, each experiment is composed of 150 members to allow for a robust climate signal to emerge; each member is run for 1 year starting on June 1st using fixed radiative forcing corresponding to the year 2000 (see “Methods” for further details).
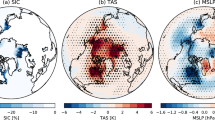
a Predefined regions over which monthly mean SIC and SST are changed to their late 21st anomalies, as predicted from an ensemble of CMIP5 simulations of a “business-as-usual” global warming scenario: Central Arctic (black), Barents–Kara seas (red), Irminger–Nordic seas (yellow), Hudson–Baffin Bays and Labrador sea (magenta), Beaufort–East Siberian–Laptev seas (green), Bering–Chukchi seas (blue), and Okhotsk sea (cyan). b Arctic sea-ice concentration (SIC) anomalies for winter (DJF) season in a 21st century, warm climate state (+2 °C from preindustrial global-mean surface temperature) derived from an ensemble of RCP8.5 CMIP5 experiments with respect to its observed 1980–2014 climatology (see “Method” for experimental protocol). c Anomalies in surface enthalpy flux, d 2-m temperature, e precipitation, and f sea-level pressure in the pan-Arctic sea-ice loss experiment. Dotted areas indicate regions where the sign of the anomalies agrees in at least 95% of the 1000 bootstrapped samples.
Using this suite of atmosphere-only regional sea-ice loss experiments, the climate response from various scenarios of regional sea-ice loss is assessed and compared to that from extensive sea-ice loss scenarios, including a pan-Arctic-sea-ice loss scenario. We focus on the tropospheric circulation response to winter sea-ice loss (December to February, DJF), that is when sea-ice loss has its strongest impact on the surface climate and tropospheric circulation11,17. Our results confirm the seemingly inconsistent climate response to sea-ice change, depending on its pattern and extent, and we attribute this behavior to a zonal-mean atmospheric circulation feedback.
Results
Surface climate response to pan-Arctic sea-ice loss
The projected pattern of sea-ice loss in winter used to force our experiments shows nearly ice-free conditions in the marginal seas that surrounds the Central Arctic, while sea-ice over the Central Arctic is mostly preserved to its present state (Fig. 1b). Positive anomalies in the net surface enthalpy flux are found over regions of sea-ice loss (Fig. 1c), consistent with an ice-free ocean warming the atmosphere in winter (here, the term anomaly will refer to the difference between the mean climate in the future and present-day experiments). Accordingly, the near-surface temperature shows localized increases of up to 10 °C over the areas of sea-ice loss (Fig. 1d).
Anomalies in SLP and precipitation suggest that sea-ice loss impacts locally the tropospheric circulation: increased precipitation over regions of sea-ice loss (Fig. 1e), directly driven by local surface enthalpy flux anomalies, is likely to induce regional updraft. Planetary teleconnections are also apparent from precipitation anomalies found in the midlatitudes and subtropical regions, in the form of anomalous stationary Rossby waves. Those are clearly outlined by the SLP anomalies, revealing at least two wave trains propagating around the polar regions and into the midlatitudes (Fig. 1f), with negative SLP anomalies found over the Okhotsk sea, the Bering Strait, the Hudson Bay, and positive SLP anomalies over the Nordic seas, Eastern Siberia, and California. In particular, the SLP high and associated precipitation reduction near California agree with recent studies predicting California to become drier in response to sea-ice loss22,23,24; yet, unlike those studies, our climate model lacks an interactive ocean and thus California winter precipitation anomalies seen in our simulations are a result of a purely atmospheric teleconnection. Positive precipitation anomalies are also found over the west coast of the Iberian peninsula (Fig. 1e), suggesting that in the midlatitudes the sign of precipitation anomalies depends on the region of sea-ice loss. This is in accordance with the phase of the Rossby wave train found there.
Tropospheric response to different sea-ice loss scenarios
To understand how the tropospheric circulation may respond to sea-ice loss, we first analyze geopotential height (GPH; see “Methods”). When evaluated at 500 hPa, GPH in the pan-Arctic experiment shows a prominent positive anomaly over the whole polar region (Fig. 2a). This pattern can be compared to the aggregated response from regional sea-ice loss, which we obtain by adding synthetically together the climate anomalies from all nonoverlapping regional experiments. Comparing climate anomalies between the pan-Arctic experiment and the aggregation of regional sea-ice loss experiments allows us to assess whether the climate response to a pan-Arctic sea-ice loss scenario can be understood as a superposition (or aggregation) of climate responses to sea-ice loss over different nonoverlapping areas. Indeed, sea-ice loss is rarely confined to one specific region of the Arctic, but rather occurs simultaneously across different regions. Hence, a comparison of various combinations of regional sea-ice loss scenarios (including the pan-Arctic sea-ice loss scenario) provides a simple way to determine whether the climatic footprint due to sea-ice loss over one area of the Arctic (as established from the relevant regional experiment) remains detectable in the presence of climate anomalies from other areas of sea-ice loss. We find that this is not the case, as the aggregated response (Fig. 2b) is profoundly different from that of the pan-Arctic experiment (Fig. 2a), the first indication that the climate response can differ dramatically between different sea-ice loss scenarios.
DJF anomalies in the future Arctic experiment (upper row) and the aggregated contributions from all future regional experiments (lower row) for: a, b the geopotential height (GPH) at 500 hPa, c, d the stationary (zonally asymmetric) component of the GPH at 500 hPa, e, f the zonal-mean component of the GPH. Anomalies (shown in colors) are computed as the difference between the future experiments and the present-day experiment climatologies. Black contours show the corresponding present-day climatologies (solid lines correspond to 5000, 5250, 5500, and 5750-m levels in (a, b); 50 and 100-m levels in (c, d) and 2000-m increments in (e, f); dashed lines represent −100 and −50-m levels in (c, d)). The stationary component in (c, d) is defined by subtracting the zonal-mean from the total anomalies. The zonal-mean panels (e, f) are pressure level [hPa]–latitude [deg] cross-sections. Dotted areas indicate regions where the sign of the anomalies agrees in at least 95% of the 1000 bootstrapped samples.
To understand why this response is different, the GPH anomaly is separated into a zonally asymmetric (Fig. 2c, d) and a zonally symmetric component (Fig. 2e, f), i.e., its stationary and zonal-mean components, respectively (see “Methods”). The stationary component shows qualitative similarities between the pan-Arctic and the aggregated response (Fig. 2c, d), such as the wave train in the Pacific sector presenting a succession of positive and negative anomalies similar to that found for the SLP (Fig. 1c). This response is comparable to what has been found in past studies using similar sea-ice loss patterns25. An investigation of the GPH500 anomalies in the regional experiments suggests that sea-ice loss in all individual regions can excite wave train responses of length scales typical of stationary Rossby waves, with significant anomalies emerging from most sectors of sea-ice loss (Supplementary Fig. 1). The zonal-mean response to pan-Arctic-sea-ice loss, on the other hand, is dominated by a positive GPH anomaly over the Arctic, a feature that is not found in any of the regional experiments: unlike for the stationary component, the pan-Arctic and the aggregated regional experiments share no common qualitative feature in their zonal-mean GPH anomaly (Fig. 2e, f).
This difference between the pan-Arctic and regional experiments is consistent with the lower troposphere over the Arctic being much warmer in the pan-Arctic than in any of the regional experiments, as is evidently clear when comparing their zonal-mean temperature anomalies (Fig. 3a vs. 3b). Likewise, the warmer Arctic troposphere in the pan-Arctic experiment leads to a weakening of the zonal wind near 60°N (Fig. 3c), while the aggregated zonal wind shows the opposite response to sea-ice loss, that is, a strengthening instead of a weakening of the subpolar jet, in agreement with a reversal of the tropospheric temperature anomalies over the Arctic. A more detailed inspection reveals that a majority of regional experiments show this behavior, with the notable exception of the Bering–Chukchi, Irminger–Nordic, and Central Arctic experiments (see Supplementary Fig. 2).
Zonal-mean anomalies of: a, b temperature, c, d zonal wind, and e, f meridional streamfunction in the pan-Arctic experiment (top row) and aggregated signal from all regional experiments (bottom row). Anomalies (shown in colors) are computed as the difference between the future experiments and the present-day experiment climatologies. The present-day climatology is shown in black contours in increments of 25 K (a, b), 4 m s−1 (c, d), and 25 × 109 kg s−1 (e, f), with dashed and solid lines for negative and positive values, respectively. All panels are pressure level [hPa]–latitude [deg] cross-sections. Dotted areas indicate regions where the sign of the anomalies agrees in at least 95% of the 1000 bootstrapped samples.
Mechanism of polar amplification from sea-ice loss
This drastic difference in the zonal-mean response of the tropospheric circulation to sea-ice loss between regional and pan-Arctic experiments may seem odd at first when considering that the zonal-mean surface forcing is applied consistently across all experiments: in particular, both the surface enthalpy flux and 2-m temperature zonal-mean anomalies increase linearly with the extent of the sea-ice loss (Fig. 4a). The drastic differences in zonal-mean temperature and zonal wind response are attributed to a tropospheric dynamical feedback.
a Scatter plot of the Arctic-mean surface enthalpy flux anomaly against the total Arctic sea-ice extent anomaly for all the future Arctic experiments [arrow I in schematic (g)]. Both quantities are computed over an Arctic polar cap north of 60°N. Anomalies are computed as the differences between the ensemble mean in each future Arctic experiment and the ensemble mean in the present-day control. The least-square regression line and its 95% confidence envelope are included as thin black lines. b–f As in a but between the anomalies of: b Arctic-mean latent heat released by precipitation (\(L_vP\)) [arrow II.a] and surface enthalpy flux. c Arctic-mean tropospheric eddy heat flux divergence and surface enthalpy flux [arrow II.b]; d Arctic-mean tropospheric adiabatic warming and the combined effect of latent heat released by precipitation and tropospheric eddy heat flux divergence [arrow III]; e subpolar jet [arrow IV.a] and Arctic-mean tropospheric adiabatic warming; and f polar cell strength and Arctic-mean tropospheric adiabatic warming [arrow IV.b]. g Schematic diagram of mechanism detailing how pan-Arctic or regional sea-ice loss influences the zonal-mean tropospheric circulation (blue/red fonts refer to climate response associated with adiabatic cooling/warming). On a–f are shown: future Arctic (black diamond), Central Arctic (black square), Barents–Kara (red square), Irminger–Nordic (yellow square), Hudson–Baffin and Labrador (magenta square), Beaufort–East Siberian–Laptev (green square), Bering–Chukchi (blue square), Okhotsk (cyan square), Central Arctic and Barents–Kara (red cross), and all Arctic except Central Arctic seas (blue cross).
The first evidence for such feedback is an amplified strengthening of the polar cell in the pan-Arctic experiment (characterized by anomalous ascent between 45° and 60°N and anomalous descent poleward of 60°N, Fig. 3e) with respect to both the aggregated (Fig. 3f) and individual regional experiments (see Supplementary Fig. 3). This stands in contrast to the Ferrel cells, whose changes in regional experiments are of comparable magnitude to those in the pan-Arctic experiment (compare Fig. 3e, f and Supplementary Fig. 3). To understand the implication of this difference in the behavior of the polar cell in response to pan-Arctic or regional sea-ice loss, we consider the thermodynamic budget of the troposphere. The latter can be approximately described by the following equation:
Here, \(\theta\) is the potential temperature, \(v\) and \(\omega\) the meridional and vertical wind, \({\Omega} = (p/p_{o})^\kappa\) a geometric factor (\(p_{o} = 10^3\) hPa), \(c_{p}\) the heat capacity of dry air at constant pressure per unit mass, \(L_{v}\) the latent release of vaporization per unit mass (here we disregard the slightly different values between sublimation and vaporization of ice and liquid droplets), and we define \(\kappa = c_{p}/r_{d}\) with \(r_{d}\) as the gas constant of dry air. \(P\) is the net precipitation at the surface, \(F^{{\mathrm{TOA}}}\) and \(F^{{\mathrm{SRF}}}\) the top-of-atmosphere and surface net upward radiative fluxes (shortwave and longwave), respectively, and \({\mathrm{SH}}\) is the upward surface sensible heat flux. The vertical integration extends from the surface pressure, \(p_{s}\), to the tropopause pressure level, \(p_{t}\) (set at 150 hPa). Relation (1) states that the left-hand-side term, i.e., the adiabatic warming integrated over the troposphere is compensated by the right-hand-side terms: the eddy meridional heat flux convergence integrated over the troposphere, the latent heat release from condensation in the troposphere, the radiative cooling in the troposphere, and the surface sensible heat fluxes. Despite being an approximation of the atmospheric thermodynamic budget (stratospheric fluxes, mean meridional heat flux, and eddy vertical heat fluxes are all neglected), changes in adiabatic warming (LHS) are nearly perfectly explained by the residual of the remaining terms (RHS).
Using relation (1), we compute a thermodynamic budget for the Arctic basin by averaging it over a polar cap extending north of 60°N. Consistent with its dependence on the vertical wind, adiabatic warming anomalies are found to scale linearly with the strength of the polar cell (Fig. 4e). Adiabatic warming anomalies also scale linearly with the anomalies in the subpolar jet strength (Fig. 4f; see “Method” for definitions of the strength of the polar cell and subpolar jet), in agreement with its influence on tropospheric temperatures.
Overall, regional experiments that show a strengthening of the subpolar jet also show a weakening of the polar cell (Fig. 4e, f): the Barents–-Kara and Beaufort–Siberian seas experiments (red and green squares, respectively), which dominate the aggregated response, are the most representative examples of this regime. Other experiments, and in particular the pan-Arctic and the two combined experiments (which impose two or more regions of sea-ice loss; see “Methods”), show climate anomalies of the opposite sign. Determining what sets the magnitude of adiabatic warming anomalies, or at least its sign, is thus essential for understanding the striking difference in the zonal wind anomalies between regional, combined, and pan-Arctic experiments.
A careful inspection of the thermodynamic budget of the polar cap reveals that adiabatic warming anomalies can be largely explained by the subtle balance between the tropospheric latent heat release and eddy heat flux convergence terms, whose anomalies, respectively, warm and cool the Arctic troposphere (Fig. 4d), with the overall sign of the anomalies being region-dependent. The remaining terms of the budget equation (i.e., radiative cooling and surface sensible heat flux), while contributing to the thermodynamics, are therefore not essential for explaining the regional differences in the adiabatic warming anomalies.
In all experiments, we find sea-ice loss to be associated with a weakening of the eddy poleward heat flux at the subpolar front (Fig. 4c). This is consistent with the low-level subpolar meridional temperature gradient weakening in response to a warming of the Arctic boundary layer, which reduces both the transient and stationary components of the eddy poleward heat flux26,27 (Fig. S5a, d). All experiments also show an increase in latent heat release over the Arctic (Fig. 4b), consistent with more areas of open ocean locally strengthening winter tropospheric convective activity (i.e., the increase in local precipitation over regions of sea-ice loss, which is apparent in Fig. 1e for the pan-Arctic experiment, is due to increases in the convective precipitation component). According to this thermodynamic balance, whether the polar cell strengthens or weakens with sea-ice loss depends primarily on how strongly Arctic precipitation increases and the poleward eddy heat flux at the subpolar front decreases with sea-ice loss.
In most experiments, eddy heat fluxes anomalies are larger than precipitation-driven anomalies, leading to adiabatic warming (Fig. 4d). However, in the Barents–Kara or Beaufort–Siberian seas experiments, the negative eddy heat flux anomalies are small and easily compensated by the positive precipitation anomalies, leading to a net adiabatic cooling of the Arctic troposphere. A careful investigation reveals that in those two experiments, a near-perfect cancellation between transient and stationary eddy heat flux occurs (Fig. S5a, c), while in most other experiments, anomalies in the transient and stationary components both drive a reduction of the net poleward eddy heat flux. This contrasting behavior in the transient and stationary eddy heat flux between experiments may be explained, to a large extent, by the geometry of their imposed sea-ice change in fall and winter: as detailed in the Supplementary Information Part B, we find that transient and stationary eddy heat flux anomalies can be predicted directly from changes in the zonal-mean and zonal variance of SIC over the Arctic, respectively.
We summarize the dynamical feedback mechanism in four main stages (Fig. 4g): a warming of the Arctic boundary layer in response to sea-ice loss (step 1) leads to an increase in convective precipitation, due to the anomalous surface heating over areas of newly open ocean (step 2a), as well as to a weakening of tropospheric eddy heat flux into the Arctic, driven by a decrease in low-level baroclinicity (step 2b). Depending on which effect is strongest, large-scale subsidence (adiabatic warming) or ascent (adiabatic cooling) is found in the Arctic troposphere (step 3), which results in opposite changes in the polar cell and subpolar tropospheric jet (step 4). In this feedback mechanism, adiabatic warming is more likely to occur when both transient and stationary eddy heat fluxes weaken, since this leads to a strong reduction of the net eddy heat flux; whether this is the case or not in each experiment depends sensitively on the geometry and extent of the sea-ice loss, which we found to control both components of the eddy heat flux. Overall, this feedback mechanism has allowed us to interpret changes in the tropospheric circulation directly from the pattern of sea-ice loss.
This feedback mechanism may explain as well climate anomalies forced by Arctic sea-ice loss simulated in climate models other than EC-Earth3: this is borne out by the aforementioned processes (i.e., adiabatic warming, eddy heat flux, and moist convection) expected to dominate the thermodynamic budget in all climate models, as well as those processes being controlled by changes in the same underlying predictors (such as meridional temperature gradient for transient eddy heat fluxes11, or surface enthalpy flux for convective rainfall28). Intermodel differences in the atmospheric circulation response to specific regional sea-ice loss scenarios may then result from the influence of model-specific physical parameterizations (e.g., convection scheme, boundary layer parameterizations) on those thermodynamic processes.
Discussion
Our findings confirm that some aspects of the climate response to sea-ice loss can be diametrically opposite depending on where the sea-ice loss occurs: in some regional experiments, the response of the Arctic troposphere is characterized by ascent anomalies and a strengthening of the subpolar jet, while an opposite response may occur when the sea-ice loss occurs over different (sometimes neighboring) regions, or when it becomes extensive (such as in the combined and pan-Arctic experiments). While the nonlinearity of the climate response to sea-ice loss pattern and amplitude has been discussed previously, the feedback mechanism proposed here is purely tropospheric, explaining the nonadditivity of the response to sea-ice loss from opposite changes in convective rainfall, transient and stationary tropospheric eddy fluxes. This differs from existing stratospheric mechanisms, which attribute the nonlinear response to changes in upwelling stationary waves and their interaction with the stratospheric polar vortex16,26,29. Our findings have important implications for assessing consistency among model studies: intermodel comparison studies of the climate response to sea-ice loss risk drawing contradictory conclusions if the imposed sea-ice loss patterns have different regional features, through a different manifestation of the zonal-mean feedback mechanism discussed here. A corollary point is that the climate response to regional sea-ice loss hotspots, such as the Barents–Kara sea30, may have little bearing on the climate response in a context of a more extensive (pan-Arctic) sea-ice loss. This feedback mechanism also has implications for climate change, as it suggests that differences in the spatial pattern of sea-ice loss modulate polar amplification through its effect on the Arctic tropospheric temperature. The quantitative framework outlined in this study may allow an assessment of this effect in individual experiments or multimodel studies.
Methods
Model and experiment description
Although oceans can be important modulators of the overall climate response to sea-ice change—through a combination of thermal inertia22 and dynamical effects31, an atmosphere-only configuration is chosen here to understand which atmospheric processes are critical to the seasonal climatic response to sea-ice loss in mid- and high-latitude regions, with no interference from ocean processes. The EC-Earth3.3 (CMIP6 production) model20 in its atmosphere-only configuration uses the Integrated Forecasting System (IFS cy36r4) atmospheric component from the European Centre for Medium Range Weather Forecasts to simulate atmospheric flows. IFS is a hydrostatic semi-implicit dynamical core, in which horizontal motions are solved on spectral reduced Gaussian grid T255 (equivalent to 1° nominal resolution) and vertical motions in grid-point space with a finite-element scheme (91 levels); a transformation scheme converts the resolved dynamics from spectral to real space on the N128 reduced Gaussian grid when solving for parameterizations and advections.
Following Smith et al.21, the prescribed present-day SIC and SST state corresponds to an observed 1979–2008 monthly climatology from the Hadley Center Sea Ice and Sea Surface Temperature data set (HadISST)32. The future state is constructed from an ensemble of 31 historical and RCP8.5 simulations (in the CMIP5 archive) by using an emergent constraint; the latter predicts a “best-fit” value of SST/SIC for every grid point by combining the present day, HadISST observed value with the intermodel spread in SST/SIC from CMIP5 simulations (for a detailed explanation of the protocol, please refer to Appendix A in Smith et al.21). This setup, which also outputs a monthly climatology, is comparable to that used in Screen12. All these SIC and SST forcing fields were retrieved from the input4MIPs data server (https://esgf-node.llnl.gov/search/input4mips). In the pan-Arctic sea-ice loss experiment, the future state monthly mean SIC distribution is prescribed in the Northern Hemisphere, while keeping the present-day monthly mean SIC in the Southern Hemisphere; furthermore, present-day monthly mean SST are prescribed everywhere except over newly ice-free areas, where the future state monthly mean SST are used instead. This implies that both changes in SST over regions of newly open oceans and SIC over all regions of the Arctic contribute directly to forcing climatic anomalies.
In order to explore the influences of sea-ice loss from specific areas of the Arctic, we run nine experiments simulating the climate response to sea-ice loss in one or more of the predefined regions of the Arctic basin (Fig. 1a) by regionally modifying the SIC and SST distribution of the present-day and future Arctic experiments over the following regions: the Barents–Kara seas, the Irminger–Nordic seas, the Hudson–Baffin–Labrador bays, the Central Arctic, the Beaufort–East Siberian–Laptev seas, the Bering–Chukchi seas, and the Okhotsk sea (see Fig. 1a for regional outlines; also note that the Barents–Kara and Okhotsk sea experiments are part of the PAMIP protocol). This set of experiments includes the PAMIP experiments33 proposed to investigate the atmospheric response to regional forcing from the Okhotsk and Barents–Kara seas, but goes beyond by adding a larger set of regional sea ice loss scenarios. While extending the PAMIP protocol precludes comparing our findings with experiments from other climate models, having additional experiments is an essential step toward quantifying and explaining the effect of regional sea-ice loss on climate. All regional experiments are designed such that their aggregated sea-ice loss pattern is identical to that of the pan-Arctic experiment. This set of regional experiments is complemented by two additional experiments, each combining two or more regions of sea-ice loss: the first includes the Central Arctic with the Barents–Kara sea, and another one combines all regions of sea-ice loss except for the Central Arctic. Those two combined experiments are designed to investigate the role of sea-ice loss in the Central Arctic, which peaks in fall, in preconditioning the tropospheric response to sea-ice loss in winter.
Regional and combined experiments are compared to a pan-Arctic sea-ice loss experiment, in which the future SST and SIC forcing fields are set everywhere in the Arctic. The impact of both the pan-Arctic and regional forcing is assessed by comparing with a baseline experiment in which present-day SST and SIC conditions are prescribed all across the Arctic. Each experiment (seven regional, two combined, one pan-Arctic, and one control) has 150 members initialized on June 1st, 2000 (itself initialized from a 5-month-spinup experiment initialized on January 1st, 2000 from a CMIP6 historical simulation) that are run for 1 year; filtering out internal variability by using a large ensemble of members is essential as the sea-ice distribution is identical across all members of the same experiment, precluding internal variability to have any connection with sea-ice changes. In all experiments, present-day SIC and SST conditions are prescribed in the Southern Hemisphere. Greenhouse gas concentrations are prescribed at their year 2000 levels; vegetation cover is set to its monthly mean distribution as obtained from an average of its observed state over the period 1980–2014. The atmospheric initial conditions were obtained from a fully coupled EC-Earth, CMIP6 historical simulation. Different members with slightly different atmospheric initial conditions are produced by applying an infinitesimal random perturbation to the 3D temperature field. The generation of the atmospheric initial conditions as well as the EC-Earth experiments were done using the Autosubmit workflow manager34.
Key dynamical definitions
GPH can be used to describe changes in the horizontal winds, as dictated by the geostrophic balance
where \(f\) is the coriolis parameter, \(u\) and \(v\) the zonal and meridional wind, and \(\phi\) the GPH (cartesian coordinates \(x\) and \(y\) were used for simplicity).
Zonal-mean and stationary components of wind anomalies can be expressed in terms of their respective GPH components
where, \(\overline {(.)}\) defines a time and zonal average, \((.)^ \ast\) a time-mean deviation from the time and zonal average.
The polar cell strength has been computed from the zonal-mean vertical wind, following the equation:
where, \(\psi\) is the mean meridional mass flux streamfunction, \(p_{m}\) is the pressure level of evaluation, \(a\) is Earth’s radius, \(g\) is the gravitational constant, and \(\varphi\) is the latitude (in radian). The polar cell strength is defined as the mean meridional mass flux streamfunction \(\psi\) averaged over 55–65°N and 500–700 hPa. An equivalent definition based on the meridional wind exists, which is more commonly applied. It could not be used for this study because the required meridional wind data were not saved for all pressure levels when the experiments were performed.
The subpolar jet strength is defined as the zonal-mean zonal wind averaged over 55–65ºN and 150–300 hPa.
Significance analysis
Statistical significance of the anomalies between the different sea-ice forcing experiments and the control is assessed by determining whether or not changes between the control and perturbation experiment have the same sign in at least 95% of 1000 bootstrap samples. A bootstrap sample is defined by computing the difference between the ensemble mean of a perturbation and control batch, with each batch corresponding to a set of 150 members randomly picked from all (150) members in that experiment (i.e., one batch for each experiment); a bootstrap batch includes repetition of members. Unlike the more commonly used t-test, our metric for statistical significance is nonparametric, i.e., it does not assume normality of the distribution. This precludes any issue when assessing changes in a non-normally distributed variable, such as precipitation.
Data availability
All experiments are stored permanently at BSC; this data is available upon request. Some experiments are also stored on the ESGF data node, grouped with other PAMIP experiments.
Code availability
The model source code (EC-Earth3.3) is the intellectual property of the ECMWF; it can be accessed via the EC-Earth portal (http://www.ec-earth.org), conditioned upon signing a licence agreement with the ECMWF. The code used to perform the analysis is available on the github page of the first author (@xlevine).
References
Stroeve, J. C. et al. The Arctic’s rapidly shrinking sea ice cover: a research synthesis. Clim. Change 110, 1005–1027 (2012).
Sigmond, M., Fyfe, J. C. & Swart, N. C. Ice-free Arctic projections under the Paris Agreement. Nat. Clim. Change 8, 404–408 (2018).
Vihma, T. Effects of Arctic sea ice decline on weather and climate: a review. Surv. Geophys. 35, 1175–1214 (2014).
Cohen, J. et al. Recent Arctic amplification and extreme mid-latitude weather. Nat. Geosci. 7, 627–637 (2014).
Overland, J. E. & Wang, M. Large-scale atmospheric circulation changes are associated with the recent loss of Arctic sea ice. Tellus Dyn. Meteorol. Oceanogr. 62, 1–9 (2010).
Liu, J., Curry, J. A., Wang, H., Song, M. & Horton, R. M. Impact of declining Arctic sea ice on winter snowfall. Proc. Natl Acad. Sci. 109, 4074–4079 (2012).
Tang, Q., Zhang, X., Yang, X. & Francis, J. A. Cold winter extremes in northern continents linked to Arctic sea ice loss. Environ. Res. Lett. 8, 014036 (2013).
Petoukhov, V., Rahmstorf, S., Petri, S. & Schellnhuber, H. J. Quasiresonant amplification of planetary waves and recent Northern Hemisphere weather extremes. Proc. Natl Acad. Sci. 110, 5336–5341 (2013).
Acosta Navarro, J. C. et al. December 2016: linking the lowest Arctic sea-ice extent on record with the lowest European precipitation event on record. Bull. Am. Meteorol. Soc. 100, S43–S48 (2019).
Barnes, E. A. Revisiting the evidence linking Arctic amplification to extreme weather in midlatitudes. Geophys. Res. Lett. 40, 4734–4739 (2013).
Barnes, E. A. & Screen, J. A. The impact of Arctic warming on the midlatitude jet-stream: Can it? Has it? Will it? WIREs Clim. Change 6, 277–286 (2015).
Screen, J. A. Simulated atmospheric response to regional and pan-Arctic sea ice loss. J. Clim. 30, 3945–3962 (2017).
Petoukhov, V. & Semenov, V. A. A link between reduced Barents-Kara sea ice and cold winter extremes over northern continents. J. Geophys. Res. Atmos. 115, (2010).
Semenov, V. A. & Latif, M. Nonlinear winter atmospheric circulation response to Arctic sea ice concentration anomalies for different periods during 1966–2012. Environ. Res. Lett. 10, 054020 (2015).
Chen, H. W., Zhang, F. & Alley, R. B. The robustness of midlatitude weather pattern changes due to Arctic sea ice loss. J. Clim. 29, 7831–7849 (2016).
McKenna, C. M., Bracegirdle, T. J., Shuckburgh, E. F., Haynes, P. H. & Joshi, M. M. Arctic sea ice loss in different regions leads to contrasting northern hemisphere impacts. Geophys. Res. Lett. 45, 945–954 (2018).
Sun, L., Deser, C. & Tomas, R. A. Mechanisms of stratospheric and tropospheric circulation response to projected Arctic sea ice loss. J. Clim. 28, 7824–7845 (2015).
Pedersen, R. A., Cvijanovic, I., Langen, P. L. & Vinther, B. M. The impact of regional Arctic sea ice loss on atmospheric circulation and the NAO. J. Clim. 29, 889–902 (2016).
Overland, J. E. et al. Nonlinear response of mid-latitude weather to the changing Arctic. Nat. Clim. Change 6, 992–999 (2016).
Wyser, K. et al. On the increased climate sensitivity in the EC-Earth model from CMIP5 to CMIP6. Geosci. Model Dev. Discuss. 1–13 https://doi.org/10.5194/gmd-2019-282 (2019).
Smith, D. M. et al. The Polar Amplification Model Intercomparison Project (PAMIP) contribution to CMIP6: investigating the causes and consequences of polar amplification. Geosci. Model Dev. 12, 1139–1164 (2019).
Cvijanovic, I. et al. Future loss of Arctic sea-ice cover could drive a substantial decrease in California’s rainfall. Nat. Commun. 8, 1–10 (2017).
Sewall, J. O. & Sloan, L. C. Disappearing Arctic sea ice reduces available water in the American west. Geophys. Res. Lett. 31, 1–4 (2004).
Simon, A., Gastineau, G., Frankignoul, C., Rousset, C. & Codron, F. Transient climate response to Arctic sea ice loss with two ice-constraining methods. J. Clim. 34, 3295–3310 (2021).
Screen, J. A. et al. Consistency and discrepancy in the atmospheric response to Arctic sea-ice loss across climate models. Nat. Geosci. 11, 155–163 (2018).
Hell, M. C., Schneider, T. & Li, C. Atmospheric circulation response to short-term Arctic warming in an idealized model. J. Atmos. Sci. 77, 531–549 (2020).
Chemke, R. & Polvani, L. M. Linking midlatitudes eddy heat flux trends and polar amplification. Npj Clim. Atmos. Sci. 3, 1–8 (2020).
Bintanja, R. & Selten, F. M. Future increases in Arctic precipitation linked to local evaporation and sea-ice retreat. Nature 509, 479–482 (2014).
Peings, Y. & Magnusdottir, G. Forcing of the wintertime atmospheric circulation by the multidecadal fluctuations of the North Atlantic ocean. Environ. Res. Lett. 9, 034018 (2014).
Lind, S., Ingvaldsen, R. B. & Furevik, T. Arctic warming hotspot in the northern Barents Sea linked to declining sea-ice import. Nat. Clim. Change 8, 634–639 (2018).
Deser, C., Tomas, R. A. & Sun, L. The role of ocean–atmosphere coupling in the Zonal-mean atmospheric response to Arctic sea ice loss. J. Clim. 28, 2168–2186 (2015).
Rayner, N. A. et al. Global analyses of sea surface temperature, sea ice, and night marine air temperature since the late nineteenth century. J. Geophys. Res. Atmos. 108 (2003).
Screen, J. A., Simmonds, I., Deser, C. & Tomas, R. The atmospheric response to three decades of observed Arctic sea ice loss. J. Clim. 26, 1230–1248 (2013).
Manubens-Gil, D., Vegas-Regidor, J., Prodhomme, C., Mula-Valls, O. & Doblas-Reyes, F. J. Seamless management of ensemble climate prediction experiments on HPC platforms. In Proc. 2016 International Conference on High Performance Computing Simulation (HPCS) 895–900 (2016). https://doi.org/10.1109/HPCSim.2016.7568429.
Acknowledgements
X.J.L. has received funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie Grant Agreement H2020-MSCA-COFUND-2016-754433 and from the H2020 project APPLICATE (Grant 727862). I.C. was supported by Generalitat de Catalunya (Secretaria d’Universitats i Recerca del Departament d’Empresa i Coneixement) through Beatriu de Pinós 2017 programme. M.G.D. and P.O. are grateful for funding by the Spanish Ministry for the Economy, Industry and Competitiveness, respectively, for the Grant references RYC-2017-22964 and RYC-2017-22772. E.T. has received funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie Grant Agreement No. 748750 (SPFireSD project). Experiments were completed on the Marenostrum IV supercomputer at the Barcelona Supercomputing Center (BSC), and support was provided by BSC’s Computational Earth Sciences (CES) department.
Author information
Authors and Affiliations
Contributions
X.J.L. performed and analyzed the experiments. X.J.L., I.C., P.O., and M.G.D. contributed to the definition of the experimental design and to the result discussion. X.J.L. wrote the manuscript, with the other authors contributing to its content. E.T. implemented critical workflow improvements, allowing experiments to run on the Marenostrum IV supercomputer.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Levine, X.J., Cvijanovic, I., Ortega, P. et al. Atmospheric feedback explains disparate climate response to regional Arctic sea-ice loss. npj Clim Atmos Sci 4, 28 (2021). https://doi.org/10.1038/s41612-021-00183-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41612-021-00183-w
This article is cited by
-
Regional scaling of sea surface temperature with global warming levels in the CMIP6 ensemble
Climate Dynamics (2024)
-
Dominant role of early winter Barents–Kara sea ice extent anomalies in subsequent atmospheric circulation changes in CMIP6 models
Climate Dynamics (2024)
-
The unprecedented Pacific Northwest heatwave of June 2021
Nature Communications (2023)
-
Arctic amplification, and its seasonal migration, over a wide range of abrupt CO2 forcing
npj Climate and Atmospheric Science (2022)
-
Robust but weak winter atmospheric circulation response to future Arctic sea ice loss
Nature Communications (2022)