Abstract
The Atlantic Meridional Overturning Circulation (AMOC), a tipping component of the climate system, is projected to slowdown during the 21st century in response to increased atmospheric CO2 concentration. The rate and start of the weakening are associated with relatively large uncertainties. Observed sea surface temperature-based reconstructions indicate that AMOC has been weakening since the mid-20th century, but its forcing factors are not fully understood. Here we provide dynamical observational evidence that the increasing atmospheric CO2 concentration affects the North Atlantic heat fluxes and precipitation rate, and weakens AMOC, consistent with numerical simulations. The inferred weakening, starting in the late 19th century, earlier than previously suggested, is estimated at 3.7 ± 1.0 Sv over the 1854–2016 period, which is larger than it is shown in numerical simulations (1.4 ± 1.4 Sv).
Similar content being viewed by others
Introduction
In the context of global warming, a major concern is related to climatic components which can suffer rapid transitions between two distinct states1 (e.g., Atlantic deep water formation, Arctic sea ice, Greenland ice-sheet, among others). Such a tipping element, AMOC, has a quasi-global impact and played a central role in past abrupt climate changes2,3. Its fate during the twenty first century is a topic of major scientific and socio-economic interest.
Most climate projections indicate that AMOC will suffer a centennial scale slowdown during the twenty-first century, mainly in response to intensified North Atlantic freshwater and heat fluxes, induced by increased atmospheric CO2 concentration4. However, there are significant quantitative differences between the results of various model simulations, which imply large uncertainties regarding the future evolution of AMOC.
Numerical integrations over the historical period simulate a modest AMOC decrease of 1.4 ± 1.4 Sverdrup (Sv) between preindustrial (1850–1900) and present day (2006–2015), which is most pronounced during the last decades, indicating that anthropogenic warming may have already weakened it5. Direct observations indicate that the overturning weakened by 30% during the 1957–2004 period6 and that it was in a relatively weak state between 2008 and 20177. Alternatively, indirect measures of ocean circulation changes, based on historical sea surface temperature (SST) fields, suggest that AMOC has been weakening since the mid-twenty century8. When calibrated with an ensemble of model simulations from the CMIP5 project, the weakening over 1870–2006 period was estimated to be of 3 ± 1 Sverdrup (Sv) (15%) and it was most pronounced since the mid-twenty century9. Proxy and reconstructed data suggest that the reduced AMOC intensity during the 1975–1995 period is at the lowest level in the last millennium10. The attribution of this reconstructed trend to external or internal factors remains an open problem of fundamental importance in climate research.
Here we investigate a potential contribution of atmospheric CO2 concentration to AMOC slowdown, based on observational and reanalysis data. First, we separate the SST-based reconstructed long-term AMOC weakening trend and emphasize the routes through which this greenhouse gas could affect AMOC. Then we probe the associated causal chains using the Convergent Cross Mapping (CCM) technique, a method based on the theory of dynamical systems used to identify causation in weakly coupled systems based on two timeseries11.
In practical terms, CCM causation is tested using the technique of “cross mapping”: a time delay embedding is constructed from the time series of Y and the ability to estimate the values of X from this embedding quantifies how much information about the later has been encoded into the former variable. The accuracy of the prediction is measured using Pearson’s correlation coefficient (ρ), between observed and predicted values. One notes the counterintuitive fact that the cross map estimate runs in the reverse direction of causality: if Y predicts X, then X causes Y. However, one key property that distinguishes causality from mere correlation is the convergence of the cross estimation. When constructing the embedding, only a given portion of the time series is used. Increasing this library length should improve the accuracy of the prediction, since the additional points fill in the trajectories in the attractor, resulting in closer nearest neighbors. At some point, the information contained in the affected variable has been exhaustively harnessed and the cross map saturates to a plateau. The asymptotic increase of the cross-map skill with library length is called convergence. The strength of the causal interaction may be linked with the rate of growth toward the convergence level with library size, but also with the level of the cross map skill.
Results
Isolating the AMOC trend
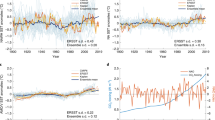
In order to investigate the AMOC response to this greenhouse gas, in a preliminary analysis, we aim to increase the signal-to-noise ratio by separating the centennial from multidecadal overturning variations emphasized in previous numerical and observational studies8,12,13, with the former having the same characteristic time scale as the increasing trend of the atmospheric CO2 concentration4. The separation is performed through two EOF analyzes performed on North Atlantic and South Atlantic annual SST anomalies from the ERSST.v5 dataset, extending over the 1854–2016 period14 (Supplementary Figs. 1–4). Similar results are obtained if the EOF method is applied to the Hadley SST fields15.
Whereas the time component of one North Atlantic mode is marked by a decreasing centennial-scale trend (hereafter Trend Mode—TM), which starts around 1890, that of the other one is dominated by multidecadal fluctuations, typical for the Atlantic Multidecadal Oscillation (AMO) (Fig. 1b). While the TM pattern is dominated by three centers of alternating signs, disposed from SW to NE of Greenland (Fig. 1a), a structure which is linked to AMOC changes9,10,16,17, the other mode has a typical monopolar AMO structure (Supplementary Fig. 2a), reflecting multidecadal AMOC variations18,19. The superposition of the time components of the two North Atlantic modes is strongly correlated (0.77) with a SST-based reconstruction9 (Fig. 1e). The time series of the corresponding modes identified based on the South Atlantic SST fields show similar centennial-scale and multidecadal variations (Fig. 1d). The South Atlantic TM pattern has a north-south oriented dipolar pattern (Fig. 1c). The other AMOC mode is marked by multidecadal fluctuations (Fig.1d) and by monopolar structures in both hemispheres of the Atlantic basin (Supplementary Figs. 2a and 4c), which are typical for AMO8,20. The TM(AMO) derived from North Atlantic SSTs has a 0.65 (0.49) maximum correlation with the corresponding mode obtained from South Atlantic fields, when the former leads the later by 19 (9) years.
The pattern of the SST Trend Mode (°C) (a) and the associated time series (dark blue line), together with the AMO time series (turquoise line) (b), derived through EOF analysis of North Atlantic sector (80°W-0°E, 0°N-80°N) annual SST fields. The corresponding pattern and time series, for the South Atlantic sector, are shown in panels c and d. The sums of the two timeseries in panel b and that of the pair of time components in panel d are shown in panel e (indigo and magenta lines, respectively), together with an AMOC reconstruction9 (orange line). Details on both EOF analyzes are presented in the supplement.
The superposition of the time components of the two South Atlantic modes is significantly correlated (0.60) with the SST-based reconstruction9 (Fig. 1e). Therefore, these two SST modes are characterized by distinct spatial and temporal features and are responsible for the largest part of decadal and longer AMOC variability.
A qualitatively identical and quantitatively similar bimodal decomposition of decadal and longer-term AMOC variability over the instrumental period was emphasized in an ensemble of historical simulations21. When these were combined with control simulations with constant radiative forcing, AMO appears associated with internal AMOC variations, whereas the centennial scale trend was interpreted as an externally forced mode. One notes that in some of the historical simulations the AMOC centennial-scale decreasing trend starts at the end of the nineteenth century21 (Fig. 11 in their study), as does the time component of TM, derived from observed SSTs (Fig. 1b). Furthermore, the Atlantic TM and AMO SST patterns were linked to forced and internal variations, respectively, based on model simulations and observations22. Consequently, hereafter we consider TM as an indicator of externally forced AMOC centennial-scale variations, separated here from the multidecadal internal fluctuations, reflected by AMO.
It was shown that the average SST anomalies over the subpolar gyre can be translated to AMOC changes, by using a calibration factor of 3.8 ± 0.5 Sv K−1, derived from CMIP5 simulations9. The fact that the dominant center of TM coincides with the SST anomalies in this area (Fig. 1a), makes possible an estimation of the AMOC change associated with this mode. Consequently, the linear decreasing trend of TM (Fig. 1b) translates in an AMOC weakening of 3.7 ± 1.0 Sv over the 1854–2016 period.
The North Atlantic SST dipole pattern located south of Greenland in the TM structure (Fig. 1a) was associated with the AMOC slowdown in climate model simulations with increasing atmospheric CO2 concentration9,23,24,25. This suggests that the TM’s weakening trend, which starts in the late nineteenth century, is induced by this greenhouse gas (Fig. 1b).
Mechanisms of CO2 influence on the AMOC trend
Model integrations indicate that an increase of atmospheric CO2 concentration can weaken AMOC through increases of North Atlantic surface heat and freshwater fluxes4,26,27,28. Here we investigate these simulated connections, based on observational (SST—ERSSTv5 dataset) and reanalysis (Sea Level Pressure (SLP), heat fluxes and precipitation rate—NOAA/CIRES/DOE 20th Century Reanalysis V3 datasets) fields14,29 (sea Methods).
The regression of spring North Atlantic Ocean heat fluxes on the time series of atmospheric CO2 concentration30 (Fig. 2a) is dominated by positive values (Fig. 2c), consistent with a direct thermodynamic influence of this greenhouse gas on ocean surface temperature. A quasi-identical pattern is obtained if a composite map is constructed as difference between average values over the 1935–2015 and 1854–1934 periods (Supplementary Fig. 5). The regression of the North Atlantic spring precipitation rate on CO2 record is dominated by negative anomalies (not shown).
a Reconstruction of annual atmospheric CO2 concentration (ppm); b Time series of the dominant North Atlantic spring SLP mode (black line) and of the SST/AMOC Trend Mode (blue line) (c) regression map of spring surface heat fluxes on the annual atmospheric CO2 concentration (W/m2/ppm); for positive values the flux is directed from the atmosphere into the ocean (d) regression map of spring precipitation rate on the SLP time series shown in panel b ([kg/(m2 × s)/Pa] × 106); the dominant North Atlantic SLP mode is also shown (solid black contour lines) (Pa); e time series of average North Atlantic ocean spring heat fluxes (orange line) and time series of the SST/AMOC Trend Mode (blue line). f Time series of average North Atlantic spring precipitation rate (violet line) and the time series of the SST Trend Mode (blue line). In panels c and d the regions for which the regression is significant above the 95% level are marked by red grids.
Model projections show that increasing atmospheric CO2 concentration results in a positive trend of the dominant atmospheric mode in this sector, the North Atlantic Oscillation31. The pattern and time series of this mode are derived through EOF analysis (not shown). The regression map of the North Atlantic precipitation rate field on the NAO index is dominated by a prominent center of positive values located in the low-pressure center of this mode, consistent with an influence from the later to the former (Fig. 2d).
A similar regression map of heat fluxes on NAO time series reveals a dipolar structure, which has a small projection on the average value of the North Atlantic sector (not shown). Therefore, these analyzes suggest influences of increased atmospheric CO2 concentration on spring North Atlantic surface heat fluxes (directly, thermodynamically) and on precipitation rate (indirectly, dynamically, through NAO), which were shown to weaken AMOC in model simulations4,26,27,28.
The dominant growing character of these two fluxes, associated with increasing atmospheric CO2 concentration (Fig. 2c, d), is reflected also in the upward trends of the integrated North Atlantic (70°W-20°E, 40°N-80°N) heat flux and precipitation rate time series (Fig. 2e, f). In order to test these observed connections linking increasing CO2 with weakening AMOC, anticipated by model simulations, we apply CCM on their associated pairs of variables.
CO2-to-AMOC causal links
TDCCM is first applied to two possible connected time series in order to estimate the lag for which the cross-map estimate is maximum and to infer the correct sense of the causal links, when an unambiguous interpretation is available11. With the identified lag, CCM is used (Supplementary Fig. 9) to check for convergence and its statistical significance, based on which a potential causal relationship can be inferred (see Methods).
The cross map skill from North Atlantic spring surface heat flux to atmospheric CO2 concentration increases with the library length and reaches a plateau around \(\rho \cong 0.8\), well above the 95% significance level (p < 0.03), indicating a causal relationship from the later to the former (Fig. 3a). The convergent (\(\rho \cong 0.7\)) and significant (p < 0.05) cross map of the TM to heat flux (Fig. 3c) suggests a causal link from the latter to the former, thus completing the first causal chain from CO2 to the AMOC weakening trend, via the heat flux. The second channel of causality starts again with CO2 as a cause, but this time its dynamic signature is found in the spring SLP attractor. This causal character is inferred from the convergent (\(\rho \cong 0.65\)) and significant (p < 0.05) cross map (Fig. 3b). SLP further influences spring precipitation rate, this link having a convergence level of \(\rho \cong 0.5\) and p value < 0.05 (Fig. 3d). Finally, the cross map from TM to spring precipitation rate shows clear convergence (\(\rho \cong 0.6\)) and statistical significance (p < 0.02), therefore indicating a causal connection from the later to the former (Fig. 3f). The CCMs in the opposite directions for all the above pairs are generally non-significant, with the exception of the TM-precipitation rate pair of time series, which are thus part of a feedback (Supplementary Figs. 6 and 7). Other potential causal channels linking CO2 with AMOC are also tested, but are not significant (Supplementary Fig. 8).
Cross map skill given by the correlation between predicted and observed values, as a function of library length for: a spring heat flux and CO2; b spring SLP and CO2; c AMOC North and heat flux; d spring precipitation rate and spring SLP; e AMOC South and AMOC North; f AMOC North and spring precipitation rate; g AMOC North and CO2. The light (dark) gray shaded areas correspond to the 95th cross map between each affected variable and the surrogate of the cause generated by a swap (Ebisuzaki) model. All variables have the embedding dimension, E = 8 and embedding lag, l = 1. The saturation of a cross map between X and Y variables, at a plateau above the significance levels, indicates a causal connection from Y to X. All cross maps exhibit statistically significant levels of convergence. In order to damp interannual fluctuations and focus on decadal and longer variations, a 3-year running mean filter was applied to the time series (excepting the heat flux record, for which the length of the filter was 5 years), before the CCM analyzes. The CCM results for the opposite causal relationships are shown in Supplementary Fig. 7.
Interhemispheric connections between the North Atlantic and South Atlantic components of TM are also explored (Fig. 3e). The CCM analysis reveals a robust causal influence from the northern component to the southern one (\(\rho \cong 0.7\)) significant above the 95% level (p < 0.03). No reversed significant convergence is detected (Supplementary Fig. 7e). Finally, the indirect link from the primary causal factor (CO2) to the final recipient (North Atlantic TM) has a clear causal nature as it is revealed by the convergent (\(\rho \cong 0.9\)) and significant (p < 0.02) cross map skill from the latter to the former (Fig. 3g).
The relatively high convergence level may reflect synchronicity, but this is dismissed by the inverse cross map, which is not statistically significant (p > 0.05, Supplementary Fig. 7g). The thermodynamical and dynamical causal links discussed above are synthesized in Fig. 4. Similar possible causal channels are investigated for all other seasons. The only significant one is found for winter: CO2\(\to\)Heat flux\(\to\)North Atlantic TM (Supplementary Figs. 10 and 11).
It includes a direct, thermodynamic branch (left route), through heat fluxes and an indirect, dynamical one (right route), through NAO-driven precipitation rates. Also, the southward interhemispheric connection is depicted in the bottom link. The diagram is the conceptual analog of the CCM results shown in Fig. 3.
An increasing CO2\(\to\)AMOC weakening causal connection inferred here based on observed and reanalysis data, is consistent with the anticorrelated millennial record levels of high atmospheric CO2 concentrations32 and the reconstructed record low level of the AMOC strength over the last decades10.
Discussion
An annual SST-based AMOC reconstruction shows a pronounced long-term slowdown since 1950s and no significant trend before9. Based on observed Atlantic SST fingerprints we separate associated centennial and multidecadal AMOC variations. The centennial-scale component indicates that an AMOC weakening trend starts earlier, in the late nineteenth century, several decades after the onset of the sustained industrial-era warming33.
In model integrations, centennial-scale increasing atmospheric CO2 concentration affects North Atlantic spring heat fluxes and precipitation rate, which results in an AMOC weakening trend4,28. We construct regression maps based on observed and reanalysis data, which support these simulated mechanisms. Furthermore, by applying the CCM method on pairs of observed and reanalysis time series, we identify the causal connections linking increasing atmospheric CO2 concentration with AMOC weakening (Fig. 4).
Our analyzes of observational and reanalysis data suggest that the AMOC linear slowdown over the 1854–2016 period, estimated at 3.7 ± 1.0 Sv, is larger than the of 1.4 ± 1.4 Sv weakening from the preindustrial period (1850–1900) to present days (2006–2015), exhibited in climate projections5.
Methods
Sea surface temperature
Due to their relatively long-time span, observed SSTs were used to infer ocean circulation variations from surface measurements9. Here we use fields from the ERSSTv5 dataset, distributed on a 2° × 2° grid and extending over the 1854–2016 period14. Similar results with that presented here, were obtained based on the SST fields from the HADISST1 dataset, distributed over 1° × 1° grids15.
Atmospheric CO2 concentration
Reconstructed values of annual means of atmospheric CO2 concentration30 were obtained from: https://climexp.knmi.nl/start.cgi.
Reanalysis SLP, heat fluxes and precipitation rate
SLP, heat fluxes and precipitation rate are from the monthly NOAA/CIRES/DOE 20th Century Reanalysis V3 data set29, were obtained from https://climexp.knmi.nl/start.cgi. They are distributed over a 1° × 1° grid and extend over the 1836–2015 period.
Preprocessing
Before all analyzes a pre-filtering procedure is applied to the SST fields in order to remove the uniform global warming trend. The yearly global average is subtracted from each grid point. The procedure has the advantage that it removes the spatially quasi-uniform nonlinear trend determined from the data, without need to a priori choose a linear or nonlinear shape to be removed. The global mean time series is quasi-identical with that of the average SST anomalies over a smaller domain (e.g., 0–360°E, 70°S–70°N) and therefore the subtracting method is not sensitive to scarcity of data in high latitudes. Because the globally uniform warming trend explains a large amount of variance in the initial SST fields, but the focus of this study is on spatially heterogeneous patterns, this preliminary operation increases significantly the signal-to-noise ratio in the SST data.
EOF analysis
The North and South Atlantic modes of SST variability, which are linked to AMOC changes, are identified through Empirical Orthogonal Functions (EOF) analyzes (Supplementary Figs. S1–S3).
This method is also used to identify the dominant mode of North Atlantic spring SLP variability and its associated time series. The first EOF, explaining 42% of variance, is the North Atlantic Oscillation.
Convergent cross mapping
The identification of causal relationships based on empirical data represents a critical problem across a wide range of scientific fields, which cannot be satisfactorily solved using correlations, which is a poor indicator of causality. A significant correlation between two variables does not imply a direct causal link between them. For example, a third variable could drive both of them. Similarly, a weak correlation between two variables does not imply a lack of causal relationship as it is often the case for systems governed by nonlinear dynamics. A recently proposed method, Convergent Cross Mapping (CCM), relying on time embedded state space reconstruction based on data, provides significant progress on this problem11.
The dynamics of the system is represented by coherent trajectories in state space which organize into an (usually lower dimensional) attractor manifold. Time is implicit and is represented by the direction along the state space trajectory. For deterministic dynamical systems, the variables are not independent and the system must be understood as a whole, rather than the sum of its parts. This non-separability translates into the fact that information about past states is carried forward through time and any variable in the system contains information about the states of the other. The historical values of a variable contain information about both, its past behavior and the instantaneous interdependence between the variables of the system. Thus Takens’ theorem applies, stating that we may reconstruct the underlying attractor manifold of a system by a time embedding of only one variable in the system, say Y. If two variables, X and Y, are bidirectionally causally linked then they contain information about each other and share a common attractor manifold. Their time embedded attractor reconstructions will be topologically equivalent (diffeomorphic) and nearby points in the attractor of Y will correspond to nearby points in the attractor of X. On the other hand, if only X causes Y, then Y will contain information about X, but the time evolution of X is independent of Y and the former variable does not contain information about the later. The CCM method extracts causal signatures using prediction as a criterion: from the E-dimensional time embedded attractor manifold of variable Y, find nearest neighbors to a given point at time t and construct weights from the identified neighbors. An estimate of X at time t is generated using these weights. This procedure is repeated for the values of Y at all times and a correlation measure between the predicted and observed time series is computed. Here we use Pearson’s correlation coefficient, ρ, as a measure of correlation. Most importantly, to truly distinguish between causality and correlation, one should check for the property of convergence of the cross estimation with the library size, that is the increase in estimation precision when considering more points for the prediction. The accuracy and convergence of the cross prediction may be limited by noise, observational error, time series length, but also by the complexity of the real-world systems, which could exhibit transitory and non-stationary causal behavior. As mentioned before, the method applies to nonlinear deterministic systems, even to stochastic ones as long as they are not completely random11. Thus, CCM becomes a necessary condition for causation.
CCM depends on several parameters. First of all, as is the case with any time embedded state space reconstruction method, we have a dependency on the embedding dimension, E and the embedding lag, l. Here we choose E = 8 and l = 1 everywhere. For our analyzes, Simplex Projection is essentially constant for any embedding dimension (Fig. S9a). On the other hand, E = 8 seems to be the right number of dimensions for cross prediction between the variables of our physical climatic system (Fig. S9b). Each cross-map value in the CCMs is computed as the average over 100 random samples (without replacement) at each library size.
Time delayed convergent cross mapping
The question still remains if CCM could indicate a false positive causal link. In cases of strong unidirectional forcing (X causes Y) the affected variable (Y) becomes a dynamical slave of its cause (X) so that they vary synchronously. In such a situation, the CCM could indicate a virtual bidirectional causal relationship, even if there is no information transfer from the effect to the cause. However, in such cases causality can still be inferred through surrogate analysis or Time Delayed CCM (TDCCM)34. Here, we preliminarily use TDCCM to find the lag for maximum predictability and use surrogate analysis to single out the unidirectional causal connections.
TDCCM consists of calculating the cross map skill for different lags in order to reveal one for which the prediction skill is optimal (i.e., maximum)34. This lag is negative since we make the prediction backwards in time, from the effect Y(t) to the cause \(X(t - \tau )\) and cause must precede effect (\(X(t - \tau )\) causes Y(t)). Each cross-map value is computed for the maximum library size available for each time delay. The identified lag is then used in CCM. As the exact value of the delay is highly unstable with respect to embedding dimension and embedding lag35, we don’t rely on its physical relevance, but rather use it as an optimization tool. TDCCM also provides qualitative insight into the correct causal directions through the sign of the maximum cross map skill lag (negative for the true causal direction). Nevertheless, the correct causal directions are primarily identified through surrogate analysis: we apply CCM between the presumed effect and the surrogate of the cause generated under two surrogate models.
This technique, together with CCM, was used, for example, to investigate potential causal relationships between atmospheric CO2 concentration and global temperature36.
Statistical significance of CCM
We estimate statistical significance under the null hypothesis that the (possible) effect does not contain information about the (possible) cause. To test it, we use surrogate randomization models for the cause. Under the null hypothesis, cross maps from the effect to the surrogate cause might be generated by information which was not destroyed by the randomization procedure, or by spurious correlation in the time series. The rejection of the null hypothesis means that we can find a cross map estimate above the 95% percentile of the estimates for the surrogates (or a p value of p < 0.05). As mentioned before, we can use statistical significance to single out the true direction of causality in the cases of synchrony or ambiguous TDCCM37. Here, we employ two surrogate tests36: (a) Ebisuzaki phase shift: one keeps the same frequency spectrum as the original time series and randomize the phases, generating 100 surrogates of the cause and try to estimate them from the effect. In Fig. 3 we have represented 95 of the cross maps obtained, eliminating the top 5; (b) Swap model: one chooses a random point in the time series and swap the two segments; this procedure randomizes the phases, while preserving nearly all short-term deterministic dependencies; 100 surrogates of the effect variable are created and 95 of them are represented in Fig. 3, eliminating the top 5.
Data availability
All data sources are mentioned in the Methods section.
Code availability
Code for CCM analysis was obtained from11. Codes to produce the figures are available from the corresponding author.
References
Lenton, T. M. et al. Tipping elements in the Earth’s climate system. Proc. Natl Acad. Sci. USA 105, 1786–1793 (2008).
Rahmstorf, S. Ocean circulation and climate during the past 120,000 years. Nature 419, 207–214 (2002).
Vellinga, M. & Wood, R. A. Global climatic impacts of a collapse of the Atlantic Thermohaline Circulation. Clim. Change 54, 251–267 (2002).
Collins, M., et al. Long-term climate change: Projections, commitments and irreversibility, in Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change (Cambridge Univ. Press, 2013).
Collins M. et al. Extremes, abrupt changes and managing risk. In: IPCC Special Report on the Ocean and Cryosphere in a Changing Climate (2019). Available online: https://www.ipcc.ch/srocc/.
Bryden, H. L., Longworth, H. R. & Cunningham, S. A. Slowing of the Atlantic meridional overturning circulation at 25°N. Nature 438, 655–657 (2005).
Smeed, D. A. et al. Observed decline of the Atlantic meridional overturning circulation 2004–2012. Ocean Sci. 10, 29–38 (2014).
Dima, M. & Lohmann, G. Evidence for two distinct modes of large-scale ocean circulation changes over the last century. J. Clim. 23, 5–16 (2010).
Caesar, L., Rahmstorf, S., Robinson, A., Feulner, G. & Saba, V. Observed fingerprint of a weakening Atlantic Ocean overturning circulation. Nature 556, 191–196 (2018).
Rahmstorf, S. et al. Exceptional twentieth-century slowdown in Atlantic Ocean overturning circulation. Nat. Clim. Change 5, 475–480 (2015).
Sugihara, G. et al. Detecting causality in complex ecosystems. Science 338, 496–500 (2012).
Park, W., & Latif, M. Multidecadal and multicentenial variability of the meridional overturning circulation. Geophys. Res. Lett. 35, https://doi.org/10.1029/2008GL035779 (2008).
Cheng, W., Chiang, J. C. H. & Zhang, D. Atlantic Meridional Overturning Circulation (AMOC) in CMIP5 models: RCP and historical simulations. J. Clim. 26, 7187–7197 (2013).
Huang, B. P. et al. Extended Reconstructed Sea Surface Temperature version 5 (ERSSTv5), upgrades, validations, and intercomparisons. J. Clim. https://doi.org/10.1175/JCLI-D-16-0826.1 (2017).
Rayner, N. A. et al. Global analyses of sea surface temperature, sea ice, and night marine air temperature since the late nineteenth century. J. Geophys. Res. 108, 4407, https://doi.org/10.1029/2002JD002670 (2003).
Born, A., Levermann, A. & Mignot, J. Sensitivity of the Atlantic Ocean circulation to a hydraulic overflow parametrisation in a coarse resolution model: response of the subpolar gyre. Oc. Model. 27, 130–142 (2009).
Zhang, R. et al. Sensitivity of the North Atlantic Ocean Circulation to an abrupt change in the Nordic Sea overflow in a high resolution global climate model, J. Geophys. Res. 116, https://doi.org/10.1029/2011JC007240 (2011).
Latif, M. et al. Reconstructing, monitoring, and predicting multidecadal-scale changes in the North Atlantic thermohaline circulation with sea surface temperature. J. Clim. 17, 1605–1614 (2004).
Knight, J. R., Allan, R. J., Folland, C. K., Vellinga, M. & Mann, M. E. A signature of persistent natural thermohaline circulation cycles in observed climate. Geophys. Res. Lett. 32, L20708, https://doi.org/10.1029/2005GL024233 (2005).
Schlesinger, M. E. & Ramankutty, N. An oscillation in the global climate system of period 65–70 years. Nature 367, 723–726 (1994).
Schmith, T., Yang, S., Gleeson, E. & Semmler, T. How much have variations in the meridional overturning circulation contributed to sea surface temperature trends since 1850? A study with the EC-Earth global climate model. J. Clim. 27, 6343–6357 (2014).
DelSole, T., Tippett, M. K., Shukla, J. A significant component of unforced multidecadal variability in the recent acceleration of global warming, J. Clim. 24, 909–926 (2011).
Saba, V. S. et al. Enhanced warming of the Northwest Atlantic Ocean under climate change. J. Geophys. Res. Oceans 120, https://doi.org/10.1002/2015JC011346 (2015).
Sgubin, G., Swingedouw, D., Drijfhout, S., Marry, Y. & Bennabi, A. Abrupt cooling over the North Atlantic in modern climate models. Nat. Commun. 8, https://doi.org/10.1038/ncomms14375 (2017).
Menary, B. M. & Wood, R. A. An anatomy of the projected North Atlantic warming hole in CMIP5 models. Clim. Dyn. 50, 3063–3080 (2018).
Dixon, K., Delworth, T., Spelman, M. & Stouffer, R. The influence of transient surface fluxes on North Atlantic overturning in a coupled GCM climate change experiment. Geophys. Res. Let. 26, 2749–2752 (1999).
Mikolajewicz, U. & Voss, R. The role of the individual air-sea flux components in CO2-induced changes of the ocean’s circulation and climate. Clim. Dyn. 16, 627–642 (2000).
Gregory, J. M. et al. A model intercomparasion of changes in the Atlantic thermohaline circulation in response to increasing atmospheric CO2 concentration. Geophys. Res. Let. 32, https://doi.org/10.1029/2005GL023209 (2005).
Slivinski, L. C. et al. Towards a more reliable historical reanalysis: Improvements for version 3 of the Twentieth Century Reanalysis System. Q. J. R. Met. Soc. 145, 2876–2908 (2019).
Ballantyne, A. P., Alden, C. B., Miller, J. B., Tans, P. P. & White, J. W. C. Increase in observed net carbon dioxide uptake by land and oceans during the last 50 years. Nature 488, 70–72 (2012).
Kuzmina, S. I., Bengtsson, L., Johannessen, O. M. & Drange, H. The North Atlantic Oscillation and greenhouse-gas forcing. Geophys. Res. Let. 32, https://doi.org/10.1029/2004GL021064 (2005).
Meure, C. M. et al. LowDome CO2, CH4 and N2O ice core records extended to 2000 years BP. Geophys. Ress. Lett. 33, L14810, https://doi.org/10.1029/2006GL026152 (2006).
Abram, J. N. et al. Early onset of industrial-era warming across the oceans and continents. Nature 536, 411–418 (2016).
Ye, H., Deyle, E. R., Gilarnanz, L. J. & Sugihara, G. Distinguishing time-delay causal interactions using convergent cross mapping. Sci. Rep. 5, 1–9 (2015).
Ma, H. et al. Detection of time delays and directional interactions based on time series from complex dynamical systems. Phys. Rev. E https://doi.org/10.1103/PhysRevE.96.012221 (2017).
van Ness, E. H. et al. Causal feedback in climate change. Nat. Clim. Change https://doi.org/10.1038/nclimate2568 (2015).
Sugihara, G., Deyle, E. R. & Ye, H. Misconceptions about causality with synchrony. PNAS 114, E2272–E2274, https://doi.org/10.1073/pnas.1700998114 (2017).
Acknowledgements
M.D. acknowledges the support from the visiting program of the Alfred Wegener Institute for Polar and Marine Research and from the EEA Grants 2014-2021, under Project contract no. 3/2019 (EEA-RO-NO-2018-0126). M.I. and G.L. are supported by Helmholtz funding through the joint program “Changing Earth - Sustaining our Future” (PoF IV) program of the AWI. Funding by the AWI Strategy Fund Project - PalEX and by the Helmholtz Climate Initiative - REKLIM is gratefully acknowledged.
Author information
Authors and Affiliations
Contributions
M.D. initiated and led this research. M.D. and D.N. performed the analyses. All authors participated in discussions during this study and contributed to the writing and revising the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Dima, M., Nichita, D.R., Lohmann, G. et al. Early-onset of Atlantic Meridional Overturning Circulation weakening in response to atmospheric CO2 concentration. npj Clim Atmos Sci 4, 27 (2021). https://doi.org/10.1038/s41612-021-00182-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41612-021-00182-x
This article is cited by
-
Data analysis evidence beyond correlation of a possible causal impact of weather on the COVID-19 spread, mediated by human mobility
Scientific Reports (2024)
-
North Atlantic Oscillation impact on the Atlantic Meridional Overturning Circulation shaped by the mean state
npj Climate and Atmospheric Science (2023)
-
Atmospheric CO2 forcing on Mediterranean biomes during the past 500 kyrs
Nature Communications (2023)
-
Atmospheric and oceanic circulation altered by global mean sea-level rise
Nature Geoscience (2023)
-
Global ocean wave fields show consistent regional trends between 1980 and 2014 in a multi-product ensemble
Communications Earth & Environment (2022)