Abstract
The North Atlantic Oscillation (NAO) is predictable in climate models at near-decadal timescales. Predictive skill derives from ocean initialization, which can capture variability internal to the climate system, and from external radiative forcing. Herein, we show that predictive skill for the NAO in a very large uninitialized multi-model ensemble is commensurate with previously reported skill from a state-of-the-art initialized prediction system. The uninitialized ensemble and initialized prediction system produce similar levels of skill for northern European precipitation and North Atlantic SSTs. Identifying these predictable components becomes possible in a very large ensemble, confirming the erroneously low signal-to-noise ratio previously identified in both initialized and uninitialized climate models. Though the results here imply that external radiative forcing is a major source of predictive skill for the NAO, they also indicate that ocean initialization may be important for particular NAO events (the mid-1990s strong positive NAO), and, as previously suggested, in certain ocean regions such as the subpolar North Atlantic ocean. Overall, we suggest that improving climate models’ response to external radiative forcing may help resolve the known signal-to-noise error in climate models.
Similar content being viewed by others
Introduction
Groundbreaking work over the last several years demonstrates that climate models can predict the North Atlantic Oscillation (NAO) out to near-decadal timescales1,2,3,4. The key insight offered by Smith et al. (2020; henceforth S20) is that decadal predictive skill for the NAO only emerges in very large multi-model ensembles4. Their team, scattered across the most advanced weather and climate modeling centers in the world, built a forecast system composed of decade-long runs of 169 ensemble members across 46 start dates. Even with over 77,000 model-years of output at their disposal, S20 still required post-processing to overcome the unrealistically low signal-to-noise ratio in climate models, tantalizingly termed the “signal-to-noise paradox”5,6. In this paper, we will build on S20 by analyzing and improving our understanding of the predictable component of the NAO in an uninitialized very large ensemble.
A successful prediction of the NAO from the ensemble mean of an initialized forecast system suggests that NAO predictability is composed of two components in yet unknown proportions: one from ocean initialization and another from external forcing7. All climate model runs require both initial conditions and boundary conditions. Researchers who run initialized forecast systems prescribe initial conditions that are designed to approximate the observed state of the climate at the time the forecast is initiated. Recent literature refers to the act of using an observationally based initial state as “initialization”. In the initialized hindcasts of S20, consistent with much of the decadal prediction literature, as the model integrates it incorporates estimates of observed external radiative forcing. The uninitialized ensembles used here eschew the incorporation of data from observations into their initial conditions but are forced by the same time history of external forcing. Averaging across a large ensemble effectively removes the uncorrelated, internally generated variability and retains the information common to all ensemble members. As above, the ensemble mean of an initialized prediction system isolates information from ocean initialization and external forcing. The ensemble mean of an uninitialized ensemble reflects the isolated influence of external forcing.
A careful comparison of initialized forecast systems and uninitialized ensembles can therefore reveal the value of ocean initialization. Analysis of the best available initialized forecast systems claims, at a minimum, regional improvements from initialization in upper ocean temperature, SST, precipitation, and surface pressure7,8. In particular, ocean temperature in parts of the North Atlantic subpolar gyre seems to have more predictive skill than the surrounding ocean in initialized models and that skill appears to be tied to the ocean circulation8,9,10,11,12,13,14. Ocean temperatures may influence the NAO15,16,17,18, so it is plausible that ocean initialization could improve skill in predicting the NAO.
There are hints that external forcing can be a source of predictive skill for the NAO at longer lead times. In both models and observations, tropical volcanic eruptions instigate the NAO to move towards its positive phase19,20. In the mid-20th century, there is a linear trend in the NAO index and this trend is one component of predictive skill in the NAO (compare Athanasiadis et al. 2020s Figs. 2c and 6c)1. In addition, on decadal timescales, in the Community Earth System Model (CESM), an uninitialized ensemble produces skill commensurate with an initialized prediction system for two NAO impacts: North American and western European summertime precipitation (as estimated via field significance in Yeager et al. 2018s Fig. 5)8.
Using a 269-member uninitialized multi-model large ensemble, in this paper we show that external forcing is the larger component of NAO predictability. In the Methods section, we provide further details of this ensemble and the methods we employ to study it. We then quantify how much NAO predictive skill can be extricated from external forcing alone, and extend this to include NAO impacts and covariates. We conclude by analyzing how our results fit within the context of previous studies by discussing the implications of a predictable, forced component of the NAO.
Results
Source of predictive skill in the NAO
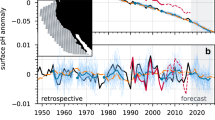
In our very large uninitialized ensemble, we find that predictive skill for the NAO is at least equal to that from S20’s initialized forecast system. For the years 1962–2015, the raw ensemble mean has an ACC of 0.62 (p = 0.025; Fig. 1a), whereas S20’s initialized “raw ensemble” ACC is 0.48. As in S20, we find a very large RPC (11.61), consistent with Scaife and Smith’s6 finding that the signal-to-noise ratio is too low in climate models. We further illustrate this in Fig. 2a, where we show that the raw ensemble mean of the uninitialized ensemble is better correlated with observations than a random ensemble member (compare to Scaife and Smith6 Fig. 1). When we mimic the lagged ensemble method of S20 (see Methods), we improve the ACC to 0.78 (p < 0.01; Fig. 1b); S20’s ACC value is 0.79. A majority of predictive skill for the NAO in the uninitialized ensemble is derived from the linear trend. When we remove this trend, ACC values decrease from 0.62 to 0.25 and from 0.78 to 0.30 for the raw and lagged ensembles, respectively. Table 1 includes a full comparison of our results to S20’s results.
We plot and report metrics of predictability for the NAO index (a–c), NASST index (d–f), AMO index (g–i), and an index of Northern European precipitation (j–l). We compare the three methods of calculating the ensemble mean employed by S20. First, we take the naïve average across all ensemble members in 8-year subsections and call it the “raw” ensemble mean (a, d, g, and j). Next, we augment our 8-year subsections with the prior 3 years, which we call our “lagged” ensemble (b, e, h, and k). Finally, we employ S20’s NAO-matching method (c, f, i, and l). These approaches are described in more detail in the methods section. In each figure, we report the ACC along with a bootstrapped p value. The years on the x-axis reflect the beginning of each 8-year period, as in S20.
a We create an ensemble of increasing size (x-axis) by subsampling (with replacement) from all ensemble members, calculate the filtered ensemble mean, and finding the ACC with observations (black) and a random ensemble member (blue). For each ensemble size, we repeat this process 10,000 times and report the mean (thick dot) and 95% confidence interval (colored cloud). When considering a random ensemble member, that member is removed from the pool of potential ensemble members. b ACC of the individual ensemble members (open markers) and ensemble means (closed markers) for the individual models in the MMLEA compared to the best ACC for the NAO we produce (0.78 from Fig. 1b; blue dashed line).
As with S20’s initialized ensemble, we find that NAO predictive skill increases with uninitialized ensemble size7. This is consistent with Zhang and Kirtman’s results in a multi-model ensemble of uninitialized CMIP5 runs and a simple statistical model21. To examine this, we create ensembles of between one and 500 members by randomly selecting ensemble members (with replacement). We find the raw ensemble mean of the NAO indices from the chosen ensemble members and calculate the ACC of that ensemble mean with observations. For each ensemble size, we repeat this process 10,000 times to create a probability distribution. In Fig. 2a, we report the mean and 95% confidence interval of this distribution. Only ensembles with more than 56 members produce ACC values that are greater than zero in 95% of realizations (which we call statistically significant). Average predictive skill generally increases with ensemble size, but with decreasing marginal improvement. The ACC we report in Fig. 1a for the raw ensemble (0.70) is slightly larger than the mean value for an ensemble of 269 random members (ACC = 0.65) in Fig. 2a, but this difference is not statistically significantly different (p = 0.66). We note that sampling with replacement is a less effective noise filter than sampling without replacement since it allows ensembles with replicated members and thus fewer different members. S20’s raw ensemble ACC of 0.48 is not statistically significantly different from our mean ACC for a 169-member ensemble (0.62; p = 0.49).
Ensembles from individual models can produce ensemble mean NAO indices with positive ACC values. In fact, all of the models we consider, except CSIRO-Mk3, produce positive ensemble mean ACC values (Fig. 2b). As exhibited by Fig. 2a, these positive values may be a matter of good luck, given the low signal-to-noise ratio in the NAO and the negative ensemble mean ACC in CSIRO-Mk3 may simply be the result of its small ensemble size (for the purposes of this problem). There is a low signal-to-noise ratio in each of the single model ensembles we consider; all models have an RPC with an absolute value greater than one. From Fig. 2a, an ensemble of 30 members has a 7.4% chance of producing a negative ensemble mean ACC with observations. Individual ensemble members from all ensembles produce both positive and negative ACCs with observations (Fig. 2b), consistent with the large internal variability of the NAO in climate models. While a multi-model ensemble clearly improves predictive skill for the NAO by allowing us to construct a very large ensemble, it also seems to improve skill relative to even our largest single model ensemble22.
The ensemble mean of our large uninitialized ensemble also has a predictive skill for NAO covariates and impacts. It is well established that on seasonal timescales the NAO drives a tripole pattern of SST anomalies across the North Atlantic basin23. The subpolar portion of this pattern persists onto decadal and longer timescales and likely contributes to the multidecadal North Atlantic SST variability24,25,26. We find robust predictability for the NASST index in our raw ensemble mean. For 1962–2015, we report ACC values of 0.92 (p < 0.01; Fig. 1d) and 0.97 (p < 0.01) for HadISST and ERSST, respectively. The lagged ensemble produces similarly high ACC values (Fig. 1e). High predictability in the uninitialized ensemble is consistent with many recent studies that suggest that low-frequency North Atlantic SSTs primarily responding to external forcing19,27,28,29,30,31,32,33,34. If we remove the component of the NASST index that covaries with global mean SST to create the AMV index, we report lower ACC values of 0.62 (p = 0.04) and 0.50 (p = 0.09) for the raw and lagged ensemble, respectively (Fig. 1g, h). These values are lower than S20’s ACC of 0.82. This is not surprising, as initialized ensembles include observations about observed SST, including correcting errors in the mean state. We also find good skill from our raw ensemble mean for a known impact of the NAO, northern European precipitation: ACC = 0.66 (p < 0.01; Fig. 1j). S20’s raw ensemble mean ACC for the same region and time period is 0.44. In our lagged ensemble the ACC value rises to 0.77 (p = 0.02).
S20 find that focusing on those ensemble members that are most like the ensemble mean, via NAO matching, enhances their predictive skill for NAO impacts and covariates. When we repeat their methodology in the uninitialized ensemble we find improvement in our forecast of northern European precipitation but not for North Atlantic SSTs. As described in more detail in “Methods”, for each eight-year period we identify the 20 ensemble members with the smallest absolute difference from the ratio of predictable signals (RPS)-adjusted raw ensemble mean. We calculate the ensemble mean NAO index, NASST index, AMV index, and the index of northern European precipitation rate from this new 20-member ensemble. As expected, the ACC for the NAO index itself increases from 0.62 (Fig. 1a) to 0.77 (Fig. 1c). NAO matching improves predictive skill for northern European precipitation from an ACC of 0.66 (p < 0.01) to 0.72 (p = 0.02; Fig. 1j, l). By chance, S20’s NAO-matched ACC for northern European precipitation is an identical 0.72 (their Fig. 2f). Nonetheless, our forecast fails to capture the full extent of the mid-1990s peak in European rainfall as in S20, which suggests a role for ocean initialization in predicting that extreme event.
We do not find an advantage to NAO matching in terms of predictive skill in either the NASST index or the AMV index. We find essentially the same ACC for the raw ensemble (0.92; p < 0.01) and the NAO matched ensemble (0.91; p < 0.01) in the NASST index from HadISST. In ERSST, for both ensembles ACC = 0.97; (p < 0.01). We find similar results for the AMV index (Fig. 1g, i). This is consistent with S20’s finding (compare their Fig. 2c, d). The reader may have expected the reduced ensemble size associated with NAO matching to degrade our ability to predict multidecadal North Atlantic SSTs. However, Murphy et al. (in review) show that for the similar AMV index an ensemble of only ten members is large enough to produce good correlations with SST observations35.
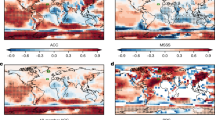
Of course, not all climate variability is explained by the indices we have discussed thus far. To generalize our results, we report maps of ACC values for the three fields we have considered: SLP, SST, and precipitation. At near-decadal timescales, both SLP and SST have high predictive skill across most of the Atlantic region in our uninitialized ensemble (Fig. 3). Following S20, we do not detrend in these maps. Therefore, the linear component of the anthropogenic warming trend contributes to high ACC values in SST. The warming trend has a less direct influence on SLP and precipitation. For SLP, there is a potential discrepancy across northern North America and Europe; however, the difference is not statistically significant in the raw ensemble to mean. For SST, there is a notable area of negative ACC values in the central North Atlantic subpolar gyre (Fig. 3b). These negative values seem to arise from the eastward displacement of the warming hole in our ensemble relative to observations. In Fig. 3b, we have contoured the negative SST trend from both the ensemble mean and observations. Ocean initialization would rectify this bias8,12 via some combination of correcting SST biases and encouraging a more realistic ocean circulation. Precipitation, an exceedingly noisy field, has regions of ACC values greater than 0.5 across northern Europe (Fig. 3c), parts of northern North America, and across the Sahel and Sahara. Positive predictive skill across the northern United States and Europe is consistent with the level of predictive skill we have shown for the NAO. Positive ACC values for equatorial African precipitation is potentially related to externally forced variations in North Atlantic SSTs and associated shifts in the ITCZ36,37, although these signals may be more prominent during the boreal summer. A lack of skill in DJFM precipitation across the southern United States is potentially related to the absence of internal variations of the El Niño Southern Oscillation in the ensemble mean.
We map ACC values for a sea-level pressure, b SST, and c precipitation. We display only the raw ensemble mean. We only color those pixels with ACC values that are statistically significant at the 95% level. In panel b, highlight the location of the warming hole by contouring the −1 °C/54-year trend in SST in observations (black) and our ensemble (gray). In panel c, we highlight the location used to calculate Northern European precipitation reported in the text.
Discussion
In agreement with S20, we find that climate models can predict the NAO on decadal and longer timescales in a sufficiently large ensemble. Further, we echo their claim that the NAO’s signal-to-noise ratio in climate models is too small via our estimates of the RPC6. This is in agreement with Zhang and Kirtman who also show the existence of the signal-to-noise paradox in uninitialized CMIP5 models21. We show that the ensemble means NAO in a 14,526 model-year multi-model uninitialized ensemble offers the commensurate predictive skill to the NAO from S20’s 77,740 model-year multi-model initialized ensemble.
Predictive skill for the NAO index over the second half of the 20th century is primarily derived from the linear trend. Unlike the global temperature signal, predicting a trend in SLP is not trivial. There is no a priori expectation that global warming should preferentially rearrange air masses into a positive and increasing NAO pattern. The newly discovered ability for models to reproduce this linear trend shows promise for models’ ability to predict NAO impacts, like northern European precipitation. Likewise, it is quite useful that models can reproduce the NASST index, even if they struggle with the AMV index (as defined by Trenberth and Shea 2006), as climate impacts likely respond to total Atlantic SST in addition to excess warming in the Atlantic compared to the rest of the globe, as well as, of course, more regional features.
Paired with S20, this work also highlights the potential importance of ocean initialization in predicting particular time periods, such as the extreme mid-1990s positive phase of the NAO, which is missed in uninitialized models. Smith et al. sum up the current view of the effectiveness of initialization for decadal prediction: “Previous studies have found fairly limited improvements from initialization, mainly in the North Atlantic, with little impact over land7”. Our results here reinforce this message, generally showing little difference between the uninitialized large ensemble analyzed here and the state-of-the-art initialized forecasts presented by S20. Consistent with prior work, our results indicate that the North Atlantic subpolar gyre is a region where initialization is clearly helpful8.
The response of the NAO to external forcing is complicated and guided by a balance between competing factors including, but not limited to the pole-to-equator temperature gradient, horizontal eddy fluxes in the atmosphere, coupling with the stratosphere, and interactions with the ocean boundary currents38. Each of these mechanisms has been suggested as a possible explanation for the signal-to-noise paradox, which is a consequence of our models’ tendency to dampen signals more than noise. O’Reilly et al. find that stratospheric initialization improves NAO forecasts and that artificially amplifying the Quasi-Biennial Oscillation—NAO wintertime teleconnection increases the signal-to-noise ratio in climate models26. Scaife et al. find that increasing atmospheric horizontal resolution from 0.8 to 0.4 degrees does not solve the signal-to-noise paradox but provides some evidence that higher resolutions that resolve high-frequency eddy feedback may amplify the signal in the NAO39. Kirtman et al. show that mesoscale ocean features can increase predictability in atmospheric circulation, particularly in eddy-rich regions, like along the Gulf Stream front and in the subpolar North Atlantic40. Each of these mechanisms also ought to respond to changes in radiative external forcing. Given that forcing impacts the predictable component of the decadal NAO and given that the predictable component is too weak in climate models, we suggest that some of the mechanisms listed above are not responding strongly enough to external forcing.
Even if all of the theoretical predictability inherent to the real-world NAO could be attributable to external forcing, ocean initialization can still improve climate model forecasts of the NAO and NAO impacts by correcting for any biases in the model’s response to external forcing. For example, in both the NAO index and the time series of northern European precipitation, our uninitialized ensemble fails to predict the magnitude of the extreme positive phase (or wet phase) in the mid-1990s. S20’s initialized ensemble seems to rectify this error. However, uninitialized climate projections cannot have this correction. Therefore, the influence of the NAO on climate around the North Atlantic basin is likely too weak in these projections. Given the predictive value that we find for the NAO in external forcing, we expect that devoting effort to the difficult and uncertain task of improving the response of climate models to external forcing will improve the signal-to-noise ratio in climate models and therefore projections and predictions of future climate.
Methods
Metrics
In this section, we identify the core metrics that we will use to quantify predictive skill in the NAO. We then describe the very large multi-model ensemble from the multi-model large ensemble archive (MMLEA) and the post-processing techniques we will employ to understand it and compare our results to S20. The MMLEA ensemble is not a precise comparison to S20’s prediction system, but it is a state-of-the-art uninitialized ensemble. We conclude this section with a brief description of our data sources and definitions.
Metrics
We assess skill in the phasing of climate indices and at individual grid points via the anomaly correlation coefficient (ACC) defined as
where m is the index in a model and o is the index in observations and overbars denote time-mean values. In each index, we compare the predictable portion of the variability in models and observations via the ratio of predictable components (RPC), defined as
where σsig is the standard deviation of the signal in the observed (“o”) and forecast (“f”) and σtot is the total standard deviation of the signal plus the noise5. As in S20, we estimate the signal in the forecasts as the ensemble mean and the total as the average standard deviation of all of the individual ensemble members. The observed total is the standard deviation of the observed time series, but, again following S20, we estimate the signal in the observed from the variance accounted for by the forecast. As they note, due to model error this is likely an underestimate of the true signal in the North Atlantic. The RPC, therefore, requires knowledge of both the observed phasing and magnitude of the NAO index. A perfect model ought to have an RPC of 1. S20 found values greater than one nearly everywhere in the North Atlantic, consistent with the signal-to-noise paradox. Finally, we will consider the RPS, defined as
where all variables are defined as above.
Multi-model large ensemble archive
The signal-to-noise paradox in climate models is a problem in two parts: (1) models agree with observations more than would be expected given the small signal-to-noise ratios in models and (2) model ensembles are more capable of simulating observations than they are of reproducing a single member of the ensemble6. Here, the “signal” is the predictable component of the NAO and the “noise” is the unpredictable component. Our “Results and discussion” will be aimed at advancing our understanding of the second part of the signal-to-noise paradox.
The first part of this problem can be overcome with sufficiently large ensembles of climate models to average over unpredictable noise, and some creative statistical post-processing4.
We take advantage of a new, publicly available archive of existing climate model large ensembles. We consider all six ensembles from the MMLEA41 for which the required output was available at the time of writing. In total, the ensemble has 269 members. To allow for direct comparison with S20, we limit our analysis to the years 1962–2015 (a total of 14,526 model-years, 19% of S20’s 77,740 model-years). All ensemble members experience CMIP5 boundary conditions, consistent with the best estimates of historical external forcing through 200542. After 2005, each ensemble member experiences scenario-based trajectories of external forcing, following either representative concentration pathway (RCP) 2.6, 4.5, or 8.5. For the time period 2006–2015, there are only minor discrepancies between these three RCPs and observed forcing43. Differences in internal variability between ensemble members are induced by varying the initial conditions once at the beginning of each run44, in all cases more than a decade earlier than the forecast start date. This contrasts with “ocean initialization”, where an estimate of the observed ocean state is prescribed at the beginning of the forecast period (as in S20). More details about each ensemble, including their size, resolution, start date, and method of initialization are included in Table 2.
Post-processing
Following S20, we apply three methods for calculating the ensemble mean of our multi-model ensemble. We often call this ensemble mean a “forecast” or “prediction”. Of course, it is neither. This jargon, adopted from the decadal forecast community, is inculcated with the hope that what we learn from hindcasts or historically-forced models will help us predict the future. In a practical sense, this word choice allows for a straight-forward qualitative comparison with S20. We also devise post-processing techniques that are conducive to direct quantitative comparison with S20, although we are somewhat limited by the differing structures of our ensembles. In each of our approaches, we subsection our ensemble into 8-year segments, thereby mimicking the year 2–9 forecasts S20 studied in their initialized forecast system.
First, we take the ensemble at face-value and calculate the “raw” ensemble mean, wherein we weigh each individual ensemble member equally. Combined with the 8-year subsections, this approach is equivalent to applying an 8-year wide boxcar filter and assigning the value to the first year. That is, our “forecast” in the raw ensemble for 1970 is the arithmetic mean of the years 1970–1977.
Our second method of calculating the ensemble mean follows S20’s “lagged ensemble” approach. For a given year two to nine forecast, S20 augments their ensemble with the previous 3 years two to nine forecasts. Effectively, they quadruple the number of ensemble members and include unique information from three previous years. In their paper, S20 acquires significant additional skills via this approach (compare their Fig. 2a, b). Our uninitialized ensemble does not have independent model runs for each year’s 8-year “forecast”. So, we simply bring the prior three years into our average. That is, the forecasted NAO index for 1970 is the arithmetic mean from 1967 to 1977, with no change in the number of ensemble members. For consistency, we also call this a “lagged ensemble”.
For these first two averaging schemes, we follow S20 in inflating the variance of the ensemble mean NAO index. For simplicity, we multiply our ensemble mean by the ratio of the standard deviation of the observed over the standard deviation of the ensemble mean NAO index, as in S20. We note in our figures when this method is applied.
Our third and final method of calculating the ensemble mean is a translation of S20’s “NAO matching”. To briefly summarize their approach, S20 first linearly amplified the ensemble mean NAO by the RPS. The RPS increases as the signal-to-noise ratio decreases (when the signal-to-noise ratio is too small), thereby allowing S20 to bring the ensemble mean NAO closer to observations. S20 then selected those 20 members with the smallest absolute differences from the RPS inflated ensemble mean NAO. We apply the same approach for each eight-year subsection to create an “NAO-matched” ensemble mean.
As an aside, we weighted each model in our multi-model ensemble equally, regardless of the number of members. The results of this approach are qualitatively similar to our raw ensemble mean. To avoid clutter, we choose not to display these results in-text.
Observations and observational products
For gridded sea-level pressure (SLP), we use the NCEP/NCAR reanalysis45. For the NAO index, we also use HadSLP2, to allow for direct comparison to S2046. For SST we use subsections of two datasets covering the years 1962–2015: The Extended Reconstructed Sea Surface Temperature version 5.1 dataset at about 2° × 2° resolution (ERSSTv5)47 and the Hadley Centre Sea Ice and Sea Surface Temperature dataset at about 1° × 1° resolution (HadISST)48. Our figures show results for HadISST, but we report results in-text from both datasets. For precipitation, we use a 1° × 1° configuration of the Global Precipitation Climatology Center version 2018 (GPCC) gridded monthly precipitation product, also for the years 1962–201549. For each of these fields, we use the output from DJFM, when the NAO’s influence is the largest, to enable comparison to S20.
Indices
Following S20, in both observations and models, we define the NAO index as the difference in mean sea level pressure between a box around the Azores (36°–40°N, 28°–20°W) and a box around Iceland (63°–70°N, 25°–16°W). The North Atlantic SST (NASST) index is calculated as the area-weighted average of SST anomalies (the seasonal cycle computed over the 1962–2015 period is removed) in the Atlantic (0°–60°N, 80°–0°W). The Atlantic Multidecadal Variability (AMV) index averages SST over the same area but then removes global average SST (60°N – 60°S)50. S20 considers the AMV index, but not the NASST index. We include both for completeness. As in S20, we define an index of northern European precipitation as the spatially weighted average precipitation rate in the box (55°–70°N, 10°W–25°E), which is outlined in Fig. 3c. We also linearly detrend each of these indices and report the results. Presumably, due to the structure of their ensemble, S20 does not include detrended results, so a direct comparison is not possible at this time.
Significance
We test for significance in the statistics discussed above via block bootstrap in which we subsample individual decades from each of the time series (with replacement) and recalculate the relevant statistic 10,000 times to create a probability distribution. We report the p value of the reported statistic relative to this distribution. This method tests the same null hypothesis as S20, that the statistic (e.g., ACC) is equal to zero. This statistical test does not establish any minimum threshold for considering a prediction system to have “useful skill”.
Data availability
The model simulations analyzed in this study is available at https://www.cesm.ucar.edu/projects/community-projects/MMLEA/.
Code availability
The code used in this study is available from the corresponding author on reasonable request.
References
Athanasiadis, P. J. et al. Decadal predictability of North Atlantic blocking and the NAO. Npj Clim. Atmos. Sci. 3, 1–10 (2020).
Dunstone, N. et al. Skilful predictions of the winter North Atlantic oscillation one year ahead. Nat. Geosci. 9, 809 (2016).
Scaife, A. A. et al. Skillful long-range prediction of European and North American winters. Geophys. Res. Lett. 41, 2514–2519 (2014).
Smith, D. M. et al. North Atlantic Climate far more predictable than models imply. Nature 583, 796–800 (2020).
Eade, R. et al. Do seasonal-to-decadal climate predictions underestimate the predictability of the real world?”. Geophys. Res. Lett. 41, 5620–5628 (2014).
Scaife, A. A. & Smith, D. A signal-to-noise paradox in climate science. Npj Clim. Atmos. Sci. 1, 1–8 (2018).
Smith, D. M. et al. Robust skill of decadal climate predictions. Npj Clim. Atmos. Sci. 2, 1–10 (2019).
Yeager, S. G. et al. Predicting near-term changes in the earth system: a large ensemble of initialized decadal prediction simulations using the community earth system model. Bull. Am. Meteorol. Soc. 99, 1867–1886 (2018).
Msadek, R. et al. Predicting a decadal shift in North Atlantic climate variability using the GFDL forecast system. J. Clim. 27, 6472–6496 (2014).
Meehl, G. A. et al. Decadal climate prediction: an update from the trenches. Bull. Am. Meteorol. Soc. 95, 243–267 (2014).
Hermanson, Leon et al. Forecast cooling of the atlantic subpolar gyre and associated impacts. Geophys. Res. Lett. 41, 5167–5174 (2014).
Karspeck, A., Yeager, S., Danabasoglu, G. & Teng, H. An evaluation of experimental decadal predictions using CCSM4. Clim. Dyn. 44, 907–923 (2015).
Piecuch, C. G., Ponte, R. M., Little, C. M., Buckley, M. W. & Fukumori, I. Mechanisms underlying recent decadal changes in subpolar North Atlantic Ocean heat content. J. Geophys. Res. Oceans 122, 7181–7197 (2017).
Yeager, S. The Abyssal Origins of North Atlantic decadal predictability. Clim. Dyn. https://doi.org/10.1007/s00382-020-05382-4 (2020).
Czaja, A. & Frankignoul, C. Observed impact of Atlantic SST anomalies on the North Atlantic oscillation. J. Clim. 15, 606–623 (2002).
Frankignoul, C. & Kestenare, E. Observed Atlantic SST Anomaly impact on the NAO: an update. J. Clim. 18, 4089–4094 (2005).
Omrani, N.-E., Keenlyside, N. S., Bader, J. & Manzini, E. Stratosphere key for wintertime atmospheric response to Warm Atlantic Decadal conditions. Clim. Dyn. 42(February 1), 649–663 (2014).
Simpson, I. R., Stephen, G. Y., McKinnon, K. A. & Deser, C. Decadal predictability of late winter precipitation in Western Europe through an ocean–jet stream connection. Nat. Geosci. 12, 613–619 (2019).
Otterå, O. H., Bentsen, M., Drange, H. & Suo., L. External forcing as a metronome for Atlantic multidecadal variability. Nat. Geosci. 3, 688–694 (2010).
Robock, A. Volcanic eruptions and climate. Rev. Geophys. 38, 191–219 (2000).
Zhang, W. & Kirtman, B. Understanding the signal-to-noise paradox with a simple Markov model. Geophys. Res. Lett. 46, 13308–13317 (2019).
Bell, R. & Kirtman, B. Seasonal forecasting of wind and waves in the North Atlantic using a grand multimodel ensemble. Weather Forecast 34, 31–59 (2019).
Deser, C., Alexander, M. A., Xie, S.-P. & Phillips., A. S. Sea surface temperature variability: patterns and mechanisms. Ann. Rev. Mar. Sci. 2, 115–143 (2010).
Delworth, T. L. et al. The central role of ocean dynamics in connecting the North Atlantic oscillation to the extratropical component of the Atlantic multidecadal oscillation. J. Clim. 30, 3789–3805 (2017).
Klavans, J. M., Clement, A. C. & Cane, M. A. Variable external forcing obscures the weak relationship between the NAO and North Atlantic multidecadal SST variability. J. Clim. 32, 3847–3864 (2019).
O’Reilly, C. H., Weisheimer, A., Woollings, T., Gray, L. J. & MacLeod, D. The importance of stratospheric initial conditions for Winter North Atlantic oscillation predictability and implications for the signal-to-noise paradox. Q. J. R. Meteor. Soc. 145, 131–146 (2019).
Bellomo, K., Murphy, L. N., Cane, M. A., Clement, A. C. & Polvani., L. M. Historical forcings as main drivers of the Atlantic multidecadal variability in the CESM large ensemble. Clim. Dyn. 50, 3687–3698 (2018).
Bellucci, A., Mariotti, A. & Gualdi, S. The role of forcings in the twentieth-century North Atlantic multidecadal variability: the 1940–75 North Atlantic cooling case study. J. Clim. 30, 7317–7337 (2017).
Birkel, S. D., Mayewski, P. A., Maasch, K. A., Kurbatov, A. V. & Lyon, B. Evidence for a volcanic underpinning of the Atlantic multidecadal oscillation. Npj Clim. Atmos. Sci. 1, 24 (2018).
Booth, B. B. B., Dunstone, N. J., Halloran, P. R., Andrews, T. & Bellouin., N. Aerosols implicated as a prime driver of twentieth-century North Atlantic climate variability. Nature 484, 228 (2012).
Mann, M. E., Steinman, B. A. & Miller., S. K. Absence of internal multidecadal and interdecadal oscillations in climate model simulations. Nat. Commun. 11, 1–9 (2020).
Murphy, L. N., Bellomo, K., Cane, M. & Clement, A. The role of historical forcings in simulating the observed Atlantic multidecadal oscillation. Geophys. Res. Lett. https://doi.org/10.1002/2016GL071337/full (2017).
Undorf, S., Bollasina, M. A., Booth, B. B. B. & Hegerl, G. C. Contrasting the effects of the 1850–1975 increase in sulphate Aerosols from North America and Europe on the Atlantic in the CESM. Geophys. Res. Lett. 45, 11,930–11,940 (2018).
Watanabe, M. & Tatebe, H. Reconciling roles of sulphate aerosol forcing and internal variability in Atlantic multidecadal climate changes. Clim. Dyn. https://doi.org/10.1007/s00382-019-04811-3 (2019).
Murphy, L. N., Klavans, J. M., Clement, A. C. & Cane, M. A. Investigating the roles of external forcing and ocean circulation on the Atlantic multidecadal SST variability in a large ensemble climate model hierarchy. J. Clim. https://doi.org/10.1175/JCLI-D-20-0167.1 (2021).
Biasutti, M. Rainfall trends in the African Sahel: characteristics, processes, and causes. Wiley Interdiscip. Rev. Clim. Change 10, e591 (2019).
Folland, C. K., Palmer, T. N. & Parker, D. E. Sahel rainfall and worldwide sea temperatures, 1901–85. Nature 320, 602–607 (1986).
Shaw, T. A. et al. Storm track processes and the opposing influences of climate change. Nat. Geosci. 9, 656–664 (2016).
Scaife, A. A. et al. Does increased atmospheric resolution improve seasonal climate predictions?” Atmos. Sci. Lett. 20, e922 (2019).
Kirtman, B. P., Perlin, N. & Siqueira., L. Ocean eddies and climate predictability. Chaos 27, 126902 (2017).
Deser, C. et al. Insights from Earth system model initial-condition large ensembles and future prospects. Nat. Clim. Change 10, 277–286 (2020).
Schmidt, G. et al. Climate forcing reconstructions for use in PMIP simulations of the last millennium (v1.0). Geosci. Model. Dev. 4, 33–45 (2011).
Peters, G. P. et al. The challenge to keep global warming below 2 °C. Nat. Clim. Change 3, 4–6 (2013).
Kay, J. E. et al. The Community Earth System Model (CESM) Large Ensemble Project: a community resource for studying climate change in the presence of internal climate variability. Bull. Am. Meteorol. Soc. 96, 1333–1349 (2015).
Kalnay, E. et al. The NCEP/NCAR 40-year reanalysis project. Bull. Am. Meteorol. Soc. 77, 437–472 (1996).
Allan, R. & Ansell, T. A new globally complete monthly historical gridded mean sea level pressure dataset (HadSLP2): 1850–2004. J. Clim. 19, 5816–5842 (2006).
Huang, B. et al. Extended reconstructed sea surface temperature, Version 5 (ERSSTv5): upgrades, validations, and intercomparisons. J. Clim. 30, 8179–8205 (2017).
Rayner, N. A. et al. Global analyses of sea surface temperature, sea ice, and night marine air temperature since the late nineteenth century. J. Geophys. Res. 108, 2156–2202 (2003).
Meyer-Christoffer, A., Becker, A., Finger, P., Schneider, U., Ziese, M. GPCC Climatology Version 2018 at 1.0°: monthly land-surface precipitation climatology for every month and the total year from rain-gauges built on GTS-based and historical data. https://doi.org/10.5676/DWD_GPCC/CLIM_M_V2018_100 (2018).
Trenberth, K. E. & Shea, D. J. Atlantic hurricanes and natural variability in 2005. Geophys. Res. Lett. 33, 1–4 (2006).
Maher, N. et al. The Max Planck Institute grand ensemble: enabling the exploration of climate system variability. J. Adv. Model. Earth Syst. 11, 2050–2069 (2019).
Jeffrey, S. et al. Australia’s CMIP5 submission using the CSIRO Mk3. 6 model. Aust. Meteor. Oceanogr. J. 63, 1–13 (2013).
Rodgers, K. B., Lin, J. & Frölicher, T. L. Emergence of multiple ocean ecosystem drivers in a large ensemble suite with an earth system model. Biogeosciences 12, 3301–3320 (2015).
Kirchmeier-Young, M. C., Zwiers, F. W. & Gillett, N. P. Attribution of extreme events in Arctic Sea Ice extent. J. Clim. 30, 553–571 (2017).
Sun, L., Alexander, M. & Deser, C. Evolution of the global coupled climate response to Arctic Sea Ice loss during 1990–2090 and its contribution to climate change. J. Clim. 31, 7823–7843 (2018).
Hawkins, E. D., Smith, R. S., Gregory, J. M. & Stainforth, D. A. Irreducible uncertainty in near-term climate projections. Clim. Dyn. 46, 3807–3819 (2016).
Acknowledgements
The authors are grateful for the helpful comments on this paper from Benjamin Kirtman, Yochanan Kushnir, and Doug Smith. Likewise, the authors would like to express their gratitude to the three anonymous reviewers. This paper is better for its constructive critiques and expert insight. GPCCv7, NCEP Reanalysis, and NOAA ERSSTv5.1 data provided by NOAA/OAR/ESRL PSD (https://www.esrl.noaa.gov/psd/). The station-based NAO index was provided by Climate Data Guide, based in NCAR, and supported by the NSF. Access and download to the MMLEA were facilitated by NCAR’s supercomputing resources provided by NSF/CISL/Cheyenne (see http://www.cesm.ucar.edu/projects/community-projects/MMLEA/). HadISST data were obtained from https://www.metoffice.gov.uk/hadobs/hadisst/ and are ©British Crown Copyright, Met Office, 2020, provided under a Non-Commercial Government License http://www.nationalarchives.gov.uk/doc/non-commercial-government-licence/version/2/. We acknowledge grants from the NSF Climate and Large-Scale Dynamics program (grant #AGS 1735245 and #AGS 1650209,) and the NSF Paleo Perspectives on Climate Change program (grant #AGS 1703076).
Author information
Authors and Affiliations
Contributions
J.M.K. and M.A.C. wrote the paper. J.M.K led data analysis with a considerable comment, contribution, and interpretation from all authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Klavans, J.M., Cane, M.A., Clement, A.C. et al. NAO predictability from external forcing in the late 20th century. npj Clim Atmos Sci 4, 22 (2021). https://doi.org/10.1038/s41612-021-00177-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41612-021-00177-8
This article is cited by
-
Causes and multiyear predictability of the rapid acceleration of U.S. Southeast Sea level rise after 2010
npj Climate and Atmospheric Science (2024)
-
Recalibration of missing low-frequency variability and trends in the North Atlantic Oscillation
Climate Dynamics (2024)
-
Tropical Atlantic multidecadal variability is dominated by external forcing
Nature (2023)
-
Reduced Southern Ocean warming enhances global skill and signal-to-noise in an eddy-resolving decadal prediction system
npj Climate and Atmospheric Science (2023)
-
Winter heavy precipitation events over Northern Europe modulated by a weaker NAO variability by the end of the 21st century
npj Climate and Atmospheric Science (2023)